Привет! Мы добрались до 18 задания из ЕГЭ по информатике 2021.
Это задание снова решается с помощью компьютера.
Восемнадцатое задание направлено на обработку вещественных чисел с помощью таблиц. Мы с вами будет использовать программу Excel от компании Microsoft.
Перейдём к к тренировке решения 18 задания из ЕГЭ по информатике 2021.
Задача (Стандартная)
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монеты с собой; это также относится к начальной и конечной клетке маршрута Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
Решение:
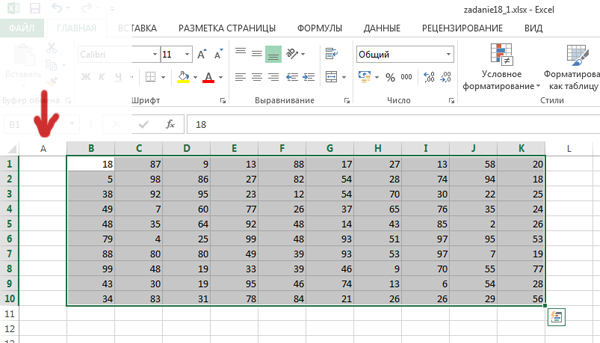
Открываем файл к данной задачке.
В начале найдём максимальную сумму.
Выделяем область всех ячеек, где написаны числа, вырезаем её и вставляем на столбец правее. Это нужно для того, чтобы при составлении формулы решения не было ошибок.
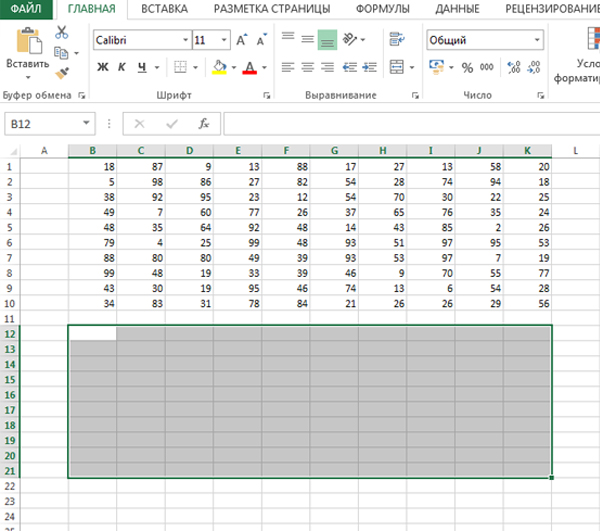
Обозначим мысленно ту область, где мы будем составлять наше решение, пропустив одну или две строчки снизу. По размеру область будет такая же.
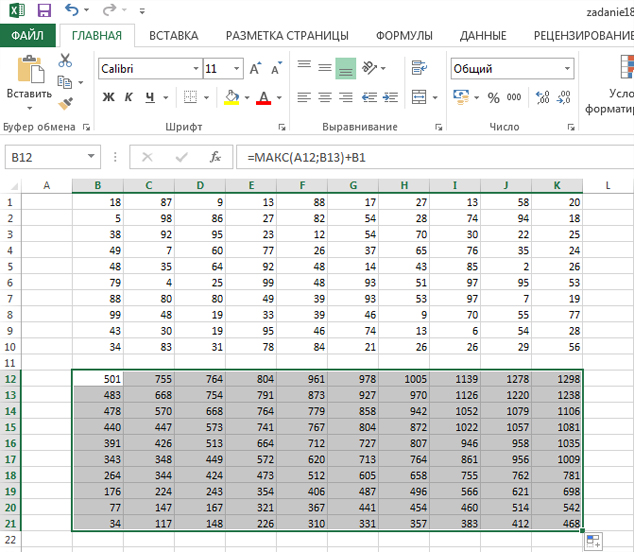
В каждой ячейке этой области будет лежать максимальная cумма, которую может собрать Робот, дойдя до этой клетки. Т.к. Робот идёт в верхнюю правую клетку, то, соответственно, в ячейке K12 будет находится нужный нам ответ.
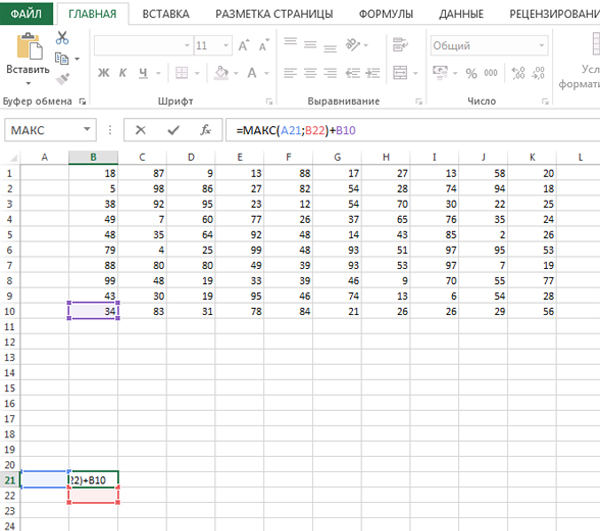
Наш Робот идёт из левой нижней клетки. Поэтому формулу, решающую эту задачу, составим сначала для ячейки B21.
Кликаем на ячейку B21 и пишем формулу:
=МАКС(A21;B22)+B10
Примечание: Чтобы в ячейке начать писать формулу, нужно поставить знак «=».
В любую ячейку нашей области можно попасть либо слева, либо снизу (Т.к. составляем формулу для любой ячейки, то не играет роли, что в данная ячейка угловая). Поэтому для ячейки B21 мы берём предыдущий результат — либо из левой ячейки, либо из правой ячейки, в зависимости от того, где собранная сумма больше.
Эту роль исполняет функция МАКС(). Она помогает выбрать откуда нужно идти, чтобы сумма всегда была максимальна.
Плюс, мы должны добавить сумму для данной ячейки к максимальной сумме предыдущей клетки. Поэтому в формулу дописываем ячейку B10
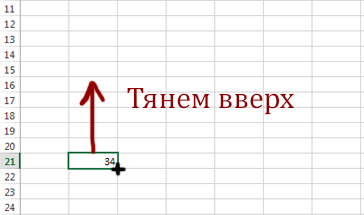
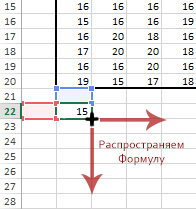
После того, как составили формулу для одной ячейки B21, можно распространить формулу на всю область.
Подносим мышку к правому нижнему углу. Как только появился чёрный крестик, кликаем левую кнопку мыши, и тянем вверх на 10 строчек вверх.
После того, как столбец готов, выделяем этот столбец, и аналогично, распространяем его на всё пространство.
В итоге получается такая картина:
Видим, что в ячейке K12 значение 1298. Это значение нам и нужно.
Аналогичным образом ищется минимальное значение, только в формуле вместо функции МАКС будет использоваться функция МИН.
Минимальное значение получилось 589.
Ответ: 1298589
Посмотрим ещё одну интересную задачу из примерны задач ЕГЭ по информатике нового образца 2021.
Задача (со стенками)
Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух
команд: вправо или вниз. По команде вправо Робот перемещается
в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю.
Квадрат ограничен внешними стенами. Между соседними клетками квадрата
также могут быть внутренние стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета
достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой;
это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые
может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем
минимальную.
Исходные данные представляют собой электронную таблицу размером
N × N, каждая ячейка которой соответствует клетке квадрата. Внутренние
и внешние стены обозначены утолщенными линиями.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел
Решение:
Открываем файл в программе Excel.
Выделим все ячейки с числами, нажмём «вырезать», используя контекстное меню. Вставим данные на 1 столбец вправо. Это делаем потому, что будем использовать для решения формулу, которая будет обращаться к ячейке слева.
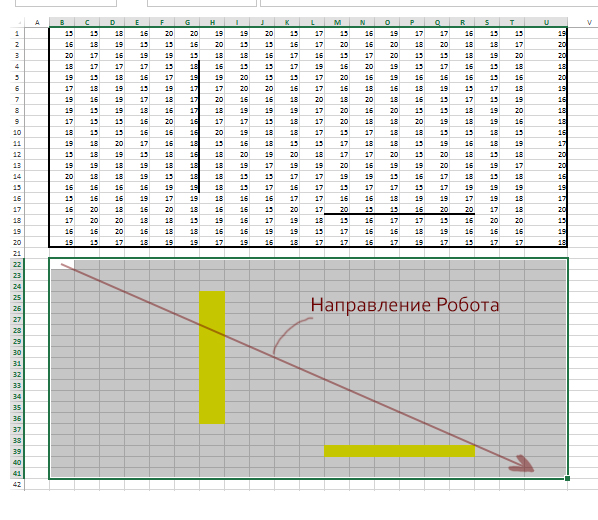
Мысленно представим пространство на 1 строчку ниже, чем область, где находятся числа. Это пространство будет таким же по размерам, как и область с числами. В этом пространстве и будет наше решение.
Отметим особым цветом те ячейки, которые «спрятаны» от движения Робота стенками.
Для этих ячеек будем составлять другие формулы, в отличии от обычных ячеек.
Цвет ячейки можно поменять, нажав на кнопку «Цвет заливки» на главной вкладке программы.
Т.к. Робот направляется из левой верхней ячейки, то мы сначала и напишем формулу для этой ячейки. Пишем для ячейки B22:
=МАКС(B21;A22)+B1
Робот в любую ячейку может прийти либо сверху, либо слева. Для подсчёта максимального количества монет, мы должны выбрать максимальное предыдущее значение. Это и делаем формула. Плюс Робот должен взять монеты с текущей клетки.
Распространим формулу на всё пространство, не трогая закрашенные клетки.
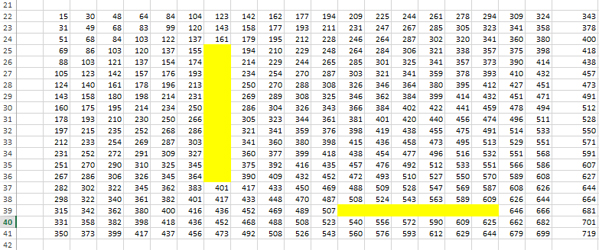
Получается такая картина:
В ячейки для первой закрашенной области, Робот может попасть только сверху! Поэтому пишем формулу для ячейки H25:
=H24+H4
Распространяем формулу по всему закрашенному столбцу.
В ячейки для второй закрашенной области, Робот может попасть только слева! Поэтому пишем формулу для ячейки М39:
=L39+M18
Распространяем формулу по всей закрашенной строчке.
В правом нижнем углу нашего рабочего пространства получается максимальное количество монет, которое может собрать Робот. В ячейке U41 получается число 721.
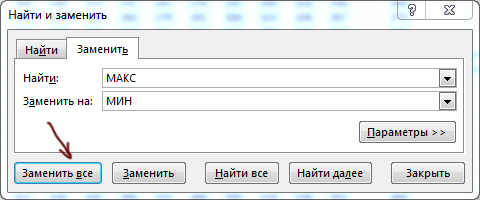
Чтобы получить минимальную возможную сумму, в главной формуле функцию МАКС нужно заменить на МИН!
Удобно воспользоваться автоматической заменой через Ctrl+F.
Минимальная сумма равна 640.
Ответ:
Задача (Два Робота)
Квадрат разлинован на N×N клеток (2 < N < 19). В каждой клетке лежат
монеты, количество которых соответствует записанному числу. Количество
монет не может быть меньше 1.
Два исполнителя – ВЕРХ и НИЗ – существуют на одинаковых полях. Первый
имеет две команды – вверх и вправо, второй – вниз и вправо, которые,
соответственно, перемещают исполнитель на одну клетку вверх, вниз или
вправо. Исполнитель ВЕРХ начинает движение в левой нижней ячейке,
исполнитель НИЗ – в левой верхней.
Откройте файл. Какой из исполнителей соберет большее количество монет в результате
своей работы, если известно, что каждый из них запрограммирован собрать
максимальное количество монет?
Исходные данные представляют собой электронную таблицу размером N×N,
каждая ячейка которой соответствует клетке квадрата.
Пример:
| 1 | 8 | 8 | 4 | 10 |
| 10 | 1 | 1 | 3 | 2 |
| 1 | 3 | 12 | 2 | 8 |
| 2 | 3 | 5 | 6 | 11 |
| 3 | 19 | 14 | 11 | 5 |
Для указанных входных данных ответом является комбинация из названия
исполнителя и количества собранных монет
ВЕРХ84
Решение:
Перенесём таблицу чисел на один столбец вправо.
Найдём, сколько соберёт монет исполнитель ВЕРХ.
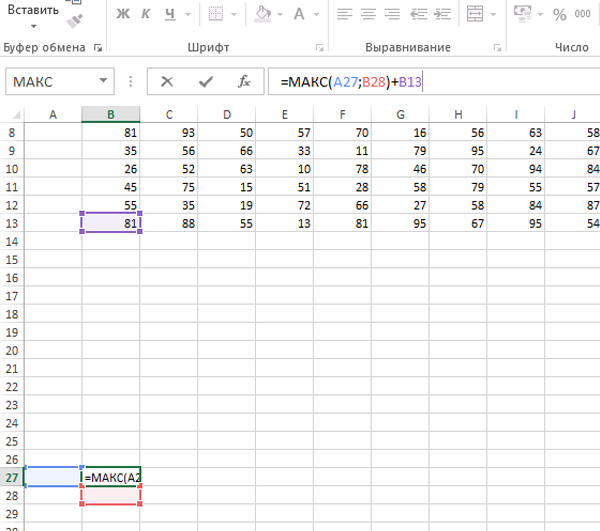
Исполнитель «ВЕРХ» начинает идти с левой нижней клетки. Поэтому первую формулу мы зададим для клетки B27. Эта ячейка является нижней левой клеткой для области, где мы будем составлять решение.
Напишем в ячейке B27:
=МАКС(A27;B28)+B13
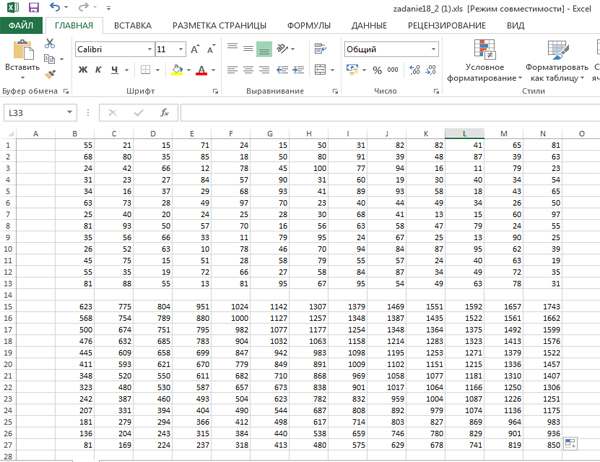
Распространим формулу на всё пространство.
Когда исполнитель пройдёт всё поле, в ячейке N15 будет находится ответ. Максимальное количество монет, которое может собрать исполнитель ВЕРХ будет 1743.
Теперь найдём максимальное количество монет, которое может собрать исполнитель НИЗ.
Решать будем аналогичным образом, удалив все следы от предыдущего исполнителя.
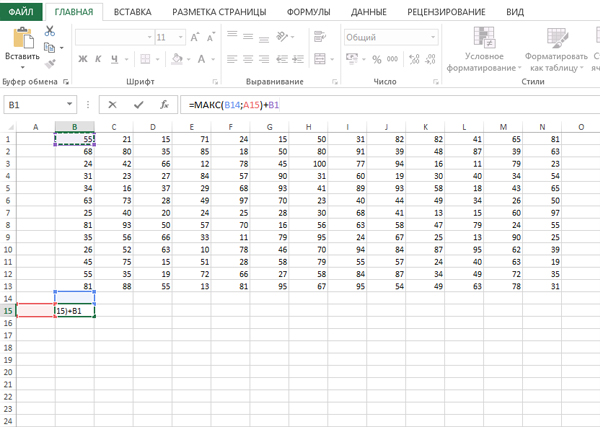
Т.к. исполнитель НИЗ стартует с левой верхней клетки, то мы сначала составим формулу для ячейки B15. Эта клетка олицетворяет левую верхнюю ячейку для области, где будет происходить решение.
=МАКС(B14;A15)+B1
В любую ячейку мы можем попасть либо сверху, либо слева. Это не относится к боковым и угловым ячейкам, но формула будет работать и для них.
При составлении максимальной суммы для любой ячейки, мы выбираем максимальное значение суммы из двух предыдущих ячеек + добавляем значение для этой ячейки.
Распространим формулу на всё пространство.
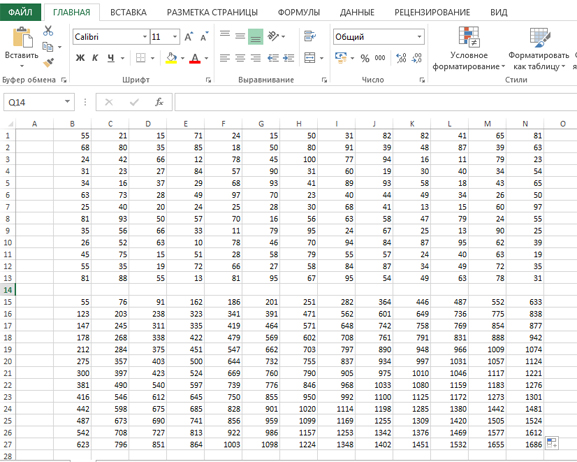
В ячейке N27 будет максимальное значение для исполнителя НИЗ. Получилось 1686.
Видим, что у исполнителя ВЕРХ получилось собрать больше монет.
Ответ: ВЕРХ1743
Спасибо за ваши советы, не знаю как без них бы я готовился к экзамену, не сдавайтесь и продолжайте помогать нам, молодёжи, удачи!
На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 18 задания. Объясняется тема об обработке числовой информации в электронных таблицах.
Содержание:
- ЕГЭ по информатике 18 задание объяснение
- Решение 18 задания ЕГЭ
- Исполнитель Робот
18-е задание: «Обработка числовой информации в электронных таблицах»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— да,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение обрабатывать вещественные выражения в электронных таблицах
Решение 18 задания ЕГЭ
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Исполнитель Робот
18 задание. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел:

Ответ: 1204 | 502
Решение подобного задания смотрите в следующем ниже разборе.
📹 YouTube здесь
Видеорешение на RuTube здесь
18_1:
Задание выполняется с использованием прилагаемых файлов
Исходные данные записаны в файле (выше) в виде электронной таблицы прямоугольной формы.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой НИЖНЕЙ клетки в правую ВЕРХНЮЮ. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — верхняя правая ячейка
J12результирующей таблицы. Робот просто соберет монету, которая находится в этой ячейке. Поэтому для ячейки возьмем значение из исходной таблицы. Введите формулу:
=J1
J12 Робот мог, либо двигаясь из ячейки I12, либо из J13. I12. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка I1). Ну и поскольку дальше он попадет только в ячейку J12, то необходимо прибавить значение этой ячейки. Поскольку значение уже просчитано для результирующей таблицы, то мы и будем его брать именно с результирующей таблицы. То есть введите формулу для ячейки I12:=I1+J12
I12, будет такой же и для всех оставшихся ячеек верхней строки.I12 в диапазон ячеек A12:H12:J13. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — J2) и добавим значение ячейки, в которую он пойдет дальше — ячейка J12 (берем значение из результирующей таблицы, поскольку оно уже просчитано):=J2+J12
J13 подходит для всех ячеек данного столбца.J13 в диапазон ячеек J14:J21:I12 и J13 Робот мог попасть, также двигаясь из ячейки I13. Рассмотрим ее.I13 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — I2), и затем у него альтернатива движения: либо в ячейку I12, либо в J13. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Для этого надо выбрать максимум из I12 и J13 и добавить к текущему значению. Введите формулу в I13:
=I2+МАКС(I12;J13)
I13, использовав маркер копирования, во все оставшиеся ячейки таблицы:I13 на =I2+МИН(I12;J13).Ответ: 1133 | 522
18_2:
Задание выполняется с использованием прилагаемых файлов
При попытке зайти на клетку со стеной Робот разрушается. Исходные данные записаны в файле в виде электронной таблицы прямоугольной формы. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю, не разрушившись. Известно, что такой путь существует. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — нижняя правая ячейка
L25результирующей таблицы. Робот просто соберет монету, которая находится в этой ячейке исходной таблицы —L12. Поэтому для ячейки возьмем значение из исходной таблицы. Введите формулу:
формула для L25:
=L12
L12 Робот мог, либо двигаясь из ячейки K12, либо из L11. К12. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка K12). Ну и поскольку дальше он попадет только в ячейку L12, то необходимо прибавить значение этой ячейки.K25:=ЕСЛИ(И(L25>0;ИЛИ(K12<=100;K12>=500));K12+L25;0)
Если выполняются одновременно два условия: L25>0 И либо K12<=100 либо K12>=500, то собираем монету с текущей ячейки (K12) и добавляем монету с L25, так как там нет стены (L25>0)
K25 будет такой же и для всех оставшихся ячеек строки.K25 в диапазон ячеек A25:J25.L24. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — L11) и добавим значение ячейки, в которую он пойдет дальше — ячейка L25 (берем значение из результирующей таблицы, поскольку оно уже просчитано):=ЕСЛИ(И(L25>0;ИЛИ(L11<=100;L11>=500));L11+L25;0)
Если выполняются одновременно два условия: L25>0 И либо L11<=100 либо L11>=500, то собираем монету с текущей ячейки (L11) и добавляем монету с L25, так как там нет стены (L25>0)
L24 в диапазон ячеек L14:L23.K24 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — K11), и затем у него альтернатива движения: либо в ячейку L24, либо в K25. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Не забудем проверять значение каждой ячейки, нет ли там стены. Для этого введите формулу в K24:=ЕСЛИ(И(K11>100;K11<500);0;ЕСЛИ(И(L24=0;K25=0);0;ЕСЛИ(L24=0;K11+K25; ЕСЛИ(K25=0;K11+L24;K11+МИН(L24;K25)))))
Здесь логика формулы следующая: если текущее значение ячейки соответствует стене, то записываем 0; ИНАЧЕ — если обе ячейки, в которые может двигаться Робот, — стены, то записываем в текущую ячейку 0; ИНАЧЕ — если ячейка справа — стена, то двигаемся вниз, собирая по пути монеты; ИНАЧЕ — если ячейка снизу — стена, то двигаемся вправо, собирая по пути монеты; ИНАЧЕ — выбираем минимальное значение из соседних ячеек и собираем монеты.
K24, использовав маркер копирования, во все оставшиеся ячейки таблицы:МАКС на МИН. И скопируйте снова данную формулу во всю оставшуюся таблицу.
Ответ: 1492 640
18_3:
Задание выполняется с использованием прилагаемых файлов
Робот может двигаться только вниз и вправо. Для сбора денег у Робота есть контейнеры вместимостью 8 монет каждый. С каждой клетки Робот забирает наибольшее количество контейнеров, полностью заполненных монетами. Если контейнер не заполнен до конца, а монеты в клетке кончились, робот высыпает из него монеты перед переходом в следующую клетку. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.
✍ Решение:
-
✎ Электронные таблицы:
- Для решения будем использовать метод динамического программирования — решать будет с конца к началу.
- Откройте файл электронной таблицы. Скопируем таблицу и вставим ее ниже — это будет шаблон для результирующей таблицы, полученной после решения задачи.
- Выделите ячейки скопированной таблицы каким-либо цветом, для обозначения ее границ. Теперь удалите все значения в результирующей таблице:
- Так как задание решается с конца, то выделим последнюю ячейку, в которой окажется Робот — нижняя правая ячейка
J21результирующей таблицы. Робот просто соберет монеты, которые находится в этой ячейке исходной таблицы —J10, если наберется целое число контейнеров (значение кратное 8). Если целое число контейнеров не набирается, — то робот забирает только то, что набралось в контейнеры (8* ЧАСТНОЕ от деления монет на 8). Поэтому для ячейки возьмем значение из исходной таблицы, проверяя его на кратность 8. Введите формулу:
формула для J21:
=ЕСЛИ(ОСТАТ(J10;8)=0;J10;8*ЧАСТНОЕ(J10;8))
J20. В ней Робот собирает монету, значение которой возьмем из исходной таблицы (ячейка J9). При этом будем проверять значение на кратность 8 и действовать так же, как описано в предыдущем пункте. Ну и поскольку дальше Робот попадет только в ячейку J21, то необходимо прибавить значение этой ячейки.формула для J20: =ЕСЛИ(ОСТАТ(J9;8)=0;J9+J21;8*ЧАСТНОЕ(J9;8)+J21)
J20 будет такой же и для всех оставшихся ячеек столбца.J20 в диапазон ячеек J12:J19.I21. Робот собирает монету с текущей ячейки (возьмём значение из ячейки исходной таблицы — I10). Проверим заполненность контейнеров, и добавим значение ячейки, в которую Робот пойдет дальше — ячейка J21 (берем значение из результирующей таблицы, поскольку оно уже просчитано):формула для I21:
=ЕСЛИ(ОСТАТ(I10;8)=0;I10+J21;8*ЧАСТНОЕ(I10;8)+J21)
I21 в диапазон ячеек A21:H21.I20 Робот собирает монету из текущей ячейки (берем значение из исходной таблицы — I9), проверяя заполненность контейнеров, и затем у него альтернатива движения: либо в ячейку J20, либо в I21. В задании необходимо найти, как максимальную, так и минимальную сумму монет. Найдем сначала максимальную. Не забудем проверять значение каждой ячейки на заполненность контейнеров. Для этого введите формулу в I20:формула для I20:
=ЕСЛИ(ОСТАТ(I9;8)=0;I9+МАКС(J20;I21);8*ЧАСТНОЕ(I9;8)+МАКС(J20;I21))
I20, использовав маркер копирования, во все оставшиеся ячейки таблицы.МАКС на МИН. И скопируйте снова данную формулу во всю оставшуюся таблицу.Ответ: 1144 448
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 41 и 22.
Источник: Демонстрационная версия ЕГЭ−2021 по информатике
2
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
3
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 41 и 22.
4
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
5
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота.
Задание 18
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 41 и 22.
Пройти тестирование по этим заданиям
Две трети выпускников проваливают 18 задание ЕГЭ по информатике. Как же его решать? Нужно знать особый подход. Давайте разберемся, как эффективно справиться с этим коварным заданием.
В ЕГЭ по информатике есть четыре задания на математическую логику. Сегодня речь пойдёт о задании №18, которое связано с анализом логического высказывания. Статистика ужасна: по оценке ФИПИ с ним справляются чуть меньше 1/3 сдающих. Почему 18 задание ЕГЭ по информатике вызывает сложности? Давайте разберемся, что надо знать, понимать и уметь, чтобы их избежать.
А если вас интересуют и другие задания, эффективно подготовиться к ЕГЭ по информатике можно на наших курсах.
Вам нужны знания не только математической логики, но и просто математики. В качестве логической переменной (которая может быть истина или ложна) выступают не просто некие x, y, z, а математические высказывания. В ответе надо определить значения некоторого параметра, зависящего от этих переменных. Что-то напоминает? Да, почти как в задании 18 из профильной математики, но тут будет намного проще. Например, логической переменной может выступать выражение «x>10» или суждение о том, что x кратен 5. Рассмотрим, как подходить к такому виду логической переменной.
Если логическая переменная — неравенство
Все просто. Выражение «x>10» истинно для всех х, которые являются решением данного неравенства, то есть для x от 10 до +∞. И это выражение ложно для всех x, которые можно описать неравенством (x≤10) или x∈(+∞; 10]. Обратите внимание на число 10, когда x=10, логическая переменная (x>10) ложна.
Если логическая переменная — утверждение
Допустим, наша переменная — «x делится на 5». Тогда она истинна для всех х, которые кратны 5 (0, 5, 10, 15,…). Обратите внимание на то, что 0 кратен любому числу, а значит кратен 5 и тоже даст истинное значение. Методом исключения, данная логическая переменная ложна при всех х, которые не делятся на 5.
Вторая сложность в 18 задании ЕГЭ по информатике
Когда такие переменные рассматриваются отдельно, все выглядит просто. Но в 18 задании у вас будет целое логическое высказывание, содержащее несколько переменных и параметр, значение которого вам надо определить.
Это и есть вторая сложность данного задания — надо знать, как правильно подходить к анализу выражения. Для этого нужно помнить о двух принципиальных шагах:
- Упрости, если есть возможность.
- Определи «красную зону»
18 задание ЕГЭ по информатике важно решать постепенно. Сначала поговорим об упрощении, так как без этого шага очень сложно начать анализ. Затем обсудим, что такое «красная зона».
Как упростить выражение?
Смысл
этого шага в двух моментах:
- Введите обозначения для удобства записи. Иначе некоторые переменные получаются слишком громоздкими.
- Упростите зависимости логических переменных. Выражение, где смешаны несколько уровней скобок и логических функций, сложно анализировать. А вот идентичное ему выражение, в котором три переменных связаны дизъюнкцией, намного проще.
Для большинства заданий вам нужно знать несколько формул матлогики. Сохраните эту картинку, пригодится.
Что такое «красная зона»?
В задании нужно определить значения параметра, чтобы логическое высказывание было тождественно истинно при любых значениях переменной x. При этом мы не можем брать произвольно большой набор значений для искомого параметра, это также определяется условием задания. Поэтому нужно подбирать такие значения параметра, чтобы они закрывали только определённый ряд случаев, не больше и не меньше. Этот ряд случаев назовем «красной зоной», теми значениями переменной x, когда логическое высказывание не будет истинно при любых значениях параметра.
Простой пример. Возьмем логическое высказывание: (X < 50) V (X > A).
Нам не важно значение параметра А. У нас есть одно логическое слагаемое, которое истинно. Второе может быть ложно — дизъюнкция все равно в итоге даст истину. Значит «красная зона» — это все х≥50. Подбирать значение для параметра А необходимо только для случаев, когда х≥50, чтобы за счет второго слагаемого (где содержится А) обеспечить истинность всего выражения, когда первая скобка ложна.
Для правильного анализа красной зоны важно помнить об основных
моментах анализа некоторых логических функций:
- Конъюнкция нескольких переменных будет истинна, только если каждый множитель истинен, и ложна, если хотя бы один множитель ложен.
- Дизъюнкция нескольких переменных будет истинна, если хотя бы одно слагаемое истинно, и ложна, только если ложны все слагаемые.
- Импликация ложна только в единственном случае — когда из истины следует ложь.
Примеры 18 задания ЕГЭ по информатике
Рассмотрим правильный подход на различных прототипах данного задания.
Пример 1
Решение
В данном логическом высказывании не требуется упрощений, так как у нас простой для анализа случай: дизъюнкция трёх переменных. Поэтому перейдём сразу к анализу и определению «красной зоны».
Вторая и третья скобки не зависят от А и обеспечат истинность всего выражения, независимо от параметра, если X>15 или Y>30. Тогда красной зоной будет ситуация, когда не выполняются ОБА из этих условий, то есть и вторая, и третья скобки одновременно ложны. Опишем этот случай системой:
В этой ситуации нам необходимо обеспечить истинность первой скобки, которая зависит от параметра. Дополним систему ещё одним условием.
Теперь мы свели задание к решению системы простейших неравенств. Определим границы для параметра А при помощи работы с неравенствами. Первое неравенство умножим на 2, затем сложим новое неравенство со вторым и сведём это всё к одному двойному неравенству за счёт одинакового выражения Y+2X.
Осталось вернуться к формулировке вопроса. Вас всегда будут спрашивать что-то конкретное относительно значений параметра А! В данном случае нам надо найти наименьшее целое значение. В случае A > 60 наименьшим подходящим целым значением будет 61. Внимание! Всегда отслеживайте строгость и нестрогость знаков, значение 60 не подходит под условие A > 60, так как 60 равно 60, но не как не больше.
Ответ:
Пример 2
Здесь необходимо начать с упрощения выражения. Введём обозначения для краткости и удобства записи.
Выражение сразу выглядит намного проще.
Теперь применим формулу для раскрытия импликации на базовые функции.
Далее воспользуемся формулой де Моргана.
Уберём двойное отрицание и лишние скобки.
И финальным шагом уберём тавтологию.
Сравните с тем, что было в условии. Стало проще, правда? Дальше мы будем анализировать именно это выражение.
«Красная зона» будет также определяться из случая, когда дизъюнкция будет истинна не из-за переменных, которые не зависят от А, а исключительно из-за переменной с параметром. Получается, для этого первое и второе слагаемые должны быть ложны. Получаем, что P = 1 и Q = 1, в таком случае и A = 1. Теперь вернёмся от наших обозначений к исходным описаниям переменных.
Значит наша «красная зона» — это пересечение отрезков P и Q. Чтобы покрыть ровно эту часть числовой прямой, отрезок А должен ровняться пересечению отрезков P и Q.

Получаем: A = [150; 171].
В ответ надо указать минимально возможную длину отрезка. Мы подбирали значение отрезка А так, чтобы сразу закрыть им только необходимое и не больше, поэтому полученный отрезок и есть отрезок минимальной длинны.
Длина отрезка считается очень просто: из большей границы вычитается меньшая. Длина отрезка А = 171 – 150 = 21.
Ответ: 21
Пример 3
Решение
В данном примере тоже нужно упростить выражение. Введём обозначения:
Получаем выражение
Дальше потребуется только раскрыть импликации, убрать двойное отрицание и лишние скобки.
Теперь переходим к определению «красной зоны». Когда D6=1 и D4 = 1, то и DA должно быть истинно.
Вернемся к математическому смыслу наших переменных. Получаем условие: числа, которые кратны 4 и 6 одновременно, должны быть кратны и А. Пользуясь понятием наименьшего общего кратного (НОК) из математики, получаем, что числа, которые одновременно кратны 4 и 6 – это числа, кратные 12.
Переформулируем условие: числа, которые кратны 12, должны быть кратны А. Отсюда уже понятно, что А = 12. Если мы возьмём число меньшее, например 2, выражение будет истинно, но это не максимальное возможное значение, которое просят по условию. А если возьмём число больше, например 24, для x=12 выражение окажется ложным. Кратность 4 и 6 будет обнулять второе и третье слагаемое, а первое окажется ложно, так как 12 не кратно 24, а наоборот 24 кратно 12.
Ответ:
12
Пример 4
Решение
В этом примере встречается поразрядная конъюнкция. Суть этого вычислительного действия проста: мы выполняем логическое умножение чисел, записанных двоичным кодом, по разрядам (нулевой с нулевым, первый с первым и т.д.). Подробнее на поразрядную конъюнкцию взглянем уже при анализе выражения. Для начала упростим то, что надо анализировать. Введём обозначения:
Получим выражение
Дальше потребуется только раскрыть импликацию и убрать лишние скобки
Теперь переходим к определению «красной зоны». Она возникает, когда Z39 = 0 и Z41 = 1, и ZA должно быть ложно.
Переходим
обратно к математическому смыслу наших переменных. Запишем условия следующим
образом: для х, для которых поразрядная конъюнкция с 41 даёт 0, а с 39 даёт не
0, поразрядная конъюнкция с А должна давать не 0.
Определим, что такое х из «красной зоны».
Посмотрим
на первое условие: поразрядная конъюнкция с 41 даёт 0. Чтобы посчитать
поразрядную конъюнкцию переводим 41 в двоичную систему счисления и получаем
1010012.
Чтобы в итоге поразрядной конъюнкции получился ноль, в тех разрядах, где в числе 41 стоят единицы, у числа х должны обязательно стоять нули. Там же, где в числе 41 стоят нули – в числе х может быть всё что угодно, так как одного нуля для обнуления произведения достаточно. Изобразим это схематически.
Мы получили некоторый «макет» чисел «красной зоны». Но он пока не полный. Переходим ко второму условию: поразрядная конъюнкция с 39 даёт не 0. Также необходимо перевести число в двоичную систему счисления. 3910 = 1001112. Чтобы в итоге поразрядной конъюнкции получить не 0, хотя бы один из разрядов, где у 39 стоят единицы, в х тоже должен содержать единицу. Достаточно одной, но она может быть на любом из доступных мест (кроме, тех, где из-за анализа первого условия мы уже поставили 0).
Теперь у нас есть полная схема чисел, которые представляют собой «красную зону». У таких чисел в нулевом, третьем, пятом разряде точно стоят нули, а в первом или во втором (или и в том и том) стоят единицы.
Теперь, чтобы определить наименьшее значение параметра А, при котором выражение будет тождественно истинно, надо обеспечить, чтобы при минимальном количестве единиц в разрядах (минимальном, но не меньше чем необходимо) можно было обеспечить ненулевое значение поразрядной конъюнкции иксов из «красной зоны» с числом А. Для этого нам обязательно надо закрыть единицами первый и второй разряды (тогда хотя бы в одном из этих разрядов точно получится 1), а остальные можно спокойно занять нулями.
Последнее, что осталось сделать — перевести число А в десятичную систему счисления. 1102 = 610.
Ответ: 6
Подведем итоги
Теперь вы умеете решать 18 задание ЕГЭ по информатике. Такой подход с упрощением выражения и постепенным анализом позволяет разбить длительную работу с заданием на небольшие этапы. Вы постепенно составляете выводы о том, каким же должен быть параметр в этом задании.
Остается закрепить знания на практике. Напомню, что эффективно подготовиться к ЕГЭ по информатике можно на наших курсах. Используйте промокод BLOG0320 до 31 марта 2020 года включительно и получите первый месяц онлайн-подготовки со скидкой 50%.
Мини-курс по 18 заданию ЕГЭ по информатике. Предназначен для тех, кто сдаёт компьютерный ЕГЭ в 2023 году.
About this course
Вы научитесь решать задание №18 с Роботом и другими исполнитеями из компьютерного ЕГЭ по информатике.
Поговорим о динамическом программировании, научимся анализировать и обрабатывать целочисленные данные в электронных таблицах.
Whom this course is for
Ученики 10-11 классов и все интересующиеся компьютерным ЕГЭ по информатике.
Initial requirements
Необходимы минимальные навыки работы с электронными таблицами. Также для выполнения заданий понадобится программа: Microsoft Excel, LibreOffice Calc или другой редактор электронных таблиц.
Meet the Instructors
Course content
Share this course
https://stepik.org/course/90950/promo