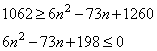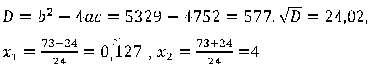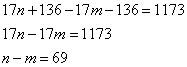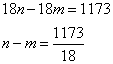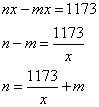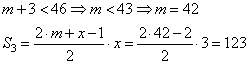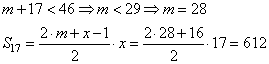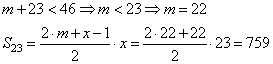Задача 19 егэ математика профильный с нуля - Помощь в подготовке к экзаменам и поступлению

Вот она! Загадочная. Нестандартная. Задача 18 Профильного ЕГЭ по математике.

Эта задача оценивается в целых 4 первичных балла, и они пересчитываются в 9-10 тестовых.

Можно ничего не знать. И удачно подобрать пример. И получить 1 балл за пункт (а). Во всяком случае, попробовать это сделать.

А можно потратить 2 часа на перебор вариантов… и так ничего и не найти. Если не знаешь секретов решения этой задачи. ОК, некоторые из секретов мы расскажем.

Действительно, пункт (а) в задаче 18 почти всегда решается сразу. Пункт (б) тоже решается быстро, но только если повезет. Пункт (в) без специальной подготовки решить невозможно.

Необходимая теория для решения задач на числа и их свойства — это всего две страницы. Делимость чисел, наибольший общий делитель и наименьшее общее кратное, основная теорема арифметики, признаки делимости на 3, на 4, на 5, на 8, 9, 10 и 11. Ничего сложного.

Повторите также темы: Арифметическая прогрессия и Геометрическая прогрессия.

Начинать лучше всего с подготовительных задач.

Затем стоит освоить метод «Оценка плюс пример». Для того чтобы применить этот метод, от строгих оценок, которые даны в условии (со знаками > или < ), переходим к нестрогим (со знаками ≥ или ≤ ).

Узнать о секретах решения задания 18 Профильного ЕГЭ по математике.

Узнать больше о решении уравнений в целых числах. В школьных учебниках этого нет.

Один из необходимых навыков для решения пункта (в) – работа с неравенствами. В школьных учебниках этого тоже нет.

Многие считают, что если в этой задаче в пункте (а) ответ «да», то во втором обязательно должно быть «нет». Авторитетно заявляем: нет, необязательно! Может быть любое сочетание из «да» и «нет». И может быть «да» в обоих пунктах, и «нет» в обоих.

Если вопрос в этой задаче (неважно, в каком пункте) формулируется как «Может ли быть…» — и дальше некоторое утверждение, и ваш ответ: «Да», — то одного вашего «Да» недостаточно. Нужен пример. И если вы его подберете, вы не обязаны объяснять, как нашли его.

Если ответ на этот вопрос: «Нет», то вам нужно это доказать. «Нет, потому что…» — и приводите свое доказательство.

В общем, проще показать это на примерах:

1. За прохождение каждого уровня игры на планшете можно получить от одной до трёх звёзд. При этом заряд аккумулятора планшета уменьшается на 3 пункта при получении трёх звёзд, на 6 пунктов при получении двух звёзд и на 9 пунктов при получении одной звезды. Витя прошёл несколько уровней игры подряд.

а) Мог ли заряд аккумулятора уменьшиться ровно на 32 пункта?

б) Сколько уровней игры было пройдено, если заряд аккумулятора уменьшился на 33 пункта и суммарно было получено 17 звёзд?

в) За пройденный уровень начисляется 9000 очков при получении трёх звёзд, 5000 — при получении двух звёзд и 2000 — при получении одной звезды. Какое наибольшее количество очков мог получить Витя, если заряд аккумулятора уменьшился на 33 пункта и суммарно было получено 17 звёзд?

а) Заметим, что заряд аккумулятора при прохождении уровня уменьшается на 3, 6 или 9 пунктов, и все эти числа делится на 3. Поскольку 32 не делится на 3, заряд не мог уменьшиться на 32 пункта.

б) Да, на 33 пункта заряд мог уменьшиться.

Пусть на х уровнях получено по 3 звезды, на у уровнях — по 2 звезды и на z уровнях — по 1 звезде.

Тогда:

, то есть .

Сложив уравнения и , получим, что x+y+z=7 (пройдено 7 уровней).

Системе удовлетворяют При этом заряд аккумулятора уменьшился на 33 пункта.

в) Поскольку и x+y+z=7 , получаем, что y+2z=4 . Возможны варианты:

z=0 , тогда, получено 47 тысяч очков.

z=1 , тогда , получено 48 тысяч очков.

z=2 , тогда , получено 49 тысяч очков – это максимально возможное количество.

Это была простая задача №18. А вот сложная.

2. В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.

а) Мог ли средний балл в школе № 1 вырасти в два раза?

б) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Мог ли первоначальный балл в школе № 2 равняться 1?

в) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.

Пусть в первой школе писали тест учеников, а во второй учеников, причем
m=51-n , .

Пусть учащиеся первой школы набрали в сумме $S_{1}$ балл, а учащиеся второй $S_{2}$ баллов.

Тогда средние баллы равны $frac{S_{1}}{n}$ и $frac{S_{2}}{m}$ .

Пусть из первой школы во вторую перешел ученик, набравший за тест баллов.

а) Предположим, что средний балл в школе № 1 вырос в два раза. Тогда $frac{2S_1}{n}= frac{S_1 - k}{n-1}$ .

Отсюда: $S_{1}left ( n-2 right )=-kn$ .

Поскольку положительно, получаем, что – противоречие с условием.

Ответ в пункте (а): нет.

б) Во втором пункте ответ тоже «нет». Предположим, что $frac{S_{2}}{m}=1$ . Получим:

$frac{S_{1}-k}{n-1}=1,1cdot frac{S_{1}}{n};$

$frac{S_{2}+k}{m+1}=1,1cdot frac{S_{2}}{m}$ .
Поскольку m=51-n ,

$frac{S_{2}+k}{52-n}=1,1cdot frac{S_{2}}{51-n}$ .

Если $frac{S_{2}}{m}=1$ ,то $frac{S_{2}}{51-n}$ .

Тогда:

$frac{51-n+k}{52-n}=1,1$ . Отсюда:

. Очевидно, kleq 6 и .

Что будет, если k=6 ? Тогда .

Подставив эти и в уравнение

$frac{S_{1}-k}{n-1}=1,1cdot frac{S_{1}}{n}$ , получим: $frac{S_{1}-6}{2-1}=1,1cdot frac{S_{1}}{2}$ , $S_{1}=frac{40}{3}$ , противоречие с условием, поскольку $S_{1}$ – целое. Значит,

С другой стороны, из условия $frac{S_{1}-k}{n-1}=1,1cdot frac{S_{1}}{n}$ получаем, что
$10kn=S_{1}left ( 11-n right )$ , значит, .

Но если , то и kgeq 6 – получили противоречие.

в) По условию, и в первой, и во второй школах первоначально средний балл был целым числом. Он не может быть равен единице (из пункта (б)). Проверим, может ли он быть равен 2, 3, 4…

Пусть первоначально средний балл равен 2. Тогда

$frac{S_{1}-k}{n-1}=1,1cdot frac{S_{1}}{n};$

$frac{S_{2}+k}{52-n}=frac{1,1cdot S_{2}}{51-n};$

$frac{S_{2}}{m}=2$ . Условие по-прежнему должно выполняться.

Преобразуя эти уравнения, получим:

$S_{2}=2left ( 51-n right )=102-2n;$

$frac{102-2n+k}{52-n}=1,1cdot 2;$

Значит, $kgeq frac{52}{5}$ и kleq 12 . Подходит k = 11 и k = 12 .

При таких значениях уравнение n=62-5k имеет решения n = 7 или n = 2 .

Подставим поочередно пары и в уравнение

$frac{S_{1}-k}{n-1}=1,1cdot frac{S_{1}}{n}$ , получим, что целых решений $S_{1}$ это уравнение не имеет.

Пусть первоначально средний балл равен 3. Тогда

$frac{S_{1}-k}{n-1}=1,1cdot frac{S_{1}}{n};$

$frac{S_{2}+k}{52-n}=frac{1,1cdot S_{2}}{51-n};$

$frac{S_{2}}{m}=3$ ,

$frac{153-3n+k}{52-n}=1,1cdot 3;$

, подходит , тогда $S_{1}=40$ .

Например, в первой школе тест писали 2 учащихся и набрали 22 и 18 баллов. В школе № 2 писали тест 49 учащихся и каждый набрал по три балла, а у перешедшего из одной школы в другую учащегося 18 баллов.

Да, непростая это задача, восемнадцатая задача из варинта ЕГЭ. Но если к ней привыкнуть, потренироваться, то вполне можно решить и заработать необходимые на ЕГЭ баллы. Мы учим решать эту задачу на наших интенсивах в ЕГЭ-Студии, а также на Онлайн-курсе. Многим нашим выпускникам она обеспечила поступление на бюджетные отделения ведущих вузов.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 18. Числа и их свойства u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

9 марта 2018

В закладки

Обсудить

Жалоба

Теория чисел

Задача 19 профильного ЕГЭ.

В данном материале приведено подробное описание тем, которые используются при решении задачи 19 ЕГЭ. Сюда входят и теория чисел, и прогрессии (арифметическая и геометрическая), и деление с остатков, и признаки делимости чисел. По каждой из этих тем приведены методы решения и разбор примеров.

Автор: Колесник Марина Анатольевна.

19pro.docx

Источник

Решение 18 задания ЕГЭ по математике (профиль)

Разбор задания 18 ЕГЭ по математике

Задача 18 считается одной из самых сложных в профильном ЕГЭ 2023 г. по математике, однако набрать 1–2 первичных балла в ней вовсе не так уж сложно.

Согласно спецификации задание 18 имеет дело с построением математических моделей.

Традиционно задача 18 содержит в себе три подзадачи — пункты а), б) и в).

В пункте а) обычно предлагается решить несложную задачу на построение примера. За какой-либо правильный пример (а их может быть и несколько!) эксперт поставит 1 первичный балл. Особых обоснований в этом пункте не требуется, нужно лишь показать, что приведённый пример действительно удовлетворяет условию задачи.

Пункт б) существенно отличается от пункта а). В нём, как правило, требуется строго доказать, что требуемый пример построить нельзя. Стоит этот пункт тоже 1 балл.

Пункт в), оцениваемый в 2 первичных балла, уже немного сложнее. В нём требуется построение примера, обладающего в некотором смысле «экстремальными» характеристиками (например, задача на максимум или минимум выражения, принимающего дискретные значения), а также доказательство того, что именно этот пример, а не какой-то другой обладает данными характеристиками.

Рассмотрим методы решения 18 задачи:

На доске написано несколько различных натуральных чисел, каждое из которых делится на 3 и оканчивается на 7.

а) Может ли сумма этих чисел быть равна 231?

б) Может ли сумма этих чисел быть равна 1590?

в) Какое наибольшее количество чисел может быть на доске, если их сумма равна 1056?

Решение.

а) Да, может. Числа 27, 57 и 147 дают в сумме 231.

б) Предположим, что это возможно. Каждое число оканчивается на 7, а их сумма на 0. Такое возможно, если количество чисел кратно 10. Значит, таких чисел в любом случае не меньше 10.

Число, делящееся на 3, оканчивается на 7 только, если оно имеет вид 3n, где n – натуральное число, оканчивающееся на 9. Найдём сумму 10 наименьших чисел, оканчивающихся на 7:

27 + 57 + 87 + … = 3·(9 + 19 + … + 99) = 3·540 = 1620 > 1590.

Противоречие. Следовательно, требуемое невозможно.

в) Чтобы узнать последнюю цифру в сумме из n чисел, оканчивающихся на 7, нужно определить последнюю цифру в числе 7n. Последняя цифра равна 6, если n = 8, 18, … и т.д.

Найдём сумму 8 наименьших чисел, оканчивающихся на 7:

27 + 57 + 87 + …+ 237 = 3·(9 + 19 + … + 79) = 3·88·4 = 1056.

Это и будет примером в данной задаче.

Таким образом, наибольшее количество чисел на доске равно 8.

Ответ
: а) да; б) нет; в) 8.

Нетрудно убедиться в том, что в пункте а) здесь возможны и другие примеры. Так, числа

27, 87 и 117 тоже делятся на 3 и дают в сумме 231.

В пункте в) рассуждения, приводящие к тому, что количество чисел обязано оканчиваться на 8, т.е. n = 8, 18, … и т.д., называются оценкой. Однако одной лишь оценки достаточно только для получения 1 балла, ведь в реальности пример, реализующий эту оценку, может и не существовать. В данной задаче построение (единственного!) примера, реализующего эту оценку, т.е. 27, 57, …, 237, даёт ещё 1 балл в пункте в).

Если же в пункте в), подобно пункту а), ограничиться только построением примера, пусть и правильного, то без оценки это, скорее всего, приведёт к выставлению 0 баллов за пункт в).

Таким образом, типичные критерии по проверке задания 18 выглядят так:

Содержание критерия

Баллы

Верно получены все перечисленные (см. критерий на 1 балл) результаты

Верно получены три из перечисленных (см. критерий на 1 балл) результатов

Верно получены два из перечисленных (см. критерий на 1 балл) результатов

Верно получен один из следующих результатов:

– обоснованное решение пункта а;

– обоснованное решение пункта б;

– искомая оценка в пункте в;

– пример в пункте в, обеспечивающий точность предыдущей оценки

Решение не соответствует ни одному из критериев, перечисленных выше

Максимальный балл

Итак, в большинстве случаев для решения задания 19 нужно запомнить следующую структуру этой задачи:

— а) Да + пример;

— б) Нет + доказательство;

— в) Оценка + пример.

Отметим, что наиболее типичной ошибкой в этом задании является приведение только ответов, как в случае заданий с кратким ответом, не подкреплённых никакими рассуждениями. Т.е. просто за ответы а) да; б) нет; в) 8 в рассмотренной задаче никаких баллов Вы не получите.

Что требуется для успешного решения задания 18 ЕГЭ?

Если времени до ЕГЭ достаточно, то рекомендуется изучить внимательно темы, представленные в части 5 книги «Математика. ЕГЭ. Алгебра: задания с развёрнутым ответом». Издательство «Легион».

Если времени мало, то рекомендуем

Повторить основные признаки делимости (на 2, 3, 4, 5, 9, 10, 11);
Изучить некоторые приёмы доказательств невозможности (от противного, принцип Дирихле, чётность–нечётность);
Повторить основные формулы, связанные с арифметической прогрессией и средним арифметическим.

Разберём пример:

Элементы теории чисел

19 задание в профильном уровне ЕГЭ по математике направлено на выявление у учеников способности оперировать числами, а именно их свойствами. Это задание наиболее сложное и требует нестандартного подхода и хорошего знания свойств чисел. Перейдем к рассмотрению типового задания.

Разбор типовых вариантов заданий №19 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно –3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно –8.

а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

Алгоритм решения:

Вводим переменные k, l, m.
Находим сумму набора чисел.
Отвечаем на пункт а).
Определяем, каких чисел больше (пункт б)).
Определяем, сколько положительных чисел.

Решение:

1. Пусть среди записанных на доске чисел положительных k. Отрицательных чисел l и нулевых m.

2. Сумма выписанных чисел равна их количеству в данной записи на доске, умноженному на среднее арифметическое. Определяем сумму:

4k −8l + 0⋅m = − 3(k + l +m)

3. Заметим, что слева в приведенном только что равенстве каждое из слагаемых делится на 4, потому сумма количества каждого типа чисел k + l + m тоже делится на 4. По условию общее число записанных чисел удовлетворяет неравенству:

40 < k + l + m < 48

Тогда k + l + m = 44, потому что 44 единственное между 40 и 48 натуральное число, которое делится на 4.

Значит, написано на доске всего 44 числа.

4. Определяем, чисел какого вида больше: положительных или отрицательных. Для этого приведем равенство 4k −8l = − 3(k + l +m) к более упрощенному виду: 5l = 7k + 3m.

5. m≥ 0. Отсюда вытекает: 5l ≥ 7k, l > k. Получается, что отрицательных чисел записано больше положительных. Подставляем вместо k + l + m число 44 в равенство

4k −8l = − 3(k + l + m).

Имеем

4k − 8l = −132, k = 2l − 33

k + l ≤ 44, тогда получается: 3l − 33 ≤ 44; 3l ≤ 77; l ≤ 25; k = 2l − 33 ≤17. Отсюда приходим к выводу, что положительных чисел не более 17.

Если же положительных чисел всего 17, то на доске 17 раз записано число 4, 25 раз – число −8 и 2 раза записано число 0. Такой набор отвечает всем требованиям задачи.

Ответ: а) 44; б) отрицательных; в) 17.

Второй вариант 1 (из Ященко, №1)

На доске написано 35 различных натуральных чисел, каждое из которых либо чётное, либо его десятичная запись оканчивается на цифру 3. Сумма написанных чисел равна 1062.

а) Может ли на доске быть ровно 27 чётных чисел?

б) Могут ли ровно два числа на доске оканчиваться на 3?

в) Какое наименьшее количество чисел, оканчивающихся на 3, может быть на доске?

Алгоритм решения:

Приведем пример набора чисел, который удовлетворяет условию (Это подтверждает возможность набора чисел).
Проверяем вероятность второго условия.
Ищем ответ на третий вопрос, введя переменную n.
Записываем ответы.

Решение:

1. Такой примерный перечень чисел на доске соответствует заданным условиям:

3,13,23,33,43,53,63,73,2,4,6,…,50,52,56

Это дает положительный ответ на вопрос а.

2. Пусть на доске написано ровно два числа, у которых последняя цифра 3. Тогда там записано 33 чётных числа. Их сумма:

Это противоречит тому, что сумма написанных чисел равна 1062, то есть, утвердительного ответа на вопрос б нет.

3. Полагаем, что на доске записано n чисел, которые оканчиваются на 3, и (35 – n)из выписанных чётные. Тогда сумма чисел, которые оканчиваются на 3, равна

а сумма чётных:

2+4+…+2(35 – n)=(35 – n)(36 – n)= n²-71 n+1260.

Тогда из условия:

Решаем получившееся неравенство:

Получается, что . Отсюда, зная, что n — натуральное, получаем .

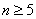
3. Наименьшее число чисел, оканчивающихся на 3, может быть только 5. И добавлено 30 чётных чисел, тогда сумма всех чисел нечётна. Значит, чисел, которые оканчиваются на 3, больше. чем пять, поскольку сумма по условию равна четному числу. Попробуем взять 6 чисел, с последней цифрой 3.

Приведём пример, когда 6 чисел, оканчиваются на три, и 29 чётных чисел. Сумма их равна 1062. Получается такой список:

3, 13, 23, 33, 43, 53, 2, 4, …, 54, 56, 82.

Ответ: а) да; б) нет; в) 6.

Третий вариант (из Ященко, №4)

Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала m фотографий, а Наташа — n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1173 фотографии больше, чем Маша, и что фотографировали они больше одного дня.

а) Могли ли они фотографировать в течение 17 дней?

б) Могли ли они фотографировать в течение 18 дней?

в) Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 45 фотографий?

Алгоритм решения:

Ответим на вопрос а).
Найдем ответ на вопрос б).
Найдем суммарное количество фотографий, сделанных Наташей.
Запишем ответ.

Решение:

1. Если Маша сделала m фотографий в 1-й день, то за 17 дней она сфотографировала снимков.

Наташа, за 1-й день сделала n фотографий, тогда за оставшиеся 17 дней она сделала

кадров.

Найдем такие m и n, чтобы выполнялось равенство:

Возьмем, к примеру, n=70 и m=1. Это ответ на вопрос а).

2. Если фотографировали девочки всего 18 дней, получается:

1173 на 18 не разделится, следовательно, выбрать такие n и m нельзя. Это ответ на вопрос б.

3. Поищем ответ на последний вопрос. Допускаем, что девочки делали фотографии x дней. Тогда Маша сделала бы в последний день снимков

То есть . А согласно условию

число x является делителем 1173. Тогда возможны только варианты: x = 23, 17 или 3.

Вычисляем наибольшее число фотографий, которые могла сделать Маша. Получаем:

Для числа x=3:

При x=17:

А при x=23:

Самое большое количество снимков, которые сделала Наташа:

759+1173=1932.

Ответ: а) да; б) нет; в) 1932.

Источник

ЕГЭ №18 (19). Теория чисел. Рекуррентная задача – самая сложная задача мартовского статграда 2021

ЕГЭ 18 (19) – это задачи на теорию чисел, на свойства чисел, на последовательности. Что такое рекуррентная последовательность?

Сейчас узнаете…

Последовательности чисел нам хорошо известны ещё с 8 – 9 класса. Например, прогрессии – арифметическая и геометрическая.

На ЕГЭ довольно часто попадаются задачи на последовательности – как на стандартные прогрессии, так и на необычные – у каждой из которых какая-то своя формула. И формулы у таких последовательностей обычно рекуррентные – то есть такие, когда каждое следующее число вычисляется через значения каких-то предыдущих.

Например, самая известная не-прогрессия – это последовательность Фибоначчи: каждое число равно сумме двух предыдущих.

Такие последовательности – это не просто очередные бессмысленные упражнения математиков (которым, как известно, делать нечего, вот и грузят всех своими задачками). Последовательности очень часто встречаются нам в жизни, и с их помощью очень удобно описывать некоторые процессы.

Например, говорят, что Фибоначчи свою последовательность придумал, наблюдая за размножением кроликов: первые 2 месяца жизни кролик просто растёт, а потом начинает каждый месяц рожать нового кролика (в среднем).

Сколько будет кроликов через полгода? Через год? В задаче 18 (19 из последнего статграда нам попалась как раз такая последовательность.

Смотрите видео, и вы научитесь исследовать такие последовательности, а также узнаете, как правильно решается эта задача.

Источник

Элементы теории чисел

Разбор типовых вариантов заданий №19 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

[/su_note]

Алгоритм решения:

Вводим переменные k, l, m.
Находим сумму набора чисел.
Отвечаем на пункт а).
Определяем, каких чисел больше (пункт б)).
Определяем, сколько положительных чисел.

Решение:

1. Пусть среди записанных на доске чисел положительных k. Отрицательных чисел l и нулевых m.

4k −8l + 0⋅m = − 3(k + l +m)

40 < k + l + m < 48

Тогда k + l + m = 44, потому что 44 единственное между 40 и 48 натуральное число, которое делится на 4.

Значит, написано на доске всего 44 числа.

4k −8l = − 3(k + l + m).

Имеем

4k − 8l = −132, k = 2l − 33

Ответ: а) 44; б) отрицательных; в) 17.

Второй вариант 1 (из Ященко, №1)

[su_note note_color=”#defae6″]

а) Может ли на доске быть ровно 27 чётных чисел?

б) Могут ли ровно два числа на доске оканчиваться на 3?

в) Какое наименьшее количество чисел, оканчивающихся на 3, может быть на доске?

[/su_note]

Алгоритм решения:

Приведем пример набора чисел, который удовлетворяет условию (Это подтверждает возможность набора чисел).
Проверяем вероятность второго условия.
Ищем ответ на третий вопрос, введя переменную n.
Записываем ответы.

Решение:

1. Такой примерный перечень чисел на доске соответствует заданным условиям:

3,13,23,33,43,53,63,73,2,4,6,…,50,52,56

Это дает положительный ответ на вопрос а.

Это противоречит тому, что сумма написанных чисел равна 1062, то есть, утвердительного ответа на вопрос б нет.

а сумма чётных:

2+4+…+2(35 – n)=(35 – n)(36 – n)= n²-71 n+1260.

Тогда из условия:

Решаем получившееся неравенство:

Получается, что . Отсюда, зная, что n — натуральное, получаем .

3, 13, 23, 33, 43, 53, 2, 4, …, 54, 56, 82.

Ответ: а) да; б) нет; в) 6.

Третий вариант (из Ященко, №4)

[su_note note_color=”#defae6″]

а) Могли ли они фотографировать в течение 17 дней?

б) Могли ли они фотографировать в течение 18 дней?

[/su_note]

Алгоритм решения:

Ответим на вопрос а).
Найдем ответ на вопрос б).
Найдем суммарное количество фотографий, сделанных Наташей.
Запишем ответ.

Решение:

1. Если Маша сделала m фотографий в 1-й день, то за 17 дней она сфотографировала снимков.

Наташа, за 1-й день сделала n фотографий, тогда за оставшиеся 17 дней она сделала

кадров.

Найдем такие m и n, чтобы выполнялось равенство:

Возьмем, к примеру, n=70 и m=1. Это ответ на вопрос а).

2. Если фотографировали девочки всего 18 дней, получается:

1173 на 18 не разделится, следовательно, выбрать такие n и m нельзя. Это ответ на вопрос б.

То есть . А согласно условию

число x является делителем 1173. Тогда возможны только варианты: x = 23, 17 или 3.

Вычисляем наибольшее число фотографий, которые могла сделать Маша. Получаем:

Для числа x=3:

При x=17:

А при x=23:

Самое большое количество снимков, которые сделала Наташа:

759+1173=1932.

Ответ: а) да; б) нет; в) 1932.

Даниил Романович | Просмотров: 10.6k

Источник

Теория чисел

РЕКОМЕНДУЕМЫЕ ТОВАРЫ

Элементы теории чисел

Разбор типовых вариантов заданий №19 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

Алгоритм решения:

Решение:

Второй вариант 1 (из Ященко, №1)

Алгоритм решения:

Решение:

Третий вариант (из Ященко, №4)

Алгоритм решения:

Решение:

ЕГЭ №18 (19). Теория чисел. Рекуррентная задача – самая сложная задача мартовского статграда 2021

Элементы теории чисел

Разбор типовых вариантов заданий №19 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

Алгоритм решения:

Решение:

Второй вариант 1 (из Ященко, №1)

Алгоритм решения:

Решение:

Третий вариант (из Ященко, №4)

Алгоритм решения:

Решение: