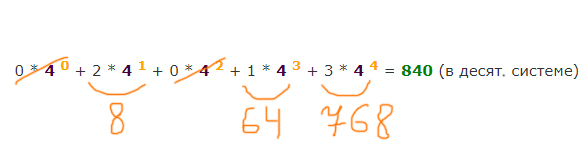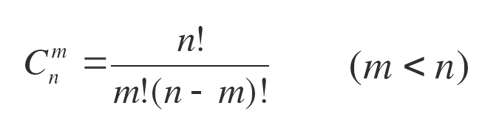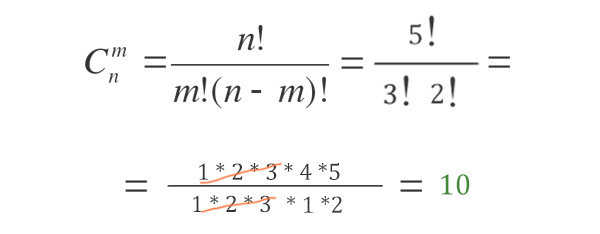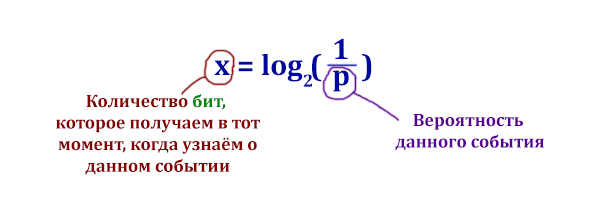На уроке рассматривается разбор 8 задания ЕГЭ по информатике про измерение количества информации
8-е задание: «Измерение количества информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 4 минуты.
Проверяемые элементы содержания: Знание о методах измерения количества информации
До ЕГЭ 2021 года — это было задание № 10 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«При использовании способа решения со системой счисления с основанием N следует помнить, что слова в списке нумеруются с единицы, поэтому числу 0 будет соответствовать первое слово»
ФГБНУ «Федеральный институт педагогических измерений»
Содержание:
- Объяснение темы
- Измерение количества информации
- Двоичное кодирование сообщений (равновероятностные события)
- Количество различных сообщений в алфавите разной мощности
- Количество сообщений при различном вхождении (встречаемости) букв
- Дополнительные формулы
- Тренировочные задания 8 ЕГЭ по информатике и их решение
- Сколько вариантов шифра или кодовых слов
- Перестановка букв в слове (каждая буква 1 раз)
- Сколько существует n-значных чисел, записанных в m-ной системе счисления
- Список в алфавитном порядке
- Вероятность событий
Объяснение темы
Рассмотрим кратко необходимые для решения 8 задания ЕГЭ понятия и формулы.
Измерение количества информации
- Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
- 1 бит – это количество информации, которое можно передать с помощью одного знака в двоичном коде (0 или 1).
- Алфавит — это набор знаков, используемый в том или ином языке.
- Мощность алфавита — это количество используемых в алфавите знаков.
- Сообщение — это любая последовательность символов какого-либо алфавита.
1 байт (bytе) = 8 бит
1 Кб (килобайт) = 1024 байта
1 Мб (мегабайт) = 1024 Кб
1 Гб (гигабайт) = 1024 Мб
1 Тб (терабайт) = 1024 Гб
1 Пб (петабайт) = 1024 Тб
8 = 23
1024 = 210
Рассмотрим еще несколько определений:
Мощность алфавита
Для вычисления количества информации применяются несколько различных формул в зависимости от ситуации:
Двоичное кодирование сообщений (равновероятностные события)
При вычислении количества информации в сообщении для равновероятностных событий, общее количество которых равно N, используется формула:
N = 2L
* следует иметь в виду, что также приняты следующие обозначения: Q = 2k
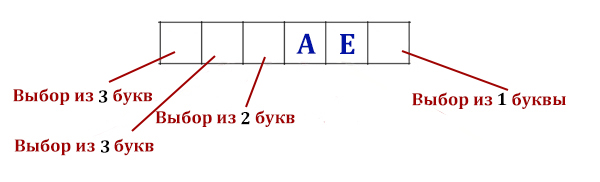
Пример 2: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:

Решение:
Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодовых слов (L = 2).
Количество сообщений длиной L битов:
N = 2L
Т.е. количество сообщений длиной 2 бита, как в примере с нашими буквами, будет равно N = 22 = 4
Ответ: 4
Количество различных сообщений в алфавите разной мощности
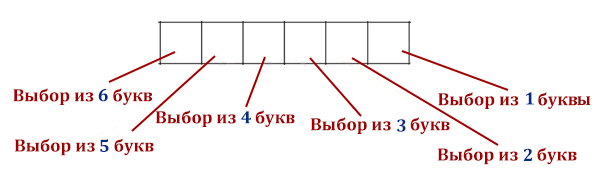
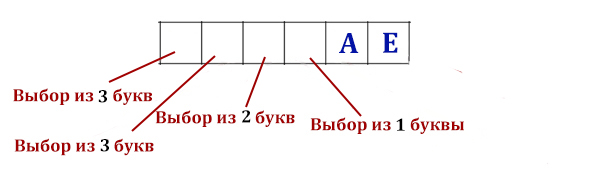
Рассмотрим вариант с 5 буквами (мощность алфавита = 5), которые надо разместить в сообщении длиной 2 символа:
Найдем формулу для нахождения количества различных сообщений в алфавите различной мощности:
Если мощность некоторого алфавита составляет N, то количество различных сообщений длиной L знаков:
- N – мощность алфавита
- L – длина сообщения
- Q – количество различных сообщений
Пример: Сколько существует всевозможных трехбуквенных слов в английском языке?
Решение:
В английском алфавите 26 букв. Значит, мощность алфавита = 26. Длина сообщения = 3. Найдем по формуле количество трехбуквенных слов:
Q = 263
или
26
*
26
*
26
= 17576
Ответ: 17576
N = n1 * n2 * … * nL
Количество сообщений при различном вхождении (встречаемости) букв
В таком случае можно использовать формулу для вычисления числа перестановок с повторениями; для двух разных символов она выглядит так:
[ P = frac{na+n*!}{na!n*!} ]
na – количество букв a n* — количество звёздочек или кол-во вариантов
Иногда в заданиях 8 можно использовать формулу комбинаторики для проверки полученных результатов перебора. Число сочетаний из n элементов по k элементов:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
n! = 1 * 2 * 3 * … * n
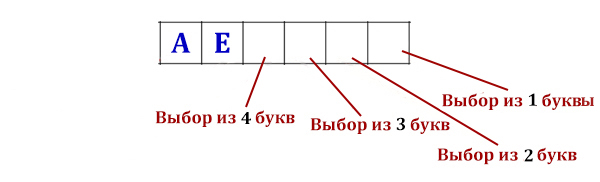
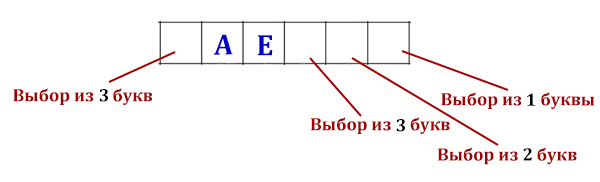
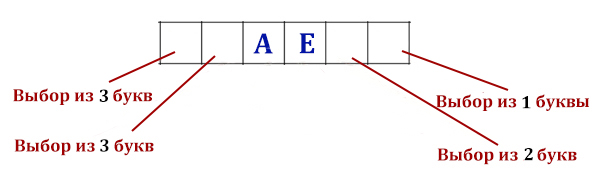
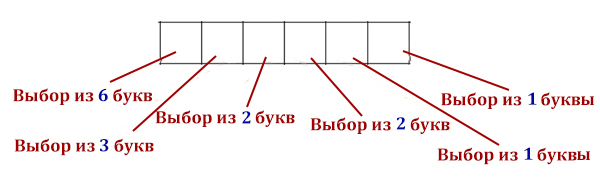
Пример: Сколько существует всевозможных четырехбуквенных слов в алфавите из 4 букв: А, Б, В, Г, если известно, что буква А встречается ровно два раза?
Решение:
- Длина сообщения = 4. Мощность алфавита = 4. Но мешает условие: буква А встречается ровно два раза.
- В таких заданиях можно использовать способ перебора всевозможных вариантов:
два раза буква А, на остальных местах - одна из трех оставшихся букв: А А 3 3 = 3 * 3 = 32 = 9 А 3 А 3 = 9 А 3 3 А = 9 3 А А 3 = 9 3 А 3 А = 9 3 3 А А = 9
Число сочетаний из n элементов по k элементов:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
[ C{binom{2}{4}}= frac{4!}{2!(4-2)!} = frac{24}{2*2} = 6 ]
* Факториал числа n! = 1 * 2 * 3 *..* n
6 * 9 = 54
Дополнительные формулы
Количество информации и равновероятные события
При определении количества информации для равновероятностных событий могут понадобиться две формулы:
x = log2(1/p)
p(A) = m / n
Количество информации и неравновероятные события
При использовании неравновероятного события, вероятность которого равна p, для вычисления количества информации используется формула:
i = -[log2p]
*квадратные скобки означают ближайшее целое, меньшее или равное значению выражения в скобках
Формула Хартли:
Формула Хартли
Алфавитный подход:
Информационный объем сообщения длиной L:
Алфавитный подход
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Сколько вариантов шифра или кодовых слов
Cartesian(n) — метод расширения последовательности, возвращающий декартову степень множества символов |
Когда применяется: Если требуется полный перебор вариантов букв для каждой позиции (каждая буква может встречаться в кодовом слове любое количество раз) |
||||||
|---|---|---|---|---|---|---|---|
| Пример: Сравним полный перебор букв слова «школа», размещенных на две позиции: |
|||||||
| Pascal | PascalABC.NET | ||||||
|
|
||||||
| Результат: | |||||||
|
[ш,ш] [ш,к] [ш,о] [ш,л] [ш,а] [к,ш] [к,к] [к,о] Итого 25 штук (5*5) |
[ш,ш] [ш,к] [ш,о] [ш,л] [ш,а] [к,ш] [к,к] [к,о] [к,л] [к,а] [о,ш] [о,к] [о,о] [о,л] [о,а] [л,ш] [л,к] [л,о] [л,л] [л,а] [а,ш] [а,к] [а,о] [а,л] [а,а] |
||||||
Permutations — метод возвращает все перестановки множества элементов, заданного массивом или последовательностью |
Когда применяется: Если требуется перестановка букв в слове. То есть количество каждой буквы в словах сохраняется, и каждая буква встречается только 1 раз |
||||||
| Пример: Сравним перестановку букв слова «мимикрия»: |
|||||||
| Pascal | PascalABC.NET | ||||||
|
|
|
||||||
| Результат: | |||||||
|
[М,И,М,И,К,Р,И,Я] [М,И,М,И,К,Р,Я,И] [М,И,М,И,К,И,Р,Я] [М,И,М,И,К,И,Я,Р] [М,И,М,И,К,Я,Р,И] [М,И,М,И,К,Я,И,Р] [М,И,М,И,Р,К,И,Я] [М,И,М,И,Р,К,Я,И] … |
Используются также следующие запросы и методы LINQ:
Фильтрация последовательностей (Where)
Метод Count([Type -> boolean]) Вычисление скаляра
Метод CountOf(s: Type) — Возвращает количество элементов, равных указанному значению
Метод First() — Возвращает первый элемент последовательности.
Метод Last() — Возвращает последний элемент последовательности.
Метод Pairwise(Self: sequence of T; func: (T,T)->Res) — Превращает последовательность в последовательность пар соседних элементов, применяет func к каждой паре полученных элементов и получает новую последовательность
8_1:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 6.
Сколько различных вариантов шифра можно задать, если известно, что цифра 1 должна встречаться в коде ровно 1 раз, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
✍ Решение:
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Длина сообщения (L) = 5 символов
- Мощность алфавита (N) = 6 (цифры от 1 до 6).
- Но так как цифра 1 встречается по условию ровно один раз, а остальные 5 цифр — любое количество раз, то будем считать, что N = 5 (цифры от 2 до 6, исключая 1). Т.е. возьмем вариант, когда 1 стоит на первом месте, а остальные 5 цифр размещаем на 4 позиции:
Q = NL
1 5 5 5 5 - 1 * Q = 54 = 625
✎ 1 способ. Найдем количество вариантов методом перебора:
1 5 5 5 5 -1 * Q=54= 625 5 1 5 5 5 -1 * Q=54= 625 5 5 1 5 5 -1 * Q=54= 625 5 5 5 1 5 -1 * Q=54= 625 5 5 5 5 1 -1 * Q=54= 625
✎ 2 способ. Найдем количество вариантов при помощи формулы комбинаторики:
[ C{binom{4}{5}}= frac{5!}{4!(5-4)!} = 5 ]
625 * 5 = 3125
Результат: 3125
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
|
С++:
|
Детальный теоретический разбор задания 8 ЕГЭ по информатике предлагаем посмотреть в видеоуроке:
📹 YouTube здесьздесь (теоретическое решение)
8_2:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является либо буквой (A или B) или цифрой (1, 2 или 3).
Сколько различных вариантов шифра можно задать, если известно, что в коде присутствует ровно одна буква, а все другие символы являются цифрами?
✍ Решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Посчитаем количество возможных шифров для одного из вариантов (например, когда буквы находятся на первой позиции). Так как цифры (1, 2, 3) могут занимать 4 позиции из пяти, а две буквы (А и В) одну из позиций, значит:
Q = NL
Q = 2 * 34 = 162
AB 123 123 123 123 = 162
"2" означает одна из двух букв: А или B, "3" - одна из трех цифр: 2 3 3 3 3 -> Q = 2 * 34 = 162 3 2 3 3 3 -> Q = 2 * 34 = 162 3 3 2 3 3 -> Q = 2 * 34 = 162 3 3 3 2 3 -> Q = 2 * 34 = 162 3 3 3 3 2 -> Q = 2 * 34 = 162
5 * 162 = 810
Результат: 810
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Подробное теоретическое решение данного задания предлагаем посмотреть на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_3:
Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 4-буквенные слова, в которых есть только буквы A, Б, В, Г, Д и Е, причём буква Г появляется ровно 1 раз и только на первом или последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.
Сколько различных кодовых слов может использовать Олег?
✍ Решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Рассмотрим варианты, когда буква Г встречается на первом или последнем месте:
N = n1 * n2 * n3 * … * nL = nL
Г ? ? ? = 1 * 5 * 5 * 5 = 53 = 125 ? ? ? Г = 5 * 5 * 5 * 1 = 53 = 125
125 + 125 = 250
Результат: 250
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Видеоразбор данного задания (теоретический способ):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_4:
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является одной из букв X, Y или Z.
Сколько различных вариантов шифра можно задать, если известно, что буква X должна встречаться в коде ровно 2 раза, а каждая из других допустимых букв может встречаться в шифре любое количество раз или не встречаться совсем?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Формула нахождения количества различных сообщений:
- Итак, что у нас дано из этой формулы:
- Начальная мощность алфавита (N) = 3 (буквы X, Y, Z). Но так как буква X встречается ровно два раза, то мы ее рассмотрим отдельно, а остальные 2 буквы — встречаются любое количество раз, значит, будем считать, что:
Q = NL
N = 3 - 1 = 2 (Y и Z)
(L) = 5 - 2 = 3 символа (остальные два символа отведем на размещение X)
X X ? ? ? -> 12 * Q = 23 = 8
✎1 способ. Перебор всех вариантов:
X X ? ? ? - 12 * Q = 23 = 8 X ? X ? ? - 12 * Q = 23 = 8 X ? ? X ? - 12 * Q = 23 = 8 X ? ? ? X - 12 * Q = 23 = 8 ? X X ? ? - 12 * Q = 23 = 8 ? X ? X ? - 12 * Q = 23 = 8 ? X ? ? X - 12 * Q = 23 = 8 ? ? X X ? - 12 * Q = 23 = 8 ? ? X ? X - 12 * Q = 23 = 8 ? ? ? X X - 12 * Q = 23 = 8
✎ 2 способ. При помощи формулы поиска числа сочетаний:
[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]
Число сочетаний из n элементов по k элементов:
[ C{binom{2}{5}}= frac{5!}{2!(5-2)!} = frac{120}{12} = 10 ]
* Факториал числа: n! = 1 * 2 * 3 * .. * n
8 * 10 = 80
* задание достаточно решить одним из способов!
Результат: 80
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Детальный теоретический разбор задания 8 ЕГЭ по информатике теоретическим способом предлагаем посмотреть в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_5:
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв ОСЕНЬ? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Из букв слова ОСЕНЬ имеем 2 гласных буквы (О, Е) и 2 согласных буквы (С, Н). Буква мягкий знак «нейтральна».
- Подсчитаем количество букв на каждой из 5 позиций:
2 5 5 5 2 СН все все все ОЕ
N = n1 * n2 * n3 * … * nL = nL
N = 2 * 5 * 5 * 5 * 2 = 500
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Результат: 500
Разбор можно также посмотреть на видео (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_6:
Вася составляет 4-буквенные слова, в которых есть только буквы Л, Е, Т, О, причём буква Е используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
✍ Решение:
-
✎ Решение теоретическое:
- Количество вариантов различных слов вычислим по формуле:
- n1 — количество вариантов выбора первой буквы и т.п.
- Рассмотрим все варианты расположения буквы Е:
✎ 1 способ:
N = n1 * n2 * n3 * …
где
1. Е ? ? ? или 2. ? Е ? ? или 3. ? ? Е ? или 4. ? ? ? Е Где вопросительный знак означает любую букву из Л, Е, Т, О.
Е ? ? ? = 1 * 4 * 4 * 4 = 64 т.е. на первой позиции - только 1 буква - Е, на каждой последующей - одна из четырех букв Л, Е, Т, О.
? Е ? ? = 3 * 1 * 4 * 4 = 48
? ? Е ? = 3 * 3 * 1 * 4 = 36
? ? ? Е = 3 * 3 * 3 * 1 = 27
64 + 48 + 36 + 27 = 175
Результат: 175
✎ 2 способ:
- Так как по условию буква Е встретится хотя бы 1 раз, значит, можно утверждать, что не может быть такого, чтобы буква Е не встретилась бы ни одного раза.
- Таким образом, рассчитаем случай, когда буква Е встречается все 4 раза (т.е. все случаи) и отнимем от результата невозможный случай: когда буква Е не встретится ни одного раза:
1. Буква Е используется 4 раза (т.е. на всех позициях): 4 * 4 * 4 * 4 = 256 2. Буква Е не используется совсем (т.е. только 3 буквы): 3 * 3 * 3 * 3 = 81
256 - 81 = 175
Результат: 175
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Теоретическое решение задания 8 смотрите в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_7:
Вася составляет 4-буквенные слова, в которых есть только буквы К, А, Т, Е, Р, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
✍ Решение:
-
✎ Решение теоретическое:
- Количество возможных вариантов слов вычислим по формуле:
- где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
- Сначала по формуле получим все варианты для всех пяти букв, включая букву Р:
N = n1 * n2 * n3 * … * nL = nL
5 * 5 * 5 * 5 = 54 = 625
4 * 4 * 4 * 4 = 44 = 256
р ? ? ? = 1 * 4 * 4 * 4 = 43 ? р ? ? = 4 * 1 * 4 * 4 = 43 ? ? р ? = 4 * 4 * 1 * 4 = 43 ? ? ? р = 4 * 4 * 4 * 1 = 43 Получим 43 * 4 = 256
625 - 256 - 256 = 113
✎ Решение с использованием программирования:
PascalABC.net (традиционный):
|
||
PascalABC.net (LINQ):
|
||
Python:
|
||
| С++: |
Результат: 113
Теоретическое решение 8 задания предлагаем посмотреть в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_8:
Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 5-буквенные слова, в которых есть только буквы A, Б, В, и Г, причём буква Г появляется не более одного раза и только на последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.
Сколько различных кодовых слов может использовать Олег?
✍ Решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Так как буква Г появляется не более одного раза и только на последнем месте, значит, она может либо появиться 1 раз на последнем месте, либо не появиться совсем.
- Рассмотрим варианты, когда буква Г встречается 1 раз на последнем месте и встречается 0 раз:
N = n1 * n2 * n3 * … * nL = nL
1 раз: ? ? ? ? Г = 3 * 3 * 3 * 3 * 1 = 34 = 81 0 раз: ? ? ? ? ? = 3 * 3 * 3 * 3 * 3 = 35 = 243
81 + 243 = 324
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: 324
8_9:
Вася составляет 4-буквенные слова, в которых есть только буквы К, О, М, А, Р, причём буква А используется в них не более 3-х раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
✍ Решение:
-
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Так как буква А по условию используется не более 3-х раз, это значит, что она используется либо 3 раза, либо 2 раза, либо 1 раз, либо не используется совсем. Рассмотрим все эти варианты отдельно.
- 1. Буква А используется 3 раза:
N = n1 * n2 * n3 * … * nL = nL
А А А _ -> 1 * 1 * 1 * 4 = 4 А А _ А -> 1 * 1 * 4 * А = 4 А _ А А -> 1 * 4 * 1 * 1 = 4 _ А А А -> 4 * 1 * 1 * 1 = 4
_ может быть любая из 4 букв: К О М Р. Значит, имеем:4 * 4 = 16 вариантов
А А _ _ -> 1 * 1 * 4 * 4 = 16 А _ А _ -> 1 * 4 * 1 * 4 = 16 А _ _ А -> 1 * 4 * 4 * 1 = 16 _ А А _ -> 4 * 1 * 1 * 4 = 16 _ А _ А -> 4 * 1 * 4 * 1 = 16 _ _ А А -> 4 * 4 * 1 * 1 = 16
_ может быть любая из 4 букв: К О М Р. Значит имеем:16 * 6 = 96 вариантов
А _ _ _ -> 1 * 4 * 4 * 4 = 64 _ А _ _ -> = 64 _ _ А _ -> = 64 _ _ _ А -> = 64
64 * 4 = 256 вариантов
_ _ _ _ -> 44 = 256
16 + 96 + 256 + 256 = 624
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов * LINQ (Language Integrated Query) — язык интегрированных запросов |
||
Python:
|
||
| С++: |
Результат: 624
Теоретическое решение смотрите также на видео:
📹 YouTube здесьздесь (теоретическое решение)
8_10:
Сколько существует различных символьных последовательностей длины 3 в четырёхбуквенном алфавите {A,B,C,D}, если известно, что одним из соседей A обязательно является D, а буквы B и C никогда не соседствуют друг с другом?
✍ Решение:
✎ Решение теоретическое:
- Вспомним формулу получения количества возможных вариантов слов:
- где n1 — количество вариантов выбора первой буквы,
- n2 — количество вариантов выбора второй буквы и т.п.
- Будем рассматривать варианты, расставляя каждую букву последовательно по алфавиту, начиная с первой буквы. При этом будем учитывать указанные ограничения для букв А, B и С:
N = n1 * n2 * n3 * … * nL = nL
Начинаем с A: A D 4ABCD = 1 * 1 * 4 = 4 Начинаем с B: B A D, B B 2BD, B D 4ABCD = 7 Начинаем с C: C A D, C C 2CD, C D 4ABCD = 7 Начинаем с D: D A 3BCD, D B 2BD, D C 2CD, D D 4ABCD = 11
4 + 7 + 7 + 11 = 29
Результат: 29
Видеоурок демонстрирует подробное теоретическое решение задания:
📹 YouTube здесьздесь (теоретическое решение)
8_22:
Лена составляет 5-буквенные слова из букв Я, С, Н, О, В, И, Д, Е, Ц, причём слово должно начинаться с согласной и заканчиваться гласной. Первая и последняя буквы слова встречаются в нем только один раз; остальные буквы могут повторяться.
Сколько слов может составить Лена?
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
| Python: | ||
| С++: |
Результат: 6860
Использование метода Pairwise()
8_11:
Из букв С, Р, Е, Д, А составляются трехбуквенные комбинации по следующему правилу – в комбинации не может быть подряд идущих гласных и одинаковых букв.
Например, комбинации ААР или ЕСС не являются допустимыми.
Сколько всего комбинаций можно составить, используя это правило?
✍ Решение:
-
✎ Решение теоретическое:
- Рассмотрим два варианта: когда слово начинается с гласной буквы, и когда оно начинается с согласной.
1. С гласной:
1.1 2 3 2 = 2 * 3 * 2 = 12 гл с с 1.2 2 3 2 = 2 * 3 * 2 = 12 гл с гл
2. С согласной:
2.1 3 2 2 = 3 * 2 * 2 = 12 с с с 2.2 3 2 3 = 3 * 2 * 3 = 18 с гл с 2.3 3 2 2 = 3 * 2 * 2 = 12 с с гл
12 + 12 + 12 + 18 + 12 = 66
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
Python:
|
||
| С++: |
Результат: 66
Перестановка букв в слове (каждая буква 1 раз)
8_12:
Дано слово КОРАБЛИКИ. Таня решила составлять новые 5-буквенные слова из букв этого слова по следующим правилам:
1) слово начинается с гласной буквы;
2) гласные и согласные буквы в слове должны чередоваться;
3) буквы в слове не должны повторяться.
✍ Решение:
-
✎ Решение теоретическое:
- Учтем, что в слове КОРАБЛИКИ две буквы К и две И.
- Всего в слове 4 гласных, но поскольку две буквы
И, то необходимо считать только 3 гласных. - Всего в слове 5 согласных, однако две из них — буквы
К, поэтому считать следует 4 согласных. - Посчитаем количество согласных и гласных для каждой из 5 позиций слова, учитывая, что с каждой последующей буквой количество используемых гласных/согласных уменьшается. Под позициями приведем пример букв:
гл с гл с гл 3 4 2 3 1 оаи крбл оа крб и
3 * 4 * 2 * 3 * 1 = 72
Результат: 72
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Результат: 72
8_21:
Ксюша составляет слова, меняя местами буквы в слове МИМИКРИЯ.
Сколько различных слов, включая исходное, может составить Ксюша?
✍ Решение:
-
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 3360
Подробное решение программным способом смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (программное решение)
8_19:
Петя составляет шестибуквенные слова
перестановкой букв
слова АДЖИКА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Посчитаем количество слов без двух подряд одинаковых букв. Будем считать относительно буквы А, которых две в заданном слове АДЖИКА. Буквы не могут повторяться, поэтому их кол-во в каждом варианте будет уменьшается:
А*А*** = 4*3*2*1 = 24 слова с данным расположением буквы А. А**А** = 4*3*2*1 = 24 А***А* = 4*3*2*1 А****А = ... *А*А** *А**А* *А***А **А*А* **А**А ***А*А
10 * 24 = 240
✎ Решение с использованием программирования:
PascalABC.net (приближенный к традиционному, долгое решение):
Смысл решения в использовании типа — множества ( |
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Ответ: 240
8_20:
Маша составляет 7-буквенные коды из букв В, Е, Н, Т, И, Л, Ь. Каждую букву нужно использовать
ровно 1 раз
, при этом код буква Ь не может стоять на последнем месте и между гласными. Сколько различных кодов может составить Маша?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Выполним задание следующим образом: 1. посчитаем общее количество слов, не учитывая никакие ограничения. 2. Затем посчитаем случаи, которые необходимо исключить. 3. Вычтем из результата пункта 1 результат пункта 2.
- Общее количество независимо от ограничений (учтем, что буквы не должны повторяться):
7 6 5 4 3 2 1 - количество возможных вариантов букв на семи позициях ИТОГО: 7! = 5040 слов
6 5 4 3 2 1 Ь = 6! = 720
И Ь Е 4 3 2 1 = 24 варианта Так как буквы смещаются по всем позициям, то получим (4 И Ь Е 3 2 1, ...): 24 * 5 = 120 Е Ь И 4 3 2 1 = 24 варианта 24 * 5 = 120
5040 - 720 - 120 - 120 = 4080
✎ Решение с использованием программирования:
Стоит заметить, что теоретическое решение занимает меньше времени, чем программный способ!
PascalABC.net (приближенный к традиционному, долгое решение):
|
||
PascalABC.net (использование LINQ, быстрое решение):
|
||
| Python: | ||
| С++: |
Ответ: 4080
8_23:
Артур составляет 6-буквенные коды перестановкой букв слова ВОРОТА. При этом нельзя ставить рядом две гласные.
Сколько различных кодов может составить Артур?
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, спортивное прогр-е):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 72
Сколько существует n-значных чисел, записанных в m-ной системе счисления
8_18: Объяснение 8 задания экзамена ЕГЭ 2020 г. (со слов учащегося):
Сколько существует восьмизначных чисел, записанных в восьмеричной системе счисления, в которых все цифры различны и рядом не могут стоять 2 чётные или 2 нечётные цифры?
Типовые задания для тренировки
✍ Решение:
-
✎ Решение теоретическое:
- Выпишем все четные и нечетные цифры, которые могут использоваться в 8-й с.с.:
четные: 0, 2, 4, 6 - итого 4 цифры нечетные: 1, 3, 5, 7 - итого 4 цифры
1) с четной цифры: 3 4 3 3 2 2 1 1 = 3*4*3*3*2*2*1*1 = 432 ч н ч н ч н ч н
Самый старший разряд не может быть равен 0 (поэтому 3 цифры из 4 возможных), так как разряд просто потеряется, и число станет семизначным). Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
2) с нечетной цифры: 4 4 3 3 2 2 1 1 = 4*4*3*3*2*2*1*1 = 576 н ч н ч н ч н ч
Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.
432 + 576 = 1008
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Ответ: 1008
Список в алфавитном порядке
8_13:
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Ниже приведено начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
…
Запишите слово, которое стоит под номером 242 от начала списка.
✍ Решение:
-
✎ Решение теоретическое:
- Данное задание лучше решать следующим образом. Подставим вместо букв цифры (А -> 0, О -> 1, У -> 2):
1. 00000 2. 00001 3. 00002 4. 00010 ...
остатки 241 | 3 | 1 80 | 3 | 2 26 | 3 | 2 8 | 3 | 2 2 | |
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
Смотрим слова и находим по номеру нужное слово: … (241,[У,У,У,У,А]) (242,[У,У,У,У,О]) (243,[У,У,У,У,У])
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: УУУУО
Подробное решение теоретическим способом смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_14: 8 задание. Демоверсия ЕГЭ 2018 информатика:
Все 4-буквенные слова, составленные из букв Д, Е, К, О, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
1. ДДДД 2. ДДДЕ 3. ДДДК 4. ДДДО 5. ДДДР 6. ДДЕД …
Под каким номером в списке идёт первое слово, которое начинается с буквы K?
✍ Решение:
-
✎ Решение теоретическое:
- Подставим вместо букв цифры (Д -> 0, Е -> 1, К -> 2, О -> 3, Р -> 4):
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010 ...
K -> 2 -> 2000
По формуле разложения числа по степеням основания: 20005 = 2 * 53 + 0 * 22 + 0 + 0 = 2 * 125 = 25010
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: 251
Подробное решение 8 (10) задания демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_15:
Все 4-буквенные слова, составленные из букв П, Р, С, Т, записаны в алфавитном порядке.
Вот начало списка:
1. ПППП 2. ПППР 3. ПППС 4. ПППТ 5. ППРП ... ...
✍ Решение:
Результат: 65
Видеоразбор задания смотрите ниже:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
8_16:
Все четырёхбуквенные слова, составленные из букв В, Е, Г, А, Н записаны в алфавитном порядке и пронумерованы, начиная с 1. Начало списка выглядит так:
1. АААА 2. АААВ 3. АААГ 4. АААЕ 5. АААН 6. ААВА …
Под каким номером в списке идёт первое слово, в котором нет буквы А?
✍ Решение:
- ✎ Решение теоретическое:
- Пронумерованный список начинается со всех букв А. Представим, что А — 0, В — 1, Г — 2, Е — 3, Н — 4. Получим следующий список:
1. 0000 2. 0001 3. 0002 4. 0003 5. 0004 6. 0010
11115 = 1 * 53 + 1 * 52 + 1 * 51 + 1 * 50 = 156
156 + 1 = 157
✎ Решение с использованием программирования:
PascalABC.net (использование LINQ, быстрое решение):
* LINQ (Language Integrated Query) — язык интегрированных запросов |
||
| Python: | ||
| С++: |
Результат: 157
Видеорешение задания (теоретическое):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
Вероятность событий
8_17:
За четверть Василий Пупкин получил 20 оценок. Сообщение о том, что он вчера получил четверку, несет 2 бита информации.
Сколько четверок получил Василий за четверть?
✍ Решение:
- Для решения данного задания необходимо вспомнить две формулы:
1. Формула Шеннона:
x = log2(1/p)
x - количество информации в сообщении о событии p - вероятность события
2. Формула вероятности случайного события:
p(A) = m/n
m - число случаев, способствующих событию А n - общее число равновозможных случаев
2 = log2(1/p);
=>
1/p = 4;
=>
p = 1/4
p = ?/20
1/4 = ?/20
? = 1/4 * 20 = 5
Результат: 5
Видеоразбор задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
Сегодня на повестке дня 8 задание из ЕГЭ по информатике 2021. Данный тип заданий включает в себя нахождение количества вариантов, элементы комбинаторики и другие математические понятия.
Перейдём к практике решения задач задания 8 ЕГЭ по информатике 2021.
Задача (Классика)
Все 4-буквенные слова, составленные из букв А, Е, И, О записаны в алфавитном порядке и пронумерованы. Вот начало списка:
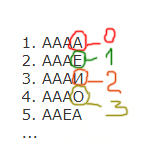
1. АААА
2. АААЕ
3. АААИ
4. АААО
5. ААЕА
…
Запишите слово, стоящее на 248-м месте от начала списка.
Решение:
Обозначим условно А — 0, Е — 1, И — 2, О — 3.
Важно: Нужно буквам присваивать цифры именно в том порядке, в котором они идут в самом правом столбце, потому что буквы могут дать в «перепутанном порядке» (например Е, А, И, О), и тогда ничего не получится.
Теперь запишем список с помощью цифр.
1. 0000
2. 0001
3. 0002
4. 0003
5. 0010
…
Получился обычный счёт в четверичной системе!! (всего используются 4 цифры: 0, 1, 2, 3). А слева нумерация показывает соответствие нашей десятичной системе. Но все числа десятичной системы в этой таблице соответствия сдвинуты на 1, ведь мы должны были начать с нуля.
Нас просят записать слово стоящее на 248, т.е. если была обычная таблица соответствия чисел десятичной системы и четверичной системы, слово стоящее на 248 месте, находилось бы на 247 (248 — 1) месте. Значит, наше искомое четверичное число соответствует 247 в десятичной системе.
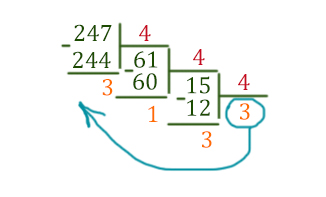
Переведём число 247 в четверичную систему!
Получилось число 33134 в четверичной системе. Сделаем обратное декодирование в буквы. Таким образом, ответ будет ООЕО.
Ответы: ООЕО
Ещё одна похожая задача 8 задания из примерных вариантов ЕГЭ по информатике, но другой вариации.
Задача (Классика, Другая вариация)
Все 5-буквенные слова, составленные из букв А, Р, У, К записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА
……
Укажите номер слова УКАРА
Решение:
Закодируем буквы цифрами: А — 0, К — 1, Р — 2, У — 3. Здесь как раз буквы даны не в том порядке, как они идут в самом правом столбце. Но мы должны кодировать именно в том порядке, как буквы идут в самом правом столбце.
У нас получилось четыре цифры! Значит снова можно слова превратить в таблицу соответствия между десятичной системой и четверичной системой. Но десятичная система смещена на 1 позицию.
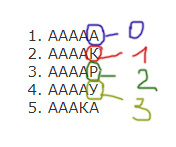
1. 00000
2. 00001
3. 00002
4. 00003
5. 00010
……
Выписываем данное нам слово и посмотрим, какое число в четверичной системе было бы, если бы у нас были в место слов числа в четверичной системе!
Получили число в четверичной системе 310204. Узнаем, какое число в десятичной системе соответствовало этому числу, если бы была обычная таблица соответствия. Для этого переведём число 310204 из четверичной системы в десятичную. Перевод делаем по аналогии перевода из двоичной системы в десятичную.
Но помним, что у нас нумерация идёт на 1 быстрее, нежели мы бы поставили десятичные числа, как в таблице соответствия, потому что нумерация начинается не с нуля, а с 1. Поэтому к числу 840 нужно прибавить 1, и в ответе будет 841
Ответ: 841
Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)
Все 4-буквенные слова, в составе которых могут быть буквы Н, О, Т, К, И,
записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
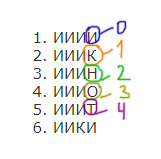
1. ИИИИ
2. ИИИК
3. ИИИН
4. ИИИО
5. ИИИТ
6. ИИКИ
…
Под каким номером в списке идёт первое слово, которое начинается
с буквы О?
Решение:
Закодируем буквы цифрами.
Получилось 5 цифр ( 0, 1, 2, 3, 4 ), значит, будем работать в пятеричной системе.
Нужно найти номер первого слова, которое начинается с буквы О. Если говорить на языке пятеричных чисел, то нужно найти номер числа 30005. Мы «забиваем нулями», чтобы число было четырёхразрядное, т.к. слова 4-х буквенные. Именно нулями, потому что нужно именно первое слово найти.
Теперь, как в предыдущей задаче, переведём число 30005 из пятеричной системы в десятичную.
0 * 5 0 + 0 * 5 1 + 0 * 5 2 +
3 * 5 3 = 375 (в десят. системе)
Но опять же должны прибавить 1 к числу 375, т.к. нумерация отличается от десятичных чисел на 1 в большую сторону.
Ответ: 376
Задача (Досрочная волна 2020 ЕГЭ по информатике, вариант 1)
Вася составляет 5-буквенные слова, в которых есть только буквы В, О, Л, К,
причём буква В используется в каждом слове ровно 1 раз. Каждая из других
допустимых букв может встречаться в слове любое количество раз или
не встречаться совсем. Словом считается любая допустимая
последовательность букв, не обязательно осмысленная. Сколько существует
таких слов, которые может написать Вася?
Решение:
Для начала решим вводную подзадачу.
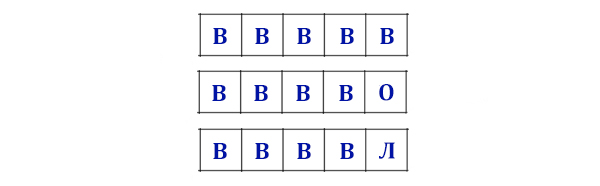
Пусть у нас есть те же буквы В, О, Л, К, каждая из букв может встречаться в слове любое количество раз или
не встречаться совсем. Сколько можно составить 5-буквенных слов ?
Т.е буквы могут повторяться!
Например
Такая конструкция сильно напоминает перебор чисел, где вместо цифр используются буквы.
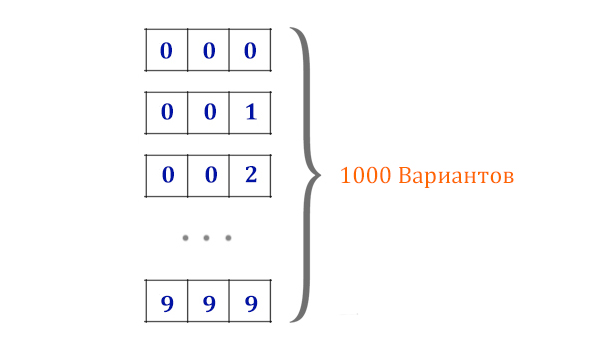
Рассмотрим перебор трёхразрядных чисел. Вместо 5 букв теперь можно использовать 10 цифр ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ). Цифры так же могут повторяться. Сколько получится вариантов ?
Выведем общую формулу для количества вариантов, когда символы могут повторяться!
Для трёхразрядных чисел от 000 до 999:
N = 103 = 1000 вариантов.
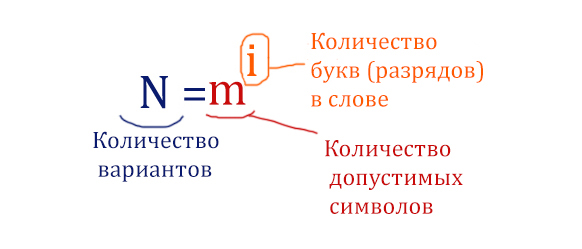
Вернёмся к пятибуквенным словам и нашей подзадаче. Здесь количество букв (разрядов) в слове равно 5, количество допустимых символов равно 4 ( В, О, Л, К ).
N = 45 = 1024 вариантов.
Вернёмся к изначальной задаче. Сначала найдём количество вариантов, когда буква В находится в самой левой ячейке!
Применим формулу! Здесь слово сократилось до четырёхразрядного. А количество букв для использования 3 (О, Л, К).
N = 34 = 81 комбинация.
Но буква В так же может стоять во второй ячейке слева. Этот случай тоже даст 81 других комбинаций. Буква В может стоять в каждой из 5-ти ячеек, и везде будет получатся 81 комбинация.
Таким образом, окончательный ответ будет:
N = 81 * 5 = 405 различных вариантов.
Ответ: 405
Разобравшись с этой задачей, больше половины тренировочных задач десятого задания из различных книг и сайтов по подготовке к ЕГЭ по информатике будут решаться, как по маслу!
Задача(Закрепление формулы)
Рассматриваются символьные последовательности длины 5 в шестибуквенном алфавите {У, Ч, Е, Н, И, К}. Сколько существует таких последовательностей, которые начинаются с буквы У и заканчиваются буквой К?
Решение:
Применим главную формулу 8 задания из ЕГЭ по информатике
N = mi = 63 = 216
Здесь буквы могут изменяться на 3 ячейках! Значит, в формуле i=3. Количество допустимых символов, которые можно поставить в каждую ячейку равно 6. Значит, в формуле m=6.
В ответе будет 216.
Примечание: Здесь можно использовать все буквы в каждой ячейке, включая У и К. В некоторых задачах их уже использовать нельзя, т.е. сказано, что буквы У и К используются один раз в слове. Тогда в формуле m, будет на 2 единицы меньше. Нужно внимательно читать задачу!
Ответ: 216
Задача (Демонстрационный вариант ЕГЭ по информатике, 2019)
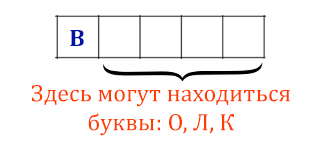
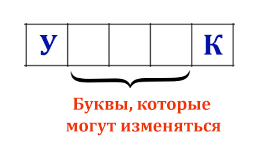
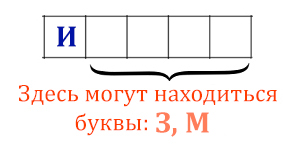
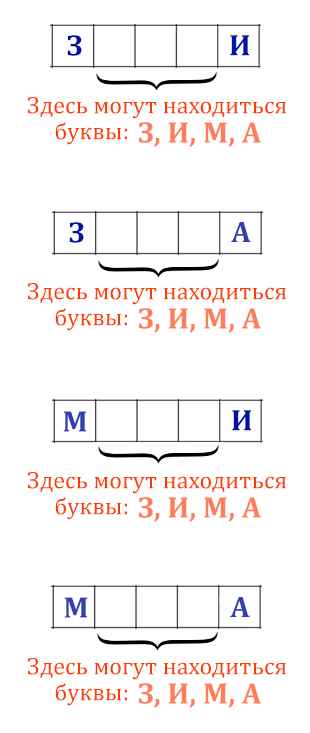
Вася составляет 5-буквенные слова, в которых есть только буквы З, И, М, А,
причём в каждом слове есть ровно одна гласная буква и она встречается
ровно 1 раз. Каждая из допустимых согласных букв может встречаться
в слове любое количество раз или не встречаться совсем. Словом считается
любая допустимая последовательность букв, не обязательно осмысленная.
Сколько существует таких слов, которые может написать Вася?
Решение:
Рассмотрим количество вариантов, когда гласная И стоит в первом месте!
Подсчитаем количество слов с помощью супер-формулы
N = mi = 24 = 16
Длина изменяющихся ячеек равна 4, а количество допустимых букв равно 2.
Но буква И может стоять не только на первом месте. Она так же может стоять и на 2, и на 3, и на 4, и на 5 месте. Каждый такое случай добавляет столько же новых слов.
Значит, при использовании только буквы И будет количество слов 16 * 5 = 80. Ещё столько же слов добавится, если в словах вместо буквы И будет использоваться буква А. Поэтому окончательный ответ будет 80 * 2 = 160
Ответ: 160
Отработаем главную формулу 8 задания из ЕГЭ по информатике.
Задача (Развиваем понимание формулы!)
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Решение:
Рассмотрим, какие варианты могут быть, если у нас на первом месте стоит согласная, а на последнем месте гласная
Получилось 4 разных случая. Подсчитаем, сколько слов можно составить при одном случае.
N = mi = 43 = 64
Длина изменяющихся ячеек равна 3, а количество возможных букв 4.
Но т.к. таких случая у нас четыре, то ответ будет 4 * 64 = 256
Ответ: 256
Рассмотрим важнейший «метод умножения» при решении 8 задания из ЕГЭ по информатике.
Задача (Другой метод решения!!)
Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз , при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?
Решение:
Эта задача отличается от уже разобранных тем, что каждую букву можно использовать один раз. В этой задаче удобнее воспользоваться немного другим методом решения! «Методом умножения»!
Решим вводную подзадачу (без дополнительных ограничений).
Сколькими способами можно составить 6-x буквенное слово из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз .
Чтобы найти возможные варианты, перемножаем для каждой ячейки количество букв из которых у нас есть выбор!
N = 6 * 5 * 4 * 3 * 2 * 1 = 720
Вернёмся к изначальной задаче!
В начале подсчитаем «методом умножения» количество слов, не обращая внимание, на условие, в котором сказано, что слово не может содержать сочетание АЕ.
N = 5 * 5 * 4 * 3 * 2 * 1 = 600
В формуле стоят почти все те же самые числа, как и в вводном примере, только первый множитель не 6, а 5. Это произошло из-за того, что у нас в задаче слово не может начинаться на букву Й. Значит, выбор на первую позицию будет не из 6 букв, а из 5.
Но в 600 комбинаций входят и те случаи, когда в слове присутствует сочетание АЕ. Теперь найдём сколько таких слов, где присутствует сочетание АЕ
Узнаем количество вариантов в каждом таком случае.
N1 = 4 * 3 * 2 * 1 = 24
На первом месте мы не можем использовать букву Й, поэтому мы на первом месте выбираем из 3 букв.
N2 = 3 * 3 * 2 * 1 = 18
Аналогично предыдущему случаю.
N3 = 3 * 3 * 2 * 1 = 18
N4 = 3 * 3 * 2 * 1 = 18
N5 = 3 * 3 * 2 * 1 = 18
Всего слов с сочетанием АЕ будет
24 + 18 + 18 + 18 + 18 = 96
Значит, всего слов, которые удовлетворяют условию задаче будет
N = 600 — 96 = 504
Примечание: Метод умножения можно было использовать и в задачах, которые мы рассмотрели ранее. Например, в задаче «Закрепление формулы» в первой свободной ячейке выбираем из 6 букв, во второй свободной ячейке тоже из 6 букв, и в третий свободной ячейке тоже можно использовать 6 букв. Значит, по методу умножения получается N = 6 * 6 * 6 = 63 = 216
Ответ: 504
Задача (Закрепления «метода умножения»)
Полина составляет 6-буквенные коды из букв П, О, Л, И, Н, А. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Полина?
Решение:
Опять сказано, что каждая буква используется 1 раз, следовательно, нужно применять «метод умножения».
На первое место можно выбрать из 6 букв, предположим, мы выберем согласную. Тогда на второе место нужно выбирать из 3 гласных. Потом опять должна идти согласная, но их у нас осталось только 2. Далее, на следующее место выбираем из 2 гласных букв. И на предпоследнее место выбирается 1 согласная, а на последнее место остаётся 1 гласная.
Т.к. количество гласных букв и согласных одинаковое, и равно трём, то если мы бы начали делать «метод умножения» с гласной буквы, количество вариантов бы не поменялось.
N = 6 * 3 * 2 * 2 * 1 * 1 = 72
Ответ: 72
Задача (Азбука Морзе)
Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее трёх и не более четырёх сигналов (точек и тире) ?
Решение:
Зная формулу, без проблем решим данную примерную задачу из ЕГЭ по информатике.
У нас есть 2 символа, которые можно использовать: точка и тире. Фраза, что сообщение может иметь «не менее трёх и не более четырёх сигналов», означает, что сообщения могут быть длиною 3 символа и длиною 4 символа.
Подсчитаем общее количество вариантов.
N = 23 + 24 = 8 + 16 = 24 комбинаций.
Значит, для 24 различных символов (цифр, букв, знаков пунктуации и т.д.) мы найдём различные комбинации, чтобы их закодировать
Ответ: 24
Задача (Обратная предыдущей)
Световое табло состоит из цветных индикаторов. Каждый индикатор может окрашиваться в четыре цвета: белый, черный, желтый и красный. Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 300 различных сигналов?
Решение:
Нам нужно закодировать 300 различных вариантов! Имеются 4 различных лампочки! (Они имеют смысл, как количество допустимых символов!) На этот раз нужно узнать количество лампочек (количество разрядов, «длину слова»). Применяем формулу.
N = 4x = 300
Не найдётся такое целое x, чтобы равенство стало верным. Поэтому берём целое минимальное x такое, чтобы 4x больше 300.
45 = 1024
Пять лампочек на табло хватит, чтобы закодировать 300 сигналов, но, к сожалению, много комбинаций просто не пригодится!
Ответ: 5
Задача (Важная!)
Нужно выбрать в подарок 3 книги из 5. Сколькими способами можно выбрать ?
Решение:
На рисунке показано две комбинации, как можно выбрать в подарок 3 книги из 5.
Данную задачку нужно решать используя формулу сочетаний из раздела комбинаторика.
n — количество книг, из которых мы выбираем подарок, m — количество книг, которое мы хотим выбрать, C — количество вариантов (способов).
Восклицательный знак — это факториал!
Факториалом числа «n» (условное обозначение n!- читается как «эн» — факториал) называется произведение чисел от 1 до «n»
Примечание: При использовании формулы сочетаний, не важен порядок, в котором мы выбираем одни и те же книги. Это будет один и тот же вариант.
Ответ: 10
Следующая задача часто встречается в книгах по подготовке к ЕГЭ по информатике.
Задача (Главная формула + сочетания)
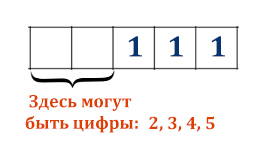
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 5. Сколько различных вариантов шифра можно задать, если известно, что цифра 1 встречается ровно три раза, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?
Решение:
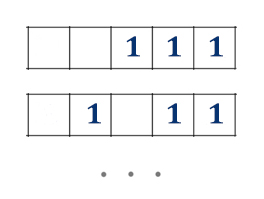
В начале нужно посчитать, сколькими способами на 5-ти ячейках можно расположить 3 единицы!
Обратите внимание, как будто мы выбираем 3 книги в подарок из 5 возможных! Значит, опять применяем формулу сочетаний из комбинаторики. Мы вычисляли уже её точно с такими же числами в прошлой задаче, количество вариантов равно 10.
Подсчитаем, сколько вариантов кодового замка можно составить при одном определённом расположении трёх единиц.
Применим формулу, есть две ячейки, в которых изменяются цифры, а в каждой ячейке может быть одна из 4 цифр.
N = mi = 42 = 16
Т.к. различных вариантов, как расположить единицы на 5 ячейках равно 10, то ответ будет 16 * 10 = 160
Ответ: 160
Ещё одна задача из примерных вариантов по подготовке к ЕГЭ по информатике.
Задача (Таблица соревнований)
Для записи результатов соревнований используется таблица, в которой для каждой из 20-ти команд по каждому из 10-ти видов состязаний записано 1, 2 или 3 (если команда заняла соответствующее место в этом состязании) или прочерк (если не заняла призовое место или не участвовала). Какое количество информации (бит) содержит таблица ?
Решение:
Есть таблица с 20 командами и для каждой команды есть результат по 10-ти видам состязаний.
| 1 команда | 2 команда | 3 команда | … | 20 команда | |
| 1 дисциплина | 1 | — | 1 | … | 3 |
| 2 дисциплина | — | 2 | 1 | … | 2 |
| … | … | … | … | … | … |
| 10 дисциплина | 1 | 1 | 2 | … | — |
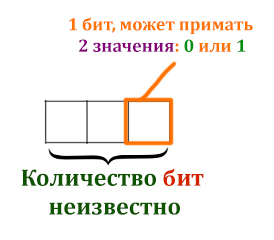
В каждой ячейке может быть 4 различных значения ( 1, 2, 3, — ). Нужно узнать, сколько бит занимает одна ячейка таблицы. Один бит может быть либо единицей, либо нулём.
Сделав рисунок, задача обрела привычные очертания.
Как будто мы решаем задачу с перебором слов. Но здесь длина слова неизвестна, а количество вариантов, которое должно получится уже дано и равно 4 (четырём). Применим главную формулу из 10 задания из ЕГЭ по информатике.
N = mi = 2i = 4
i=2 бита (длина равна «2 буквам», если воспринимать задачу, как со словами.)
Одна ячейка таблицы весит 2 бита. Найдём количество ячеек во всей таблице соревнований.
Всего ячеек = 20 * 10 = 200
Тогда вся таблица будет весит:
V = 2 бита * 200 = 400 бит.
Ответ: 400
Формула Шеннона
Задача (Формула Шеннона)
В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?
Решение:
Данную задачу нужно решать по формуле Шеннона
Найдём вероятность p того, что вытащили чёрный шарик.
p = (количество чёрных шаров) / (количество всех шаров) = 8 / (24 + 
p = 1 / 4
Применим формулу Шеннона.
x = log2(4)
2x = 4
x = 2 бита
Ответ: 2
Доброго времени суток ! Помогите пожалуйста решить задачу .) Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз, при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?
В закрытом ящике находится 32 карандаша, некоторые из них синего цвета. Наугад вынимается один карандаш. Сообщение «этот карандаш – НЕ синий» несёт 4 бита информации. Сколько синих карандашей в ящике?
Был бы очень рад , если вы разберете и эту задачку
Добрый день. Полностью разобрал этот номер, но наткнулся на один интересный пример. Объясните доступным языком, пожалуйста. На решу егэ вообще не понял их решение:
Тимофей составляет 5-буквенные коды из букв Т, И, М, О, Ф, Е, Й. Буква Т должна входить в код не менее одного раза, а буква Й — не более одного раза. Сколько различных кодов может составить Тимофей? (ответ: 8006)
Добрый день! Подскажите пожалуйста, как решить следующую задачу: Сколько существует чисел, шестнадцатеричная запись которых содержит 3 цифры, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом.
Петя составляет семибуквенные слова перестановкой букв слова АССАСИН. Сколько всего различных слов может составить Петя? Мое решение: 21 вариант с буквой А, 35- с буквой С, и 4 на буквы И и Н. Всего 60 и умножаем на 7. Получается 420. Не уверена, что применила верный алгоритм. Прокомментируйте, пожалуйста, решение
Можете заказать решение задачи через раздел «связь».
В Задаче (Другой метод решения!!) допущена ошибка в решении, ведь 24 + 18 + 18 + 18 + 18 = 114,значит N = 600 — 114 = 486!
Добрый день! Помогите пожалуйста решить задачку
Сколько чисел длиной 6 можно составить, если известно, что цифры идут в порядке убывания, при этом четные и нечетные цифры чередуются?
У меня только один вопрос. Почему в школах на уроках информатики вместо действительно полезного изучения какого нибудь языка программирования, заставляют заниматься вот этой вот ересью и решать какое по счету слово напишет Вася? Я могу только составить в ответ на это только слова которые нельзя здесь писать. От таких знаний и занятий ни один ребенок не захочет стать программистом, потому что это непонятно, и неизвестно зачем уметь решать такие задачи. Я сам программист с 10 летним стажем не смог объяснить ребенку как решать некоторые задачи и самое главное, я не знаю зачем дети должны уметь это решать.
Дмитрий, согласен с Вами. Особенно 11 задание и формула Шеннона. Надо либо излагать задание корректно, либо исключить вообще: «В корзине лежат черные и белые шары. Среди них 18 черных шаров. Сообщение о том, что достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине?» — для двух состояний достаточно одного бита.
marvell special for u
c = 0
from itertools import*
for i in permutations(‘МАТВЕЙ’, r=6):
i = ».join(i)
if i[0] != ‘Й’ and i.count(‘АЕ’) == 0:
print(i)
c += 1
print(c)
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Сколько слов длины 5, начинающихся с гласной буквы, можно составить из букв Е, Г, Э? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
2
Сколько слов длины 6, начинающихся с согласной буквы, можно составить из букв Г, О, Д? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
3
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
4
Вася составляет 5-буквенные слова, в которых есть только буквы С, Л, О, Н, причём буква С используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Источник: ЕГЭ 05.05.2015. Досрочная волна.
5
Сколько слов длины 6, начинающихся и заканчивающихся согласной буквой, можно составить из букв Г, О, Д? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.
Пройти тестирование по этим заданиям
Задание 8. Анализ программ. Циклы for и while. ЕГЭ 2023 по информатике
За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 85.3%
Ответом к заданию 8 по информатике может быть цифра (число) или слово.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Саша составляет шестибуквенные слова, в которых есть только буквы А, М, О, К, Т и С, причём в каждом слове буква Т используется один или два раза и при этом может стоять только на первом или на втором местах, а буква О встречается в слове ровно 2 раза, на пятом и шестом месте. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Сколько существует таких слов, которые может написать Саша?
Решение
Поскольку на двух последних позициях обязательно стоит буква О, там всегда ровно один вариант расстановки букв. Количество вариантов зависит только от первых 4-х символов. Дальше будем считать именно для 4-х символов.
Рассмотрим все варианты расстановки буквы Т:
1. Буква Т встречается ровно 2 раза на первом и втором месте. Тогда на 3 и 4 месте могут стоять только буквы А/М/К/С. 4·4 = 16 вариантов.
2. Буква Т встречается ровно 1 раз на первом месте. Тогда на 2, 3 и 4 месте могут стоять только буквы А/М/К/С. 4·4·4 = 64 варианта.
3. Буква Т встречается ровно 1 раз на втором месте. Тогда на 1, 3 и 4 месте могут стоять только буквы А/М/К/С. 4·4·4 = 64 варианта.
Всего вариантов: 64+64+16 = 144.
Ответ: 144
Ответ: 144
Задача 2
Саша составляет шестизначные числа, в которых есть только цифры 1, 2 и 3, причём цифра 1 используется в каждом числе не более двух раз и при этом может стоять только на первом или втором местах. Каждая из других допустимых цифр может встречаться в числе любое количество раз или не встречаться совсем. Сколько существует таких чисел, которые может написать Саша?
Решение
1) без цифры 1: 2*2*2*2*2*2=64
2) с одной 1 на первом месте: 1*2*2*2*2*2=32
3) с одной 1 на втором месте: 2*1*2*2*2*2=32
1) с двумя 1: 1*1*2*2*2*2=16
Итого: 64+32+32+16=144
Ответ: 144
Задача 3
Саша составляет пятибуквенные слова, в которых есть только буквы А, Б, В, Г, Д, Е, причём в каждом слове буква Г используется ровно 2 раза. Каждая из других допустимых букв может встречаться любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Сколько существует таких слов, которые может написать Саша?
Решение
Количество перестановок букв Т на 5 позициях = 10. можно вычислить по формуле n!/(n-m)! где n — это количество позиций (в данном случае 5), а m — количество букв, которые необходимо расположить (в данном случае 2 буквы Т). по формуле получается 20, но у нас абсолютно одинаковые элементы (буквы Т) поэтому делим на факториал 2, чтобы не учитывать повторы.
На каждой из оставшихся трёх позиций в слове могут стоять по 5 букв — итого 125 комбинаций.
В итоге: для каждого из 10 вариантов расположения букв Т получается по 125 комбинаций оставшихся трёх букв: 10 * 125 = 1250.
Ответ: 1250
Задача 4
Аня составляет 5-буквенные слова, в которых встречаются только буквы А, Б, В. Причем буква A может встречаться только первой или последней (двух букв А в слове быть не может), но при этом должна присутствовать обязательно. Каждая из других допустимых букв может встречаться в слове на любом месте или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная.
Сколько существует таких слов, которые может написать Аня?
Решение
Поскольку буква А должна стоять либо на первом, либо на последнем месте (должна встретиться в слове, но не на обеих позициях), то получаем такие комбинации размещения букв:
A 2 2 2 2 = 16 слов
2 2 2 2 A = 16 слов
Итого: 16+16=32 слова
Ответ: 32
Задача 5
Все пятибуквенные слова, составленные из букв А, Л, Е, Т, Б записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ААААА
2. ААААБ
3. ААААЕ
4. ААААЛ
5. ААААТ
6. АААБА
. . .
Под каким номером в списке идёт первое слово, которое начинается с буквы Л и заканчивается буквой Т?
Решение
Каждому слову поставим в соответствие пятизначное число в пятеричной системе счисления. Для этого каждой букве поставим в соответствие цифру в том порядке, в котором она появляетс в списке.
А — 0, Б — 1, Е — 2, Л — 3, Т — 4
Первое слово, которое начинается на Л — это слово ЛАААА и заканчивающееся на Т — то есть ЛАААТ. Этому слову соответствует число $30004_5$ = $1879_10$, которое стоит под номером 1880.
Ответ: 1880
Задача 6
Все шестибуквенные слова, составленные из букв Б, Л, О, Т записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ББББББ
2. БББББЛ
3. БББББО
4. БББББТ
5. ББББЛБ
6. ББББЛЛ
. . .
Под каким номером стоит слово БОЛОТО?
Решение
Для составления слов используются 4 различных буквы. Поставим в соответствие каждой из букв цифры системы счисления с основанием 4 (с учётом порядка их следования в алфавите): Б — 0, Л — 1, О — 2, Т — 3.
Тогда упорядоченной по алфавиту последовательности слов
1. ББББББ
2. БББББЛ
3. БББББО
4. БББББТ
5. ББББЛБ
6. ББББЛЛ
. . .
будут соответствовать числа в системе счисления с основанием 4:
1. 0000004 = 010
2. 0000014 = 110
3. 0000024 = 210
4. 0000034 = 310
5. 0000104 = 410
5. 0000114 = 510
. . .
Слову БОЛОТО будет соответствовать число 0212324. Переведём это число из системы счисления с основанием 4 в десятичную.
0212324 = 0 · 45 + 2 · 44 + 1 · 43 + 2 · 42 + 3 · 41 + 2 · 40 = 62210.
Заметим, что соответствующая последовательность чисел, записанных в десятичной системе счисления, на 1 меньше номера строки, содержащей данное число. Значит, десятичное число 622 будет находиться на 623-м месте.
Ответ: 623
Задача 7
Саша составляет 6-значные числа, в которых есть только цифры 1, 2, 3 и 4 причём цифра 1 используется в каждом числе ровно 1 раз. Каждое из других допустимых цифр может встречаться в числе любое количество раз или не встречаться совсем. Сколько существует таких чисел, которые может написать Саша?
Решение
Пусть цифра 1 стоит в числе на первом месте. Тогда на оставшихся 5 местах может стоять одна из оставшихся цифр 2, 3 или 4. Причём каждая из этих цифр может встречаться в числе любое количество раз. Таким образом нам нужно определить количество 5-значных чисел, состоящих из трёх цифр.
Если M — количество символов в некотором алфавите (мощность алфавита), K — количество всех возможных «слов» (символьных цепочек) длиной N , то = MN.
Следовательно, количество пятизначных чисел, состоящих из трёх цифр, равно 35 = 243. А значит такое же количество 6-значных чисел, в которых на первом месте стоит цифра 1, а на остальных местах цифры 2, 3 или 4, возможно с повтором.
Рассуждая аналогичным образом, мы получим, что такое же количество чисел в 6-значных числах, в которых цифра 1 на втором, третьем, четвёртом, пятом и шестом местах.
То есть всего искомых чисел 6 · 243 = 1458.
Ответ: 1458
Задача 8
Саша составляет четырёхбуквенные слова, в которых есть только буквы Е, Д, О, Н и К, причём в каждом слове буква О используется ровно 2 раза. Каждое из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Сколько существует таких слов, которые может написать Саша?
Задача 9
Саша составляет трёхбуквенные слова, в которых есть только буквы E, C, B, Н, К и У, причём в каждом слове буква К используется ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.
Сколько существует таких слов, которые может написать Саша?
Задача 10
Все шестибуквенные слова, составленные из букв М, Н, О, П, Р, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ММММММ
2. МММММН
3. МММММО
4. МММММП
5. МММММР
6. ММММНМ
. . .
Укажите слово, которое стоит под номером 267.
Задача 11
Все пятибуквенные слова, составленные из букв А, М, Н, Т, У, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ААААА
2. ААААМ
3. ААААН
4. ААААТ
5. ААААУ
6. АААМА
. . .
Под каким номером стоит слово ТУМАН?
Рекомендуемые курсы подготовки
Лада Есакова, преподаватель информатики и математики, автор книги «Информатика. Полный курс подготовки к ЕГЭ».
Добрый день, дорогие друзья! С вами я, Есакова Лада, преподаватель информатики с 20-летним стажем.
Сегодня разберем основы комбинаторики и буквенные цепочки.
Задача:
«Все 4-буквенные слова, составленные из букв В, Н, Р, Т, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ВВВВ
2. ВВВН
3. ВВВР
4. ВВВТ
5. ВВНВ
………
Запишите слово, которое стоит под номером 251.»
Обозначим В = 0, Н = 1, Р = 2, Т = 3 и получим вот такой ряд:
1. 0000
2. 0001
3. 0002
4. 0003
5. 0010
Это числовой ряд в четверичной системе исчисления. Нам нужно найти слово, которое стоит под номером 251.
Здесь важный нюанс, на котором часто ребята теряют балл. На первом месте стоит 0, то есть номер строчки на единицу больше самого числа. Поэтому на 251 месте у нас будет стоять число на единицу меньше – 250, но только в четверичной системе исчисления.
Переведем 250 в четверичную систему. Будем делить столбиком. У нас получается 250 = 33224. Теперь переводим цифры в буквы — ТТРР. Вот такой ответ должен получиться.
Вот такие буквенные цепочки – это, по сути, числовые ряды.
Следующая задача:
«Все 6-буквенные слова, составленные из букв С, В, Е, Т, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ВВВВВВ
2. ВВВВВЕ
3. ВВВВВС
4. ВВВВВТ
5. ВВВВЕВ
………
Под каким номером стоит первое из слов, которое начинается с буквы Т?»
Здесь есть еще одна ловушка: нам сказали, что все 6-буквенные слова составлены из этих букв, и очень хочется пронумеровать букву в том же порядке, в котором они представлены – С = 0, В = 1, Е = 2, Т = 3. Вот здесь-то и ошибка.
Если посмотрим на числовой ряд, то увидим, что на первой строчке у нас стоит В, значит, она будет равна 0. Далее появляется Е, значит, она равна 1, С = 2 и Т = 3.
И снова у нас четверичная система исчисления. Необходимо определить, под каким номером стоит первое из слов, которое начинается с буквы Т. Перефразирую вопрос: под каким номером стоит четверичное число, которое начинается на 3? Значит, оно должно выглядеть как 300000. Это число стоит на месте, которое на единицу больше, чем оно само, но в десятичной записи. Необходимо это число, 300000, из четверичной системы перевести в десятичную.
3000004=3*45=3*1024=3072
У нас получается число 3072, а номер строки на единицу больше, то есть номер строки будет 3073. Это и есть ответ задачи.
С такими цифровыми цепочками на сегодня мы закончим. Перейдем к более интересной теме, к элементам комбинаторики, хотя это громко сказано, потому что там от комбинаторики только одна маленькая формула.
Чтобы понять, о чем я сейчас буду говорить, давайте представим такую ситуацию: допустим, надоело нам жить в Москве и решили переехать на необитаемый остров. Для связи с внешним миром мы запасли некоторое количество цветных флажков, которые мы можем прикрепить к флагштокам и при необходимости подать сигнал. У нас есть два флагштока и флажки только двух цветов: красные и синие. Что же при помощи этого мы можем сообщить во внешний мир?
Мы можем составить 4 комбинации:
Если нам этого не хватает, мы можем добавить флажки еще одного цвета. Допустим, у нас еще есть зеленые флажки, и мы можем составить следующие комбинации:
У нас получилось 9 комбинаций.
Если же все-таки у нас флажки только двух цветов, третьего нет, у нас есть другой путь увеличить количество комбинаций, увеличив количество флагштоков. Получаем следующие комбинации:
и их получилось 8 штук.
Мы видим, что количество сообщений, которые мы можем передать внешнему миру, зависит от двух параметров: от количества букв в нашем алфавите (или, в нашем случае, от разных цветов флажков) и от длины слова (или от количества флагштоков).
Количество слов, которые мы можем закодировать, равно количеству букв в нашем алфавите (еще это называется мощностью алфавита) в степени «длина слова» A=ai
«Сколько различных символов можно закодировать, используя код азбуки Морзе длиной не менее четырех и не более пяти сигналов (точек и тире)?»
Если я делаю слово из четырех сигналов, то таких слов я могу сделать 24, если я делаю из пяти сигналов, то таких слов я могу придумать 25. А в задаче как раз этот интервал, то есть и те, и те мне подойдут. Вот столько разных слов я могу составить 24 + 25 = 48.
«Коля составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует свое кодовое слово. В качестве кодовых слов Коля использует 4-буквенные слова, в которых есть буквы А, Б, В, Г, Д, причем буква Д появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Коля?»
Не буду мудрить, придумывать какие-то сложные формулы, а просто распишу, как буква Д может встречаться ровно один раз. Это выглядит так
Д — — —
— Д — —
— — Д —
— — — Д
то есть она может встретиться на каком-то из четырех мест. На остальных трех местах может стоять все, кроме Д, то есть 4 любые буквы по трем позициям, 43. И так в каждом ряду. Все это сложим и получим 4*43=44=256
«Паша составляет таблицу кодовых слов для передачи сообщений. В качестве кодовых слов Паша использует 4-буквенные слова, в которых есть только буквы А, Б, В, Г, Д, Е, Ж. При этом первая буква кодового слова – это буква Д, Е или Ж, а далее в кодовом слове буквы Д, Е и Ж не встречаются. Сколько различных кодов может использовать Паша?»
У нас получается такой вид
Д — — —
Е — — —
Ж — — —
А в остальных местах используются остальные буквы, кроме Д, Е и Ж. Получаем 3*43=3*64=192
«Герасим составляет 7-буквенные коды из букв Г, Е, Р, А, С, И, М. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Герасим?»
Тут немного схитрим. Необходимо обязательно чередовать гласные и согласные, а для этого посмотрим, сколько у нас гласных. 3. А согласных 4. Поэтому на гласную начать слово я не могу, иначе их не хватит на все слово, и согласные где-то обязательно повторятся. Поэтому слово будет выглядеть таким образом: согласная – гласная – согласная – гласная – согласная – гласная – согласная.
Далее каждую букву я должна использовать ровно один раз.
Вначале состава слова согласных у нас 4, гласных – 3, далее согласных остается 3, т.к. одну я уже использовала, а согласных – 2, затем согласных 2, гласных – одна и согласная осталась одна. Теперь мы перемножаем все эти цифры
и получаем 144.
«Ольга составляет 5-буквенные коды из букв О, Л, Ь, Г, А. Каждую букву нужно использовать ровно 1 раз, при этом Ь нельзя ставить первым и нельзя ставить после гласной. Сколько различных кодов может составить Ольга?»
Давайте пойдем от противного: посчитаем все варианты, а потом выбросим те, которые нам запретили, но сразу выкинем вариант с мягким знаком на первом месте. То есть на первом месте мы можем поставить 4 различные буквы. На втором месте могу поставить все, кроме этой буквы, но зато мы можем добавить Ь, то есть тоже 4. Две буквы уже использовали. Осталось 3, 2 и 1. Все это перемножаю и получаю 96. То есть это все возможные слова, где используется буквы по одному разу, но только не начинающиеся на Ь.
Теперь из этого числа нужно выбросить ситуации, когда Ь стоит после гласной. Это, например, вот так
О Ь — — —
— О Ь — —
— — О Ь —
— — — О Ь
Таких слов 24
О Ь — — — 3*2*1
— О Ь — — 3*2*1
— — О Ь — 3*2*1
— — — О Ь 3*2*1
——
24
Абсолютно такая же ситуация с буквой А
А Ь — — —
— А Ь — —
— — А Ь —
— — — А Ь
———
24
И их тоже 24. То есть 96-48=48.
На этом прощаемся. Если вопросов нет, пока!
Все видео по информатике
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «8 Задание ЕГЭ 2021 | Комбинаторика» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
ЕГЭ информатика 8 задание разбор, теория, как решать.
Перебор слов и комбинаторика, (Б) — 1 балл
Е8.44 Определите количество пятизначных чисел, записанных в восьмеричной
Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6. Ответ: Демонстрационный вариант ЕГЭ 2023 г. – задание №8
Читать далее
Е8.43 Леонид составляет коды из букв слова ЛЕОНИД.
Леонид составляет коды из букв слова ЛЕОНИД. Код должен состоять из 6 букв, буква Л должна встречаться в нём ровно два раза, буква О – как минимум один раз. Сколько различных кодов может составить Леонид? Ответ: СтатГрад Вариант ИН2110402 30.03.2022 – задание №8
Читать далее
Е8.42 Определите количество семизначных чисел, записанных в семеричной системе счисления
Определите количество семизначных чисел, записанных в семеричной системе счисления, учитывая, что числа не могут начинаться с цифр 3 и 5 и не должны содержать сочетания цифр 22 и 44 одновременно. Ответ: Апробация ЕГЭ по информатике 19 февраля 2022 – задание №8 Тренировочный экзамен по информатике и ИКТ (КЕГЭ) в компьютерной форме
Читать далее
Е8.41 Светлана составляет коды из букв слова РОСОМАХА
Светлана составляет коды из букв слова РОСОМАХА. Код должен состоять из 8 букв, и каждая буква в нём должна встречаться столько же раз, сколько в заданном слове. Кроме того, в коде не должны стоять рядом две гласные и две согласные буквы. Сколько кодов может составить Светлана? Ответ: СтатГрад Вариант ИН2110301 08.02.2022 – задание №8
Читать далее
Е8.40 согласная буква не может стоять в начале слова
Федя составляет 7-буквенные слова из букв П, Л, Ю, С, Ё, Н, О, К, причём согласная буква не может стоять в начале слова, а также рядом с буквой Ё. Буквы в слове могут повторяться. Сколько таких слов может составить Федя? Ответ: «Некрыловские варианты» от Евгения Джобса (И. Женецкий) — Вариант 6
Читать далее
Е8.39 никакие две четные или две нечетные цифры не должны стоять рядом
Аня составляет шестизначные числа в десятичной системе счисления. Цифры в числе не должны повторяться, и никакие две четные или две нечетные цифры не должны стоять рядом. Сколько чисел может составить Аня? Ответ: «Некрыловские варианты» от Евгения Джобса (А. Куканова) — Вариант 5
Читать далее
Е8.38 каждая буква в нём должна встречаться столько же раз, сколько в имени
Светлана составляет коды из букв своего имени. Код должен состоять из 8 букв, и каждая буква в нём должна встречаться столько же раз, сколько в имени Светлана. Кроме того, одинаковые буквы в коде не должны стоять рядом. Сколько кодов может составить Светлана? Ответ: Источник: СтатГрад 17 декабря 2021 года Вариант ИН2110201
Читать далее
Е8.37 Валерия составляет 3-буквенные коды и букв В, А, Л, Е, Р, И, Я, причём буква В
Валерия составляет 3-буквенные коды и букв В, А, Л, Е, Р, И, Я, причём буква В должна входить в код ровно один раз. Все полученные коды Валерия записала в алфавитном порядке и пронумеровала. Начало списка выглядит так: 1. ААВ 2. АВА 3. АВЕ … На каком месте будет записан первый код, не содержащий ни одной …
Читать далее
Е8.36 Настя составляет 6-буквенные коды из букв Н, А, С, Т, Я
Настя составляет 6-буквенные коды из букв Н, А, С, Т, Я. Каждая допустимая гласная буква может входить в код не более одного раза. Сколько кодов может составить Настя? Ответ: СтатГрад Вариант ИН2010501 26.04.2021– задание №8
Читать далее
Е8.35 Под каким номером в списке идёт слово ВАТА?
Под каким номером в списке идёт слово ВАТА? Все четырёхбуквенные слова, в составе которых могут быть только буквы А, В, Т , О , Р , записаны в алфавитном порядке и пронумерованы, начиная с 1. Ниже приведено начало списка: 1. АААА 2. АААВ 3. АААО 4. АААР 5. АААТ 6. ААВА Под каким номером в …
Читать далее