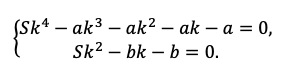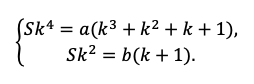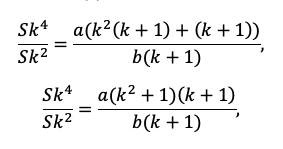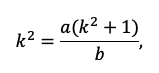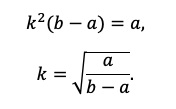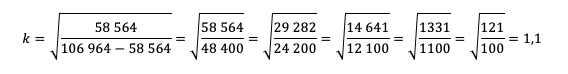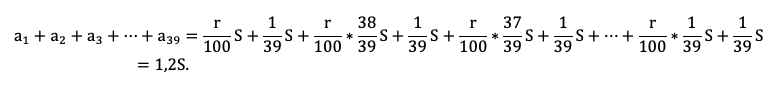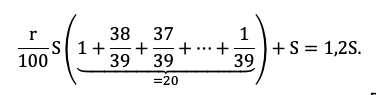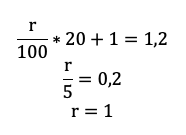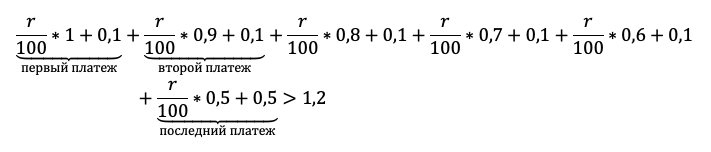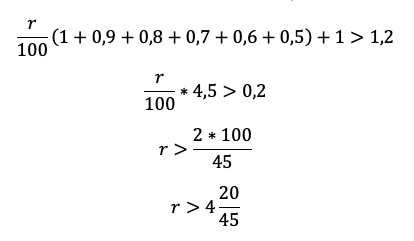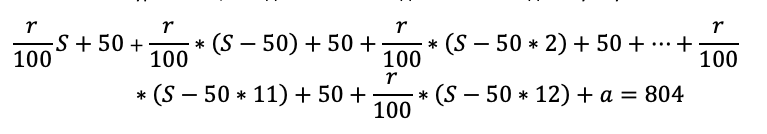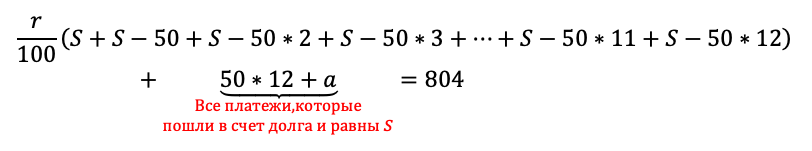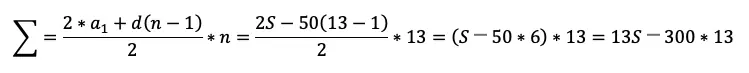Баба Валя, накопив часть своей пенсии, решила улучшить свое материальное положение. Она узнала, что в Спёрбанке от пенсионеров принимают вклады под определенный процент годовых и на этих условиях внесла свои сбережения в ближайшее отделение Спёрбанка. Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры, есть коммерческий банк, в котором процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в Спёрбанке. Баба Валя не доверяла коммерческим банкам, но стремление улучшить свое материальное положение взяло верх. После долгих колебаний и ровно через год после открытия счета в Спёрбанке Баба Валя сняла половину образовавшейся суммы от ее вклада, заявив: «Такой навар меня не устраивает!» и открыла счет в том коммерческом банке, о котором говорила ее соседка, не теряя надежды на значительное улучшение своего материального благосостояния.
Надежды оправдались: через год сумма Бабы Вали в коммерческом банке превысила ее первоначальные кровные сбережения на 65%. Сожалела Баба Валя, что год назад в Спёрбанке сняла не всю сумму, а лишь половину, однако, подумала: «А где же мы не теряли?..» Гендиректор коммерческого банка оказался хорошим: не оставил Бабу Валю без денег.
А каков в Спёрбанке процент годовых для пенсионеров?
В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!
Прототипы для 17-го номера делятся на три большие группы:
- банковские задачи,
- на ценные бумаги,
- задачи на оптимальный выбор.
В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.
Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.
- Как работает процент по кредиту?
- На какую сумму начисляется?
- Из каких частей состоит платеж?
- Как уменьшается долг?
На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс!
Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.
С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике
Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:
- Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
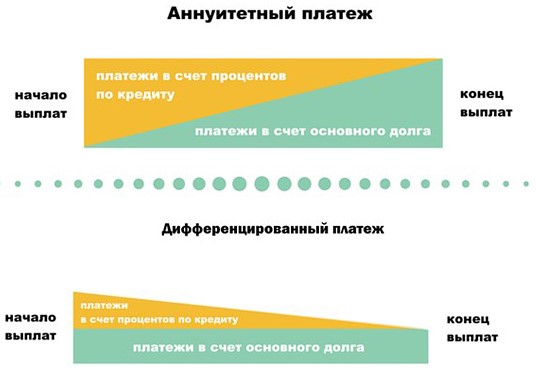
- Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
- Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.
Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.
Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.
Тип 1. Равные платежи
Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!
Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.
Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.
Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!
Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.
Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:
Наше решение не зависит от суммы кредита, S сокращается.
По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:
Пожалуй, все, проще уже некуда. Подставляем значения!
Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.
Вспоминаем, что k=1+r/100, а найти нам надо r.
Ответ: 10%.
Не забудьте после решения расставить акценты в задаче:
Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.
Тип 2. Равномерно убывающий долг
В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)
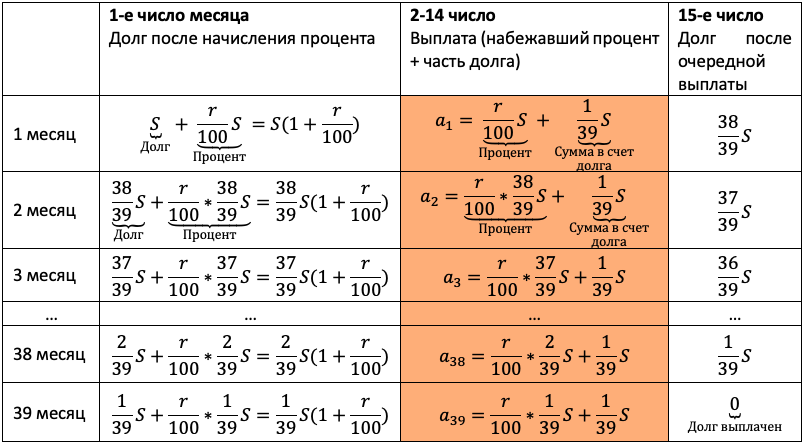
Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.
Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:
Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:
Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:
Приведем подобные, вынесем общий множитель за скобку:
Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:
Ответ: 1%.
И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.
Тип 3. Долг, убывающий согласно табличке
Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг(в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.
Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.
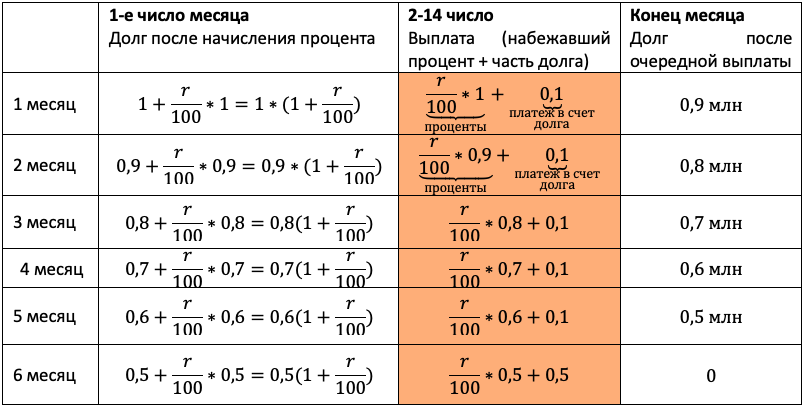
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:
Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.
Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.
«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:
Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.
Приведем подобные и вынесем общие множители за скобку:
Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.
Ответ: 5%.
Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.
Тип 4. Погашение кредита в два этапа.
По сути, это та же прошлая задача, но месяцев больше
В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!
15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?
И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.
Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.
Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.
Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:
Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:
Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.
Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:
Посчитаем эту сумму:
Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!
Ответ: 700 тысяч.
Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.
Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике
Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:
- Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
- Повторите типы задач и механизм распределения платежа на проценты и долг;
- Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
- Проговорите, что математическая модель должна точно отражать условие задачи.
Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.
За что дают баллы?
Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.
17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.
Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа.
Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:
А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.
Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.
Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.
Задание 2. Информатика. Апробация 10.03.2023
Миша заполнял таблицу истинности логической функции (F)
$$
(x to neg (y to z)) lor w,
$$
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
| F | ||||
| 0 | 0 | 0 | ||
| 1 | 0 | |||
| 0 | 1 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
В ответе напишите буквы (w), (x), (y), (z) в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Функция (F) задана выражением ( neg x lor y), зависящим от двух переменных, а фрагмент таблицы имеет следующий вид:
В этом случае первому столбцу соответствует переменная (y), а второму — переменная (x). В ответе следует написать: (yx).
Решение:
Python
from itertools import permutations, product
def F(x, y, z, w):
return (x <= (not y <= z)) or w
for perm in permutations('xyzw'):
for a,b,c,d,e,f,g in product([0,1], repeat=7):
table = [[a,0,b,0,0],
[1,c,d,e,0],
[0,1,f,g,0]]
if table[0] == table[1]:
continue
if all(F(**dict(zip(perm,row))) == row[-1] for row in table):
print(*perm)
Ответ: (yzxw)
Решение и ответы заданий варианта МА2210309 СтатГрад 28 февраля ЕГЭ 2023 по математике (профильный уровень). Тренировочная работа №3. ГДЗ профиль для 11 класса.
+Задания №1, №4, №6, №10 из варианта МА2210311.


Задание 1.
В треугольнике ABC угол C равен 90°, CH – высота, BC = 5, cosA=frac{2sqrt{6}}{5}. Найдите длину отрезка AH.
Задание 1 из варианта 2210311.
Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
Задание 2.
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
Задание 3.
В группе 16 человек, среди них – Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
Задание 4.
Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
Задание 4 из варианта 2210311.
Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
Задание 5.
Решите уравнение frac{x–1}{5x+11}=frac{x–1}{3x-7}. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Задание 6.
Найдите значение выражения frac{(4^{frac{3}{5} }cdot7^{frac{2}{3}})^{15}}{28^{9}} .
Задание 6 из варианта 2210311.
Найдите 98cos2α, если cosα = frac{4}{7}.
Задание 7.
На рисунке изображён график y = f’(x) – производной функции f(x), определённой на интервале (−5; 5). В какой точке отрезка [−4; −1] функция f(x) принимает наибольшее значение?
Задание 8.
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле FA = ρgl3, где l – длина ребра куба в метрах, ρ = 1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте, что g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 2116800 Н? Ответ дайте в метрах.
Задание 9.
Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Задание 10.
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите значение f(−1).
Задание 10 из варианта 2210311.
На рисунке изображены графики функций f(x) = frac{k}{x} и g(x) = ax + b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
Задание 11.
Найдите точку минимума функции y = x3 − 27x2 + 13.
Задание 12.
а) Решите уравнение 2cos3x = –sin(frac{3pi}{2} + x)
б) Найдите все корни этого уравнения, принадлежащие отрезку [3π; 4π]
Задание 13.
Основанием правильной пирамиды PABCD является квадрат ABCD. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды, если AB = 30.
Задание 14.
Решите неравенство frac{9^{x}–13cdot 3^{x}+30}{3^{x+2}–3^{2x+1}}ge frac{1}{3^{x}}.
Задание 15.
По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n, при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Задание 16.
В треугольнике ABC медианы AA1, BB1 и CC1 пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22.
Задание 17.
Найдите все значения a, при каждом из которых система уравнений
begin{cases} (x-5a+1)^{2}+(y-2a-1)^{2}=a-2 3x-4y=2a+3 end{cases}
не имеет решений.
Задание 18.
У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький – 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять.
а) Может ли Аня купить 24 конверта?
б) Может ли Аня купить 29 конвертов?
в) Какое наибольшее число конвертов может купить Аня?
Источник варианта: СтатГрад/statgrad.org.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Решу егэ профиль математика 517739
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Задание 12 № 517747
Ответ а 3 и 27; б 3.
Ege. sdamgia. ru
12.01.2020 13:48:01
2020-01-12 13:48:01
Источники:
Https://ege. sdamgia. ru/test? likes=517739
Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 517746
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.
Ответ: а) −3 и 27; б) −3.
Аналоги к заданию № 517739: 517746 517747 Все
Задание 12 № 517747
Задание 12 № 517746
Б Заметим, что Значит, указанному отрезку принадлежит корень 3.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Запишем исходное уравнение в виде:
Б) Поскольку отрезку принадлежит единственный корень −2.
Ответ: а) −2; 1, б) −2.
Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)
Екатерина, в решении не находили ОДЗ.
В решении было использован равносильный переход, при котором условия достаточно для решения примера
А у Вас ОДЗ найдено с ошибкой.
Задание 12 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Из уравнения получаем:
Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2.
В пункте «а» ответ только 16,вы не проверили ОДЗ
В этом уравнении не нужно искать ОДЗ. Это лишнее действие
Задание 12 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
А) Заметим, что преобразуем исходное уравнение:
Пусть тогда уравнение запишется в виде откуда или
При получим: откуда
При получим: откуда
Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку
Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013
В строчке а) откуда-то взялась «3»
Путём каких преобразований мы получили ответ log(3)5 ?
1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.
2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?
Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.
Задание 12 № 517739
Задание 12 № 502094
Задание 12 502094.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
16.06.2020 6:45:22
2020-06-16 06:45:22
Источники:
Https://dankonoy. com/ege/ege11/archives/10087
Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739
Материал для подготовки к экзамену по математике 1 курс
Материал для подготовки к экзамену по математике 1 курс.
Материал для подготовки к экзамену по математике для 1 курса СПО.
Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»
Логарифмические уравнения
1. Задание 5 № 26646
Найдите корень уравнения
2. Задание 5 № 26647
Найдите корень уравнения
3. Задание 5 № 26648
Найдите корень уравнения
4. Задание 5 № 26649
Найдите корень уравнения
5. Задание 5 № 26657
Найдите корень уравнения
6. Задание 5 № 26658
Найдите корень уравнения
7. Задание 5 № 26659
Найдите корень уравнения
8. Задание 5 № 77380
Решите уравнение
9. Задание 5 № 77381
Решите уравнение
10. Задание 5 № 77382
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.
11. Задание 5 № 315120
Найдите корень уравнения
12. Задание 5 № 315535
Найдите корень уравнения
13. Задание 5 № 525399
Решите уравнение
Тригонометрические уравнения
1. Задание 5 № 26669
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.

Значениям соответствуют положительные корни.
Если, то и
Если, то и
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
2. Задание 5 № 77376
Решите уравнение В ответе напишите наибольший отрицательный корень.
Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.
3. Задание 5 № 77377
Решите уравнение В ответе напишите наименьший положительный корень.
Значениям соответствуют отрицательные корни.
Если, то и
Если, то и
Значениям соответствуют большие положительные корни.
Наименьшим положительным решением является 0,5.
Преобразования числовых логарифмических выражений
1. Задание 9 № 26843
Найдите значение выражения
2. Задание 9 № 26844
Найдите значение выражения
3. Задание 9 № 26845
Найдите значение выражения
4. Задание 9 № 26846
Найдите значение выражения
5. Задание 9 № 26847
Найдите значение выражения
6. Задание 9 № 26848
Найдите значение выражения
7. Задание 9 № 26849
Найдите значение выражения
8. Задание 9 № 26850
Найдите значение выражения
9. Задание 9 № 26851
Найдите значение выражения
10. Задание 9 № 26852
Найдите значение выражения
11. Задание 9 № 26853
Найдите значение выражения
12. Задание 9 № 26854
Найдите значение выражения
13. Задание 9 № 26855
Найдите значение выражения
14. Задание 9 № 26856
Найдите значение выражения
15. Задание 9 № 26857
Найдите значение выражения
16. Задание 9 № 26858
Найдите значение выражения
17. Задание 9 № 26859
Найдите значение выражения
18. Задание 9 № 26860
Найдите значение выражения
19. Задание 9 № 26861
Найдите значение выражения
20. Задание 9 № 26862
Найдите значение выражения
21. Задание 9 № 26882
Найдите значение выражения
22. Задание 9 № 26883
Найдите значение выражения
23. Задание 9 № 26885
Найдите значение выражения
24. Задание 9 № 26889
Найдите значение выражения
25. Задание 9 № 26892
Найдите значение выражения
26. Задание 9 № 26893
Найдите значение выражения
27. Задание 9 № 26894
Найдите значение выражения
28. Задание 9 № 26896
Найдите значение выражения
29. Задание 9 № 77418
Вычислите значение выражения:
30. Задание 9 № 505097
Найдите значение выражения
31. Задание 9 № 509086
Найдите значение выражения
32. Задание 9 № 510939
Найдите значение выражения
33. Задание 9 № 525403
Найдите значение выражения
Вычисление значений тригонометрических выражений
1. Задание 9 № 26775
Найдите, если и
2. Задание 9 № 26776
Найдите, если и
3. Задание 9 № 26777
Найдите, если и
4. Задание 9 № 26778
Найдите, если и
5. Задание 9 № 26779
Найдите, если
6. Задание 9 № 26780
Найдите, если
7. Задание 9 № 26783
Найдите значение выражения, если
8. Задание 9 № 26784
Найдите, если и
9. Задание 9 № 26785
Найдите, если и
10. Задание 9 № 26786
Найдите, если
11. Задание 9 № 26787
Найдите, если
12. Задание 9 № 26788
Найдите, если
13. Задание 9 № 26789
Найдите, если
14. Задание 9 № 26790
Найдите, если
15. Задание 9 № 26791
Найдите, если
16. Задание 9 № 26792
Найдите значение выражения, если
17. Задание 9 № 26793
Найдите значение выражения, если
18. Задание 9 № 26794
Найдите, если
19. Задание 9 № 316350
Найдите, если
20. Задание 9 № 501598
Найдите значение выражения
21. Задание 9 № 502014
Найдите значение выражения
22. Задание 9 № 502045
Найдите значение выражения
23. Задание 9 № 502106
Найдите значение выражения
24. Задание 9 № 502285
Найдите значение выражения
25. Задание 9 № 502305
Найдите значение выражения если и
26. Задание 9 № 504410
Найдите значение выражения:
27. Задание 9 № 504824
Найдите значение выражения
28. Задание 9 № 508966
Найдите если
29. Задание 9 № 510424
Найдите если и
30. Задание 9 № 549336
Найдите если и
Преобразования числовых тригонометрических выражений
1. Задание 9 № 26755
Найдите значение выражения
2. Задание 9 № 26756
Найдите значение выражения
3. Задание 9 № 26757
Найдите значение выражения
4. Задание 9 № 26758
Найдите значение выражения
5. Задание 9 № 26759
Найдите значение выражения
6. Задание 9 № 26760
Найдите значение выражения
7. Задание 9 № 26761
Найдите значение выражения
8. Задание 9 № 26762
Найдите значение выражения
9. Задание 9 № 26763
Найдите значение выражения
10. Задание 9 № 26764
Найдите значение выражения
11. Задание 9 № 26765
Найдите значение выражения
12. Задание 9 № 26766
Найдите значение выражения
13. Задание 9 № 26767
Найдите значение выражения
14. Задание 9 № 26769
Найдите значение выражения
15. Задание 9 № 26770
Найдите значение выражения
16. Задание 9 № 26771
Найдите значение выражения
17. Задание 9 № 26772
Найдите значение выражения
18. Задание 9 № 26773
Найдите значение выражения
19. Задание 9 № 26774
Найдите значение выражения
20. Задание 9 № 77412
Найдите значение выражения
21. Задание 9 № 77413
Найдите значение выражения
22. Задание 9 № 77414
Найдите значение выражения:
23. Задание 9 № 245169
Найдите значение выражения
24. Задание 9 № 245170
Найдите значение выражения
25. Задание 9 № 245171
Найдите значение выражения
26. Задание 9 № 245172
Найдите значение выражения
27. Задание 9 № 501701
Найдите значение выражения
28. Задание 9 № 502994
Найдите значение выражения
29. Задание 9 № 503310
Найдите значения выражения
30. Задание 9 № 510013
Найдите если и
31. Задание 9 № 510312
Найдите значение выражения
32. Задание 9 № 510386
Найдите значение выражения
33. Задание 9 № 510405
Найдите значение выражения
34. Задание 9 № 510824
Найдите значение выражения
35. Задание 9 № 510843
Найдите значение выражения
36. Задание 9 № 525113
Найдите значение выражения
37. Задание 9 № 526009
Найдите значение выражения
Логарифмические и показательные уравнения
1. Задание 13 № 514082
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
2. Задание 13 № 517739
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
3. Задание 13 № 502094
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие промежутку
4. Задание 13 № 516760
А) Решите уравнение:
Б) Определите, какие из его корней принадлежат отрезку
5. Задание 13 № 514623
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
6. Задание 13 № 502053
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
7. Задание 13 № 525377
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
8. Задание 13 № 513605
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
9. Задание 13 № 503127
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
10. Задание 13 № 514081
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащего отрезку
11. Задание 13 № 502999
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].
12. Задание 13 № 528517
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
13. Задание 13 № 550261
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
14. Задание 13 № 555265
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
15. Задание 13 № 555583
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
16. Задание 13 № 561853
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].
17. Задание 13 № 562032
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].
18. Задание 13 № 562757
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Укажите корни этого уравнения, принадлежащие отрезку
Решите уравнение В ответе напишите наименьший положительный корень.
Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»
Б Укажите корни этого уравнения, принадлежащие отрезку.
Multiurok. ru
06.02.2020 18:29:01
2020-02-06 18:29:01
Источники:
Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html
Тренировочная работа №3 статград пробник ЕГЭ 2023 по математике 11 класс 12 тренировочных вариантов МА2210301-МА2210312 с ответами и решением базовый и профильный уровень (БАЗА И ПРОФИЛЬ). Официальная дата проведения работы: 28 февраля 2023 года.
Скачать ответы и решения для вариантов
Пробник ЕГЭ 2023 математика 11 класс статград база
Варианты профильного уровня ЕГЭ 2023 математика статград
Вариант МА2210301 и ответы
1. Каждый день во время конференции расходуется 60 пакетиков чая. Конференция длится 9 дней. В пачке чая 50 пакетиков. Какого наименьшего количества пачек чая хватит на все дни конференции?
2. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
3. В таблице показано расписание пригородных электропоездов по направлению Москва Курская – Крутое – Петушки. Владислав пришёл на станцию Москва Курская в 18:20 и хочет уехать в Петушки на электропоезде без пересадок. Найдите номер ближайшего электропоезда, который ему подходит.
5. В коробке вперемешку лежат чайные пакетики с чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с чёрным чаем в 4 раза больше, чем пакетиков с зелёным. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с чёрным чаем.
8. Некоторые учащиеся 10-х классов школы ходили в апреле на спектакль «Гроза». В мае некоторые десятиклассники пойдут на постановку по пьесе «Бесприданница», причём среди них не будет тех, кто ходил в апреле на спектакль «Гроза». Выберите утверждения, которые будут верны при указанных условиях независимо от того, кто из десятиклассников пойдёт на постановку по пьесе «Бесприданница».
- 1) Каждый учащийся 10-х классов, который не ходил на спектакль «Гроза», пойдёт на постановку по пьесе «Бесприданница».
- 2) Нет ни одного десятиклассника, который ходил на спектакль «Гроза» и пойдёт на постановку по пьесе «Бесприданница».
- 3) Среди учащихся 10-х классов этой школы, которые не пойдут на постановку по пьесе «Бесприданница», есть хотя бы один, который ходил на спектакль «Гроза».
- 4) Найдётся десятиклассник, который не ходил на спектакль «Гроза» и не пойдёт на постановку по пьесе «Бесприданница».
9. На фрагменте географической карты схематично изображены границы деревни Покровское и очертания озёр (площадь одной клетки равна одному гектару). Оцените приближённо площадь озера Малого. Ответ дайте в гектарах с округлением до целого значения.
10. Диагональ прямоугольного экрана ноутбука равна 40 см, а ширина экрана ― 32 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
11. Пирамида Снофру имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 220 м, а высота — 104 м. Сторона основания точной музейной копии этой пирамиды равна 55 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах.
12. В треугольнике ABC проведена биссектриса AL, угол ALC равен 112° , угол ABC равен 106° . Найдите угол ACB . Ответ дайте в градусах.
13. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
15. В школе мальчики составляют 55 % от числа всех учащихся. Сколько в этой школе мальчиков, если их на 50 человек больше, чем девочек?
19. Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из исходного числа вычли второе и получили 3366. В ответе укажите какое-нибудь одно такое исходное число.
20. Имеется два сплава. Первый содержит 45 % никеля, второй — 5 % никеля. Из этих двух сплавов получили третий сплав, содержащий 15 % никеля. Масса первого сплава равна 40 кг. На сколько килограммов масса первого сплава была меньше массы второго?
21. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 2, 3 и 18. Найдите периметр четвёртого прямоугольника.
Вариант МА2210305 и ответы
1. Для покраски 1 кв. м потолка требуется 230 г краски. Краска продаётся в банках по 2 кг. Какое наименьшее количество банок краски нужно для покраски потолка площадью 44 кв. м?
3. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года. Какова налоговая ставка (в рублях за 1 л. с. в год) на автомобиль мощностью 115 л. с.?
5. Помещение освещается двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года обе лампы перегорят.
6. В таблице даны результаты олимпиад по русскому языку и биологии в 9 «А» классе. Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 110 или хотя бы по одному предмету набрано не меньше 60 баллов. Укажите номера учащихся 9 «А» класса, набравших меньше 60 баллов по русскому языку и получивших похвальные грамоты, без пробелов, запятых и других дополнительных символов.
7. На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D. В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
8. Некоторые учащиеся 10-х классов школы ходили в ноябре на оперу «Евгений Онегин». В марте некоторые десятиклассники пойдут на оперу «Руслан и Людмила», причём среди них не будет тех, кто ходил в ноябре на оперу «Евгений Онегин». Выберите утверждения, которые будут верны при указанных условиях независимо от того, кто из десятиклассников пойдёт на оперу «Руслан и Людмила».
- 1) Каждый учащийся 10-х классов, который не ходил на оперу «Евгений Онегин», пойдёт на оперу «Руслан и Людмила».
- 2) Нет ни одного десятиклассника, который ходил на оперу «Евгений Онегин» и пойдёт на оперу «Руслан и Людмила».
- 3) Найдётся десятиклассник, который не ходил на оперу «Евгений Онегин» и не пойдёт на оперу «Руслан и Людмила».
- 4) Среди учащихся 10-х классов этой школы, которые не пойдут на оперу «Руслан и Людмила», есть хотя бы один, который ходил на оперу «Евгений Онегин».
9. План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
10. Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец лестницы? Ответ дайте в метрах.
11. Прямолинейный участок трубы длиной 4 м, имеющей в сечении окружность, необходимо покрасить снаружи (торцы трубы открыты, их красить не нужно). Найдите площадь поверхности, которую необходимо покрасить, если внешний обхват трубы равен 19 см. Ответ дайте в квадратных сантиметрах.
12. В треугольнике ABC стороны AC и BC равны. Внешний угол при вершине B равен 146° . Найдите угол C. Ответ дайте в градусах.
13. Даны два шара радиусами 4 и 2. Во сколько раз объём большего шара больше объёма меньшего?
15. Число больных гриппом в школе уменьшилось за месяц в пять раз. На сколько процентов уменьшилось число больных гриппом?
19. Найдите пятизначное число, кратное 15, любые две соседние цифры которого отличаются на 3. В ответе укажите какое-нибудь одно такое число.
20. Теплоход, скорость которого в неподвижной воде равна 19 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 43 часа после отправления из него. Сколько километров проходит теплоход за весь рейс?
21. На кольцевой дороге расположены четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 55 км, между А и В — 40 км, между В и Г — 40 км, между Г и А — 30 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.
Вариант МА2210309 и ответы
2. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
3. В группе 16 человек, среди них — Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
4. Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
9. Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
13. Основанием правильной пирамиды PABCD является квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если AB = 30.
15. По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16. В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M . Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22 .
18. У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький — 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять. а) Может ли Аня купить 24 конверта? б) Может ли Аня купить 29 конвертов? в) Какое наибольшее число конвертов может купить Аня?
Вариант МА2210311 и ответы
1. Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
2. Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 78. Найдите площадь поверхности шара.
3. В магазине в среднем из 120 сумок 15 имеют скрытые дефекты. Найдите вероятность того, что выбранная в магазине сумка окажется со скрытыми дефектами.
4. Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
9. Игорь и Паша, работая вместе, могут покрасить забор за 40 часов. Паша и Володя, работая вместе, могут покрасить этот же забор за 48 часов, а Володя и Игорь, работая вместе, — за 60 часов. За сколько часов мальчики покрасят забор, работая втроём?
13. Основанием правильной пирамиды PABCD является квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если AB = 24 .
15. По вкладу «А» банк в конце каждого года планирует увеличивать на 11 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16. В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M . Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 18.
18. У Ани есть 400 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 22 рубля, а маленький — 17 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять. а) Может ли Аня купить 19 конвертов? б) Может ли Аня купить 23 конверта? в) Какое наибольшее число конвертов может купить Аня?
Работы статград по математике для 9 и 11 класса
Share the post «Математика 11 класс ЕГЭ 2023 статград база и профиль варианты и ответы с решением»
- VKontakte
Метки: ЕГЭ 2023заданияматематика 11 классответыстатградтренировочная работа
B вариантах ЕГЭ по математике 2022 года задача с экономическим содержанием, № 15, оценивалась в 2 первичных балла. B прошлые годы она стоила дороже –целых 3 первичных балла.
Зато и набор тем в задании 15 в этом году был сокращенным: только задачи на кредиты. И никаких заданий на оптимизацию.
Напоминаем, что задачи на кредиты бывают двух основных типов. О решении «экономических» задач – читайте в этом разделе.
Первый тип, аннуитет. Кредит погашается равными платежами или есть информация о платежах.
Подробно об этой схеме погашения кредита – здесь.
Bторой тип, схема с дифференцированными платежами. Сумма долга уменьшается равномерно, или же есть информация об изменении суммы долга. B задачах этого типа часто применяются формулы суммы арифметической прогрессии.
Подробно о схеме с дифференцированными платежами здесь.
На этой странице мы разберем задачи по финансовой математик, предложенные на ЕГЭ-2022 в разных регионах России.
1. ЕГЭ-2022, Москва
B июле 2022 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Найдите сумму кредита, если известно, что кредит будет полностью выплачен за 3 года, причем в первый и второй год будет выплачено по 300 тыс. руб., а в третий 417,6 тыс. руб.
Решение:
Пусть S — сумма кредита,
р — процент банка,
— коэффициент, показывающий во сколько раз увеличивается сумма долга после начисления процентов,
x=300 тыс. руб. – платеж в первый и второй годы,
– платеж в третий год.
Составим схему погашения кредита.
– сумма долга после первого начисления процентов,
— сумма долга после первого платежа,
— сумма долга после второго начисления процентов,
— сумма долга после второго платежа,
— сумма долга после третьего начисления процентов,
— сумма долга после третьего платежа.
отсюда
Будем вести расчеты в тысячах рублей.
тыс.руб.
Ответ: 700 000 рублей
2. Дальний Bосток
B июле 2016 г. планируется взять кредит на 5 лет в размере 1050 тысяч рублей.
Условия его возврата таковы:
— Каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— B июле 2017, 2018 и 2019 годов долг остается равным 1050 тысяч рублей,
— выплаты в 2020 и 2021 годах равны по X тысяч рублей,
— к июлю 2021 года долг будет выплачен полностью.
Найдите общую сумму выплат за 5 лет.
Решение:
Пусть A = 1050 тыс. рублей – сумма кредита,
,
B 2017 – 2019 годы долг остается равен 1050 тыс. рублей,
B 2020 и 2021 годы выплаты равны по X тыс. рублей.
Составим таблицу погашения долга.
| Год | Долг | Долг после начисления процентов | Выплаты | Остаток долга |
| 2017 | ||||
| 2018 | ||||
| 2019 | ||||
| 2020 | ||||
| 2021 |
Поскольку к июлю 2021 года долг будет выплачен полностью, то
отсюда найдем X
605 ( тыс. рублей).
Общая сумма выплат за 5 лет составит:
тыс рублей.
Ответ: 1525тыс. рублей.
3. Досрочная волна, Санкт-Петербург
15-го декабря планируется взять кредит в банке на 19 месяцев. Условия возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 18-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 19-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 18-го месяца, если общая сумма выплат после полного погашения кредита составит 1209 тысяч рублей?
Решение:
Обозначим S — сумму кредита,
n = 19 месяцев,
p = 2%,
— коэффициент, показывающий, во сколько раз увеличивается долг после начисления процентов,
x — сумма, на которую уменьшается долг с 1-го и по 18-й месяц; x=50тыс. руб.
составим схему погашения кредита.
Общая сумма выплат B = 1209 тыс. рублей.
Bыплаты:
Общая сумма выплат:
Найдем сумму арифметической прогрессии.
тыс.руб.
По условию, тыс. руб.
Ответ: 100 тысяч рублей.
4. Основная волна, Bосток
B июле 2026 года планируется взять кредит на пять лет в размере 3,3 млн руб. Условия его возврата таковы:
– каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле 2027, 2028 и 2029 годах долг остаётся равен 3,3 млн руб.;
– платежи в 2030 и 2031 годах должны быть равны;
– к июлю 2031 года долг должен быть выплачен полностью.
Найдите разницу между первым и последним платежами.
Решение:
Bведем переменные:
S=3,3 млн. руб. – сумма кредита;
p=20% — процентная ставка;
— коэффициент, показывающий, во сколько раз увеличивается сумма долга после начисления процентов.
Рисуем схему погашения кредита:
Общая сумма выплат:
Кроме того, долг был полностью погашен последней выплатой .
Это значит, что
и тогда первая выплата: а последняя выплата Y, и разница между последней и первой выплатами:
млн. рублей
Ответ: 1,5 млн. рублей
5. Основная волна, Bосток
B июле 2022 года планируется взять кредит на пять лет в размере 1050 тыс. рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года, необходимо выплатить одним платежом часть долга;
– в июле 2023, 2024 и 2025 годах сумма долга остается равной 1050 тыс. руб.;
– выплаты в 2026 и 2027 годах равны;
– к июлю 2027 года долг будет выплачен полностью.
На сколько рублей последняя выплата будет больше первой?
Решение:
Bведем переменные:
S=1050 тыс. руб. – сумма кредита;
p=10% — процентная ставка;
— коэффициент, показывающий во сколько раз, увеличивается долг после начисления процентов
Рисуем схему погашения кредита:
Общая сумма выплат:
Кроме того, долг был полностью погашен последней выплатой .
Это значит, что
и тогда первая выплата: а последняя выплата Y, и разница между последним и первым платежами:
тысяч рублей.
Ответ: 500 тысяч рублей
6. Санкт-Петербург, Москва
B июле 2026 года планируется взять кредит на три года. Условия его возврата таковы:
– каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– платежи в 2027 и в 2028 годах должны быть по 300 тыс. руб.;
– к июлю 2029 года долг должен быть выплачен полностью.
Известно, что платёж в 2029 году будет равен 417,6 тыс. руб. Какую сумму планируется взять в кредит?
Решение:
Конечно, это задача первого типа. Есть информация о платежах. B условии сказано, что кредит будет выплачен сначала двумя равными платежами, а затем третьим платежом выплачивается остаток долга.
Bведем обозначения:
S тыс. рублей — сумма долга. Расчеты будем вести в тысячах рублей.
p=20% — процент банка,
— коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,
X=300 тыс. руб – сумма ежегодного платежа в 2027 и 2028 годах;
Y=417,6 тыс. руб. — платеж в 2029 году
Составим схему погашения кредита.
Sk — сумма долга увеличивается в k раз,
Клиент вносит на счет сумму X в счет погашения кредита, и сумма долга уменьшается на X . Bот что получается:
Снова долг увеличивается в k раз и сумма долга уменьшается на X . Bот что получается: left(Sk-Xright)k-X
И в третий раз увеличивается долг в k раз и сумма долга уменьшается на Y. Bот что получается:
Раскроем скобки:
Что же, можно подставить численные данные.
тыс. руб.
Ответ: 700 тысяч рублей
7. Основная волна, Москва, Санкт-Петербург
B июле 2026 года планируется взять кредит на три года в размере 634,5 тыс. руб. Условия его возврата таковы:
– каждый январь долг будет возрастать на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– платёж в 2027 и 2028 годах должен быть по 100 тыс. руб.;
– к июлю 2029 года долг должен быть выплачен полностью.
Найдите сумму всех платежей после полного погашения кредита.
Решение:
Это задача первого типа. Есть информация о платежах. B условии сказано, что кредит будет выплачен двумя равными платежами и третьим весь остаток долга.
Bведем обозначения:
S=634,5 тыс. рублей — сумма долга. Расчеты будем вести в тысячах рублей.
p=10% — процент банка,
— коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,
X=100 тыс. руб – сумма ежегодного платежа в 2027 и 2028 годах;
Y тыс. руб. — платеж в 2029 году
Составим схему погашения кредита.
Sk — сумма долга увеличивается в k раз,
Клиент вносит на счет сумму X в счет погашения кредита, и сумма долга уменьшается на X . Bот что получается:
Снова долг увеличивается в k раз и сумма долга уменьшается на X . Bот что получается:
И в третий раз увеличивается долг в k раз и сумма долга уменьшается на Y. Bот что получается:
Раскроем скобки:
Подставим численные данные.
тыс. руб.
Сумма всех платежей: тыс. руб.
Ответ: 813,5195тыс.рублей = 813519,5 рублей.
Эта задача отличается от предыдущих только вычислительными трудностями. Получается, что задачи неравноценны: в одних вариантах удачные численные данные, в других – нет. Не повезло тем, кому она досталась. Пришлось считать сумму выплат с точностью до 50 копеек.
8. ЕГЭ, резервная волна
15-го января планируется взять кредит в банке на девять месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r процентов по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.
Решение:
Это задача на дифференцированные платежи с равномерным погашением долга.
Пусть S тыс. рублей – сумма кредита;
n=9 месяцев – срок кредита;
r% — процент банка,
— коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов,
— ежемесячная выплата основного долга
— сумма выплат
Составим схему погашения кредита.
Ежемесячные выплаты:
Общая сумма выплат:
Найдём
Мы нашли суммы арифметических прогрессий:
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит.
Ответ: 5
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Финансовая математика на ЕГЭ-2022. Задача 15» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Экономическая задача 17 на проценты из 87 варианта Ларина 2015
№ задачи в базе 909
Вкладчик внёс некоторую сумму под определённый процент в Сбербанк. Через год он взял половину полученной суммы и положил в коммерческий банк, процент годовых которого в 32 раза выше чем в сбербанке. Ещё через год сумма вкладчика в коммерческом банке превысила первоначальную на 4 %. Какой процент годовых в сбербанке?
Ответ:
0.125 %
ФИПИ 2023 🔥 …
Примечание: Экономическая задача 17 на проценты из 87 варианта Ларина 2015
Рейтинг сложности задачи:
ЕГЭ 2022 ФИПИ. Вариант 3. Задача 15.
По вкладу «А» банк в конце каждого года увеличивает на 20 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает эту сумму на 12 % в течение каждого из первых двух лет. Найдите наибольшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет менее выгоден, чем вклад «А».
Решение.
Обозначим искомое число процентов через r.
Оформим рассуждения по условию задачи в виде таблицы.
Так как вклад «Б» будет менее выгоден, чем вклад «А», то справедливо неравенство:
1,122 ∙S + 1,122 ∙S ∙0,01r < 1,23 ∙S.
Разделим обе части неравенства на S.
1,122 ∙0,01r < 1,23 -1,122;
1,2544 ∙0,01r < 1,728 -1,2544;
1,2544 ∙0,01r < 0,4736;
1,2544r < 47,36;
r < 47,36 : 1,2544;
r < 37,75…
r = 37 – наибольшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет менее выгоден, чем вклад «А».
Ответ: 37.
Экономические задачи ЕГЭ Это страница с нужной вам задачей
ЕГЭ 2022 ФИПИ. Вариант 4. Задача 15.
По вкладу «А» банк в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает эту сумму на 14 % в течение каждого из первых двух лет. Найдите наименьшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет более выгоден, чем вклад «А».
Решение.
Обозначим искомое число процентов через r.
Оформим рассуждения по условию задачи в виде таблицы.
Так как вклад «Б» будет менее выгоден, чем вклад «А», то справедливо неравенство:
1,142 ∙S + 1,142 ∙S ∙0,01r > 1,13 ∙S.
Разделим обе части неравенства на S.
1,142 ∙0,01r > 1,13 -1,142;
1,2996 ∙0,01r > 1,331 -1,2996;
1,2996 ∙0,01r > 0,0304;
1,2996 > 3,04;
r > 3,04 : 1,2996;
r > 2,33…
r = 3 – наименьшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет более выгоден, чем вклад «А».
Ответ: 3.
ЕГЭ 2022 ФИПИ. Вариант 17. Задача 15.
Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоил 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и туже сумму, а в конце месяца пакет дорожает, но не более чем на 30 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
Решение.
1-й месяц. Александр не смог купить акции за 100 тысяч рублей. Он отложил Х тысяч рублей
2-й месяц. Акции стоят 1,3 ∙100 тыс. рублей. Александр отложил Хтыс. рублей.
3-й месяц. Акции стоят 1,32 ∙100 тыс. рублей. Александр отложил Х тыс. рублей.
4-й месяц. Акции стоят 1,33 ∙100 тыс. рублей. Александр отложил Хтыс. рублей.
…………………………………………………………………………………………………
n-й месяц. Акции стоят 1,3n-1 ∙100 тыс. рублей. Александр отложил Х тыс. рублей.
Итак, за n месяцев Александр отложил nХ тысяч рублей, и наконец, может купить акции, т.е.
Нужно найти минимальное целое значение n, при котором производная будет менять знак с минуса на плюс. Это значение n и будет точкой минимума функции
Производная отрицательна при n ∙ ln1,3 -1 < 0. Решаем неравенство:
ln1,3n < 1;
ln1,3n < lne;
1,3n < e. Помним, что е ≈ 2,72…
Так как n – количество месяцев, то будем подбирать целое значение показателя степени так, чтобы знак неравенства поменялся.
Если n = 2, то 1,32 = 1,69 < e;
Если n = 3, то 1,33 = 2,197 < e;
Если n = 4, то 1,34 = 2,8561 > e.
Таким образом, производная X’(n) поменяет знак с минуса на плюс на промежутке, содержащем n = 4. Это наименьшее целое значение n, при котором функция
Это означает, что Александру достаточно было откладывать по 54925 рублей в течение четырёх месяцев, чтобы купить пакет акций быстрорастущей компании.
Ответ: 54925 рублей.
ЕГЭ 2022 ФИПИ. Вариант 18. Задача 15.
Сергей хочет купить пакет акций быстрорастущей компании. В начале года у Сергея не было денег на покупку акций, а пакет стоил 160 000 рублей. В середине каждого месяца Сергей откладывает на покупку пакета акций одну и туже сумму, а в конце месяца пакет дорожает, но не более чем на 25 %. Какую наименьшую сумму нужно откладывать Сергею каждый месяц, чтобы через некоторое время купить желаемый пакет акций?
Решение.
1-й месяц. Сергей не смог купить акции за 160 тысяч рублей. Он отложил Х тысяч рублей
2-й месяц. Акции стоят 1,25 ∙160 тыс. рублей. Александр отложил Х тыс. рублей.
3-й месяц. Акции стоят 1,252 ∙160 тыс. рублей. Александр отложил Х тыс. рублей.
4-й месяц. Акции стоят 1,253 ∙160 тыс. рублей. Александр отложил Х тыс. рублей.
…………………………………………………………………………………………………
n-й месяц. Акции стоят 1,25n-1 ∙160 тыс. рублей. Александр отложил Х тыс. рублей.
Итак, за n месяцев Александр отложил nХ тысяч рублей, и наконец, может купить акции, т.е.
Нужно найти минимальное целое значение n, при котором производная будет менять знак с минуса на плюс. Это значение n и будет точкой минимума функции
Производная отрицательна при n ∙ ln1,25 -1 < 0. Решаем неравенство:
ln1,25n < 1;
ln1,25n < lne;
1,25n < e. Помним, что е ≈ 2,72…
Так как n – количество месяцев, то будем подбирать целое значение показателя степени так, чтобы знак неравенства поменялся.
Если n = 2, то 1,252 = 1,5625 < e;
Если n = 3, то 1,253 ≈ 1,953 < e;
Если n = 4, то 1,254 ≈ 2,4 < e;
Если n = 5, то 1,255 ≈ 3,05 > e.
Таким образом, производная X’(n) поменяет знак с минуса на плюс на промежутке, содержащем n = 5. Это наименьшее целое значение n, при котором функция
Это означает, что Сергею достаточно было откладывать по 78125 рублей в течение пяти месяцев, чтобы купить пакет акций быстрорастущей компании.
Ответ: 78125 рублей.
ЕГЭ 2022 ФИПИ. Вариант 19. Задача 15.
Цена ценной бумаги на конец года вычисляется по формуле
S=1,1So + 2000, где So – цена этой ценной бумаги на начало года в рублях. Максим может приобрести ценную бумагу, а может положить деньги на банковский счёт, на котором сумма увеличивается за год на 12 %. В начале любого года Максим может продать бумагу и положить все вырученные деньги на банковский счёт, а также снять деньги с банковского счёта и купить ценную бумагу. В начале 2021 года у Максима было 80 тыс. рублей, которые он может положить на банковский счёт или может приобрести на них ценную бумагу. Какая наибольшая сумма может быть у Максима через четыре года? Ответ дайте в рублях.
Решение.
По условию у Максима 80 тыс. рублей, которые он может или положить на счёт или купить ценную бумагу, т.е. So = 80 тыс. рублей.
Если в начале 2021 года Максим положит деньги на банковский счёт, то на конец года у него будет 1,12 So.
Запишем эту сумму в виде: 1,1So + 0,02So и сравним её с ценой ценной бумаги на конец года: 1,1So + 2000.
Так как 0,02So = 0,02 ∙ 80000 = 1600 < 2000, то выгоднее купить ценную бумагу.
Итак, если в начале 2021 года Максим купит ценную бумагу, то на конец года у него будет 1,1 ∙ 80000 + 2000 = 90000 рублей. Оставить ценную бумагу или продать?
Проверим значение 0,02So = 0,02 ∙ 90000 = 1800 < 2000. Значит, продавать ценную бумагу рано.
На конец 2022 года у Максима будет
1,1 ∙ 90000 + 2000 = 101000 рублей.
Оцениваем значение 0,02So = 0,02 ∙ 101000 = 2020 > 2000.
Следовательно, в начале 2023 года Максиму выгоднее продать ценную бумагу и положить деньги на банковский счёт.
На конец 2023 года у него может быть 1,12So = 1,12 ∙ 101000 = 113120 рублей.
На конец 2024 года у Максима может быть 1,12So = 1,12 ∙ 113120 = 126694,4 рублей.
Ответ: 126694,4 рублей.
ЕГЭ 2022 ФИПИ. Вариант 33. Задача 15.
15 июня планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев. Условия его возврата таковы:
— 11-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа 15-го месяца долг составит 100 тысяч рублей;
— к 15-му числу 16-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1636 тысяч рублей.
Решение.
За 15 месяцев банку заплатили 1300-100=1200 тысяч рублей основного долга,
что составляет 1200 : 15 = 80 тысяч рублей – сумму, на которую ежемесячно уменьшается долг.
Однако, r % ежемесячно нужно выплачивать с суммы остатка долга, начиная с выданной суммы кредита 1300 тысяч рублей, а затем с суммы за вычетом 80 тысяч рублей ежемесячно. Проценты считаются так:
1 месяц. 1300 ∙ 0,01r = 13r;
2 месяц (1300-80) ∙ 0,01r = 1220 ∙ 0,01r = 12,2r;
3 месяц (1220-80) ∙ 0,01r =1140 ∙ 0,01r = 11,4r;
4 месяц (1140-80) ∙ 0,01r =1060 ∙ 0,01r = 10,6r и так далее.
Заметим, что последовательность чисел 13r; 12,2r; 11,4r; 10,6r и т.д. представляет собой арифметическую прогрессию с первым членом
а1 = 13r и разностью d=-0,8r. Нам нужно найти сумму 15-ти членов этой арифметической прогрессии. Воспользуемся формулой:
Итак, банку придётся отдать 1200 тысяч рублей плюс 111r тысяч рублей процентов за первые 15 месяцев и ещё за 16-й месяц долг 100 тысяч рублей плюс проценты с этой суммы, т.е. r % от 100 тысяч (это 0,01r ∙ 100 = r). Общая сумма выплат по условию равна 1636 тысяч рублей. Получим равенство:
1200+111r+100+r = 1636;
112r = 336;
r = 3.
Ответ: 3%.
ЕГЭ 2022 ФИПИ. Вариант 34. Задача 15.
15 мая планируется взять кредит в банке на 17 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 16-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 17-го месяца кредит должен быть полностью погашен. Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1472 тысячи рублей?
Решение.
Обозначим через Х сумму, которую нужно будет выплатить банку к 15-му числу 17-го месяца в счёт основного долга.
За 16 месяцев банку заплатят 16 ∙ 50 = 800 тысяч рублей основного долга.
Значит, 1472-800=672 тысячи рублей – это проценты за 16 месяцев,
а также за 17-й месяц сумма Х с процентами, т.е. Х+0,02Х=1,02Х.
Итак, взятая сумма кредита (800+Х) тысяч рублей, и нам надо подсчитать проценты с этой суммы за первые 16 месяцев кредитования.
Рассуждаем: в первый месяц банк начислит 2 % на сумму (800+Х), во второй месяц 2 % на сумму (750+Х), затем на (700+Х), на (650+х) и т.д. А в 16-й месяц кредитования банк начислит 2 % на сумму (50+Х) тысяч рублей.
Таким образом, нам надо найти значение выражения:
0,02 ∙ ((800+Х)+(750+Х)+(700+Х)+…+(50+Х)).
Сумма в скобках – это сумма арифметической прогрессии с первым членом
Это проценты за первые 16 месяцев кредитования.
Итак, получим равенство:
1,02Х+136+0,32Х= 672;
1,34Х=672-136;
1,34Х=536;
Х=400.
За 17 месяц в счёт основного долга нужно выплатить 400 тысяч рублей. Тогда в кредит планируется взять 800+400=1200 тысяч рублей.
Ответ: 1 200 000 рублей.
ЕГЭ 2022 ФИПИ. Вариант 36. Задача 15.
31 декабря 2014 года Михаил взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Михаил переводит в банк 2928200 рублей. Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?
I способ решения. Если кредит на S рублей полностью погашается за n ежегодных выплат, равных X1, X2, X3, …, Xn, осуществленных после начисления r% по вкладу, то применяем формулу:
Кредит Михаила S полностью погашается за 4 платежа по 2928200 рублей каждый, после начисления r = 10% годовых каждый год на оставшуюся сумму долга. Таким образом, так как X1=X2=X3=X4=2928200, получаем сумму взятого кредита:
Окончательно S = 2000000 ∙ 4,641 = 9282000 рублей.
Ответ: 9282000.
II способ решения (традиционный).
Пусть Михаил взял в банке S рублей.
1) Банк начислил на эту сумму 10% и долг составил 1,1S рублей. Михаил выплатил 2928200 рублей. Долг составил (1,1S-2928200) рублей.
2) Банк начислил 10% и долг составил 1,1(1,1S-2928200) рублей. Михаил выплатил 2928200 рублей. Долг составил (1,1(1,1S-2928200)-2928200) рублей.
3) Банк начислил 10% и долг составил 1,1(1,1(1,1S-2928200)-2928200) рублей. Михаил выплатил 2928200 рублей.
Долг составил (1,1(1,1(1,1S-2928200)-2928200)-2928200) рублей.
4) Банк начислил 10% и долг составил
1,1(1,1(1,1(1,1S-2928200)-2928200)-2928200). Банк выплатил 2928200 рублей, и долг был полностью погашен. Составим равенство:
1,1(1,1(1,1(1,1S-2928200)-2928200)-2928200)-2928200=0;
1,14⋅ S-1,13⋅2928200-1,12⋅2928200-1,1⋅2928200-2928200=0;
1,4641S-1,331⋅2928200-1,21⋅2928200-1,1⋅2928200-2928200=0;
1,4641S-4,641⋅2928200=0;
1,4641S=4,641⋅2928200;
S=4,641⋅2000000;
S=9 282000.
Ответ: 9 282 000.
Примечание. Если обозначить 2 928 200 рублей через Х, то записи решения были бы короче.
Смотрите сами.
Итак, обозначим каждый из четырёх ежегодных платежей через Х.
Пусть Х=2928200 рублей, а взял Михаил в банке S рублей.
1) Банк начислил на эту сумму 10% и долг составил 1,1S. Михаил выплатил Х рублей. Долг составил 1,1S-Х.
2) Банк начислил 10% и долг составил 1,1(1,1S-Х)=1,12 ∙ S-1,1X. Михаил выплатил X. Долг составил 1,12 ∙ S-1,1X-X.
3) Банк начислил 10% и долг составил 1,1(1,12∙S-1,1X-X)=1,13∙S-1,12X-1,1X. Михаил выплатил X рублей.
Долг составил 1,13∙S-1,12X-1,1X-X.
4) Банк начислил 10% и долг составил
1,1(1,13∙S-1,12X-1,1X-X)=1,14∙S-1,13X-1,12 X-1,1X.
Банк выплатил X, и долг был полностью погашен. Получаем равенство:
1,14∙S-1,13X-1,12 X-1,1X-Х=0.
1,14∙S=1,13X+1,12 X+1,1X+Х=0;
1,4641S=1,331X+1,21X+1,1X+X;
1,4641S=4,641X;
S=4,641X :1,4641. Так как Х=2928200, то
S=4,641∙2928200 :1,4641;
S=4,641⋅2000000;
S=9 282 000.
Ответ: 9 282 000.
Ниже простые и очень полезные формулы:
k2 ⋅ S = (k +1) ⋅ Х . ( I**)
k 3 ⋅ S = (k2 + k + 1) ⋅ Х. ( II**)
k 4 ⋅ S = (k3 + k2 + k + 1) ⋅ Х. ( III**)
Здесь: S – сумма кредита, выданная банком под r%, которая полностью погашается платежами по Х рублей каждый. Значение k=1+0,01r. Показатель степени с основанием k – это количество платежей по Х рублей.
В рассмотренной задаче мы рассуждениями получили формулу ( III**).
Навигация
17. Сложные задачи прикладного характера
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи про банковский вклад
Банковский вклад — это сумма денег, переданная банку на хранение с целью получить доход в виде начисленных процентов.
Раз в какой-то промежуток времени (в задачах это, как правило, месяц или год) банк начисляет на текущую сумму некоторое количество (r%) процентов.
Раз в год после начисления процентов клиент, как правило, имеет право доложить на счет любую сумму денег. Также клиент имеет право снимать со счета любую сумму (естественно, не превышающую имеющуюся). Время, когда он может это сделать, указывается в задаче.
Пример: В январе (2014) года клиент положил в банк (30,000) рублей под (10%) годовых, которые банк начисляет раз в год в декабре. Сколько рублей будет на счете у клиента в январе (2017) года?
То, что банк начисляет на текущую сумму (10%), значит, что после начисления процентов сумма будет составлять (110%) от суммы, находящейся на счете до начисления процентов.
Составим таблицу: [begin{array}{|l|c|c|}
hline text{Год}&text{Сумма на счете до начисления} %&text{Сумма на счете после начисления} %\
&text{(январь)}&text{(декабрь)}\
hline 2014&30,000&1,1cdot 30,000\
hline 2015&1,1cdot 30,000&1,1^2cdot 30,000\
hline 2016&1,1^2cdot 30,000&1,1^3cdot 30,000\
hline
end{array}]
Таким образом, в декабре (2016) года после начисления процентов на счете у клиента будет (1,1^3cdot 30,000) рублей. Эта же сумма будет у него на счете и в январе (2017) года (т.к. проценты начисляются только в декабре).
Значит, ответом будет (39,930) рублей.
Задание
1
#2934
Уровень задания: Равен ЕГЭ
Клиент вложил некоторую сумму под (10%) годовых, начисляемых на вклад раз в год. Известно, что в конце первого года (после начисления процентов) он снял со своего счета (10%) от имеющейся на тот момент суммы, а в конце второго года (также после начисления процентов) он доложил на счет (10%) от имеющейся суммы. Определите, в конце третьего года (после начисления процентов) увеличилась или уменьшилась сумма на счете после таких манипуляций по сравнению с первоначальным вкладом и на сколько процентов.
Пусть клиент сделал вклад в размере (A) рублей. Тогда после начисления процентов в первый год на счете у него уже будет (1,1A) рублей. Так как он снял (10%) от этой суммы, то у него осталось (90%) или (0,9cdot 1,1A) рублей.
Тогда в конце второго года банк снова начислил проценты и сумма на счете стала равна (1,1cdot (0,9cdot 1,1A)) рублей. Далее он доложил (10%), следовательно, на счете у него стало (110%) или (1,1cdot (1,1cdot (0,9cdot 1,1A))) рублей.
На третьем году после начисления процентов у него стало (1,1cdot
1,1cdot (1,1cdot (0,9cdot 1,1A))) рублей.
Удобно следить за данными операциями, составив таблицу: [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& 1,1A& -,0,1cdot (1,1A)\
hline 2&0,9cdot (1,1A)& 1,1cdot (0,9cdot 1,1A)& +,0,1cdot (1,1cdot 0,9cdot 1,1A)\
hline 3& 1,1cdot (1,1cdot 0,9cdot 1,1A)& 1,1cdot (1,1cdot 1,1cdot 0,9cdot 1,1A)&\
hline
end{array}]
Следовательно, на счете у него стало [1,1^4cdot 0,9A=1,31769A,] что больше первоначального вклада (A) на (31,769%).
Ответ: 31,769
Задание
2
#2841
Уровень задания: Равен ЕГЭ
Владелец автосалона решил разделить свой капитал на (3) части и вложить их в (3) различных банка, причем годовые процентные ставки в этих банках относятся как (2:3:5). В каком отношении он должен поделить свой капитал, чтобы через год чистая прибыль от вкладов во всех трех банках была одинакова?
Обозначим за (2y) процентную ставку в первом банке, тогда в остальных банках ставки будут (3y%) и (5y%). Пусть вклад в первый банк составил (A_{1}), во второй – (A_{2}), в третий – (A_{3}). Составим таблицу:
[begin{array}{|l|c|c|c|}
hline text{Банк}&text{Размер вклада до} &text{Размер вклада после} &text{Чистая прибыль}\
&text{начисления }%&text{начисления }%&\
hline &&&\
1&A_{1} &dfrac{100+2y}{100}cdot A_{1}&A_{1}cdot left(dfrac{100+2y}{100}-1right)\
&&&\
hline &&&\
2&A_{2} &dfrac{100+3y}{100}cdot A_{2}&A_{2}cdot left(dfrac{100+3y}{100}-1right)\
&&&\
hline &&&\
3&A_{3} &dfrac{100+5y}{100}cdot A_{3}&A_{3}cdot left(dfrac{100+5y}{100}-1right)\
&&&\
hline
end{array}]
Т.к. чистая прибыль во всех банках должна быть одинакова, то
(A_{1}cdot left(dfrac{100+2y}{100}-1right)=A_{2}cdot
left(dfrac{100+3y}{100}-1right)=A_{3}cdot
left(dfrac{100+5y}{100}-1right)
Leftrightarrow )
(2A_{1}=3A_{2}=5A_{3} Rightarrow A_{1}:A_{2}:A_{3}=15:10:6).
Ответ:
(15:10:6).
Задание
3
#2840
Уровень задания: Равен ЕГЭ
Алексей решил внести некоторую сумму (A) рублей в банк под целое число (y) процентов годовых. Каждый год после начисления процентов он дополнительно вносит на счет сумму, равную половине от той, которая находилась на счете у Алексея в начале текущего года. Какая наименьшая процентная ставка (y) должна быть у банка, чтобы к концу третьего года (после внесения третьей дополнительной суммы) сумма на счете была не менее (8A) рублей?
Составим таблицу, обозначив за (t=dfrac{100+y}{100}): [begin{array}{|l|c|c|c|}
hline text{Год} & text{Сумма на счете} & text{Сумма на счете} & text{Сумма на счете}\
& text{до начисления }% & text{после начисления }% & text{после дополнительного взноса} \
hline &&&\
1 & A & tA & tA+frac{1}{2}A\
&&&\
hline &&&\
2 & tA+frac{1}{2}A & t(tA+frac{1}{2}A) & t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A) \
&&&\
hline &&&\
3 & t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A) & t(t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A)) & t(t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A))+\
&&&\
&&& +frac{1}{2}(t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A))\
&&&\
hline
end{array}]
По условию итоговая сумма на счете должна быть не менее (8A
Rightarrow)
(t(t(tA+frac{A}{2})+frac{1}{2}(tA+frac{1}{2}A))+frac{1}{2}(t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A))
geqslant 8A)
Преобразовав левую часть неравенства, получим:
(t^3A+dfrac{3t^2A}{2}+dfrac{3tA}{4}+dfrac{A}{8} geqslant 8A
Longleftrightarrow dfrac{A(2t+1)^3}{8} geqslant 8A)
Решив данное неравенство, получим: (t geqslant 1,5 Rightarrow y
geqslant
50)
Таким образом, наименьшее целое значение (y=50%).
Ответ:
(50%).
Задание
4
#2936
Уровень задания: Равен ЕГЭ
В банке оформили два одинаковых вклада под один и тот же процент годовых на 3 года. По первому вкладу были проделаны следующие манипуляции: в конце первого года (после начисления процентов) со счета было снято (20%) от имеющейся там суммы, а в конце второго (после начисления процентов) доложено (30%) от имеющейся там суммы. По второму вкладу: в конце первого года (после начисления процентов) на счет было доложено (20%) от имеющейся там суммы, а в конце второго (после начисления процентов) снято (30%) от имеющейся там суммы.
Определите, на каком из двух счетов в конце третьего года после проделанных действий оказалось больше денег? Найдите отношение суммы, находящейся на первом счете, к сумме, находящейся на втором счете.
Пусть оба вклада были размером (A) рублей. Пусть после начисления процентов вклад увеличивался в (t) раз.
Составим таблицу для первого вклада: [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& tA
& -,0,2cdot (tA)\
hline 2&0,8cdot (tA)& tcdot (0,8cdot tA)
& +,0,3cdot (tcdot 0,8cdot tA)\
hline 3& 1,3cdot (tcdot 0,8cdot tA)& tcdot (1,3cdot tcdot 0,8cdot tA)&\
hline
end{array}]
Следовательно, в конце третьего года на счете было [1,3cdot
0,8cdot t^3A=1,04t^3A quad {small{text{рублей.}}}]
Составим таблицу для второго вклада: [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& tA
& +,0,2cdot (tA)\
hline 2&1,2cdot (tA)& tcdot (1,2cdot tA)
& -,0,3cdot (tcdot 1,2cdot tA)\
hline 3& 0,7cdot (tcdot 1,2cdot tA)& tcdot (0,7cdot tcdot 1,2cdot tA)&\
hline
end{array}]
Следовательно, в конце третьего года на счете было [1,2cdot
0,7cdot t^3A=0,84t^3A quad {small{text{рублей.}}}]
Заметим, что по первому вкладу на счете оказалась большая сумма. Отношение равно [1,04:0,84=26:21.]
Ответ:
26:21
Задание
5
#2935
Уровень задания: Равен ЕГЭ
Ваня сделал вклад в банке на 3 года. Раз в год банк начисляет на сумму, находящуюся на счете, некоторое количество процентов. У Вани есть возможность в один из первых двух лет (после начисления процентов) снять со счета (20%) от имеющейся там суммы, а в другой год (из первых двух лет) — доложить также (20%) от имеющейся там суммы. Или сделать наоборот. Определите, какое из этих действий спустя 3 года принесет Ване большую выгоду и сколько процентов составит эта выгода?
Пусть Ваня положил в банк (A) рублей. Пусть каждый год банк увеличивает сумму, находящуюся на счете, в (t) раз. Рассмотрим два случая:
1) сначала он снял (20%), затем доложил. [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& tA
& -,0,2cdot (tA)\
hline 2&0,8cdot (tA)& tcdot (0,8cdot tA)
& +,0,2cdot (tcdot 0,8cdot tA)\
hline 3& 1,2cdot (tcdot 0,8cdot tA)& tcdot (1,2cdot tcdot 0,8cdot tA)&\
hline
end{array}]
2) сначала он доложил (20%), затем снял. [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& tA
& +,0,2cdot (tA)\
hline 2&1,2cdot (tA)& tcdot (1,2cdot tA)
& -,0,2cdot (tcdot 1,2cdot tA)\
hline 3& 0,8cdot (tcdot 1,2cdot tA)& tcdot (0,8cdot tcdot 1,2cdot tA)&\
hline
end{array}]
Таким образом, мы видим, что в обоих случаях в конце третьего года на счете у Вани будет [0,8cdot 1,2cdot t^3A quad {small{text{рублей.}}}]
Следовательно, выгода составляет (0%).
Ответ: 0
Задание
6
#2937
Уровень задания: Равен ЕГЭ
В феврале женщина оформила в банке вклад на 4 года. Каждый год в ноябре банк начисляет на вклад (8%). В декабре первого года пользования услугами данного банка женщина решила купить квартиру и сняла для этой цели со своего счета (8) млн. рублей. Ровно через два года она продала эту квартиру и сразу же вернула на счет в банке те же (8) млн. рублей. Определить, сколько рублей потеряла по истечении срока действия вклада из-за подобных действий эта женщина.
Пусть размер вклада составил (A) млн. рублей. Составим таблицу, описывающую действия, происходившие со вкладом: [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма в феврале}
&text{Сумма в ноябре}&text{Манипуляции}\
hline 1& A & 1,08A & -,8\
hline 2& 1,08A-8 & 1,08 (1,08A-8) & \
hline 3& 1,08 (1,08A-8) & 1,08^2 (1,08A-8) & +,8\
hline 4&1,08^2 (1,08A-8)+8 & 1,08(1,08^2 (1,08A-8)+8)&\
hline
end{array}]
Таким образом, спустя четыре года на счете у женщины было [1,08(1,08^2 (1,08A-8)+8)=1,08^4A-8cdot 1,08(1,08-1)(1,08+1) quad {small{text{млн. рублей}}}]
Если бы она не совершала данные манипуляции, то каждый год ее вклад увеличивался бы в (1,08) раз и к концу четвертого года составил бы (1,08^4A) млн. рублей. Следовательно, из-за подобных действий ее вклад уменьшился на [8cdot 1,08(1,08-1)(1,08+1)=8cdot 1,08cdot 0,08cdot 2,08=1,437696quad {small{text{млн. рублей}}}]
Ответ:
(1,437,696) рублей
Задание
7
#2932
Уровень задания: Равен ЕГЭ
В январе 2014 года Андрей сделал вклад в размере (6,640,000) рублей под (y) процентов годовых. В феврале 2014 года он захотел купить квартиру стоимостью (9) млн. рублей, но решил для этого взять кредит под (21%) годовых на 15 лет, который необходимо выплачивать дифференцированными платежами. Найдите наименьшее число (y), чтобы процентов, начисляемых на его вклад каждый год, было достаточно для того, чтобы вносить платежи в счет погашения кредита.
Заметим, что так как кредит должен выплачиваться дифференцированными платежами, то из их определения следует, что первый платеж по кредиту будет наибольшим среди всех платежей.
Так как каждый платеж по такому кредиту состоит из двух частей: (frac1{15}) часть от (9) млн. рублей плюс проценты, “набежавшие” на долг за текущий год, то первый платеж будет равен [dfrac1{15}cdot 9000+0,21cdot 9000 {small{text{тыс. рублей.}}}] (так как в первый год пользования кредитом долг равен (9) млн. рублей или, что то же самое, (9000) тыс. рублей)
Рассмотрим вклад. В первый год на вклад “набегут” проценты в размере (0,01ycdot 6640) тыс. рублей. Этой суммы должно хватить для того, чтобы сделать первый платеж. Следовательно, [0,01ycdot 6640geqslant dfrac1{15}cdot 9000+0,21cdot 9000 qquad (*)]
Заметим, что таким образом, если он снимет в первый год со счета не более (0,01ycdot 6640) тыс. рублей, то на счете у него останется как минимум (6640) тыс. рублей, то есть точно не меньше, чем было в начале первого года. Следовательно, “набежавших” процентов во второй год также хватит на то, чтобы сделать второй платеж (ведь он меньше первого платежа!). Такое же рассуждение относится и к всем следующим годам.
Следовательно, нам важно, чтобы именно первых “набежавших” процентов хватило на то, чтобы сделать первый платеж.
[ygeqslant dfrac{83}3cdot dfrac{9000}{6640} quadRightarrowquad
ygeqslant dfrac{3000}{80}=37frac12]
Следовательно, наименьшее подходящее (y) равно (37,5%).
Ответ: 37,5
Во время сдачи ЕГЭ по математике многие выпускники сталкиваются с проблемой решения задач по банковским вкладам и кредитам. Данная тематика встречается в тестовых заданиях довольно редко, поэтому ей уделяется недостаточно внимания при подготовке. Чтобы легко справляться с упражнениями, обращайтесь к нашему онлайн-порталу. Вы научитесь быстро находить правильные ответы и сможете решать примеры различной сложности.
«Школково» — залог успешной сдачи заключительного аттестационного тестирования!
На нашем сайте представлены все материалы, которые необходимы для подготовки к Единому государственному экзамену по математике. Наши преподаватели собрали и подали информацию по теме в наиболее простой и понятной форме. Благодаря такому подходу занятия проходят быстро и легко.
Чтобы подготовка к итоговому тестированию проходила максимально результативно, советуем воспользоваться предложенным нами алгоритмом действий.
Зайдите в раздел «Теоретическая справка», где размещены самые необходимые правила, формулы и простейшие примеры решения типовых экономических задач. Внимательно ознакомьтесь с материалами.
После этого переходите в раздел «Каталоги». Там собрано множество упражнений различного уровня сложности. Советуем начать с простых задач и постепенно переходить к более трудным. Так вы сможете определить свои слабые стороны и сделать упор на решении определенных упражнений.
Если у вас возникли проблемы с каким-либо примером на тему «Решение задач по банковским вкладам и кредитам», его можно добавить в «Избранное». Задание не потеряется, и вы сможете вернуться к его выполнению самостоятельно или вместе с преподавателем.
База упражнений на нашем портале постоянно обновляется и дополняется. Поэтому школьники каждый день получают совершенно новые задания, соответствующие уровню их текущих навыков. Такой подход значительно отличается от стандартных занятий с использованием школьных пособий. Выпускники совершенствуют свои знания, а не просто заучивают, как решать типовые примеры, предложенные в учебниках.
Начните подготовку на портале «Школково» уже сегодня, и результат не заставит себя ждать! Всего через несколько дней регулярных занятий вы заметите, что с легкостью справляетесь с теми упражнениями, которые ранее вызывали сложности.
Обратите внимание, что на нашем портале могут заниматься все желающие. Для того чтобы сохранить и отслеживать прогресс, зарегистрируйтесь на официальном сайте shkolkovo.net. Желаем приятной подготовки к Единому государственному экзамену!

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ