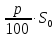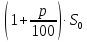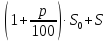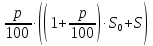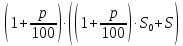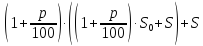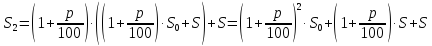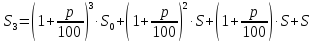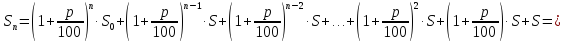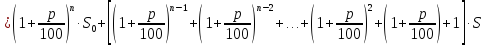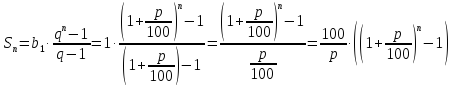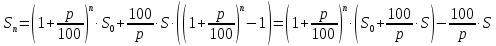Задача про бабу валю егэ

Баба Валя, накопив часть своей пенсии, решила улучшить свое материальное положение. Она узнала, что в Спёрбанке от пенсионеров принимают вклады под определенный процент годовых и на этих условиях внесла свои сбережения в ближайшее отделение Спёрбанка. Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры, есть коммерческий банк, в котором процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в Спёрбанке. Баба Валя не доверяла коммерческим банкам, но стремление улучшить свое материальное положение взяло верх. После долгих колебаний и ровно через год после открытия счета в Спёрбанке Баба Валя сняла половину образовавшейся суммы от ее вклада, заявив: «Такой навар меня не устраивает!» и открыла счет в том коммерческом банке, о котором говорила ее соседка, не теряя надежды на значительное улучшение своего материального благосостояния.

Надежды оправдались: через год сумма Бабы Вали в коммерческом банке превысила ее первоначальные кровные сбережения на 65%. Сожалела Баба Валя, что год назад в Спёрбанке сняла не всю сумму, а лишь половину, однако, подумала: «А где же мы не теряли?..» Гендиректор коммерческого банка оказался хорошим: не оставил Бабу Валю без денег.

А каков в Спёрбанке процент годовых для пенсионеров?

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

«Такой навар меня не устраивает!»

Как вы думаете, что это за текст?

«Баба Валя, накопив часть своей пенсии, решила улучшить свое материальное положение. Она узнала, что в Сбербанке от пенсионеров принимают вклады под определенный процент годовых, и на этих условиях внесла свои сбережения в ближайшее отделение. Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры, есть коммерческий банк, где процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в Сбербанке. Баба Валя не доверяла коммерческим банкам, но стремление улучшить свое материальное положение взяло верх. После долгих колебаний и ровно через год после открытия счета в Сбербанке баба Валя сняла половину образовавшей суммы от ее вклада, заявив: «Такой навар меня не устраивает!» И открыла счет в том коммерческом банке, о котором говорила ее соседка. Через год сумма бабы Вали в коммерческом банке превысила ее первоначальные кровные сбережения на 65%. Сожалела баба Валя, что год назад в Сбербанке сняла не всю сумму, а лишь половину, однако подумала: «А где же мы не теряли?..» Гендиректор коммерческого банка оказался хорошим: не оставил бабу Валю без навара! А каков в Сбербанке процент годовых для пенсионеров?»

Итак, что это такое? Рекламный проспект? Плутовской роман? Водевиль? Криминальная драма на вечный российский сюжет «Не гонялся бы ты, поп, за дешевизной»? А вот и не угадали! Это реальное задание №18.С5 №506959 из недавно написанного в Москве пробного ЕГЭ по математике.

Родители сего порождения креативщиков от математики, мягко говоря, не оценили. Кто-то сразу перешел на ненормативную лексику. Детей же задание про бабу Валю повергло в ступор:

— Получи я эту задачу в стрессовом состоянии на экзамене, она бы вызвала у меня приступ хохота, и я не смогла бы сосредоточиться, — не сомневается 11-классница Даша.

— А меня, — говорит ее подруга Люба, — испугали бы размеры задачи: дочитывая до конца, теряешь нить повествования.

Но хуже всех пришлось Лизе, которой чудо-задача досталась реально:

— Я дорешала ее до конца. Но могу сказать, что шутки в задаче должны хотя бы ограничиваться содержанием. Говоря о числовом эквиваленте, процент в коммерческом банке по вычислениям равен 200% (в Сбербанке 10%). Но я всегда боюсь ошибиться. А такие цифры меня точно выведут из душевного равновесия, и я попросту все зачеркну, убедившись в ошибочности собственного решения.

Примечательно, что использование на экзамене «банковской тематики» носит целенаправленный характер, разъяснил «МК» главный «куратор» ЕГЭ по математике, директор Центра педагогического мастерства Иван Ященко:

— В 2015 году в профильный ЕГЭ по математике обязательно включается задача практического содержания с экономическим смыслом — ситуация из жизни с нормальными числами. Отсюда в данном случае и подсчет процента в банке. Другое дело, что эта задача составлена в стиле Остера и совершенно не соответствует стилистике такого серьезного мероприятия, как ЕГЭ. Поэтому на официально проводимых Единых госэкзаменах таких задач-шуток нет и быть не может. Однако на школьном уровне при подготовке к ЕГЭ, включая пробные экзамены, могут быть использованы любые задания — в Интернете их полно. Этим и пользуются учебные заведения. К слову сказать, в последнее время вузы на «пробниках» стали практиковать такой трюк: раздают заведомо сложные задания, чтобы дети схватились от ужаса за голову, — и тут же раздают листочки с телефоном своих подготовительных курсов, где их готовят за дополнительную плату…

Короче, вузы в любом случае не остаются без навара. Совсем как баба Валя!

Опубликован в газете «Московский комсомолец» №26759 от 11 марта 2015

Заголовок в газете:
«Такой навар меня не устраивает!»

12 марта 2015, 09:05, ИА Амител

Не прошло и десяти лет, как из заданий
ЕГЭ исчезли вопросы типа «Как звали лошадь Вронского?» или «О скольких
пуговицах была гоголевская шинель?». Но легче от этого, увы, не стало.
Нелепые вопросы, как показал последний пробник ЕГЭ по математике, не
исчезли, а лишь переместились из основных заданий во вспомогательные. Подробности сообщает МК.

Как вы думаете, что это за текст?

«Баба Валя, накопив часть
своей пенсии, решила улучшить свое материальное положение. Она узнала,
что в Сбербанке от пенсионеров принимают вклады под определенный процент
годовых, и на этих условиях внесла свои сбережения в ближайшее
отделение. Но через некоторое время соседка ей рассказала, что недалеко
от той местности, где проживают пенсионеры, есть коммерческий банк, где
процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в
Сбербанке. Баба Валя не доверяла коммерческим банкам, но стремление
улучшить свое материальное положение взяло верх. После долгих колебаний и
ровно через год после открытия счета в Сбербанке баба Валя сняла
половину образовавшей суммы от ее вклада, заявив: «Такой навар меня не
устраивает!» И открыла счет в том коммерческом банке, о котором говорила
ее соседка. Через год сумма бабы Вали в коммерческом банке превысила ее
первоначальные кровные сбережения на 65%. Сожалела баба Валя, что год
назад в Сбербанке сняла не всю сумму, а лишь половину, однако подумала:
«А где же мы не теряли?..» Гендиректор коммерческого банка оказался
хорошим: не оставил бабу Валю без навара! А каков в Сбербанке процент
годовых для пенсионеров?»

Итак, что это такое? Рекламный
проспект? Плутовской роман? Водевиль? Криминальная драма на вечный
российский сюжет «Не гонялся бы ты, поп, за дешевизной»? А вот и не
угадали! Это реальное задание №18.С5 №506959 из недавно написанного в
Москве пробного ЕГЭ по математике.

Родители сего порождения
креативщиков от математики, мягко говоря, не оценили. Кто-то сразу
перешел на ненормативную лексику. Детей же задание про бабу Валю
повергло в ступор:

— Получи я эту задачу в стрессовом состоянии
на экзамене, она бы вызвала у меня приступ хохота, и я не смогла бы
сосредоточиться, — не сомневается 11-классница Даша.

— А меня, — говорит ее подруга Люба, — испугали бы размеры задачи: дочитывая до конца, теряешь нить повествования.

Но хуже всех пришлось Лизе, которой чудо-задача досталась реально:

—
Я дорешала ее до конца. Но могу сказать, что шутки в задаче должны хотя
бы ограничиваться содержанием. Говоря о числовом эквиваленте, процент в
коммерческом банке по вычислениям равен 200% (в Сбербанке 10%). Но я
всегда боюсь ошибиться. А такие цифры меня точно выведут из душевного
равновесия, и я попросту все зачеркну, убедившись в ошибочности
собственного решения.

Примечательно, что использование на
экзамене «банковской тематики» носит целенаправленный характер,
разъяснил «МК» главный «куратор» ЕГЭ по математике, директор Центра
педагогического мастерства Иван Ященко:

— В 2015 году в
профильный ЕГЭ по математике обязательно включается задача практического
содержания с экономическим смыслом — ситуация из жизни с нормальными
числами. Отсюда в данном случае и подсчет процента в банке. Другое дело,
что эта задача составлена в стиле Остера и совершенно не соответствует
стилистике такого серьезного мероприятия, как ЕГЭ. Поэтому на официально
проводимых Единых госэкзаменах таких задач-шуток нет и быть не может.
Однако на школьном уровне при подготовке к ЕГЭ, включая пробные
экзамены, могут быть использованы любые задания — в Интернете их полно.
Этим и пользуются учебные заведения. К слову сказать, в последнее время
вузы на «пробниках» стали практиковать такой трюк: раздают заведомо
сложные задания, чтобы дети схватились от ужаса за голову, — и тут же
раздают листочки с телефоном своих подготовительных курсов, где их
готовят за дополнительную плату…

Короче, вузы в любом случае не остаются без навара. Совсем как баба Валя!, — иронизирует Марина Лемуткина.

ЗАДАНИЕ 17 ЕГЭ.

ФИНАНСОВАЯ МАТЕМАТИКА. ВКЛАДЫ

1. БАНКОВСКИЕ ЗАДАЧИ НА ВКЛАДЫ

1. Нахождение срока вклада.

2. Вычисление процентной ставки по вкладу.

3. Нахождение суммы вклада.

4. Нахождение ежегодной суммы пополнения вклада.

5. Нахождение прибыли от вклада.

Разберём задачи на вклады. Обычно встречаются задачи на вклады двух типов: без ежегодного взноса определённой суммы и с внесением такой суммы.

Для определённости введём обозначения, используемые при решении задач.

– сумма первоначального вклада.

– сумма ежегодного вклада (часто ).

– временной промежуток (количество месяцев, лет).

– сумма через n лет (месяцев).

– процентная ставка.

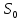
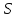
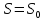
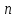
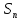
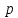
Задачи на вклады решаются двумя способами: с помощью таблиц и с помощью формул. Рассмотрим задачу на вклад с ежегодным пополнением на определённую сумму.

I способ. Приведём пример таблицы накопления вклада. Таблицы удобны, если временной промежуток вклада невелик.

дата или № года (месяца)	% на сумму в конце года (месяца)	сумма с учётом %	сумма вклада	сумма в конце года (месяца)
0
1
2
…	………	…………….		………….

Из таблицы видно, что чем больше срок вклада, тем сложнее вычисления. Поэтому, при больших сроках удобнее пользоваться формулами.

II способ. Чтобы понять, откуда берётся формула, приведём её вывод. Воспользуемся таблицей выше. Рассмотрим сумму вклада в конце второго года (месяца).

Аналогично,

И так далее,

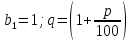
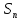
В последнем выражении, в квадратных скобках стоит сумма п членов геометрической прогрессии, в которой . Воспользуемся формулой для .

Тогда общая сумма вклада через п лет (с учётом пополнения) будет:

Если же в n-ом году счёт будет закрыт, то последнего пополнения не будет! Тогда формула имеет вид:

Если сумма ежегодного пополнения равна первоначальному взносу , то формула принимает более компактный вид:

В задачах на вклады без ежегодного пополнения ситуация немного проще.

дата или № года (месяца)	% на сумму в конце года (месяца)	сумма в конце года (месяца) с учётом %
0
1
2
…	………	…………….
через п лет

В виде формулы это выглядит так:

Приведём примеры.

1. Банк выплачивает 4 % годовых. Через сколько лет внесённая сумма удвоится?

Решение.

– сумма вклада, , .

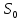
По окончании первого года, после начисления процентов, на счёте станет:

По окончании второго года, после начисления процентов, на счёте станет:

………………………………………………………………….

Так как , то

Ответ: лет

1. На какой срок необходимо вложить 5000 рублей при 30% годовых, чтобы сумма дохода составила 560 рублей?

Решение.

, , .

Так как сумма дохода равна , то срок вклада будем рассчитывать в днях, и т.к. нас интересует только доход, то . Эта формула означает следующее: на первоначальный взнос назначается годовой процент р, но т.к. срок вклада меньше года, то эту сумму делят на 365 дней и умножают на количество дней, в течении которых вклад находился в банке (п). Важно, что здесь не добавляется сам первоначальный взнос, т.е. формула отражает чистую прибыль.

Так как , то

Ответ: дней

1. На какой срок необходимо вложить 15 000 рублей при 9 % годовых, чтобы сумма дохода составила 2 000 рублей?

Решение.

, , .

Так как нас интересует только доход, то

Так как , то

Ответ: дней

1. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на . Определите срок хранения вклада.

Решение.

– сумма вклада;

месяцев – срок начисления 5% ставки;

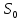
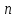
месяцев – срок начисления 12% ставки;

месяцев – срок начисления % ставки;

месяцев – срок начисления 12,5% ставки.

При ставке 5% через месяц сумма вклада составила . Через два месяца сумма вклада составила . И так далее, через п месяцев сумма вклада составит .

При ставке 12% через месяц сумма вклада составит:

. Через два месяца –

. И так далее, через т месяцев сумма вклада составит .

Аналогично, при ставке через k месяцев сумма вклада будет .

Так же, при ставке 12,5% через l месяцев сумма вклада будет .

По условию задачи известно, что по истечении срока хранения первоначальная сумма увеличилась на , т.е. составила .

Составляем уравнение:

Значит, весь срок вклада составляет: месяцев.

Ответ: 7 месяцев

1. Гражданин Петров по случаю рождения сына открыл 1 сентября 2008 года в банке счёт, на который он ежегодно кладёт 1000 рублей. По условиям вклада банк ежегодно начисляет 20% на сумму, находящуюся на счёте. Через 6 лет у гражданина Петрова родилась дочь, и 1 сентября 2014 года он открыл в другом банке счёт, на который ежегодно кладёт по 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают?

Решение. Сначала рассмотрим как происходит накопление денежных средств на счёте сына. Так как каждый год банк начисляет 20% на сумму, которая была в конце предыдущего года, то вся сумма будет составлять 120%. Затем прибавляем ежегодный взнос 1000 руб.

дата	сумма на счёте сына
01.09.2008
01.09.2009
01.09.2010
01.09.2011
……………	…………………………………………………………………………………
через n лет

Теперь рассмотрим сумму на счёте сына через n лет.

В этой сумме слагаемое (слагаемых со степенями п плюс первое слагаемое). Нетрудно заметить, что эта сумма представляет собой сумму геометрической прогрессии, у которой . Воспользуемся формулой суммы членов геометрической прогрессии:

Это сумма, которая будет на счёте сына через п лет.

дата	сумма на счёте дочери
01.09.2014
01.09.2015
01.09.2016
01.09.2017
……………	…………………………………………………………………………………
через n-6 лет

Рассчитаем сумму на счёте дочери. Так как каждый год банк начисляет 44% на сумму, которая была в конце предыдущего года, то вся сумма будет составлять 144%. Затем прибавляем ежегодный взнос 2200 руб. и учитываем, что срок вклада дочери будет на 6 лет меньше, чем срок вклада сына, т.е. лет.

Теперь рассмотрим сумму на счёте дочери через n — 6 лет.

В этой сумме слагаемых (слагаемых со степенями п — 6 плюс первое слагаемое). Эта сумма представляет собой сумму геометрической прогрессии, у которой . Воспользуемся формулой суммы членов геометрической прогрессии:

Это сумма, которая будет на счёте дочери через п — 6 лет.

В задаче поставлено условие, что суммы вкладов сына и дочери должны сравняться, поэтому приравниваем их.

Значит, суммы на счетах сына и дочери сравняются через 11 лет после открытия счёта сына. И это произойдёт в году.

Ответ: в 2019 году.

1. Алексей приобрёл ценную бумагу за 8 тыс. рублей. Цена бумаги каждый год возрастает на 1 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 8%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через двадцать пять лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Решение. Рассмотрим два способа решения данной задачи.

I способ. Составим сравнительную таблицу стоимости ценной бумаги после увеличения цены и банковского процента.

№ года	стоимость ценной бумаги в начале года	сумма увеличения стоимости ценной бумаги	общая стоимость ценной бумаги в конце года	банковский процент (8%)
1	8 000	1 000	9 000	720
2	9 000	1 000	10 000	800
3	10 000	1 000	11 000	880
4	11 000	1 000	12 000	960
5	12 000	1 000	13 000	1040

Из таблицы видно, что банковский процент превысит сумму увеличения стоимости ценной бумаги через 5 лет, значит, продавать бумаги надо в течение 6 лет.

II способ. Если ценная бумага будет находится у Алексея n лет, то через n лет он получит   рублей. Если в начале го года Алексей продаст бумагу и положит деньги в банк, то по итогам года получит Это следует делать, если . Найдем, каким должно быть число n.

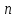
– число целое, значит, . Так как Алексей положил деньги в банк в течении года, то максимальную прибыль он получит, если положит деньги в банк в течении 6 года.

Ответ: в течении 6 года.

1. В январе 2000 года ставка по депозитам в банке «Возрождение» составила х% годовых, тогда как в январе 2001 года она была у% годовых, причём известно, что x + y = 30%. В январе 2000 года вкладчик открыл счёт в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, по прошествии года с того момента, вкладчик снял со счёта пятую часть этой суммы. Укажите значение х, при котором сумма на счёте вкладчика в январе 2002 года станет максимально возможной.

Решение. Пусть 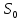– первоначальный вклад. При годовых через год на счёте будет . После снятия со счёта , на нём осталось:

. На эту сумму через год начислили и на счёте стало . Так как , то . Тогда:

Мы получили функцию относительно переменной х:

Наибольшее значение эта квадратичная функция достигает в своей вершине, т.к. ветви её направлены вниз. Найдём абсциссу вершины параболы:

.

Итак, при сумма на счёте вкладчика в январе 2002 года будет максимально возможной.

Ответ: 25%

1. Баба Валя, накопив часть своей пенсии, решила улучшить своё материальное положение. Она узнала, что в Спёрбанке от пенсионеров принимают вклады под определённый процент годовых и на этих условиях внесла свои сбережения в ближайшее отделение Спёрбанка. Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры, есть коммерческий банк, в котором процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в Спёрбанке. Баба Валя не доверяла коммерческим банкам, но стремление улучшить своё материальное положение взяло верх. После долгих колебаний и ровно через год после открытия счёта в Спёрбанке, Баба Валя сняла половину образовавшейся суммы от её вклада, заявив: «Такой навар меня не устраивает!» И открыла счёт в том коммерческом банке, о котором говорила её соседка, не теряя надежды на значительное улучшение своего материального благосостояния. Надежды оправдались: через год сумма Бабы Вали в коммерческом банке превысила её первоначальные кровные сбережения на 65%. Сожалела Баба Валя, что год назад в Спёрбанке сняла не всю сумму, а лишь половину, однако, подумала: «А где же мы не теряли?..» Гендиректор коммерческого банка оказался хорошим: не оставил Бабу Валю без навара! А каков в Спёрбанке процент годовых для пенсионеров?

Решение. Пусть 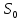– первоначальные накопления; — процентная ставка в Спёрбанке, тогда — процентная ставка в коммерческом банке. Открыв счёт в Спёрбанке, через год на нём образуется сумма . В коммерческий банк была внесена сумма, равная половине этой, т.е. . Через год в коммерческом банке на счёте, после начисления процентов, будет . По условию задачи известно, что эта сумма на 65% больше, чем первоначальные накопления, т.е. составляет 165% от и равна . 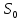Составляем уравнение:

не удовлетворяет условию задачи, значит, в Спёрбанке процентная ставка равна 10%.

Ответ: 10%

1. Банк под определённый процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счёта. Банк увеличил процент годовых на 40 процентных пунктов (то есть увеличил ставку а% до (а + 40)%). К концу следующего года накопленная сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?

Решение. Обозначим первоначальный вклад через 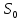, а первоначальную процентную ставку через а%. Тогда через год, после начисления процентов на счёте станет Четверть этой суммы сняли со счёта, тогда осталось:

. На эту оставшуюся сумму через год начислили проценты в размере . В итоге, к концу года на счёте накопилась сумма: . По условию задачи известно, что она превысила первоначальный вклад в 1,44 раз, т.е. стала равной . Составим уравнение:

не удовлетворяет условию задачи. Значит, первоначальная процентная ставка составляла 20%. Поэтому новая процентная ставка равна: .

Ответ: 60%.

1. По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает на 11 % в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А».

Решение. Обозначим через 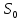— первоначальную сумму по обоим вкладам, а через – процентную ставку вклада «Б» на третий год. Составим таблицу:

№ года	сумма в конце года с учётом процентов вклада «А»	сумма в конце года с учётом процентов вклада «Б»
0
1
2
3

Чтобы выполнялось условие задачи (вклад «Б» должен остаться более выгодным, чем вклад «А»), необходимо выполнение условия:

Т.к. 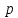должно быть целым и наименьшим, то .

Ответ: 9%.

1. По вкладу «А» банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 10% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.

Решение.

№ года	сумма в конце года с учётом процентов вклада «А»	сумма в конце года с учётом процентов вклада «Б»
0
1
2
3

Чтобы выполнялось условие задачи (вклад «Б» должен остаться более выгодным, чем вклад «А»), необходимо выполнение условия:

Так как , то .

Стоит заметить, что при . Это не удовлетворяет условию, как, впрочем, и все остальные значения, меньшие 26.

Итак, наименьшее целое .

Ответ: 26%.

1. В начале года 5/6 некоторой суммы денег вложили в банк А, а то, что осталось — в банк Б. Если вклад находится в банке с начала года, то к концу года он возрастает на определённый процент, величина которого зависит от банка. Известно, что к концу первого года сумма вкладов стала равна 670 у. е., к концу следующего — 749 у. е. Если первоначально 5/6 суммы было бы вложено в банк Б, а оставшуюся вложили бы в банк А, то по истечении одного года сумма выросла бы до 710 у. е. Определите сумму вкладов по истечении второго года в этом случае.

Решение. Обозначим 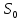– общую первоначальную сумму, тогда в банк А вложили , а в банк Б вложили . Процентную ставку банка А обозначим через р, а процентную ставку банка Б – через q. Тогда через год на счёте в банке А стало , а на счёте в банке Б — . Через два года в банке А стало , а в банке Б — . Если бы изначально в банк А вложили бы , а в банк Б — , то через год в банке А было бы , а в банке Б — . Через два года в банке А было бы , а в банке Б — . Для наглядности сведём всё это в таблицу:

№ года	сумма в конце года банка А при сумме вложения	сумма в конце года банка Б при сумме вложения	общая сумма в конце года
1			670
2			749
№ года	сумма в конце года банка А при сумме вложения	сумма в конце года банка Б при сумме вложения	общая сумма в конце года
1			710
2			?

Итак, получаем систему уравнений:

Второе уравнение умножим на -5 и сложим с первым.

Теперь мы можем найти общую сумму в конце второго года во втором случае:

Ответ: 841 у.е.

1. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 2 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 15 млн рублей.

Решение.

№ года	сумма на счёте
0
1
2
3
4

Итоговая сумма должна быть меньше 15 млн. рублей, поэтому:

Так как первоначальный вклад является целым числом и должен быть наибольшим, то млн. рублей.

Ответ: 7 млн. рублей.

1. По бизнес-плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором они за два года станут больше 125 миллионов, а за четыре года станут больше 200 миллионов рублей.

Решение.

№ года	сумма с учётом процентов и вложений
0	млн
1
2
3
4

По условию задачи через два года сумма должна быть больше 125 млн. рублей, а через 4 года – больше 200 млн. рублей, поэтому:

Так как 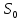– наименьшее целое, то млн. рублей.

Ответ: 57 млн. рублей.

1. В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырёх лет хранения после начисления процентов вкладчик дополнительно вносил на счёт одну и ту же фиксированную сумму. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%. Какую сумму вкладчик ежегодно добавлял ко вкладу?

Решение. В данной задаче рассматривается вклад с пополнением. Обозначим через 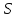тыс. рублей ежегодную сумму пополнения. Тогда сведём данные в таблицу:

№ года	сумма на счёте
0
1
2
3
4
5

Итак, в конце пятого года, после начисления процентов на счёте оказалась сумма:

По условию задачи известно, что в конце пятого года размер вклада увеличился по сравнению с первоначальным на 725%, т.е. стал составлять 825% от первоначального.. Составляем уравнение:

Значит, ежегодное пополнение составляло 210 тыс. рублей.

Ответ: 210 000 рублей

1. По бизнес-плану предполагается изначально вложить в четырёхлетний проект 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по целому числу n млн рублей в первый и второй годы, а также по целому числу m млн рублей в третий и четвёртый годы. Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся.

Решение. Составим таблицу:

№ года	сумма с учётом процентов и вложений
0	10 млн
1
2
3
4

По условию задачи за два года вложения должны как минимум удвоиться, поэтому,

Значит, наименьшее целое .

Через четыре года первоначальные вложения должны утроиться, учитывая, что , получаем:

Значит, наименьшее целое

Итак, чтобы выполнялось условие задачи, первые два года необходимо добавлять по 4 млн. рублей, а в третий и четвёртый годы – по 1 млн. рублей.

Ответ: 4 млн. и 1 млн. рублей.

1. Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 30 млн рублей.

Решение. Обозначим через S млн. рублей фиксированную сумму пополнения.

№ года	сумма с учётом процентов и пополнения
0	10 млн
1
2
3
4

Итоговая сумма должна быть не меньше 30 млн. рублей, поэтому:

Так как сумма должна быть целым наименьшим числом, то млн. рублей.

Ответ: 7 млн. рублей.

1. В конце августа 2001 года администрация Приморского края располагала некой суммой денег, которую предполагалось направить на пополнение нефтяных запасов края. Надеясь на изменение конъюнктуры рынка, руководство края, отсрочив закупку нефти, положила эту сумму 1 сентября 2001 года в банк. Далее известно, что сумма вклада в банке увеличивалась первого числа каждого месяца на 26% по отношению к сумме на первое число предыдущего месяца, а цена барреля сырой нефти убывала на 10% ежемесячно. На сколько процентов больше (от первоначального объёма закупок) руководство края смогло пополнить нефтяные запасы края, сняв 1 ноября 2001 года всю сумму, полученную из банка вместе с процентами, и направив её на закупку нефти?

Решение. Обозначим сумму, которой располагала администрация в конце августа 2001 года через 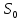, а цену барреля сырой нефти через у.е. Тогда, на конец августа объём закупок нефти составил бы баррелей. Так как деньги были вложены в банк 01.09.2001, то на 01.10.2001 на счёте стало (с учётом процентов); на 01.11.2001 сумма стала равной . Эта сумма и была снята со счёта. Цена барреля снижалась каждый месяц на 10%, значит, на 01.10.2001 года баррель стоил у.е., а на 01.11.2001 года он стал стоить у.е. Значит, объём закупок нефти в ноябре 2001 года составил баррелей. Процентное отношение этого объёма к первоначально возможному составляет . Поэтому разница составляет .

Ответ: 96%.

1. Банк планирует вложить на 1 год 30% имеющихся у него средств клиентов в акции золотодобывающего комбината, а остальные 70% — в строительство торгового комплекса. В зависимости от обстоятельств первый проект может принести банку прибыль в размере от 32% до 37% годовых, а второй проект — от 22 до 27% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке, уровень которой должен находиться в пределах от 10% до 20% годовых. Определите, какую наименьшую и наибольшую чистую прибыль в процентах годовых от суммарных вложений в покупку акций и строительство торгового комплекса может при этом получить банк.

Решение. Минимальную прибыль банк получит при соблюдении двух условий: по двум проектам получен минимальный процент прибыли и вкладчикам выплачен максимальный годовой процент. В первый проект (акции золотодобывающего комбината) банком была вложена сумма: . Через год, учитывая минимальный процент, из этого проекта выйдет сумма: . Во второй проект (строительство торгового комплекса) банком вложена сумма: . Через год, учитывая минимальный процент, из этого проекта выйдет сумма: .

Общая сумма с двух проектов составит .

Из этой суммы банк обязан отдать вкладчикам их вложения, т.е. 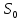, и тогда у банка останется . Из этих денег банку нужно выплатить вкладчикам проценты (процент должен быть максимальный – 20%), т.е. . Значит, у банка останется . В процентах это составляет . Итак, минимальная прибыль банка – 5%.

Аналогично рассчитываем максимальную прибыль.

Через год, учитывая максимальный процент, из первого проекта выйдет сумма: .

Из второго проекта выйдет сумма: .

Общая сумма с двух проектов составит .

Из этой суммы банк обязан отдать вкладчикам их вложения, т.е. 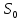, и тогда у банка останется . Из этих денег банку нужно выплатить вкладчикам проценты (процент должен быть минимальный – 10%), т.е. . Значит, у банка останется . В процентах это составляет . Итак, максимальная прибыль банка – 20%.

Ответ: 5%, 20%.

1. В банк был положен вклад под банковский процент 10%. Через год, после начисления процентов, хозяин вклада снял со счета 2000 рублей, а ещё через год снова внёс 2000 рублей. Однако, вследствие этих действий через три года со времени первоначального вложения вклада он получил сумму, меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы получил в итоге вкладчик?

Решение. Обозначим вклад через 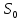. Если бы вкладчик не совершал промежуточных действий с вкладом (не снимал, не вкладывал), то через 3 года на счёте была бы сумма . Теперь рассмотрим, что происходило с вкладом в реальности.

Через год, после начисления процентов, на счёте было . Вкладчик снял 2000, значит, осталось . Ещё через год на эту сумму начислены проценты и она стала равной . Теперь к этой сумме вкладчик добавил 2000 рублей и на счёте стало . И ещё через год, после начисления процентов на эту сумму, счёт в банке составил . В итоге, вкладчик, из-за своих действий потерял 220 рублей.

Ответ: на 220 рублей.

1. Миша и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а ещё через год снова внёс 5000 рублей. Маша, наоборот, через год доложила на свой счёт 5000 рублей, а ещё через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей?

Решение. Пусть 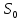– сумма, которую положили и Миша, и Маша в банк. Через год, после начисления процентов, у них на счетах было по . Т.к. Миша снял 5000 рублей, то у него осталось рублей. Маша доложила 5000 рублей и у неё стало рублей. Ещё через год, после начисления процентов на получившиеся суммы, у Миши на счёте было рублей, а у Маши стало рублей. Теперь Миша к своей сумме доложил 5000 рублей и у него стало руб., а Маша сняла со своей суммы 5000 руб. и у неё стало рублей. Ещё через год, после начисления процентов, у Миши на счёте было рублей, а у Маши – рублей. В итоге, через три года Маша получит сумму больше на 1100 рублей, т.к.

.

Ответ: на 1100 рублей.

1. Василий кладёт в банк 1 000 000 рублей под 10% годовых на 4 года (проценты начисляются один раз после истечения года) с правом докладывать три раза (в конце каждого года) на счёт фиксированную сумму 133 000 рублей. Какая сумма будет на счёте у Василия через 4 года?

Решение. Составим таблицу накопления вклада.

№ года	сумма на счёте
0	1 000 000
1	1,1∙1 000 000+133 000=1 100 000+133 000=1 233 000
2	1,1∙1 233 000+133 000=1 356 300+133 000=1 489 300
3	1,1∙1 489 300+133 000=1 638 230+133 000=1 771 230
4	1,1∙1 771 230=1 948 353

Если записать в виде формулы, то она выглядит так:

Ответ: 1 948 353 рубля.

1. Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик пополняет вклад на х млн рублей, где х — целое число. Найдите наименьшее значение х, при котором банк за четыре года начислит на вклад больше 6 млн рублей.

Решение.

№ года	сумма с учётом процентов и пополнения
0	10 млн
1
2
3
4

Чтобы найти сумму, которую банк начислит за четыре года, необходимо от итоговой суммы вклада вычесть первоначальную сумму и сумму пополнений за два года:

Так как х – наименьшее целое число млн., то млн. рублей.

Ответ: 5 млн. рублей.

1. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.

1. (Аналог задачи 1.3.1.) Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определённый процент, свой для каждого банка. В начале года Степан положил 60% некоторой суммы денег в первый банк, а оставшуюся часть суммы во второй банк. К концу года сумма этих вкладов стала равна 590 000 руб., а к концу следующего года 701 000 руб. Если бы Степан первоначально положил 60% своей суммы во второй банк, а оставшуюся часть в первый, то по истечении одного года сумма вкладов стала бы равной 610 000 руб. Какова была бы сумма вкладов в этом случае к концу второго года? (Ответ: 749 000 рублей)

1. (Аналог задачи 1.1.6.) Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей? (Ответ: в течении 8 года)

1. (Аналог задачи 1.5.4.) Близнецы Саша и Паша положили в банк по 50 000 рублей на три года под 10% годовых Однако через год и Саша, и Паша сняли со своих счетов соответственно 10% и 20% имеющихся денег. Ещё через год каждый из них снял со своего счёта соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу третьего года на счёте окажется большая сумма денег? На сколько рублей? (Ответ: у Саши больше на 1155 рублей)

1. (Аналог задачи 1.4.1.) Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения, после начисления процентов, он дополнительно вносил на счёт одну и ту же фиксированную сумму. К концу третьего года, после начисления процентов, оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму Владимир ежегодно добавлял ко вкладу? (Ответ: 240 000 рублей)

1. (Аналог задачи 1.2.4.) По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 20 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает на 21 % в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А». (Ответ: 19%)

1. (Аналог задачи 1.2.4.) По вкладу «А» банк в конце каждого года планирует увеличивать на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 5% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов. (Ответ: 13%)

1. (Аналог задачи 1.3.2.) Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 25 млн рублей. (Ответ: 12 млн. рублей)

1. (Аналог задачи 1.1.6.) В начале 2001 года Алексей приобрёл ценную бумагу за 19 000 рублей. В конце каждого года цена бумаги возрастает на 3000 рублей. В начале любого когда Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей? (Ответ: в начале 2005 года)

1. (Аналог задачи 1.2.4.) По вкладу «А» банк в конце каждого года планирует увеличивать на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 9 % в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов. (Ответ: 11)

1. (Аналог задачи 1.4.2.) По бизнес-плану предполагается изначально вложить в четырёхлетний проект 20 млн рублей. По итогам каждого года планируется прирост вложенных средств на 13% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по целому числу n млн рублей в первый и второй годы, а также по целому числу m млн рублей в третий и четвёртый годы. Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся. (Ответ: 7 млн. и 4 млн. рублей)

1. (Аналог задачи 1.4.3.) Вклад в размере 6 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размеров в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 15 млн рублей. (Ответ: 3 млн. рублей)

1. (Аналог задачи 1.5.6.) Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х млн рублей, где х — целое число. Найдите наименьшее значение х, при котором банк за четыре года начислит на вклад больше 7 млн рублей. (Ответ:

1. (Аналог задачи 1.5.6.) Вклад в размере 20 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х млн рублей, где х — целое число. Найдите наибольшее значение х, при котором банк за четыре года начислит на вклад меньше 17 млн рублей. (Ответ: 24)

1. (Аналог задачи 1.3.2.) Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на 3 млн рублей. Найдите наименьший размер первоначального вклада, при котором банк за четыре года начислит на вклад больше 5 млн рублей. (Ответ: 9 млн. рублей)

1. (Аналог задачи 1.3.3.) По бизнес-плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором они за два года станут больше 100 миллионов, а за четыре года станут больше 170 миллионов рублей. (Ответ: 41 млн. рублей)

1. (Аналог задачи 1.2.5.) По вкладу «А» банк в конце каждого года планирует увеличивать на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 8 % в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов. (Ответ: 12%)

1. (Аналог задачи 1.1.5.) Мистер Джонсон по случаю своего тридцатилетия открыл 1 октября 2010 года в банке счёт, на который он ежегодно кладёт 6000 рублей. По условиям вклада банк ежегодно начисляет 30% на сумму, находящуюся на счёте. Через 7 лет 1 октября 2017 года октября, следуя примеру мистера Джонсона, мистер Браун по случаю своего тридцатилетия тоже открыл в банке счёт, на который ежегодно кладёт по 13 800 рублей, а банк начисляет 69% в год. В каком году после очередного пополнения суммы вкладов мистера Джонсона и мистера Брауна сравняются, если деньги со счетов не снимают? (Ответ: в 2023 году)

10

Баба Валя — бизнесменша!
Баба Валя, накопив часть своей пенсии, решила улучшить своё материальное положение.
Она узнала, что в Сбербанке от пенсионеров принимают вклады под определенный процент годовых
и на этих условиях внесла свои сбережения в ближайшее отделение Сбербанка.
Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры,
есть коммерческий банк, в котором процент годовых для пенсионеров-вкладчиков в `43 3/4` раза выше, чем в Сбербанке.
Баба Валя не доверяла коммерческим банкам, но стремление улучшить свое материальное положение взяло верх.
После долгих колебаний и ровно через год после открытия счета в Сбербанке
баба Валя сняла половину образовавшейся суммы от ее вклада, заявив: «Такой навар меня не устраивает!»
И открыла счет в том коммерческом банке, о котором говорила ее соседка,
не теряя надежды на улучшение своего материального благосостояния.
Надежды-то оправдались: через год сумма бабы Вали в коммерческом банке превысила ее первоначальные кровные сбережения на 43%.
Сожалела баба Валя, что год назад в Сбербанке сняла не всю сумму, а лишь половину, однако, подумала: «А где же мы не теряли?.. «
Гендиректор коммерческого банка оказался хорошим: не оставил бабу Валю без навара!
А каков в Сбербанке процент годовых для пенсионеров?
Решение: