Задача про бензол физика егэ - Помощь в подготовке к экзаменам и поступлению

В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол (С₆H₆) при температуре кипения t = 80 °C. При сообщении бензолу некоторого количества теплоты часть его превращается в пар, который, расширяясь при постоянном давлении, совершает работу, поднимая поршень. Удельная теплота парообразования бензола L = 396·10³ Дж/кг, его молярная масса M = 78·10⁻³ кг/моль. Какая часть подводимого к бензолу количества теплоты идёт на увеличение внутренней энергии системы? Объёмом жидкого бензола и трением между поршнем и цилиндром пренебречь.

Спрятать решение

Решение.

Состояние идеального газа описывается уравнение Менделеева  — Клапейрона При кипении масса пара увеличивается, температура пара равна температуре кипения и остаётся постоянной пока весь бензол не выкипит, давление по условию также постоянно. Значит, выполняется соотношение

При передаче газу теплоты Q испаряется бензола. Найдём работу, которую совершает пар:

И по первому началу термодинамики

увеличение внутренней энергии составляет 90,5% от подводимого количества теплоты.

Ответ: 90,5%.

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: уравнение Менделеева—Клапейрона, первый закон термодинамики, выражения для работы газа при изобарном процессе и для внутренней энергии идеального одноатомного газа); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины.	3
Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.). И (ИЛИ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И (ИЛИ) Отсутствует пункт IV, или в нём допущена ошибка	2
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи	1
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла	0
Максимальный балл	3

Источник: ЕГЭ по физике 2020. Досрочная волна. Вариант 1

Источник

Физика — Разбор демоверсии ЕГЭ 2021

Физика ЕГЭ 2021 Демоверсия Решение задания 30

30. В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол (С₆H₆) при температуре кипения t = 80^оC . При сообщении бензолу количества теплоты Q часть его превращается в пар, который при изобарном расширении совершает работу А. Удельная теплота парообразования бензола L = 396 ⋅10³ Дж/кг, его молярная масса M = 78 ⋅ 10⁻³ кг/моль. Какая часть подведённого к бензолу количества теплоты переходит в работу? Объёмом жидкого бензола пренебречь.

Решение:

1. В соответствии с первым законом термодинамики подводимое количество теплоты равно сумме изменения внутренней энергии системы и совершённой механической работы:

При кипении бензола происходит его изобарное расширение. Работа пара

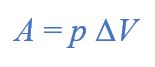
где p – атмосферное давление, Δ V – изменение объёма.

2. Считая пар идеальным газом, воспользуемся уравнением Клапейрона – Менделеева для определения изменения объёма за счёт испарившегося бензола массой

где M = 78⋅10⁻³ кг/моль – молярная масса бензола, T = 80 + 273 = 353 K – температура кипения бензола.

Отсюда

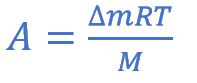
3. Количество теплоты Q, необходимое для испарения массы Δm бензола, пропорционально удельной теплоте парообразования L:

Искомая величина определяется отношением

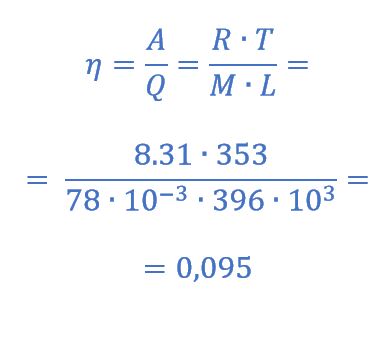
Ответ: 0,095

В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол (С₆Н₆) при температуре кипения t = 80 °C. При сообщении бензолу некоторого количества теплоты часть его превращается в пар, который при изобарном расширении совершает работу, поднимая поршень. Удельная теплота парообразования бензола L = 396 ∙ 10³ Дж/кг, а его молярная масса М = 78 • 10^-3 кг/моль. Какая часть подводимого к бензолу количества теплоты идёт на увеличение внутренней энергии системы? Объёмом жидкого бензола и трением между поршнем и цилиндром пренебречь.

Обоснуйте применимость используемых законов к решению задачи.

РЕШЕНИЕ

Обоснование

Согласно условию объёмом жидкого бензола следует пренебречь. В то же время возникающие при кипении пары бензола изобарно расширяются, увеличивая свой объём. И это увеличение объёма судя по условию, заметно. В объёме AV находятся только пары бензола, образовавшиеся при кипении. Следовательно, объём массы пара во много раз больше объёма жидкости, из которой он образовался. Отсюда следует, что объём в паре, приходящийся в среднем на одну молекулу Ugj12gsUdhhea1

ΔV/N, много больше объёма одной молекулы и поэтому среднее расстояние между соседними молекулами пара много больше их размера. Таким образом, пары бензола в этой задаче являются разреженным газом и их можно описывать моделью идеального газа.

Решение

1. В соответствии с первым началом термодинамики подводимое количество

теплоты равно сумме изменения внутренней энергии системы и совершённой механической работы: При кипении бензола происходит его изобарное

расширение. Работа пара где р — атмосферное давление, — изменение

объёма.

2. Считая пар идеальным газом, воспользуемся уравнением Менделеева —

Клапейрона для определения изменения объёма за счёт испарившегося бензола массой — молярная масса бензола,

Т = 80 + 273 = 353 К — температура кипения бензола. Отсюда

3. Количество теплоты Q, необходимое для испарения массы Δт бензола, пропорционально удельной теплоте парообразования Q = ΔmL.

4. Искомая величина определяется отношением

Ответ:

Источник

Молекулярная физика. Расчетная задача

В. З. Шапиро

Это задание также относится к высокому уровню сложности. Как правило, тематика этого задания «МКТ» и «Термодинамика». Какие-то задачи требуют только формульного решения, какие-то необходимо сопровождать графическими пояснениями термодинамических процессов. В любом случае, теоретический материал полностью соответствует кодификатору элементов содержания и спецификации контрольных измерительных материалов.

1. В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол $(C_{6}H_{6}),$ при температуре кипения При сообщении бензолу некоторого количества теплоты часть его превращается в пар, который при изобарном расширении совершает работу, поднимая поршень. Удельная теплота парообразования бензола $L = 396 cdot 10^{3}$ Дж/кг, а его молярная масса $M = 78cdot 10^{-3}$ кг/моль. Какая часть подводимого к бензолу количества теплоты идёт на увеличение внутренней энергии системы? Объёмом жидкого бензола и трением между поршнем и цилиндром пренебречь.

Необходимая теория:

Первый закон термодинамики

Внутренняя энергия

Дано: «СИ»

$L= 396 cdot 10^{3}$ Дж/кг;

$M = 78cdot 10^{3}$ кг/моль.

Найти: $displaystyle frac{Delta U}{Q}$ — ?

Решение:

Запишем первый закон термодинамики для изобарного процесса:

Выразим из этого равенства изменение внутренней энергии:

Для $displaystyle frac{Delta U}{Q}$ запишем:

$displaystyle frac{Delta U}{Q}=frac{Q - A$ (1).

Работу газа в изобарном процессе можно рассчитать по формуле:

с учетом уравнения Менделеева-Клапейрона получим:
(2).
При совершении работы давление бензола не изменяется, так как поршень в цилиндре легкоподвижный. Давление бензола все время остается равным атмосферному.

При этом
Delta m – масса бензола, превратившегося в газообразное состояние.

Количество теплоты, которое идет на превращение бензола в это состояние можно рассчитать по формуле:

Выражение для работы бензола (2) и количества теплоты (3) подставим в уравнение (1).

$displaystyle frac{Delta U}{Q}=1 - frac{frac{Delta m}{M}RT}{Delta mcdot L} .$

После сокращения на получим искомую формулу:
$displaystyle frac{Delta U}{Q}=1 - frac{RT}{Mcdot L}.$

Подставим численные значения и проведем расчет:

$displaystyle frac{Delta U}{Q}=1 - frac{8,31cdot 353}{78cdot {10}^{-3 }cdot 396cdot {10}^{-3 }}approx 0,905.$

Ответ: 0,905.

Секрет решения. На первый взгляд задача кажется несложной, но в ней «спрятаны» несколько искусственных приемов, до которых додуматься достаточно сложно. Первый прием – выражение $displaystyle frac{Delta U}{Q}=frac{Q-A$ Это математический ход, который сразу подсказывает, что конкретно надо находить в этой задаче.

Второй прием – получение равенства, используя уравнения Менделеева-Клапейрона Здесь надо придерживаться следующих рассуждений: если в левой части уравнения есть переменная величина (в этой задаче Delta V ), то и в правой части должна изменяться какая-то физическая величина (в этой задаче Delta m ). Можно сказать еще проще: если в левой части равенства есть знак дельта « Delta «, то и в правой части он должен обязательно появиться. В крайнем случае, можно «перебрать» все величины из правой части: температура не может изменяться, так как при парообразовании она всегда постоянна; молярная масса также неизменна, потому что речь идет об одном и том же газе; R – табличная величина. Остается только Эти рассуждения помогут понять ситуацию, описанную в задаче и правильно ее решить.

2. Одно и то же постоянное количество одноатомного идеального газа расширяется из одного и того же начального состояния $p_{1}, V_{1}$ до одного и того же конечного объёма $V_{2}$ первый раз по изобаре 1–2, а второй по адиабате 1–3 (см. рисунок). Отношение работы газа в процессе 1–2 к работе газа в процессе 1–3 равно $displaystyle frac{A$ =к=2. Чему равно отношение х количества теплоты $Q_{12},$ полученного газом от нагревателя в ходе процесса 1–2, к модулю изменения внутренней энергии газа $left|U_{3} - U_{1} right|$ в ходе процесса 1–3?

Необходимая теория:

Первый закон термодинамики

Внутренняя энергия

Изопроцессы

Дано:

1–2 р=const;

2–3 Q=const;
$displaystyle frac{A$ =к=2.
Найти: $displaystyle frac{Q_{12}}{left| U_3 - U_1right|}?$

Решение:

Для участка 1–2 применим первый закон термодинамики с учетом изобарного процесса.

$Q_{12}=A$

Работу газа при расширении найдем как площадь прямоугольника под графиком.

Изменение внутренней энергии одноатомного идеального газа запишем в виде формулы:

$displaystyle {Delta U}_{12}=frac{3}{2}vartheta Rleft(T_2 - T_1right) (3).$
Применим уравнение Менделеева-Клапейрона:

Тогда (3) примет вид:

$displaystyle {Delta U}_{12}=frac{3}{2}left(vartheta RT_2 - vartheta RT_1right)=frac{3}{2}left(p_1V_2 - p_1V_1right)=frac{3}{2}p_1left(V_2 - V_1right)$ (4).

Таким образом количество теплоты на участке 12 равно:

$displaystyle Q_{12}=p_1left(V_2 - V_1right)+frac{3}{2}p_1left(V_2 - V_1right)=frac{5}{2}p_1left(V_2 - V_1right)$ (5).

Для участка 1–3 применим первый закон термодинамики с учетом адиабатного процесса.

$Q_{13}=A$ но так как $Q_{13}=0,$ запишем:

0=A или Это выражение означает, что газ на участке 13 совершает работу за счет уменьшения своей внутренней энергии.

Учтем, что по условию $displaystyle frac{A$ =к=2, тогда:

$- displaystyle {Delta U}_{13}=A$

Используя (5) и (6) получим искомую формулу:

$displaystyle frac{Q_{12}}{left| U_3 - U_1right|}=frac{Q_{12}}{| - {Delta U}_{13}|}=frac{frac{5}{2}p_1left(V_2 - V_1right)}{frac{p_1left(V_2 - V_1right)}{2}}=frac{5}{2}:frac{1}{2}=5.$

Ответ: 5.

Секрет решения. Несмотря на громоздкие расчеты и обилие разных индексов в уравнениях, задача является среднего уровня сложности. Надо знать:

— первый закон термодинамики;

— его применение к изопроцессам;

— формулы, выражающие работу газа и его внутреннюю энергию (только для одноатомного идеального газа);

— уметь «читать» графики;

— понимать, что при расширении газ совершает положительную работу, при сжатии – отрицательную работу;

— проводить рассуждения о том, откуда газ берет энергию для совершения работы (за счет своей внутренней энергии или за счет поступления энергии извне);

— указанные пункты описывать соответствующими уравнениями.

Суть любой задачи по физике – описание физических процессов математическими уравнениями, которые надо решить удобным (рациональным) способом.

3. В тепловом двигателе 1 моль одноатомного разряженного газа совершает цикл 1–2–3–4–1, показанный на графике в координатах p–T, где p – давление газа, Т – абсолютная температура. Температуры в точках 2 и 4 равны и превышают температуру в точке 1 в 2 раза. Определите КПД цикла.

Дано:

$T_{2} =T_{4} = 2T_{1}.$

Найти: eta – ?

Решение:

КПД теплового двигателя определяется формулой:

– полезная работа, совершенная газом за цикл, Q – полученное за цикл количество теплоты. Можно графически рассчитать работу, если перерисовать данный цикл в координатах рV. Проведем анализ каждого процесса.

12: V=const, p↑, T↑;

23: p=const, T↑, V↑;

34: V=const, p↓, T↓;

41: p=const, T↓, V↓.

В координатах рV график будет иметь вид:

Работа газа за цикл будет определяться площадью прямоугольника 1-2-3-4.

Учтем, что $T_{2} =T_{4} = 2T_{1}.$

Поэтому (на основании закона Шарля).

$V_3=V_4={2V}_2={2V}_1$ (на основании закона Гей-Люссака).

Таким образом, можно выразить полезную работу через p_1 и V_1.

Газ получает положительное количество теплоты на участках 1–2 и 2–3.
$Q=Q_{12}+Q_{23}.$

Применим к этим участкам первый закон термодинамики.
$Q_{12}=Delta U_{12}+A$

Но работа газа на этом участке равна нулю, так как процесс изохорный.
$displaystyle Q_{12}=Delta U_{12}=frac{3}{2}vartheta Rleft(T_2 - T_1right)=frac{3}{2}(vartheta RT_2 - vartheta RT_1).$

С учетом уравнения Менделеева-Клапейрона и получим:

$displaystyle Q_{12}=frac{3}{2}left(p_2V_2 - p_1V_1right)=frac{3}{2}left(2p_1V_1 - p_1V_1right)=frac{3}{2}p_1V_1=1,5p_1V_1$ (2).

Для участка 23 первый закон термодинамики примет вид:

$Q_{23}=Delta U_{23}+A$
Работа определяется площадью прямоугольника под участком 23.

$displaystyle Delta U_{23}=frac{3}{2} vartheta Rleft(T_3 - T_2right)=frac{3}{2}(vartheta RT_3 - vartheta RT_2)$ (4).

С учетом уравнения Менделеева-Клапейрона (4) примет вид:

$displaystyle Delta U_{23}=frac{3}{2}left(p_3V_3 - p_2V_2right)=frac{3}{2}left(2p_1cdot 2V_1 - 2p_1cdot V_1right)=frac{3}{2}cdot 2p_1cdot V_1=3p_1V_1$ (5).

Таким образом, полученное количество теплоты на участке 23 равно:
$Q_{23}=2p_1V_1+3p_1V_1=5p_1V_1.$

Общее количество теплоты, полученное за цикл:

(6).

Полученные выражения из (1) и (6) подставим в формулу КПД.

Ответ: 15,3%.

Секрет решения. За задачи на определение КПД тепловой машины по графику надо получать максимальные 3 балла. Эти задания сопровождаются большими расчетами, поэтому на первое место надо ставить внимательность их выполнения.

Необходимо выделить следующие моменты в решении:

— определять работу графически можно только в координатах рV;

— если в условии дан график в других координатах, то его надо перечертить в рV;

— поэтапно применять первый закон термодинамики и газовые законы для всех процессов;

— свести в единую формулу полученные данные для расчета КПД.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 30 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.03.2023

Источник

Обоснование:
Согласно условию объёмом жидкого бензола следует пренебречь. В то же время возникающие при кипении пары бензола изобарно расширяются, увеличивая свой объём. И это увеличение объёма ( Delta V ), судя по условию, заметно. В объёме ( Delta V ) находятся только пары бензола, образовавшиеся при кипении. Следовательно, объём массы пара во много раз больше объёма жидкости, из которой он образовался. Отсюда следует, что объём в паре, приходящийся в среднем на одну молекулу ( Delta V/N ), много больше объёма одной молекулы и поэтому среднее расстояние между соседними молекулами пара много больше их размера. Таким образом, пары бензола в этой задаче являются разреженным газом и их можно описывать моделью идеального газа.

Решение:
1. В соответствии с первым началом термодинамики подводимое количество теплоты равно сумме изменения внутренней энергии системы и совершённой механической работы: ( Q = Delta U + A ). При кипении бензола происходит его изобарное расширение. Работа пара ( A = pDelta V ), где ( p ) — атмосферное давление, ( Delta V ) — изменение объёма.

2. Считая пар идеальным газом, воспользуемся уравнением Менделеева Клапейрона для определения изменения объёма за счёт испарившегося бензола ( Delta m:pDelta V = frac{{Delta m}}{M}RT ), где ( M = 78 cdot {10^{ — 3}} ) кг/моль — молярная масса бензола, ( T = 80 + 273 = 353 ) К — температура кипения бензола. Отсюда ( A = frac{{Delta mRT}}{M} ).

3. Количество теплоты ( Q ), необходимое для испарения массы ( Delta m ) бензола, пропорционально удельной теплоте парообразования ( Q = Delta mL ).

4. Искомая величина определяется отношением

( eta = frac{{Delta U}}{Q} = frac{{Q — A}}{Q} = )( 1 — frac{{RT}}{{ML}} = 1 — frac{{8,31 cdot 353}}{{78 cdot {{10}^{ — 3}} cdot 396 cdot {{10}^3}}} )( approx 0,905 ).

Ответ: ( eta ) ≈ 0,905.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке
При обращении указывайте id этого вопроса — 15468.

Источник

Задание №10322

В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол (С₆H₆) при температуре кипения t = 80^o C. При сообщении бензолу количества теплоты Q часть его превращается в пар, который при изобарном расширении совершает работу А. Удельная теплота парообразования бензола L =396⋅10³ Дж/кг, его молярная масса M=78⋅10⁻³кг/моль. Какая часть подведённого к бензолу количества теплоты переходит в работу? Объёмом жидкого бензола пренебречь.

Задание состоит в варианте: