На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Спрятать решение
Решение.
Введём обозначения, приведённые на рисунке. Здесь AC — плечи «журавля» до опускания, BD — после, AH — высота, на которую поднялся конец короткого плеча, CK — высота, на которую опустился конец длинного. Рассмотрим треугольники AOB и COD, углы AOB и COD равны, как вертикальные, следовательно, равны и углы при основаниях:
Следовательно, треугольники AOB и COD подобны по двум углам, то есть
Рассмотри прямые AB и CD, их пересекает секущая BD углы, обозначенные на рисунке 1 и 2 накрест лежащие и равны друг другу, следовательно, прямые AB и CD параллельны. Стороны углов 3 и 4 параллельны друг другу, следовательно, они равны.
Рассмотрим треугольники AHB и CDK, они прямоугольные, имеют равные углы, следовательно, они подобны, значит:
Ответ: 2.
Примечание
Можно привести несколько иное доказательство подобия треугольников AHB и На приведённой ниже картинке есть два маленьких треугольника обозначенные AHM и DKL, они прямоугольные и одна пара углов равна друг другу как накрест лежащие при параллельных прямых, следовательно, они подобны.
Затем, можно заметить, что у треугольников AMB и DLC соответственные углы, не важно какие, равны друг другу, потому что их стороны параллельны, следовательно, треугольники подобны. Аналогично с треугольниками AHB и Из трёх пар подобий этих треугольников следует, что треугольники AHB и CDK подобны.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо – 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Решение
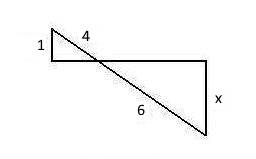
Данный рисунок можно перерисовать в следующий вид для облегчения:
Рассмотрим треугольники (AOD) и (BOC).
Углы (AOD) и (COB) раны, т.к. они вертикальные.
Угол (OAD) равен углу (OCB) и равен (90^{circ}).
Углы (ADO) и (CBO) равны, т.к. они внутренние накрест-лежащие.
Получается, что треугольники (AOD) и (BOC) подобны (если два угла одного треугольника равны двум угла другого треугольника). Значит, можно составить следующее соотношение сторон:
(displaystyle frac{BO}{OD}=frac{BC}{AD};)
(displaystyle frac{3}{1}=frac{BC}{0,5};)
(BC=1,5).
Получилось, что на (1,5) метра опустится конец длинного плеча.
Ответ: (1,5).
Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 10) (Купить книгу)
Решение:
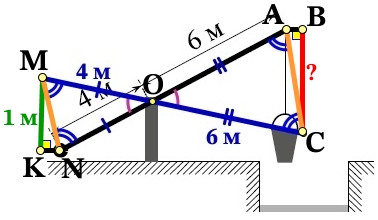
Изобразим условие задания:
Получим подобные треугольники ΔОMN и ΔОАС, по трём равным углам (по равному вертикальному углу и равные углы при основаниях равнобедренных треугольников).
В подобных треугольниках, соответствующие стороны пропорциональны:
frac{MN}{AC}=frac{MO}{AO}\frac{MN}{AC}=frac{4}{6}\frac{MN}{AC}=frac{2}{3}
ΔMNK и ΔАВС подобные по двум равным углам (по одному прямому углу и ∠MNK = CAB, величины которых являются разностью между равными накрест лежащими углами ∠KNA = ∠BAN, при АВ||KN и секущей АN и равными углами ∠MNO = ∠CAO при основаниях равнобедренных треугольников ΔОMN и ΔОАС).
В подобных треугольниках, соответствующие стороны пропорциональны:
frac{MN}{AC}=frac{MK}{BC}\frac{2}{3}=frac{1}{BC}\BC=frac{1cdot 3}{2}=1,5
Ответ: 1,5.
Привет! Цель нашего проекта помочь тебе подготовиться к ЕГЭ (или ОГЭ).
У нас более 1000 заданий с подробным решением, сервис, запоминающий твои ответы, и удивительная система тестирования.
Обо всем по порядку расскажу тебе после быстрой регистрации.
Присоединиться к ExamMe
ОГЭ по Математике
Задание 1. Числа и вычисления (0/10)
Задание 2. Числовые неравенства, координатная прямая (0/10)
Задание 3. Числа, вычисления и алгебраические выражения (0/10)
Задание 4. Уравнения и неравенства (0/10)
Задание 5. Чтение графиков функций (0/10)
Задание 6. Арифметические и геометрические прогрессии (0/10)
Задание 7. Алгебраические выражения (0/10)
Задание 8. Уравнения, неравенства и их системы (0/10)
Задание 9. Треугольники, четырёхугольники, многоугольники и их элементы (0/10)
Задание 10. Окружность, круг и их элементы (0/10)
Задание 11. Площади фигур (0/10)
Задание 12. Фигуры на квадратной решётке (0/10)
Задание 13. Верные и неверные геометрические высказывания (0/10)
Задание 14. Анализ диаграмм, таблиц, графиков (0/10)
Задание 15. Анализ диаграмм, таблиц, графиков (0/10)
Задание 16. Простейшие текстовые задачи (0/10)
Задание 17. Практические задачи по геометрии (0/10)
Задание 18. Анализ диаграмм (0/10)
Задание 19. Статистика и вероятности (0/10)
Задание 20. Расчеты по формулам (0/10)
Задание 21. Алгебраические выражения, уравнения, неравенства и их системы (0/10)
Задание 22. Текстовые задачи (0/10)
Задание 23. Функции и их свойства. Графики функций (0/10)
Задание 24. Геометрическая задача на вычисление (0/10)
Задание 25. Геометрическая задача на доказательство (0/10)
Задание 26. Геометрическая задача повышенной сложности (0/10)
Начать проверочный тест
На рисунке изображен колодец с…
Задание:
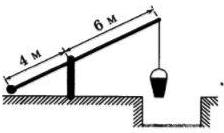
На рисунке изображен колодец с «журавлем». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Решение:
Изобразим схематично колодец с «журавлем», когда конец короткого плеча поднимется на 1 м(см. рис.):
Получили два подобных треугольника(по двум углам).
Значит, стороны пропорциональны.
Найдем $x$(искомую величину):
$frac{4}{6}=frac{1}{x}$
$4cdot x=1cdot 6$
$x=6:4$
$x=1,5$
Значит, на 1,5 метра опустится конец длинного плеча.
Ответ:
1,5
Задание добавил(а)
О задание:
Источник условия: Книга: ОГЭ 2017. Математика. 3 модуля. Типовые тестовые задания. Под ред. Ященко И.В.
Источник решения: авторское
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
Перейти к содержанию
На чтение 1 мин Просмотров 2 Опубликовано 5 марта, 2023
Решение №3663 На рисунке изображён колодец с «журавлём». Решение и ответы на задачи на официальном сайте источника онлайн.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Варианты ответов и решение задачи ТУТ: https://ege314.ru/8-prikladnaya-geometriya/reshenie-3663/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.