Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Тип 8 № 41895 
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием 
см. Расстояние 
от линзы до лампочки может изменяться в пределах от 330 до 350 см, а расстояние 
от линзы до экрана — в пределах от 80 до 105 см. Изображение на экране будет четким, если выполнено соотношение 
Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
Аналоги к заданию № 27970: 28205 41891 41895 519511 519537 541052 541257 28207 28209 28211 … Все
Классификатор алгебры: Рациональные уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 60 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 92 до 115 см, а расстояние d2 от линзы до экрана – в пределах от 140 до 160 см. Изображение на экране будет четким, если выполнено соотношение frac{1}{d_{1}}+frac{1}{d_{2}}=frac{1}{f}. На каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было чётким. Ответ выразите в сантиметрах.
Источники: fipi, os.fipi, Пробный ЕГЭ 2018, Основная волна 2017
Решение:
f = 60 см
frac{1}{d_{1}}+frac{1}{d_{2}}=frac{1}{f}\frac{1}{d_{1}}+frac{1}{d_{2}}=frac{1}{60}\frac{1}{d_{1}}=frac{1}{60}-frac{1}{d_{2}}
По условию расстояние до лампочки d1 должно быть наименьшим, тогда выражение frac{1}{d_{1}} будет наибольшим, что бы оно было наибольшим в правой части должны вычитать как можно меньше frac{1}{d_{1}}, тогда d2 должно быть максимальным, т.е. d2 = 160.
frac{1}{d_{1}}=frac{1}{60}-frac{1}{160}\frac{1}{d_{1}}=frac{8-3}{480}\frac{1}{d_{1}}=frac{5}{480}\frac{1}{d_{1}}=frac{1}{96}\d_{1}=96
Ответ: 96.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 32
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Выразим d1 из соотношения, при выполнении которого увеличенное изображение будет чётким:
frac{1}{d_{1}} + frac{1}{d_{2}} = frac{1}{f}
frac{1}{d_{1}} = frac{1}{f} — frac{1}{d_{2}}
Приводим правую часть к общему знаменателю и выражаем d1:
frac{1}{d_{1}} = frac{d_{2}-f}{fcdot d_{2}}
d_{1} = frac{fcdot d_{2}}{d_{2}-f}
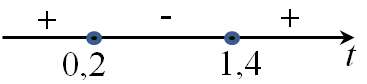
Определим, какое расстояние d1 будет при граничных значениях d2 (d2 = 90 см и d2 = 120 см) и найдем среди них наименьшее. Фокусное расстояние линзы f = 30 см.
Для d2 = 120 см получим:
d_{1} = frac{30 cdot 120}{120-30} = frac{30 cdot 120}{90} = 40 см
Для d2 = 90 см:
d_{1} = frac{30 cdot 90}{90-30} = frac{30 cdot 90}{60} = 45 см
Наименьшее из них – 40 см.
Условие задачи
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием 
см.
Расстояние 
от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние 
от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение 
Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.
Решение
Фокусное расстояние линзы известно.
Но какое же значение 
(расстояние от линзы до экрана) надо подставлять в формулу?
Нам надо найти наименьшее расстояние от лампочки до линзы .
Если – наименьшее, то обратная величина 
будет наибольшей.
Поскольку 
– константа, второе слагаемое 
в формуле линзы должно быть наименьшим, а обратная ему величина – наибольшей, то есть равной 180. Подставим данные в формулу:
Ответ:
36.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Решение. Задание 10, Вариант 3» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Для получения на экране увеличенного изображения
Дата: 2014-10-10
16580
Категория: Физические задачи
Метка: ЕГЭ-№8
27970. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f =30 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение
Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было четким. Ответ выразите в сантиметрах.
Первый способ. Расстояние d2 лежит в пределах от 150 до 180 см. Решим два уравнения, подставив пограничные значения в формулу и выберем меньшее d1:
Наименьшее расстояние равно 36 сантиметрам.
Второй способ. Выразим из формулы d2:
Сказано, что d2 лежит в пределах от 150 до 180 см, значит
Это двойное неравенство можно записать в виде двух неравенств
Получили 36 ≤ d1 ≤ 37,5. Наименьшее расстояние 36 сантиметров.
Ответ: 36
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
ЕГЭ Профиль №8. Рациональные уравнения и неравенства
Скачать файл в формате pdf.
ЕГЭ Профиль №8. Рациональные уравнения и неравенства
| Задача 1. При температуре ({0^ circ }{text{C}}) рельс имеет длину ({l_0} = 10) м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону (lleft( {{t^ circ }} right) = {l_0}left( {1 + alpha cdot {t^ circ }} right)), где (alpha = 1,2 cdot {10^{ — 5}}{left( {{}^ circ {text{C}}} right)^{ — 1}}) — коэффициент теплового расширения, ({t^ circ }) — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
Ответ
ОТВЕТ: 25. Решение
l – длина рельса. Так как рельс должен удлиниться на 3 мм, то его длина будет равна: l = 10 м + 3 мм = 10 м + 0,003 м = 10,003 м. (10,003 = 10left( {1 + 1,2 cdot {{10}^{ — 5}} cdot {t^ circ }} right)) (10,003 = 10 + 12 cdot {10^{ — 5}} cdot {t^ circ }) (12 cdot {10^{ — 5}} cdot {t^ circ } = 0,003) ({t^ circ } = frac{{0,003}}{{12 cdot {{10}^{ — 5}}}} = frac{{0,003 cdot {{10}^5}}}{{12}} = frac{{300}}{{12}} = 25) Ответ: 25. |
| Задача 2. Некоторая компания продает свою продукцию по цене (p = 500) руб. за единицу, переменные затраты на производство одной единицы продукции составляют (v = 300) руб., постоянные расходы предприятия (f = 700,,000) руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле ( pileft( q right) = qleft( {p — v} right) — f. ) Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300 000 руб.
Ответ
ОТВЕТ: 5 000. Решение
(pi left( q right)) – операционная прибыль предприятия должна быть не меньше 300 000 руб. Следовательно, (pi left( q right) geqslant 300,,000) (qleft( {500 — 300} right) — 700,,000 geqslant 300,,000) (200,q geqslant 1,,000,,000) (q geqslant 5,,000) Наименьший месячный объём производства: (q = 5,,000.) Ответ: 5 000. |
| Задача 3. После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле (h = 5,{t^2}), где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Ответ
ОТВЕТ: 1. Решение
До дождя время падения камешков: ({t_1} = 0,6,,c.) Тогда до дождя расстояние до воды: ({h_1} = 5 cdot {0,6^2} = 1,8,) м. Так как уровень воды после дождя поднялся, то время падения камешков уменьшится на 0,2 с; то есть: ({t_2} = 0,6 — 0,2 = 0,4,,c.) Тогда после дождя расстояние до воды: ({h_2} = 5 cdot {0,4^2} = 0,8,) м. Следовательно, уровень воды должен подняться на: (vartriangle h = {h_1} — {h_2} = 1,8 — 0,8 = 1,) м. Ответ: 1. |
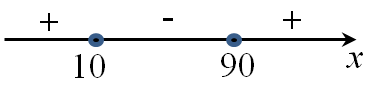
| Задача 4. Зависимость объeма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаeтся формулой (q = 100 — 10p). Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле (rleft( p right) = q cdot p). Определите наибольшую цену p, при которой месячная выручка (rleft( p right)) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.
Ответ
ОТВЕТ: 6. Решение
Задача сводится к решению неравенства: (rleft( p right) geqslant 240;,,,,,,q cdot p geqslant 240;,,,,pleft( {100 — 10p} right) geqslant 240) ( — 10{p^2} + 100p — 240 geqslant 0,,|,,:,left( { — 10} right)) ({p^2} — 10p + 24 leqslant 0) ({p^2} — 10p + 24 = 0;,,,,{p_1} = 4,,,,,,{p_2} = 6) Ответ: 6. |
| Задача 5. Высота над землeй подброшенного вверх мяча меняется по закону (hleft( t right) = 1,6 + 8t — 5{t^2}), где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?
Ответ
ОТВЕТ: 1,2. Решение
Так как мяч должен находиться на высоте не менее трёх метров, то задача сводится к решению неравенства: (hleft( t right) geqslant 3). (1,6 + 8t — 5{t^2} geqslant 3) (5{t^2} — 8t + 1,4 leqslant 0) (5{t^2} — 8t + 1,4 = 0;,,,,,,{t_1} = 0,2,,,,,,,{t_2} = 1,4) Ответ: 1,2. |
| Задача 6. Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна (P = mleft( {frac{{{v^2}}}{L} — g} right)), где m — масса воды в килограммах, v — скорость движения ведёрка в м/с, L — длина верёвки в метрах, g — ускорение свободного падения (считайте (g = 10) м/с2). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с.
Ответ
ОТВЕТ: 2. Решение
Вода не будет выливаться, если (Pleft( v right) geqslant 0.) Следовательно, задача сводится к решению неравенства: (mleft( {frac{{{v^2}}}{L} — g} right) geqslant 0). Так как m > 0, то (frac{{{v^2}}}{L} — g geqslant 0), где g = 10 м/c2 и L = 40 см = 0,4 м. (frac{{{v^2}}}{{0,4}} — 10 geqslant 0;,,,,,,,,{v^2} geqslant 4) Следовательно, (v in left( { — infty ;, — 2} right] cup left[ {2;,infty } right)), но так как v > 0, то (v in left[ {2;,infty } right)). Наименьшая скорость v = 2 м/с. Ответ: 2. |
| Задача 7. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону (Hleft( t right) = {H_0} — sqrt {2g{H_0}} ,k,t + frac{g}{2}{k^2}{t^2}), где t — время в секундах, прошедшее с момента открытия крана, ({H_0} = 20) м — начальная высота столба воды, (k = frac{1}{{50}}) — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте (g = 10) м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?
Ответ
ОТВЕТ: 50. Решение
Так как в баке должна остаться четверть первоначального объёма воды, то (H = frac{1}{4}{H_0} = frac{1}{4} cdot 20 = 5). (frac{g}{2}{k^2}{t^2} — sqrt {2g{H_0}} ,k,t + {H_0} = H) Пусть k t = x. Тогда: (frac{{10}}{2}{x^2} — sqrt {2 cdot 10 cdot 20} ,x + 20 = 5) (5{x^2} — 20,x + 15 = 0,,|,,:,,,5,,,,,,,,, Leftrightarrow ,,,,,,,,,{x^2} — 4,x + 3 = 0,) ({x_1} = 1;,,,,,,,,,,,,,,,,,,,,,,{x_2} = 3) (k,t = 1;,,,,,,,,,,,,,,,,,,,,k,t = 3) (frac{1}{{50}},t = 1;,,,,,,,,,,,,,,,,,,,,frac{1}{{50}},t = 3) (,{t_1} = 50;,,,,,,,,,,,,,,,,,,,,,{t_2} = 150) Следовательно, через t1 = 50 с в баке останется четверть первоначального объёма. Ответ: 50 Замечание: Почему не подходит t2 = 150 с? Если в исходную формулу вместо H подставить 0, то есть определить за какое время вода полностью вытечет из бака, то получим t = 100. Следовательно, через 100 секунд в баке не останется воды. Поэтому t2 = 150 с не подходит. |
| Задача 8. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону (Hleft( t right) = a,{t^2} + b,t + {H_0}), где ({H_0} = 4) м — начальный уровень воды, (a = frac{1}{{100}}) м/мин2, и (b = — frac{2}{5}) м/мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
Ответ
ОТВЕТ: 20. Решение
Так как спрашивают в течение какого времени вода будет вытекать из бака, то H = 0. Следовательно, задача сводится к решению квадратного уравнения: (frac{1}{{100}}{t^2} — frac{2}{5}t + 4 = 0,,|, cdot ,100,,,,, Leftrightarrow ,,,,{t^2} — 40t + 400 = 0,,,, Leftrightarrow ,,,,t = 20.) Следовательно, за 20 минут вся вода вытечет из бака. Ответ: 20. |
| Задача 9. Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой (y = a,{x^2} + b,x), где (a = — frac{1}{{100}}) м-1, (b = 1) — постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
Ответ
ОТВЕТ: 90. Решение
Высота стены равна 8 м. Так как камни должны пролетать над стеной на высоте не менее 1 метра, то задача сводится к решению неравенства: (y geqslant 8 + 1 = 9) ( — frac{1}{{100}}{x^2} + x geqslant 9,,|, cdot ,left( { — 100} right),,,,,,, Leftrightarrow ,,,,,,{x^2} — 100x + 900 leqslant 0,) ({x^2} — 100x + 900 = 0,,,,,,,, Leftrightarrow ,,,,,,{x_1} = 10;,,,,,,{x_2} = 90) Следовательно, (x in left[ {10;,90} right]) и наибольшее расстояние на котором нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра равно 90 метров. |
| Задача 10. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением (Tleft( t right) = {T_0} + b,t + a,{t^2}), где t — время в минутах, ({T_0} = 1400) К, (a, = — 10) К/мин2, (b = 200,) К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах
Ответ
ОТВЕТ: 2. Решение
Определим когда температура нагревателя будем не более 1 760 К. Для этого необходимо решить неравенство: (Tleft( t right) leqslant 1760.) (1400 + 200t — 10{t^2} leqslant 1760,,,,, Leftrightarrow ,,,,, — 10{t^2} + 200t — 360 leqslant 0,,|,:,left( { — 10} right)) ({t^2} — 20t + 36 geqslant 0,,,,, Leftrightarrow ,,,,,t in left( { — infty ;,2} right] cup left[ {18;,infty } right).) Через 2 минуты после включения прибор нагреется до 1760 К, и при дальнейшем нагревании может испортиться. Таким образом, наибольшее время после начала работы когда прибор нужно отключить это 2 минуты. Ответ: 2. |
| Задача 11. Для сматывания кабеля на заводе используют лебедку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону (varphi = omega ,t + frac{{beta ,{t^2}}}{2}), где t — время в минутах, — начальная угловая скорость вращения катушки, а — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки (varphi ) достигнет ({1200^ circ }). Определите время после начала работы лебедки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
Ответ
ОТВЕТ: 20. Решение
Задача сводится к решению следующего неравенства: (varphi leqslant 1200.) (20t + frac{{4{t^2}}}{2} leqslant 1200,,,,, Leftrightarrow ,,,,,{t^2} + 10t — 600 leqslant 0,,,,, Leftrightarrow ,,,,,t in left[ { — 30;,20} right].) Следовательно, не позже чем через 20 минут рабочий должен проверить работу лебёдки. Ответ: 20. |
| Задача 12. Мотоциклист, движущийся по городу со скоростью ({v_0} = 57) км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением (a = 12) км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением (S = {v_0}t + frac{{a,{t^2}}}{2}). Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
Ответ
ОТВЕТ: 30. Решение
Мотоциклист будет находиться в зоне функционирования сотовой связи, если (S leqslant 30.) Следовательно, задача сводится к решению следующего неравенства: (57t + frac{{12{t^2}}}{2} leqslant 30,,,,, Leftrightarrow ,,,,,2{t^2} + 19t — 10 leqslant 0,,,,, Leftrightarrow ,,,,,t in left[ { — 10;,0,5} right].) Так как (t geqslant 0,) то (t in left[ {0;,0,5} right].) Следовательно, наибольшее время t = 0,5 ч = 30 минут. Ответ: 30. |
| Задача 13. Автомобиль, движущийся в начальный момент времени со скоростью ({v_0} = 20) м/с, начал торможение с постоянным ускорением (a = 5) м/с2. За t секунд после начала торможения он прошёл путь (S = {v_0}t — frac{{a,{t^2}}}{2})(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
Ответ
ОТВЕТ: 2. Решение
Задача сводится к решению следующего квадратного уравнения: (30 = 20t — frac{{5{t^2}}}{2},,,,, Leftrightarrow ,,,,,{t^2} — 8t + 12 = 0,,,,, Leftrightarrow ,,,,,{t_1} = 2,,,,,{t_2} = 6.) Следовательно, через 2 секунды автомобиль проедет 30 метров. Ответ: 2. Замечание: Почему не подходит t2 = 6 с? Автомобиль остановится в тот момент, когда будет пройден наибольший путь: (S = 20t — frac{{5{t^2}}}{2}.) Парабола, направленная ветвями вверх, достигнет наибольшего значения в вершине: ({t_0} = — frac{b}{{2a}} = — frac{{20}}{{2 cdot left( { — 2,5} right)}} = 4.) Следовательно, через 4 секунды автомобиль остановится, поэтому t2 = 6 с не подходит. |
Следовательно, 
Задача 14. Деталью некоторого прибора является вращающаяся катушка. Она состоит из трех однородных соосных цилиндров: центрального массой (m =  кг и радиуса (R = 10) см, и двух боковых с массами (M = 1) кг и с радиусами (R + h). При этом момент инерции катушки относительно оси вращения, выражаемый в , задается формулой (I = frac{{left( {m + 2M} right){R^2}}}{2} + Mleft( {2Rh + {h^2}} right)). При каком максимальном значении h момент инерции катушки не превышает предельного значения ? Ответ выразите в сантиметрах
Ответ
ОТВЕТ: 5. Решение
Задача сводится к нахождению наибольшего решения следующего неравенства: (I leqslant 625.) (frac{{left( {8 + 2 cdot 1} right) cdot {{10}^2}}}{2} + 1 cdot left( {2 cdot 10 cdot h + {h^2}} right) leqslant 625,,,,,, Leftrightarrow ,,,,,{h^2} + 20h — 125 leqslant 0,,,,, Leftrightarrow ,,,,,h in left[ { — 25;,5} right].) Следовательно, наибольшее значение h = 5 см. Ответ: 5. |
| Задача 15. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: ({F_A} = rho ,g,{l^3}), где l — длина ребра куба в метрах, — плотность воды, а g — ускорение свободного падения (считайте (g = 9,8) Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78 400 Н? Ответ выразите в метрах.
Ответ
ОТВЕТ: 2. Решение
Задача сводится к нахождению наибольшего решения следующего неравенства: ({F_A} leqslant 78,400.) (1000 cdot 9,8 cdot {l^3} leqslant 78400,,,,,, Leftrightarrow ,,,,,{l^3} leqslant 8,,,,, Leftrightarrow ,,,,,l leqslant 2.) Следовательно, наибольшее значение l = 2 м. Ответ: 2. |
| Задача 16. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: ({F_A} = alpha ,rho ,g,{r^3}), где (alpha = 4,2) — постоянная, r — радиус аппарата в метрах, — плотность воды, а g — ускорение свободного падения (считайте (g = 10) Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах
Ответ
ОТВЕТ: 2. Решение
Задача сводится к нахождению наибольшего решения следующего неравенства: ({F_A} leqslant 336,000.) (4,2 cdot 1000 cdot 10 cdot {r^3} leqslant 336000,,,,,, Leftrightarrow ,,,,,{r^3} leqslant 8,,,,, Leftrightarrow ,,,,,r leqslant 2.) Следовательно, наибольшее значение r = 2 м. Ответ: 2. |
| Задача 17. Для определения эффективной температуры звезд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвёртой степени температуры: (P = sigma ,S,{T^4}), где (sigma = 5,7 cdot {10^{ — 8}}) — постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь (S = frac{1}{{16}} cdot {10^{20}})м2, а излучаемая ею мощность P не менее (9,12 cdot {10^{25}}) Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
Ответ
ОТВЕТ: 4 000. Решение
Задача сводится к решению следующего уравнения: (9,12 cdot {10^{25}} = 5,7 cdot {10^{ — 8}} cdot frac{1}{{16}} cdot {10^{20}} cdot {T^4},,,,, Leftrightarrow ,,,,,{T^4} = frac{{16 cdot 9,12 cdot {{10}^{25}}}}{{5,7 cdot {{10}^{12}}}}) (T = sqrt[4]{{frac{{16 cdot 912 cdot {{10}^{12}}}}{{57}}}} = sqrt[4]{{16 cdot 16 cdot {{10}^{12}}}} = 2 cdot 2 cdot {10^3} = 4,000,,{text{K}}{text{.}}) Ответ: 4 000. |
| Задача 18. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием (f = 30) см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение (frac{1}{{{d_1}}} + frac{1}{{{d_2}}} = frac{1}{f}). Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было четким. Ответ выразите в сантиметрах.
Ответ
ОТВЕТ: 36. Решение
Так как f = 30 см, то (frac{1}{{{d_1}}} + frac{1}{{{d_2}}} = frac{1}{{30}}.) Расстояние от линзы до лампочки d1 должно быть наименьшим, тогда слагаемое (frac{1}{{{d_1}}}) должно принимать наибольшее значение, а слагаемое (frac{1}{{{d_2}}}) соответственно наоборот наименьшее, которое будет получено при наибольшем значении d2. Следовательно, d2 = 180. (frac{1}{{{d_1}}} + frac{1}{{180}} = frac{1}{{30}},,,,, Leftrightarrow ,,,,,frac{1}{{{d_1}}} = frac{1}{{30}}, — frac{1}{{180}},,,,, Leftrightarrow ,,,,,frac{1}{{{d_1}}} = frac{1}{{36}},,,,, Leftrightarrow ,,,,,{d_1} = 36) см. По условию задачи расстояние d1 от линзы до лампочки меняется в пределах от 30 до 50. Следовательно, найденное значение удовлетворяет условию задачи. Ответ: 36. |
| Задача 19. Перед отправкой тепловоз издал гудок с частотой ({f_0} = 440) Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону (fleft( v right) = frac{{{f_0}}}{{1 — frac{v}{c}}}) (Гц), где c — скорость звука в (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а (c = 315) м/с. Ответ выразите в м/с.
Ответ
ОТВЕТ: 7. Решение
Так как частота второго гудка f больше первого и человек, стоящий на платформе, различает сигналы по тону, то задача сводится к решению рационального неравенства: (fleft( v right) geqslant 440 + 10 = 450.) (frac{{440}}{{1 — frac{v}{{315}}}} geqslant 450,,,,, Leftrightarrow ,,,,frac{{440}}{{450}} geqslant 1 — frac{v}{{315}},,,, Leftrightarrow ,,,,,frac{v}{{315}} geqslant 1 — frac{{44}}{{45}},,,, Leftrightarrow ,,,,frac{v}{{315}} geqslant frac{1}{{45}},,,, Leftrightarrow ,,,v geqslant 7) м/с. Следовательно, наименьшая скорость тепловоза v = 7 м/с. Ответ: 7. |
| Задача 20. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна (I = frac{varepsilon }{{R + r}}), где (varepsilon ) — ЭДС источника (в вольтах), (r = 1) Ом — его внутреннее сопротивление, R — сопротивление цепи (в Омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более (20% ) от силы тока короткого замыкания? (Ответ выразите в Омах.)
Ответ
ОТВЕТ: 4. Решение
По условию задачи сила тока должна составлять не более 20% от силы тока короткого замыкания, то есть (I leqslant {I_{k3}} cdot frac{{20}}{{100}}.) (fracvarepsilon{{R{text{ + 1}}}} leqslant fracvarepsilon{1} cdot frac{1}{5},,|,:,varepsilon > 0,,,, Leftrightarrow ,,,,,frac{1}{{R + 1}} leqslant frac{1}{5},,|, cdot 5left( {R + 1} right) > 0,,,,,, Leftrightarrow ,,,,,R + 1 geqslant 5,,,,,, Leftrightarrow ,,,,,,R geqslant 4) Ом. Следовательно, наименьшее сопротивление цепи R = 4 Ом. Ответ: 4. |
| Задача 21. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: (I = frac{U}{R}), где U — напряжение в вольтах, R — сопротивление электроприбора в Омах. В электросеть включен предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
Ответ
ОТВЕТ: 55. Решение
Задача сводится к решению неравенства: (I leqslant 4,{text{A}}{text{.}}) (frac{{220}}{R} leqslant 4,,|, cdot ,R > 0,,,,,,,, Leftrightarrow ,,,,220 leqslant 4R,,,,,, Leftrightarrow ,,,,,,R geqslant 55) Ом. Следовательно, наименьшее сопротивление R = 55 Ом. Ответ: 55. |
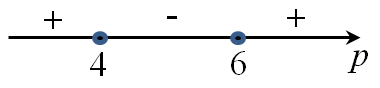
| Задача 22. Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле (Aleft( omega right) = frac{{{A_0},omega _p^2}}{{left| {,omega _p^2 — {omega ^2},} right|}}), где (omega ) — частота вынуждающей силы (в ({{text{c}}^{ — 1}})), ({A_0}) — постоянный параметр, (omega _p^{} = 360,{{text{c}}^{ — 1}}) — резонансная частота. Найдите максимальную частоту (omega ), меньшую резонансной, для которой амплитуда колебаний превосходит величину ({A_0}) не более чем на 12,5%. Ответ выразите в ({{text{c}}^{ — 1}})
Ответ
ОТВЕТ: 120. Решение
Так как амплитуда колебаний A(ω) должна превосходить величину А0 не более чем на 12,5%, то должно выполняться неравенство: (Aleft( omega right) leqslant {A_0} cdot frac{{112,5}}{{100}},,,,,, Leftrightarrow ,,,,,,frac{{A{_0}omega _p^2}}{{left| {,omega _p^2 — omega _{}^2} right|}} leqslant {A_0} cdot 1,125,,|,,:,,{A_0} > 0,,,,, Leftrightarrow ,,,,,,frac{{omega _p^2}}{{left| {,omega _p^2 — omega _{}^2} right|}} leqslant 1frac{1}{8}.) По условию задачи (omega < {omega _p},,,, Leftrightarrow ,,,,{omega _p} > omega ,,,,, Leftrightarrow ,,,,omega _p^2 > {omega ^2},,,,, Leftrightarrow ,,,,,,omega _p^2 — {omega ^2}, > 0). Поэтому: (left| {omega _p^2 — {omega ^2}} right|, > omega _p^2 — {omega ^2}.) (,frac{{omega _p^2}}{{omega _p^2 — omega _{}^2}} leqslant frac{9}{8},,|,, cdot ,8left( {omega _p^2 — omega _{}^2} right) > 0,,,,, Leftrightarrow ,,,,,8omega _p^2 leqslant 9 cdot omega _p^2 — 9omega _{}^2,,,,, Leftrightarrow ,,,,,,9omega _{}^2 leqslant omega _p^2,,,, Leftrightarrow ) (omega _{}^2 leqslant frac{{omega _p^2}}{9},,,,,, Leftrightarrow ,,,,,,omega leqslant frac{{{omega _p}}}{3},,,,,,, Leftrightarrow ,,,,,,omega leqslant frac{{360}}{3},,,,,,, Leftrightarrow ,,,,,,omega leqslant 120,{c^{ — 1}}.) Следовательно, максимальная частота ω = 120 с-1. Ответ: 120. |
| Задача 23. В розетку электросети подключены приборы, общее сопротивление которых составляет ({R_1} = 90) Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление ({R_2}) этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями ({R_1}) Ом и ({R_2}) Ом их общее сопротивление дается формулой (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.
Ответ
ОТВЕТ: 10. Решение
Задача сводится к решению следующего неравенства: Rобщ ≥ 9 Ом и нахождению наименьшего значения R2 при заданном R1 = 90 Ом. (frac{{90{R_2}}}{{90 + {R_2}}} geqslant 9,,|,, cdot left( {90 + {R_2}} right) > 0,,,, Leftrightarrow ,,,,90{R_2} geqslant 810 + 9{R_2},,,, Leftrightarrow ,,,,81{R_2} geqslant 810,,, Leftrightarrow ,,,{R_2} geqslant 10) Ом. Следовательно, наименьшее значение R2 = 10 Ом. Ответ: 10. |
| Задача 24. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой (eta = frac{{{T_1} — {T_2}}}{{{T_1}}} cdot 100% ), где ({T_1}) — температура нагревателя (в градусах Кельвина), ({T_2}) — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя ({T_1}) КПД этого двигателя будет не меньше 15%, если температура холодильника ({T_2} = 340) К? Ответ выразите в градусах Кельвина.
Ответ
ОТВЕТ: 400. Решение
Задача сводится к решению следующего неравенства: (eta geqslant 15% ) и нахождению наименьшего значения T1 при заданном T2 = 340 K. (frac{{{T_1} — 340}}{{{T_1}}} cdot 100 geqslant 15,,|, cdot {T_1} > 0,,, Leftrightarrow ,,,100{T_1} — 34000 geqslant 15{T_1},, Leftrightarrow ,,85{T_1} geqslant 34000,, Leftrightarrow ,,{T_1} geqslant 400)K. Следовательно, наименьшее значение T1 = 400 K. Ответ: 400. |
| Задача 25. Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой (в килограммах) от температуры ({t_1}) до температуры ({t_2}) (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы кг. Он определяется формулой (eta = frac{{{c_в} cdot {m_в}left( {{t_2} — {t_1}} right)}}{{{q_{др}},{m_{др}}}} cdot 100% ), где ({c_в} = 4,2 cdot {10^3}) Дж/(кгК) — теплоёмкость воды, ({q_{др}} = 8,3 cdot {10^6}) Дж/кг — удельная теплота сгорания дров. Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть (m = 83) кг воды от ({10^ circ }{text{C}}) до кипения, если известно, что КПД кормозапарника не больше 21%. Ответ выразите в килограммах
Ответ
ОТВЕТ: 18.
Решение
Задача сводится к решению следующего неравенства: (eta leqslant 21% ) и нахождению наименьшего значения mдр. (frac{{4,2 cdot {{10}^3} cdot 83 cdot left( {100 — 10} right)}}{{8,3 cdot {{10}^6} cdot m}} cdot 100 leqslant 21,,|, cdot m > 0,,,, Leftrightarrow ,,,,frac{{42 cdot {{10}^3} cdot 83 cdot 9 cdot {{10}^2}}}{{83 cdot {{10}^5}}} leqslant 21m,,,, Leftrightarrow ,) ( Leftrightarrow ,,,,42 cdot 9 leqslant 21m,,, Leftrightarrow ,,,m geqslant 18) кг. Следовательно, наименьшее значение m = 18 кг. Ответ: 18. |
| Задача 26. Опорные башмаки шагающего экскаватора, имеющего массу (m = 1260) тонн представляют собой две пустотелые балки длиной (l = 18) метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой (p = frac{{m,g}}{{2,l,s}}), где m — масса экскаватора (в тоннах), l — длина балок в метрах, s — ширина балок в метрах, g — ускорение свободного падения (считайте (g = 10) м/с). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 140 кПа. Ответ выразите в метрах.
Ответ
ОТВЕТ: 2,5. Решение
Задача сводится к решению следующего неравенства: (p leqslant 140)кПа и нахождению наименьшего значения s. (frac{{1260 cdot 10}}{{2 cdot 18 cdot s}} leqslant 140,,|, cdot s > 0,,,, Leftrightarrow ,,,,350 leqslant 140;s,,,, Leftrightarrow ,,,,,s geqslant 2,5)м. Следовательно, наименьшее значение s = 2,5 м. Ответ: 2,5. |
| Задача 27. К источнику с ЭДС (varepsilon = 55) В и внутренним сопротивлением (r = 0,5) Ом, хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, дается формулой (U = frac{{varepsilon ,R}}{{R + r}}). При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 50 В? Ответ выразите в Омах.
Ответ
ОТВЕТ: 5. Решение
Задача сводится к решению следующего неравенства: (U geqslant 50) В и нахождению наименьшего значения R. (frac{{55 cdot R}}{{R + 0,5}} geqslant 50,,|, cdot left( {R + 0,5} right) > 0,,,, Leftrightarrow ,,,,55R geqslant 50R + 25,,,, Leftrightarrow ,,,,,R geqslant 5) Ом. Следовательно, наименьшее значение R = 5 Ом. Ответ: 5. |
| Задача 28. При сближении источника и приёмника звуковых сигналов движущихся в некоторой среде по прямой навстречу друг другу частота звукового сигнала, регистрируемого приемником, не совпадает с частотой исходного сигнала ({f_0} = 150) Гц и определяется следующим выражением: (f = {f_0}frac{{c + u}}{{c — v}}) (Гц), где c — скорость распространения сигнала в среде (в м/с), а (u = 10) м/с и (v = 15) м/с — скорости приемника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приемнике f будет не менее 160 Гц?
Ответ
ОТВЕТ: 390. Решение
Задача сводится к решению следующего неравенства: (f geqslant 160) Гц и нахождению наибольшего значения с. (150 cdot frac{{c + 10}}{{c — 15}} geqslant 160,,|, cdot left( {c — 15} right) > 0,,,, Leftrightarrow ,,,,150c + 1500 geqslant 160c — 2400,,,, Leftrightarrow ,,,,,,c leqslant 390) м/с. Следовательно, наибольшее значение с = 390 м/с. Ответ: 390. |
| Задача 29. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле (v = cfrac{{f — {f_0}}}{{f + {f_0}}}), где (c = 1500) м/с — скорость звука в воде, ({f_0}) — частота испускаемых импульсов (в МГц), f — частота отраженного от дна сигнала, регистрируемая приемником (в МГц). Определите наибольшую возможную частоту отраженного сигнала f, если скорость погружения батискафа не должна превышать 2 м/с.
Ответ
ОТВЕТ: 751. Решение
Задача сводится к решению следующего неравенства: (v leqslant 2) м/c и нахождению наибольшего значения f. (1500 cdot frac{{f — 749}}{{f + 749}} leqslant 2,,|, cdot frac{{f + 749}}{2} > 0,,,, Leftrightarrow ,,,,750f — 750 cdot 749 leqslant f + 749,,,, Leftrightarrow ,) ( Leftrightarrow ,,,,749f leqslant 750 cdot 749 + 749,,,, Leftrightarrow ,,,,,749f leqslant 751 cdot 749,,,,, Leftrightarrow ,,,,,f leqslant 751) МГц. Следовательно, наибольшее значение f = 751 МГц. Ответ: 751. |
| Задача 30. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч, вычисляется по формуле ({v^2} = 2,l,a). Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 1 километра от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 5000 км/ч2. Ответ выразите в км/ч.
Ответ
ОТВЕТ: 100. Решение
Так как (a = frac{{{v^2}}}{{2,,l}}), то задача сводится к решению неравенства: (a geqslant 5000) км/ч2 и нахождению наименьшего значения v. (frac{{{v^2}}}{{2 cdot 1}} geqslant 5000,,,,,, Leftrightarrow ,,,,{v^2} geqslant 10000,,,, Leftrightarrow ,,,,,,v geqslant 100) км/ч. Следовательно, наименьшее значение v = 100 км/ч. Ответ: 100. |
| Задача 31. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле (P = frac{{4,m,g}}{{pi ,{D^2}}}), где (m = 1200) кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения (g = 10) м/с2, а (pi = 3), определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па. Ответ выразите в метрах.
Ответ
ОТВЕТ: 0,2. Решение
Задача сводится к решению неравенства: (P leqslant 400000) Па и нахождению наименьшего значения D. (frac{{4 cdot 1200 cdot 10}}{{3 cdot {D^2}}} leqslant 400000,|, cdot ,{D^2} > 0,,,,, Leftrightarrow ,,,,4 cdot 4 leqslant 400{D^2},,,, Leftrightarrow ,,,,,,{D^2} geqslant frac{1}{{25}},,,,, Leftrightarrow ,,,,,D geqslant 0,2) м. Следовательно, наименьшее значение D = 0,2 м. Ответ: 0,2. |
| Задача 32. Автомобиль, масса которого равна (m = 2160) кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь (S = 500) метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно (F = frac{{2,m,S}}{{{t^2}}}). Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 2400 Н. Ответ выразите в секундах
Ответ
ОТВЕТ: 30. Решение
Задача сводится к решению неравенства: (F geqslant 2400) Н и нахождению наибольшего значения t. (frac{{2 cdot 2160 cdot 500}}{{{t^2}}} geqslant 2400,,|, cdot ,{t^2} > 0,,,,, Leftrightarrow ,,,,21600 geqslant 24{t^2},,,, Leftrightarrow ,,,,,,{t^2} leqslant 900,,,, Leftrightarrow ,,,,,t leqslant 30) c. Следовательно, наибольшее значение t = 30 c. Ответ: 30. |
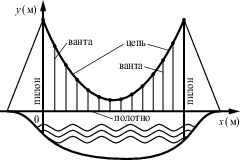 Задача 33. На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: ось Oy направим вертикально вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой (y = 0,005{x^2} — 0,74x + 25), где x и y измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах.
Ответ
ОТВЕТ: 7,3. Решение
Вычислим длину ванты на расстоянии 30 метров от пилона, то есть найдём y (30). (yleft( {30} right) = 0,005 cdot {30^2} — 0,74 cdot 30 + 25 = 4,5 — 22,2 + 25 = 7,3) м. Ответ: 7,3. |