Задача про линзы на егэ по математике

Каталог заданий

Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word

15
Мар 2012

07 Задание (2022)

Выразим d₁ из соотношения, при выполнении которого увеличенное изображение будет чётким:

frac{1}{d_{1}} + frac{1}{d_{2}} = frac{1}{f}

frac{1}{d_{1}} = frac{1}{f} — frac{1}{d_{2}}

Приводим правую часть к общему знаменателю и выражаем d₁:

frac{1}{d_{1}} = frac{d_{2}-f}{fcdot d_{2}}

d_{1} = frac{fcdot d_{2}}{d_{2}-f}

Определим, какое расстояние d₁ будет при граничных значениях d₂ (d₂ = 90 см и d₂ = 120 см) и найдем среди них наименьшее. Фокусное расстояние линзы f = 30 см.

Для d₂ = 120 см получим:

d_{1} = frac{30 cdot 120}{120-30} = frac{30 cdot 120}{90} = 40 см

Для d₂ = 90 см:

d_{1} = frac{30 cdot 90}{90-30} = frac{30 cdot 90}{60} = 45 см

Наименьшее из них – 40 см.

13 апреля 2011

Если в задаче B12 дано уравнение, которое содержит несколько переменных, ни одна из которых не рассматривается как «основная» — перед нами задача на работу с формулами. За примерами далеко ходить не надо:

Как видно, формулы могут связывать по три, а то и по четыре переменных. Но решаются такие задачи всегда одинаково.

Взгляните на них: значения переменных, входящих в формулу, указаны прямо в тексте. За исключением одной — ее-то и требуется найти. Таким образом, решение задачи B12 с формулой состоит из трех шагов:

1. Найти и выписать из текста все известные переменные. Не забудьте перевести все в единую систему измерений. Если одна величина указана в км/ч, а другая — в м/с, то все надо перевести в м/с.
2. Подставить эти переменные в формулу. Получится уравнение с одной неизвестной.
3. Решить полученное уравнение — получим ответ.

И еще: прежде чем решать задачу, постарайтесь преобразовать исходную формулу в максимально простой вид — избавляйтесь от корней, дробей и прочего бреда. Это правило распространяется на все задачи ЕГЭ по математике.

Задача. В электросеть включен предохранитель, рассчитанный на силу тока 20 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Сила тока в цепи I связана с напряжением U соотношением:

где R — сопротивление прибора. Ответ выразите в Омах.

Для начала перепишем формулу: U = I · R. По условию, нам известно напряжение U = 220 В и сила тока I = 20 А. Ничего переводить в другую систему счисления не надо — все и так переведено. Поэтому находим R:

220 = 20 · R;
R = 11.

Задача. Если наблюдатель находится на небольшой высоте h над поверхностью Земли, то расстояние от него до линии горизонта можно найти по формуле:

где R = 6400 км — радиус Земли. Найдите наименьшую высоту, с которой должен смотреть наблюдатель, чтобы он видел линию горизонта на расстоянии не менее 6,4 км. Ответ выразите в метрах.

Перепишем формулу: l² = 2Rh. Поскольку нам известны две величины — l = 6,4 км и R = 6400 км — и обе выражены в километрах, можно подставить в формулу и найти h:

6,4² = 2 · 6400 · h;
40,96 = 12 800 · h;
h = 0,0032.

Итак, h = 0,0032 км. Но ответ просят дать в метрах. В одном километре 1000 метров, поэтому имеем:

h = 0,0032 · 1000 = 3,2 м.

Задача. Коэффициент полезного действия некоторого двигателя определяется по формуле:

При каком наименьшем значении температуры нагревателя T₁ КПД этого двигателя будет не меньше 70%, если температура холодильника T₂ = 150?

Перепишем формулу, избавившись от дроби: η · T₁ = (T₁ − T₂) · 100. В этой формуле известны КПД η = 70 и температура холодильника T₂ = 150. Подставляем — получаем уравнение относительно T₁:

70 · T₁ = (T₁ − 150) · 100;
70 · T₁ = 100 · T₁ − 15 000;
−30 · T₁ = −15 000;
T₁ = 500.

Задача. В розетку электросети подключены приборы, общее сопротивление которых составляет 60 Ом. Параллельно с ними в розетку хотят подключить обогреватель. Определите наименьшее допустимое сопротивление этого обогревателя, если для нормального функционирования электросети общее сопротивление в ней должно быть не менее 10 Ом.

При этом известно, что при параллельном соединении двух проводников с сопротивлениями R₁ и R₂ их общее сопротивление определяется по формуле:

Преобразуем формулу, избавившись от дроби: R · (R₁ + R₂) = R₁ · R₂.

Теперь разберемся с терминологией. Общее сопротивление должно быть не менее 10 Ом — значит, R = 10. Что касается R₁ и R₂, то, не умаляя общности (в силу симметрии формулы), положим R₁ = 60. Соответственно, R₂ — сопротивление обогревателя, которое требуется найти. Имеем:

10 · (60 + R₂) = 60 · R₂;
600 + 10 · R₂ = 60 · R₂;
50 · R₂ = 600;
R₂ = 12.

Задача. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d₁ от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d₂ от линзы до экрана — в пределах от 180 до 210 см. Изображения на экране будет четким, если выполнено соотношение:

Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было четким. Ответ выразите в сантиметрах.

Снова перепишем формулу, избавившись от дробей:
f · (d₁ + d₂) = d₁ · d₂.

Итак, нам нужно найти d₁. При этом значение f = 30 нам дано, а вот d₂ изменяется от 180 до 210. Получим два уравнения:

30 · (d₁ + 180) = d₁ · 180;
30 · d₁ + 5400 = 180 · d₁;
150 · d₁ = 5400;
d₁ = 36.

30 · (d₁ + 210) = d₁ · 210;
… (решается аналогично предыдущему)
d₁ = 35.

По условию, оба значения d₁ допустимы, поэтому выбираем наименьшее: d₁ = 35.

Небольшое пояснение к задаче с линзами. Многие, увидев волшебную фразу «в пределах от … до … », даже не приступают к решению этой задачи. А на самом деле это обычная формула — просто для переменных указаны два значения, поэтому надо составить два уравнения. Получим два значения искомой величины — из них выбираем нужное с учетом ограничений.

Смотрите также:

1. Задачи B12, сводящиеся к линейным уравнениям
2. Решение задач B12: №440—447
3. Тест к уроку «Что такое логарифм» (средний)
4. Иррациональные неравенства. Часть 2
5. Тест по задачам B14: легкий уровень, 2 вариант
6. B14 и эскалаторы: считаем скорость

Задачи по геометрической оптике не такие уж и сложные, если уделить их разбору немного временени. Сегодня в нашей регулярной рубрике «Физика для чайников» рассмотрим несколько примеров задач на тонкие линзы.

Хотите быть в курсе актуальных новостей, связанных с учебой? Присоединяйтесь к нам в телеграме! А тем, кто хочет получать скидки и бонусы, рекомендуем заглянуть на наш второй канал для клиентов.

Тонкая линза: задачи

Чтобы успешно решать задачи по геометрической оптике на тему «Тонкие линзы», нужно знать всего лишь пару формулу. Правда, формул много не бывает, и мы собрали их вместе: пригодятся в решении задач по другим темам. А тем, кто не знает, как вообще подступиться к задачам по физике, рекомендуем почитать общую памятку по решению. 

Задача №1. Формула тонкой линзы

Условие 

Линзу с оптической силой 2,5 дптр поместили на расстоянии 0,5 м от ярко освещённого предмета. На каком расстоянии следует поместить экран, чтобы увидеть на нём чёткое изображение предмета?

Решение

Линза является собирающей (оптическая сила положительна). Запишем формулу тонкой линзы:

1F=1d+1f

Учтем, что F=1D, подставим значения из условия, и запишем:

2,5=10,5+1+ff=2 м

Ответ: 2м

Задача №2. Формула тонкой линзы

Условие

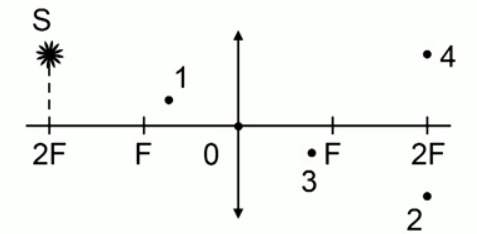
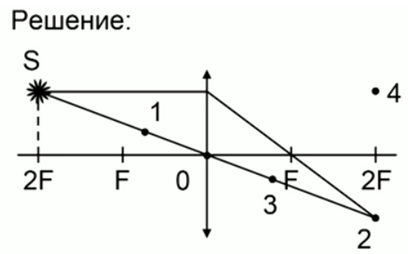
Светящаяся точка лежит в плоскости, проходящей через двойной фокус тонкой линзы, у которой указана главная оптическая ось. Определите, какая из четырех точек на чертеже соответствует правильному изображению  светящейся точки.

Решение

Как видим, на рисунке изображена собирающая линза с оптическим центром в точке 0. Светящася точка S находится от линзы на расстоянии, равном двум фокусам.

Построим изображение точки: один луч проходит через оптический центр линзы, а второй луч, параллельный главной оптической оси, после преломления проходит через фокус. Точка пересечения лучей на расстоянии двойного фокуса и будет являться изображением точки S.

Ответ: изображению точки S соответствует точка 2.

Денное решение получено геометрическим путем, но его можно проверить, используя формулу линзы. Подставим в нее 2F вместо d, и получим тот же результат.

Задача №3. Формула тонкой линзы

Условие

Предмет высотой 3 см находится на расстоянии 40 см от собирающей тонкой линзы. Определите высоту изображения, если оптическая сила линзы равна 4 диоптриям.

Решение

Запишем форумулу тонкой собирающей линзы и формулу увеличения линзы:

1F=1d+1f ; Г=Hh=fd

Перепишем эти соотношения, с учетом того, что F=1D

H=h·fd1f=D-1d

Отсюда найдем f:

f=dD·d-1

Осталось подставить значения в формулу для H и вычислить:

H=hdD·d-1=0,03·0,44·0,4-1=0,05 м

Ответ: 0,05 м.

Задача №4. Формула тонкой линзы

Условие

Предмет имеет высоту 2 см. Какое фокусное расстояние должна иметь линза, расположенная на расстоянии f=4 м от экрана, чтобы изображение предмета на экране имело высоту H=1 м?

Решение

Фокусное расстояние найдем из формулы линзы:

1F=1d+1fF=fdd+f

Запишем формулу увеличения линзы и выразим d:

Г=Hh=fd ; d=fhH

Запишем окончательный ответ:

F=hfH+h≈0,08 м

Ответ: 0,08 м.

Задача №5. Формула тонкой линзы

Условие

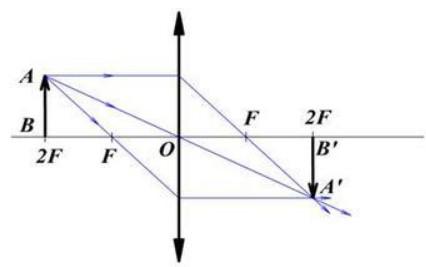
Постройте изображение отрезка AB, расположенного перед собирающей линзой так, что расстояние от предмета до линзы d=2F. Каким будет изображение?

Решение

Посторим изображение в соответствии с правилами геометрической оптики:

Данное изображение:

• действительное;
• перевернутое;
• равное предмету.

Ответ: см. выше.

Вопросы на тему «Тонкая линза»

Вопрос 1. Какое равенство называют формулой тонкой линзы?

Ответ. Формула тонкой линзы имеет следующий вид:

1F=1d+1±f

Здесь:

• F – фокусное расстояние;
• d – расстояние от линзы до предмета;
• f – расстояние от линзы до изображения. 

Вопрос 2. В чем разница в формуле линзы для собирающей и рассеивающей линз?

Ответ. Для собирающей линзы f берется положительным, а для рассеивающей – отрицательным. Соответственно, собирающая линза строит действительное изображение, а рассеивающая – мнимое.

Вопрос 3. Что такое фокусное расстоняние линзы?

Ответ. Фокусное расстояние линзы – это расстояние между ее оптическим центром и главным фокусом.

Вопрос 4. Что такое оптическая сила линзы?

Ответ. Оптическая сила – это величина, обратная фокусному расстоянию. Она характеризует преломляющую способность линзы.

Вопрос 5. Может ли оптическая сила линзы быть отрицательной?

Ответ. Да. Для рассеивающей линзы оптическая сила берется со знаком минус.

Проблемы с решением задач или других заданий? Обращайтесь в профессиональный сервис помощи учащимся!

Для получения на экране увеличенного изображения

Дата: 2014-10-10

16581

Категория: Физические задачи

Метка: ЕГЭ-№8

27970. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f =30 см. Расстояние d₁ от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d₂ от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение

Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было четким.  Ответ выразите в сантиметрах. 

Первый способ. Расстояние d₂  лежит в пределах от 150 до 180 см. Решим два уравнения, подставив пограничные значения в формулу и выберем меньшее  d₁:

Наименьшее расстояние равно 36 сантиметрам.

Второй способ. Выразим из формулы d₂:

Сказано, что d₂  лежит в пределах от 150 до 180 см, значит

Это двойное неравенство можно записать в виде двух неравенств

Получили 36 ≤ d₁ ≤ 37,5. Наименьшее расстояние 36 сантиметров.

Ответ: 36

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Ok