Задача о шарике и мертвой петле
В этой статье будет рассмотрена всего одна задача: задача на закон сохранения энергии. Задача такая:
Шарик скатывается с возвышенности и делает мертвую петлю радиусом . Какова минимальная высота такой возвышенности? Трением пренебречь.
Задача Григория Левиева
Рассмотрим картинку. В начале своего движения шарик еще не обладает скоростью, поэтому его кинетическая энергия нулевая. Зато он обладает потенциальной энергией, поскольку находится на высоте . Примем основание петли за нулевой уровень потенциальной энергии, тогда
.
Когда шарик скатится вниз, его потенциальная энергия перейдет в кинетическую, и он будет обладать скоростью .Кинетическая энергия шарика будет равна
. Эта энергия равна его потенциальной энергии в точке старта:
Тогда искомая исходная высота будет:
Потом шарик оказывается в верхней точке петли. Здесь, чтобы удержаться, он должен обладать минимальным центростремительным ускорением. А минимальным оно будет, если будет равно ускорению свободного падения:
Одновременно вспомним, что , поэтому
Кинетическая энергия шарика в верхней точке петли:
Потенциальная энергия шарика в верхней точке петли:
Таким образом, кинетическая энергия шарика, которая наличествовала в нижней точке петли, частично перейдет в потенциальную, когда он поднимется в верхнюю ее точку:
Масса шарика сокращается:
Домножим на 2:
Вспомним, что , следовательно,
Найдем теперь высоту старта:
Ответ:
14 комментариев
Сергей
✉️
15.12.2016 21:07:54
Мой Е-мэйл действительный, но система не хочет его принимать.
Пропал весь набранный текст комментария. Если возможна связь, то пришлю свои предложения по теме «мертвая петля».
Сергей
✨
06.09.2021 15:43:40
Анна. Я случайно увидел, что мое предложение по теме «мертвая петля», кажется. пропало. Они касалоь учета вращательного движения шарика. Если нужно, то могу переслать его Вам по мэйлу.
С уважением Сергей
Анна Валерьевна
✨
07.09.2021 07:24:05
Да, Сергей, будьте так добры — почта denisova.anna@mail.ru
Donaldkibra
✉️
05.04.2022 00:19:30
Donaldkibra
✉️
05.04.2022 08:07:58
Duanelig
✉️
10.04.2022 12:09:14
Duanelig
✉️
10.04.2022 20:21:20
JasonReott
✉️
11.04.2022 18:43:08
LarryGot
✉️
12.04.2022 10:52:14
LarryGot
✉️
12.04.2022 16:46:49
Замечательно, это весьма ценная фраза
——-
https://my-lkcabinet.com/bilajn-kontakty/
Замечательно, весьма забавный ответ
——-
https://modscraft.net/mods/2406-basic-nether-ores-addon-mod.html
Это просто замечательное сообщение
——-
купить аккаунт battlefield hardline
Я не знаю как мои родители, а я пожалуй посмотрю . . .
——-
top subscribers youtube
Любопытно, а аналог есть?
——-
https://portotecnica.su/category/show/id/259/
Я думаю, что это — серьёзная ошибка.
——-
дизайн города сочи
По моему мнению Вы допускаете ошибку. Пишите мне в PM.
——-
экскурсии калининград купить
Абсолютно не согласен с предыдущей фразой
——-
Накрутка Instagram
Прошу прощения, что я вмешиваюсь, но, по-моему, есть другой путь решения вопроса.
——-
софт для чпу фрезера
нормуль,давно искал! всем спасибо…
——-
nakrutka.com free followers
Jessievob
✉️
13.04.2022 00:07:21
Jessievob
✉️
13.04.2022 06:00:53
Stevetaind
✉️
16.04.2022 14:23:07
Stevetaind
✉️
16.04.2022 18:14:34
Каталог заданий.
Движение по окружности
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д29 C2 № 2952
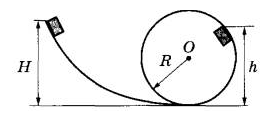
Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рис.).
В точке В наклонная плоскость без излома переходит в наружную поверхность горизонтальной трубы радиусом R. Если в точке А скорость шайбы превосходит то в точке В шайба отрывается от опоры. Длина наклонной плоскости
угол
Коэффициент трения между наклонной плоскостью и шайбой
Найдите внешний радиус трубы R.
2
Задания Д29 C2 № 2954
В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью движется тележка в верхней точке круговой траектории радиусом 20 м, если в этой точке сила давления человека на сидение тележки равна 700 Н? Ускорение свободного падения принять равным
3
Задания Д29 C2 № 2955
В аттракционе человек массой 60 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости по круговой траектории радиусом 25 м. Какова сила давления человека на сидение тележки при скорости прохождения нижней точки 10 м/с? Ускорение свободного падения принять равным
4
Задания Д29 C2 № 2956
В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если в верхней точке сила давления человека на сидение тележки равна 700 Н при скорости движения тележки 10 м/с? Ускорение свободного падения принять равным
5
Задания Д29 C2 № 2957
В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если в верхней точке сила давления человека на сидение тележки равна 200 Н при скорости движения тележки 7,5 м/с? Ускорение свободного падения принять равным
Пройти тестирование по этим заданиям
[latexpage]
В этой статье будет рассмотрена всего одна задача: задача на закон сохранения энергии. Задача такая:
Шарик скатывается с возвышенности и делает мертвую петлю радиусом $R$. Какова минимальная высота такой возвышенности? Трением пренебречь.
Задача Григория Левиева
Рассмотрим картинку. В начале своего движения шарик еще не обладает скоростью, поэтому его кинетическая энергия нулевая. Зато он обладает потенциальной энергией, поскольку находится на высоте $H$. Примем основание петли за нулевой уровень потенциальной энергии, тогда $E_{pot1}=mgH$.
Когда шарик скатится вниз, его потенциальная энергия перейдет в кинетическую, и он будет обладать скоростью $upsilon_1$.Кинетическая энергия шарика будет равна $E_{k1}=frac{m{upsilon_1}^2}{2}$. Эта энергия равна его потенциальной энергии в точке старта:
$$ E_{k1}= E_{pot1}$$
$$frac{m{upsilon_1}^2}{2}= mgH$$
$${upsilon_1}^2= 2gH$$
Тогда искомая исходная высота будет:
$$H=frac{{upsilon_1}^2}{2g}$$
Потом шарик оказывается в верхней точке петли. Здесь, чтобы удержаться, он должен обладать минимальным центростремительным ускорением. А минимальным оно будет, если будет равно ускорению свободного падения:
$$a_{z}=g$$
Одновременно вспомним, что $a_{z}=frac{{upsilon_2}^2}{R}=g$, поэтому
$${upsilon_2}^2=gR$$
Кинетическая энергия шарика в верхней точке петли:
$$E_{k2}=frac{m{upsilon_2}^2}{2}$$
Потенциальная энергия шарика в верхней точке петли:
$$E_{pot2}=2mgR$$
Таким образом, кинетическая энергия шарика, которая наличествовала в нижней точке петли, частично перейдет в потенциальную, когда он поднимется в верхнюю ее точку:
$$E_{k2}+ E_{pot2}= E_{k1}$$
$$frac{m{upsilon_2}^2}{2}+2mgR=frac{m{upsilon_1}^2}{2}$$
Масса шарика сокращается:
$$frac{{upsilon_2}^2}{2}+2gR=frac{{upsilon_1}^2}{2}$$
Домножим на 2:
$${upsilon_2}^2+4gR={upsilon_1}^2$$
Вспомним, что ${upsilon_2}^2=gR$, следовательно,
$${upsilon_1}^2=5gR$$
Найдем теперь высоту старта:
$$H=frac{{upsilon_1}^2}{2g}=frac{5gR}{2g}=2,5R$$
Ответ: $H=2,5R$
Условие задачи:
В школьном опыте с “мертвой петлей” шарик массой 0,1 кг отпущен с высоты (h=3R). С какой силой шарик давит на опору в верхней точке петли?
Задача №2.8.44 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=0,1) кг, (h=3R), (P-?)
Решение задачи:
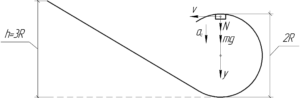
[P = N;;;;(1)]
На тело в верхней точке петли действуют две силы: сила тяжести и сила реакции опоры. Запишем второй закон Ньютона в проекции на ось (y).
[N + mg = m{a_ц}]
[N = mleft( {{a_ц} – g} right)]
Центростремительное ускорение равно отношению квадрата скорости шарика в этой точке к радиусу кривизны (петли).
[{a_ц} = frac{{{upsilon ^2}}}{R}]
[N = mleft( {frac{{{upsilon ^2}}}{R} – g} right);;;;(2)]
Так как сила трения отсутствует, то по закону сохранения энергии полная механическая энергия шарика сохраняется. Значит начальная потенциальная энергия шарика преобразуется в верхней точке петли в кинетическую и потенциальную энергии.
[mgh = frac{{m{upsilon ^2}}}{2} + mg cdot 2R]
По условию (h=3R), поэтому:
[mg cdot 3R = frac{{m{upsilon ^2}}}{2} + mg cdot 2R]
[gR = frac{{{upsilon ^2}}}{2}]
[{upsilon ^2} = 2gR;;;;(3)]
Подставим выражение (3) в (2), тогда:
[N = mleft( {frac{{2gR}}{R} – g} right)]
[N = mg]
Согласно равенству (1) следует:
[P = mg]
Посчитаем численный ответ к задаче:
[P = 0,1 cdot 10 = 1; Н]
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.43 Тело скользит вниз по наклонной плоскости, плавно переходящей в вертикальную
2.8.45 Вертикальный невесомый стержень длиной 6 м подвешен одним концом к оси
2.8.46 Колодец, имеющий глубину 5 м, площадь дна 0,5 м2, наполовину заполнен водой
На картинке внизу изображена установка, с которой мы будем работать.
Эта конструкция расположена у подножия горки, с которой в определенный момент времени спускают шар для боулинга, проходящий петлю благодаря хорошей скорости.
Какая сила в данном случае заставляет тело двигаться по кругу? Прежде всего, сила реакции опоры. Если бы конструкция была хрупкой и непрочной, шар бы просто сломал ее и полетел бы дальше, не совершая красивый вираж.
Пусть масса шара равна 3 килограммам. Радиус окружности – 3 метра. Давайте найдем величину силы реакции опоры в тот момент, когда шар будет находиться в верхней точке своей траектории (допустим, его мгновенная скорость v=8thickspaceм/с).
Будем придерживаться стандартного плана: сначала поймем, какие силы действуют на тело, а затем применим второй закон Ньютона.
На шар действуют две силы – сила тяжести и сила реакции опоры.
Иногда у людей возникают сомнения насчет направления второй силы. Но все очень просто. Сила реакции опоры препятствует «погружению» тела, поэтому всегда направлена перпендикулярно к поверхности соприкосновения. В нашем случае она направлена вертикально вниз.
Теперь применим второй закон Ньютона. Тело движется по кругу, направление вектора скорости меняется, значит, есть центростремительное ускорение. Применим второй закон Ньютона в радиальном направлении:
vec{a}_ц=dfrac{varSigmavec{F}_ц}{m}
dfrac{v^2}{r}=dfrac{varSigmavec{F}_ц}{m}
Обе силы, действующие на тело, направлены к центру окружности. Поставим положительные знаки перед их модулями в уравнении:
dfrac{v^2}{r}=dfrac{mg+N}{m}
Отсюда нетрудно выразить величину силы реакции опоры:
N=dfrac{mv^2}{r}-mg=dfrac{3thickspaceкг×(8thickspaceм/с)^2}{3thickspaceм}-(3thickspaceкг×9.8thickspaceм/с^2)=34.6thickspaceН
Давайте для сравнения попробуем найти силу реакции опоры еще в одной точке.
Теперь сила тяжести действует по касательной к окружности и не способствует тому, чтобы шар оставался на своем треке. Только сила реакции опоры действует в радиальном направлении:
vec{a}_ц=dfrac{varSigmavec{F}_ц}{m}
dfrac{v^2}{r}=dfrac{varSigmavec{F}_ц}{m}
dfrac{v^2}{r}=dfrac{N}{m}
N=dfrac{mv^2}{r}
Осталось подсчитать, чему она будет равна:
N=dfrac{mv^2}{r}=dfrac{3thickspaceкг×(8thickspaceм/с)^2}{3thickspaceм}=64thickspaceН
На самом деле, она даже будет немного больше: сила тяжести сообщит дополнительную скорость шару, пока он будет перемещаться из верхней точки в рассматриваемое положение.
Задача 1
К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.
Решение
1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину
Тогда конечная энергия системы равна потенциальной энергии сжатой пружины:
Изменение полной энергии системы равно работе силы трения
где — модуль силы реакции опоры.
2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.
Запишем закон Ньютона для горизонтальной и вертикальной осей:
3. Подставим полученное выражение для в равенство из пункта 1:
После подстановки получим
Ответ:
Задача 2
Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?
Решение
Согласно закону сохранения механической энергии, имеем два равенства:
где и
— скорости летящей пули соответственно на высоте и непосредственно перед мишенью. Вся энергия подлетевшей к мишени пули потрачена на механическую работу, так что
Решая полученную систему уравнений, находим массу пули:
Задача 3
Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закрепленного кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?
Решение
Согласно закону сохранения энергии:
, (1)
где — скорость шайбы в момент отрыва от кольца на высоте
.
В точке отрыва сила нормальной реакции опоры равна 0; . Центростремительное ускорение шайбы
найдём из второго закона Ньютона (см. рис.):
. (2)
. (3)
Объединяя (1), (2) и (3), получим:
м.
Ответ: 0,18.
Задача 4
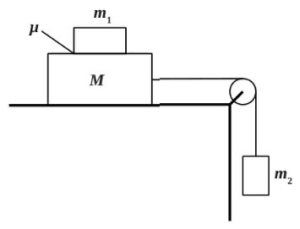
Грузы массами M = 1 кг и m связаны легкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рис.). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту а = 30°, коэффициент трения = 0,3). Чему равно минимальное значение массы m, при котором система грузов еще не выходит из первоначального состояния покоя?
Решение
Если масса m достаточно мала, но грузы ещё покоятся, то сила трения покоя, действующая на груз массой М, направлена вверх вдоль наклонной плоскости. Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат. На первое тело действуют сила тяжести, сила нормальной реакции опоры, сила натяжения нити и сила трения:
(ось направлена вниз вдоль наклонной плоскости);
(ось направлена вверх перпендикулярно наклонной плоскости).
На второе тело действуют сила тяжести и сила натяжения нити:
(ось направлена вертикально вниз).
Учитывая, что (нить легкая, между блоком и нитью трения нет), то
(сила трения покоя). Получим:
кг.
Ответ: 0,24.
Задача 5
Тело, брошено с поверхности земли со скоростью v под углом a к горизонту. Сопротивление воздуха пренебрежимо мало.
Установите соответствие между физическими величинами, характеризующими движение тела, и формулами, по которым их можно определить.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.

Решение
Рассмотрим динамику движения тела, брошенного под углом к горизонту с начальной скоростью
. В задаче нас интересует вертикальное движение тела.
Из рисунка видно, что проекция начальной скорости на ось Oy равна
.
Проекция ускорения равна
,
где м/с2 – ускорение свободного падения. Таким образом, скорость тела вдоль оси Oy будет меняться по закону
.
Можно заметить, что в точке максимального подъема скорость , получаем уравнение
То есть для буквы «А» соответствует формула под номером 4.
Для определения максимальной высоты , запишем формулу движения тела, подброшенного вертикально вверх:
и, учитывая, что ,
, а время для достижения максимальной высоты составляет
, получаем выражение:
.
То есть для буквы «Б» соответствует формула под номером 1.
Ответ: А4, Б1.
Задача 6
Воздушный шар объемом V = 2500 м3 с массой оболочки = 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры t1 нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой
= 200 кг? Температура окружающего воздуха t = 7 °С, его плотность
= 1,2 кг/м3. Оболочку шара считать нерастяжимой.
Решение
Шар взлетает, когда сила тяжести, действующая на него, равна силе Архимеда
, (1)
где m — масса воздуха в шаре. Из уравнения Менделеева-Клапейрона
,
, (2)
где ,
,
— молярная масса воздуха. Объединяя (1) и (2), получим:
К
соответственно °С.
Ответ: 350.
Задача 7
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Решение
Кинетическая энергия брусков после столкновения где v — скорость системы после удара, определяемая из закона сохранения импульса на горизонтальном участке: m1v1 = (m1 + m2)v.
Исключая из системы уравнений скорость v, получим:
Кинетическая энергия первого бруска перед столкновением определяется из закона сохранения механической энергии при скольжении по наклонной плоскости: что даёт выражение
Подставляя значения масс и энергии из условия, получим численное значение h = 0,8 м
Ответ: h = 0,8 м.
Задача 8
Небольшой груз, прикрепленный к нити длиной l = 15 см, вращается вокруг вертикальной оси так, что нить отклоняется от вертикали на угол a = 60°. С какой скоростью движется груз?
Решение
На груз действуют сила натяжения нити и сила тяжести
, как указано на рисунке.
В инерциальной системе отсчёта, связанной с Землёй, ускорение тела определяется вторым законом Ньютона:
Здесь — центростремительное ускорение. Решая полученную систему, получим:
м/с.
Ответ: 1,5.
Задача 9
Камень массой m = 4 кг падает под углом a = 30° к вертикали со скоростью 10 м/с в тележку с песком общей массой M = 16 кг, покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в нее камня.
Решение
Общая инерция камня, падающего в тележку, равна . Величина инерции, в горизонтальном направлении от падения камня составит
. Тогда из закона сохранения инерции, учитывая, что тележка вначале была неподвижной, а после падения в нее камня увеличила свою массу на массу камня, получаем
,
откуда
и

Ответ: 1.
Задача 10
Два груза одинаковой массы М, связанные нерастяжимой и невесомой нитью, движутся прямолинейно по гладкой горизонтальной поверхности под действием горизонтальной силы F, приложенной к одному из грузов (см. рис.). Минимальная сила F, при которой нить обрывается, равна 12 Н. При какой силе натяжения обрывается нить?
Решение
Сила, под действием которой движутся грузы массой M – это равнодействующая, то есть учитывающая силу трения. Следовательно, из второго закона Ньютона можно записать , где
— ускорение, с которым движутся грузы. Сила натяжения нити T создается последним грузом, который перемещается с тем же ускорением
, но имеет массу M, т.е.
. Выражая ускорение как
, получаем силу натяжения, равную
Н.
Ответ: 6.
Задача 11
Груз, лежащий на столе, связан легкой нерастяжимой нитью, переброшенной через идеальный блок, с грузом массой 0,25 кг. На первый груз действует горизонтальная постоянная сила F, равная 9 Н (см. рис.). Второй груз движется с ускорением 2 м/с2, направленным вверх. Трением между грузом и поверхностью стола пренебречь. Какова масса первого груза?
Решение
На второй груз действует сила тяжести и противоположная сила тяги первого груза
Н (трение здесь не учитывается). Таким образом, для системы из двух грузов массами
и
можем записать
,
где — масса первого груза. Отсюда получаем:
Подставляем числовые значения, находим
кг.
Ответ: 3.
Задача 12
Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.
Решение
Выберем следующую систему координат: ось направим вдоль плоскости, а ось
— перпендикулярно ей. Тогда кинематические уравнения движения шарика имеют вид:
В момент второго соударения шарика с плоскостью
Решая систему уравнений, получаем:
и
Из рисунка видно, что
Ответ:
Задача 13
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и 5/2*h (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной v. Найдите отношение масс шайбы и горки.
Решение
На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), направленные по вертикали, поэтому проекция импульса системы на горизонтальную ось Ох системы отсчёта, связанной со столом, сохраняется.
В начальный момент , а в момент
. Из закона сохранения импульса
получим:
, где m — масса шайбы, М — масса горки.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
.
Решение системы дает отношение масс
.
Ответ: .
Задача 14
Снаряд, движущийся со скоростью v0 разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆E. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна v1. Найдите массу m осколка.
Решение
Введём обозначение: v2 — модуль скорости летящего назад осколка снаряда. Система уравнений для решения задачи:
Выразим v2 из первого уравнения: — и подставим во второе уравнение. Получим:
. Отсюда следует:

Ответ: 
Задача 15
Снаряд массой 2m разрывается в полёте на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆Е. Модуль скорости осколка, движущегося по направлению движения снаряда, равен v1, а модуль скорости второго осколка равен v2. Найдите ∆Е.
Решение
Введём обозначение: v0 — модуль скорости снаряда до разрыва. Система уравнений для решения задачи:
Выразим v0 из первого уравнения: и подставим во второе уравнение. Получим:
.
Отсюда следует:
.
Ответ: .
Задача 16
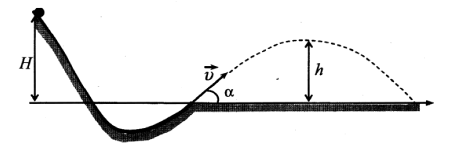
При выполнении трюка «Летающий велосипедист» гонщик движется по гладкому трамплину под действием силы тяжести, начиная движение из состояния покоя с некоторой высоты (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 60° к горизонту. Пролетев по воздуху, он приземляется на горизонтальный стол, поднявшись в полёте на высоту h над краем трамплина. С какой высоты H начинал движение гонщик?
Решение
Применим закон сохранения энергии и найдём скорость велосипедиста при отрыве от трамплина.
Рассмотрим проекции скорости на горизонтальную и вертикальную оси:
В тот момент, когда велосипедист достигнет наивысшей точки полёта вертикальная проекция его скорости станет равной нулю, при этом в горизонтальном направлении он пролетит половину пути. Найдём время, за которое велосипедист достигнет наивысшей точки.
Координата зависит от времени по закону
Значит, максимальная высота полёта велоспедиста
Откуда
Ответ:
Задача 17
После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме.
В некоторый момент времени льдинка находилась в точке А с координатой и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
Решение
1) Льдинка сможет выскользнуть из ямы через ее правый край.
2) Трения при движении льдинки нет, поэтому ее механическая энергия сохраняется. Запас кинетической энергии льдинки в точке A позволяет ей подняться до уровня, где ее потенциальная энергия составит 4 Дж.
3) Левый край ямы поднят до большей высоты. Следовательно, этого края льдинка не достигнет и заскользит вправо. Правый же край ямы ниже: на верху этого края потенциальная энергия льдинки меньше 4 Дж. Поэтому льдинка выскользнет из ямы через правый край.
Задача 18
Гладкий клин массой M с углом при основании стоит на горизонтальной плоскости, часть которой под ним и левее — гладкая, а часть — справа от него — шероховатая (см. рис.). На вершине клина, на высоте H над плоскостью находится маленький брусок массой m, коэффициент трения которого о шероховатую часть плоскости равен
Брусок отпускают без начальной скорости, он скатывается по клину и далее скользит по шероховатой плоскости и останавливается на некотором расстоянии L по горизонтали от своего начального положения. Найдите это расстояние L, если в точке перехода с клина на плоскость есть гладкое закругление, так что скорость бруска при переходе с клина на плоскость не уменьшается.
Решение
При соскальзывании бруска с клина выполняются законы сохранения горизонтальной проекции импульса и механической энергии данной системы тел:
где v и V — скорости бруска и клина, соответственно, после соскальзывания бруска с клина. Из этих уравнений следует, что скорость бруска перед его попаданием на шероховатый участок плоскости равна:
До попадания на этот участок брусок сдвинется из начального положения по горизонтали без трения на расстояние равное, очевидно, длине основания клина, а затем пройдёт по шероховатой плоскости расстояние
на котором его кинетическая энергия будет израсходована на работу против силы сухого трения скольжения. По закону Амонтона — Кулона эта сила равна
так как сила N давления бруска на неподвижную горизонтальную плоскость равна mg. Таким образом,
и
Искомое расстояние L в результате равно сумме l1 и l2:
Ответ:
Задача 19
В системе, изображённой на рисунке, трения нет, блоки невесомы, нить невесома и нерастяжима, m1 = 2 кг, m2 = 4 кг, m3 = 1 кг. Найдите модуль и направление ускорения груза массой m3.
Решение
1. Введём на рисунке неподвижную систему координат, у которой ось x горизонтальна и направлена вправо, а ось y направлена вертикально вниз. Обозначим также силы, определяющие ускорения тел вдоль направлений их движения: силу T натяжения нити, которая, как следует из условия задачи, постоянна по модулю вдоль всей нити, и силу тяжести
2. Записывая второй закон Ньютона в проекциях на оси x и y для трёх грузов, имеем:
3. Поскольку нить нерастяжима, из постоянства её длины получаем следующее соотношение для координат грузов:
Отсюда следует связь между ускорениями грузов:
4. Решая полученную систему уравнений, находим модуль искомого ускорения:
вектор направлен вниз.
Ответ: вектор
направлен вниз.
Задача 20
К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.
Решение
1. Укажем на рисунке силы действующие на стержень. Приравняем моменты сил, действующих на стержень, относительно центра стержня, т.е. точки А:
Учтем, что стержень расположен горизонтально, т.е. удлинения пружин равны, а также, что жесткость правой пружины в два раза больше левой:
2. Приравняем моменты сил, действующих на стержень, относительно точки Б, которая находится в месте крепления правой пружины:
3. Найдем массу стержня:
Ответ:
Задача 21
Найдите модуль ускорения a груза массой m в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза M, ускорение свободного падения равно g.
Решение
Введём координатную ось Х, направленную вниз, и отметим на ней координаты грузов М и m: xM и xm (см. рис.). Пронумеруем блоки цифрами 1, 2, 3 и укажем на рисунке силы натяжения нитей и силы тяжести, действующие на грузы. Согласно условию, в силу невесомости нитей и блоков, а также отсутствия сил трения, первая нить, охватывающая блоки 1 и 2, натянута с силой T, а вторая — с силой 2T, так что на груз m действует направленная вверх сила 4T. Если сместить груз М вдоль оси Х вниз на расстояние ΔxM, то в силу нерастяжимости нитей блок 2 сместится, как следует из рисунка, на −ΔxM/2, а блок 3 и груз m — на Δxm = −ΔxM/4. Таким образом, ΔxM + 4Δxm = 0.
Отсюда получаем уравнение кинематической связи: A + 4a = 0, где A и a — проекции ускорений грузов М и m на ось Х. Уравнения движения грузов (второй закон Ньютона) в проекциях на ось Х имеют вид: МA = Мg – T, ma = mg – 4T. Решая полученную систему из трех уравнений, находим, что модуль ускорения груза М равен:
Ответ:
Задача 22
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Решение
1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.
Здесь — сила натяжения нити,
— сила тяжести,
и
— вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.
2. В положении равновесия равны нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:
где
— длина стержня; (1)
(2)
(3)
3. Модуль силы реакции шарнира
Из (1) получим Окончательно
Ответ:
Задача 23
Из двух ровных досок сделан желоб, представляющий собой двугранный угол с раствором Желоб закреплен так, что его ребро горизонтально, а доски симметричны относительно вертикали. В желобе на боковой поверхности лежит цилиндр массой
Коэффициент трения между досками и цилиндром равен
К торцу цилиндра приложена горизонтально направленная сила
Найдите модуль ускорения цилиндра.
Решение
Изобразим вид на желоб со стороны торца цилиндра. На цилиндр в плоскости чертежа действуют направленная вниз сила тяжести
и две равные по модулю силы реакции
досок, направленные перпендикулярно стенкам желоба. Так как цилиндр не движется в вертикальном направлении, то, в соответствии со вторым законом Ньютона, сумма проекций этих трех сил на вертикаль равна нулю:
где
Отсюда В горизонтальном направлении (вдоль желоба) на цилиндр действуют сила
а также, в противоположном направлении, две силы сухого трения
Предположим, что цилиндр будет двигаться по желобу. Тогда по закону Амонтона — Кулона для силы сухого трения скольжения можно записать:
Записывая второй закон Ньютона в проекции на горизонтальную ось, направленную вдоль ребра желоба, получим:
где — модуль искомого ускорения цилиндра. Заметим, что
Это означает, что приложенная к торцу цилиндра сила превышает силу трения покоя, то есть цилиндр и в самом деле будет скользить вдоль желоба.
Следовательно, Подставляя числовые данные и проверяя размерность, окончательно получим:
Ответ:
Задача 24
Равносторонний треугольник, состоящий из трёх жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплён массивный грузик (см. рисунок). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом к горизонту?
Решение
Обозначим расстояние от оси вращения треугольника до грузика через Тогда период колебаний при горизонтальном положении оси равен, очевидно,
После наклона оси на угол возвращающая сила при отклонении треугольника от положения равновесия уменьшится: составляющая силы тяжести вдоль оси, равная
(здесь
— масса грузика), будет компенсироваться силами реакции со стороны подшипников, в которых закреплена эта ось, а в направлении, перпендикулярном оси, будет действовать эффективная «сила тяжести», равна
Поэтому период малых колебаний грузика при наклоненной оси будет равен
Таким образом, период колебаний увеличится в раз.
Ответ: период колебаний увеличится в раз.
Задача 25
На гладкой горизонтальной плоскости лежат два груза массами и
соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена направленная вертикально вниз сила F = 4 Н. Найдите ускорение этой оси. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.
Решение
Нарисуем силы Т натяжения нити, одинаковые, в силу условия задачи, вдоль всей нити и действующие на грузы и блок О (см. рисунок). Введём систему координат XY, как показано на рисунке, и запишем уравнения движения грузов в проекции на ось X:
В силу невесомости блока О имеем или
В силу нерастяжимости нити (длиной L) и неподвижности блоков А и В (их координаты и
постоянны) имеется следующая кинематическая связь между координатами
и
грузов и координатой
блока О (здесь
— радиус блоков А и В, R — радиус блока О):
или
и значит
Решаем записанную систему уравнений и получаем ответ:
Ответ:
Задача 26
Два вращающихся вала соединены замкнутым ремнём, который не проскальзывает относительно валов. Радиус первого вала равен R, радиус второго вала равен 2R. Чему равно отношение угловой скорости точки A к угловой скорости вращения первого вала
Решение
Скорость движения точек первого вала, находящихся на расстоянии от его центра, даётся формулой
Угловая скорость вращения точки А равна угловой скорости вращения второго вала. Валы связаны ремнём, поэтому скорости ободов
у валов одинаковы, а их угловые скорости
В итоге получаем
Ответ: 0,5.
Задача 28
Два велосипедиста совершают кольцевую гонку с одинаковой угловой скоростью. Положения и траектории движения велосипедистов показаны на рисунке. Чему равно отношение центростремительных ускорений велосипедистов ?
Решение
При движении по окружности угловая и линейная
скорости тела связаны с радиусом окружности
соотношением:
Центростремительное ускорение равно
Поскольку велосипедисты едут с одинаковым угловыми скоростями, для отношения центростремительных ускорения велосипедистов имеем:
Ответ: 2.
Задача 29
Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и высоту
м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии
м от места его обнаружения. Известно, что снаряды данного типа вылетают из ствола пушки со скоростью 800 м/с. Какова была максимальная высота Н траектории снаряда, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.
Первое решение
Найдём горизонтальную скорость снаряда:
Найдём вертикальную проекцию скорости снаряда в момент обнаружения:
Определим, за какое время снаряд долетел из верхней точки траектории в точку, в которой был зафиксирован:
Таким образом, время опускания снаряда составляет
Таким образом, максимальная высота снаряда:
Второе решение
Найдём горизонтальную скорость снаряда: эта скорость остается постоянной на протяжении всего полета. Определим величину вертикальной проекции скорости в начальный момент:
Используя формулу для максимальной высоты брошенного под углом к горизонту тела, получаем:
Ответ: около 16 км.
Задача 30
К концу вертикального стержня привязана лёгкая нерастяжимая нить с маленьким грузиком на конце. Грузик раскрутили на нити так, что она отклонилась от вертикали на угол α = 30º (см. рисунок). Как и во сколько раз надо изменить угловую скорость ω вращения грузика вокруг стержня для того, чтобы этот угол стал равным β = 60º?
Решение
1. Обозначим силу натяжения нити T, массу грузика m, длину нити l, радиус окружности, по которой вращается грузик, R, и изобразим систему на рисунке (см. рисунок).
2. Запишем уравнение движения грузика по окружности вокруг стержня в проекциях на вертикальную ось и на радиус окружности с учётом выражения для центростремительного ускорения грузика:
,
.
3. Из написанных соотношений следует, что , а
.
4. Для того, чтобы угол отклонения нити стал равным β, угловая скорость вращения грузика должна увеличиться в
раза.
Ответ: 1,3 раза.
Задача 31
В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если при скорости 10 м/с, направленной вертикально вверх, сила нормального давления человека на сидение тележки равна 1 600 Н? Ускорение свободного падения равно
Задача 32
На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с2.
Решение
Из графика видно, что скорость в интервале времени от 40 с до 50 с меняется линейно, значит, ускорение постоянно. На всём этом интервале времени ускорение такое же, как и в момент времени 45 с. Найдём это ускорение:
Ответ: 2.
Задача 32
Два небольших тела с массами 2 кг и 3 кг висят на разных концах невесомой нерастяжимой нити, перекинутой через гладкий неподвижный блок. Первое тело находится на высоте 40 см ниже второго. Тела пришли в движение без начальной скорости. Через какое время они окажутся на одной высоте? Сделайте схематический рисунок с указанием сил, действующих на тела. Обоснуйте применимость используемых законов к решению задачи.
Решение
Задача 33
Система грузов M, m1 и m2, показанная на рисунке, движется из состояния покоя. Поверхность стола — горизонтальная гладкая. Коэффициент трения между грузами M и m1 равен μ = 0,3. Грузы M и m2 связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 2,4 кг, m1 = m2 = m. При каких значениях m грузы M и m1 движутся как одно целое? Сделайте рисунок с указанием сил, действующих на грузы.
Решение
Задача 34
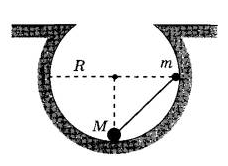
Небольшие шарики, массы которых m и M, соединены лёгким стержнем и помещены в гладкую сферическую выемку радиусом R = 20 см. В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Минимальная высота, на которой оказался шарик m в процессе движения, равна 4 см от нижней точки выемки. Определите отношение масс M и m.
Решение
Задача 35
Небольшой брусок массой m начинает соскальзывать с высоты H по гладкой горке, переходящей в мёртвую петлю (см. рисунок). Определите высоту отрыва бруска, если высота горки H. Радиус окружности R. Сделайте рисунок с указанием сил, поясняющий решение.
Решение
Направим ось Ох вдоль ускорения и пусть сила тяжести образует с этой осью угол α Запишем второй закон Ньютона для бруска на высоте h:
Выразим отсюда скорость бруска, учитывая, что и по третьему закону Ньютона
:
На высоте h брусок обладает как кинетической, так и потенциальной энергией. Из закона сохранения энергии найдём искомую высоту H:
откуда
Задача 36
В маленький шар массой M=100г, висящий на нити длиной l=50 см, попадает и застревает в нем пулька массой m=20г, летящая под углом 30 град к горизонту (см рисунок). Какую скорость v имела пуля перед попаданием в шар, если после соударения шар с застрявшей в нем пулей отклонился по вертикали на угол 60 град? Сопротивлением воздуха пренебречь. Какие законы вы использовали для описания взаимодействия пульки с шаром и подьема тел? Обоснуйте их применимость к данному случаю.
Решение
Задача 37
При выполнение трюка летающий велосипедист гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты H. На краю трамплина скорость гонщика направлена под таим углом к горизонту, что дальность его полета максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящейся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Решение