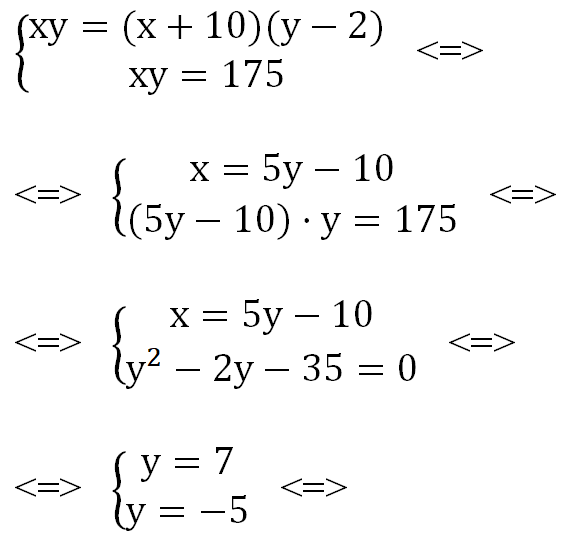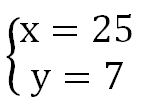Плиточник планирует уложить 175 м2 плитки. Если он будет укладывать на 10 м2 в день больше, чем запланировал, то закончит работу на 2 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Спрятать решение
Решение.
Пусть плиточник планирует укладывать x кв. м плитки в течение y дней. Если он будет укладывать кв. м плитки в течение
дней, то выполнит ту же работу. Поскольку всего нужно уложить 175 кв. м плитки, можно составить систему уравнений:
Таким образом, плиточник планирует в течение 7 дней укладывать по 25 кв. м плитки в день.
Ответ: 25.
Приведём другое решение.
Пусть плиточник планирует укладывать x кв. м плитки в день и справиться с работой за дней. Если укладывать
кв. м плитки в день, то работа будет выполнена за
дня. Имеем:
Таким образом, плиточник должен укладывать по 25 кв. м плитки в день.
Приведём другое решение.
Пусть плиточник планирует был укладывать x кв. м плитки в день. Тогда он уложит всю плитку за дней. Если бы он укладывал на 10 кв. м в день больше, то уложил бы плитку на два дня раньше и сделал это за
дней. Получаем уравнение:
Отрицательный корень не подходит по условию задачи, следовательно, плиточник планирует ежедневно укладывать по 25 кв. м плитки.
Примечание редакции Решу ЕГЭ.
В открытом банке заданий первое предложение таково: «плиточник должен уложить…». Мы отредактировали условие для более ясного его понимания.
Плиточник должен уложить 120 м2 плитки. Если он будет укладывать на 8 м2 в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Источник: mathege
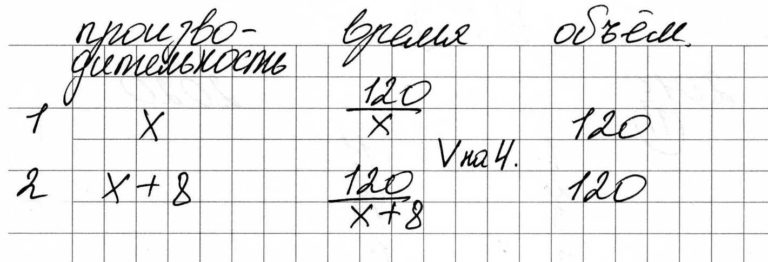
Представим, что у нас есть два плиточника, настоящий и воображаемый, оба должны уложить 120 м2 плитки.
Пусть настоящий укладывает x плитки в день, тогда воображаемый х + 8. Время работы настоящего будет frac{120}{x}, а воображаемого frac{120}{x+8}, зная, что первый будет укладывать на 4 дня дольше, составим уравнение:
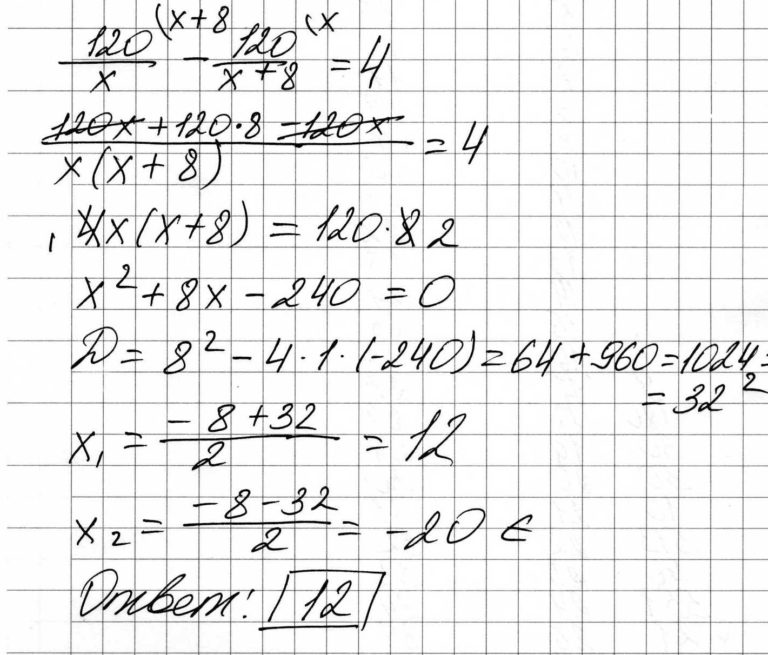
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 12
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задание 11. ЕГЭ. Плиточник должен уложить 120 м^2 плитки.
Задание. Плиточник должен уложить 120 м2 плитки. Если он будет укладывать на 8 м2 в день больше, чем запланировал, то закончит работу на 4 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Решение:
Пусть x м2/дн. планирует укладывать плиточник (производительность рабочего по плану),
а x + 8 м2/дн. плиточник будет укладывать сверх плана (производительность рабочего сверх плана).
Тогда на укладку 120 м2 по плану плиточник потратит
дней,
а на укладку 120 м2 сверх плана плиточник потратит
дней.
Работая сверх плана плиточник закончит работу на 4 дня раньше, составим уравнение
Учитывая, что x ≠ 0, x ≠ — 8 умножим обе части уравнения на x(x + 8), получим
120·(x + 

Раскроем скобки и приравняем к нулю:
120x + 960 – 120x =4x2 + 32x
4x2 + 32x – 960 = 0
x2 + 8x – 240 = 0
Так как x1 < 0, тогда плиточник планирует укладывать 12 квадратных метров плитки в день.
Ответ: 12
- Альфашкола
- Статьи
- Задачи на совместную работу (вариант 3)
Задача №1
Плиточник должен уложить 175 м2 плитки. Если он будет укладывать на 10 м2 в день больше, чем запланировал, то закончит работу на 2 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Решение
Пусть плиточник должен был укладывать «х» кв. м. плитки в течение «у» дней. Если он будет укладывать:
(х + 10) кв. м. плитки в течение:
(у — 2) дней,
то выполнит ту же работу.
Поскольку всего нужно уложить 175 кв. м. плитки, получим систему уравнений:
Решим эту систему уравнений:
Отрицательный корень не подходит по условию задачи, получаем:
Таким образом, плиточник планировал в течение 7 дней укладывать по 25 кв. м. плитки в день.
Ответ: 25.
Задача №2
Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Решение
Наименьшее общее кратное чисел 9, 14 и 18 равно 126.
За 126 минут первый и второй, второй и третий, первый и третий насосы (каждый учтен дважды) заполнят:
14 + 9 + 7 = 30 бассейнов.
Следовательно, работая одновременно, первый, второй и третий насосы заполняют 15 бассейнов за 126 минут, а значит, 1 бассейн за 8,4 минуты.
Ответ: 8,4.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Репетитор по математике
Стерлитамакский государственный педагогический институт
Репетитор по математике
Белорусский государственный педагогический университет
Репетитор по математике
Челябинский государственный университет