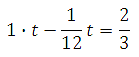Задача с часами егэ профиль - Помощь в подготовке к экзаменам и поступлению

Часы со стрелками показывают 4 часа 45 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 11 часов 20 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 45 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 2 часа ровно. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 8 часов 20 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 5 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 1 час 55 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 25 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 3 часа 10 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 3 часа 25 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 4 часа 5 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 7 часов 5 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 5 часов 45 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 8 часов 50 минут. Через сколько минут минутная стрелка в третий раз поравняется с часовой?

Часы со стрелками показывают 1 час 25 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 11 часов 55 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Часы со стрелками показывают 1 час 30 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 1 час 40 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 4 часа 40 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 4 часа 35 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 7 часов 20 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 9 часов 15 минут. Через сколько минут минутная стрелка в третий раз поравняется с часовой?

Часы со стрелками показывают 3 часа 30 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 2 часа 40 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 50 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 9 часов 45 минут. Через сколько минут минутная стрелка в третий раз поравняется с часовой?

Часы со стрелками показывают 7 часов 40 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 10 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 4 часа 25 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 10 часов ровно. Через сколько минут минутная стрелка в второй раз поравняется с часовой?

Часы со стрелками показывают 9 часов 30 минут. Через сколько минут минутная стрелка в третий раз поравняется с часовой?

Часы со стрелками показывают 8 часов 35 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 10 часов 20 минут. Через сколько минут минутная стрелка в второй раз поравняется с часовой?

Часы со стрелками показывают 4 часа 15 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 5 часов 25 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 7 часов 15 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 5 часов 5 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 5 часов 30 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 6 часов ровно. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 8 часов 5 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 10 часов 15 минут. Через сколько минут минутная стрелка в второй раз поравняется с часовой?

Часы со стрелками показывают 6 часов 55 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 1 час ровно. Через сколько минут минутная стрелка в одиннадцатый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 15 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 1 час 45 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 10 часов 25 минут. Через сколько минут минутная стрелка в второй раз поравняется с часовой?

Часы со стрелками показывают 6 часов 5 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 4 часа 10 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 8 часов 15 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 11 часов 30 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 10 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 8 часов 30 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 7 часов 25 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 30 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 2 часа 55 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 5 часов 10 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 5 часов 35 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 11 часов 50 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 35 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 7 часов 50 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 40 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 5 часов ровно. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Источник

28 января 2022

В закладки

Обсудить

Жалоба

Движение по окружности.

m8dvi.pptx
m8dvi.pdf

1. Часы со стрелками показывают 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

2. Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

3. Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

4. Часы со стрелками показывают 11 часов 20 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

5. Часы со стрелками показывают 6 часов 45 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

6. Часы со стрелками показывают 2 часа ровно. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

7. Часы со стрелками показывают 8 часов 20 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

8. Часы со стрелками показывают 2 часа 5 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

9. Часы со стрелками показывают 1 час 55 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

10. Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Ответы

1) 325
2) 625
3) 540
4) 40
5) 315
6) 600
7) 220
2
9) 605
10) 240

Автор: Бабошкина Любовь Юрьевна.

Источник

18
Апр 2012

08 Задание (2022)ТЕКСТОВЫЕ ЗАДАЧИ

Задача про стрелки часов. Задание 11

1. Задание 11 (№ 99600)

Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Эта задача ничуть не сложнее, чем задача на движение по кругу. У нас по кругу движутся часовая и минутная стрелки. Минутная стрелка за час проходит полный круг, то есть 360°. Значит, ее скорость равна 360° в час. Часовая стрелка за час проходит угол 30° ( это угол между двумя соседними числами на циферблате). Значит, ее скорость 30° в час.

В 8 часов 00 минут расстояние между стрелками составляет 240°:

360°t-30°t=240°

t=240°/330°=8/11

То есть через 8/11 часа стрелки первый раз встретятся.

Теперь до следующей встречи минутная стрелка пройдет на 360° больше, чем часовая. Пусть это произойдет через х часов.

Получим уравнение:

360°х-30°х=360°. Отсюда х=12/11. И так еще два раза.

Получаем, что минутная стрелка в четвертый раз поравняется с часовой через 8/11+12/11+12/11+12/11= 4 часа= 240 мин.

Ответ: 240 мин.

2. Задание 11 (№ 114773). Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

В этой задаче скорость движения стрелок будем выражать в градусах/минуту.

Скорость минутной стрелки равна 360˚/60=6˚ в минуту.

Скорость часовой стрелки равна 30˚/60=0,5˚ в минуту.

В 0 часов положение часовой и минутной стрелок совпадало. 1 час 35 минут — это 95 минут. За это время минутная стрелка прошла 95х6=570˚=360˚+210˚, а часовая прошла 95×0,5˚=47,5˚. И у нас такая картинка:

Первый раз стрелки встретятся через время t_1 , когда часовая стрелка повернется на $0,5{t_1}^{circ}$ , а минутная на 150˚+47,5˚ больше. Получаем уравнение для t_1 :

$150^{circ}+47,5^{circ}+0,5{t_1}=6t_1$

Отсюда $t_1={395^{circ}}/{11}$

Следующий раз стрелки встретятся, когда минутная пройдет на круг больше часовой: $6t_2-0,5t_2=360^{circ}$

$t_2={360^{circ}}/{5,5}={720^{circ}}/{11}$

И так 9 раз.

Минутная стрелка в десятый раз поравняется с часовой через $t_1+9t_2={395^{circ}}/{11}+9{720^{circ}}/{11}={6875^{circ}}/{11}=625$ минут

Ответ: 625

И.В. Фельдман, репетитор по математике.

Для вас другие записи этой рубрики:

Текстовая задача. ДВИ МГУ 2016
Видеолекция «Решение текстовых задач на движение по кругу и воде»
Задача про вклады. Задание В14 (2014) (Диагностическая работа 24 сентября)
Задача на проценты. Пакеты акций. Задание 19
Видеолекция «Решение текстовых задач на работу и прогрессии»
Видеолекция «Решение текстовых задач на движение по прямой»

Источник

Секрет задач на движение по окружности: тот, кто обгоняет, проезжает на 1 круг больше, если это первый обгон. И на n кругов больше, если обогнал другого в n-ный раз.

Из одной точки круговой трассы, длина которой равна 8 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 114 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Автомобили стартовали одновременно, и первый автомобиль через 20 минут после старта опережал второй автомобиль на один круг. Значит, за эти 20 минут, то есть за $frac{1}{3}$ часа он проехал на 1 круг больше – то есть на 8 км больше.

За час первый автомобиль проедет на км больше второго. Скорость второго автомобиля на 24 км/ч меньше, чем у первого, и равна 114 — 24 = 90 км/ч.

Ответ: 90.

Из пункта круговой трассы выехал велосипедист, а через минут следом за ним отправился мотоциклист. Через минут после отправления он догнал велосипедиста в первый раз, а еще через минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна км. Ответ дайте в км/ч.

Во-первых, переведем минуты в часы, поскольку скорость надо найти в км/ч. Скорости участников обозначим за и . В первый раз мотоциклист обогнал велосипедиста через минут, то есть через $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 6}$ часа после старта. До этого момента велосипедист был в пути минут, то есть $genfrac{}{}{}{0}{displaystyle 2}{displaystyle 3}$ часа.

Запишем эти данные в таблицу:


велосипедист	$genfrac{}{}{}{0}{displaystyle 2}{displaystyle 3}$	$genfrac{}{}{}{0}{displaystyle 2}{displaystyle 3}x$
мотоциклист	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle 6}$	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle 6}y$

Оба проехали одинаковые расстояния, то есть $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 6}y=genfrac{}{}{}{0}{displaystyle 2}{displaystyle 3}x$ .

Затем мотоциклист второй раз обогнал велосипедиста. Произошло это через минут, то есть через $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}$ часа после первого обгона.

Нарисуем вторую таблицу.


велосипедист	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}$	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}x$
мотоциклист	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}$	$genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}y$

А какие же расстояния они проехали? Мотоциклист обогнал велосипедиста. Значит, он проехал на один круг больше. Это и есть секрет данной задачи. Один круг — это длина трассы, она равна км. Получим второе уравнение:

$genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}y-genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}x=30$

Решим получившуюся систему.

$left{begin{matrix}genfrac{}{}{}{0}{displaystyle 1}{displaystyle 6}y=genfrac{}{}{}{0}{displaystyle 2}{displaystyle 3}x\genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}y-genfrac{}{}{}{0}{displaystyle 1}{displaystyle 2}x=30end{matrix}right.$

$left{begin{matrix}y=4x\ y-x=60end{matrix}right.$

Получим, что . В ответ запишем скорость мотоциклиста.

Ответ: .

Часы со стрелками показывают часов минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Это, пожалуй, самая сложная задача из вариантов ЕГЭ. Конечно, есть простое решение — взять часы со стрелками и убедиться, что в четвертый раз стрелки поравняются через часа, ровно в 12.00 .
А как быть, если у вас электронные часы и вы не можете решить задачу экспериментально?

За один час минутная стрелка проходит один круг, а часовая $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 12}$ часть круга. Пусть их скорости равны (круг в час) и $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 12}$ (круга в час). Старт — в 8.00 . Найдем время, за которое минутная стрелка в первый раз догонит часовую.

Минутная стрелка пройдет на $genfrac{}{}{}{0}{displaystyle 2}{displaystyle 3}$ круга больше, поэтому уравнение будет таким:
$1 cdot t - genfrac{}{}{}{0}{displaystyle 1}{displaystyle 12}t=genfrac{}{}{}{0}{displaystyle 2}{displaystyle 3}$

Решив его, получим, что $genfrac{}{}{}{0}{displaystyle 8}{displaystyle 11}$ часа. Итак, в первый раз стрелки поравняются через $genfrac{}{}{}{0}{displaystyle 8}{displaystyle 11}$ часа. Пусть во второй раз они поравняются через время . Минутная стрелка пройдет расстояние , а часовая $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 12}z$ , причем минутная стрелка пройдет на один круг больше. Запишем уравнение:

$1 cdot z-genfrac{}{}{}{0}{displaystyle 1}{displaystyle 12}z=1$

Решив его, получим, что $z=genfrac{}{}{}{0}{displaystyle 12}{displaystyle 11}$ часа. Итак, через $genfrac{}{}{}{0}{displaystyle 12}{displaystyle 11}$ часа стрелки поравняются во второй раз, еще через $genfrac{}{}{}{0}{displaystyle 12}{displaystyle 11}$ часа — в третий, и еще через $genfrac{}{}{}{0}{displaystyle 12}{displaystyle 11}$ часа — в четвертый.

Значит, если старт был в 8.00 , то в четвертый раз стрелки поравняются через $genfrac{}{}{}{0}{displaystyle 8}{displaystyle 11}+3genfrac{}{}{}{0}{displaystyle 12}{displaystyle 11}$ часа.

Ответ полностью согласуется с «экспериментальным» решением!

На экзамене по математике вам может также встретиться задача о нахождении средней скорости. Запомним, что средняя скорость не равна среднему арифметическому скоростей. Она находится по специальной формуле:

$v_{cp}=genfrac{}{}{}{0}{displaystyle S_o}{displaystyle t_o}$ ,

где $v_{cp}$ — средняя скорость, S_o — общий путь, t_o — общее время.

Если участков пути было два, то

$v_{cp}=genfrac{}{}{}{0}{displaystyle S_1 + S_2}{displaystyle t_1+t_2}$

А сейчас покажем вам один из секретов решения текстовых задач. Что делать, если у вас получился в уравнении пятизначный дискриминант? Да, это реальная ситуация! Это может встретиться в варианте ЕГЭ.

Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.

Первый гонщик через 15 минут после старта обогнал второго на 1 круг. Значит, за 15 минут он проехал на 1 круг, то есть на 3 километра больше. За час он проедет на километров больше. Его скорость на 12 км/ч больше, чем скорость второго.

Как всегда, составляем таблицу и уравнение. 10 минут переведем в часы. Это $frac{1}{4}$ часа.

$frac{180}{x}-frac{180}{x+12}=frac{1}{6};$

Честно преобразовав это уравнение к квадратному, получим:

Пятизначный дискриминант, вот повезло! Но есть и другой способ решения, и он намного проще.
Посмотрим еще раз на наше уравнение:

$frac{180}{x}-frac{180}{x+12}=frac{1}{6}$

Заметим, что 180 делится на 12. Сделаем замену: x=12z.

Это уравнение легко привести к квадратному и решить.
Целый положительный корень этого уравнения: z=9. Тогда

Ответ: 108

Мы решили текстовую задачу с помощью замены переменной. Этот прием в математике используется везде: в решении задач, уравнений и неравенств, в задачах с параметрами и интегрировании. Общее правило: можете сделать замену переменной – сделайте.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи ЕГЭ на движение по окружности» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.03.2023

Источник

Задачи с часами. ЕГЭ, профиль. (видео обзоры)

Дополнительные материалы

Все Задания 9 ЕГЭ 2023 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать

✓ Как решать сложные текстовые задачи почти в уме | ЕГЭ. Задание 9. Математика| Борис ТрушинСкачать

Через сколько минут минутная стрелка в девятый раз поравняется с часовой (ЕГЭ и ОГЭ)Скачать

ЕГЭ математика профиль № 11 Часы со стрелками показывают 1 час 35 минут.Скачать

Профильный ЕГЭ 2023. Задача 8. Текстовые задачи на движение. 10 классСкачать

Разбор ВСЕХ экономических задач №15 из ЕГЭ за 7 часов! ЕГЭ 2022!Скачать

14 задания с 0 и до уровня ЕГЭ за 7 часов. Неравенства профильная математика. ЕГЭ 2022.Скачать

Задача про часовые стрелки. Задание 9 ЕГЭСкачать

Текстовые задачи. Движение по прямой и воде | Математика ЕГЭ 2023 | УмскулСкачать

№11 ЕГЭ | Как решать задачи на движение? | PARTAСкачать

Задача про часы / ЕГЭ прикладная геометрияСкачать

Источник

Разбираем задачи В13. Речь пойдёт о задачах про стрелки часов. Это тоже движение по кругу. И принципы решения те же самые.

Вот пример простейшей задачи:

1. Часы со стрелками показывают 11 часов 20 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Ответ очевиден, через 40 минут, когда будет ровно двенадцать. Даже если сразу не смогли понять, то нарисовав циферблат (сделав эскиз) на листке, вы без труда определите ответ.

Ответ: 40

2. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Это, пожалуй, самая сложная задача из вариантов ЕГЭ про циферблат. Но…
Эта задача ничуть не сложнее, чем задача на движение по кругу. У нас по кругу движутся часовая и минутная стрелки. Минутная стрелка за час проходит полный круг, то есть 360°. Значит, ее скорость равна 360° в час. Часовая стрелка за час проходит угол 30° ( это угол между двумя соседними числами на циферблате). Значит, ее скорость 30° в час.

В 8 часов 00 минут расстояние между

стрелками составляет 240°:

Пусть минутная стрелка в первый раз встретится с часовой через t часов. За это время минутная стрелка пройдет 360°t, а часовая 30°t, причем минутная пройдет на 240° больше, чем часовая. Получим уравнение:

360°t-30°t=240°

t=240°/330°=8/11

То есть через 8/11 часа стрелки первый раз встретятся.

Теперь до следующей встречи минутная стрелка пройдет на 360° больше, чем часовая. Пусть это произойдет через х часов.

Получим уравнение:

360°х-30°х=360°. Отсюда х=12/11. И так еще два раза.

Получаем, что минутная стрелка в четвертый раз поравняется с часовой через 8/11+12/11+12/11+12/11= 4 часа= 240 мин.

Ответ: 240 мин.

Конечно, есть простое решение — взять часы со стрелками и убедиться, что в четвертый раз стрелки поравняются через 4 часа, ровно в 12.00.
А как быть, если у вас электронные часы и вы не можете решить задачу экспериментально?

За один час минутная стрелка проходит один круг, а часовая 1/12 часть круга. Пусть их скорости равны 1 (круг в час) и 1/12 (круга в час). Старт — в 8.00. Найдем время, за которое минутная стрелка в первый раз догонит часовую.

Минутная стрелка пройдет на 2/3 круга больше, поэтому уравнение будет таким:

(1 — 1/12)x = 2/3

Решив его, получим, что x = 8./11 часа. Итак, в первый раз стрелки поравняются через 8/11 часа. Пусть во второй раз они поравняются через время z. Минутная стрелка пройдет расстояние 1 * z, а часовая 1/12 z, причем минутная стрелка пройдет на один круг больше. Запишем уравнение:

Решив его, получим, что z = 12/11 часа. Итак, через 12/11 часа стрелки поравняются во второй раз, еще через 12/11 часа — в третий, и еще через 12/11 часа — в четвертый.

Значит, если старт был в 8.00, то в четвертый раз стрелки поравняются через

Ответ полностью согласуется с «экспериментальным» решением!

Ответ: 240

Вы убедились, что запутаться очень легко?

СОВЕТЫ БЫВАЛОГО:

На ЕГЭ с такой задачей можно легко запутаться, вычислить неверно или просто потерять много времени на решение.

Вы можете решить данную задачу за одну минуту. Как? Просто!

Возьмите с собой на ЕГЭ механические часы со стрелками… Догадались?

Если вам попадёт такая задача, то берёте часы, ставите исходное время оговоренное в условии (например, 8.00) и прокручиваете заданное число раз. А затем смотрите: сколько «отмотали» минут от исходного времени. Вот и всё.

3. Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

В этой задаче скорость движения стрелок будем выражать в градусах/минуту.

Скорость минутной стрелки равна 360˚/60=6˚ в минуту.

Скорость часовой стрелки равна 30˚/60=0,5˚ в минуту. В 0 часов положение часовой и минутной стрелок совпадало. 1 час 35 минут — это 95 минут. За это время минутная стрелка прошла 95х6=570˚=360˚+210˚, а часовая прошла 95×0,5˚=47,5˚.

Первый раз стрелки встретятся через время t1, когда часовая стрелка повернется на 0,5t1, а минутная на 150˚+47,5˚ больше. Получаем уравнение для t1:

Отсюда

Следующий раз стрелки встретятся, когда минутная пройдет на круг больше часовой:

И так 9 раз.

Минутная стрелка в десятый раз поравняется с часовой через 625 минут

Ответ: 625

Источник

Дата: 2015-01-22

13481

Категория: Движение

Метка: ЕГЭ-№9

99600. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

За один час минутная стрелка проходит один круг, а часовая 1/12 часть круга. Пусть их скорости равны 1 (круг в час) и 1/12 (круга в час). Старт — в 8.00.

Найдем время, за которое минутная стрелка в первый раз догонит часовую. Минутная стрелка пройдет на 2/3 круга больше, поэтому уравнение будет таким:

Получим t=8/11 часа.

Итак, в первый раз стрелки поравняются через 8/11часа.

Пусть во второй раз они поравняются через время z.

Минутная стрелка пройдет расстояние 1∙z, а часовая (1/12)∙z, причем минутная стрелка пройдет на один круг больше. Запишем уравнение:

Решив его, получим z=12/11 часа .

Итак, через 12/11 часа стрелки поравняются во второй раз, еще через 12/11 часа — в третий, и еще через 12/11 часа — в четвертый.

Значит если старт был в 8.00, то в четвертый раз стрелки поравняются через:

Ответ: 240

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Источник

Для вас другие записи этой рубрики:

Задачи с часами. ЕГЭ, профиль. (видео обзоры)

Похожие видео

Дополнительные материалы