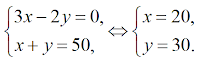Задача с кузнечиком егэ математика

Версия для печати и копирования в MS Word

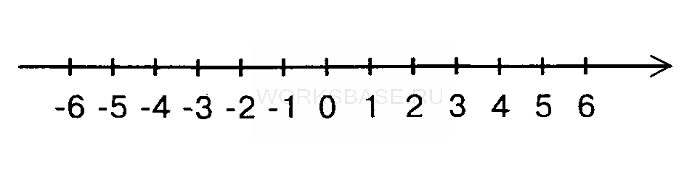
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно (8) прыжков, начиная прыгать из начала координат?

---

Решение

Рассмотрим несколько вариантов, при которых кузнечик сможет сделать прыжки влево и вправо за весь путь:

(1) вариант – (8) прыжков вправо – кузнечик будет в точке (8).

(2) вариант – (7) прыжков вправо и (1) влево – кузнечик будет в точке (6).

(3) вариант – (6) прыжков вправо и (2) влево – кузнечик будет в точке (4).

(4) вариант – (5) прыжков вправо и (3) влево – кузнечик будет в точке (2).

Уже видно, что в итоге кузнечик всегда оказывается в точках с четными координатами (из-за того что он делает четное количество прыжков. Если бы кузнечик делал нечетное количество прыжков, то он бы оказывался в точках с нечетными координатами). Т.к. кузнечик делает ровно (8) прыжков, то он может оказаться в точках, модуль которых не превышает (8). Получается, что кузнечик может оказаться в следующих точках: (-8, -6, -4, -2, 0, 2, 4, 6) и (8). Всего получилось (9) точек.

Ответ: (9).

---

Источник: ЕГЭ-2017. Математика. Базовый уровень. 30 вариантов. Типовые экзаменационные варианты. (вариант №6) (Купить книгу)

Задание № 20. Задачи на логику и смекалку

Тип №1 (про кузнечика)

1. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков, начиная прыгать из начала координат.

Решение.

Заметим, что кузнечик может оказаться только в точках с нечётными координатами, т.к. количество прыжков, которое он делает, — нечётно. Максимально кузнечик может оказаться в точках, модуль которых не превышает одиннадцати. Таким образом, кузнечик может оказаться в точках: −11, −9, −7, −5, −3, −1, 1, 3, 5, 7, 9 и 11; всего 12 точек.

Ответ: 12.

2. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 6 прыжков, начиная прыгать из начала координат?

Решение.

Заметим, что кузнечик может оказаться только в точках с чётными координатами, поскольку число прыжков, которое он делает, — чётно. Максимально кузнечик может оказаться в точках, модуль которых не превышает шести. Таким образом, кузнечик может оказаться в точках: −6, −4, −2, 0, 2, 4 и 6; всего 7 точек.

Ответ: 7.

Вывод. Из решения представленных задач видно, что количество различных точек на координатной прямой, в которых кузнечик может оказаться, на 1 больше числа совершённых им прыжков.

Задания для самостоятельного решения

1. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 8 прыжков, начиная прыгать из начала координат.

2. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 9 прыжков, начиная прыгать из начала координат.

Тип № 2 (про улитку)

1. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?

Решение.

За день улитка заползёт на 4 метра, а за ночь — сползёт на 3 метра. Итого за сутки она заползёт на метр.

За шестеро суток она поднимется на высоту шести метров. И днём следующего дня она уже окажется на вершине дерева.

Ответ: 7.

2. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 12 м. За сколько дней улитка впервые доползёт до вершины дерева?

Решение.

За день улитка заползёт на 4 метра, а за ночь — сползёт на 2 метра. Итого за сутки она заползёт на 2 метра.

За четверо суток она поднимется на высоту восьми метров. И днём следующего дня она уже окажется на вершине дерева.

Ответ: 5.

Примечание. Можно рассуждать так: В последний день улитка может подняться вверх на 4 метра. Значит, 12 – 4 = 8 (м) надо преодолеть за предыдущие дни. Так как за сутки улитка заползёт на 2 метра, то 8 : 2 = 4 (дня) ей понадобится, чтобы подняться на 8 метров. Следовательно, всего 1 + 4 = 5 дней.

Задания для самостоятельного решения

1. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 1 м. Высота дерева 13 м. За сколько дней улитка впервые доползёт до вершины дерева?

2. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 14 м. За сколько дней улитка впервые доползёт до вершины дерева?

3. Улитка за день заползает вверх по дереву на 2 м, а за ночь сползает на 1 м. Высота дерева 11 м. За сколько дней улитка доползёт от основания до вершины дерева?

Формулировка задачи: Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно N прыжков, начиная прыгать из начала координат?

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку).

Рассмотрим, как решаются подобные задачи на примере.

В
ЕГЭ базового уровня есть задача на
смекалку под №20. Большинство таких
задач решаются довольно просто.
Распределим задачи, представленные в
открытом банке ЕГЭ по типам и дадим им
условное название:

Тип 1. (про кузнечика) Тип 2. (про улитку) Тип 3. (с квартирами) Тип 4. (с монетами) Тип 5. (про работу) Тип 6. (про грибы) Тип 7. (про палку) Тип 8. (про лекарства)	Тип 9. (о продажах) Тип 10. (с глобусом) Тип 11. (с прямоугольником) Тип 12. (про числа) Тип 13. (с ящиками) Тип 14. (с таблицей) Тип 15. (про викторину) Тип 16. (про кольцевую дорогу)
Тип 17 (разные задачи на смекалку)

Рассмотрим
первые четыре типа.

Тип
1.  

Кузнечик прыгает
вдоль координатной прямой в любом
направлении на единичный отрезок за
один прыжок. Кузнечик начинает прыгать
из начала координат. Сколько существует
различных точек на координатной прямой,
в которых кузнечик может оказаться,
сделав ровно 11 прыжков?

Решение. Заметим,
что кузнечик в
итоге может
оказаться только в точках с нечётными
координатами, так как
количество прыжков, которое он делает,
нечётно. 

Максимально кузнечик может оказаться
в точках, модуль
которых не превышает
одиннадцати. Таким образом, кузнечик
может оказаться в точках: −11, −9, −7, −5,
−3, −1, 1, 3, 5, 7, 9 и 11; всего
12 точек.

Ответ:
12

Задачи
для самостоятельного решения.

• Заяц
  прыгает вдоль координатной прямой в
  любом направлении на единичный отрезок
  за прыжок. Сколько существует различных
  точек на координатной прямой, в которых
  заяц может оказаться, сделав ровно 6
  прыжков, начиная прыгать из начала
  координат?

• Воробей
  прыгает вдоль прямой в любом направлении.
  Длина прыжка равна единичному отрезку.
  Сколько существует точек, в которых
  воробей может оказаться, сделав 5 прыжков?

• Кузнечик
  прыгает вдоль координатной прямой в
  любом направлении на единичный отрезок
  за прыжок. Сколько существует различных
  точек на координатной прямой, в которых
  кузнечик может оказаться, сделав ровно
  12 прыжков, начиная прыгать из начала
  координат?

Тип
2.

Задача
1.Улитка за день заползает вверх по
дереву на 4 м, а за ночь сползает на 3 м.
Высота дерева 10 м. За сколько дней улитка
впервые доползёт до вершины дерева?

Решение.
За день улитка заползёт на 4 метра, а за
ночь — сползёт на 3 метра. Итого за сутки
она заползёт на метр. За шестеро суток
она поднимется на высоту шести метров.
И днём следующего дня она уже окажется
на вершине дерева.

Ответ:
7

Задача
2. Нефтяная компания бурит скважину для
добычи нефти, которая залегает, по данным
геологоразведки, на глубине 3 км. В
течение рабочего дня бурильщики проходят
300 метров в глубину, но за ночь скважина
вновь «заиливается», то есть заполняется
грунтом на 30 метров. За сколько рабочих
дней нефтяники пробурят скважину до
глубины залегания нефти?

Решение.
За день скважина увеличивается на 300 −
30 = 270 м. К началу одиннадцатого рабочего
дня нефтяники пробурят 2700 метров. За
одиннадцатый рабочий день нефтяники
пробурят ещё 300 метров, то есть дойдут
до глубины 3 км. 

Ответ: 11

Задача
3. В результате паводка котлован заполнился
водой до уровня 2 метра. Строительная
помпа непрерывно откачивает воду,
понижая её уровень на 20 см в час.
Подпочвенные воды, наоборот, повышают
уровень воды в котловане на 5 см в час.
За сколько часов работы помпы уровень
воды в котловане опустится до 80 см?

Решение.
За
час уровень воды в котловане уменьшается
на 20 − 5 = 15 см. Нужно откачать 2 · 100
− 80 = 120 см воды. Следовательно, уровень
воды в котловане опустится до 80 см за 120
: 15 = 8 часов.

Ответ:
8

Задача
4. В бак объёмом 38 литров каждый час,
начиная с 12 часов, наливают полное ведро
воды объёмом 8 литров. Но в днище бака
есть небольшая щель, и из неё за час
вытекает 3 литра. В какой момент времени
(в часах) бак будет заполнен полностью.

Решение.
К
концу каждого часа объём воды в баке
увеличивается на 8 − 3 = 5 литров. Через
6 часов, то есть в 18 часов, в баке будет
30 литров воды. В 18 часов в бак дольют 8
литров воды и объём воды в баке станет
равным 38 литров.

Ответ:
18

Решите
самостоятельно.

• Улитка
  за день заползает вверх по дереву на 4
  м, а за ночь сползает на 1 м. Высота дерева
  13 м. За сколько дней улитка впервые
  доползёт до вершины дерева?

• Улитка
  за день заползает вверх по дереву на 4
  м, а за ночь сползает на 2 м. Высота дерева
  26 м. За сколько дней улитка впервые
  доползёт до вершины дерева?

• Улитка
  за день заползает вверх по дереву на 3
  м, а за ночь сползает на 2 м. Высота дерева
  28 м. За сколько дней улитка впервые
  доползёт до вершины дерева?

Тип
3.

Задача
1. Саша пригласил Петю в гости, сказав,
что живёт в седьмом подъезде в квартире
№ 462, а этаж сказать забыл. Подойдя к
дому, Петя обнаружил, что дом семиэтажный.
На каком этаже живёт Саша? (На всех этажах
число квартир одинаково, номера квартир
в доме начинаются с единицы.)

Решение.
Поскольку в первых 7 подъездах не меньше
462 квартир, в каждом подъезде не меньше
462 : 7 = 66 квартир. Следовательно, на каждом
из 7 этажей в подъезде не меньше 9 квартир.

Пусть
на каждой лестничной площадке по 9
квартир. Тогда в первых семи подъездах
всего 9 · 7 · 7 = 441 квартира, и квартира
462 окажется в восьмом подъезде, что
противоречит условию.

Пусть
на каждой площадке по 10 квартир. Тогда
в первых семи подъездах 10 · 7 · 7 = 490
квартир, а в первых шести — 420. Следовательно,
квартира 462 находится в седьмом подъезде.
Она в нем 42-ая по счету, поскольку на
этаже по 10 квартир, она расположена на
пятом этаже.

Если
бы на каж­дой площадке было по 11
квартир, то в первых шести подъездах
оказалось бы 11 · 7 · 6 = 462 квартиры, то
есть 462 квартира в шестом подъезде, что
противоречит условию.

Значит
Саша живёт на пятом этаже.

Ответ:
5

Задача
2. Во всех подъездах дома одинаковое
число этажей, а на каждом этаже одинаковое
число квартир. При этом число этажей в
доме больше числа квартир на этаже,
число квартир на этаже больше числа
подъездов, а число подъездов больше
одного. Сколько этажей в доме, если всего
в нём 110 квартир?

Решение.
Число квартир, этажей и подъездов может
быть только целым числом.

Заметим,
что число 110 делится на 2, 5 и 11. Следовательно,
в доме должно быть 2 подъезда, 5 квартир
и 11 этажей.

Ответ:
11

Решите
самостоятельно.

• Саша
  пригласил Петю в гости, сказав, что живёт
  в восьмом подъезде в квартире № 468, а
  этаж сказать забыл. Подойдя к дому, Петя
  обнаружил, что дом 12-тиэтажный. На каком
  этаже живёт Саша? (На всех этажах число
  квартир одинаково, номера квартир в
  доме начинаются с единицы.)

• Саша
  пригласил Петю в гости, сказав, что живёт
  в двенадцатом подъезде в квартире №
  465, а этаж сказать забыл. Подойдя к дому,
  Петя обнаружил, что дом пятиэтажный. На
  каком этаже живёт Саша? (На всех этажах
  число квартир одинаково, номера квартир
  в доме начинаются с единицы.)

• Катя
  с подружкой Леной пошли в гости к Свете,
  зная, что она живёт в 364-й квартире в 6-ом
  подъезде. Подойдя к дому, они обнаружили,
  что дом 16-тиэтажный. На каком этаже живёт
  Света? (На всех этажах число квартир
  одинаковое, номера квартир начинаются
  с единицы).

• Игорь
  решил сделать домашнее задание по
  математике с Колей и пошёл к нему домой,
  зная, что он живёт рядом с доме, в пятом
  подъезде и в 206 квартире. Подойдя к дому,
  Игорь обнаружил, что он девятиэтажный.
  На каком этаже живёт Коля? (На всех этажах
  число квартир одинаковое, номера квартир
  в доме начинаются с единицы).

• Во
  всех подъездах дома одинаковое число
  этажей, а на каждом этаже одинаковое
  число квартир. При этом число этажей в
  доме больше числа квартир на этаже,
  число квартир на этаже больше числа
  подъездов, а число подъездов больше
  одного. Сколько этажей в доме, если всего
  в нём 170 квартир?

Тип
4. 

В обменном пункте можно совершить
одну из двух операций:

• за
  2 золотых монеты получить 3 серебряных
  и одну медную;

• за
  5 серебряных монет получить 3 золотых и
  одну медную.

У
Николая были только серебряные монеты.
После нескольких посещений обменного
пункта серебряных монет у него стало
меньше, золотых не появилось, зато
появилось 50 медных. На сколько уменьшилось
количество серебряных монет у Николая?

Решение.
Пусть Николай сделал сначала х операций
второго типа, а затем у операций
первого типа. Так как после нескольких
операций золотых монет не осталось, а
количество
медных монет увеличилось на 50, составим
и решим систему уравнений:

Тогда
серебряных монет стало на 3у -5х = 90 – 100
= -10 то есть на 10 меньше.

Ответ:
10

Решите
самостоятельно.

• В
  обменном пункте можно совершить одну
  из двух операций: за
  3 золотых монеты получить 4 серебряных
  и одну медную; за
  6 серебряных монет получить 4 золотых и
  одну медную. У
  Николая были только серебряные монеты.
  После посещений обменного пункта
  серебряных монет у него стало меньше,
  золотых не появилось, зато появилось
  35 медных. На сколько уменьшилось
  количество серебряных монет у Николая?

• В
  обменном пункте можно совершить одну
  из двух операций: за
  2
  золотые
  монеты получить 3
  серебряные
  и одну медную; за
  5
  серебряных монет получить 3
  золотые
  и одну медную. У
  Андрея
  были только серебряные монеты. После
  посещений обменного пункта серебряных
  монет у него стало меньше, золотых не
  появилось, зато появилось 100
  медных. На сколько уменьшилось количество
  серебряных монет у Андрея?

Практика по заданию №21 ЕГЭ по математике базового уровня — задачи на смекалку.

Практика

Примеры заданий:

1. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок, делая первый прыжок из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, совершив ровно 8 прыжков?

2. В корзине лежит 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов – хотя бы один груздь. Сколько рыжиков в корзине?

3. Девять столбов соединены между собой проводами так, что от каждого столба отходит ровно 8 проводов. Сколько всего проводов протянуто между этими девятью столбами?

4. На поверхности глобуса фломастером проведены 13 параллелей и 25 меридианов. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан – это дуга окружности, соединяющая Северный и Южный полюсы. Параллель – это окружность, лежащая в плоскости, параллельной плоскости экватора.

5. В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 85, во втором – 77, в третьем – 71, а сумма чисел в каждой строке больше 12, но меньше 15. Сколько всего строк в таблице?

6. В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 954. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,1 округляется до 3; 4,5 – до 5; а 2,8 – до 3.)

7. Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами – 298, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?

8. На ленте по разные стороны от середины отмечены две тонкие поперечные полоски: синяя и красная. Если разрезать ленту по красной полоске, то одна часть будет на 35 см длиннее другой. Если разрезать ленту по синей полоске, то одна часть будет на 75 см длиннее другой. Найдите расстояние (в сантиметрах) между красной и синей полосками.

9. На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б – 60 км, между А и В – 45 км, между В и Г – 40 км, между Г и А – 35 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.

10. Про натуральные числа A, B и С известно, что каждое из них больше 5, но меньше 9. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 172. Какое число было загадано?

Смотрите также:

 Итак, продолжаем испытывать нашу смекалку, решая задания под номером 20 базового ЕГЭ по математике. Сегодня следим за кузнечиком.

Задача 1. Кузнечик прыгает вдоль координатной прямой в любом направлении на

единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 8 прыжков, начиная прыгать из начала координат?

Решение:

Немного подумав, мы можем за­ме­тить, что куз­не­чик может ока­зать­ся толь­ко в точ­ках с чётными ко­ор­ди­на­та­ми, по­сколь­ку число прыж­ков, ко­то­рое он де­ла­ет, чётно. Например, если он сделает пять прыжков в одну сторону, то в обратную сторону он сделает три прыжка и окажется в точках 2 или −2.

Мак­си­маль­но куз­не­чик может ока­зать­ся в точ­ках, мо­дуль ко­то­рых не пре­вы­ша­ет восьми. Таким об­ра­зом, куз­не­чик может ока­зать­ся в точ­ках: −8, −6, −4, −2, 0, 2, 4, 6 и 8; всего 9 точек.

Ответ 9.

Потренируйтесь в решении подобных задач.

1.     Кузнечик прыгает вдоль координатной прямой в любом направлении
на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 4 прыжка, начиная прыгать из начала координат?

2.     Кузнечик прыгает вдоль координатной прямой в любом направлении
на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 10 прыжков, начиная прыгать из начала координат?

3.     Кузнечик прыгает вдоль координатной прямой в любом направлении
на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 9 прыжков, начиная прыгать из начала координат?

4.     Куз­не­чик пры­га­ет вдоль ко­ор­ди­нат­ной пря­мой в любом на­прав­ле­нии на еди­нич­ный от­ре­зок за пры­жок. Сколь­ко су­ще­ству­ет раз­лич­ных точек на ко­ор­ди­нат­ной пря­мой, в ко­то­рых куз­не­чик может ока­зать­ся, сде­лав ровно 6 прыж­ков, на­чи­ная пры­гать из на­ча­ла ко­ор­ди­нат?

5.     Куз­не­чик пры­га­ет вдоль ко­ор­ди­нат­ной пря­мой в любом на­прав­ле­нии на еди­нич­ный от­ре­зок за пры­жок. Сколь­ко су­ще­ству­ет раз­лич­ных точек на ко­ор­ди­нат­ной пря­мой, в ко­то­рых куз­не­чик может ока­зать­ся, сде­лав ровно 11 прыж­ков, на­чи­ная пры­гать из на­ча­ла ко­ор­ди­нат?