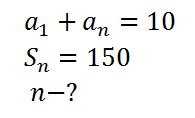Всего: 13 1–13
Добавить в вариант
Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.
Улитка за день залезает вверх по дереву на 3 м, а за ночь спускается на 2 м. Высота дерева 10 м. За сколько дней улитка поднимется на вершину дерева?
Источник: Демонстрационная версия ЕГЭ—2015 по математике. Базовый уровень. Вариант 1.
Улитка за день залезает вверх по дереву на 3 м, а за ночь спускается на 2 м. Высота дерева 10 м. За сколько дней улитка поднимется на вершину дерева?
Источник: Демонстрационная версия ЕГЭ — 2015.
Улитка за день заползает вверх по дереву на 3 м, а за ночь сползает на 1 м. Высота дерева равна 13 м. За сколько дней улитка доползёт до вершины дерева, начав путь от его основания?
Улитка за день заползает вверх по дереву на 3 м, а за ночь сползает на 1 м. Высота дерева равна 11 м. За сколько дней улитка доползёт до вершины дерева, начав путь от его основания?
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 14 м. За сколько дней улитка доползёт от основания до вершины дерева?
Установите соответствие между величинами и их возможными значениями:
ВЕЛИЧИНЫ
А) скорость движения автомобиля
Б) скорость движения пешехода
В) скорость движения улитки
Г) скорость звука в воздушной среде
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 0,5 м/мин
2) 60 км/час
3) 330 м/сек
4) 4 км/час
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Источник: РЕШУ ЕГЭ
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166214., Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166704.
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 1 м. Высота дерева 13 м. За сколько дней улитка впервые доползёт до вершины дерева?
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 153694.
Улитка за день заползает вверх по дереву на 2 м, а за ночь сползает на 1 м. Высота дерева 11 м. За сколько дней улитка доползёт от основания до вершины дерева?
Улитка за день заползает вверх по дереву на 3 м, а за ночь сползает на 2 м. Высота дерева 10 м. За сколько дней улитка доползёт до вершины дерева, начав путь от его основания?
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 1
Улитка за день заползает вверх по дереву на 2 м, а за ночь сползает на 1 м. Высота дерева равна 10 м. За сколько дней улитка доползёт до вершины дерева, начав путь от его основания?
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) скорость гоночной машины
Б) скорость улитки
В) скорость пешехода
Г) скорость звука
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 1,5 мм/с
2) 200 км/ч
3) 1,5 м/с
4) 330 м/с
Источник: РЕШУ ЕГЭ
Всего: 13 1–13
Формулировка задачи: Улитка за день заползает вверх по дереву на K м, а за ночь сползает на L м. Высота дерева N м. За сколько дней улитка впервые доползёт до вершины дерева?
Задача с улитками входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку).
Рассмотрим, как решаются подобные задачи на примере.
Пример задачи:
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?
Решение:
Чтобы правильно решать подобные задачи нужно понимать следующее: если подсчитать на сколько метров улитка продвигается ровно за сутки и разделить высоту дерева на это число, ответ будет неверным. Поскольку улитка могла добраться до вершины дерева в течение дня, а потом уже за ночь сползти вниз. Кроме того, если решать задачу про улитку и дерево таким способом, получится, что в какой-то момент улитка заползает выше, чем находится вершина дерева. Именно поэтому подобный подход использовать нельзя.
Проще всего будет решать эту задачу постепенно. За первый день улитка заползла на 4 метра. Это меньше высоты дерева, значит она достигла вершины не в первый день. За ночь она спустилась на 3 метра, поэтому высота, на которой она находится стала равна:
H = 4 — 3 = 1
За второй день улитка добралась до высоты:
H = 1 + 4 = 5 < 10
За ночь она опять сползла на 3 метра:
H = 5 — 3 = 2
За третьи сутки:
H = 2 + 4 = 6 < 10
H = 6 — 3 = 3
За четвертые сутки:
H = 3 + 4 = 7 < 10
H = 7 — 3 = 4
За пятые сутки:
H = 4 + 4 = 8 < 10
H = 8 — 3 = 5
За шестые сутки:
H = 5 + 4 = 9 < 10
H = 9 — 3 = 6
За седьмые сутки:
H = 6 + 4 = 10
Таким образом, улитка впервые доползла до вершины на 7 день.
Данную задачу можно решить и другим способом: для начала вычесть из высоты дерева дневной подъем улитки, чтобы получить высоту улитки накануне достижения вершины:
10 — 4 = 6
После этого нужно получить перемещение улитки за сутки:
4 — 3 = 1
И, наконец, разделить высоту накануне достижения вершины на суточное перемещение, чтобы получить число суток, за которые улитка и поднималась и спускалась, и прибавить к нему 1 день (последний подъем):
6 / 1 + 1 = 6 + 1 = 7
Если после деления получилось дробное число, его нужно округлить в большую сторону.
Ответ: 7
Задача егэ по математике про улитку
Улитка за день заползает вверх по дереву
Формулировка задачи: Улитка за день заползает вверх по дереву на K м, а за ночь сползает на L м. Высота дерева N м. За сколько дней улитка впервые доползёт до вершины дерева?
Задача с улитками входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку).
Рассмотрим, как решаются подобные задачи на примере.
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?
Чтобы правильно решать подобные задачи нужно понимать следующее: если подсчитать на сколько метров улитка продвигается ровно за сутки и разделить высоту дерева на это число, ответ будет неверным. Поскольку улитка могла добраться до вершины дерева в течение дня, а потом уже за ночь сползти вниз. Кроме того, если решать задачу про улитку и дерево таким способом, получится, что в какой-то момент улитка заползает выше, чем находится вершина дерева. Именно поэтому подобный подход использовать нельзя.
Проще всего будет решать эту задачу постепенно. За первый день улитка заползла на 4 метра. Это меньше высоты дерева, значит она достигла вершины не в первый день. За ночь она спустилась на 3 метра, поэтому высота, на которой она находится стала равна:
Формулировка задачи Улитка за день заползает вверх по дереву на K м, а за ночь сползает на L м.
Worksbase. ru
30.07.2017 19:48:26
2017-07-30 19:48:26
Источники:
Http://worksbase. ru/matematika/kak-reshat/9-ulitka-za-den-zapolzaet. html
Улитка ползет от одного дерева до другого | Подготовка к ОГЭ по математике » /> » /> .keyword { color: red; } Задача егэ по математике про улитку
Улитка ползет от одного дерева до другого
Улитка ползет от одного дерева до другого
Улитка ползет от одного дерева до другого
Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.
Задача очень легкая. Единственное, что может смутить — это то, что здесь неизвестен первый член прогрессии и разность прогрессии.
Но зато мы знаем сразу сумму первого и последнего элемента, а также сумму всех членов данной арифметической прогрессии.
Теперь запишем формулу суммы всех членов прогрессии, подставим в нее то, что известно и решим простое уравнение.
Улитка ползет от одного дерева до другого
Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.
Задача очень легкая. Единственное, что может смутить — это то, что здесь неизвестен первый член прогрессии и разность прогрессии.
Но зато мы знаем сразу сумму первого и последнего элемента, а также сумму всех членов данной арифметической прогрессии.
Теперь запишем формулу суммы всех членов прогрессии, подставим в нее то, что известно и решим простое уравнение.
Единственное, что может смутить это то, что здесь неизвестен первый член прогрессии и разность прогрессии.
Ogematematika. ru
30.12.2018 5:19:54
2018-12-30 05:19:54
Источники:
Https://ogematematika. ru/ulitka-polzet-ot-odnogo-dereva-do-drugogo/
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задача егэ по математике про улитку
Задача егэ по математике про улитку
Задача егэ по математике про улитку
—>
Д. Д. Гущин Готовимся к ЕГЭ по профильной математике
Определите желаемый балл. (Будьте скромнее. Потом можно изменить.) Укажите дни, когда вы будете заниматься. (Понадобится 2−3 раза в неделю по 1−2 часа.) Пройдите входное тестирование. (Будет построен ваш индивидуальный образовательный маршрут.) Изучайте указанные темы, следуя расписанию занятий. (Можно опережать.) Сдав контрольную работу, переходите на следующий уровень.
Математика это сложно, получить больше 85 баллов трудно. Но если серьёзно относиться к делу, то к концу года можно получить прибавку в 27 баллов к начальному уровню. #математиканедлявсех #математикаэтосложно
Вы можете узнать свой текущий уровень прямо сейчас. Пройдите входное тестирование по заданиям из открытого банка ЕГЭ.
—>
Д. Д. Гущин Готовимся к ЕГЭ по профильной математике
Сдав контрольную работу, переходите на следующий уровень.
Ege. sdamgia. ru
07.10.2019 16:17:07
2019-10-07 16:17:07
Источники:
Https://ege. sdamgia. ru/lesson
Задание 20 Базовый уровень ЕГЭ
1)Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 1 м. Высота дерева 13 м. За сколько дней улитка впервые доползёт до вершины дерева? (4-1 =3, утро 4 дня окажется на высоте 9м, и за день проползет 4м.
Ответ: 4
)
2)Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева? Ответ: 7
3)Улитка за день залезает вверх по дереву на 3 м, а за ночь спускается на 2 м. Высота дерева 10 м. За сколько дней улитка поднимется на вершину дерева?Ответ:8
4) На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов? (Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14. Если распилить палку по желтым — 5 кусков, следовательно, линий — 4. Если распилить по зеленым — 7 кусков, линий — 6. Всего линий: 14 + 4 + 6 = 24 линии. Ответ:
25
)
5) На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 5 кусков, если по жёлтым — 7 кусков, а если по зелёным — 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов? Ответ
:
21
6)На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 10 кусков, если по жёлтым — 8 кусков, если по зелёным — 8 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов? Ответ
:
24
7) В обменном пункте можно совершить одну из двух операций:
За 2 золотых монеты получить 3 серебряных и одну медную;
За 5 серебряных монет получить 3 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая? Ответ: 10
8)В обменном пункте можно совершить одну из двух операций:
· за 2 золотые монеты получить 3 серебряные и одну медную;
· за 5 серебряных монет получить 3 золотые и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 100 медных. На сколько уменьшилось количество серебряных монет у Николая
?
Ответ: 20
9) В обменном пункте можно совершить одну из двух операций:
1) за 3 золотых монеты получить 4 серебряных и одну медную;
2) за 6 серебряных монет получить 4 золотых и одну медную.
У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николы? Ответ: 10
10) В обменном пункте можно совершить одну из двух операций:
1) за 3 золотых монеты получить 4 серебряных и одну медную;
2) за 7 серебряных монет получить 4 золотых и одну медную.
У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 42 медных. На сколько уменьшилось количество серебряных монет у Николы? Ответ: 30
11) В обменном пункте можно совершить одну из двух операций:
1) за 4 золотых монеты получить 5 серебряных и одну медную;
2) за 8 серебряных монет получить 5 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 45 медных. На сколько уменьшилось количество серебряных монет у Николая? Ответ: 35
12)В корзине лежит 50 грибов: рыжики и грузди. Известно, что среди любых 28 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько груздей в корзине? ( (50-28)+1=23
— должно быть рыжиков.
(50-24)+1=27
— должно быть груздей. Ответ: груздей в корзине
27
.)
13)В корзине лежит 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине? (Согласно условию задачи:
(40-17)+1=24
— должно быть рыжиков.
(40-25)+1=16
24
.)
14) корзине лежит 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов хотя бы один груздь. Сколько рыжиков в корзине? (Согласно условию задачи:
(30-12)+1=19
— должно быть рыжиков.
(30-20)+1=11
— должно быть груздей. Ответ: рыжиков в корзине
19
.)
15)В корзине лежит 45 грибов: рыжики и грузди. Известно, что среди любых 23 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько рыжиков в корзине? (Согласно условию задачи:
(45-23)+1=23
— должно быть рыжиков.
(45-24)+1=22
— должно быть груздей. Ответ: рыжиков в корзине
23
.)
16)В корзине лежит 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик, а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине? (Так как среди любых 11 грибов хотя бы один – рыжик, то груздей не больше 10. Так как среди любых 16 грибов хотя бы один – груздь, то рыжиков не больше 15. А так как всего в корзине 25 грибов, то груздей ровно 10, а рыжиков ровно
Ответ:15.
17)Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?(Ответ: 117700)
18) Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3700 рублей, а за каждый следующий метр — на 1700 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 8 метров? (77200
)
19) Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров? (89100
)
20) Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3900 рублей, а за каждый следующий метр будет платить на 1200 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 6 метров? (41400)
21) Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 15 минут, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 7 минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности 2 часа 25 минут, если будет следовать советам тренера? (5
)
22) Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 22 минуты, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 4 минуты, пока оно не достигнет 60 минут, а дальше продолжать тренироваться по 60 минут каждый день. За сколько занятий, начиная с первого, Андрей проведёт на беговой дорожке в сумме 4 часа 48 минут? (8
)
23) В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду? (38
)
24)Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)? (2)
сумму арифметической прогрессии с первым членом, равным 3, разностью, равной 3 и последним членом, равным 30.; 165 + 90 + 135 = 390 капель; 3+ 3(n
-1)=30;
n
=10 и 27- 3(n
-1)=3;
n
=9
25)
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 20 капель, а в каждый следующий день — на 3 капли больше, чем в предыдущий. После 15 дней приёма пациент делает перерыв в 3 дня и продолжает принимать лекарство по обратной схеме: в 19-й день он принимает столько же капель, сколько и в 15-й день, а затем ежедневно уменьшает дозу на 3 капли, пока дозировка не станет меньше 3 капель в день. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 200 капель? (7
) выпьет 615 + 615 + 55 = 1285 ;1285: 200 = 6,4
26)В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год? (360) (5*10+2*25+2*40+2*55+70=360
27)
На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса?
Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора. (13 · 22=
286)
28)
На поверхности глобуса фломастером проведены 17 параллелей и 24 меридиана. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора. (18 · 24 =
432)
29)Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 7? (2)
Если бы условие задачи звучало так: «Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение
гарантировано
делилось на 7?» То нужно было бы взять семь подряд идущих чисел.
30)Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 9? (2)
31)Произведение десяти идущих подряд чисел разделили на 7. Чему может быть равен остаток? (0)
Среди 10 подряд идущих чисел одно из них обязательно будет делиться на 7, поэтому произведение этих чисел кратно семи. Следовательно, остаток от деления на 7 равен нулю.
32)Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 6 прыжков, начиная прыгать из начала координат? ( кузнечик может оказаться в точках: −6, −4, −2, 0, 2, 4 и 6; всего 7 точек.)
33)Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 12 прыжков, начиная прыгать из начала координат? (кузнечик может оказаться в точках: −12, −10, −8, −6, −4, −2, 0, 2, 4, 6, 8, 10 и 12; всего 13 точек.)
34)Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков, начиная прыгать из начала координат?(может оказаться в точках: −11, −9, −7, −5, −3, −1, 1, 3, 5, 7, 9 и 11; всего 12 точек.)
35)Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 8 прыжков, начиная прыгать из начала координат?
Заметим, что кузнечик может оказаться только в точках с чётными координатами, поскольку число прыжков, которое он делает, — чётно. Максимально кузнечик может оказаться в точках, модуль которых не превышает восьми. Таким образом, кузнечик может оказаться в точках: −8, −6,
-2
; −4, 0,2 , 4, 6, 8 всего 9 точек.
Рассмотрим такого плана задачи. Мы имеем следующие условия:
Общее количество:
N
Из А штук хотя бы 1 другого вида, а из В штук хотя бы 1 первого вида
Тогда: (А-1) – минимальное количество первого вида, а (В-1) – второго.
После делаем проверку: (А-1)+(В-1)=
N
.
ПРИМЕР
В
РЕШЕНИЕ
Итак: всего рыб у нас 35 (окуни и плотвички)
Рассмотрим условия: среди любых 21 рыбы имеется хотя бы одна плотвичка, значит минимум 1 плотвичка есть в данном условии, следовательно (21-1)=20 это минимум окуней. Среди любых 16 рыб — хотя бы один окунь, рассуждая аналогично, (16-1)=15 – это минимум плотвичек. Теперь делаем проверку: 20+15=35, то есть мы получили общее количество рыб, а значит 20 окуней и 15 плотвичек.
ОТВЕТ: 15 плотвичек
Викторина и количество правильных ответов
Список заданий викторины состоял из А вопросов. За каждый правильный ответ ученик получал а очков, за неправильный ответ с него списывали
b
очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший
N
очков, если известно, что по крайней мере один раз он ошибся?
Мы знаем сколько баллов он заработал, знаем цену правильного и неправильного ответа. Исходя из того был дан хотя бы один неправильный ответ, то количество баллов за правильные ответы должны превышать количество штрафных баллов на
N
баллов. Пусть было дано х правильных ответов и у неправильных, тогда:
а*
x
=
N
+
b
*
y
х=(
N
+
b
*
y
)/а
из данного равенства видно, что число в скобках должно быть кратным а. С учетом этого мы можем оценить у(он тоже целое число). При этом надо учесть что количество правильных и не правильных ответов не должно превышать общего числа вопросов.
ПРИМЕР
РЕШЕНИЕ:
вводим обозначения (для удобства) х — правильные, у – неправильные, тогда
5*х=75+11*у
Х=(75+11*у)/5
Так как 75 делится нацело на пять, то и 11*у тоже должно делиться нацело на пять. Поэтому у может принимать значения кратные пяти (5, 10, 15, и т.д.). берем первое значение у=5 тогда х=(75+11*5)/5=26 всего вопросов 26+5=31
У=10 х=(75+11*10)=37 всего ответов 37+10= 47 (больше чем вопросов) не подходит.
Значит всего было: 26 верных и 5 неверных ответов.
ОТВЕТ: 26 верных ответов
На каком этаже?
Саша пригласил Петю в гости, сказав, что живёт в а подъезде в квартире №
N
, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом
y-
этажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
РЕШЕНИЕ
По условию задачи мы знаем номер квартиры, подъезд и количество этажей в доме. Исходя из этих данных, можно сделать оценку количества квартир на этаже. Пусть х — количество квартир на этаже, тогда должно выполняться следующее условие:
А*у*х должно быть больше или равно
N
Из этого неравенства оцениваем х
Берем для начала минимальное целое значение х, пусть оно равно с, и делаем проверку: (а-1)*у*с меньше
N
, а а*у*с больше или равно
N
.
Выбрав необходимое нам значение х, мы легко можем рассчитать этаж (в): в=(N
-(
a
-1)*
c
)/
c
, причем в – целое число и получая дробное значение, мы берем ближайшее целое(в большую сторону)
ПРИМЕР
РЕШЕНИЕ
Оценим количество квартир на этаже: 7*7*х больше или равно 462, отсюда хбольше или равен 462/(7*7)=9,42 значит минимальный х=10. Делаем проверку: 6*7*10=420 и 7*7*10=490 в итоге мы получили,что квартира по номеру попадает в данный диапозон. Теперь найдем этаж: (462-6*7*10)/10=4,2 значит мальчик живет на пятом этаже.
ОТВЕТ: 5 этаж
Квартиры, этажи, подъезды
Во всех подъездах дома одинаковое число этажей, и па всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём Х квартир?
Данный тип задач базируется на следующем условии: если в доме Э – этажей, П – подъездов и К – квартир на этаже, то общее количество квартир в доме должно быть равно Э*П*К=Х. значит нам необходимо Х представить в виде произведения трех чисел не равны 1(по условию задачи). Для этого сделаем разложение числа Х на простые множители. Сделав разложение и учитывая условия задачи мы делаем выборку соответствия чисел и тех условий, которые указаны в задачи.
ПРИМЕР
РЕШЕНИЕ
Представим число 105 в виде произведения простых множителей
105=5*7*3, теперь вернемся к условию задачи: так как число этажей самое большое, то оно равно 7, число квартир на этаже 5, а подъездов – 3.
ОТВЕТ: подъездов — 7, квартир на этаже – 5, подъездов – 3.
Обмен
В
За а золотых монет получить у серебряные и с медную;
За х серебряных монет получить в золотых и с 1 медную.
У Николая были только серебряные монеты. После обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось С медных. На сколько уменьшилось количество серебряных монет у Николая?
В обменом пунукте есть две схемы обмена:
ПРИМЕР
В
обменном пункте можно совершить одну из двух операций:
РЕШЕНИЕ
5 золотых=4 серебрянных+1 медная
10 серебрянных=7 золотых+1 медная
так как не появилось золотых монет, то нам необходима схема обмена без золоты монет. Поэтому количество золотых монет должно быть равным в обоих случаях. Нам надо найти наименьшее общее кратное чисел 5 и 7, и привести наше золото в обоих случаях к нему:
35 золотых=28 серебрянных+7 медных
50 серебрянных=35 золотых+5 медных
в итоге получаем
50 серебрянных=28 серебрянных+12 медных
Мы нашли схему обмена минуя золотые монеты, теперь нам надо,зная количество медных монет, найти сколько раз такая операция выполнялась
N
=60/12=5
В итоге получаем
250 серебрянных=140 серебрянных+60 медных
Подставив, и получив конечный обмен мы найдем какое количество серебра было поменяно. Значит — количество уменьшилось на 250-140=110
ОТВЕТ на 110 монет
6.
ГЛОБУС
На поверхности глобуса маркером проведены х параллелей и у меридиана. На сколько частей проведенные линии разделили поверхность глобуса? (меридиан — это дуга окружности, соединяющая Северный и Южный полюсы, а параллель — это граница сечения глобуса плоскостью, параллельной плоскости экватора).
РЕШЕНИЕ:
Так как параллель эо граница сечения глобуса плоскостью, то одна разобьет глобус на 2 части, две на три части, х на х+1 частей
Меридиан же это дуга окружности(точнее полуокружность) и у меридиан разбивают поверхность на у частей следовательно всего получиться (х+1)*у частей.
ПРИМЕР
Проведя аналогичные рассуждения мы получим:
(30+1)*24=744 (части)
ОТВЕТ: на 744 части
7.
РАСПИЛЫ
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится А кусков, если по жёлтым — В кусков, а если по зелёным — С кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
РЕШЕНИЕ
Для решения учтем, что количество кусков на 1 больше количества распилов. Теперь необходимо найти сколько линий отмечено на палке. Получаем красных (А-1), желтых – (В-1), зеленных – (С-1). Найдя количество линий каждого цвета и просуммировав их получим общее количество линий: (А-1)+(В-1)+(С-1). Прибавляем к полученному числу единицу (так как количество кусков на один больше количества распилов) получаем количество кусков, если пилить по всем линиям.
ПРИМЕР
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 7 кусков, если по жёлтым — 13 кусков, а если по зелёным — 5 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
РЕШЕНИЕ
Находим количество линий
Красных: 7-1=6
Желтых: 13-1=12
Зеленых: 5-1=4
Общее количество линий: 6+12+4=22
Тогда количество кусков: 22+1=23
ОТВЕТ: 23 куска
8.
СТОЛБЦЫ И СТРОКИ
В
каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна С1, во втором — С2, в третьем — С3, а сумма чисел в каждой строке больше У1, но меньше У2. Сколько всего строк в таблице?
РЕШЕНИЕ
Так как числа в ячейках таблицы не меняются, то сумма всех чисел таблицы равна: С=С1+С2+С3.
Теперь обратим внимание на то, что таблица состоит из натуральных чисел, а значит сумма чисел по строкам должны быть целыми числами и находиться в пределах от (У1+1) до (У2-1)(так как сумма строк ограниченна строго). Теперь мы можем оценить количесво строк:
С/(У1+1) – максимальное количество
С/(У2-1) – минимальное количество
ПРИМЕР
В
таблице три столбца и несколько строк. В
РЕШЕНИЕ
Найдем сумму таблицы
С=85+77+71=233
Определим границы суммы строк
12+1=13 – минимальная
15-1=14 – максимальная
Оценим количество строк в таблице
233/13=17,92 максимальное
233/14=16,64 минимальное
В этих пределах заключено только одно целое число – 17
ОТВЕТ: 17
9.
ЗАПРАВКА НА КОЛЬЦЕВОЙ
и Г. Расстояние между А
и Б
— 35 км, между А
и В
— 20 км, между В
и Г — 20 км, между Г и А
и В.
РЕШЕНИЕ
Внимательно прочитав задачу, мы заметим, что практически окружность разбита на три дуги АВ, ВГ и АГ. На основании этого мы найдем длину всей окружности(кольцевой). Для данной задачи она равна 20+20+30=70 (км).
Теперь расставив все точки на окружности и подписав длины соответствующих дуг, легко определить искомое расстояние. В данной задаче БВ=АБ-АВ, то есть БВ=35-20=15
ОТВЕТ: 15 км
10.
КОМБИНАЦИИ
РЕШЕНИЕ
Для решения данного типа задач следует вспомнить что такое факториал
Факториалом числа
N
! называется произведение последовательных чисел от 1 до
N
, то есть 4!=1*2*3*4.
Теперь вернемся к задаче. Найдем общее количество кубиков: 3+1+1=5. Так как одного цвета у нас три кубика, то общее количество кубиков можно найти по формуле 5!/3! Получим (5*4*3*2*1)/(1*2*3)=5*4=20
ОТВЕТ: 20 способов расстановки
11
. КОЛОДЦЫ
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им Х рублей, а за каждый следующий метр — на У рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной
N
метров?
РЕШЕНИЕ:
Так как хозяин увеличивает цену за каждый метр, то за второй он заплатит (Х+У), за третий – (Х+2У), за четвертый (Х+3У) и т.д. Не сложно увидеть, что данная система оплаты напомин6ает арифметическую прогрессия, где а1=Х,
d
=
Y
,
n
=
N
. Тогда
Оплата за работу есть ничто иное как сумма данной прогрессии:
S
=
(
(2a
₁
+d(n-1))/2)·n
ПРИМЕР:
РЕШЕНИЕ
Исходя из выше сказанного получаем
a
1=4200
d=1300
n=11
подставляя эти данные в нашу формулу получаем
S=((2*4200+1300(11-1)/2)*11=((8400+13000)/2)*11=10700*11=117700
ОТВЕТ: 117700
12
.
СТОЛБЫ И ПРОВОДА
Х столбов, соеденны между собой проводами, так что от каждого отходит ровно У проводов. Сколько всего проводов натянуто между столбами?
РЕШЕНИЕ
Найдем сколько промежутков между столбами. Между двумя один промежуток, между тремя – два, между четырьмя – 3, между Х – (Х-1).
На каждом промежутке У проводов, тогда (Х-1)*У это всего проводов между столбами.
ПРИМЕР
Десять столбов соеденны между собой проводами, так что от каждого отходит ровно 6 проводов. Сколько всего проводов натянуто между столбами?
РЕШЕНИЕ
Возвращаясь к предыдущим обозначениям получаем:
Х=9 У=6
Тогда получаем (9-1)*6=8*6=48
ОТВЕТ: 48
13. ПИЛИМ ДОСКИ И БРЕВНА
Было несколько брёвен. Сделали Х распилов и получилось У чурбачков. Сколько брёвен распилили?
РЕШЕНИЕ
При решении сделаем одно замечание: некоторые задачи не всегда имеют математическое решение.
Теперь к задаче. При решении надо учесть, что бревен больше чем одно и при распили каждого бревна получается =1 кусок.
Данный вид задачи решать удобнее методом подбора:
Пусть будет два бревна тогда кусков получиться 13+2=15
Возьмем три получим 13+3=16
И тут можно увидеть зависимость, что количество распилов и кусков увеличивается одинаково, то есть количество бревен которые надо распилить равно У-Х
ПРИМЕР
Было несколько брёвен. Сделали 13 распилов и получилось 20 чубачков. Сколько брёвен распилили?
РЕШЕНИЕ
Вернувшись к нашим рассуждениям мы можем подбирать, или можно просто 20-13=7 значит всего 7 бревен
Ответ 7
14
. ВЫПАВШИЕ СТРАНИЦЫ
Из книги выпало подряд несколько страниц. Первая из выпавших страниц имеет номер Х, а номер последней записывается такими же цифрами в каком-то другом порядке. Сколько страниц выпало из книги?
РЕШЕНИЕ
Нумерация страниц, которые выпали, начинаются с нечетного числа и должны оканчиваться четным числом. Поэтому, мы, зная.что номер последней выпавшей записывается теми же цифрами, что первая выпавшая знаем ее последнюю цифру. Путем перестановок оставшихся цифр и, учитывая, что нумерация страницы должна быть больше, чем первая выпавшая, получаем ее номер. Зная номера страниц, можно посчитать сколько их выпало, при этом учтем что страница Х тоже выпала. Значит из получившегося номера мы должны вычисть число (Х-1)
ПРИМЕР
Из книги выпало подряд несколько страниц. Первая из выпавших страниц имеет номер 387, а номер последней записывается такими же цифрами в каком-то другом порядке. Сколько страниц выпало из книги?
РЕШЕНИЕ
Опираясь, на наши рассуждения получаем, что номер последней выпавшей страницы должен оканчиваться на цифру 8. Значит у нас всего два варианта чисел это 378 и 738. 378 нам не подходит так как оно меньше номера первой выпавшей страницы значит последняя выпавшая это 738.
738-(387-1)=352
ОТВЕТ: 352
Следует добавить следующее: иногда просят указать количество листов, тогда следует количество страниц разделить пополам.
15.
ИТОГОВАЯ ОЦЕНКА
В конце четверти Вовочка выписал подряд в строчку свои текущие отметки по пению и поставил между некоторых из них знак умножения. Произведения получившихся чисел оказалось равны Х. Какая отметка выходит у Вовочки в четверти по пению?
РЕШЕНИЕ
При решении данного типа задач необходимо учитывать, что его оценки должны быть 2,3,4 и 5. Поэтому нам необходимо разложить число Х на множители 2,3,4 и 5. Причем остаток от разложения тоже должен состоять из этих чисел.
ПРИМЕР1
В конце четверти Вовочка выписал подряд в строчку свои текущие отметки по пению и поставил между некоторых из них знак умножения. Произведения получившихся чисел оказалось равны 2007. Какая отметка выходит у Вовочки в четверти по пению?
РЕШЕНИЕ
Разложим число 2007 на множители
Получим 2007=3*3*223
Значит его отметки: 3 3 2 2 3 теперь найдем среднее арифметическое его оценок для данного набора это 2,6 следовательно его оценка три (больше чем 2,5)
ОТВЕТ 3
ПРИМЕР 2
В конце четверти Вовочка выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалась равным 690. Какая отметка выходит у Вовочки в четверти по этому предмету, если учитель ставит только отметки 2, 3, 4 и 5 и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленная по правилам округления? (Например: 2,4 округляется до двух; 3,5 – до 4; а 4,8 – до 5.)
РЕШЕНИЕ
690 разложим на множители так что бы остаток от разложения состоял из цифр 2 3 4 5
690=3*5*2*23
Следовательно его оценки: 3 5 2 2 3
Найдем среднее арифметическое этих чисел: (3+5+2+2+3)/5=3
Это и будет его оценкой
ОТВЕТ: 3
16
. МЕНЮ
В меню ресторана имеется Х видов салатов, У вида первых блюд, А видов вторых блюд и В вида десерта. Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана?
РЕШЕНИЕ
При решении немного урежем меню: пусть есть только салат и первое тогда вариантов становиться (Х*У). Теперь добавим второе блюдо количество вариантов возрастает в А раз и становиться (Х*У*А). ну а теперь добавим десерт. Количество вариантов возрастет в В раз
Теперь мы получаем окончательный ответ:
N=
Х*У*А*В
ПРИМЕР
РЕШЕНИЕ
Опираясь на выше изложенное получаем:
N=6*3*5*4=360
ОТВЕТ: 360
17
. ДЕЛИМ БЕЗ ОСТАТКА
В данном разделе рассмотрим задачи на конкретном примере, для большей наглядности
Так как у нас произведение последовательно идущих чисел и их больше чем 7, то хотя бы одно должно делиться на 7. Значит мы имеем произведение, один из множителей которого делиться на 7, следовательно и все произведение тоже делиться на семь, а значит остаток от деления будет равен нулю, или для второй задачи количество множителей должно равняться делителю.
18.ТУРИСТЫ
Данный тип задач тоже рассмотрим на конкретном примере.
Для начала определим, что нам необходимо найти: времямаршрута=подъем+отдых+спуск
Отдых мы знаем, теперь надо найти время подъема и спуска
Читая задачу, мы видим что в обоих случая (подъем и спуск) время зависит как арифметическая прогрессия, но мы еще не знаем на какую высоту было восхождение, хотя ее нетрудно найти:
H
=(95-50)15+1=4
Мы нашли высоту подъема, теперь найдем время подъема как сумму арифметической прогрессии: Тподьема= ((2*50+15*(4-1))*4)/2=290 минут
Аналогично находим, учитывая что теперь разность прогрессии равна -10. Получаем Тспуска=((2*60-10(4-1))*4)/2= 180 минут.
Зная все составляющие можно посчитать общее время маршрута:
Тмаршрута=290+180+10=480 минут или переводя в часы(делим на 60) получим 8 часов.
ОТВЕТ: 8 часов
19.ПРЯМОУГОЛЬНИКИ
На прямоугольники встречается два типа задач: на периметры и на площади
Для решения такого плана задач, нетрудно доказать, что при разбитии любого прямоугольника двумя прямолинейными разрезами, мы получим четыре прямоугольника для которых всегда будут выполняться следующие соотношения:
Р1+Р2=Р3+Р4
S1*S2=S3*S4,
где
Р
–
периметр
,
S
— площадь
Основываясь на этих соотношениях, мы легко можем решить следующие задачи
19.1.Периметры
РЕШЕНИЕ
Опираясь на выше сказанное получаем
24+16=28+Х
Х=(24+16)-28=12
ОТВЕТ: 12
19.2 ПЛОЩАДИ
Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них начиная с левого верхнего и далее по часовой стрелке равны 18, 12 и 20. Найдите площадь четвёртого прямоугольника.
РЕШЕНИЕ
Для полученных прямоугольников должно выполняться:
18*20=12*Х
Тогда Х=(18*20)/12=30
20. ТУДА-СЮДА
Улитка за день заползает вверх по дереву на А м, а за ночь сползает на В м. Высота дерева С м. За сколько дней улитка впервые доползёт до вершины дерева?
РЕШЕНИЕ
За одни сутки улитка может подняться на высоту (А-В) метров. Так как она за один день может подняться на высоту А, то до последнего подъема ей необходимо преодолеть высоту (С-А). Исходя из этого, получаем что она будет подниматься (С-А)(А-В)+1 (единицу прибавляем так как она за один день поднимается на высоту А).
ПРИМЕР
РЕШЕНИЕ
Возвращаясь к нашим рассуждениям получаем
(10-4)/(4-3)+1=7
ОТВЕТ за 7 дней
Следует отметить что таким способ можно решать задачи на наполнение чего либо, когда поступает что-то и что-то вытекает.
21. ПРЫЖКИ ПО ПРЯМОЙ
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав Х прыжков, начиная прыгать из начала координат?
РЕШЕНИЕ
Предположим, что кузнечик делает все прыжки в одну сторону, тогда он попадет в точку с координатой Х. Теперь он прыгает вперед на (Х-1) прыжков и один обратно: попадает в точку с координатой (Х-2). Рассматривая таким способом все его прыжки можно заметить, что он будет находиться в точках с координатами Х, (Х-2),(Х-4) и т.д. Данная зависимость является не чем иным как арифметической прогрессией с разностью
d
=-2 и а1=Х, а
an
=-
X
. Тогда количество членов этой прогрессии и есть количество точек в которых он может оказаться. Найдем их
an=a1+d(n-1)
X=X+d(n-1)
2X=-2(n-1)
n=X+1
ПРИМЕР
РЕШЕНИЕ
Основываясь на выше приведенных выводах получаем
10+1=11
ОТВЕТ 11 точек
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:
1.
Каждую секунду бактерия делится на две новые бактерии. Известно, что весь объём одного стакана бактерии заполняют за 1 час. За сколько секунд стакан будет заполнен бактериями наполовину?
2.
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
3.
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Кузнечик начинает прыгать из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков?
4.
В корзине лежит 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине?
5.
Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
6.
Саша пригласил Петю в гости, сказав, что живёт в восьмом подъезде в квартире № 468, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом двенадцатиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
7.
Саша пригласил Петю в гости, сказав, что живёт в двенадцатом подъезде в квартире № 465, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом пятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
8.
Саша пригласил Петю в гости, сказав, что живёт в десятом подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
9.
Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 15 минут, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 7 минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности 2 часа 25 минут, если будет следовать советам тренера?
10.
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
11.
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 20 капель, а в каждый следующий день — на 3 капли больше, чем в предыдущий. После 15 дней приёма пациент делает перерыв в 3 дня и продолжает принимать лекарство по обратной схеме: в 19-й день он принимает столько же капель, сколько и в 15-й день, а затем ежедневно уменьшает дозу на 3 капли, пока дозировка не станет меньше 3 капель в день. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 200 капель?
12.
Произведение десяти идущих подряд чисел разделили на 7. Чему может быть равен остаток?
13.
Сколькими способами можно поставить в ряд два одинаковых красных кубика, три одинаковых зелёных кубика и один синий кубик?
14.
В бак объёмом 38 литров каждый час, начиная с 12 часов, наливают полное ведро воды объёмом 8 литров. Но в днище бака есть небольшая щель, и из неё за час вытекает 3 литра. В какой момент времени (в часах) бак будет заполнен полностью.
15.
Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 7?
16.
В результате паводка котлован заполнился водой до уровня 2 метра. Строительная помпа непрерывно откачивает воду, понижая её уровень на 20 см в час. Подпочвенные воды, наоборот, повышают уровень воды в котловане на 5 см в час. За сколько часов работы помпы уровень воды в котловане опустится до 80 см?
17.
В меню ресторана имеется 6 видов салатов, 3 вида первых блюд, 5 видов вторых блюд и 4 вида десерта. Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана?
18.
Нефтяная компания бурит скважину для добычи нефти, которая залегает, по данным геологоразведки, на глубине 3 км. В течение рабочего дня бурильщики проходят 300 метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на 30 метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?
19.
Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 9?
20.
за 2 золотых монеты получить 3 серебряных и одну медную;
за 5 серебряных монет получить 3 золотых и одну медную.
21.
На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса?
Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
22.
В корзине лежит 50 грибов: рыжики и грузди. Известно, что среди любых 28 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько груздей в корзине?
23.
Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут.
24.
На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 35 км, между A и C — 20 км, между C и D — 20 км, между D и A — 30 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. Ответ дайте в километрах.
25.
На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 50 км, между A и C — 40 км, между C и D — 25 км, между D и A — 35 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C.
26.
В классе учится 25 учащихся. Несколько из них ходили в кино, 18 человек ходили в театр, причём и в кино, и в театр ходили 12 человек. Известно, что трое не ходили ни в кино, ни в театр. Сколько человек из класса ходили в кино?
27.
По эмпирическому закону Мура среднее число транзисторов на микросхемах каждый год удваивается. Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось 520 млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году.
28.
В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
29.
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, то получится 5 кусков, если по жёлтым — 7 кусков, а если по зелёным — 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
30.
В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год?
31.
В обменном пункте можно совершить одну из двух операций:
1) за 3 золотых монеты получить 4 серебряных и одну медную;
2) за 6 серебряных монет получить 4 золотых и одну медную.
У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николы?
32.
Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.)
33.
Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 110 квартир?
34.
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 6 прыжков, начиная прыгать из начала координат?
35.
В корзине лежат 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине?
36.
В корзине лежат 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик, а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?
37.
В корзине лежат 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов хотя бы один груздь. Сколько рыжиков в корзине?
38.
На глобусе фломастером проведены 17 параллелей (включая экватор) и 24 меридиана. На сколько частей проведённые линии разделяют поверхность глобуса?
39.
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?
40.
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 1 м. Высота дерева 13 м. За сколько дней улитка впервые доползёт до вершины дерева?
41.
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
42.
Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров?
43.
В корзине лежит 45 грибов: рыжики и грузди. Известно, что среди любых 23 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько рыжиков в корзине?
44.
В корзине лежит 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик, а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?
45.
Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 10 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 42 очка, если известно, что по крайней мере один раз он ошибся?
46.
На палке отмечены поперечные линии красного, желтого и зеленого цвета. Если распилить палку по красным линиям, то получится 5 кусков, если по желтым ― 7 кусков, а если по зеленым ― 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трех цветов?
47.
Улитка за день заползает вверх по дереву на 2 м, а за ночь сползает на 1 м. Высота дерева 11 м. За сколько дней улитка доползёт от основания до вершины дерева?
48.
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 14 м. За сколько дней улитка доползёт от основания до вершины дерева?
49.
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
50.
В обменном пункте можно совершить одну из двух операций:
1) за 2 золотых монеты получить 3 серебряных и одну медную;
2) за 5 серебряных монет получить 3 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
51.
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
52.
В обменном пункте можно совершить одну из двух операций:
1) за 4 золотых монеты получить 5 серебряных и одну медную;
2) за 7 серебряных монет получить 5 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет у Николая?
53.
Во всех подъездах дома одинаковое число этажей, а на каждом этаже — одинаковое число квартир. При этом число подъездов дома меньше числа квартир на этаже, число квартир на этаже меньше числа этажей, число подъездов больше одного, а число этажей не более 24. Сколько этажей в доме, если в нем всего 156 квартир?
54.
В
классе учится 26 учащихся. Несколько из них слушают рок, 14 человек слушают рэп, причем и рок, и рэп слушают всего лишь трое. Известно, что четверо не слушают ни рок, ни рэп. Сколько человек из класса слушают рок?
55.
В
садке лежат 35 рыб: окуни и плотвички. Известно, что среди любых 21 рыбы имеется хотя бы одна плотвичка, а среди любых 16 рыб — хотя бы один окунь. Сколько плотвичек в садке?
56.
На поверхности глобуса маркером проведены 30 параллелей и 24 меридиана. На сколько частей проведенные линии разделили поверхность глобуса? (меридиан — это дуга окружности, соединяющая Северный и Южный полюсы, а параллель — это граница сечения глобуса плоскостью, параллельной плоскости экватора).
57.
В
доисторическом обменном пункте можно было совершить одну из двух операций:
— за 2 шкуры пещерного льва получить 5 шкур тигра и 1 шкуру кабана;
— за 7 шкур тигра получить 2 шкуры пещерного льва и 1 шкуру кабана.
У Уна, сына Быка, были только шкуры тигра. После нескольких посещений обменного пункта шкур тигра у него не прибавилось, шкур пещерного льва не появилось, зато появилось 80 шкур кабана. На сколько, в итоге, уменьшилось количество шкур тигра у Уна, сына Быка?
58.
В
войсковой части 32103 имеется 3 вида салата, 2 вида первого блюда, 3 вида второго блюда и на выбор компот или чай. Сколько вариантов обеда, состоящего обязательно из одного салата, одного первого блюда, одного второго блюда и одного напитка, могут выбрать военнослужащие этой войсковой части?
59.
Улитка за день заползает вверх по дереву на 5 метров, а за ночь сползает вниз на 3 метра. Высота дерева 17 метров. На какой день улитка впервые доползет до вершины дерева?
60.
Сколькими способами можно поставить в ряд три одинаковых желтых кубика, один синий кубик и один зеленый кубик?
61.
Произведение шестнадцати идущих подряд натуральных чисел разделили на 11. Чему может быть равен остаток от деления?
62.
Каждую минуту бактерия делится на две новые бактерии. Известно, что весь объем трехлитровой банки бактерии заполняют за 4 часа. За сколько секунд бактерии заполняют четверть банки?
63.
Список заданий викторины состоял из 36 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 75 очков, если известно, что по крайней мере один раз он ошибся?
64.
Кузнечик прыгает по прямой дороге длина одного прыжка 1 см. сначала он прыгает 11 прыжков вперед потом 3 назад потом опять 11 прыжков и затем назад 3 прыжка и так далее сколько прыжков он сделает к моменту когда впервые окажется на расстоянии 100 см. от начала.
65.
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, то получится 7 кусков, если по жёлтым — 13 кусков, а если по зелёным — 5 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
66.
В
обменном пункте можно совершить одну из двух операций:
за 2 золотых монеты получить 3 серебряных и одну медную;
за 5 серебряных монет получить 3 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
67.
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами.
Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
68.
В
обменном пункте можно совершить одну из двух операций:
1) за 4 золотых монеты получить 5 серебряных и одну медную;
2) за 7 серебряных монет получить 5 золотых и одну медную.
У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет?
69.
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 12 м. За сколько дней улитка доползёт от основания до вершины дерева?
70.
Список заданий викторины состоял из 32 вопросов. За каждый правильный ответ ученик получает 5 очков. За неправильный списывали 9, при отсуттвии ответа давали 0 очков.
Сколько верных ответов дал ученик, набравший 75 баллов, если он по крайней мере 2 раза ошибся?
71.
Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 10 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 42 очка, если известно, что по крайней мере один раз он ошибся?
72.
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
73.
Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них начиная с левого верхнего и далее по часовой стрелке равны 18, 12 и 20. Найдите площадь четвёртого прямоугольника.
74.
Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трёх из них начиная с левого верхнего и далее по часовой стрелке равны 12, 18 и 30. Найдите площадь четвёртого прямоугольника.
75.
В
таблице три столбца и несколько строк. В
каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 85, во втором — 77, в третьем — 71, а сумма чисел в каждой строке больше 12, но меньше 15. Сколько всего строк в таблице?
76.
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав 10 прыжков, начиная прыгать из начала координат?
77.
Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
78.
В
обменном пункте можно совершить одну из двух операций:
за 2 золотые монеты получить 3 серебряные и одну медную;
за 7 серебряных монет получить 3 золотые и одну медную.
У Николая были только серебряные монеты. После обменного пункта золотых монет у него не появилось, зато появилось 20 медных. На сколько уменьшилось количество серебряных монет у Николая?
79.
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав 11 прыжков, начиная прыгать из начала координат?
80.
На кольцевой дороге расположены четыре бензоколонки: А, Б, В
и Г. Расстояние между А
и Б
— 35 км, между А
и В
— 20 км, между В
и Г — 20 км, между Г и А
— 30 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б
и В.
81.
В
обменном пункте можно совершить одну из двух операций:
за 4 золотые монеты получить 5 серебряных и одну медную;
за 7 серебряных монет получить 5 золотых и одну медную.
У Николая были только серебряные монеты. После обменного пункта серебряных монет у него стало меньше, Золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет у Николая.
82. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 8 прыжков, начиная прыгать из начала координат?
83.
В
обменном пункте можно совершить одну из двух операций:
за 5 золотых монет получить 4 серебряные и одну медную;
за 10 серебряных монет получить 7 золотых и одну медную.
У Николая были только серебряные монеты. После обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 60 медных. На сколько уменьшилось количество серебряных монет у Николая?
84.
В
обменном пункте можно совершить одну из двух операций:
за 5 золотых монет получить 6 серебряных и одну медную;
за 8 серебряных монет получить 6 золотых и одну медную.
У Николая были только серебряные монеты. После обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 55 медных. На сколько уменьшилось количество серебряных монет у Николая?
85.
Во всех подъездах дома одинаковое число этажей, и па всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 105 квартир?
86.
В
обменном пункте можно совершить одну из двух операций:
1) за 3 золотых монеты получить 4 серебряных и одну медную;
2) за 7 серебряных монет получить 4 золотых и одну медную.
У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 42 медных. На сколько уменьшилось количество серебряных монет у Николы?
ОТВЕТЫ
Единый государственный экзамен по математике базового уровня состоит из 20 заданий. В задании 20 проверяются навыки решения логических задач. Школьник должен уметь применять свои знания для решения задач на практике, в том числе на арифметическую и геометрическую прогрессию. Здесь вы можете узнать, как решать задание 20 ЕГЭ по математике базового уровня, а также изучить примеры и способы решения на основе подробно разобранных заданий.
Все задания
ЕГЭ база все задания (263)
ЕГЭ база задание 1 (5)
ЕГЭ база задание 2 (6)
ЕГЭ база задание 3 (45)
ЕГЭ база задание 4 (33)
ЕГЭ база задание 5 (2)
ЕГЭ база задание 6 (44)
ЕГЭ база задание 7 (1)
ЕГЭ база задание 8 (12)
ЕГЭ база задание 10 (22)
ЕГЭ база задание 12 (5)
ЕГЭ база задание 13 (20)
ЕГЭ база задание 15 (13)
ЕГЭ база задание 19 (23)
ЕГЭ база задание 20 (32)
На ленте с разных сторон от середины отмечены две поперечные полоски
На ленте с разных сторон от середины отмечены две поперечные полоски: синяя и красная. Если разрезать ленту по синей полоске, то одна часть будет длиннее другой на A см. Если разрезать по красной, то одна часть будет длиннее другой на B см. Найдите расстояние от красной до синей полоски.
Задача про ленту входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
Биологи открыли разновидность амёб
Биологи открыли разновидность амёб, каждая из которых ровно через минуту делится на две. Биолог кладёт амёбу в пробирку, и ровно через N часов пробирка оказывается полностью заполненной амёбами. Сколько минут потребуется, чтобы вся пробирка заполнилась амёбами, если в неё положить не одну, а K амёб?
При демонстрации летней одежды наряды каждой манекенщицы
При демонстрации летней одежды наряды каждой манекенщицы отличаются хотя бы одним из трёх элементов: блузкой, юбкой и туфлями. Всего модельер приготовил для демонстрации A видов блузок, B вида юбок и C вида туфель. Сколько различных нарядов будет показано на этой демонстрации?
Задача про наряды входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
Группа туристов преодолела горный перевал
Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели за K минут, а каждый следующий километр проходили на L минут дольше предыдущего. Последний километр перед вершиной был пройден за M минут. После отдыха N минут на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за P минут, а каждый следующий на R минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за S минут.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
Врач прописал пациенту принимать лекарство по такой схеме
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять K капель, а в каждый следующий день — на N капель больше, чем в предыдущий. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится M капель?
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
По эмпирическому закону Мура среднее число транзисторов на микросхемах
По эмпирическому закону Мура среднее число транзисторов на микросхемах каждый год увеличивается в N раз. Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось K млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
Нефтяная компания бурит скважину для добычи нефти
Нефтяная компания бурит скважину для добычи нефти, которая залегает, по данным геологоразведки, на глубине N км. В течение рабочего дня бурильщики проходят L метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на K метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
В магазине бытовой техники объём продаж холодильников носит сезонный характер
В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано K холодильников, и в три последующих месяца продавали по L холодильников. С мая продажи увеличивались на M единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на N холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год?
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке
Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке L минут, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на M минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности N часов K минут, если будет следовать советам тренера?
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
Каждую секунду бактерия делится на две новые бактерии
Каждую секунду бактерия делится на две новые бактерии. Известно, что весь объём одного стакана бактерии заполняют за N часов. За сколько секунд стакан будет заполнен бактериями на 1/K часть?
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г
На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — K км, между А и В — L км, между В и Г — M км, между Г и А — N км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.
Задача про бензоколонки входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
Саша пригласил Петю в гости, сказав, что живёт
Саша пригласил Петю в гости, сказав, что живёт в K подъезде в квартире № M, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом N-этажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
Задача про квартиры и дома входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20.
Среднее общее образование
Линия УМК Г. К. Муравина. Алгебра и начала математического анализа (10-11) (углуб.)
Линия УМК Мерзляка. Алгебра и начала анализа (10-11) (У)
Математика
Подготовка к ЕГЭ по математике (профильный уровень): задания, решения и объяснения
Разбираем задания и решаем примеры с учителем
Экзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут).
Минимальный порог
— 27 баллов.
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.
Определяющим признаком каждой части работы является форма заданий:
- часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
- часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).
Панова Светлана Анатольевна
, учитель математики высшей категории школы, стаж работы 20 лет:
«Для того чтобы получить школьный аттестат, выпускнику необходимо сдать два обязательных экзамена в форме ЕГЭ, один из которых математика. В соответствии с Концепцией развития математического образования в Российской Федерации ЕГЭ по математике разделен на два уровня: базовый и профильный. Сегодня мы рассмотрим варианты профильного уровня».
Задание № 1
— проверяет у участников ЕГЭ умение применять навыки, полученные в курсе 5 — 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.
Пример 1.
В квартире, где проживает Петр, установили прибор учета расхода холодной воды (счетчик). Первого мая счетчик показывал расход 172 куб. м воды, а первого июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м холодной воды составляет 34 руб 17 коп? Ответ дайте в рублях.
Решение:
1) Найдем количество потраченной воды за месяц:
177 — 172 = 5 (куб м)
2) Найдем сколько денег заплатят за потраченную воду:
34,17 · 5 = 170,85 (руб)
Ответ:
170,85.
Задание № 2
-является одним из простейших заданий экзамена. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований — это задание на использования приобретённых знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит из описания с помощью функций различных реальных зависимостей между величинами и интерпретация их графиков. Задание № 2 проверяет умение извлекать информацию, представленную в таблицах, на диаграммах, графиках. Выпускникам нужно уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по её графику. Также необходимо уметь находить по графику функции наибольшее или наименьшее значение и строить графики изученных функций. Допускаемые ошибки носят случайный характер в чтении условия задачи, чтении диаграммы.
#ADVERTISING_INSERT#
Пример 2.
На рисунке показано изменение биржевой стоимости одной акции добывающей компании в первой половине апреля 2017 года. 7 апреля бизнесмен приобрёл 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько потерял бизнесмен в результате этих операций?
Решение:
2) 1000 · 3/4 = 750 (акций) — составляют 3/4 от всех купленных акций.
6) 247500 + 77500 = 325000 (руб) — бизнесмен получил после продажи 1000 акций.
7) 340000 – 325000 = 15000 (руб) — потерял бизнесмен в результате всех операций.
Ответ:
15000.
Задание № 3
— является заданием базового уровня первой части, проверяет умения выполнять действия с геометрическими фигурами по содержанию курса «Планиметрия». В задании 3 проверяется умение вычислять площадь фигуры на клетчатой бумаге, умение вычислять градусные меры углов, вычислять периметры и т.п.
Пример 3.
Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение:
Для вычисления площади данной фигуры можно воспользоваться формулой Пика:
Для вычисления площади данного прямоугольника воспользуемся формулой Пика:
где В = 10, Г = 6, поэтому
Ответ:
20.
Читайте также: ЕГЭ по физике: решение задач о колебаниях
Задание № 4
— задача курса «Теория вероятностей и статистика». Проверяется умение вычислять вероятность события в простейшей ситуации.
Пример 4.
На окружности отмечены 5 красных и 1 синяя точка. Определите, каких многоугольников больше: тех, у которых все вершины красные, или тех, у которых одна из вершин синяя. В ответе укажите, на сколько одних больше, чем других.
Решение:
1) Воспользуемся формулой числа сочетаний из n
элементов по k
:
у которых все вершины красные.
3) Один пятиугольник, у которого все вершины красные.
4) 10 + 5 + 1 = 16 многоугольников, у которых все вершины красные.
у которых вершины красные или с одной синей вершиной.
у которых вершины красные или с одной синей вершиной.

9) 20 + 15 + 6 + 1 = 42 многоуголника, у которых все вершины красные или с одной синей вершиной.
10) 42 – 16 = 26 многоугольников, в которых используется синяя точка.
11) 26 – 16 = 10 многоугольников – на сколько многоугольников, у которых одна из вершин — синяя точка, больше, чем многоугольников, у которых все вершины только красные.
Ответ:
10.
Задание № 5
— базового уровня первой части проверяет умения решать простейшие уравнения (иррациональные, показательные, тригонометрические, логарифмические).
Пример 5.
Решите уравнение 2 3 + x
= 0,4 · 5 3 + x
.
Решение.
Разделим обе части данного уравнения на 5 3 + х
≠ 0, получим
|
2 3 + x |
= 0,4 или | 2 |
3 + х |
= | 2 | , | ||
|
5 3 + х |
5 | 5 |
откуда следует, что 3 + x
= 1, x
= –2.
Ответ:
–2.
Задание № 6
по планиметрии на нахождение геометрических величин (длин, углов, площадей), моделирование реальных ситуаций на языке геометрии. Исследование построенных моделей с использованием геометрических понятий и теорем. Источником трудностей является, как правило, незнание или неверное применение необходимых теорем планиметрии.
Площадь треугольника ABC
равна 129. DE
– средняя линия, параллельная стороне AB
. Найдите площадь трапеции ABED
.
Решение.
Треугольник CDE
подобен треугольнику CAB
по двум углам, так как угол при вершине C
общий, угол СDE
равен углу CAB
как соответственные углы при DE
|| AB
секущей AC
. Так как DE
– средняя линия треугольника по условию, то по свойству средней линии | DE
= (1/2)AB
. Значит, коэффициент подобия равен 0,5. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
Следовательно, S ABED
= S
ΔABC
– S
ΔCDE
= 129 – 32,25 = 96,75.
Задание № 7
— проверяет применение производной к исследованию функции. Для успешного выполнения необходимо содержательное, не формальное владение понятием производной.
Пример 7.
К графику функции y
= f
(x
) в точке с абсциссой x
0 проведена касательная, которая перпендикулярна прямой, проходящей через точки (4; 3) и (3; –1) этого графика. Найдите f
′(x
0).
Решение.
1) Воспользуемся уравнением прямой, проходящей через две заданные точки и найдём уравнение прямой, проходящей через точки (4; 3) и (3; –1).
(y
– y
1)(x
2 – x
1) = (x
– x
1)(y
2 – y
1)
(y
– 3)(3 – 4) = (x
– 4)(–1 – 3)
(y
– 3)(–1) = (x
– 4)(–4)
–y
+ 3 = –4x
+ 16| · (–1)
y
– 3 = 4x
– 16
y
= 4x
– 13, где k
1 = 4.
2) Найдём угловой коэффициент касательной k
2 , которая перпендикулярна прямой y
= 4x
– 13, где k
1 = 4, по формуле:
3) Угловой коэффициент касательной – производная функции в точке касания. Значит, f
′(x
0) = k
2 = –0,25.
Ответ:
–0,25.
Задание № 8
— проверяет у участников экзамена знания по элементарной стереометрии, умение применять формулы нахождения площадей поверхностей и объемов фигур, двугранных углов, сравнивать объемы подобных фигур, уметь выполнять действия с геометрическими фигурами, координатами и векторами и т.п.
Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
Решение.
1) V
куба = a
3 (где а
– длина ребра куба), поэтому
а
3 = 216
а
= 3 √216
2) Так как сфера вписана в куб, значит, длина диаметра сферы равна длине ребра куба, поэтому d
= a
, d
= 6, d
= 2R
, R
= 6: 2 = 3.
Задание № 9
— требует от выпускника навыков преобразования и упрощения алгебраических выражений. Задание № 9 повышенного уровня сложности с кратким ответом. Задания из раздела «Вычисления и преобразования» в ЕГЭ подразделяются на несколько видов:
- преобразования числовых/буквенных тригонометрических выражений.
преобразования числовых рациональных выражений;
преобразования алгебраических выражений и дробей;
преобразования числовых/буквенных иррациональных выражений;
действия со степенями;
преобразование логарифмических выражений;
Пример 9.
Вычислите tgα, если известно, что cos2α = 0,6 и
Решение.
1) Воспользуемся формулой двойного аргумента: cos2α = 2 cos 2 α – 1 и найдём
| tg 2 α = | 1 | – 1 = | 1 | – 1 = | 10 | – 1 = | 5 | – 1 = 1 | 1 | – 1 = | 1 | = 0,25. |
| cos 2 α | 0,8 | 8 | 4 | 4 | 4 |
Значит, tg 2 α = ± 0,5.
3) По условию
значит, α – угол II четверти и tgα < 0, поэтому tgα = –0,5.
Ответ:
–0,5.
#ADVERTISING_INSERT#
Задание № 10
— проверяет у учащихся умение использовать приобретенные раннее знания и умения в практической деятельности и повседневной жизни. Можно сказать, что это задачи по физике, а не по математике, но все необходимые формулы и величины даны в условии. Задачи сводятся к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства. Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ. Ответ должен получиться в виде целого числа или конечной десятичной дроби.
Два тела массой m
= 2 кг каждое, движутся с одинаковой скоростью v
= 10 м/с под углом 2α
друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением Q
= mv
2 sin 2 α. Под каким наименьшим углом 2α
(в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
Решение.
Для решения задачи нам необходимо решить неравенство Q ≥ 50, на интервале 2α
∈ (0°; 180°).
mv
2 sin 2 α ≥ 50
2· 10 2 sin 2 α ≥ 50
200 · sin 2 α ≥ 50
Так как α
∈ (0°; 90°), то будем решать только
Изобразим решение неравенства графически:
Так как по условию α
∈ (0°; 90°), значит 30° ≤ α < 90°. Получили, что наименьший угол α равен 30°, тогда наименьший угол 2α = 60°.
Задание № 11
— является типовым, но оказывается непростым для учащихся. Главным источником затруднений является построение математической модели (составление уравнения). Задание № 11 проверяет умение решать текстовые задачи.
Пример 11.
На весенних каникулах 11-классник Вася должен был решить 560 тренировочных задач для подготовки к ЕГЭ. 18 марта в последний учебный день Вася решил 5 задач. Далее ежедневно он решал на одно и то же количество задач больше по сравнению с предыдущим днём. Определите, сколько задач Вася решил 2 апреля в последний день каникул.
Решение:
Обозначим a
1 = 5 – количество задач, которые Вася решил 18 марта, d
– ежедневное количество задач, решаемых Васей, n
= 16 – количество дней с 18 марта по 2 апреля включительно, S
16 = 560 – общее количество задач, a
16 – количество задач, которые Вася решил 2 апреля. Зная, что ежедневно Вася решал на одно и то же количество задач больше по сравнению с предыдущим днём, то можно использовать формулы нахождения суммы арифметической прогрессии:
560 = (5 + a
16) · 8,
5 + a
16 = 560: 8,
5 + a
16 = 70,
a
16 = 70 – 5
a
16 = 65.
Ответ:
65.
Задание № 12
— проверяют у учащихся умение выполнять действия с функциями, уметь применять производную к исследованию функции.
Найти точку максимума функции y
= 10ln(x
+ 9) – 10x
+ 1.
Решение:
1) Найдем область определения функции: x
+ 9 > 0, x
> –9, то есть x ∈ (–9; ∞).
2) Найдем производную функции:
4) Найденная точка принадлежит промежутку (–9; ∞). Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума x
= –8.
Скачать бесплатно рабочую программу по математике к линии УМК Г.К. Муравина, К.С. Муравина, О.В. Муравиной 10-11
Скачать бесплатно методические пособия по алгебре
Задание № 13
-повышенного уровня сложности с развернутым ответом, проверяющее умение решать уравнения, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.
а) Решите уравнение 2log 3 2 (2cosx
) – 5log 3 (2cosx
) + 2 = 0
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Решение:
а) Пусть log 3 (2cosx
) = t
, тогда 2t
2 – 5t
+ 2 = 0,
|
log 3 (2cosx ) = |
2 | ⇔ |
2cosx = 9 |
⇔ |
cosx = |
4,5 |
⇔ т.к. |cosx | ≤ 1, |
|||
|
log 3 (2cosx ) = |
1 |
2cosx = √3 |
cosx = |
√3 | ||||||
| 2 | 2 |
|
x = |
π |
+ 2πk |
|
| 6 | |||
|
x = – |
π |
+ 2πk , k ∈ Z |
|
| 6 |
б) Найдём корни, лежащие на отрезке .
Из рисунка видно, что заданному отрезку принадлежат корни
|
Ответ: а) |
π |
+ 2πk ; – |
π |
+ 2πk , k ∈ Z ; б) |
11π | ; | 13π | . |
| 6 | 6 | 6 | 6 |
Задание № 14
-повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить.
Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Расстояние между хордами равно 2√197.
а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Решение:
а) Хорда длиной 12 находится на расстоянии = 8 от центра окружности основания, а хорда длиной 16, аналогично, – на расстоянии 6. Поэтому расстояние между их проекциями на плоскость, параллельную основаниям цилиндров, составляет либо 8 + 6 = 14, либо 8 − 6 = 2.
Тогда расстояние между хордами составляет либо
= = √980 = = 2√245
= = √788 = = 2√197.
По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее. Что требовалось доказать.
б) Обозначим центры оснований за О 1 и О 2 . Проведем из центра основания с хордой длины 12 серединный перпендикуляр к этой хорде (он имеет длину 8, как уже отмечалось) и из центра другого основания — к другой хорде. Они лежат в одной плоскости β, перпендикулярной этим хордам. Назовем середину меньшей хорды B, большей A и проекцию A на второе основание — H (H ∈ β). Тогда AB,AH ∈ β и значит, AB,AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.
Значит, искомый угол равен
| ∠ABH = arctg | AH | = arctg | 28 | = arctg14. |
| BH | 8 – 6 |
Задание № 15
— повышенного уровня сложности с развернутым ответом, проверяет умение решать неравенства, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.
Пример 15.
Решите неравенство |x
2 – 3x
| · log 2 (x
+ 1) ≤ 3x
– x
2 .
Решение:
Областью определения данного неравенства является интервал (–1; +∞). Рассмотри отдельно три случая:
1) Пусть x
2 – 3x
= 0, т.е. х
= 0 или х
= 3. В этом случае данное неравенство превращается в верное, следовательно, эти значения входят в решение.
2) Пусть теперь x
2 – 3x
> 0, т.е. x
∈ (–1; 0) ∪ (3; +∞). При этом данное неравенство можно переписать в виде (x
2 – 3x
) · log 2 (x
+ 1) ≤ 3x
– x
2 и разделить на положительное выражение x
2 – 3x
. Получим log 2 (x
+ 1) ≤ –1, x
+ 1 ≤ 2 –1 , x
≤ 0,5 –1 или x
≤ –0,5. Учитывая область определения, имеем x
∈ (–1; –0,5].
3) Наконец, рассмотрим x
2 – 3x
< 0, при этом x
∈ (0; 3). При этом исходное неравенство перепишется в виде (3x
– x
2) · log 2 (x
+ 1) ≤ 3x
– x
2 . После деления на положительное выражение 3x
– x
2 , получим log 2 (x
+ 1) ≤ 1, x
+ 1 ≤ 2, x
≤ 1. Учитывая область, имеем x
∈ (0; 1].
Объединяя полученные решения, получаем x
∈ (–1; –0.5] ∪ ∪ {3}.
Ответ:
(–1; –0.5] ∪ ∪ {3}.
Задание № 16
— повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами, координатами и векторами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить.
В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E – на отрезке AB. а) Докажите, что FH = 2DH. б) Найдите площадь прямоугольника DEFH, если AB = 4.
Решение:
а)
1) ΔBEF – прямоугольный, EF⊥BC, ∠B = (180° – 120°) : 2 = 30°, тогда EF = BE по свойству катета, лежащего против угла 30°.
2) Пусть EF = DH = x
, тогда BE = 2x
, BF = x
√3 по теореме Пифагора.
3) Так как ΔABC равнобедренный, значит, ∠B = ∠C = 30˚.
BD – биссектриса ∠B, значит ∠ABD = ∠DBC = 15˚.
4) Рассмотрим ΔDBH – прямоугольный, т.к. DH⊥BC.
| 2x |
= | 4 – 2x |
| 2x (√3 + 1) |
4 |
√3 – 1
= 2 – x
x
= 3 – √3
EF = 3 – √3
2) S
DEFH = ED · EF = (3 – √3
) · 2(3 – √3
)
S
DEFH = 24 – 12√3.
Ответ:
24 – 12√3.
Задание № 17
— задание с развернутым ответом, это задание проверяет применение знаний и умений в практической деятельности и повседневной жизни, умение строить и исследовать математические модели. Это задание — текстовая задача с экономическим содержанием.
Пример 17.
Вклад в размере 20 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х
млн. рублей, где х
— целое
число. Найдите наибольшее значение х
, при котором банк за четыре года начислит на вклад меньше 17 млн рублей.
Решение:
В конце первого года вклад составит 20 + 20 · 0,1 = 22 млн рублей, а в конце второго – 22 + 22 · 0,1 = 24,2 млн рублей. В начале третьего года вклад (в млн рублей) составит (24,2 + х
), а в конце — (24,2 + х)
+ (24,2 + х)
· 0,1 = (26,62 + 1,1х
). В начале четвёртого года вклад составит (26,62 + 2,1х)
, а в конце — (26,62 + 2,1х
) + (26,62 + 2,1х
) · 0,1 = (29,282 + 2,31х
). По условию, нужно найти наибольшее целое х, для которого выполнено неравенство
(29,282 + 2,31x
) – 20 – 2x
< 17
29,282 + 2,31x
– 20 – 2x
< 17
0,31x
< 17 + 20 – 29,282
0,31x
< 7,718
Наибольшее целое решение этого неравенства — число 24.
Ответ:
24.
Задание № 18
— задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности — это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 18 необходим, кроме прочных математических знаний, также высокий уровень математической культуры.
При каких a
система неравенств
| x 2 + y 2 ≤ 2ay – a 2 + 1 |
|
| y + a ≤ |x | – a |
имеет ровно два решения?
Решение:
Данную систему можно переписать в виде
| x 2 + (y – a ) 2 ≤ 1 |
|
| y ≤ |x | – a |
Если нарисовать на плоскости множество решений первого неравенства, получится внутренность круга (с границей) радиуса 1 с центром в точке (0, а
). Множество решений второго неравенства – часть плоскости, лежащая под графиком функции y
= |
x
| –
a
,
причём последний есть график функции
y
= |
x
|
, сдвинутый вниз на а
. Решение данной системы есть пересечение множеств решений каждого из неравенств.
Следовательно, два решения данная система будет иметь лишь в случае, изображённом на рис. 1.
Точки касания круга с прямыми и будут двумя решениями системы. Каждая из прямых наклонена к осям под углом 45°. Значит, треугольник PQR
– прямоугольный равнобедренный. Точка Q
имеет координаты (0, а
), а точка R
– координаты (0, –а
). Кроме того, отрезки PR
и PQ
равны радиусу окружности, равному 1. Значит,
Задание № 19
— задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности — это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 19 необходимо уметь осуществлять поиск решения, выбирая различные подходы из числа известных, модифицируя изученные методы.
Пусть Sn
сумма п
членов арифметической прогрессии (а п
). Известно, что S n
+ 1 = 2n
2 – 21n
– 23.
а) Укажите формулу п
-го члена этой прогрессии.
б) Найдите наименьшую по модулю сумму S n
.
в) Найдите наименьшее п
, при котором S n
будет квадратом целого числа.
Решение
: а) Очевидно, что a n
= S n
– S n
– 1 . Используя данную формулу, получаем:
S n
= S
(n
– 1) + 1 = 2(n
– 1) 2 – 21(n
– 1) – 23 = 2n
2 – 25n
,
S n
– 1 = S
(n
– 2) + 1 = 2(n
– 1) 2 – 21(n
– 2) – 23 = 2n
2 – 25n
+ 27
значит, a n
= 2n
2 – 25n
– (2n
2 – 29n
+ 27) = 4n
– 27.
Б) Так как S n
= 2n
2 – 25n
, то рассмотрим функцию S
(x
) = |
2x
2 – 25x|
. Ее график можно увидеть на рисунке.
Очевидно, что наименьшее значение достигается в целочисленных точках, расположенных наиболее близко к нулям функции. Очевидно, что это точки х
= 1, х
= 12 и х
= 13. Поскольку, S
(1) = |S
1 | = |2 – 25| = 23, S
(12) = |S
12 | = |2 · 144 – 25 · 12| = 12, S
(13) = |S
13 | = |2 · 169 – 25 · 13| = 13, то наименьшее значение равно 12.
в) Из предыдущего пункта вытекает, что Sn
положительно, начиная с n
= 13. Так как S n
= 2n
2 – 25n
= n
(2n
– 25), то очевидный случай, когда данное выражение является полным квадратом, реализуется при n
= 2n
– 25, то есть при п
= 25.
Осталось проверить значения с 13 до 25:
S
13 = 13 · 1, S
14 = 14 · 3, S
15 = 15 · 5, S
16 = 16 · 7, S
17 = 17 · 9, S
18 = 18 · 11, S
19 = 19 · 13, S
20 = 20 · 13, S
21 = 21 · 17, S
22 = 22 · 19, S
23 = 23 · 21, S
24 = 24 · 23.
Получается, что при меньших значениях п
полный квадрат не достигается.
Ответ:
а) a n
= 4n
– 27; б) 12; в) 25.
________________
*С мая 2017 года объединенная издательская группа «ДРОФА-ВЕНТАНА» входит в корпорацию «Российский учебник». В корпорацию также вошли издательство «Астрель» и цифровая образовательная платформа «LECTA». Генеральным директором назначен Александр Брычкин, выпускник Финансовой академии при Правительстве РФ, кандидат экономических наук, руководитель инновационных проектов издательства «ДРОФА» в сфере цифрового образования (электронные формы учебников, «Российская электронная школа», цифровая образовательная платформа LECTA). До прихода в издательство «ДРОФА» занимал позицию вице-президента по стратегическому развитию и инвестициям издательского холдинга «ЭКСМО-АСТ». Сегодня издательская корпорация «Российский учебник» обладает самым крупным портфелем учебников, включенных в Федеральный перечень — 485 наименований (примерно 40%, без учета учебников для коррекционной школы). Издательствам корпорации принадлежат наиболее востребованные российскими школами комплекты учебников по физике, черчению, биологии, химии, технологии, географии, астрономии — областям знаний, которые нужны для развития производственного потенциала страны. В портфель корпорации входят учебники и учебные пособия для начальной школы, удостоенные Премии Президента в области образования. Это учебники и пособия по предметным областям, которые необходимы для развития научно-технического и производственного потенциала России.
Сборник для подготовки к ЕГЭ (базовый уровень)
Прототип задания № 20
1.
В обменном пункте можно совершить одну из двух операций:
За 2 золотых монеты получить 3 серебряных и одну медную;
За 5 серебряных монет получить 3 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
2.
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 5 кусков, если по жёлтым — 7 кусков, а если по зелёным — 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
3.
В корзине лежит 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов — хотя бы один груздь. Сколько рыжиков в корзине?
4.
В корзине лежат 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине?
5.
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 4200 рублей, а за каждый следующий метр — на 1300 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 11 метров?
6.
Улитка за день залезает вверх по дереву на 3 м, а за ночь спускается на 2 м. Высота дерева 10 м. За сколько дней улитка поднимется на вершину дерева?
7.
На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса?
8.
В корзине лежат 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов хотя бы один груздь. Сколько рыжиков в корзине?
9.
1) за 2 золотые монеты получить 3 серебряные и одну медную;
2) за 5 серебряных монет получить 3 золотые и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
10.
В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год?
11.
В корзине лежит 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик, а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?
12.
Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 10 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 42 очка, если известно, что по крайней мере один раз он ошибся?
13.
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Кузнечик начинает прыгать из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков?
14.
В обменном пункте можно совершить одну из двух операций:
· за 2 золотые монеты получить 3 серебряные и одну медную;
· за 5 серебряных монет получить 3 золотые и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 100 медных. На сколько уменьшилось количество серебряных монет у Николая?
15.
В корзине лежит 45 грибов: рыжики и грузди. Известно, что среди любых 23 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько рыжиков в корзине?
16.
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3700 рублей, а за каждый следующий метр — на 1700 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 8 метров?
17.
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 20 капель, а в каждый следующий день — на 3 капли больше, чем в предыдущий. После 15 дней приёма пациент делает перерыв в 3 дня и продолжает принимать лекарство по обратной схеме: в 19-й день он принимает столько же капель, сколько и в 15-й день, а затем ежедневно уменьшает дозу на 3 капли, пока дозировка не станет меньше 3 капель в день. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 200 капель?
18.
В корзине лежит 50 грибов: рыжики и грузди. Известно, что среди любых 28 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько груздей в корзине?
19.
Саша пригласил Петю в гости, сказав, что живёт в десятом подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
20.
В обменном пункте можно совершить одну из двух операций:
1) за 5 золотых монеты получить 6 серебряных и одну медную;
2) за 8 серебряных монет получить 6 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 55 медных. На сколько уменьшилось количество серебряных монет у Николая?
21.
Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 22 минуты, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 4 минуты, пока оно не достигнет 60 минут, а дальше продолжать тренироваться по 60 минут каждый день. За сколько занятий, начиная с первого, Андрей проведёт на беговой дорожке в сумме 4 часа 48 минут?
22.
Каждую секунду бактерия делится на две новые бактерии. Известно, что весь объём одного стакана бактерии заполняют за 1 час. За сколько секунд стакан будет заполнен бактериями наполовину?
23.
В меню ресторана имеется 6 видов салатов, 3 вида первых блюд, 5 видов вторых блюд и 4 вида десерта. Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана?
24.
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?
25.
Сколькими способами можно поставить в ряд два одинаковых красных кубика, три одинаковых зелёных кубика и один синий кубик?
26.
Произведение десяти идущих подряд чисел разделили на 7. Чему может быть равен остаток?
27.
В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
28.
Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 11 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 84 очка, если известно, что по крайней мере один раз он ошибся?
29.
На поверхности глобуса фломастером проведены 13 параллелей и 25 меридианов. На сколько частей проведённые линии разделили поверхность глобуса?
Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
30.
На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 35 км, между A и C — 20 км, между C и D — 20 км, между D и A — 30 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. Ответ дайте в километрах.
31.
Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, нумерация квартир в доме начинается с единицы.)
32.
В корзине лежит 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов — хотя бы один груздь. Сколько рыжиков в корзине?
33.
Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров?
34.
Саша пригласил Петю в гости, сказав, что живёт в десятом подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На каком этаже живёт Саша? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.)
35.
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
36.
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.
37.
На кольцевой дороге расположено четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 50 км, между А и В — 30 км, между В и Г — 25 км, между Г и А — 45 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге).
Найдите расстояние (в километрах) между Б и В.
38.
Нефтяная компания бурит скважину для добычи нефти, которая залегает, по данным геологоразведки, на глубине 3 км. В течение рабочего дня бурильщики проходят 300 метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на 30 метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?
39.
Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут.
40.
В обменном пункте можно совершить одну из двух операций:
За 3 золотые монеты получить 4 серебряных и одну медную;
За 7 серебряных монет получить 4 золотые и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 42 медные. На сколько уменьшилось количество серебряных монет у Николая?
41.
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
42.
В обменном пункте можно совершить одну из двух операций:
1) за 4 золотые монеты получить 5 серебряных и одну медную;
2) за 8 серебряных монет получить 5 золотых и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 45 медных. На сколько уменьшилось количество серебряных монет у Николая?
43.
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 12 прыжков, начиная прыгать из начала координат?
44.
В бак объёмом 38 литров каждый час, начиная с 12 часов, наливают полное ведро воды объёмом 8 литров. Но в днище бака есть небольшая щель, и из неё за час вытекает 3 литра. В какой момент времени (в часах) бак будет заполнен полностью.
45.
В корзине лежит 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине?
46.
Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 7?
47.
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков, начиная прыгать из начала координат?
48.
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 1 м. Высота дерева 13 м. За сколько дней улитка впервые доползёт до вершины дерева?
49.
На глобусе фломастером проведены 17 параллелей (включая экватор) и 24 меридиана. На сколько частей проведённые линии разделяют поверхность глобуса?
50.
На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса?
Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Ответы к прототипу задания № 20
-
Ответ: 117700
-
Ответ: 77200
-
Ответ: 3599
-
Ответ: 89100
Улитка за день заползает вверх по дереву на (4) м, а за ночь сползает на (2) м. Высота дерева (14) м. За сколько дней улитка впервые доползет до вершины дерева?
Решение
Если подсчитать на сколько метров улитка продвигается ровно за сутки и разделить высоту дерева на это число, ответ будет неверным. Потому что улитка могла добраться до вершины дерева в течение дня, а потом уже за ночь сползти вниз. Кроме того, если решать задачу про улитку и дерево таким способом, получится, что в какой-то момент улитка заползает выше, чем находится вершина дерева. Поэтому такой подход использовать нельзя. Будем решать задачу постепенно.
В первый день улитка заползла на (4) метра. Данная высота меньше высоты дерева, получается что улитка не достигла заданной высота в первый день. За ночь она спустилась на (2) метра, значит, она поднялась за сутки на высоту (4−2=2) метра.
Во второй день улитка заползла на высоту: (2+4=6) метров и спустилась ночью на (2) метра: (6-2=4) метра.
За третьи сутки:
поднялась на высоту (4+4=8) метров;
спустилась до высоты (8-2=6) метров.
За четвертые сутки:
поднялась на высоту (6+4=10) метров;
спустилась до высоты (10-2=8) метров.
За пятые сутки:
поднялась на высоту (8+4=12) метров;
спустилась до высоты (12-2=10) метров.
За шестые сутки:
поднялась на высоту (10+4=14) метров.
Таким образом, впервые улитка доползет до высоты (14) метров на шестой день.
Ответ: (6).
Источник: ЕГЭ-2017. Математика. Базовый уровень. 30 вариантов. Типовые экзаменационные варианты. (вариант №9) (Купить книгу)
Задание № 20. Задачи на логику и смекалку
Тип №1 (про кузнечика)
1. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков, начиная прыгать из начала координат.
Решение.
Заметим, что кузнечик может оказаться только в точках с нечётными координатами, т.к. количество прыжков, которое он делает, — нечётно. Максимально кузнечик может оказаться в точках, модуль которых не превышает одиннадцати. Таким образом, кузнечик может оказаться в точках: −11, −9, −7, −5, −3, −1, 1, 3, 5, 7, 9 и 11; всего 12 точек.
Ответ: 12.
2. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 6 прыжков, начиная прыгать из начала координат?
Решение.
Заметим, что кузнечик может оказаться только в точках с чётными координатами, поскольку число прыжков, которое он делает, — чётно. Максимально кузнечик может оказаться в точках, модуль которых не превышает шести. Таким образом, кузнечик может оказаться в точках: −6, −4, −2, 0, 2, 4 и 6; всего 7 точек.
Ответ: 7.
Вывод. Из решения представленных задач видно, что количество различных точек на координатной прямой, в которых кузнечик может оказаться, на 1 больше числа совершённых им прыжков.
Задания для самостоятельного решения
1. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 8 прыжков, начиная прыгать из начала координат.
2. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 9 прыжков, начиная прыгать из начала координат.
Тип № 2 (про улитку)
1. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?
Решение.
За день улитка заползёт на 4 метра, а за ночь — сползёт на 3 метра. Итого за сутки она заползёт на метр.
За шестеро суток она поднимется на высоту шести метров. И днём следующего дня она уже окажется на вершине дерева.
Ответ: 7.
2. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 12 м. За сколько дней улитка впервые доползёт до вершины дерева?
Решение.
За день улитка заползёт на 4 метра, а за ночь — сползёт на 2 метра. Итого за сутки она заползёт на 2 метра.
За четверо суток она поднимется на высоту восьми метров. И днём следующего дня она уже окажется на вершине дерева.
Ответ: 5.
Примечание. Можно рассуждать так: В последний день улитка может подняться вверх на 4 метра. Значит, 12 – 4 = 8 (м) надо преодолеть за предыдущие дни. Так как за сутки улитка заползёт на 2 метра, то 8 : 2 = 4 (дня) ей понадобится, чтобы подняться на 8 метров. Следовательно, всего 1 + 4 = 5 дней.
Задания для самостоятельного решения
1. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 1 м. Высота дерева 13 м. За сколько дней улитка впервые доползёт до вершины дерева?
2. Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 14 м. За сколько дней улитка впервые доползёт до вершины дерева?
3. Улитка за день заползает вверх по дереву на 2 м, а за ночь сползает на 1 м. Высота дерева 11 м. За сколько дней улитка доползёт от основания до вершины дерева?
Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние меньше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в сумме 8,5 метра. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 34 метрам.
Источник: ОГЭ Ященко 2023 (50 вар)
Решение:
Из справочных материалов ОГЭ используем формулу суммы первых n членов арифметической прогрессии:
S_{n}=frac{(a_{1}+a_{n})cdot n}{2}
Sn = 34 метра, расстояние между деревьев;
a1 – проползла метров за первый день;
аn – проползла метров за последний день;
n – количество дней;
По условию а1 + аn = 8,5 метров. Подставим всё в формулу и найдём n:
34=frac{8,5cdot n}{2}\34cdot 2=8,5cdot n\68=8,5cdot n\n=frac{68}{8,5}=8
Ответ: 8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.