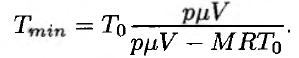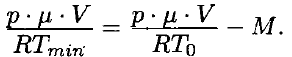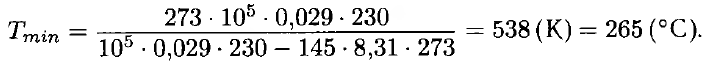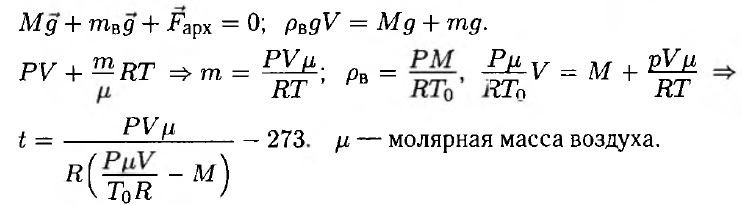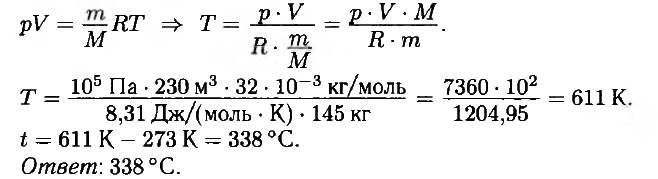Задача с воздушным шаром физика егэ - Помощь в подготовке к экзаменам и поступлению

Спрятать решение

Решение.

Условие подъёма шара: где m_в   — масса воздуха внутри оболочки. Отсюда

где rho_0   — плотность окружающего воздуха.

Используя уравнение Менделеева  — Клапейрона для воздуха внутри и снаружи оболочки, находим:

После подставки в неравенство (1) получаем:

Минимальная разность температур составляет

Ответ: 72 K.

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом; II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ	3
Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.). И (ИЛИ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И (ИЛИ) Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины)	2
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи	1
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла	0
Максимальный балл	3

Источник: ЕГЭ 20.06.2016 по физике. Основная волна. Вариант 1 (Часть С)

Источник

Решение задание 30 демоверсии ЕГЭ по физике 2019:

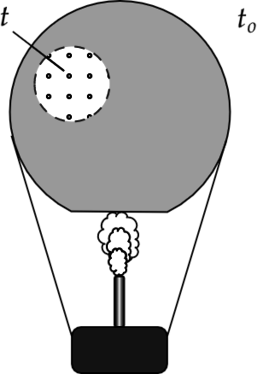
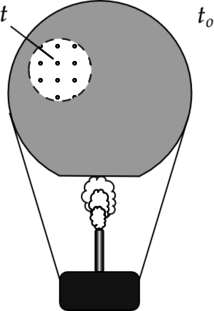
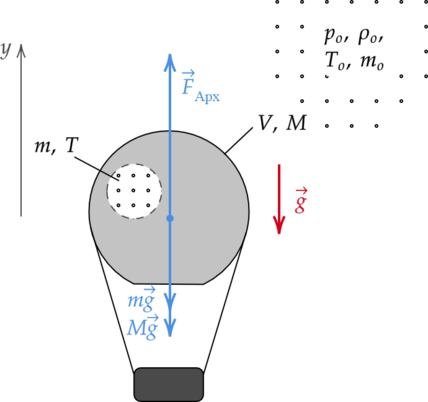
Воздушный шар, оболочка которого имеет массу М = 145 кг и объём V = 230 м³, наполняется при нормальном атмосферном давлении горячим воздухом, нагретым до температуры t = 265 °С. Определите максимальную температуру t0 окружающего воздуха, при которой шар начнёт подниматься. Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие (см. рисунок).

Будем благодарны, если вы поделитесь данной записью со своими друзьями в социальных сетях, оставите отзыв и посмотрите другие материалы на нашем сайте.

Источник

30. Молекулярная физика (расчетная задача)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Смешанные задачи

Воздушный шар, оболочка которого имеет массу (M) = 145 кг и объём (V) = 230 м(^3), наполняется при нормальном атмосферном давлении горячим воздухом, нагретым до температуры (t) = 265 (^{circ})С. Определите максимальную температуру (t_o) окружающего воздуха, при которой шар начнёт подниматься. Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие (см. рисунок).

“Демоверсия 2019”

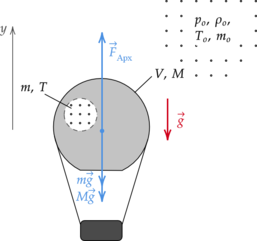
Покажем на рисунке все силы, действущие на воздушный шар и введем вертикальную ось (y):

Рассмотрим предельный случай, когда шар вот-вот оторвется от поверхности земли, и запишем для него второй закон Ньютона: [vec{F}_text{Арх} + mvec{g} +Mvec{g} = 0] где (F_text{Арх}) — выталкивающая сила, (m) — масса горячего воздуха, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на ось (y), направленную вертикально вверх: [; ; ; ; F_text{Арх} — mg-Mg = 0 ; ; ; ; (1)] Выталкивающая сила равна: [; ; ; ; F_text{Арх} = rho_o gV ; ; ; ; (2)] где (rho_o) — плотность холодного воздуха, (V) — объем шара.
Подставим (2) в (1) и разделим на (g): [; ; ; ; rho_o V — m — M = 0 ; ; ; ; (3)] Заметим, что (rho_o V = m_o), где (m_o) — масса холодного воздуха.
Тогда уравнение (3) будет иметь вид: [; ; ; ; m_o — m — M = 0 ; ; ; ; (4)] Чтобы найти массы горячей и холодного воздуха, запишем для них уравнение Менделеева – Клапейрона: [; ; ; ; p_oV = dfrac{m}{Mr}RT ; ; ; Rightarrow ; ; ; m = dfrac{p_o VMr}{RT} ; ; ; ; (5)] [; ; ; ; p_oV = dfrac{m_o}{Mr}RT_o ; ; ; Rightarrow ; ; ; m_o = dfrac{p_o VMr}{RT_o} ; ; ; ; (6)] где (p_o) — атмосферное давление, (Mr) — молярная масса воздуха, (R) — универсальная газовая постоянная, (T) (T_o) — абсолютные температуры горячего и холодного воздуха соответственно.
Подставим (5), (6) в (4) и выразим максимальную температуру окружающего воздуха, при которой шар начнет подниматься: [dfrac{p_o VMr}{RT_o} — dfrac{p_o VMr}{RT} — M = 0 ; ; ; / :dfrac{p_o VMr}{RT}] [dfrac{1}{T_o} — dfrac{1}{T} — dfrac{MR}{p_oVMr} = 0] [T_o=dfrac{mu p_oVT}{mu p_oV+MRT}] [T_o = dfrac{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3cdot(265+273)text{ К}}{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3+145text{ кг}cdot8,31text{ Дж/(моль$cdot$К)}cdot(265+273)text{ К}}approx273 text{ К}=0^{circ}text{С}]

Ответ: 0 ∘С (273 К)

В теплоизолированном сосуде в начальный момент находится одноатомный газ при температуре (T_o) = 300 К и кусочек железа массой (m) = 2 кг, нагретый до температуры (T_1) = 500 К. Начальное давление газа (p_o) = 10(^5) Па, его объем (V_o) = 10000 см(^3), удельная теплоемкость железа (c) = 0,45 кДж/(кг(cdot)К). Найдите давление газа в равновесном состоянии, считая объем газа неизменным.

Так как по условию задачи система замкнута, то внутренняя энергия ее неизменна. Поэтому равновесное состояние системы будет устанавливаться при передаче тепла газу от более горячего куска железа. По первому закону термодинамики: [Delta U=Q-A,] где (Delta U) — изменение внутренней энергии, (Q) — количество теплоты, которое подводили к телу, (A) — работа газа.
В данном случае работа газа равна нулю, так как (V=const). Уравнение теплового баланса в этом случае имеет вид: [dfrac{3}{2}nu R(T-T_o)=cm(T_1-T), hspace{7 mm} (1)] где (nu) — количество вещества газа, (R) — универсальная газовая постоянная.
Запишем уравнение Менделеева – Клапейрона: [p_oV_o=nu R T_o] Выразим отсюда: [hspace{5 mm} nu R=dfrac{p_oV_o}{T_o} hspace{7 mm} (2)] Выразим из (1) температуру газа (T): [T=dfrac{cmT_1+1,5nu RT_0}{cm+1,5nu R}hspace{5 mm} (3)] Так как объем постоянен и количество вещества газа не меняется, то по закону Шарля: [dfrac{p_1}{T_1} = dfrac{p_o}{T_o}hspace{3 mm} Rightarrow hspace{3 mm} p_1=p_ocdotdfrac{T}{T_o}hspace{5 mm} (4)] Подставим (3) в (4): [p_1=p_ocdotdfrac{cmT_1+1,5nu RT_o}{T_o(cm+1,5nu R)}hspace{5 mm} (5)] Подставим (2) в (5): [p_1=p_ocdotdfrac{cmT_1+1,5dfrac{p_oV_o}{T_o}T_o}{T_oleft(cm+1,5dfrac{p_oV_o}{T_o}right)} = p_ocdotdfrac{cmT_1+1,5p_oV_o}{T_ocm+1,5p_oV_o}] Найдем давление газа в равновесном состоянии: [p_1 = 10^5 text{ Па}cdotdfrac{450text{ Дж}/(text{кг}cdottext{К})cdot2 text{ кг} cdot500 text{ К}+1,5cdot10^5text{ Па}cdot10^{-2}text{ м$^3$}}{300text{ К}cdot450text{ Дж}/(text{кг}cdottext{К})cdot2 text{ кг}+1,5cdot10^5text{ Па}cdot10^{-2}text{ м$^3$}} approx 166 text{ кПа}]

Ответ: 166 кПа

Два литра жидкого аргона находится при температуре своего кипения -186 (^{circ})С. Какое количество теплоты нужно сообщить этому количеству аргона для того, чтобы при постоянном давлении перевести его в газ, имеющий температуру 0 (^{circ})С? Плотность жидкого аргона 1400 кг/м(^3), его удельная теплота испарения 87 кДж/кг.

Чтобы перевести аргон в газ, имеющий температуру 0 (^circ)С, сначала необходимо перевести его из жидкого состояния в газообразное, а затем нагреть до нужной температуры.
Общее количество теплоты (Q), которое необходимо для этого, будет складываться из двух составяющих: [; ; ; ; Q = Q_1 + Q_2 ; ; ; ; (1)] Количество теплоты, которое потребуется для парообразования аргона: [; ; ; ; Q_1=rm, ; ; ; ; (2)] где (m) — масса аргона, (r) — удельная теплота испарения.
Когда аргон превратится в газ, мы будем его рассматривать как идеальный одноатомный газ. Значит, для нагрева аргона до 0 (^{circ}) С запишем перове начало термодинамики: [Q_2=Delta U+A,] где (Q_2) — количество теплоты, необходимое для нагревания, (Delta U) — изменение внутренней энергии аргона, (A) — работа аргона.
[Q_2=dfrac{3}{2}nu RDelta T+p(V_2-V_1), hspace{7 mm} (3)] где (nu) — количество вещества, (Delta T) — изменение температуры, (p) — давление, (V_2) и (V_1) — конечное и начальное давлени газа, а в дальнейшнем (mu) — молярная масса газа, (rho) — плотность аргона.
По уравнению Клапейрона — Менделеева: [p(V_2-V_1)=nu R Delta T hspace{7 mm} (4)] Подставим (4) в (3): [Q_2=dfrac{3}{2}nu RDelta T+nu RDelta T] [; ; ; ; Q_2 = dfrac{5}{2}nu RDelta T ; ; ; ; (5)] Подставим (2), (5) в (1): [Q=rm+dfrac{5}{2}nu RDelta T] Количество вещества аргона можно найти по формуле: (nu = dfrac{m}{mu}), где (mu) — молярная масса аргона.
Массу аргона можно найти, зная его плотность и объем: (m = rho V).
С учетом этого: [Q=rrho V+dfrac{5}{2}cdotdfrac{rho V}{mu}RDelta T] [Q=87cdot10^3text{ кДж/кг}cdot2cdot10^{-3}text{ м$^3$}cdot1400text{ кг/м$^3$} +dfrac{5}{2}cdotdfrac{1400text{ кг/м$^3$}cdot2cdot10^{-3}text{ м$^3$}}{40cdot10^{-3}text{кг/моль}}cdot8,31cdot186^circtext{C} approx 591 text{ кДж}]

Ответ: 591 кДж

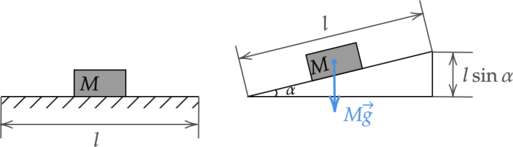
Когда легковой автомобиль едет с постоянной скоростью по горизонтальному шоссе, расход бензина составляет (mu_1) = 7 л/100 км. Каков будет расход бензина (mu_2), если этот автомобиль поедет с той же скоростью вверх по наклонному участку шоссе, образующему угол (alpha) = 0,01 рад с горизонтом? Качество дорожного покрытия на горизонтальном и наклонном участках шоссе одинаково. Масса автомобиля (M) = 1000 кг, коэффициент полезного действия двигателя (eta = 30%), удельная теплота сгорания бензина (q) = 42 МДж/кг, плотность бензина (rho) = 0,7 кг/л. При расчетах положить (sin alpha approx alpha).

По условию задачи КПД двигателя автомобиля равен 30%. Это означает, что только 30% от выделевшегося количества теплоты пойдет на совершение работы по перемещению автомомбиля: [; ; ; ; A = 0,3Q ; ; ; ; (1)] Количество теплоты, которое выделится при сгорании бензина, равно: [; ; ; ;Q = qm ; ; ; ; (2)] где (m) — масса сгоревшего бензина.
Массу бензина можно найти, зная его плотность: [; ; ; ; rho = dfrac{m}{V} ; ; ; Rightarrow ; ; ; m = rho V ; ; ; ; (3)] где (V) — объем сгоревшего бензина.
Зная расход бензина и пройденное расстояние, найдем объем израсходованного бензина: [; ; ; ;V = mu l ; ; ; ;(4)] Подставим последовательно (4), (3), (2) в (1): [; ; ; ;A = 0,3qrhomu l ; ; ; ; (5)] В то же время работа при перемещении автомобиля на расстояние (l) по определению равна: [A = Flcosalpha_o] где (F) — модуль равнодействующей всех сил, действующих на автомобиль, (alpha_o) — угол между направлением силы и направлением перемещения.
В рассматриваемых случаях и для горизонтального движения и для движения под углом к гори3 зонту (cosalpha = 1): [; ; ; ; A = Fl ; ; ; ;(6)]
Рассмотрим движение автомобиля по горизонтальному участку шоссе.
В этом случае работа, совершенная двигателем, по величине равна работе сил сопротивления.
Исходя из формул (5) и (6), получаем, что: [0,3qrhomu_1 l = Fl] Выразим отсюда силу (F): [; ; ; ; F = 0,3qrhomu_1 ; ; ; ; (7)] Рассмотрим движение автомобиля по наклонному участку шоссе той же длины.
В этом случае работа двигателя равна сумме величины работы сил сопротивления и изменения (приращения) потенциальной энергии автомобиля в поле силы тяжести: [A = Fl + Mglsinalpha] С учетом формулы (5) имеем, что: [0,3qrhomu_2 l = Fl + Mglsinalpha] Выразим отсюда силу (F): [; ; ; ; F = 0,3qrhomu_2 — Mgsinalpha ; ; ; ; (8)] Приравняем (7) и (8) с учетом того, что по условию (sinalpha approx alpha), и выразим искомый расход бензина: [0,3qrhomu_1 = 0,3qrhomu_2 — Mgsinalpha] [mu_2 = mu_1 + dfrac{Mgalpha}{0,3rho q}] [mu_2 = 7(text{ л/$100$ км}) + dfrac{1000text{ кг}cdot10text{ м/с}^2cdot0,01}{0,3cdot0,7text{ кг/л}cdot 42cdot10^6text{ Дж/кг}}cdot10^5 approx 8,13text{ л/100 км}]

Ответ: 8,13 л/100 км

Мальчик решил подняться в воздух на воздушных шарах с гелием. Известно, что мальчик весит 40 кг, а на улице нормальное атмосферное давление и температура 27 (^{circ})С. Учитывая, что объем одного шара составляет 10 литров, найдите, сколько потребуется шаров для такого путешествия. Массой оболочки шаров и объемом мальчика пренебречь.

Cила тяжести, действующая на систему, уравновешивается силой Архимеда.
Рассмотрим предельный случай, когда мальчик на воздушных шарах вот-вот оторвется от поверхности земли, и запишем второй закон Ньютона для данной системы: [vec{F}_text{Арх} + Mvec{g} + nmvec{g} = 0] где (M) — масса мальчика, (m) — масса гелия в одном шарике, (n) — количество шаров, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на вертикальную ось, направленную вверх: [F_text{Арх} — Mg — nmg = 0] [; ; ; ; F_text{Арх} = Mg + nmg ; ; ; ; (1)] Сила Архимеда равна: [F_text{Арх} = rho_o gnV] где (rho_o) — плотность воздуха, (V) — объем одного шарика.
Подставим (2) в (1): [rho_o gnV = Mg + nmg] [; ; ; ; rho_o nV = M + nm ; ; ; ; (3)] Запишем уравнение Менделеева-Клапейрона для воздуха: [; ; ; ; p_oV_o = dfrac{m_o}{mu_o} RT_o ; ; ; ; (4)] где (p_o) — атмосферное давление, (V_o) — объем, занимаемый воздухом, (m_o) — (mu_o) — масса воздуха, (R) — универсальная газовая постоянная, (T_o) — абсолютная температура воздуха.
Плотность воздуха равна: [; ; ; ; rho_o = dfrac{m_o}{V_o} ; ; ; ; (5)] Подставим (5) в (4) и выразим плотность воздуха: [; ; ; ; p_o = dfrac{rho_o}{mu_o}RT_o ; ; ; Rightarrow ; ; ; rho_o = dfrac{p_omu_o}{RT_o} ; ; ; ; (6)] Найдем массу гелия в одном шарике из уравнения Менделеева-Клапейрона: [; ; ; ; p_o V = dfrac{m}{mu}RT_o ; ; ; Rightarrow ; ; ; m = dfrac{p_o Vmu}{RT_o} ; ; ; ; (7)] где (m) — масса гелия, (mu) — молярная масса гелия.
Подставим (6), (7) в (3) и выразим количество шариков: [M + ndfrac{p_o Vmu}{RT_o} = dfrac{p_o mu_o}{RT_o}nV] [n = dfrac{MRT_o}{p_o V(mu_o — mu)}] [n = dfrac{40text{ кг}cdot8,31text{Дж/(моль$cdot$К)}cdot300text{ К}}{10^5text{ Па}cdot10^{-2}text{ м}^3cdot(29-4)cdot10^{-3} text{кг/моль}}=3989]

Ответ: 3989

Покажем на рисунке все силы, действущие на воздушный шар и введем вертикальную ось (y):

Рассмотрим предельный случай, когда шар вот-вот оторвется от поверхности земли, и запишем для него второй закон Ньютона: [vec{F}_text{Арх} + mvec{g} +Mvec{g} = 0] где (F_text{Арх}) — выталкивающая сила, (m) — масса горячего воздуха, (g) — ускорение свободного падения.
Спроецируем второй закон Ньютона на ось (y), направленную вертикально вверх: [; ; ; ; F_text{Арх} — mg-Mg = 0 ; ; ; ; (1)] Выталкивающая сила равна: [; ; ; ; F_text{Арх} = rho_o gV ; ; ; ; (2)] где (rho_o) — плотность холодного воздуха, (V) — объем шара.
Подставим (2) в (1) и разделим на (g): [; ; ; ; rho_o V — m — M = 0 ; ; ; ; (3)] Заметим, что (rho_o V = m_o), где (m_o) — масса холодного воздуха.
Тогда уравнение (3) будет иметь вид: [; ; ; ; m_o — m — M = 0 ; ; ; ; (4)] Чтобы найти массы горячей и холодного воздуха, запишем для них уравнение Менделеева – Клапейрона: [; ; ; ; p_oV = dfrac{m}{Mr}RT ; ; ; Rightarrow ; ; ; m = dfrac{p_o VMr}{RT} ; ; ; ; (5)] [; ; ; ; p_oV = dfrac{m_o}{Mr}RT_o ; ; ; Rightarrow ; ; ; m_o = dfrac{p_o VMr}{RT_o} ; ; ; ; (6)] где (p_o) — атмосферное давление, (Mr) — молярная масса воздуха, (R) — универсальная газовая постоянная, (T) (T_o) — абсолютные температуры горячего и холодного воздуха соответственно.
Подставим (5), (6) в (4) и выразим максимальную температуру окружающего воздуха, при которой шар начнет подниматься: [dfrac{p_o VMr}{RT_o} — dfrac{p_o VMr}{RT} — M = 0 ; ; ; / :dfrac{p_o VMr}{RT}] [dfrac{1}{T_o} — dfrac{1}{T} — dfrac{MR}{p_oVMr} = 0] [T_o=dfrac{mu p_oVT}{mu p_oV+MRT}] [T_o = dfrac{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3cdot(265+273)text{ К}}{0,029text{ кг/моль}cdot10^5text{ Па}cdot230text{ м}^3+145text{ кг}cdot8,31text{ Дж/(моль$cdot$К)}cdot(265+273)text{ К}}approx273 text{ К}=0^{circ}text{С}]

Ответ: 0 ∘С (273 К)

Сосуд объемом (V) л, содержащий (nu) моль воздуха при давлении (p) Па и температуре (T_o) К, сверху заткнут пробкой массой (m) кг с площадью (S) см(^2). Найдите на какую величину надо увеличить температуру газа, чтобы пробка вылетела из сосуда, если коэффицент трения пробки о стенки сосуда равен (mu), а атмосферное давление равно (p_o).

Запишем 2 закон Ньютона для предельного случая, когда пробка вот-вот вылетит из сосуда: [; ; ; ; F = F_text{тяж}+F_text{тр}+F_text{атм}, ; ; ; ; ; (1)] где (F) — сила, с которой газ воздействует на пробку, (F_text{тяж}) — сила тяжести, действующая на пробку , (F_text{тр}) — сила трения пробки о стенки сосуда, (F_text{атм}) — сила давления атмосферы на пробку.
Сила, с которой газ воздействует на пробку, равна: [; ; ; ; p=dfrac{F}{S} ; ; ; Rightarrow ; ; ; F=pS ; ; ; ; (2)] По уравнению Клайперона – Менделеева: [; ; ; ; pV=nu R T ; ; ; Rightarrow ; ; ; p=dfrac{nu R T}{V},; ; ; ; (3)] где (T) — абсолютная температура газа, (Delta T) — изменение температуры газа.
Подставим (3) в (2): [; ; ; ; F = dfrac{nu R T}{V}S ; ; ; ; (4)] Сила давления атмосферы на пробку равна: [; ; ; ; F_text{атм}=p_oS ; ; ; ; (5)] Силу тяжести и силу трения найдем по формулам: [; ; ; ; F_text{тяж}=mg ; ; ; (6) ; ; ; ; ; ; ; ; ; ; ; F_text{тр}=mu mg, ; ; ; (7)] где (g) — ускорение свободного падения.
Подставим (4), (5), (6), (7) в (1) и получим: [; ; ; ; S dfrac{nu R T}{V} = mg +mu m g +p_o S ; ; ; ; (8)] Конечная температура газа равна: [; ; ; ; T=T_o + Delta T ; ; ; ; (9)] Подставим (9) в (8) и выразим (Delta T), на которую нужно увеличить температуру газа, чтобы пробка вылетела: [S dfrac{nu R (T_o + Delta T)}{V} = mg +mu m g +p_o S] [Delta T =dfrac{V}{nu R}left(dfrac{mg}{S}+dfrac{mu m g }{S}+p_oright)-T_o]

Ответ: $Delta T =dfrac{V}{nu R}left(dfrac{mg}{S}+dfrac{mu m g }{S}+p_oright)-T_o$

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задачи из ДЕМОВАРИАНТОВ (с решениями)

1. Воздушный шар, оболочка
которого имеет массу М = 145 кг и объем V =
230 м³, наполняется горячим воздухом при нормальном
атмосферном давлении и температуре окружающего воздуха t_о
= 0^оС. Какую минимальную температуру t должен
иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка
шара нерастяжима и имеет в нижней части небольшое отверстие.
Образец возможного решения

2. Воздушный
шар с газонепроницаемой оболочкой массой 400 кг заполнен гелием.
Он может удерживать в воздухе на высоте, где температура воздуха
17^оС, а давление 10⁵ Па, груз массой 225
кг. Какова масса гелия в оболочке шара? Считать, что оболочка
шара не оказывает сопротивления изменению объема шара.
Образец возможного решения

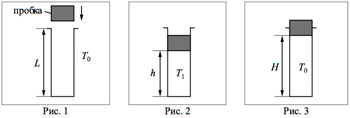
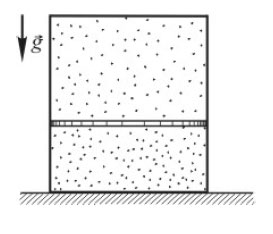
2*. В камере, заполненной азотом, при температуре T = 300 К находится открытый цилиндрический сосуд (см. рис. 1). Высота сосуда L = 50 см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до температуры T₁. В результате расстояние от дна сосуда до низа пробки становится равным h = 40 см (см. рис. 2). Затем сосуд нагревают до первоначальной температуры T₀. Расстояние от дна сосуда до низа пробки при этой температуре становится равным H = 46 см (см. рис. 3). Чему равна температура T₁? Величину силы трения между пробкой и стенками сосуда считать одинаковой при движении пробки вниз и вверх. Массой пробки пренебречь. Давление азота в камере во время эксперимента поддерживается постоянным.
Образец возможного решения

3. В медный
стакан калориметра массой 200 г, содержащий 150 г воды, опустили
кусок льда, имевший температуру 0°С. Начальная температура калориметра
с водой 25°С. В момент времени, когда наступит тепловое равновесие,
температура воды и калориметра стала равной 5°С. Рассчитайте массу
льда. Удельная теплоемкость меди 390 Дж/кг•К, удельная теплоемкость
воды 4200 Дж/кг•К, удельная теплота плавления льда 3,35•10⁵
Дж/кг. Потери тепла калориметром считать пренебрежимо малыми.
Образец возможного решения

4. Необходимо расплавить лёд массой 0,2 кг,
имеющий температуру 0^оС. Выполнима ли эта задача,
если потребляемая мощность нагревательного элемента – 400 Вт,
тепловые потери составляют 30%, а время работы нагревателя не
должно превышать 5 минут?
Образец возможного решения

4*. Теплоизолированный горизонтальный сосуд разделён пористой перегородкой на две равные части. В начальный момент в левой части сосуда находится ν = 2 моль гелия, а в правой – такое же количество моль аргона. Атомы гелия могут проникать через перегородку, а для атомов аргона перегородка непроницаема. Температура гелия равна температуре аргона: Т = 300 К. Определите отношение внутренних энергий газов по разные стороны перегородки после установления термодинамического равновесия.
Образец возможного решения

4**. Теплоизолированный цилиндр разделён подвижным теплопроводным поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 300 К, а аргона – 900 К; объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Поршень медленно перемещается без трения. Теплоёмкость поршня и цилиндра пренебрежимо мала. Чему равно отношение внутренней энергии гелия после установления теплового равновесия к его энергии в начальный момент?
Образец возможного решения

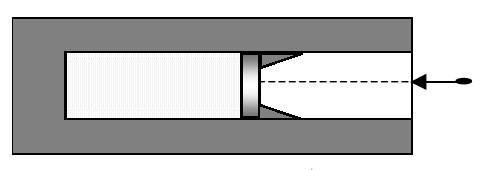
5. В вакууме
закреплен горизонтальный цилиндр с поршнем. В цилиндре находится
0,1 моль гелия. Поршень удерживается упорами и может скользить
влево вдоль стенок цилиндра без трения. В поршень попадает пуля
массой 10 г, летящая горизонтально со скоростью 400 м/с, и застревает
в нем. Температура гелия в момент остановки поршня в крайнем левом
положении возрастает на 64 К. Какова масса поршня? Считать, что
за время движения поршня газ не успевает обменяться теплом с поршнем
и цилиндром.
Образец возможного решения

6. В горизонтальном цилиндрическом сосуде,
закрытом поршнем, находится одноатомный идеальный газ. Первоначальное
давление газа p₁ = 4•10⁵
Па. Расстояние от дна сосуда до поршня равно L. Площадь
поперечного сечения поршня S = 25 см². В
результате медленного нагревания газ получил количество теплоты
Q = 1,65 кДж, а поршень сдвинулся на расстояние x
= 10 см. При движении поршня на него со стороны стенок сосуда
действует сила трения величиной F_тр = 3•10³
Н. Найдите L. Считать, что сосуд находится в вакууме.
Образец возможного решения

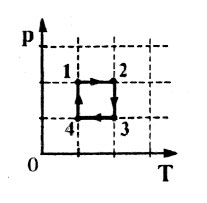
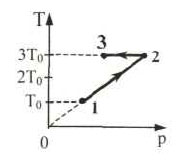
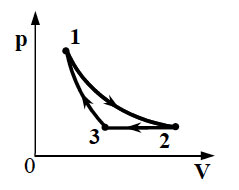
7. На pT-диаграмме показан
цикл тепловой машины, у которой рабочим телом является идеальный
газ (см. рисунок). На каком из участков цикла 1 – 2, 2 – 3, 3
– 4, 4 – 1 работа газа наибольшая по модулю?
Образец возможного решения

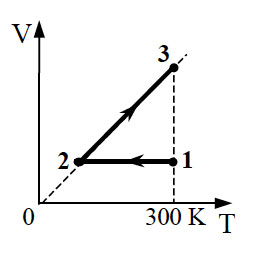
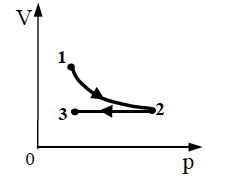
8. 10 моль одноатомного идеального
газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели
до первоначальной температуры 300 К (см. рисунок). Какое количество
теплоты получил газ на участке 2 — 3?
Образец возможного решения

9. 10 моль идеального одноатомного газа охладили,
уменьшив давление в 3 раза. Затем газ нагрели до первоначальной
температуры 300 К (см. рисунок). Какое количество теплоты сообщено
газу на участке 2 — 3?
Образец возможного решения

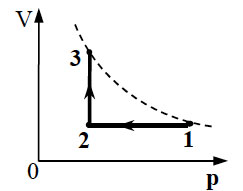
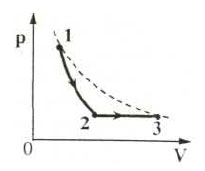
10. 1 моль идеального одноатомного газа сначала
охладили, а затем нагрели до первоначальной температуры 300
К, увеличив объем газа в 3 раза (см. рисунок). Какое количество
теплоты отдал газ на участке 1 — 2?
Образец возможного решения

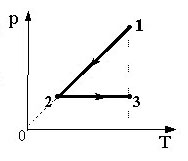
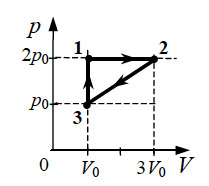
10*. Над одноатомным идеальным газом проводится циклический процесс, показанный на рисунке. На участке 1–2 газ совершает работу А₁₂ = 1000 Дж. На адиабате 3–1 внешние силы сжимают газ, совершая работу |A₃₁| = 370 Дж. Количество вещества газа в ходе процесса не меняется. Найдите количество теплоты |Q_хол|, отданное газом за цикл холодильнику.
Образец возможного решения

11. Рассчитайте КПД тепловой
машины, использующей в качестве рабочего тела одноатомный идеальный
газ и работающей по циклу, изображенному на рисунке.
Образец возможного решения

Избранные задачи прошлых лет (с ответами)

12. Вертикально расположенный
замкнутый цилиндрический сосуд высотой 50 см разделен подвижным
поршнем весом 110 Н на две части, в каждой из которых содержится
одинаковое количество идеального газа при температуре 361 К. Сколько
молей газа находится в каждой части цилиндра, если поршень находится
на высоте 20 см от дна сосуда? Толщиной поршня пренебречь.

13. В калориметре
находился лед при температуре t₁ = — 5 °С.
Какой была масса m₁ льда, если после добавления
в калориметр m₂ = 4 кг воды, имеющей температуру
t₂ = 20 °С, и установления теплового равновесия
температура содержимого калориметра оказалась равной t
= 0 °С, причем в калориметре была только вода?

14. Теплоизолированный
цилиндр разделен подвижным теплопроводным поршнем на две части.
В одной части цилиндра находится гелий, а в другой — аргон. В
начальный момент температура гелия равна 300 К, а аргона — 900
К. При этом объемы, занимаемые газами одинаковы. Какую температуру
будут иметь газы в цилиндре после установления теплового равновесия,
если поршень перемещается без трения? Теплоемкостью сосуда и поршня
пренебречь.

15. Теплоизолированный
сосуд объемом V = 2 м³ разделен теплопроводящей
перегородкой на две части одинакового объема. В одной части находится
m = 1 кг гелия, а в другой части m = 1 кг аргона.
Средняя квадратичная скорость атомов аргона равна средней квадратичной
скорости атомов гелия и составляет υ = 500 м/с. Рассчитайте
парциальное давление гелия после удаления перегородки.

16. Теплоизолированный
сосуд объемом V = 2 м³ разделен пористой перегородкой
на две равные части. В начальный момент в одной части сосуда находится
ν_He = 2 моль гелия, а в другой – ν_Ar
= 1 моль аргона. Температура гелия Т_He = 300
К, а температура аргона Т_Ar = 600 К. Атомы
гелия могут свободно проникать через поры в перегородке, а атомы
аргона – нет. Определите температуру гелия после установления
теплового равновесия в системе.

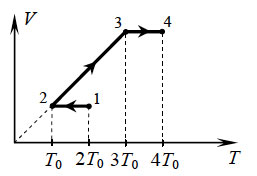
17. С одним молем идеального
одноатомного газа совершают процесс 1-2-3-4, показанный на рисунке
в координатах V-Т. Во сколько раз количество теплоты,
полученное газом в процессе 1-2-3-4 больше работы газа в этом
процессе?

18. Один моль одноатомного
идеального газа совершает процесс 1-2-3 (см. рисунок). На участке
2 — 3 к газу подводят 3 кДж теплоты. Т₀ =
100 К. Найдите отношение работы, совершаемой газом в ходе всего
процесса А₁₂₃, к соответствующему полному
количеству подведенной к нему теплоты Q₁₂₃.

19. Один моль идеального
одноатомного газа сначала изотермически сжали (Т₁
= 300 К). Затем газ изохорно охладили, понизив давление в 3 раза
(см. рисунок). Какое количество теплоты отдал газ на участке 2
— 3?

20. Идеальный одноатомный
газ расширяется сначала адиабатно, а затем изобарно. Конечная
температура газа равна начальной (см. рисунок). За весь процесс
1-2-3 газом совершается работа, равная 5 кДж. Какую работу совершает
газ при адиабатном расширении?

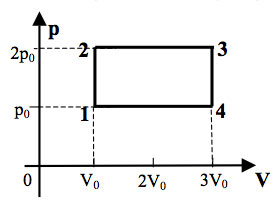
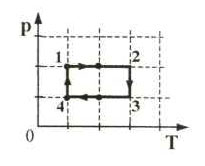
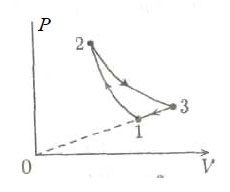
21. На рисунке в координатах
p,T показан цикл тепловой машины, у которой
рабочим телом является идеальный газ. На каком участке цикла работа
газа наименьшая по модулю?

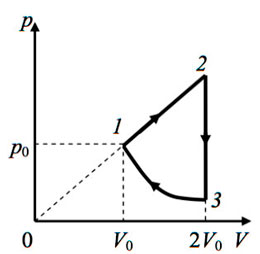
22. Один моль одноатомного
идеального газа совершает цикл, изображенный на pV-диаграмме
(см. рисунок). Участок 1 – 2 –– изотерма, 2 – 3 –– изобара, 3
– 1 –– адиабата. Работа, совершаемая газом за цикл, равна А.
Разность температур в состояниях 1 и 3 составляет ΔТ.
Какую работу совершает газ при изотермическом процессе?

23. Газообразный гелий находится
в цилиндре под подвижным поршнем. Газ сжимают в адиабатическом
процессе, переводя его из состояния 1 в состояние 2 (см. рис.).
Над газом совершается при этом работа сжатия А₁₂
(А₁₂> 0). Затем газ расширяется в изотермическом
процессе 2-3, и, наконец, из состояния 3 газ переводят в состояние
1 в процессе, когда его давление Р прямо пропорционально
объему V. Найти работу А₂₃, которую
совершил газ в процессе изотермического расширения, если во всем
замкнутом цикле 1-2-3-1 он совершил работу А.

24. Температура
гелия увеличилась в k = 3 раза в процессе P²V
= const (Р — давление, V — объем газа), а его
внутренняя энергия изменилась на 100 Дж. Найти: 1) начальный объем
V₁ газа; 2) начальное давление P₁
газа. Максимальный объем, который занимал газ в процессе нагрева,
равнялся V_max = 3 л.

25. Одноатомный идеальный
газ неизменной массы совершает циклический процесс, показанный
на рисунке. За цикл от нагревателя газ получает количество теплоты
Q_H = 8 кДж. Чему равна работа газа за цикл?

Ответы к избранным задачам
прошлых лет

Источник

Подготовка к ЕГЭ по физике. Задания высокого уровня сложности с развернутыми ответами. ЗАДАНИЕ № 30 с несколькими вариантами решения. Расчетная задача. Максимальная оценка 3 балла.

Задания 29 — 32 представляют собой расчётные задачи. В текстах заданий нет указаний на требования к полноте решения, эту функцию выполняет общая инструкция. В каждом варианте экзаменационной работы перед заданиями 29 — 32 приведена инструкция, которая в целом отражает требования к полному правильному решению расчётных задач.

ЕГЭ по физике. ЗАДАНИЕ № 30

Воздушный шар, оболочка которого имеет массу М = 145 кг и объём V = 230 м³, наполняется горячим воздухом при нормальном атмосферном давлении и температуре окружающего воздуха t₀ = 0°С. Какую минимальную температуру t должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара нерастяжима и имеет в нижней части небольшое отверстие.

Примерный ход рассуждений при решении задачи

Проведём физический анализ условия задачи. Для того чтобы шар начал подниматься, должно выполниться условие плавания тел — компенсация всех сил, действующих на тело. На шар действуют две силы: сила тяжести и выталкивающая сила Архимеда F_A. Запишем условие начала подъёма шара: F_A ≥ Mg + mg, где М — масса оболочки, m — масса воздуха внутри оболочки.

Отсюда, используя связь массы тела и его плотности, можно получить: p₀gV ≥ MG + pgV => p₀V ≥ М + pV, где р₀ — плотность окружающего воздуха, р — плотность воздуха внутри оболочки, V — объём шара.

Как видно, здесь полностью выполнены условия пункта 2 критериев оценки.

Для воздуха внутри шара находим его плотность p = m/V = pμ/RT, где р — атмосферное давление, Т — температура воздуха внутри шара.

Найдём плотность воздуха в атмосфере: p₀ = pμ/RT₀, где Т₀ — температура окружающего воздуха.

Запишем условие начала подъёма шара в виде

Откуда следует:

После подстановки числовых значений получим окончательный ответ:

Решение № 1 (на 2 балла)

Комментарий: Здесь приведены все исходные формулы, получен ответ в общем виде, не проведён численный расчёт. Эксперты оценили работу в 2 балла.

Решение № 2 (на 1 балл)

Комментарий: Здесь эксперты выставили достаточно спорный 1 балл. Условие подъёма шара записано неверно, и, следовательно, больше не о чем говорить.

Решение № 3 (на 1 балл)

Комментарий: В данном решении достаточно грамотно (в векторном виде) записаны все необходимые уравнения, но учащийся не учитывает массу оболочки шара и неверно записывает выражение для плотности воздуха в шаре (через массу оболочки и объём шара). Следовательно, одно из исходных уравнений ошибочно, работа оценивается 1 баллом.