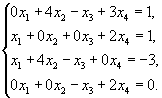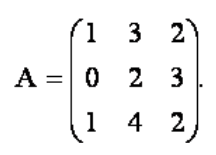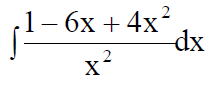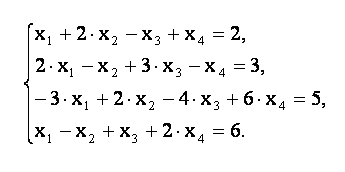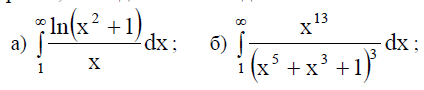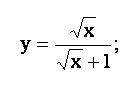Примеры решений задач по высшей математике
На этой странице мы собрали простые и сложные примеры из курса высшей математики — от векторов и матриц до дифференциальных уравнений. На каждую тему приведен один решенный пример и даны ссылки на разделы, где собраны другие решения. Фактически, это шпаргалка-каталог типовых задач и решений к ним.
Если вам нужна помощь, узнайте больше о заказе решений по высшей математике.
Далее решенные задачи по темам:
Высшая математика. Комплексные числа
Задача. Вычислить сумму $(z_1 + z_2)$ и разность $(z_1 — z_2)$ комплексных чисел, заданных в показательной форме, переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости.
$$ z_1 = 2 e^{-pi i}, z_2=4 e^{pi i}.$$
Все решения о комплексных числах
Высшая математика. Матрицы
Задача. Найти матрицу, обратную матрице $A$. Сделать проверку.
$$A=
begin{pmatrix}
1 & 2 & 1 & -1\
1 & 1 & 0 & 0\
0 & 2 & 0 & -1\
1 & 1 & 1 & 0\
end{pmatrix}
$$
Высшая математика. Определители
Задача. Вычислить определитель матрицы $A$
$$A=
begin{pmatrix}
4 & 5 & 6 & 5 & 11\
1 & 4 & 2 & 0 & 13\
1 & 1 & 0 & -1 & 5\
3 & 2 & 3 & 0 & 7\
4 & 1 & 2 & 3 & 8\
end{pmatrix}
$$
Высшая математика. Системы уравнений
Задача. Исследовать на совместность и решить систему уравнений:
Все решения по линейной алгебре
Высшая математика. Векторы
Задача. Написать разложение вектора $X$ по векторам $(a, b, c)$.
$$X=(-4;4;4), a=(3;1;0), b=(-1;0;6), c=(-1;2;0).$$
Все решения по векторной алгебре
Аналитическая геометрия на плоскости
Задача. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Все решения по АГ на плоскости
Аналитическая геометрия в пространстве
Задача. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.
$$A_1(2,3,1), A_2(4,1,-2), A_3(6,3,7), A_4(-5,-4,8).$$
Все решения по АГ в пространстве
Высшая математика. Пределы
Задача. Найти предел функции
$$
lim_{xto infty}left(frac{3x^2+1}{3x^2-x+1} right)^{3x+4}.
$$
Все решения по пределам
Высшая математика. Производные
Задача. Найти производную от следующей функции
$$
y=left[sqrt[3]{frac{1}{7+x^2}}+frac{sqrt{x}}{sqrt{x}+1} right]cdot 24; quad
y'(1).
$$
Все решения по производным
Высшая математика. Исследование функции
Задача. Провести полное исследование функции и построить график.
$$y=frac{x}{sqrt{x^2+x}}.$$
Все решения на исследование функции
Высшая математика. Интегралы
Задача. Найти неопределенный интеграл
$$intfrac{4x^2+7x-23}{(x^2-4x+8)(x+1)^2}dx.$$
Все решения по интегралам
Высшая математика. Применение интегралов
Задача. Найти длину дуги кривой, заданной параметрическими уравнениями:
$$
x=3(1-cos t)cos t, quad y=3(1-cos t)sin t, quad 0leq t leq pi.
$$
Все решения о применении интегралов
Высшая математика. Ряды
Задача. Исследовать сходимость числового ряда
$$sum_{n=1}^{infty} u_n=sum_{n=1}^{infty}frac{2n+1}{sqrt{n 2^n}}.$$
Все решения по рядам
Высшая математика. Дифференциальные уравнения
Задача. Найти общее решение линейного дифференциального уравнения первого порядка
$$ xy’+x^2+xy-y=0.$$
Все решения по дифф.уравнениям
Высшая математика. Теория вероятностей
Задача. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит 8; б) произведение числа очков не превосходит 8; в) произведение числа очков делится на 8.
Все решения по теории вероятностей
Подробное решим любые задачи высшей математики
Полезное на сайте
|
|
Экзаменационные билеты, вопросы и задачи по курсу высшей математики для студентов 1 курса (1 и 2 учебный семестр) и 2 курса (3 и 4 семестр) очной и заочной форм обучения технических и гуманитарных специальностей ВУЗов.
Допуск к экзамену получают учащиеся, выполнившие и сдавшие все контрольные и расчетные работы, предусмотренные учебным планом кафедры математики.
Для успешной сдачи экзамена необходимо выполнить 60 или более процентов заданий указанных в билете, решив минимум одну задачу.
Ответы на теоретические вопросы экзамена должны включать точные определения и основные положения рассматриваемой темы с выводами соответствующих формул.
Если Вам требуется помощь в решении задач, наши специалисты готовы ответить на все вопросы по математике.
Экзаменационный билет по высшей математике
Билет для сдачи экзамена по высшей математике включает решение задач и ответы на вопросы по темам, изучавшимся в пройденном учебном семестре, и может содержать от трех до 5, а в некоторых случаях и до 10 пунктов.
Например, в билете могут быть три теоретических вопроса и две задачи, либо задание в виде теста.
Пример экзаменационного билета
Примерный билет содержит задачи и вопросы по разделам высшей математики:
1. Определители. Свойства определителей.
2. Угол между векторами. Проекция вектора на ось.
3. Векторное произведение двух векторов и его свойства.
4. Найти обратную матрицу A-1, если:
5. Вычислить неопределенный интеграл
Вопросы к экзаменам по математике
Примерный перечень экзаменационных вопросов по теории курса высшей математики, включаемых в билет:
Раздел матрицы и векторы
- Матрицы. Виды матриц. Действия над матрицами.
- Алгебраические дополнения и миноры.
- Вычисление определителей методом треугольников и разложением по элементам строки или столбца.
- Невырожденная матрица. Обратная матрица. Нахождение обратной матрицы.
- Матричный метод решения систем линейных уравнений. Формулы Крамера.
- Метод Гаусса решения систем алгебраических линейных уравнений.
- Действия над векторами.
- Линейная зависимость и независимость векторов.
- Векторный базис. Координаты вектора.
- Прямоугольная декартова система координат. Деление отрезка в заданном отношении. Определение расстояния между точками.
- Скалярное произведение двух векторов и его свойства.
- Смешанное произведение трех векторов и его свойства.
Неопределённый интеграл
- Первообразная функция и неопределенный интеграл.
- Простейшие свойства неопределенного интеграла и его геометрический смысл.
- Интегрирование методом разложения и методом замены переменной.
- Метод интегрирования по частям.
- Интегрирование простейших дробей.
- Интегрирование дробно-рациональной функции.
- Интегрирование тригонометрических функций.
- Интегрирование иррациональных функций.
Определённый интеграл
- Определение определенного интеграла. Свойства определенного интеграла.
- Определенный интеграл с переменным верхним пределом интегрирования. Формула Ньютона-Лейбница.
- Замена переменной и интегрирование по частям в определенном интеграле.
- Несобственные интегралы с бесконечными пределами интегрирования и от неограниченных функций.
- Геометрические приложения определенного интеграла. Вычисление площадей фигур в декартовых и полярных координатах.
- Длина дуги плоской кривой в декартовых и полярных координатах, объем тела вращения.
- Решение физических задач с помощью определенных интегралов.
Кратные интегралы
- Определение двойного интеграла. Его геометрический смысл
- Свойства двойного интеграла
- Понятие о правильных областях. Двукратный интеграл
- Сведение двойного интеграла к двукратному
- Замена переменных в двойном интеграле. Вычисление двойного интеграла полярных координатах
- Вычисление объемов тел и площадей плоских областей
- Задачи механики
- Определение тройного интеграла. Его механический смысл. Свойства
- Вычисление тройного интеграла
- Вычисление тройного интеграла в декартовых координатах
- Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах
- Приложения тройных интегралов к задачам геометрии и механики
- Вычисление объемов тел
- Задачи механики
Криволинейные и поверхностные интегралы
- Криволинейные интегралы первого рода (или по длине дуги)
- Определение и физический смысл криволинейного интеграла первого рода. Свойства
- Вычисление криволинейного интеграла первого рода
- Криволинейный интеграл для пространственного случая
- Некоторые применения криволинейного интеграла первого рода
- Криволинейный интеграл второго рода (или по координатам)
- Задача о работе силового поля. Определение криволинейного интеграла второго рода
- Существование и вычисление криволинейного интеграла второго рода
- Связь между криволинейными интегралами первого и второго рода
- Формула Грина
- Условия независимости интеграла от пути интегрирования
- Поверхностный интеграл первого рода (или по площади поверхности). Теорема существования
- Вычисление поверхностного интеграла первого рода
- Некоторые применения поверхностного интеграла первого рода
- Поверхностный интеграл второго рода или по координатам. Физический смысл
- Применение поверхностного интеграла второго рода
Экзаменационные задачи по математике
Примеры экзаменационных задач по курсу высшей математики, которые могут быть включены в билет для сдачи экзамена:
1. Решить систему уравнений методом Гаусса
2. Используя признаки сходимости несобственных интегралов, исследовать на сходимость
3. Применяя основные правила дифференцирования, найти производную функции
Ответы на экзаменационные вопросы по математике
Ответы на некоторые теоретические вопросы в экзаменационных билетах по высшей математике:
- Однородные функции, однородные дифференциальные уравнения
- Линейное дифференциальное уравнение первого порядка
- Уравнение Бернулли
- Уравнение в полных дифференциалах
- Интегрирующий множитель
- Дифференциальные уравнения высших порядков. Задача Коши
- Числовые ряды. Основные понятия
- Ряд геометрической прогрессии со знаменателем
- Остаток ряда
- Свойства, сходящихся числовых рядов
- Необходимый признак сходимости числового ряда
- Признак сравнения рядов с неотрицательными членами
- Признак Даламбера
- Признак Коши
Другие ответы можно найти, воспользовавшись поиском на нашем сайте.
Наш коллектив математиков желает Вам успешной подготовки и сдачи экзамена, и в случае необходимости готов оказать студентам всю необходимую помощь.
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Изложены определение двойного интеграла и его геометрический смысл. Решены задачи на изменение порядка интегрирования в повторном интеграле, вычисление площади фигуры, вычисление двойного интеграла.
Тройные интегралы в прямоугольных координатах
Изложено определение тройного интеграла и решены задачи на его вычисление, а также на вычисление объема тела, ограниченного поверхностями.
Замена переменных в двойном и тройном интегралах
Изложен порядок замены переменных в двойном и тройном интегралах. Приведены формулы вычисления якобиана. Вычисление двойных и тройных интегралов с переходом к полярным, цилиндрическим и сферическим координатам.
Приложения кратных интегралов в механике
Рассмотрены формулы для вычисления массы плоской пластинки и тела с помощью двойных и тройных интегралов, а также формулы статистических моментов, моментов инерции и координат центра тяжести пластинки и тела.
Криволинейные интегралы 1-го рода
Рассмотрены криволинейные интегралы I рода (криволинейные интегралы по длине дуги), их свойства и формулы вычисления. Приведены примеры вычисления криволинейных интегралов I рода, заданных различными способами.
Криволинейные интегралы 2-го рода
Рассмотрены криволинейные интегралы II рода (криволинейные интегралы по координатам), их свойства и формулы вычисления. Формула Грина. Условие независимости криволинейного интеграла от пути интегрирования. Приведены примеры вычисления криволинейных интегралов II рода, заданных различными способами.
Приложения криволинейных интегралов
Приведены формулы и примеры вычисления массы дуги кривой, работы, совершаемой силой вдоль кривой. Формулы вычисления статистических моментов и моментов инерции кривой. Длина дуги кривой и площадь фигуры, которая вычисляется с помощью криволинейного интеграла.
Поверхностные интегралы 1-го рода
Рассмотрены поверхностные интегралы I рода (поверхностные интегралы по площади поверхности), их свойства и формулы вычисления. Приведены примеры вычисления поверхностных интегралов I рода, заданных различными способами.
Поверхностные интегралы 2-го рода
Рассмотрены поверхностные интегралы II рода (поверхностные интегралы по координатам), их свойства и формулы вычисления. Приведены примеры вычисления поверхностных интегралов II рода, заданных различными способами.