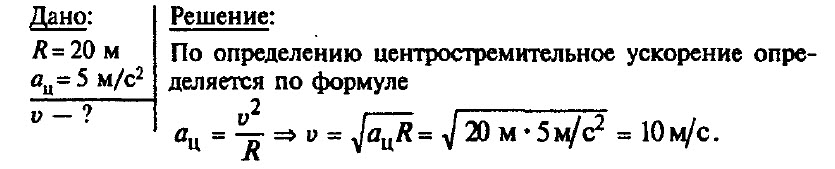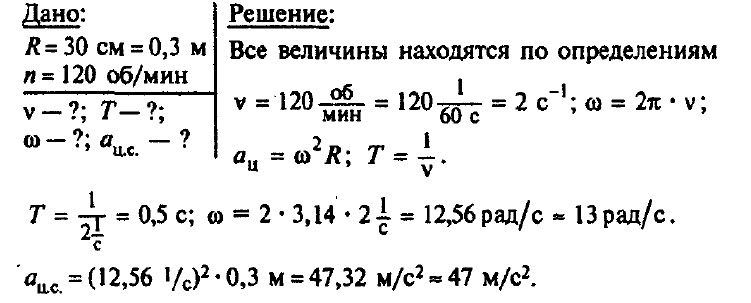Секрет задач на движение по окружности: тот, кто обгоняет, проезжает на 1 круг больше, если это первый обгон. И на n кругов больше, если обогнал другого в n-ный раз.
Из одной точки круговой трассы, длина которой равна 8 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 114 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Автомобили стартовали одновременно, и первый автомобиль через 20 минут после старта опережал второй автомобиль на один круг. Значит, за эти 20 минут, то есть за часа он проехал на 1 круг больше – то есть на 8 км больше.
За час первый автомобиль проедет на км больше второго. Скорость второго автомобиля на 24 км/ч меньше, чем у первого, и равна 114 — 24 = 90 км/ч.
Ответ: 90.
Из пункта
круговой трассы выехал велосипедист, а через
минут следом за ним отправился мотоциклист. Через
минут после отправления он догнал велосипедиста в первый раз, а еще через
минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна
км. Ответ дайте в км/ч.
Во-первых, переведем минуты в часы, поскольку скорость надо найти в км/ч. Скорости участников обозначим за и
. В первый раз мотоциклист обогнал велосипедиста через
минут, то есть через
часа после старта. До этого момента велосипедист был в пути
минут, то есть
часа.
Запишем эти данные в таблицу:
| велосипедист | |||
| мотоциклист |
Оба проехали одинаковые расстояния, то есть .
Затем мотоциклист второй раз обогнал велосипедиста. Произошло это через минут, то есть через
часа после первого обгона.
Нарисуем вторую таблицу.
| велосипедист | |||
| мотоциклист |
А какие же расстояния они проехали? Мотоциклист обогнал велосипедиста. Значит, он проехал на один круг больше. Это и есть секрет данной задачи. Один круг — это длина трассы, она равна км. Получим второе уравнение:
Решим получившуюся систему.
Получим, что . В ответ запишем скорость мотоциклиста.
Ответ: .
Часы со стрелками показывают
часов
минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
Это, пожалуй, самая сложная задача из вариантов ЕГЭ. Конечно, есть простое решение — взять часы со стрелками и убедиться, что в четвертый раз стрелки поравняются через часа, ровно в
.
А как быть, если у вас электронные часы и вы не можете решить задачу экспериментально?
За один час минутная стрелка проходит один круг, а часовая часть круга. Пусть их скорости равны
(круг в час) и
(круга в час). Старт — в
. Найдем время, за которое минутная стрелка в первый раз догонит часовую.
Минутная стрелка пройдет на круга больше, поэтому уравнение будет таким:
Решив его, получим, что часа. Итак, в первый раз стрелки поравняются через
часа. Пусть во второй раз они поравняются через время
. Минутная стрелка пройдет расстояние
, а часовая
, причем минутная стрелка пройдет на один круг больше. Запишем уравнение:
Решив его, получим, что часа. Итак, через
часа стрелки поравняются во второй раз, еще через
часа — в третий, и еще через
часа — в четвертый.
Значит, если старт был в , то в четвертый раз стрелки поравняются через
часа.
Ответ полностью согласуется с «экспериментальным» решением! 
На экзамене по математике вам может также встретиться задача о нахождении средней скорости. Запомним, что средняя скорость не равна среднему арифметическому скоростей. Она находится по специальной формуле:
,
где — средняя скорость,
— общий путь,
— общее время.
Если участков пути было два, то
А сейчас покажем вам один из секретов решения текстовых задач. Что делать, если у вас получился в уравнении пятизначный дискриминант? Да, это реальная ситуация! Это может встретиться в варианте ЕГЭ.
Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
Первый гонщик через 15 минут после старта обогнал второго на 1 круг. Значит, за 15 минут он проехал на 1 круг, то есть на 3 километра больше. За час он проедет на километров больше. Его скорость на 12 км/ч больше, чем скорость второго.
Как всегда, составляем таблицу и уравнение. 10 минут переведем в часы. Это часа.
Честно преобразовав это уравнение к квадратному, получим:
Пятизначный дискриминант, вот повезло! Но есть и другой способ решения, и он намного проще.
Посмотрим еще раз на наше уравнение:
Заметим, что 180 делится на 12. Сделаем замену:
Это уравнение легко привести к квадратному и решить.
Целый положительный корень этого уравнения: Тогда
Ответ: 108
Мы решили текстовую задачу с помощью замены переменной. Этот прием в математике используется везде: в решении задач, уравнений и неравенств, в задачах с параметрами и интегрировании. Общее правило: можете сделать замену переменной – сделайте.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи ЕГЭ на движение по окружности» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на круговое движение
Верны те же формулы: [{large{S=vcdot t quad quad quad v=dfrac
St quad quad quad
t=dfrac Sv}}]
(blacktriangleright) Пусть два тела начали движение из одной точки в одном направлении со скоростями (v_1>v_2).
Тогда если (l) — длина круга, (t_1) — время, через которое они окажутся в одной точке в первый раз, то:
То есть за (t_1) первое тело пройдет расстояние на (l) большее, чем второе тело.
Если (t_n) — время, через которое они в (n)–ый раз окажутся в одной точке, то справедлива формула: [{large{t_n=ncdot t_1}}]
(blacktriangleright) Пусть два тела начали движение из разных точек в одном направлении со скоростями (v_1>v_2).
Тогда задача легко сводится к предыдущему случаю: нужно найти сначала время (t_1), через которое они окажутся в одной точке в первый раз.
Если на момент начала движения расстояние между ними (buildrelsmileover{A_1A_2}=s), то:
Задание
1
#2677
Уровень задания: Легче ЕГЭ
Два спортсмена стартуют в одном направлении из диаметрально противоположных точек круговой дорожки. Они бегут с разными непостоянными скоростями. Известно, что в тот момент, когда спортсмены впервые поравнялись, они прекратили тренировку. На сколько кругов больше пробежал спортсмен с большей средней скоростью, чем другой спортсмен?
Назовём спортсмена с большей средней скоростью первым. Сначала первому спортсмену нужно было пробежать полкруга, чтобы достичь места старта второго спортсмена. После этого ему предстояло пробежать столько же, сколько пробежал второй спортсмен (грубо говоря, после того, как первый спортсмен пробежал полкруга, ему до встречи надо было пробежать каждый метр дорожки, который пробежал второй спортсмен, причём столько же раз, сколько этот метр пробежал второй).
Таким образом, первый спортсмен пробежал на (0,5) круга больше.
Ответ: 0,5
Задание
2
#2115
Уровень задания: Легче ЕГЭ
Кот Мурзик бегает от пса Шарика по кругу. Скорости Мурзика и Шарика постоянны. Известно, что Мурзик бежит в (1,5) раза быстрее Шарика и за (10) минут они в сумме пробегают два круга. За сколько минут Шарик пробежит один круг?
Так как Мурзик бежит в (1,5) раза быстрее Шарика, то за (10) минут Мурзик и Шарик в сумме пробегают такое же расстояние, которое пробежал бы Шарик за (10cdot (1 + 1,5) = 25) минут. Следовательно, Шарик пробегает два круга за (25) минут, тогда один круг Шарик пробегает за (12,5) минут
Ответ: 12,5
Задание
3
#823
Уровень задания: Равен ЕГЭ
Из точки A круговой орбиты далёкой планеты одновременно в одном направлении вылетели два метеорита. Скорость первого метеорита на 10000 км/ч больше, чем скорость второго. Известно, что впервые после вылета они встретились через 8 часов. Найдите длину орбиты в километрах.
В тот момент, когда они впервые встретились, разница расстояний, которые они пролетели, равна длине орбиты.
За 8 часов разница стала (8 cdot 10000 = 80000) км.
Ответ: 80000
Задание
4
#821
Уровень задания: Равен ЕГЭ
Вор, укравший сумочку, убегает от хозяйки сумочки по круговой дороге. Скорость вора на 0,5 км/ч больше, чем скорость хозяйки сумочки, которая бегает за ним. Через сколько часов вор догонит хозяйку сумочки во второй раз, если длина дороги, по которой они бегают, равна 300 метрам (считайте, что в первый раз он её догнал уже после кражи сумочки)?
Первый способ:
Вор догонит хозяйку сумочки во второй раз в тот момент, когда расстояние, которое он пробежит, станет на 600 метров больше, чем расстояние, которое пробежит хозяйка сумочки (с момента кражи).
Так как его скорость на (0,5) км/ч больше, то за час он пробегает на 500 метров больше, тогда за (1 : 5 = 0,2) часа он пробегает на (500 : 5 = 100) метров больше. На 600 метров больше он пробежит за (1 + 0,2 = 1,2) часа.
Второй способ:
Пусть (v) км/ч – скорость хозяйки сумочки, тогда
(v + 0,5) км/ч – скорость вора.
Пусть (t) ч – время, через которое вор догонит хозяйку сумочки во второй раз, тогда
(vcdot t) – расстояние, которое пробежит хозяйка сумочки за (t) ч,
((v + 0,5)cdot t) – расстояние, которое пробежит вор за (t) ч.
Вор догонит хозяйку сумочки во второй раз в тот момент, когда пробежит ровно на 2 круга больше неё (то есть на (600) м = (0,6) км), тогда [(v + 0,5)cdot t — vcdot t = 0,6qquadLeftrightarrowqquad 0,5cdot t = 0,6,] откуда (t = 1,2) ч.
Ответ: 1,2
Задание
5
#822
Уровень задания: Равен ЕГЭ
Два мотоциклиста стартуют одновременно из одной точки круговой трассы в разных направлениях. Скорость первого мотоциклиста в два раза больше, чем скорость второго. Через час после старта они встретились в третий раз (считайте, что в первый раз они встретились уже после старта). Найдите скорость первого мотоциклиста, если длина трассы 40 км. Ответ дайте в км/ч.
В тот момент, когда мотоциклисты встретились в третий раз, суммарное расстояние, которое они проехали, было (3 cdot 40 = 120) км.
Так как скорость первого в 2 раза больше, чем скорость второго, то он проехал из 120 км часть в 2 раза большую, чем второй, то есть 80 км.
Так как встретились в третий раз они через час, то 80 км первый проехал за час. Его скорость 80 км/ч.
Ответ: 80
Задание
6
#824
Уровень задания: Равен ЕГЭ
Два бегуна стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой дорожки, длина которой 400 метров. Через сколько минут бегуны поравняются в первый раз, если первый бегун за час пробегает на 1 километр больше, чем второй?
За час первый бегун пробегает на 1000 метров больше, чем второй, значит на 100 метров больше он пробежит за (60 : 10 = 6) минут.
Изначальное расстояние между бегунами равно 200 метров. Они поравняются, когда первый бегун пробежит на 200 метров больше, чем второй.
Это произойдёт через (2 cdot 6 = 12) минут.
Ответ: 12
Задание
7
#825
Уровень задания: Равен ЕГЭ
Из города M по круговой дороге длиной 220 километров вышел турист, а через 55 минут следом за ним из города M отправился автомобилист. Через 5 минут после отправления он догнал туриста в первый раз, а еще через 4 часа после этого догнал его во второй раз. Найдите скорость туриста. Ответ дайте в км/ч.
Первый способ:
После первой встречи автомобилист догнал туриста (во второй раз) через 4 часа. К моменту второй встречи автомобилист проехал на круг больше, чем прошёл турист (то есть на (220) км).
Так как за эти 4 часа автомобилист обогнал туриста на (220) км, то скорость автомобилиста на (220 : 4 = 55) км/ч больше, чем скорость туриста.
Пусть теперь скорость туриста (v) км/ч, тогда до первой встречи он успел пройти [v cdot left(dfrac{55}{60} + dfrac{5}{60}right) = v text{км},] автомобилист успел проехать [(v + 55)dfrac{5}{60} = dfrac{v + 55}{12} text{км}.] Тогда [dfrac{v + 55}{12} = v,] откуда находим (v = 5) км/ч.
Второй способ:
Пусть (v) км/ч – скорость туриста.
Пусть (w) км/ч – скорость автомобилиста. Так как (55) минут (+ 5) минут (= 1) час, то
(vcdot 1) км – расстояние, которое прошёл турист до первой встречи. Так как (5) минут (= dfrac{1}{12}) часа, то
(wcdot dfrac{1}{12}) км – расстояние, которое проехал автомобилист до первой встречи. Расстояния, которые они проехали до первой встречи, равны: [wcdot dfrac{1}{12} = vcdot 1.] За следующие 4 часа автомобилист проехал больше, чем прошёл турист на круг (на (220) км), тогда (wcdot 4 = vcdot 4 + 220), итого: [v = dfrac{1}{12}w,] что равносильно (w = 12cdot v)
(4w = 4v + 220), откуда с учётом предыдущего уравнения [48v = 4v + 220.] Решая эту систему на (v) и (w), находим (v = 5) км/ч, (w = 60) км/ч.
Ответ: 5
Как научиться быстро и правильно решать задачи на круговое движение в ЕГЭ по математике? Этот вопрос в преддверии аттестационного испытания возникает у школьников все чаще. О том, как максимально эффективно подготовиться к экзамену, расскажет образовательный портал «Школково».
Основные моменты
В задачах ЕГЭ на круговое движение перемещение могут осуществлять 2 объекта. В этом случае следует учитывать их скорость сближения или удаления.
[T=dfrac S {V_1-V_2}]
[T=dfrac S {V_1+V_2}]
При использовании в упражнении величин, которые связаны с расстоянием (скорость, длина круга), решить их можно путем сведения к перемещению по прямой.
[S=Vcdot t]
Наибольшую сложность у школьников Москвы и других городов, как показывает практика, вызывают задачи на круговое движение в ЕГЭ, поиск ответа в которых связан с применением угла. Для решения упражнения длину окружности можно задать как часть круга.
Повторить эти и другие алгебраические формулы вы можете в разделе «Теоретическая справка». Для того чтобы научиться применять их на практике, прорешайте упражнения по данной теме в «Каталоге».

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
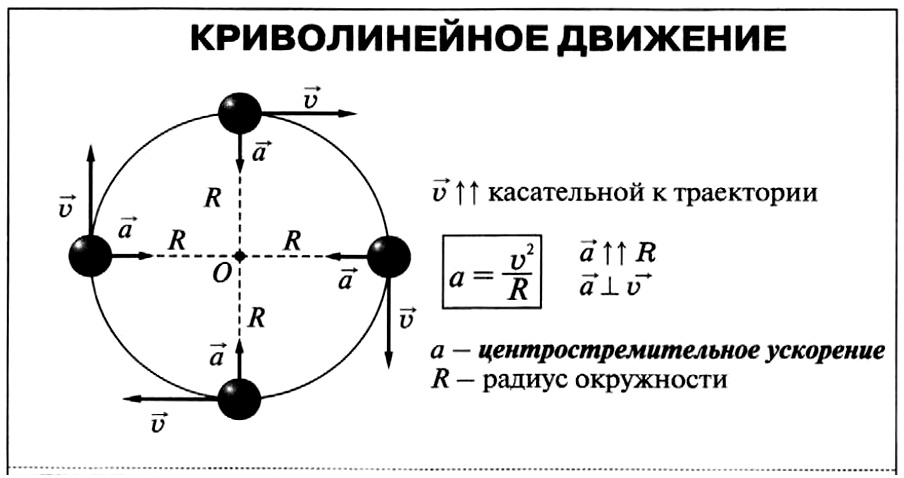
Задачи на Движение тела по окружности с решениями
Формулы, используемые на уроках «Задачи на Движение тела по окружности».
Название величины |
Обозначение |
Единица измерения |
Формула |
Радиус окружности |
r |
м |
|
Линейная скорость (модуль) |
v |
м/с |
|
Центростремительное ускорение (модуль) |
a |
м/с2 |
|
Центростремительная сила (модуль) |
F |
Н |
|
Масса тела |
m |
кг |
|
Угловая скорость при равномерном вращении |
ω |
рад/с |
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Какова линейная скорость тела, движущегося по окружности радиусом 40 м с ускорением 2,5 м/с2 ?
Задача № 2.
С какой наибольшей скоростью может двигаться автомобиль массой 1 т на повороте радиусом 100 м, чтобы его не «занесло», если максимальная сила трения 4 кН?
Задача № 3.
Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.
Задача № 4.
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Задача № 5.
Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?
Задача № 6.
Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.
Задача № 7.
Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с2.
Задача № 8.
Шкив радиусом 30 см имеет частоту вращения 120 об/мин. Определите частоту, период обращения, угловую скорость шкива и центростремительное ускорение точек шкива, наиболее удаленных от оси вращения.
Задача № 9.
Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли. Радиус Земли считайте равным 6370 км.
Задача № 10.
ОГЭ
Точка движется равномерно по окружности. Как изменится её центростремительное ускорение, если скорость возрастёт вдвое, а радиус окружности вдвое уменьшится?
Задача № 11.
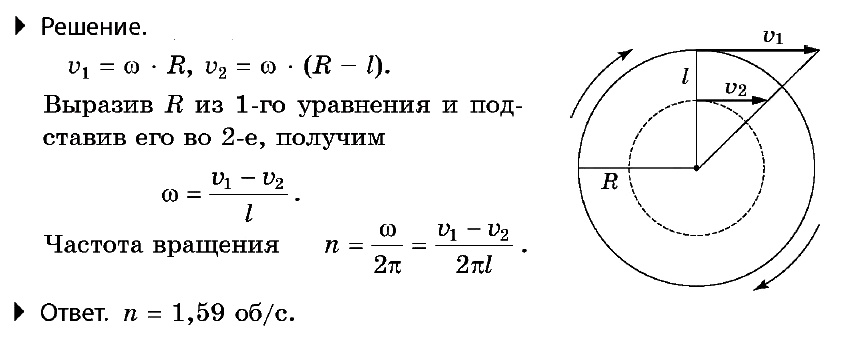
ЕГЭ
Линейная скорость точек обода вращающегося диска v1 = 3 м/с, а точек, находящихся на l = 10 см ближе к оси вращения, v2 = 2 м/с. Найти частоту вращения диска.
Задача № 12.
Груз, привязанный к шнуру длиной l = 50 см, описывает окружность в горизонтальной плоскости. Какой угол φ образует шнур с вертикалью, если частота вращения n = 1 с-1 ?
Рассуждение: На схеме покажем груз, подвешенный на нити и движущийся по окружности некого радиуса R в горизонтальной плоскости так, что нить составляет с вертикалью угол φ. На груз действуют две силы: 1) сила тяжести mg; 2) сила натяжения нити T. Так как груз не движется вдоль оси y, то запишем первый закон Ньютона в проекции на эту ось: T⋅• cos φ = mg. Поскольку груз описывается окружность, то второй закон Ньютона запишется так: T⋅• sin φ = ma.
Ответ: 60º.
Краткая теория для решения Задачи на Движение тела по окружности.
Это конспект по теме «ЗАДАЧИ на Движение тела по окружности». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Искусственные спутники планет.
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.