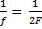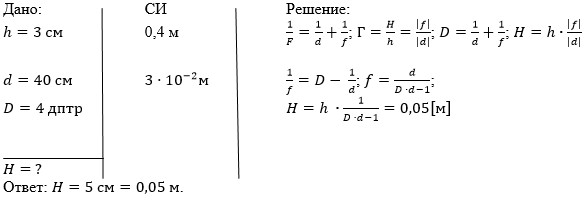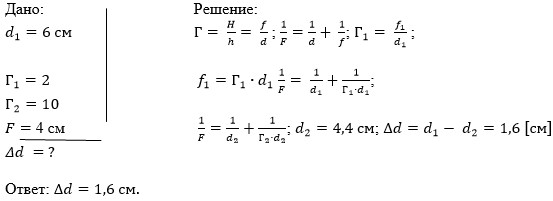Всего: 89 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Небольшой предмет располагают на расстоянии a от тонкой собирающей линзы и получают с её помощью изображение этого предмета, расположенное на расстоянии b от линзы. На рисунке изображены графики зависимостей b от a для двух тонких собирающих линз 1 и 2.
Выберите все верные утверждения на основании анализа представленных графиков.
1) Фокусное расстояние линзы 1 равно 3 см.
2) Фокусное расстояние линзы 1 больше фокусного расстояния линзы 2 на 1,5 см.
3) Оптическая сила линзы 1 больше оптической силы линзы 2.
4) Если предмет расположен на расстоянии 5 см от линзы 1, то изображение этого предмета будет увеличено в 2 раза.
5) При одинаковом расстоянии от линз до предметов линза 1 будет давать изображение с меньшим увеличением.
Небольшой предмет располагают на расстоянии a от тонкой собирающей линзы и получают с её помощью изображение этого предмета, расположенное на расстоянии b от линзы. На рисунке изображены графики зависимостей b от a для двух тонких собирающих линз 1 и 2.
Выберите все верные утверждения на основании анализа представленных графиков.
1) Фокусное расстояние линзы 2 равно 14 см.
2) Фокусное расстояние линзы 1 меньше фокусного расстояния линзы 2 на 0,5 см.
3) Оптическая сила линзы 1 меньше оптической силы линзы 2.
4) Если предмет расположен на расстоянии 10 см от линзы 2, то изображение этого предмета будет увеличено в 2 раза.
5) При одинаковом расстоянии от линз до предметов линза 2 будет давать изображение с бóльшим увеличением.
На оптической скамье установлена тонкая собирающая линза с фокусным расстоянием F, а слева от неё на расстоянии d > F от линзы помещён предмет (стрелка, перпендикулярная оси). В линзе получилось действительное изображение высотой h. Затем справа от этой линзы поместили на расстоянии F от неё вторую такую же линзу. Главные оптические оси линз совпадали. Правее второй линзы получилось новое изображение исходного предмета высотой h′. Изобразите на чертеже ход лучей в системе из двух линз, постройте новое изображение предмета и вычислите отношение
Оптическая система состоит из тонкой собирающей линзы и предмета S. Установите соответствие между схемами оптических систем и увеличениями оптических систем.
СХЕМА ОПТИЧЕСКОЙ СИСТЕМЫ
УВЕЛИЧЕНИЕ ОПТИЧЕСКОЙ СИСТЕМЫ
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Оптическая система состоит из тонкой собирающей линзы и предмета S. Установите соответствие между схемами оптических систем и увеличениями оптических систем.
СХЕМА ОПТИЧЕСКОЙ СИСТЕМЫ
УВЕЛИЧЕНИЕ ОПТИЧЕСКОЙ СИСТЕМЫ
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
На рисунке показаны предмет П и его изображение И, даваемое тонкой собирающей линзой с главной оптической осью
Чему равно даваемое этой линзой увеличение?
Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.
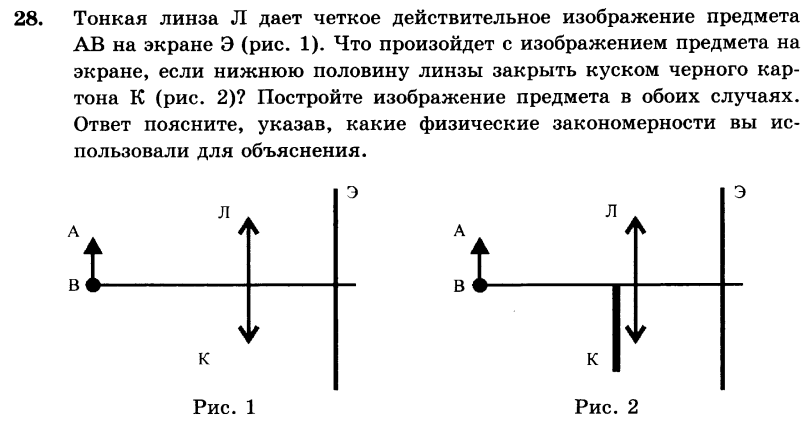
Небольшой предмет находится на главной оптической оси тонкой собирающей линзы, на двойном фокусном расстоянии от нее. Как изменятся при удалении предмета от линзы следующие три величины: размер изображения, его расстояние от линзы, оптическая сила линзы?
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
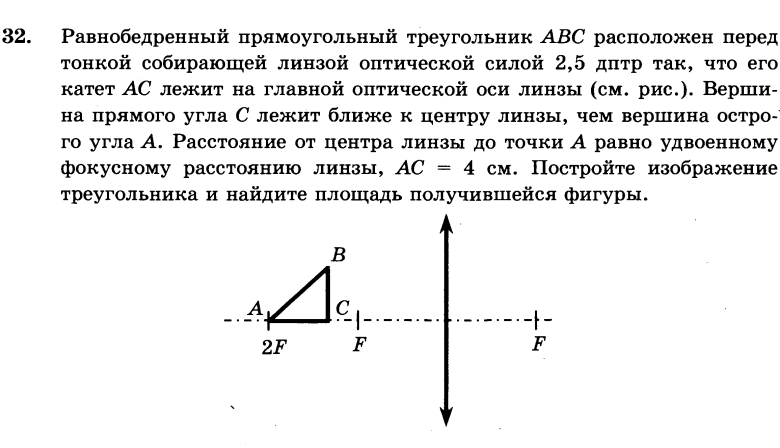
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Размер
изображения |
Расстояние
изображения от линзы |
Оптическая
сила линзы |
Предмет расположен на расстоянии 9 см от собирающей линзы с фокусным расстоянием 6 см. Линзу заменили на другую собирающую линзу с фокусным расстоянием 8 см. На каком расстоянии от новой линзы нужно расположить предмет для того, чтобы увеличения в обоих случаях были одинаковыми? Ответ приведите в сантиметрах.
Линза с фокусным расстоянием F = 0,1 м даёт на экране изображение предмета, увеличенное в 6 раз. Каково расстояние от линзы до изображения? Ответ приведите в метрах.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 2.
Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи
Источник: ЕГЭ по физике 06.06.2022. Основная волна. Центр
Источник: ЕГЭ по физике 06.06.2022. Основная волна. Ростовская область
Источник: ЕГЭ по физике 06.06.2022. Основная волна. Краснодар
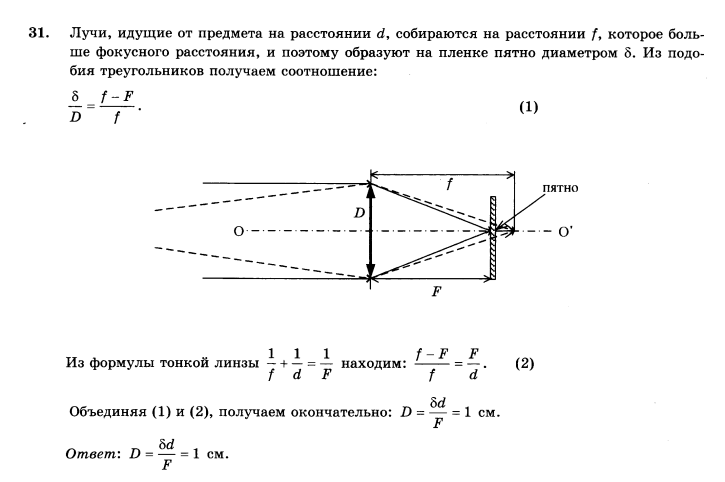
На экране, перпендикулярном главной оптической оси некоторой тонкой линзы, получили действительное изображение небольшого предмета, находящегося на расстоянии a = 25 см от этой линзы, с линейным увеличением Г = 2. После замены этой линзы на другую, находящуюся в том же месте и на том же расстоянии до предмета, увеличение изображения предмета при новом положении экрана, соответствующем резкому изображению, стало больше в n = 2,5 раза. Чему равна оптическая сила D2 второй линзы?
При изучении законов геометрической оптики ученик расположил небольшой предмет на расстоянии 50 см от тонкой собирающей линзы. Оптическая сила линзы равна 2,5 дптр. После этого он стал перемещать предмет вдоль главной оптической оси линзы. Выберите все верные утверждения о результатах этого опыта. В ответе укажите их номера.
1) Первоначально изображение предмета находилось на расстоянии 2 м от линзы.
2) Первоначальное изображение предмета получилось мнимым и увеличенным.
3) При перемещении предмета на 20 см ближе к линзе изображение предмета стало уменьшенным.
4) Фокусное расстояние линзы равно 40 см.
5) При перемещении предмета на 30 см дальше от линзы размер изображения предмета стал равен размеру самого предмета.
Груз на пружине совершает гармонические колебания перпендикулярно главной оптической оси собирающей линзы с оптической силой 5 дптр (см. рисунок). С помощью этой линзы на экране получено чёткое изображение груза, находящегося на расстоянии 0,5 м от линзы. Максимальная скорость изображения равна 1 м/с. Определите максимальную скорость самого груза, считая груз материальной точкой.
Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи
Предмет расположен на горизонтальной главной оптической оси тонкой собирающей линзы. Фокусное расстояние линзы равно 30 см. Изображение предмета действительное, а увеличение составило k = 3. Найдите расстояние от предмета до линзы. Ответ приведите в сантиметрах.
Фокусное расстояние тонкой собирающей линзы равно F. На главной оптической оси слева от линзы на расстоянии a = 2,5F от неё находится точечный источник света. Горизонтальная ось Ox совпадает с главной оптической осью линзы.
Выберите все верные утверждения.
1) Изображение точечного источника света будет находиться справа от линзы на расстоянии b > a от неё.
2) Если линзу переместить вдоль главной оптической оси так, что расстояние от точечного источника света до линзы уменьшится на величину l = F , то изображение источника будет находиться справа от линзы на расстоянии b > a от неё.
3) Если линзу переместить вдоль главной оптической оси так, что расстояние от точечного источника света до линзы станет равным 3,5F, то изображение источника будет находиться справа от линзы на расстоянии b > a от неё.
4) Если линзу сместить перпендикулярно главной оптической оси, не изменяя расстояния a от точечного источника света до линзы, то оптическая сила линзы не изменится.
5) Если линзу повернуть относительно главной оптической оси на угол α, то изображение точечного источника света повернется относительно оси Ox на угол 2α.
Точечный источник света удаляется от тонкой собирающей линзы, двигаясь вдоль её главной оптической оси. Фокусное расстояние линзы равно 10 см. На рисунке показан график зависимости расстояния x между источником и линзой от времени t.
Из приведённого ниже списка выберите все верные утверждения.
1) В момент времени t0 = 0 с изображение источника в линзе было мнимым и находилось в фокальной плоскости линзы.
2) Изображение источника в линзе в любой момент времени действительное.
3) В момент времени t = 25 с увеличение линзы меньше единицы.
4) Изображение источника в линзе движется с постоянной скоростью в течение всего времени наблюдения.
5) В момент времени t = 10 с пучок световых лучей, прошедших через линзу, становится параллельным её главной оптической оси.
Всего: 89 1–20 | 21–40 | 41–60 | 61–80 …
Задачи по геометрической оптике не такие уж и сложные, если уделить их разбору немного временени. Сегодня в нашей регулярной рубрике «Физика для чайников» рассмотрим несколько примеров задач на тонкие линзы.
Хотите быть в курсе актуальных новостей, связанных с учебой? Присоединяйтесь к нам в телеграме! А тем, кто хочет получать скидки и бонусы, рекомендуем заглянуть на наш второй канал для клиентов.
Тонкая линза: задачи
Чтобы успешно решать задачи по геометрической оптике на тему «Тонкие линзы», нужно знать всего лишь пару формулу. Правда, формул много не бывает, и мы собрали их вместе: пригодятся в решении задач по другим темам. А тем, кто не знает, как вообще подступиться к задачам по физике, рекомендуем почитать общую памятку по решению.
Задача №1. Формула тонкой линзы
Условие
Линзу с оптической силой 2,5 дптр поместили на расстоянии 0,5 м от ярко освещённого предмета. На каком расстоянии следует поместить экран, чтобы увидеть на нём чёткое изображение предмета?
Решение
Линза является собирающей (оптическая сила положительна). Запишем формулу тонкой линзы:
1F=1d+1f
Учтем, что F=1D, подставим значения из условия, и запишем:
2,5=10,5+1+ff=2 м
Ответ: 2м
Задача №2. Формула тонкой линзы
Условие
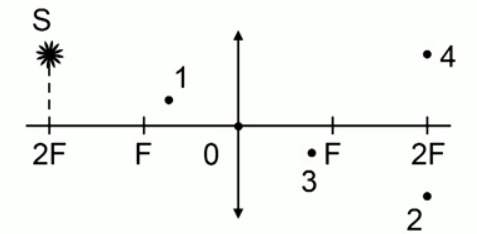
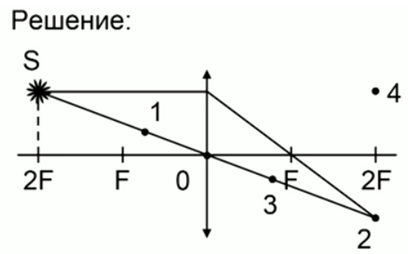
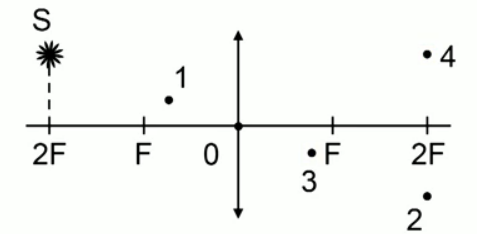
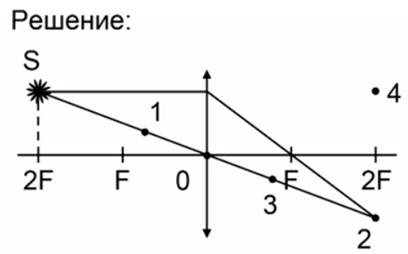
Светящаяся точка лежит в плоскости, проходящей через двойной фокус тонкой линзы, у которой указана главная оптическая ось. Определите, какая из четырех точек на чертеже соответствует правильному изображению светящейся точки.
Решение
Как видим, на рисунке изображена собирающая линза с оптическим центром в точке 0. Светящася точка S находится от линзы на расстоянии, равном двум фокусам.
Построим изображение точки: один луч проходит через оптический центр линзы, а второй луч, параллельный главной оптической оси, после преломления проходит через фокус. Точка пересечения лучей на расстоянии двойного фокуса и будет являться изображением точки S.
Ответ: изображению точки S соответствует точка 2.
Денное решение получено геометрическим путем, но его можно проверить, используя формулу линзы. Подставим в нее 2F вместо d, и получим тот же результат.
Задача №3. Формула тонкой линзы
Условие
Предмет высотой 3 см находится на расстоянии 40 см от собирающей тонкой линзы. Определите высоту изображения, если оптическая сила линзы равна 4 диоптриям.
Решение
Запишем форумулу тонкой собирающей линзы и формулу увеличения линзы:
1F=1d+1f ; Г=Hh=fd
Перепишем эти соотношения, с учетом того, что F=1D
H=h·fd1f=D-1d
Отсюда найдем f:
f=dD·d-1
Осталось подставить значения в формулу для H и вычислить:
H=hdD·d-1=0,03·0,44·0,4-1=0,05 м
Ответ: 0,05 м.
Задача №4. Формула тонкой линзы
Условие
Предмет имеет высоту 2 см. Какое фокусное расстояние должна иметь линза, расположенная на расстоянии f=4 м от экрана, чтобы изображение предмета на экране имело высоту H=1 м?
Решение
Фокусное расстояние найдем из формулы линзы:
1F=1d+1fF=fdd+f
Запишем формулу увеличения линзы и выразим d:
Г=Hh=fd ; d=fhH
Запишем окончательный ответ:
F=hfH+h≈0,08 м
Ответ: 0,08 м.
Задача №5. Формула тонкой линзы
Условие
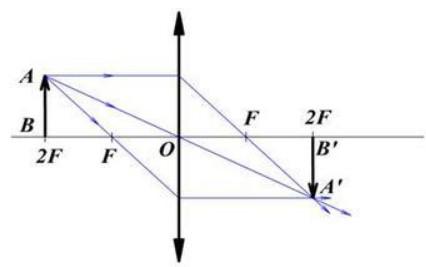
Постройте изображение отрезка AB, расположенного перед собирающей линзой так, что расстояние от предмета до линзы d=2F. Каким будет изображение?
Решение
Посторим изображение в соответствии с правилами геометрической оптики:
Данное изображение:
- действительное;
- перевернутое;
- равное предмету.
Ответ: см. выше.
Вопросы на тему «Тонкая линза»
Вопрос 1. Какое равенство называют формулой тонкой линзы?
Ответ. Формула тонкой линзы имеет следующий вид:
1F=1d+1±f
Здесь:
- F – фокусное расстояние;
- d – расстояние от линзы до предмета;
- f – расстояние от линзы до изображения.
Вопрос 2. В чем разница в формуле линзы для собирающей и рассеивающей линз?
Ответ. Для собирающей линзы f берется положительным, а для рассеивающей – отрицательным. Соответственно, собирающая линза строит действительное изображение, а рассеивающая – мнимое.
Вопрос 3. Что такое фокусное расстоняние линзы?
Ответ. Фокусное расстояние линзы – это расстояние между ее оптическим центром и главным фокусом.
Вопрос 4. Что такое оптическая сила линзы?
Ответ. Оптическая сила – это величина, обратная фокусному расстоянию. Она характеризует преломляющую способность линзы.
Вопрос 5. Может ли оптическая сила линзы быть отрицательной?
Ответ. Да. Для рассеивающей линзы оптическая сила берется со знаком минус.
Проблемы с решением задач или других заданий? Обращайтесь в профессиональный сервис помощи учащимся!
15. Магнитное поле. Оптика
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Геометрическая оптика (Линзы)
Расстояние от изображения до рассеивающей линзы составляет 0,75 фокусного расстояния. Во сколько раз больше фокусного расстояние от предмета до линзы?
Формула тонкой линзы для данного случая: [-frac{1}{F}=frac{1}{d}-frac{1}{f}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы, (f=0,75F) [frac{1}{f}-frac{1}{F}=frac{1}{d}] [d=frac{fF}{F-f}=frac{0,75FF}{0,25F}=3F]
Ответ: 3
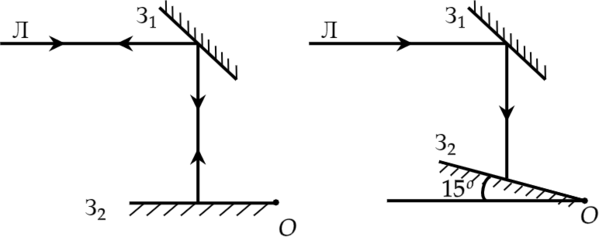
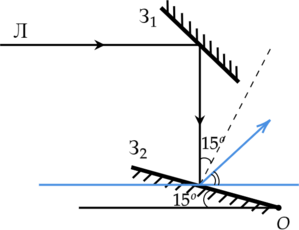
На рисунке слева изображены два плоских зеркала (З1 и З2) и луч, горизонтально падающий на зеркало 1. Зеркало 2 поворачивают относительно горизонтальной оси, проходящей через точку О, на угол (15 ^{circ}) (рисунок справа). Под каким углом к горизонту будет распространяться луч, отражённый от зеркала 2?
Из рисунка видно, что во втром случае угол падения и угол отражения равны по (15^{circ}).
Следовательно, отраженный луч по отношению к горизонту направлен под углом (gamma=90-15^{circ}-15^{circ}=60^{circ})
Ответ: 60
Иголка высотой 3 см расположена перпендикулярно главной оптической оси тонкой собирающей линзы на расстоянии 40 см от линзы. Оптическая сила линзы 4 дптр. Чему равна высота изображения иголки? Ответ приведите в метрах.
Формула тонкой линзы: [D=frac{1}{d}+frac{1}{f}] [f=frac{d}{Dd-1}] Увеличение линзы: [Gamma=frac{f}{d}=frac{H}{h}] [H=frac{fh}{d}=frac{h}{Dd-1}=frac{0,03text{ м}}{4text{ дптр}cdot0,4text{ м}-1}=0,05 text{ м}]
Ответ: 0,05
Рассеивающая линза с фокусным расстоянием 8 см уменьшает предмет в два раза. Найдите расстояние (в см) от предмета до линзы.
Формула тонкой линзы для рассеивающей линзы: [-frac{1}{F}=frac{1}{d}-frac{1}{f}=frac{1}{d}-frac{2}{d}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [d=F=8 text{ см}]
Ответ: 8
Расстояние между предметом и его увеличенным в 5 раз мнимым изображением 80 см. Найдите расстояние (в см) от предмета до линзы.
Расстояние от предмета до линзы [f-d=4d=80 text{ см}] [d=20 text{ см}]
Ответ: 20
Расстояние от предмета до собирающей линзы составляет 1,25 от фокусного расстояния. Найдите увеличение линзы.
Формула тонкой линзы для собирающей линзы: [frac{1}{F}=frac{1}{d}+frac{1}{f}=frac{1}{1,25F}+frac{1}{f}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [f=frac{1,25F}{1,25-1}=5F]
Уведичение линзы: [Gamma=frac{f}{d}=frac{5F}{1,25F}=4]
Ответ: 4
На каком расстоянии (в см) от собирающей линзы с фокусным расстоянием 30 см следует поместить предмет, чтобы получить действительное изображение, увеличенное в 3 раза?
Уведичение линзы: [Gamma=frac{h}{H}frac{f}{d}=3]
Формула тонкой линзы для собирающей линзы: [frac{1}{F}=frac{1}{d}+frac{1}{f}=frac{1}{d}+frac{1}{3d}] где (F) – фокусное расстояние,
(d) – расстояние от предмета до линзы
(f) – растояние от изображения до линзы [d=frac{4}{3}F=40 text{см}]
Ответ: 40

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Решение задач по теме «Формула тонкой линзы»
Задача 1
Представлена тонкая линза, у которой указана главная оптическая ось, и указано, что в плоскости, проходящей через двойной фокус, располагается светящаяся точка. Необходимо определить, какая из четырех точек на чертеже соответствует правильному изображению этого предмета, то есть светящейся точке.
Задача может быть решена несколькими способами, рассмотрим два из них.
Рис. 1. Задача 1
На рис. 1 изображена собирающая линза с оптическим центом (0), фокусы (
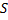
Решение задачи начнем с вопроса построения изображения.
Светящаяся точка (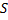

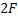
Одновременно с этим можно воспользоваться формулой тонкой линзы и вместо 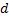
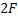
Рис. 2. Задача 1, решение
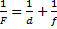
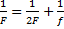
Ответ: 2.
Задачу можно было бы решить и с помощью таблицы, которую мы рассматривали ранее, там указано, что если предмет находится на расстоянии двойного фокуса, то изображение тоже получится на расстоянии двойного фокуса, то есть, помня таблицу, ответ можно было бы получить сразу.
Задача 2
Предмет высотой 3 сантиметра находится на расстоянии 40 сантиметров от собирающей тонкой линзы. Определить высоту изображения, если известно, что оптическая сила линзы составляет 4 диоптрии.
Записываем условие задачи и, поскольку величины указаны в разных системах отсчета, переводим их в единую систему и запишем уравнения, необходимые для решения задачи:
Мы использовали формулу тонкой линзы для собирающей линзы с положительным фокусом, формулу увеличения (
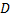
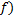
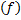
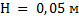
Задача 3
Перед тонкой собирающей линзой поместили предмет, в результате такого размещения увеличение получилось равным 2. Когда предмет передвинули относительно линзы, то увеличение стало равно 10. Определить на сколько передвинули предмет и в каком направлении, если первоначальное расстояние от линзы до предмета составляло 6 сантиметров.
Для решения задачи мы будем использовать формулу вычисления увеличения и формулу собирающей тонкой линзы.
Из этих двух уравнений мы и будем искать решение. Выразим расстояние от линзы до изображения в первом случае, зная увеличение и расстояние. Подставив значения в формулу тонкой линзы, мы получим значение фокуса 
Заключение
Геометрическая оптика остается очень важной темой в физике, все задачи решаются исключительно на понимании вопросов построении изображения в линзах и, конечно, знании необходимых уравнений.
Тонкие линзы: решение задач с помощью графика
Тема этой и следующей статей – использование графиков при решении задач на оптику, а именно – задач с линзами. Конспект занятий Пенкина М.А.
Сначала давайте построим график, использование которого сильно облегчит решение задач.
Собирающая линза. Для нее известно, что если расстояние от предмета до линзы меньше, чем фокусное, то формула линзы
А линейное увеличение
Если расстояние от предмета до линзы больше, чем фокусное, то формула линзы
А линейное увеличение
Тогда график зависимости имеет вид
Как видно, увеличение в точках
и
. Обе ветви симметричны относительно асимптоты
. И одно и то же увеличение может быть получено при двух расстояниях предмета от линзы —
и
.
Рассеивающая линза.
Для нее формула линзы
А линейное увеличение
График зависимости будет выглядеть так
Пользуясь этими графиками, давайте решим несколько задач.
Задача 1. Тонкая линза создаёт прямое изображение предмета, расположенного перпендикулярно главной оптической оси, с некоторым увеличением . Предмет перемещают (не трогая линзу) вдоль главной оптической оси на расстояние
(
– фокусное расстояние линзы) и получают изображение с тем же увеличением. При этом предмет остаётся по одну сторону линзы.
- Найти увеличение
.
- На какое расстояние переместилось изображение?
Согласно графику одно и то же увеличение достигается при двух положениях предмета. Для правой и левой ветвей я подписала функциональную зависимость. При имеем мнимое изображение (левая ветвь), при
— действительное (правая ветвь).
К задаче 1
По условию линза дает ПРЯМОЕ изображение – а значит, оно мнимое и изначально предмет находится на расстоянии ближе фокусного к линзе. Пусть мы (предмет) находится на расстоянии . Поскольку увеличение не изменилось, то предмет переместили за фокус – на расстояние
от линзы.
И
Пусть сдвиг предмета
Расстояние, на которое переместилось изображение будет суммой и
, так как изображение было мнимым, а стало действительным, то есть сначала оно располагалось с той же стороны, что и предмет, а затем – с противоположной.
Теперь запишем расстояние от линзы до изображения
Ответ: 1) ; 2)
.
Задача 2.
Тонкая линза создаёт изображение предмета, расположенного перпендикулярно главной оптической оси, с некоторым увеличением. Если расстояние от предмета до линзы увеличить вдвое, то получается перевёрнутое изображение предмета с увеличением, вчетверо большим первоначального увеличения. С каким увеличением изображался предмет вначале?
К задаче 2
По условию, изображение стало действительным, значит, стало больше
. Это означает, что мы оказались на правой ветви графика. Это же обстоятельство говорит о том, что линза собирающая. Также по условию увеличение выросло вчетверо, значит, было в 4 раза меньше, то есть мы находились на левой ветви графика в точке 1, которая ниже точки 2 (так как расстояние выросло вдвое также по условию).
Для точки 1
Для точки 2
Тогда
Ответ:
Тонкие линзы. Ход лучей.
-
Понятие тонкой линзы.
-
Оптический центр и фокальная плоскость.
-
Ход луча через оптический центр.
-
Ход лучей в собирающей линзе.
-
Ход лучей в рассеивающей линзе.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: линзы, оптическая сила линзы
Взгляните ещё раз на рисунки линз из предыдущего листка: эти линзы обладают заметной толщиной и существенной кривизной своих сферических границ. Мы намеренно рисовали такие линзы — чтобы основные закономерности хода световых лучей проявились как можно более чётко.
к оглавлению ▴
Понятие тонкой линзы.
Теперь, когда эти закономерности достаточно ясны, мы рассмотрим очень полезную идеализацию, которая называется тонкой линзой.
В качестве примера на рис. 1 приведена двояковыпуклая линза; точки и
являются центрами её сферических поверхностей,
и
— радиусы кривизны этих поверхностей.
— главная оптическая ось линзы.
 |
| Рис. 1. К определению тонкой линзы |
Так вот, линза считается тонкой, если её толщина очень мала. Нужно, правда, уточнить: мала по сравнению с чем?
Во-первых, предполагается, что и
. Тогда поверхности линзы хоть и будут выпуклыми, но могут восприниматься как «почти плоские». Этот факт нам очень скоро пригодится.
Во-вторых, , где
— характерное расстояние от линзы до интересующего нас предмета. Собственно, лишь в таком случае мы и
сможем корректно говорить о «расстоянии от предмета до линзы», не уточняя, до какой именно точки линзы берётся это самое расстояние.
Мы дали определение тонкой линзы, имея в виду двояковыпуклую линзу на рис. 1. Это определение без каких-либо изменений переносится на все остальные виды линз. Итак: линза является тонкой, если толщина линзы много меньше радиусов кривизны её сферических границ и расстояния от линзы до предмета.
Условное обозначение тонкой собирающей линзы показано на рис. 2.
 |
| Рис. 2. Обозначение тонкой собирающей линзы |
Условное обозначение тонкой рассеивающей линзы показано на рис. 3.
 |
| Рис. 3. Обозначение тонкой рассеивающей линзы |
В каждом случае прямая — это главная оптическая ось линзы, а сами точки
— её
фокусы. Оба фокуса тонкой линзы расположены симметрично относительно линзы.
к оглавлению ▴
Оптический центр и фокальная плоскость.
Точки и
, обозначенные на рис. 1, у тонкой линзы фактически сливаются в одну точку. Это точка
на рис. 2 и 3, называемая оптическим центром линзы. Оптический центр находится на Пересечении линзы с её главной оптической осью.
Расстояние от оптического центра до фокуса называется фокусным расстоянием линзы. Мы будем обозначать фокусное расстояние буквой
. Величина
, обратная фокусному расстоянию, есть оптическая сила — линзы:
.
Оптическая сила измеряется в диоптриях (дптр). Так, если фокусное расстояние линзы равно 25 см, то её оптическая сила:
дптр
Продолжаем вводить новые понятия. Всякая прямая, проходящая через оптический центр линзы и отличная от главной оптической оси, называется побочной оптической осью . На рис. 4 изображена побочная оптическая ось — прямая .
 |
| Рис. 4. Побочная оптическая ось, фокальная плоскость и побочный фокус |
Плоскость , проходящая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. Фокальная плоскость, таким образом, параллельна плоскости линзы. Имея два фокуса, линза соответственно имеет и две фокальных плоскости, расположенных симметрично относительно линзы.
Точка , в которой побочная оптическая ось пересекает фокальную плоскость, называется побочным фокусом. Собственно, каждая точка фокальной плоскости (кроме
) есть побочный фокус — мы ведь всегда сможем провести побочную оптическую ось, соединив данную точку с оптическим центром линзы. А сама точка
— фокус линзы — в связи с этим называется ещё главным фокусом.
То, что на рис. 4 изображена собирающая линза, никакой роли не играет. Понятия побочной оптической оси, фокальной плоскости и побочного фокуса совершенно аналогично определяются и для рассеивающей линзы — с заменой на рис. 4 собирающей линзы на рассеивающую.
Теперь мы переходим к рассмотрению хода лучей в тонких линзах. Мы будем предполагать, что лучи являются параксиальными, то есть образуют достаточно малые углы с главной оптической осью. Если параксиальные лучи исходят из одной точки, то после прохождения линзы преломлённые лучи или их продолжения также пересекаются в одной точке. Поэтому изображения предметов, даваемые линзой, в параксиальных лучах получаются весьма чёткими.
к оглавлению ▴
Ход луча через оптический центр.
Как мы знаем из предыдущего раздела, луч, идущий вдоль главной оптической оси, не преломляется. В случае тонкой линзы оказывается, что луч, идущий вдоль побочной оптической оси, также не преломляется!
Объяснить это можно следующим образом. Вблизи оптического центра обе поверхности линзы неотличимы от параллельных плоскостей, и луч в данном случае идёт как будто через плоскопараллельную стеклянную пластинку (рис. 5).
 |
| Рис. 5. Ход луча через оптический центр линзы |
Угол преломления луча равен углу падения преломлённого луча
на вторую поверхность. Поэтому второй преломлённый луч
выходит из плоскопараллельной пластинки параллельно падающему лучу
. Плоскопараллельная пластинка лишь смещает луч, не изменяя его направления, и это смещение тем меньше, чем меньше толщина пластинки.
Но для тонкой линзы мы можем считать, что эта толщина равна нулю. Тогда точки фактически сольются в одну точку, и луч
окажется просто продолжением луча
. Вот поэтому и получается, что луч, идущий вдоль побочной оптической оси, не преломляется тонкой линзой (рис. 6).
 |
| Рис. 6. Луч, идущий через оптический центр тонкой линзы, не преломляется |
Это единственное общее свойство собирающих и рассеивающих линз. В остальном ход лучей в них оказывается различным, и дальше нам придётся рассматривать собирающую и рассеивающую линзу по отдельности.
к оглавлению ▴
Ход лучей в собирающей линзе.
Как мы помним, собирающая линза называется так потому, что световой пучок, параллельный главной оптической оси, после прохождения линзы собирается в её главном фокусе (рис. 7).
 |
| Рис. 7. Параллельный пучок собирается в главном фокусе |
Пользуясь обратимостью световых лучей, приходим к следующему выводу: если в главном фокусе собирающей линзы находится точечный источник света, то на выходе из линзы получится световой пучок, параллельный главной оптической оси (рис. 8).
 |
| Рис. 8. Преломление пучка, идущего из главного фокуса |
Оказывается, что пучок параллельных лучей, падающих на собирающую линзу наклонно, тоже соберётся в фокусе — но в побочном. Этот побочный фокус отвечает тому лучу, который проходит через оптический центр линзы и не преломляется (рис. 9).
 |
| Рис. 9. Параллельный пучок собирается в побочном фокусе |
Теперь мы можем сформулировать правила хода лучей в собирающей линзе. Эти правила вытекают из рисунков 6-9,
1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления пойдёт через главный фокус (рис. 10).
 |
| Рис. 10. К правилу 2 |
3. Если луч падает на линзу наклонно, то для построения его дальнейшего хода мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Вот через этот побочный фокус и пойдёт преломлённый луч (рис. 11).
 |
| Рис. 11. К правилу 3 |
В частности, если падающий луч проходит через фокус линзы, то после преломления он пойдёт параллельно главной оптической оси.
к оглавлению ▴
Ход лучей в рассеивающей линзе.
Переходим к рассеивающей линзе. Она преобразует пучок света, параллельный главной оптической оси, в расходящийся пучок, как бы выходящий из главного фокуса (рис. 12)
 |
| Рис. 12. Рассеяние параллельного пучка |
Наблюдая этот расходящийся пучок, мы увидим светящуюся точку, расположенную в фокусе позади линзы.
Если параллельный пучок падает на линзу наклонно, то после преломления он также станет расходящимся. Продолжения лучей расходящегося пучка соберутся в побочном фокусе , отвечающем тому лучу, который проходит через через оптический центр линзы и не преломляется (рис. 13).
 |
| Рис. 13. Рассеяние наклонного параллельного пучка |
Этот расходящийся пучок создаст у нас иллюзию светящейся точки, расположенной в побочном фокусе за линзой.
Теперь мы готовы сформулировать правила хода лучей в рассеивающей линзе. Эти правила следуют из рисунков 6, 12 и 13.
1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления начнёт удаляться от главной оптической оси; при этом продолжение преломлённого луча пройдёт через главный фокус (рис. 14).
 |
| Рис. 14. К правилу 2 |
3. Если луч падает на линзу наклонно, то мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Преломлённый луч пойдёт так, словно он исходит из этого побочного фокуса (рис. 15).
 |
| Рис. 15. К правилу 3 |
Пользуясь правилами хода лучей 1–3 для собирающей и рассеивающей линзы, мы теперь научимся самому главному — строить изображения предметов, даваемые линзами.
Разберем задачи ЕГЭ по теме: Тонкие линзы.
1. На экране с помощью тонкой линзы получено изображение предмета с пятикратным увеличением. Экран передвинули на 30 см вдоль главной оптической оси линзы. Затем при неизменном положении линзы передвинули предмет, чтобы изображение снова стало резким. В этом случае получилось изображение с трехкратным увеличением. На сколько пришлось передвинуть предмет относительно первоначального положения?
Дано:
Г₁=5
Г₂=3
а = 30 см = 0,3 м.
Найти:
Δd — ?
Решение.
При решении этой задачи главным является создание модели, которая поясняет изменения в увеличении линзы и позволяет правильно определить перемещение экрана и предмета. На представленных ниже рис.1 и рис.2 выполнены все необходимые построения для двух случаев задачи. Так как увеличение линзы уменьшается, то предмет смещается в сторону двойного фокуса. Именно в этом случае возможно уменьшение изображения, по сравнению с первым случаем.
Особое внимание надо обратить на фразу, что изображение снова стало резким. Это возможно только при выполнении всех соотношений в формуле тонкой линзы
Для каждого случая запишем формулу тонкой линзы и учтем соотношения между d и f через значение увеличения (Г), даваемое линзой.
Г₁
, отсюда
Г₂
, отсюда
Тогда формулы (1) и (2) примут вид:
Остается решить следующую систему из двух уравнений:
Решение этой системы можно провести с подстановкой численных значений.
(м). Тогда
(м)
(м)
(м)
(м).
Ответ: 0,02 м
2. На оси ОХ в точке находится оптический центр тонкой рассеивающей линзы с фокусным расстоянием
см, а в точке
см – тонкой собирающей линзы. Главные оптические ос обеих линз лежат на оси ОХ. На рассеивающую линзу вдоль оси ОХ падает параллельный пучок света из области х<0. Пройдя данную оптическую систему, лучи собираются в точке с координатой
см. Найдите фокусное расстояние собирающей линзы
.
Дано:
см = -0,2 м
см = 0,2 м
см = 0,6 м
Найти:
— ?
Решение
На рисунке представлен ход лучей через систему рассеивающей и собирающей линз. При решении подобных задач необходимо рассматривать отдельно ход лучей сквозь каждую линзу.
Рассмотрим сначала ход лучей через рассеивающую линзу. Для этого воспользуемся формулой тонкой линзы и учтем, что , так как на рассеивающую линзу падает параллельный пучок света из области
. Тогда дробь
и формула примет вид:
Перед стоит знак (-), так как линза рассеивающая и она дает всегда мнимое изображение.
Поэтому (м).
В точке S сформировалось мнимое изображение светового пучка, который падает на собирающую линзу из области
Теперь отдельно рассмотрим собирающую линзу. Для нее расстояние будет равно 0,4 м (согласно рисунку). Применим для собирающей линзы формулу тонкой линзы с учетом
и
. Расстояние
;
(м).
(м) = 20 (см).
Ответ: 20 см.
3. Точечный источник света движется со скоростью v вокруг главной оптической оси собирающей линзы в плоскости, параллельной плоскости линзы на расстоянии d=15 см от линзы. Фокусное расстояние линзы F= 10 cм. Скорость движения изображения точечного источника света V=10 м/с. Найдите скорость движения источника света.
Дано:
d=15 см = 0,15 м
F= 10 см = 0,1 м
V=10 м/с
Найти: v-?
Решение.
Для решения этой задачи воспользуемся формулой тонкой линзы.
Проведем расчет для определения расстояния от линзы до изображения.
(м).
Полученный результат говорит о том, что увеличение линзы Г>1.
Г =
Точечный источник и его изображение будут двигаться с разными линейными скоростями, но в тоже самое время период их обращения, частота обращения и угловые скорости у них будут равными. Радиусы окружностей, которые будут описывать источник света и его изображения, будут отличаться в 2 раза. Радиус окружности изображения R будет превышать радиус окружности источника r в 2 раза или
Воспользуемся формулой равенства периодов обращения.
(м/с)
4. Точечный источник света S расположен на расстоянии 40 cм от оптического центра тонкой собирающей линзы с фокусным расстоянием 0,2 м на её главной оптической оси АВ. На сколько сместиться вдоль прямой АВ изображение источника, если линзу повернуть на угол =30° относительно оси, перпендикулярной плоскости рисунка и проходящей через оптический центр линзы? Сделайте пояснительный чертеж, указав ход лучей в линзе для обоих случаев её расположения.
Дано:
cм = 0,4 м
F = 0,2 м
= 30°
Найти:
— ?
Решение.
Применим формулу тонкой линзы для первого случая.
(м).
Применим формулу тонкой линзы для второго случая.
Здесь необходимо учесть, что (м).
(м).
Изображение источника во втором случае также формируется на прямой АВ. Для нахождения расстояния необходимо
(м).
Таким образом, изображения источников в обоих случаях получились на прямой АВ на расстоянии (м).
Ответ: 0,14 м.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Тонкие линзы. Ход лучей.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023
Возможное решение
Возможное решение
Возможное решение
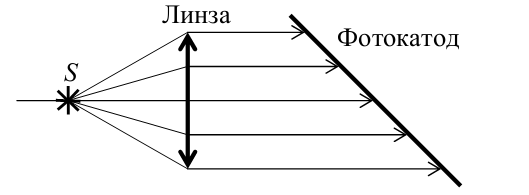
28. В установке по наблюдению фотоэффекта свет от точечного источника S , пройдя через собирающую линзу, падает на фотокатод параллельным пучком. В схему внесли изменение: на место первоначальной линзы поставили другую того же диаметра, но с бóльшим фокусным расстоянием.
Источник света переместили вдоль главной оптической оси линзы так, что на фотокатод свет снова стал падать параллельным пучком. Как изменился при этом ( уменьшился или увеличился ) фототок насыщения ? Объясните, почему изменяется фототок насыщения , и укажите , какие физические
закономерности Вы использовали для объяснения .