Задачи егэ на объем информации - Помощь в подготовке к экзаменам и поступлению

Документ объёмом 10 Мбайт можно передать с одного компьютера на другой двумя способами:

А)  сжать архиватором, передать архив по каналу связи, распаковать;

Б)  сжать суперархиватором, передать суперархив по каналу связи, распаковать.

Какой способ быстрее и насколько, если

— средняя скорость передачи данных по каналу связи составляет 2²⁰ бит в секунду,

— объём сжатого архиватором документа равен 20% от исходного,

— при использовании архиватора время, требуемое на сжатие документа,  — 18 секунд, на распаковку  — 2 секунды,

— объём сжатого суперархиватором документа равен 10% от исходного,

— при использовании суперархиватора время, требуемое на сжатие документа,  — 26 секунд, на распаковку  — 4 секунды?

В ответе напишите букву А, если способ А быстрее, или Б, если быстрее способ Б. Сразу после буквы напишите, на сколько секунд один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23. Слов «секунд», «сек.», «с.» к ответу добавлять не нужно.

Источник

На уроке рассматривается разбор 8 задания ЕГЭ по информатике про измерение количества информации

8-е задание: «Измерение количества информации»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 4 минуты.

Проверяемые элементы содержания: Знание о методах измерения количества информации

До ЕГЭ 2021 года — это было задание № 10 ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«При использовании способа решения со системой счисления с основанием N следует помнить, что слова в списке нумеруются с единицы, поэтому числу 0 будет соответствовать первое слово»

ФГБНУ «Федеральный институт педагогических измерений»

Содержание:

Объяснение темы
- Измерение количества информации
- Двоичное кодирование сообщений (равновероятностные события)
- Количество различных сообщений в алфавите разной мощности
- Количество сообщений при различном вхождении (встречаемости) букв
- Дополнительные формулы
Тренировочные задания 8 ЕГЭ по информатике и их решение
- Сколько вариантов шифра или кодовых слов
- Перестановка букв в слове (каждая буква 1 раз)
- Сколько существует n-значных чисел, записанных в m-ной системе счисления
- Список в алфавитном порядке
- Вероятность событий

Объяснение темы

Рассмотрим кратко необходимые для решения 8 задания ЕГЭ понятия и формулы.

Измерение количества информации

Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
1 бит – это количество информации, которое можно передать с помощью одного знака в двоичном коде (0 или 1).

1 байт (bytе) = 8 бит
1 Кб (килобайт) = 1024 байта
1 Мб (мегабайт) = 1024 Кб
1 Гб (гигабайт) = 1024 Мб
1 Тб (терабайт) = 1024 Гб
1 Пб (петабайт) = 1024 Тб

8 = 2³
1024 = 2¹⁰

Рассмотрим еще несколько определений:

Алфавит — это набор знаков, используемый в том или ином языке.
Мощность алфавита — это количество используемых в алфавите знаков.

Мощность алфавита

Сообщение — это любая последовательность символов какого-либо алфавита.

Для вычисления количества информации применяются несколько различных формул в зависимости от ситуации:

Двоичное кодирование сообщений (равновероятностные события)

При вычислении количества информации в сообщении для равновероятностных событий, общее количество которых равно N, используется формула:

N = 2^L

N — количество сообщений

L — длиной битов

* следует иметь в виду, что также приняты следующие обозначения: Q = 2^k

Пример 2: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:

Решение:

Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодовых слов (L = 2).

Количество сообщений длиной L битов:

N = 2^L

Т.е. количество сообщений длиной 2 бита, как в примере с нашими буквами, будет равно N = 2² = 4

Ответ: 4

Количество различных сообщений в алфавите разной мощности

Рассмотрим вариант с 5 буквами (мощность алфавита = 5), которые надо разместить в сообщении длиной 2 символа:

Найдем формулу для нахождения количества различных сообщений в алфавите различной мощности:

Если мощность некоторого алфавита составляет N, то количество различных сообщений длиной L знаков:

N – мощность алфавита
L – длина сообщения
Q – количество различных сообщений

Пример: Сколько существует всевозможных трехбуквенных слов в английском языке?

Решение:

В английском алфавите 26 букв. Значит, мощность алфавита = 26. Длина сообщения = 3. Найдем по формуле количество трехбуквенных слов:
Q = 26³
или

= 17576

Ответ: 17576

Таким, образом, если слово состоит из L букв, причем есть n1 вариантов выбора первой буквы, n2 вариантов выбора второй буквы и т.д., то число возможных слов вычисляется как произведение:

N = n1 * n2 * … * nL

Количество сообщений при различном вхождении (встречаемости) букв

В таком случае можно использовать формулу для вычисления числа перестановок с повторениями; для двух разных символов она выглядит так:

[ P = frac{na+n*!}{na!n*!} ]

na – количество букв a

n* — количество звёздочек или кол-во вариантов

Иногда в заданиях 8 можно использовать формулу комбинаторики для проверки полученных результатов перебора. Число сочетаний из n элементов по k элементов:

[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]

I – количество информации в битах

N – количество вариантов

n! = 1 * 2 * 3 * … * n

Пример: Сколько существует всевозможных четырехбуквенных слов в алфавите из 4 букв: А, Б, В, Г, если известно, что буква А встречается ровно два раза?

Решение:

Длина сообщения = 4. Мощность алфавита = 4. Но мешает условие: буква А встречается ровно два раза.
В таких заданиях можно использовать способ перебора всевозможных вариантов:

два раза буква А, на остальных местах - одна из трех оставшихся букв:
А А 3 3     = 3 * 3 = 3² = 9
А 3 А 3     = 9
А 3 3 А     = 9 
3 А А 3     = 9
3 А 3 А     = 9
3 3 А А     = 9

Получили 6 вариантов, каждый из которых равен 9.
Проверим формулой числа сочетаний:

Число сочетаний из n элементов по k элементов:

[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]

В задаче:

[ C{binom{2}{4}}= frac{4!}{2!(4-2)!} = frac{24}{2*2} = 6 ]

* Факториал числа n! = 1 * 2 * 3 *..* n

Т.е. проверка прошла успешно, мы получили 6 вариантов.
Осталось посчитать количество всех сообщений:

6 * 9 = 54

Дополнительные формулы

Количество информации и равновероятные события

При определении количества информации для равновероятностных событий могут понадобиться две формулы:

Формула Шеннона:

x = log₂(1/p)

x — количество информации в сообщении о событии

p — вероятность события

Формула вероятности случайного события:

p(A) = m / n

m — количество благоприятных исходов (число случаев, способствующих событию А)

n — количество общих исходов (общее число равновозможных случаев)

Количество информации и неравновероятные события

При использовании неравновероятного события, вероятность которого равна p, для вычисления количества информации используется формула:

i = -[log₂p]

*квадратные скобки означают ближайшее целое, меньшее или равное значению выражения в скобках

Формула Хартли:

Формула Хартли

I – количество информации в битах

N – количество вариантов

Алфавитный подход:

Информационный объем сообщения длиной L:

Алфавитный подход

N — мощность алфавита

L — длина сообщения

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Сколько вариантов шифра или кодовых слов

Такие задания можно решить программированием.

На языке PascalAbc.net можно использовать язык интегрированных запросов LINQ (Language Integrated Query).

Cartesian(n) — метод расширения последовательности, возвращающий декартову степень множества символов Когда применяется:
Если требуется полный перебор вариантов букв для каждой позиции (каждая буква может встречаться в кодовом слове любое количество раз)

Пример:
Сравним полный перебор букв слова «школа», размещенных на две позиции:

Pascal PascalABC.NET

##
var str:='школа';
foreach var s1 in str do
  foreach var s2 in str do
         print(|s1,s2|)

## // 1 вариант
var str:='школа';
str.cartesian(2).print
 
## // 2 вариант
'школа'.cartesian(2).print
 
### // 3 вариант (спортивное прогр-е)
'школа'.cart(2).print

Результат:

[ш,ш] [ш,к] [ш,о] [ш,л] [ш,а] [к,ш] [к,к] [к,о]
[к,л] [к,а] [о,ш] [о,к] [о,о] [о,л] [о,а] [л,ш]
[л,к] [л,о] [л,л] [л,а] [а,ш] [а,к] [а,о] [а,л] [а,а]

Итого 25 штук (5*5)

[ш,ш] [ш,к] [ш,о] [ш,л] [ш,а] [к,ш] [к,к] [к,о]
[к,л] [к,а] [о,ш] [о,к] [о,о] [о,л] [о,а] [л,ш]
[л,к] [л,о] [л,л] [л,а] [а,ш] [а,к] [а,о] [а,л] [а,а]

Permutations — метод возвращает все перестановки множества элементов, заданного массивом или последовательностью Когда применяется:
Если требуется перестановка букв в слове. То есть количество каждой буквы в словах сохраняется, и каждая буква встречается только 1 раз

Пример:
Сравним перестановку букв слова «мимикрия»:

Pascal PascalABC.NET

## // 1 вариант
 'мимикрия'.Permutations
  // собираем в строку:
  // к строкам можно distinct применять, а к массивам - нет
 .Select(w->w.JoinToString('')) 
 .Distinct  // выбираем уникальные, т.к. от перестановки двух букв "м" 
            // и букв "и" слово не меняется
 .Count.Print

1	## // 2 вариант

### // 3 вариант (спортивное прогр-е)
'мимикрия'.Prm
 .Sel(w->w.ToS('')) 
 .Dst  
 .Cnt.Pr

Результат:

[М,И,М,И,К,Р,И,Я] [М,И,М,И,К,Р,Я,И] [М,И,М,И,К,И,Р,Я] [М,И,М,И,К,И,Я,Р] [М,И,М,И,К,Я,Р,И] [М,И,М,И,К,Я,И,Р] [М,И,М,И,Р,К,И,Я] [М,И,М,И,Р,К,Я,И]
…

Используются также следующие запросы и методы LINQ:

Фильтрация последовательностей (Where)
Метод Count([Type -> boolean]) Вычисление скаляра
Метод CountOf(s: Type) — Возвращает количество элементов, равных указанному значению
Метод First() — Возвращает первый элемент последовательности.
Метод Last() — Возвращает последний элемент последовательности.
Метод Pairwise(Self: sequence of T; func: (T,T)->Res) — Превращает последовательность в последовательность пар соседних элементов, применяет func к каждой паре полученных элементов и получает новую последовательность

8_1:

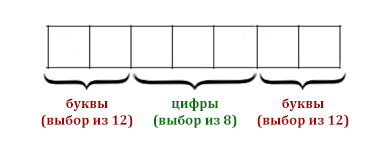
Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 6.

Сколько различных вариантов шифра можно задать, если известно, что цифра 1 должна встречаться в коде ровно 1 раз, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?

Типовые задания для тренировки

✍ Решение:

✎ Решение теоретическое:

Формула нахождения количества различных сообщений:

Q = N^L

Итак, что у нас дано из этой формулы:
Длина сообщения (L) = 5 символов
Мощность алфавита (N) = 6 (цифры от 1 до 6).
Но так как цифра 1 встречается по условию ровно один раз, а остальные 5 цифр — любое количество раз, то будем считать, что N = 5 (цифры от 2 до 6, исключая 1). Т.е. возьмем вариант, когда 1 стоит на первом месте, а остальные 5 цифр размещаем на 4 позиции:

1 5 5 5 5 - 1 * Q = 5⁴ = 625

✎ 1 способ. Найдем количество вариантов методом перебора:

Методом перебора найдем количество вариантов размещения:

1 5 5 5 5 - 1 * Q=5⁴ = 625
5 1 5 5 5 - 1 * Q=5⁴ = 625
5 5 1 5 5 - 1 * Q=5⁴ = 625
5 5 5 1 5 - 1 * Q=5⁴ = 625
5 5 5 5 1 - 1 * Q=5⁴ = 625

получили 5 вариантов;

✎ 2 способ. Найдем количество вариантов при помощи формулы комбинаторики:

[ C{binom{4}{5}}= frac{5!}{4!(5-4)!} = 5 ]

получили 5 вариантов;
В итоге получим:

625 * 5 = 3125

Результат: 3125

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := '123456';
  foreach var s1 in str do
    foreach var s2 in str do
      foreach var s3 in str do
        foreach var s4 in str do
          foreach var s5 in str do
          begin
            if (s1 + s2 + s3 + s4 + s5).CountOf('1') = 1 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='123456'.Cartesian(5) 
.where(w->w.countOf('1')=1)// кол-во '1' в слове
.count.print

Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='123456'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
        for s5 in str:
          if (s1+s2+s3+s4+s5).count('1')==1:
            n+=1
print(n)

С++:

Детальный теоретический разбор задания 8 ЕГЭ по информатике предлагаем посмотреть в видеоуроке:

📹 YouTube здесьздесь (теоретическое решение)

8_2:

Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является либо буквой (A или B) или цифрой (1, 2 или 3).

Сколько различных вариантов шифра можно задать, если известно, что в коде присутствует ровно одна буква, а все другие символы являются цифрами?

✍ Решение:

✎ Решение теоретическое:

Формула нахождения количества различных сообщений:

Q = N^L

Посчитаем количество возможных шифров для одного из вариантов (например, когда буквы находятся на первой позиции). Так как цифры (1, 2, 3) могут занимать 4 позиции из пяти, а две буквы (А и В) одну из позиций, значит:

Q = 2 * 3⁴ = 162

Имеем 162 вариантов шифра для слова, в котором буквы могут стоять на первой позиции:

AB  123 123 123 123 = 162

Получим все варианты размещения:

"2" означает одна из двух букв: А или B, "3" - одна из трех цифр:

2 3 3 3 3 -> Q = 2 * 3⁴ = 162
3 2 3 3 3 -> Q = 2 * 3⁴ = 162
3 3 2 3 3 -> Q = 2 * 3⁴ = 162
3 3 3 2 3 -> Q = 2 * 3⁴ = 162
3 3 3 3 2 -> Q = 2 * 3⁴ = 162

Получили 5 вариантов с размещением букв А и B.
Осталось умножить:

5 * 162 = 810

Результат: 810

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'AB123';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5];
            if (res.CountOf('A') = 1) and (res.CountOf('B') = 0) 
            or (res.CountOf('B') = 1) and (res.CountOf('A') = 0) then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='АВ123'.Cartesian(5) 
.where(w->w.count(letter -> letter in 'АВ')=1)// кол-во букв в слове
.count.print

Cartesian(5) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 5-знаковых слов из заданных символов

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='AB123'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
        for s5 in str:
          if ((s1+s2+s3+s4+s5).count('A')==1 and (s1+s2+s3+s4+s5).count('B')==0) 
          or ((s1+s2+s3+s4+s5).count('B')==1 and (s1+s2+s3+s4+s5).count('A')==0):
            n+=1
print(n)

С++:

Подробное теоретическое решение данного задания предлагаем посмотреть на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_3:

Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 4-буквенные слова, в которых есть только буквы A, Б, В, Г, Д и Е, причём буква Г появляется ровно 1 раз и только на первом или последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.

Сколько различных кодовых слов может использовать Олег?

✍ Решение:

✎ Решение теоретическое:

Вспомним формулу получения количества возможных вариантов слов:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
Рассмотрим варианты, когда буква Г встречается на первом или последнем месте:

Г ? ? ? = 1 * 5 * 5 * 5 = 5³ = 125 
? ? ? Г = 5 * 5 * 5 * 1 = 5³ = 125

Вместо знаков ? может стоять одна из пяти букв (А, Б, В, Д, Е), т.к. буква Г там стоять не может
Теперь суммируем количество найденных вариантов:

125 + 125 = 250

Результат: 250

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'АБВГДЕ';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4];
            if (res[1]='Г') and (res[2]<>'Г') and (res[3]<>'Г') and (res[4]<>'Г')
            or (res[1]<>'Г') and (res[2]<>'Г') and (res[3]<>'Г') and (res[4]='Г') then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='АБВГДЕ'.Cartesian(4)
.where(w->(w.countOf('Г')=1)and((w.First='Г')or(w.Last='Г'))) // или: 
// .where(w->(w.countOf('Г')=1)and(w[1]<>'Г')and(w[2]<>'Г'))
.count.print

Cartesian(4) — метод расширения последовательности, возвращающий декартову степень множества символов, т.е. в нашем случае перебор 4-знаковых слов из заданных символов

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='АБВГДЕ'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
        if (s1 =='Г') and (s2!='Г') and (s3!='Г') and (s4!='Г') 
        or (s1 !='Г') and (s2!='Г') and (s3!='Г') and (s4=='Г'):
            n+=1
print(n)

С++:

Видеоразбор данного задания (теоретический способ):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_4:

Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является одной из букв X, Y или Z.

Сколько различных вариантов шифра можно задать, если известно, что буква X должна встречаться в коде ровно 2 раза, а каждая из других допустимых букв может встречаться в шифре любое количество раз или не встречаться совсем?

Типовые задания для тренировки

✍ Решение:

✎ Решение теоретическое:

Формула нахождения количества различных сообщений:

Q = N^L

Итак, что у нас дано из этой формулы:
Начальная мощность алфавита (N) = 3 (буквы X, Y, Z). Но так как буква X встречается ровно два раза, то мы ее рассмотрим отдельно, а остальные 2 буквы — встречаются любое количество раз, значит, будем считать, что:

N = 3 - 1 = 2 (Y и Z)

Исходя из предыдущего пункта, длина сообщения тоже сократится:

(L) = 5 - 2 = 3 символа (остальные два символа отведем на размещение X)

Количество различных сообщений (вариантов шифра) = Q = ?
Т.е. для одного варианта размещения (для одного варианта шифра) имеем:

X X ? ? ? -> 1² * Q = 2³ = 8

Согласно условию получим следующие варианты размещения:

✎1 способ. Перебор всех вариантов:

X X ? ? ? - 1² * Q = 2³ = 8
X ? X ? ? - 1² * Q = 2³ = 8
X ? ? X ? - 1² * Q = 2³ = 8
X ? ? ? X - 1² * Q = 2³ = 8
? X X ? ? - 1² * Q = 2³ = 8
? X ? X ? - 1² * Q = 2³ = 8
? X ? ? X - 1² * Q = 2³ = 8
? ? X X ? - 1² * Q = 2³ = 8
? ? X ? X - 1² * Q = 2³ = 8
? ? ? X X - 1² * Q = 2³ = 8

✎ 2 способ. При помощи формулы поиска числа сочетаний:

[ C{binom{k}{n}}= frac{n!}{k!(n-k)!} ]

Число сочетаний из n элементов по k элементов:

[ C{binom{2}{5}}= frac{5!}{2!(5-2)!} = frac{120}{12} = 10 ]

* Факториал числа: n! = 1 * 2 * 3 * .. * n

Количество вариантов найдено верно, т.к. результат обоих способов = 10. В итоге получаем:

8 * 10 = 80

* задание достаточно решить одним из способов!

Результат: 80

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'xyz';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5];
            if res.countOf('x') = 2 then // или if res.Count(y -> y = 'x') = 2 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='XYZ'.Cartesian(5)
.where(w->w.countOf('X')=2)
.count.print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='xyz'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
        for s5 in str:
          if (s1+s2+s3+s4+s5).count('x') == 2:
            n+=1
print(n)

С++:

Детальный теоретический разбор задания 8 ЕГЭ по информатике теоретическим способом предлагаем посмотреть в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_5:

Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв ОСЕНЬ? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

Типовые задания для тренировки

✍ Решение:

✎ Решение теоретическое:

Из букв слова ОСЕНЬ имеем 2 гласных буквы (О, Е) и 2 согласных буквы (С, Н). Буква мягкий знак «нейтральна».
Подсчитаем количество букв на каждой из 5 позиций:

2   5   5   5   2
^{СН   все  все  все   ОЕ}

Вспомним формулу получения количества возможных вариантов слов:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
Т.е. количество вариантов равно произведению полученных чисел:

N = 2 * 5 * 5 * 5 * 2 = 500

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'ОСЕНЬ';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5];
            if ((res[1] = 'С') or (res[1] = 'Н')) and ((res[5] = 'О') or (res[5] = 'Е')) then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

1	'ОСЕНЬ'.Cartesian(5).Where(w->w[0] in 'СН').Where(w->w[4] in 'ОЕ').Count.Print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

str = 'ОСЕНЬ'
n = 0
for s1 in str:
    for s2 in str: 
        for s3 in str:
            for s4 in str:
                for s5 in str:
                    res = s1 + s2 + s3 + s4
                    if (s1 == 'С' or s1 == 'Н') and (s5 == 'О' or s5 == 'Е'):
                        n += 1
print(n)

С++:

Результат: 500

Разбор можно также посмотреть на видео (теоретическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_6:

Вася составляет 4-буквенные слова, в которых есть только буквы Л, Е, Т, О, причём буква Е используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.

✍ Решение:

✎ Решение теоретическое:

✎ 1 способ:

Количество вариантов различных слов вычислим по формуле:

N = n1 * n2 * n3 * …
где

n1 — количество вариантов выбора первой буквы и т.п.
Рассмотрим все варианты расположения буквы Е:

1. Е ? ? ? или 
2. ? Е ? ? или 
3. ? ? Е ? или
4. ? ? ? Е 

Где вопросительный знак означает любую букву из Л, Е, Т, О.

Подсчитаем по формуле количество слов для варианта 1:

Е ? ? ? = 1 * 4 * 4 * 4 = 64

т.е. на первой позиции - только 1 буква - Е, на каждой последующей - одна из четырех букв Л, Е, Т, О.

Подсчитаем по формуле количество слов для варианта 2; учтем, что на первой позиции букву Е мы уже посчитали для первого варианта!:

? Е ? ? = 3 * 1 * 4 * 4 = 48

Подсчитаем по формуле количество слов для варианта 3; учтем, что на первой и второй позициях букву Е мы уже посчитали в предыдущих вариантах!:

? ? Е ? = 3 * 3 * 1 * 4 = 36

Подсчитаем по формуле количество слов для варианта 4; учтем, что на первой, второй и третьей позициях букву Е мы уже посчитали в предыдущих вариантах:

? ? ? Е = 3 * 3 * 3 * 1 = 27

Поскольку у нас каждый вариант связан операцией логическое ИЛИ, то теперь суммируем все варианты:

64 + 48 + 36 + 27 = 175

Результат: 175
✎ 2 способ:

Так как по условию буква Е встретится хотя бы 1 раз, значит, можно утверждать, что не может быть такого, чтобы буква Е не встретилась бы ни одного раза.
Таким образом, рассчитаем случай, когда буква Е встречается все 4 раза (т.е. все случаи) и отнимем от результата невозможный случай: когда буква Е не встретится ни одного раза:

1. Буква Е используется 4 раза (т.е. на всех позициях):
4 * 4 * 4 * 4 = 256

2. Буква Е не используется совсем (т.е. только 3 буквы):
3 * 3 * 3 * 3 = 81

Вычтем из первого варианта невозможный вариант № 2:

256 - 81 = 175

Результат: 175

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'ЛЕТО';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4];
            if res.countOf('Е') >= 1 then // или if res.Count(y -> y = 'Е') >= 1 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

1 2	## var d:='лето'.Cartesian(4).where(w->w.countOf('е')>=1).count.print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

n=0
str='ЛЕТО'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
          if (s1+s2+s3+s4).count('Е') >= 1:
            n+=1
print(n)

С++:

Теоретическое решение задания 8 смотрите в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_7:

Вася составляет 4-буквенные слова, в которых есть только буквы К, А, Т, Е, Р, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.

✍ Решение:

✎ Решение теоретическое:

Количество возможных вариантов слов вычислим по формуле:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы, n2 — количество вариантов выбора второй буквы и т.п.
Сначала по формуле получим все варианты для всех пяти букв, включая букву Р:

5 * 5 * 5 * 5 = 5⁴ = 625

Из общего количества вариантов нам необходимо исключить те варианты, где Р не встречается вообще и Р встречается только 1 раз. Найдем их последовательно:
1. Буква Р не встречается совсем:

4 * 4 * 4 * 4 = 4⁴ = 256

2. Буква Р встречается только один раз:

р ? ? ? = 1 * 4 * 4 * 4 = 4³
? р ? ? = 4 * 1 * 4 * 4 = 4³
? ? р ? = 4 * 4 * 1 * 4 = 4³
? ? ? р = 4 * 4 * 4 * 1 = 4³

Получим  4³ * 4 = 256

Теперь вычтем из общего количества найденные варианты (№ 1 и № 2):

625 - 256 - 256 = 113

✎ Решение с использованием программирования:

PascalABC.net (традиционный):

begin
  var n := 0;
  var str := 'КАТЕР';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4];
            if res.CountOf('Р') >= 2 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (LINQ):

1 2	## var d:='катер'.Cartesian(4).where(w->w.countOf('р')>=2).count.print

Python:

n=0
str='КАТЕР'
for s1 in str:
  for s2 in str:
    for s3 in str:
      for s4 in str:
          if (s1+s2+s3+s4).count('Р') >= 2:
            n+=1
print(n)

С++:

Результат: 113

Теоретическое решение 8 задания предлагаем посмотреть в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_8:

Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 5-буквенные слова, в которых есть только буквы A, Б, В, и Г, причём буква Г появляется не более одного раза и только на последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем.

Сколько различных кодовых слов может использовать Олег?

✍ Решение:

✎ Решение теоретическое:

Вспомним формулу получения количества возможных вариантов слов:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы,
n2 — количество вариантов выбора второй буквы и т.п.
Так как буква Г появляется не более одного раза и только на последнем месте, значит, она может либо появиться 1 раз на последнем месте, либо не появиться совсем.
Рассмотрим варианты, когда буква Г встречается 1 раз на последнем месте и встречается 0 раз:

1 раз: ? ? ? ? Г = 3 * 3 * 3 * 3 * 1 = 3⁴ = 81 
0 раз: ? ? ? ? ? = 3 * 3 * 3 * 3 * 3 = 3⁵ = 243

Вместо знаков ? может стоять одна из трех букв (А, Б, В), т.к. буква Г там стоять не может
Теперь суммируем количество найденных вариантов:

81 + 243 = 324

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'АБВГ';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s4];
            if (res[1]<>'Г') and (res[2]<>'Г')and (res[3]<>'Г') and (res[4]<>'Г') then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='абвг'.Cartesian(5)
.where(w->(w.countOf('г')<=1)and(w[0]<>'г')and(w[1]<>'г')and(w[2]<>'г')
     and(w[3]<>'г')).count.print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

Результат: 324

8_9:

Вася составляет 4-буквенные слова, в которых есть только буквы К, О, М, А, Р, причём буква А используется в них не более 3-х раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, необязательно осмысленная.

✍ Решение:

✎ Решение теоретическое:

Вспомним формулу получения количества возможных вариантов слов:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы,
n2 — количество вариантов выбора второй буквы и т.п.
Так как буква А по условию используется не более 3-х раз, это значит, что она используется либо 3 раза, либо 2 раза, либо 1 раз, либо не используется совсем. Рассмотрим все эти варианты отдельно.
1. Буква А используется 3 раза:

А А А _  -> 1 * 1 * 1 * 4 = 4
А А _ А  -> 1 * 1 * 4 * А = 4
А _ А А  -> 1 * 4 * 1 * 1 = 4
_ А А А  -> 4 * 1 * 1 * 1 = 4

Итого получаем 4 варианта, в которых вместо символа _ может быть любая из 4 букв: К О М Р. Значит, имеем:

 4 * 4 = 16 вариантов

2. Буква А используется 2 раза:

А А _ _  -> 1 * 1 * 4 * 4 = 16
А _ А _  -> 1 * 4 * 1 * 4 = 16
А _ _ А  -> 1 * 4 * 4 * 1 = 16
_ А А _  -> 4 * 1 * 1 * 4 = 16
_ А _ А  -> 4 * 1 * 4 * 1 = 16
_ _ А А  -> 4 * 4 * 1 * 1 = 16

Итого получаем 6 вариантов, в которых вместо символа _ может быть любая из 4 букв: К О М Р. Значит имеем:

 16 * 6 = 96 вариантов

3. Буква А используется 1 раз:

А _ _ _  -> 1 * 4 * 4 * 4 = 64
_ А _ _  -> = 64
_ _ А _  -> = 64
_ _ _ А  -> = 64

Итого имеем:

64 * 4 = 256 вариантов

Буква А используется 0 раз:

_ _ _ _ -> 4⁴ = 256

Суммируем результаты всех трех случаев:

16 + 96 + 256 + 256 = 624

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'КОМАР';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          begin
            var res := str[s1] + str[s2] + str[s3] + str[s4];
            if res.CountOf('А') <=3 then
              n += 1;
          end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

1
2
3

##
var d:='комар'.Cartesian(4)
.where(w->w.countOf('а')<=3).count.print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

str = 'КОМАР'
n = 0
for s1 in str:
    for s2 in str: 
        for s3 in str:
            for s4 in str:
                res = s1 + s2 + s3 + s4
                if res.count('А')<=3:
                    n += 1
print(n)

С++:

Результат: 624

Теоретическое решение смотрите также на видео:

📹 YouTube здесьздесь (теоретическое решение)

8_10:

Сколько существует различных символьных последовательностей длины 3 в четырёхбуквенном алфавите {A,B,C,D}, если известно, что одним из соседей A обязательно является D, а буквы B и C никогда не соседствуют друг с другом?

✍ Решение:

✎ Решение теоретическое:

Вспомним формулу получения количества возможных вариантов слов:

N = n1 * n2 * n3 * … * nL = n^L

где n1 — количество вариантов выбора первой буквы,
n2 — количество вариантов выбора второй буквы и т.п.
Будем рассматривать варианты, расставляя каждую букву последовательно по алфавиту, начиная с первой буквы. При этом будем учитывать указанные ограничения для букв А, B и С:

Начинаем с A: A D 4_ABCD = 1 * 1 * 4 = 4 
Начинаем с B: B A D, B B 2_BD, B D 4_ABCD = 7
Начинаем с C: C A D, C C 2_CD, C D 4_ABCD = 7
Начинаем с D: D A 3_BCD, D B 2_BD, D C 2_CD, D D 4_ABCD = 11

Теперь суммируем количество найденных вариантов:

4 + 7 + 7 + 11 = 29

Результат: 29

Видеоурок демонстрирует подробное теоретическое решение задания:

📹 YouTube здесьздесь (теоретическое решение)

8_22:

Лена составляет 5-буквенные слова из букв Я, С, Н, О, В, И, Д, Е, Ц, причём слово должно начинаться с согласной и заканчиваться гласной. Первая и последняя буквы слова встречаются в нем только один раз; остальные буквы могут повторяться.

Сколько слов может составить Лена?

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='ясновидец'.Cartesian(5) 
.where(l->(l[0] in 'снвдц') and (l[4] in 'яоие'))// учитываем гласные и согласные
.where(l->(l.countOf(l[0])=1)and(l.countOf(l[4])=1))//учитываем, что они не повторяются
.count.print

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var str := 'ЯСНОВИДЕЦ';
  var n := 0;
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
          begin
            var slovo := str[s1] + str[s2] + str[s3] + str[s4] + str[s5];
            if (slovo[1] in 'СНВДЦ') and (slovo[5] in 'ЯОИЕ') then
              if (slovo[1] <> slovo[2]) and (slovo[1] <> slovo[3]) and (slovo[1] <> slovo[4])            
              and (slovo[1] <> slovo[5]) and (slovo[5] <> slovo[1]) and (slovo[5] <> slovo[2]) 
              and (slovo[5] <> slovo[3]) and (slovo[5] <> slovo[4]) then
              begin
                n += 1
              end;
          end;
  print(n)
end.

Python:

С++:

Результат: 6860

Использование метода Pairwise()

8_11:

Из букв С, Р, Е, Д, А составляются трехбуквенные комбинации по следующему правилу – в комбинации не может быть подряд идущих гласных и одинаковых букв.

Например, комбинации ААР или ЕСС не являются допустимыми.

Сколько всего комбинаций можно составить, используя это правило?

✍ Решение:

✎ Решение теоретическое:

Рассмотрим два варианта: когда слово начинается с гласной буквы, и когда оно начинается с согласной.

1. С гласной:

1.1
2 3 2 = 2 * 3 * 2 = 12
^{гл с  с}

1.2
2 3 2 = 2 * 3 * 2 = 12
^{гл с гл}

2. С согласной:

2.1
3  2  2 = 3 * 2 * 2 = 12
с  с  с

2.2
3  2  3 = 3 * 2 * 3 = 18
с гл  с

2.3
3  2  2 = 3 * 2 * 2 = 12
с  с  гл

Подсчитаем общее количество вариантов:

12 + 12 + 12 + 18 + 12 = 66

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

### 
'среда'.cart(3)// 
 .Select(w -> w.JoinToString('')) // собираем в строку;
 .where(w->w.Pairwise.All((a,b) -> a+b not in 'еае'))
 .where(w->w.Pairwise.All((a,b) -> a<>b))
 .count.print

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'СРЕДА';
  var glas := 'ЕА';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
      begin
        var res := str[s1] + str[s2] + str[s3];
        // условие для подряд идущих гласных
        if not ((res[1] in glas) and (res[2] in glas) or
           (res[2] in glas) and (res[3] in glas)) then
        // условие для подряд идущих одинаковых букв
          if not ((res[1] = res[2]) or (res[2] = res[3])) then
            n += 1;
      end;
  print(n)
end.

Python:

str = 'СРЕДА'
glas = 'ЕА'
n = 0
for s1 in str:
    for s2 in str: 
        for s3 in str:
            res = s1 + s2 + s3 
            if not (s1 in glas and s2 in glas or
           s2 in glas and s3 in glas) :
                if not (s1 == s2 or s2 == s3) :
                    n += 1
print(n)

С++:

Результат: 66

Перестановка букв в слове (каждая буква 1 раз)

8_12:

Дано слово КОРАБЛИКИ. Таня решила составлять новые 5-буквенные слова из букв этого слова по следующим правилам:
1) слово начинается с гласной буквы;
2) гласные и согласные буквы в слове должны чередоваться;
3) буквы в слове не должны повторяться.

✍ Решение:

✎ Решение теоретическое:

Учтем, что в слове КОРАБЛИКИ две буквы К и две И.
Всего в слове 4 гласных, но поскольку две буквы И, то необходимо считать только 3 гласных.
Всего в слове 5 согласных, однако две из них — буквы К, поэтому считать следует 4 согласных.
Посчитаем количество согласных и гласных для каждой из 5 позиций слова, учитывая, что с каждой последующей буквой количество используемых гласных/согласных уменьшается. Под позициями приведем пример букв:

гл   с   гл   с   гл  
3    4    2   3    1
^{оаи   крбл   оа   крб    и}

Количество слов вычисляется как произведение полученных чисел:

3 * 4 * 2 * 3 * 1 = 72

Результат: 72

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

###
'кораблики'
.Cart(5)
.select(w->w.JoinToString(''))
.Distinct //Обязательно!
.where(w-> w.First in 'оаи')
.where(w->w.Pairwise.All((a,b)->not ((a in 'оаи') and (b in 'оаи')) 
       and not( ( a in'крбл') and (b in 'крбл' ))))
.where(w->'корабли'.All(c->w.countOf(c)<=1))
.count.print

Python:

С++:

Результат: 72

8_21:

Ксюша составляет слова, меняя местами буквы в слове МИМИКРИЯ.
Сколько различных слов, включая исходное, может составить Ксюша?

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var str := 'МИМИКРИЯ';
  var set1: set of string;
  set1 := [];
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do 
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do 
          for var s5 := 1 to length(str) do  
            for var s6 := 1 to length(str) do
              for var s7 := 1 to length(str) do  
                for var s8 := 1 to length(str) do 
                begin
                  var slovo := str[s1] + str[s2] + str[s3] + str[s4] + str[s5] + str[s6] + str[s7] + str[s8];
                  if (slovo.CountOf('М') = 2) and (slovo.CountOf('И') = 3)
                  and (slovo.CountOf('К') = 1)
                  and (slovo.CountOf('Р') = 1)
                  and (slovo.CountOf('Я') = 1) then
                    include(set1, slovo);
                end;
  print(set1.count);
end.

Смысл решения в использовании типа множества (set). При добавлении новых элементов к множеству исключаются повторения.

PascalABC.net (использование LINQ, быстрое решение):

### 
 'МИМИКРИЯ'.Permutations // перестановки букв
 .Select(w->w.JoinToString('')) // собираем в строку
 .Distinct  // выбираем уникальные
 .Count.Print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

Ответ: 3360

Подробное решение программным способом смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (программное решение)

8_19:

Петя составляет шестибуквенные слова

перестановкой букв

слова АДЖИКА. При этом он избегает слов с двумя подряд одинаковыми буквами. Сколько всего различных слов может составить Петя?

Типовые задания для тренировки

✍ Решение:

✎ Решение теоретическое:

Посчитаем количество слов без двух подряд одинаковых букв. Будем считать относительно буквы А, которых две в заданном слове АДЖИКА. Буквы не могут повторяться, поэтому их кол-во в каждом варианте будет уменьшается:

А*А*** = 4*3*2*1 = 24 слова с данным расположением буквы А. 
А**А** = 4*3*2*1 = 24
А***А* = 4*3*2*1
А****А = ...
*А*А**
*А**А*
*А***А
**А*А*
**А**А
***А*А

Получили 10 вариантов, и в каждом из них можно составить по 24 слова.
Таким образом, получим общее количество слов:

10 * 24 = 240

✎ Решение с использованием программирования:

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var s: set of string;
  s := [];
  var str := 'АДЖИКА';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
            for var s6 := 1 to length(str) do
            begin
              var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5] + str[s6];
              if (res.CountOf('А') = 2) and (res.CountOf('Д') = 1) 
                  and (res.CountOf('Ж') = 1) and (res.CountOf('И') = 1) 
                  and (res.CountOf('К') = 1) then
                     if (res[1] <> res[2]) and (res[2] <> res[3]) and (res[3] <> res[4]) 
                        and (res[4] <> res[5]) and (res[5] <> res[6]) then
                           include(s, res);
            end;
  print(s.count)
end.

Смысл решения в использовании типа — множества (set). При добавлении новых элементов к множеству исключаются повторения.

PascalABC.net (использование LINQ, быстрое решение):

### 
'аджика'.Permutations
 .Select(w -> w.JoinToString('')) // собираем в строку;
 .distinct // исключаем дубли
 .where(s -> not ('аа' in s)) // исключаем две подряд буквы 'а'
  // или так: .where(w->w.Pairwise.All((a,b) -> a<>b))
 .count.pr

Python:

С++:

Ответ: 240

8_20:

Маша составляет 7-буквенные коды из букв В, Е, Н, Т, И, Л, Ь. Каждую букву нужно использовать

ровно 1 раз

, при этом код буква Ь не может стоять на последнем месте и между гласными. Сколько различных кодов может составить Маша?

Типовые задания для тренировки

✍ Решение:

✎ Решение теоретическое:

Выполним задание следующим образом: 1. посчитаем общее количество слов, не учитывая никакие ограничения. 2. Затем посчитаем случаи, которые необходимо исключить. 3. Вычтем из результата пункта 1 результат пункта 2.
Общее количество независимо от ограничений (учтем, что буквы не должны повторяться):

7 6 5 4 3 2 1 - количество возможных вариантов букв на семи позициях

ИТОГО:
7! = 5040 слов

Посчитаем варианты, которые необходимо исключить. Их будет несколько:
а) буква ь — на последнем месте:

6 5 4 3 2 1 Ь = 6! = 720

б) буква ь — между гласными:

И Ь Е 4 3 2 1  = 24 варианта
Так как буквы смещаются по всем позициям, то получим (4 И Ь Е 3 2 1, ...):
24 * 5 = 120
Е Ь И 4 3 2 1  = 24 варианта
24 * 5 = 120

Посчитаем количество слов, согласно условию задачи:

5040 - 720 - 120 - 120 = 4080

✎ Решение с использованием программирования:
Стоит заметить, что теоретическое решение занимает меньше времени, чем программный способ!

PascalABC.net (приближенный к традиционному, долгое решение):

begin
  var n := 0;
  var str := 'ВЕНТИЛЬ';
  var glas := 'ЕИ';
  for var s1 := 1 to length(str) do
    for var s2 := 1 to length(str) do
      for var s3 := 1 to length(str) do
        for var s4 := 1 to length(str) do
          for var s5 := 1 to length(str) do
            for var s6 := 1 to length(str) do
              for var s7 := 1 to length(str) do
              begin
                var res := str[s1] + str[s2] + str[s3] + str[s4] + str[s5] + str[s6] + str[s7];
                if (res.CountOf('В') = 1) and (res.CountOf('Е') = 1) 
                    and (res.CountOf('Н') = 1) and (res.CountOf('Т') = 1) 
                    and (res.CountOf('И') = 1) and (res.CountOf('Л') = 1)
                    and (res.CountOf('Ь') = 1) then
                  if not (res[7] = 'Ь') then
                    if not ((res[1] in glas) and (res[3] in glas) and (res[2] = 'Ь') or
                        (res[2] in glas) and (res[4] in glas) and (res[3] = 'Ь') or
                        (res[3] in glas) and (res[5] in glas) and (res[4] = 'Ь') or
                        (res[4] in glas) and (res[6] in glas) and (res[5] = 'Ь') or
                        (res[5] in glas) and (res[7] in glas) and (res[6] = 'Ь')) then
                      n += 1
              end;
  print(n)
end.

PascalABC.net (использование LINQ, быстрое решение):

### 
'вентиль'.Permutations// здесь можно без distinct, т.к. буквы не повторяются
 .Select(w -> w.JoinToString('')) // собираем в строку
 .where(s -> not ('еьи' in s) and not ('иье' in s) and (s.last <> 'ь'))
.Count.Print

Python:

С++:

Ответ: 4080

8_23:

Артур составляет 6-буквенные коды перестановкой букв слова ВОРОТА. При этом нельзя ставить рядом две гласные.
Сколько различных кодов может составить Артур?

✍ Решение:

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, спортивное прогр-е):

###
'ВОРОТА'.prm
.Sel(w->w.ToS('')).dst
.Wh(w-> not w.Pairwise.Any((a,b)->a+b in 'АООАА'))
.Cnt.pr

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

Ответ: 72

Сколько существует n-значных чисел, записанных в m-ной системе счисления

8_18: Объяснение 8 задания экзамена ЕГЭ 2020 г. (со слов учащегося):

Сколько существует восьмизначных чисел, записанных в восьмеричной системе счисления, в которых все цифры различны и рядом не могут стоять 2 чётные или 2 нечётные цифры?

Типовые задания для тренировки

✍ Решение:

✎ Решение теоретическое:

Выпишем все четные и нечетные цифры, которые могут использоваться в 8-й с.с.:

четные: 0, 2, 4, 6 - итого 4 цифры
нечетные: 1, 3, 5, 7 - итого 4 цифры

Рассмотрим два случая построения числа по заданию: 1) начиная с четной цифры и 2) начиная с нечетной цифры. Изобразим схематично числа, указывая сверху возможное количество цифр на разряд:

1) с четной цифры:
3  4  3  3  2  2  1  1 = 3*4*3*3*2*2*1*1 = 432
ч  н  ч  н  ч  н  ч  н

Самый старший разряд не может быть равен 0 (поэтому 3 цифры из 4 возможных), так как разряд просто потеряется, и число станет семизначным). Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.

2) с нечетной цифры:
4  4  3  3  2  2  1  1 = 4*4*3*3*2*2*1*1 = 576
н  ч  н  ч  н  ч  н  ч

Каждый последующий разряд включает на одну цифру меньше, так как по заданию цифры не могут повторяться.

Сложим количество вариантов в обеих случаях:

432 + 576 = 1008

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

###
'01234567'.Permutations // т.к. цифр итак 8 штук
.where(w->w.First<>'0') // первая цифра не может быть 0
.where(w->w.Pairwise.All((a,b)-> (a.ToDigit + b.ToDigit).IsOdd)) // проверка пар четных и нечетных
.count.print

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

Ответ: 1008

Список в алфавитном порядке

8_13:

Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Ниже приведено начало списка:

1. ААААА
2. ААААО
3. ААААУ
4. АААОА
…

Запишите слово, которое стоит под номером 242 от начала списка.

✍ Решение:

✎ Решение теоретическое:

Данное задание лучше решать следующим образом. Подставим вместо букв цифры (А -> 0, О -> 1, У -> 2):

Видим, что каждая последующее число получается путем прибавления в столбик единицы к предыдущему числу. В троичной системе счисления! Т.к. цифр всего три.
Порядковый номер, написанный рядом с пунктом, всегда на единицу больше располагающейся рядом цифры в троичной системе счисления.
Значит, пункту под номером 242 будет соответствовать число 241 в троичной системе счисления.
Переведем 241 в 3-ю систему делением на 3:

        ^{остатки}
241 | 3 | 1
 80 | 3 | 2
 26 | 3 | 2
  8 | 3 | 2
  2 |   |

Перепишем остатки снизу вверх: 22221, им соответствуют буквы УУУУО

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

##
var d:='АОУ'.Order // сортируем по алфавиту
.Cartesian(5)
.Numerate.print

Смотрим слова и находим по номеру нужное слово:

… (241,[У,У,У,У,А]) (242,[У,У,У,У,О]) (243,[У,У,У,У,У])

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

Результат: УУУУО

Подробное решение теоретическим способом смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_14: 8 задание. Демоверсия ЕГЭ 2018 информатика:

Все 4-буквенные слова, составленные из букв Д, Е, К, О, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.

1. ДДДД
2. ДДДЕ
3. ДДДК
4. ДДДО
5. ДДДР
6. ДДЕД
…

Под каким номером в списке идёт первое слово, которое начинается с буквы K?

✍ Решение:

✎ Решение теоретическое:

Подставим вместо букв цифры (Д -> 0, Е -> 1, К -> 2, О -> 3, Р -> 4):

Видим, что каждое последующее число получается путем прибавления единицы в столбик к предыдущему (в пятеричной системе счисления! т.к. цифр всего пять).
Порядковый номер, написанный рядом с пунктом, всегда на единицу больше располагающейся рядом цифры в пятеричной системе счисления.
Определим число, которое получится, если мы в начале слова поставим букву К (остальные должны остаться нулями, т.к. числа идут по порядку, а нам необходимо первое, начинающееся с К):

K -> 2 -> 2000

Полученное число — 2000 — необходимо перевести из пятеричной системы счисления в десятичную, чтобы узнать порядковый номер:

По формуле разложения числа по степеням основания:

2000₅ = 2 * 5³ + 0 * 2² + 0 + 0 = 2 * 125 = 250₁₀

Поскольку порядковый номер числа всегда на единицу больше самого числа, то имеем 251.

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

###
var d:='декор'.Order // сортируем по алфавиту
.Cartesian(4) // d - массива из массивов символов 
.Numerate // нумерация
.where((i,w)->w[0] = 'к') // рассматриваем и номер и слово
.first[0].print // выводим именно номер

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

Результат: 251

Подробное решение 8 (10) задания демоверсии ЕГЭ 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_15:

Все 4-буквенные слова, составленные из букв П, Р, С, Т, записаны в алфавитном порядке.
Вот начало списка:

1. ПППП
2. ПППР
3. ПППС
4. ПППТ
5. ППРП
... ...

✍ Решение:

Результат: 65

Видеоразбор задания смотрите ниже:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

8_16:

Все четырёхбуквенные слова, составленные из букв В, Е, Г, А, Н записаны в алфавитном порядке и пронумерованы, начиная с 1. Начало списка выглядит так:

1. АААА
2. АААВ
3. АААГ
4. АААЕ
5. АААН
6. ААВА
…

Под каким номером в списке идёт первое слово, в котором нет буквы А?

✍ Решение:

✎ Решение теоретическое:

Пронумерованный список начинается со всех букв А. Представим, что А — 0, В — 1, Г — 2, Е — 3, Н — 4. Получим следующий список:

Такой список представляет из себя увеличивающиеся числа 5-й системы счисления.
Так как букве А соответствует 0, то первое (самое младшее) четырехзначное число без нуля — это 1111.
Чтобы вычислить под каким номером стоит данное число, переведем его в 10-ю систему и прибавим к результату единицу (так как порядковые номера в списке на единицу больше самих чисел):

1111₅ = 1 * 5³ + 1 * 5² + 1 * 5¹ + 1 * 5⁰ = 156
156 + 1 = 157

✎ Решение с использованием программирования:

PascalABC.net (использование LINQ, быстрое решение):

###
var d:='веган'.Order // сортируем по алфавиту
.Cartesian(4) // d - массива из массивов символов
.Select(x->x.JoinToString(''))// d - массив из строк 
.Numerate // нумерация
.where((i,w)->'а' not in w) // рассматриваем и номер и слово
.first[0].print // выводим именно номер

* LINQ (Language Integrated Query) — язык интегрированных запросов

Python:

С++:

Результат: 157

Видеорешение задания (теоретическое):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

Вероятность событий

8_17:

За четверть Василий Пупкин получил 20 оценок. Сообщение о том, что он вчера получил четверку, несет 2 бита информации.

Сколько четверок получил Василий за четверть?

✍ Решение:

Для решения данного задания необходимо вспомнить две формулы:

1. Формула Шеннона:

x = log₂(1/p)

x - количество информации в сообщении о событии
p - вероятность события

2. Формула вероятности случайного события:

p(A) = m/n

m - число случаев, способствующих событию А
n - общее число равновозможных случаев

Подставим в первую формулу известное значение — вероятность того, что Василий получил четверку:

2 = log₂(1/p);
    => 
1/p = 4; 
    =>
p = 1/4

Затем подставим известное по условию значение в формулу вероятности случайного события:

p = ?/20

Поскольку p мы уже нашли, подставим найденное значение и найдем искомое число — количество четверок за четверть:

1/4 = ?/20

? = 1/4 * 20 = 5

Результат: 5

Видеоразбор задания:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)

Источник

Урок посвящён 11 заданию из ЕГЭ по информатике нового формата 2022. Проанализируем основные примеры и научимся решать это задание!

В 11 задании из ЕГЭ по информатике часто даются задачи на умение работать с количеством информации.

Приступим к делу! Раньше это задание было под номером тринадцать.

Задача (Демонстрационный вариант ЕГЭ по информатике, 2018)

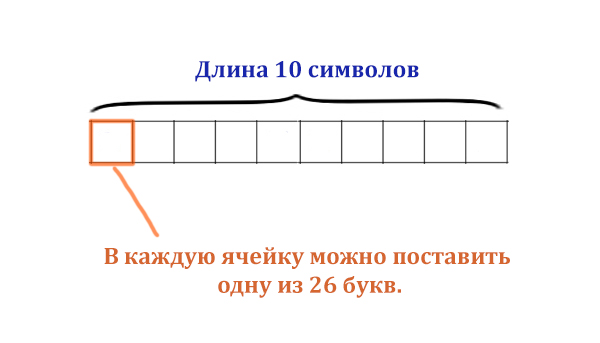
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 10 символов. В качестве символов используют прописные буквы латинского алфавита, т.е. 26 различных символов. В базе данных для хранения каждого пароля отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Определите объём памяти (в байтах), необходимый для хранения данных о 50 пользователях. В ответе запишите только целое число – количество байт.

Решение:

У каждого пользователя есть пароль, состоящий из 10 символов. Это значит, длина пароля 10 символов!

И в каждую ячейку мы может выбрать символ из 26 букв!

Здесь важно различать длину пароля и количество символов из которых пользователь выбирает для каждой ячейки пароля.

Теперь нужно определить: сколько бит занимает одна ячейка (1 символ пароля!).

Когда речь идёт о количестве бит, применяем формулу, которую мы использовали в 7 задании из ЕГЭ по информатике. Там мы кодировали цвета для одного пикселя, а здесь нужно закодировать 26 букв для одного поля пароля.

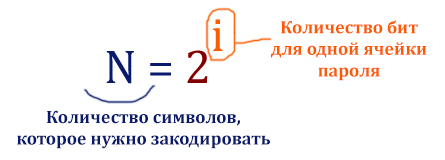
Применяем:

N = 2ⁱ = 26

Целого числа нету для i (количества бит), чтобы равенство было верным. Значит берём столько количество бит, сколько точно будет достаточно, чтобы закодировать 26 букв (символов).

N = 2⁵ > 26

Получаем одна ячейка (одно поле) пароля занимаем 5 бит! А в пароле их 10! Значит, весь пароль будет занимать:

V_пароля = 5 бит * 10 символов = 50 бит (в одном пароле!)

В условии сказано: для хранения каждого пароля отведено одинаковое и минимально возможное целое число байт. Это означает, что мы не может выделять память по одному биту. Память выделяется блоками по 8 бит (по одному байту).

Если взять 7 блоков по 8 бит (1 байту), то нам хватит этого на один пароль.

7 блоков (байт) * 8 бит = 56 бит > 50 бит

Таким образом, на 1 пароль потребуется 7 байт!

Тогда на 50 пользователей потребуется:

50 пользователей * 7 байт = 350 байт (для 50 пользователей).

Ответ: 350

Разберём задачу, которая была на реальном экзамене в Москве

Задача (ЕГЭ по информатике, 2020, Москва)

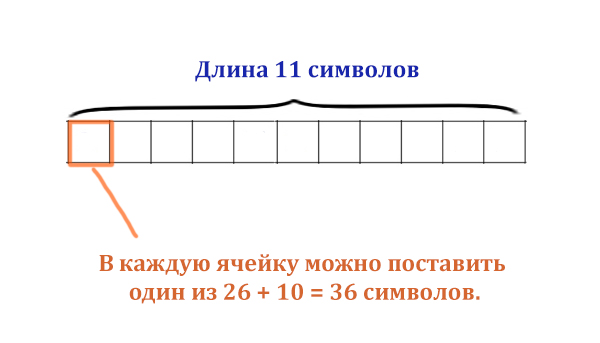
При регистрации в компьютерной системе каждому пользователю выдаётся
пароль, состоящий из 11 символов. В качестве символов используют 26
прописных букв из латинского алфавита и десять цифр. В базе
данных для хранения каждого пароля отведено одинаковое и минимально
возможное целое число байт. При этом используют посимвольное
кодирование паролей, все символы кодируют одинаковым
и минимально возможным количеством бит.
Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения.
Для кодирования данных о 30 сотрудниках было выделено 750 байт. Сколько памяти(в байтах) выделено для хранения дополнительных сведений об одном пользователе. В ответ запишите только целое число — количество байт.

Решение:

Здесь длина пароля составляет 11 символов!

Найдём сколько бит занимает одна ячейка пароля.

N = 2ⁱ = 36

N = 2⁶ = 64 > 36

Значит, 6 бит — минимальное количество бит, которое нужно, чтобы была возможность разместить любой из 36 символов в одной ячейке пароля.

Найдём сколько бит нужно на весь пароль.

V_пароля = 6 бит * 11 символов = 66 бит (в одном пароле!)

Теперь найдём, а сколько байт нужно на 1 пароль:

9 * 8 бит = 72 бит > 66 бит

Следовательно, 9 байт достаточно, чтобы покрыть 66 бит на 1 пароль.

Сказано, что для 30 сотрудников выделено 750 байт. Подсчитаем, сколько байт будет выделено на одного сотрудника.

V_{пользователя} = 750 байт / 30 = 25 байт (приходится на одного пользователя)

Мы выяснили, что на пароль из этих 25 байт потребуется 9 байт. Тогда на дополнительную информацию о каждом пользователе потребуется:

V_{доп. о 1 пол.} = 25 байт — 9 байт = 16 байт

Это и будет ответ.

Ответ: 16

Ещё один важный пример из запасов тренировочных задач ЕГЭ по информатике.

Задача (Номера спортсменов)

В велокроссе участвуют 48 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Какой объём памяти будет использован устройством, когда все спортсмены прошли промежуточный финиш? (Ответ дайте в байтах.)

Решение:

Узнаем сколько бит потребуется выделить на каждого спортсмена, чтобы была возможность записать любой номер от 1 до 48.

В этой задаче сказано: записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена . Это означает что у нас есть 48 различных позиций (номеров), которые нужно закодировать с помощью определённого количества бит. В предыдущей задаче, у нас было 62 различные позиции (символа), которые нужно было закодировать с помощью определённого количества бит. Мы там использовали формулу N = 2ⁱ.

Поэтому будем опять применять формулу N = 2ⁱ.

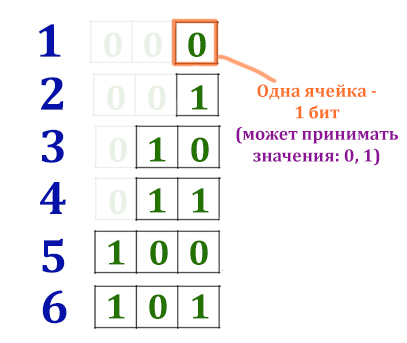
На рисунке показано, как может происходить кодирование чисел. Например, для двух номеров потребуется 1 бит (2¹ = 2), для четырёх номеров потребуется два бита (2² = 4). Нам нужно закодировать 48 чисел! Причём для каждого участника отведено одинаковое количество бит!

Можно сказать, что здесь работает формула, которую рассматривали в 8 задании. Всего нужно составить 48 различных комбинаций (закодировать 48 номеров). В каждой ячейке можно писать либо 0, либо 1 (Свойство бита информации). Какова должна быть длина «слова» (количество бит) ?

N = 2ⁱ = 2^{6 бит} = 64 > 48

Получается 6 бит потребуется для того, чтобы была возможность записать любой номер от 1 до 48 для каждого спортсмена. Если взять пять бит, то мы будем иметь возможность записать номера только от 1 до 2⁵ = 32 для каждого спортсмена (этого не хватает).

Т.к. все участники пересекли финиш, а на каждого участника выделено по 6 бит, то получается:

6 бит * 48 = 288 бит = 36 байт

Ответ: 36

Задача (Автомобильный номер)

В некоторой стране автомобильный номер состоит из 7 символов: сначала 2 буквы, затем 3 цифры, затем ещё 2 буквы. При этом буквы могут быть выбраны только из 12 строчных букв местного алфавита. Среди цифр не используются цифры 6 и 9. Автоматизированная система хранит номера автомобилей следующим образом. Используется посимвольное кодирование. В памяти системы для кодирования каждого символа используется минимально возможное и одинаковое целое количество бит (для букв и цифр отдельно). А для номера используется минимально возможное целое количество байт. Какое количество информации (в байтах) требуется для хранения номеров 160 автомобилей ?

Решение:

Найдём сколько бит потребуется для кодирования 4-х букв.

N = 2ⁱ = 2^{4 бита} = 16 > 12

4 бита хватит для кодирования 12 букв. Всего таких ячейки 4! Поэтому в одном номере на все буквы уйдёт 4 * 4 бита = 16 бит.

Найдём сколько бит потребуется на кодирование 3 ячеек, где находятся цифры.

N = 2ⁱ = 2^{3 бита} = 8

Для кодирования одной ячейки, где находится цифра, потребуется 3 бита.

Все цифры в одном номере будут закодированы 3 бита * 3 = 9 битами.

Всего на один номер уйдёт 16 бит + 9 бит = 25 бит.

Найдём сколько байт потребуется для кодирования одного номера.

4 * 8 бит (1 байт) = 32 бита > 25 бит

4-х байт достаточно, чтобы закодировать 25 бит. Если взять 3 байта, то 3 * 8 бит (1 байт) = 24 бита. Этого будет не достаточно.

Найдём количество байт, которое нужно для кодирования 160 автомобилей

160 автомобилей * 4 байта = 640 байт

Это и будет ответ.

Ответ: 640

Задача (Закрепление формулы)

Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного наблюдения является целое число от 0 до 100%, записываемое при помощи минимально возможного количества бит. Станция сделала 800 измерений. Определите информационный объем результатов наблюдений. (Ответ дайте в байтах.)

Решение:

Здесь, нужно закодировать сто одно число (от 0 до 100). Ситуация похоже на ту, где мы кодировали номера спортсменов.

N = 2ⁱ = 2^{7 бит} = 128 > 101

Получается, что 7 бит потребуется, чтобы полностью закодировать 101 число.

Всего было сделано 800 таких измерений

800 * 7 бит = 5600 бит = 700 байт

Ответ: 700

На этом всё! Удачи при решении 11 задания на ЕГЭ по информатике!

Источник

Слайд 1

Количество информации ЕГЭ № 13 (А11) Презентация выполнена учителем МОУ «СОШ №4» г.о.Шуя Ермошиной М.Ю.

Слайд 2

Вычисление информационного объема сообщения с помощью k бит можно закодировать Q=2 k различных вариантов ( чисел, символов, цветов в палитре) чтобы найти информационный объем сообщения (текста) I , нужно умножить количество символов (отсчетов) N на число бит на символ (отсчет) k : I=N*k

Слайд 3

Алфавитный подход мощность алфавита M – это количество символов в этом алфавите если алфавит имеет мощность M , то количество всех возможных «слов» (символьных цепочек) длиной N (без учета смысла) равно Q=M N ; для двоичного кодирования (мощность алфавита M – 2 символа ) получаем известную формулу: Q=2 N

Слайд 4

Задачи Считая, что каждый символ кодируется двумя байтами, оцените информационный объем следующего предложения в кодировке Unicode : Один пуд – около 16,4 килограмм . 1) 32 Кбайта 2) 512 бит 3) 64 бита 4) 32 байта 32 символа (N=32) , 16 бит (k=16) на 1 символ ( Unicod е). Информационный объём I=N*k, I=32*16=2 9 =512 бит

Слайд 5

Световое табло состоит из лампочек, каждая из которых может находиться в двух состояниях («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 200 различных сигналов? 1) 8 2) 9 3) 100 4) 200 Алфавит – « вкл » и « выкл » (2 символа), длина кода -? Количество вариантов ( Q ) = 200. 200 < =2 k k =8

Слайд 6

Метеорологическая станция ведет наблюдение за атмосферным давлением. Результатом одного измерения является целое число, принимающее значение от 720 до 780 мм ртутного столба, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Каков информационный объем результатов наблюдений? 1) 60 байт 2) 80 бит 3) 80 байт 4) 480 байт Количество вариантов «от 720 до 780», т.е 61, для кодирования 61 числа надо 6 бит (2 6 =64 >=60 ) 6*80=480 бит = 60 байт

Слайд 7

Для передачи секретного сообщения используется код, состоящий из прописных букв кириллицы и цифр (всего используется 43 различных символа). При этом все символы кодируются одним и тем же (минимально возможным) количеством бит. Определите информационный объём сообщения длиной в 140 символов. 1) 105 байт 2) 70 байт 3) 140 бит 4) 140 байт Алфавит – 43 символа, 43 <= 2 6 , на 1 символ k= 6 бит , I=N*k, N=140, I=6*140=840 бит=105 байт

Слайд 8

Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля – ровно 8 символов. В качестве символов могут быть использованы десятичные цифры и 11 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение). Под хранение каждого такого пароля на компьютере отводится одинаковое и минимально возможное целое количество байтов . При этом используется посимвольное кодирование, и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который используется для хранения 100 паролей. 1) 500 байт 2) 600 байт 3) 700 байт 4) 800 байт Алфавит: 10(цифры)+11(маленьких букв)+11(заглавных букв)=32 символа, на 1 символ 5 бит (32=2 5 ), в пароле 8 символов: I=8*5=40 бит (40 бит на 1 пароль). Объём пароля переводим в целые байты: 40/8=5 байт (если дробь, то округляем в сторону увеличения: 5,3- >6) 5 байт на 1 пароль => 5*100= 500 байт на 100 паролей

Слайд 9

В марафоне участвуют 118 бегунов. Специальное устройство регистрирует прохождение каждым из спортсменов промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Какой объём памяти будет использован устройством, когда промежуточный финиш прошли 80 бегунов? 1) 70 бит 2) 70 байт 3) 80 бит 4) 80 байт 118 <=2 7 => 7 бит на 1 бегуна, 80*7=560 бит=70 байт

Слайд 10

Автомобильный номер состоит из 8 символов: четырёх цифр, за которыми следуют 4 буквы. Допустимыми символами считаются 10 цифр и 25 заглавных латинских букв (кроме буквы O). Для хранения каждой из цифр используется одинаковое и наименьшее возможное количество бит. Аналогично, для хранения каждой из букв используется одинаковое и наименьшее возможное количество бит. При этом количество бит, используемых для хранения одной буквы и одной цифры могут быть разными. Для хранения каждого номера используется одинаковое и минимально возможное количество байт. Сколько байт памяти потребуется для хранения 400 автомобильных номеров? Номера хранятся без разделителей. 1) 1200 2) 1600 3) 2000 4) 2400 Для цифр: 10 <=2 4 , 4 бита, для букв 25<=2 5 , 5 бит, на пароль 4*4+4*5=36 бит 36 бит в целые байты = > 36/8 ~ 5 байт 5*400=2000 байт

Слайд 11

Автомобильный номер состоит из 7 символов: четырёх цифр, за которыми следуют 3 буквы. Допустимыми символами считаются 7 цифр (кроме нуля, 6 и 9) и 6 заглавных букв: А, Е, К, М, О, Т. Для хранения каждой из цифр используется одинаковое и наименьшее возможное количество бит. Аналогично, для хранения каждой из букв используется одинаковое и наименьшее возможное количество бит. При этом количество бит, используемых для хранения одной буквы и одной цифры могут быть разными. Для хранения каждого номера используется одинаковое и минимально возможное количество байт. Сколько байт памяти потребуется для хранения 200 автомобильных номеров? Номера хранятся без разделителей. 1) 400 2) 600 3) 800 4) 1000 Цифра 7 <=2 3 , , буква 6<=2 3 , т.е. по 3 бита и на букву и на цифру. Автомобильный номер: 4*3+3*3=21 бит, в целые байты: 21/8 ~3 байта. 3*200=600 байт

Слайд 12

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 30 символов и содержащий только символы А, Б, В, Г, Д. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит. Определите, сколько байт необходимо для хранения 50 паролей. В алфавите 5 букв: 5 <=2 3 , i =3 бита на 1 символ. Пароль 30*3=90 (бит), переводим в целые байты 90:8= округляем в большую сторону 12 байт. 12*50=600 (байт) Ответ: для хранения 50 паролей необходимо 600 байт.

Слайд 13

При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора: А, В, C, D, Е, F, G, H, К, L, M, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 12 байт на одного пользователя. Определите объём памяти (в байтах), необходимый для хранения сведений о 50 пользователях. В ответе запишите только целое число – количество байт. Алфавит 12 символов, 12 <16=2 4 , i =4 бита на 1 символ. Пароль 15*4=60 (бит). Переводим в целые байты: 60:8 округляем до целого =8 байт. Прибавляем дополнительные сведения 8+12=20 (байт). Необходимый объём памяти= 20*50=1000 (байт) Ответ: 1000 байт

Слайд 14

Источники: Сайт Полякова К.Ю. http://kpolyakov. spb . ru Решение Ермошиной М.Ю.

Источник

Автор материалов — Лада Борисовна Есакова.

При оцифровке звука в памяти запоминаются только отдельные значения сигнала. Чем чаще записывается сигнал, тем лучше качество записи.

Частота дискретизации f – это количество раз в секунду, которое происходит преобразование аналогового звукового сигнала в цифровой. Измеряется в Герцах (Гц).

Глубина кодирования (а также, разрешение) – это количество бит, выделяемое на одно преобразование сигнала. Измеряется в битах (Бит).

Возможна запись нескольких каналов: одного (моно), двух (стерео), четырех (квадро).

Обозначим частоту дискретизации – f (Гц), глубину кодирования – B(бит), количество каналов – k, время записи – t(Сек).

Количество уровней дискретизации d можно рассчитать по формуле: d = 2^B.

Тогда объем записанного файла V(бит) = f * B * k * t.

Или, если нам дано количество уровней дискретизации,

V(бит) = f * log₂d * k * t.

Единицы измерения объемов информации:

1 б (байт) = 8 бит

1 Кб (килобайт) = 2¹⁰ б

1 Мб (мегабайт) = 2²⁰ б

1 Гб (гигабайт) = 2³⁰ б

1 Тб (терабайт) = 2⁴⁰ б

1 Пб (петабайт) = 2⁵⁰ б

При оцифровке графического изображения качество картинки зависит от количества точек и количества цветов, в которые можно раскрасить точку.

Если X – количество точек по горизонтали,

Y – количество точек по вертикали,

I – глубина цвета (количество бит, отводимых для кодирования одной точки), то количество различных цветов в палитре N = 2^I. Соответственно, I = log₂N.

Тогда объем файла, содержащего изображение, V(бит) = X * Y * I

Или, если нам дано количество цветов в палитре, V(бит) = X * Y * log₂N.

Скорость передачи информации по каналу связи (пропускная способность канала) вычисляется как количество информации в битах, переданное за 1 секунду (бит/с).

Объем переданной информации вычисляется по формуле V = q * t, где q – пропускная способность канала, а t – время передачи.

Кодирование звука

Пример 1.

Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 32 бит. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 30 2) 45 3) 75 4) 90

Решение:

V(бит) = f(Гц)* B(бит) * k * t(Сек),

где V – размер файла, f – частота дискретизации, B – глубина кодирования, k – количество каналов, t – время.

Значит, V(Мб) = (f * B * k * t ) / 2²³

Переведем все величины в требуемые единицы измерения:

V(Мб) = (16*1000 * 32 * 2 * 12 * 60 ) / 2²³

Представим все возможные числа, как степени двойки:

V(Мб) = (2⁴ * 2³ * 125 * 2⁵ * 2 * 2² * 3 * 15 * 2²) / 2²³ = (5625 * 2¹⁷) / 2²³ = 5625 / 2⁶ =

5625 / 64 ≈ 90.

Ответ: 4

!!! Без представления чисел через степени двойки вычисления становятся намного сложнее.

!!! Частота – это физическая величина, а потому 16 кГц = 16 * 1000 Гц, а не 16 * 2¹⁰. Иногда этой разницей можно пренебречь, но на последних диагностических работах она влияла на правильность ответа.

Пример 2.

В течение трех минут производилась четырёхканальная (квадро) звукозапись с частотой дискретизации 16 КГц и 24-битным разрешением. Сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

1) 25 Мбайт

2) 35 Мбайт

3) 45 Мбайт

4) 55 Мбайт

Решение:

V(бит) = f(Гц)* B(бит) * k * t(Сек),

где V – размер файла, f – частота дискретизации, B – глубина кодирования (или разрешение), k – количество каналов, t – время.

Значит, V(Мб) = (f * B * k * t ) / 2²³= (16 * 1000 * 24 * 4 * 3 * 60) / 2²³ = (2⁴ * 2³ * 125 * 3 * 2³ * 2² * 3 * 15 * 2²) / 2²³ = (125 * 9 * 15 * 2¹⁴) / 2²³ = 16875 / 2⁹ = 32, 96 ≈ 35

Ответ: 2

Пример 3.

Аналоговый звуковой сигнал был записан сначала с использованием 64 уровней дискретизации сигнала, а затем с использованием 4096 уровней дискретизации сигнала. Во сколько раз увеличился информационный объем оцифрованного звука?

1) 64

2) 8

3) 2

4) 12

Решение:

V(бит) = f * log₂d * k * t, где V – размер файла, f – частота дискретизации, d – количество уровней дискретизации, k – количество каналов, t – время.

V₁= f * log₂64 * k * t = f * 6 * k * t

V₂= f * log₂4096 * k * t = f * 12 * k * t

V₂ / V₁ = 2

Правильный ответ указан под номером 3.

Ответ: 3

Кодирование изображения

Пример 4.

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64×64 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

V(бит) = X * Y * log₂N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.

V (Кб) = (64 * 64 * log₂256) / 2¹³ = 2¹² * 8 / 2¹³ = 4

Ответ: 4

Пример 5.

Для хранения растрового изображения размером 64×32 пикселя отвели
1 килобайт памяти. Каково максимально возможное число цветов в палитре изображения?

Решение:

log₂N = V /( X*Y) = 2¹³ / (2⁶* 2⁵) = 4

N = 16

Ответ:16

Сравнение двух способов передачи данных

Пример 6.

Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:

А) Сжать архиватором, передать архив по каналу связи, распаковать.

Б) Передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если

– средняя скорость передачи данных по каналу связи составляет 2¹⁸ бит в секунду,

– объем сжатого архиватором документа равен 80% от исходного,

– время, требуемое на сжатие документа – 35 секунд, на распаковку – 3 секунды?

В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого. Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23. Слов «секунд», «сек.», «с.» к ответу добавлять не нужно.

Решение:

Способ А. Общее время складывается из времени сжатия, распаковки и передачи. Время передачи t рассчитывается по формуле t = V / q, где V — объём информации, q — скорость передачи данных.

Объем сжатого документа: 5 * 0,8 = 4 Мб =4 * 2²³ бит.

Найдём общее время: t = 35 с + 3 с + 4 * 2²³ бит / 2¹⁸ бит/с = 38 + 2⁷ с = 166 с.

Способ Б. Общее время совпадает с временем передачи: t = 5 * 2²³ бит / 2¹⁸ бит/с = 5 * 2⁵ с = 160 с.

Способ Б быстрее на 166 — 160 = 6 с.

Ответ: Б6

Определение времени передачи данных

Пример 7.

Скорость передачи данных через ADSL─соединение равна 128000 бит/c. Через данное соединение передают файл размером 625 Кбайт. Определите время передачи файла в секундах.

Решение:

Время t = V / q, где V — объем файла, q — скорость передачи данных.

t = 625 * 2¹⁰ байт / (2 ⁷ * 1000) бит/c = 625 * 2¹³ бит / (125 * 2¹⁰) бит/c = 5 * 2³ с = 40 с.

Ответ: 40

Пример 8.

У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 2¹⁷ бит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 2¹⁵ бит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 4 Мбайта по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

Решение:

Нужно определить, сколько времени будет передаваться файл объемом 4 Мбайта по каналу со скоростью передачи данных 2¹⁵ бит/с; к этому времени нужно добавить задержку файла у Васи (пока он не получит 512 Кбайт данных по каналу со скоростью 2¹⁷ бит/с).

Время скачивания данных Петей: t₁= 4*2²³ бит / 2¹⁵ бит/с = 2¹⁰ c.

Время задержки: t₂ = 512 кб / 2¹⁷ бит/с = 2^{(9 + 10 + 3) — 17} c = 2⁵ c.

Полное время: t₁ + t₂ = 2¹⁰ c + 2⁵ c = (1024 + 32) c = 1056 c.

Ответ: 1056

Пример 9.

Данные объемом 60 Мбайт передаются из пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 2¹⁹ бит в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 2²⁰ бит в секунду. Задержка в пункте Б (время между окончанием приема данных из пункта А и началом передачи в пункт В) составляет 25 секунд. Сколько времени (в секундах) прошло с момента начала передачи данных из пункта А до их полного получения в пункте В? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

Решение:

Полное время складывается из времени передачи из пункта А в пункт Б (t₁), задержки в пункте Б (t2) и времени передачи из пункта Б в пункт В (t₃).

t₁= (60 * 2²³) / 2¹⁹ =60 * 16 = 960 c

t₂ = 25 c

t₃ = (60 * 2²³) / 2²⁰ =60 * 8 = 480 c

Полное время t₁ + t₂ +t₃ = 960 + 25 + 480 = 1465 c

Ответ: 1465

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №9. Кодирование звуковой и графической информации. Передача информации, Время записи звукового файла, время передачи данных, определение объема информации.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Источник

Набор символов знаковой системы (алфавит) можно рассматривать как различные возможные состояния (события).
Тогда, если считать, что появление символов в сообщении равновероятно, количество возможных событийN можно вычислить как N=2ⁱ
Количество информации в сообщении I можно подсчитать умножив количество символов K на информационный вес одного символа i
Итак, мы имеем формулы, необходимые для определения количества информации в алфавитном подходе:

Если к этим задачам добавить задачи на соотношение величин, записанных в разных единицах измерения, с использованием представления величин в виде степеней двойки мы получим 9 типов задач.
Рассмотрим задачи на все типы. Договоримся, что при переходе от одних единиц измерения информации к другим будем строить цепочку значений. Тогда уменьшается вероятность вычислительной ошибки.

Задача 1. Получено сообщение, информационный объем которого равен 32 битам. чему равен этот объем в байтах?

Решение: В одном байте 8 бит. 32:8=4
Ответ: 4 байта.

Задача 2. Объем информацинного сообщения 12582912 битов выразить в килобайтах и мегабайтах.

Решение: Поскольку 1Кбайт=1024 байт=1024*8 бит, то 12582912:(1024*8)=1536 Кбайт и
поскольку 1Мбайт=1024 Кбайт, то 1536:1024=1,5 Мбайт
Ответ:1536Кбайт и 1,5Мбайт.

Задача 3. Компьютер имеет оперативную память 512 Мб. Количество соответствующих этой величине бит больше:

1) 10 000 000 000бит 2) 8 000 000 000бит 3) 6 000 000 000бит 4) 4 000 000 000бит Решение: 512*1024*1024*8 бит=4294967296 бит.
Ответ: 4.

Задача 4. Определить количество битов в двух мегабайтах, используя для чисел только степени 2.
Решение: Поскольку 1байт=8битам=2³битам, а 1Мбайт=2¹⁰Кбайт=2²⁰байт=2²³бит. Отсюда, 2Мбайт=2²⁴бит.
Ответ: 2²⁴бит.

Задача 5. Сколько мегабайт информации содержит сообщение объемом 2²³бит?
Решение: Поскольку 1байт=8битам=2³битам, то
2²³бит=2²³*2²³*2³бит=2¹⁰2¹⁰байт=2¹⁰Кбайт=1Мбайт.
Ответ: 1Мбайт

Задача 6. Один символ алфавита «весит» 4 бита. Сколько символов в этом алфавите?
Решение:
Дано:

i=4	По формуле N=2ⁱ находим N=2⁴, N=16
Найти: N — ?

Ответ: 16

Задача 7. Каждый символ алфавита записан с помощью 8 цифр двоичного кода. Сколько символов в этом алфавите?
Решение:
Дано:

i=8	По формуле N=2ⁱ находим N=2⁸, N=256
Найти:N — ?

Ответ: 256

Задача 8. Алфавит русского языка иногда оценивают в 32 буквы. Каков информационный вес одной буквы такого сокращенного русского алфавита?
Решение:
Дано:

N=32	По формуле N=2ⁱ находим 32=2ⁱ, 2⁵=2ⁱ,i=5
Найти: i— ?

Ответ: 5

Задача 9. Алфавит состоит из 100 символов. Какое количество информации несет один символ этого алфавита?
Решение:
Дано:

N=100	По формуле N=2ⁱ находим 32=2ⁱ, 2⁵=2ⁱ,i=5
Найти: i— ?

Ответ: 5

Задача 10. У племени «чичевоков» в алфавите 24 буквы и 8 цифр. Знаков препинания и арифметических знаков нет. Какое минимальное количество двоичных разрядов им необходимо для кодирования всех символов? Учтите, что слова надо отделять друг от друга!
Решение:
Дано:

N=24+8=32	По формуле N=2ⁱ находим 32=2ⁱ, 2⁵=2ⁱ,i=5
Найти: i— ?

Ответ: 5

Задача 11. Книга, набранная с помощью компьютера, содержит 150 страниц. На каждой странице — 40 строк, в каждой строке — 60 символов. Каков объем информации в книге? Ответ дайте в килобайтах и мегабайтах
Решение:
Дано:

K=360000	Определим количество символов в книге 1504060=360000. Один символ занимает один байт. По формуле I=Ki*находим I=360000байт 360000:1024=351Кбайт=0,4Мбайт
Найти: I— ?

Ответ: 351Кбайт или 0,4Мбайт

Задача 12. Информационный объем текста книги, набранной на компьютере с использованием кодировки Unicode, — 128 килобайт. Определить количество символов в тексте книги.
Решение:
Дано:

I=128Кбайт,i=2байт	В кодировке Unicode один символ занимает 2 байта. Из формулыI=Ki* выразимK=I/i,K=128*1024:2=65536
Найти: K— ?

Ответ: 65536

Задача 13.Информационное сообщение объемом 1,5 Кб содержит 3072 символа. Определить информационный вес одного символа использованного алфавита
Решение:
Дано:

I=1,5Кбайт,K=3072	Из формулы I=Ki* выразимi=I/K,i=1,510248:3072=4
Найти: i— ?

Ответ: 4

Задача 14.Сообщение, записанное буквами из 64-символьного алфавита, содержит 20 символов. Какой объем информации оно несет?
Решение:
Дано:

N=64, K=20	По формуле N=2ⁱ находим 64=2ⁱ, 2⁶=2ⁱ,i=6. По формуле I=Ki* I=20*6=120
Найти: I— ?

Ответ: 120бит

Задача 15. Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если его объем составил 1/16 часть мегабайта?
Решение:
Дано:

N=16, I=1/16 Мбайт	По формуле N=2ⁱ находим 16=2ⁱ, 2⁴=2ⁱ,i=4. Из формулы I=Ki* выразим K=I/i, K=(1/16)10241024*8/4=131072
Найти: K— ?

Ответ: 131072

Задача 16. Объем сообщения, содержащего 2048 символов,составил 1/512 часть мегабайта. Каков размер алфавита, с помощью которого записано сообщение?
Решение:
Дано:

K=2048,I=1/512 Мбайт	Из формулы I=Ki* выразим i=I/K, i=(1/512)102410248/2048=8. По формулеN=2ⁱ*находим N=2⁸=256
Найти: N— ?

Ответ: 256

Задачи для самостоятельного решения:

Каждый символ алфавита записывается с помощью 4 цифр двоичного кода. Сколько символов в этом алфавите?
Алфавит для записи сообщений состоит из 32 символов, каков информационный вес одного символа? Не забудьте указать единицу измерения.
Информационный объем текста, набранного на компьюте¬ре с использованием кодировки Unicode (каждый символ кодируется 16 битами), — 4 Кб. Определить количество символов в тексте.
Объем информационного сообщения составляет 8192 бита. Выразить его в килобайтах.
Сколько бит информации содержит сообщение объемом 4 Мб? Ответ дать в степенях 2.
Сообщение, записанное буквами из 256-символьного ал¬фавита, содержит 256 символов. Какой объем информации оно несет в килобайтах?
Сколько существует различных звуковых сигналов, состоящих из последовательностей коротких и длинных звонков. Длина каждого сигнала — 6 звонков.
Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 20 до 100%, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем результатом наблюдений.
Скорость передачи данных через ADSL-соединение равна 512000 бит/с. Через данное соединение передают файл размером 1500 Кб. Определите время передачи файла в секундах.
Определите скорость работы модема, если за 256 с он может передать растровое изображение размером 640х480 пикселей. На каждый пиксель приходится 3 байта. А если в палитре 16 миллионов цветов?

Тема определения количества информации на основе алфавитного подхода используется в заданиях А1, А2, А3, А13, В5 контрольно-измерительных материалов ЕГЭ.

Источник

ГБПОУ города Москвы «Спортивно-педагогический колледж»

Департамент спорта и туризма города Москвы

Преподаватель информатики и ИКТ: Макеева Е.С.

Задачи ЕГЭ. Кодирование текстовой информации

Задача 1

Считая, что каждый символ кодируется одним байтом, оцените объем следующего предложения (в битах) в кодировке ASCII: http://www.fipi.ru В ответе укажите только число.

Задача 2

В кодировке КОИ-8 каждый символ кодируется 8 битами. Определите информационный объем (в байтах) следующего предложения: Mail.ru – почтовый сервер. В ответе укажите только число.

Задача 3

Каждый символ в Unicode закодирован двухбайтовым словом. Определите информационный объем (в битах) следующей фразы А.П. Чехова в этой кодировке: Что непонятно, то и чудо. В ответе укажите только число.

Задача 4

В текстовом редакторе включена кодировка текста КОИ-8 (1 байт на 1 символ). Мальчик набрал несколько слов. Сколько символов набрано в редакторе, если общий объем информации, набранный мальчиком, составил 592 бита?

Задача 5

Информационный объем предложения Кашу маслом не испортишь. составляет 50 байт. Определите, сколькими битами кодируется один символ. В ответе укажите только число.

Задача 6

Во сколько раз уменьшится информационный объем страницы текста (текст не содержит управляющих символов форматирования) при его преобразовании из кодировки Unicode (таблица кодировки содержит 65 536 символов) в кодировку Windows (таблица кодировки содержит 256 символов)? В ответе укажите только число.

Задача 7

Используется кодовая таблица CP1251 (Windows Cyrillic). Сколько килобайт будет занимать файл в простом текстовом формате (plain text), если в тексте 200 страниц, на странице 32 строки, а в строке в среднем 48 символов? В ответе укажите только число.

Задача 8

Система оптического распознавания символов позволяет преобразовывать отсканированные изображения страниц документа в текстовый формат со скоростью 4 страницы в минуту и использует алфавит мощностью 65 536 символов. Какое количество информации (в килобайтах) будет нести текстовый документ, каждая страница которого содержит 40 строк по 50 символов, после 10 минут работы приложения? В ответе укажите только число.

Задача 9

Сообщение на греческом языке, содержащее 150 символов, было записано в 16-битном коде Unicode. Каков информационный объем сообщения в байтах? В ответе укажите только число.

Задача 10

Автоматическое устройство осуществило автоматическую перекодировку информационного сообщения на русском языке из 16-битного представления Unicode в 8-битную кодировку КОИ-8. До перекодировки информационный объем сообщения составлял 30 байт. Определите информационный объем сообщения (в битах) после перекодировки. В ответе укажите только число.

Задачи ЕГЭ. Кодирование текстовой информации.

Задача 1

Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на 640 бит. Какова длина сообщения в символах?

Задача 2

Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке длиной в 50 символов, первоначально записанного в 2-байтном коде Unicode, в 8-битную кодировку КОИ-8. На сколько бит уменьшилась длина сообщения? В ответе запишите только число.

Задача 3

Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке длиной в 55 символов, первоначально записанного в 2-байтном коде Unicode, в 8-битную кодировку КОИ-8. На сколько бит уменьшилась длина сообщения? В ответе запишите только число.

Задача 4

Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке длиной в 100 символов, первоначально записанного в 2-байтном коде Unicode, в 8-битную кодировку КОИ-8. На сколько бит уменьшилась длина сообщения? В ответе запишите только число.

Задача 5

Сообщение на русском языке первоначально было записано в 16-битном коде Unicode. При его перекодировке в 8-битную кодировку КОИ-8 информационное сообщение уменьшилось на 80 бит. Сколько символов содержит сообщение?

Задача 6

Сообщение на русском языке первоначально было записано в 16-битном коде Unicode. При его перекодировке в 8-битную кодировку КОИ-8 информационное сообщение уменьшилось на 320 бит. Сколько символов содержит сообщение?

Задача 7

Текстовый документ, состоящий из 10240 символов, хранился в 8-битной кодировке КОИ-8. Этот документ был преобразован в 16-битную кодировку Unicode. Укажите, какое дополнительное количество Кбайт потребуется для хранения документа. В ответе запишите только число.

Задача 8

Текстовый документ, состоящий из 11264 символов, хранился в 8-битной кодировке КОИ-8. Этот документ был преобразован в 16-битную кодировку Unicode. Укажите, какое дополнительное количество Кбайт потребуется для хранения документа. В ответе запишите только число.

Задача 9

Сообщение на русском языке первоначально было записано в 16-битном коде Unicode. Автоматическое устройство осуществило его перекодировку в 8-битную кодировку Windows 1251. При этом информационное сообщение уменьшилось на 320 байт. Определите длину сообщения в символах.

Задача 10

Пользователь электронного почтового ящика написал письмо на русском языке, выбрав кодировку Unicode. Но потом он решил использовать 8-битную кодировку КОИ-8. При этом информационный объем его письма уменьшился на 2 Кбайта. Какова длина сообщения в символах?

Задачи ЕГЭ. Кодирование графической информации

Задача 1

Черно-белое (без градаций серого цвета) растровое графическое изображение имеет размер 10х10 точек. Какой объем памяти в битах займет это изображение? В ответе запишите только число.

Задача 2

Черно-белое (без градаций серого цвета) растровое графическое изображение имеет размер 20х20 точек. Какой объем памяти в байтах займет это изображение? В ответе запишите только число.

Задача 3

Цветное (с палитрой из 256 цветов) растровое графическое изображение имеет размер 10х10 точек. Какой объем памяти в битах займет это изображение? В ответе запишите только число.

Задача 4

В процессе преобразования растрового графического изображения количество цветов уменьшилось с 65 536 до 16. Во сколько раз уменьшился информационный объем графического файла?

Задача 5

В процессе преобразования растрового графического файла количество цветов уменьшилось с 1024 до 32. Во сколько раз уменьшился информационный объем файла?

Задача 6

Для хранения растрового изображения размером 32×32 пикселя отвели 512 байтов памяти. Каково максимально возможное число цветов в палитре изображения? В ответе запишите только число.

Задача 7

Для хранения растрового изображения размером 64×64 пикселя отвели 3 килобайта памяти. Каково максимально возможное количество цветов в палитре изображения? В ответе запишите только число.

Задача 8

Какой объем памяти в килобайтах необходимо выделить под хранение растрового изображения размером 240×192 пикселей, если в палитре изображения 65 тысяч цветов? В ответе запишите только число.

Задача 9

Разрешение экрана монитора 1024х768 точек, глубина цвета – 16 бит. Каков необходимый объем видеопамяти (в мегабайтах) для данного графического режима? В ответе запишите только число.

Задача 10

Какой объем памяти в килобайтах необходимо выделить под хранение растрового изображения размером 640×480 пикселей, если в палитре изображения 16 миллионов цветов? В ответе запишите только число.

Задачи ЕГЭ. Кодирование звуковой информации.

Задача 1

Аналоговый звуковой сигнал был дискретизирован сначала с использованием 65 536 уровней интенсивности сигнала (качество звучания аудио-CD), а затем – с использованием 256 уровней интенсивности сигнала (качество звучания радиотрансляции). Во сколько раз различаются информационные объемы оцифрованных звуковых сигналов? В ответе запишите только число.

Задача 2

Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Запись длится 8 минут, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

Задача 3

Двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением велась в течение 5 минут. Сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

Задача 4

Двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 24-битным разрешением велась в течение 5 минут. Сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

Задача 5

Проводилась одноканальная (моно) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. В результате был получен файл размером 20 Мбайт, сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к времени, в течение которого проводилась запись?

Задача 6

Проводилась одноканальная (моно) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. В результате был получен файл размером 40 Мбайт, сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к времени, в течение которого проводилась запись?

Задача 7

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. В результате был получен файл размером 30 Мбайт, сжатие данных не производилось. Какая из приведенных ниже величин наиболее близка к времени, в течение которого производилась запись?

Задача 8

Двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением велась в течение 10 минут. Сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

Задача 9

Пользователю необходимо записать цифровой аудиофайл (моно) длительностью 1 минута и разрешением 16 бит. Какой должна быть частота дискретизации, если в распоряжении пользователя есть 2,6 Мбайт памяти?

Задача 10

Цифровой аудиофайл (моно) имеет продолжительность звучания 1 минута. При этом он занимает 2,52 Мбайт. С какой частотой дискретизации записан звук, если разрядность звуковой платы 8 бит?

Контрольная работа. Вариант 1

Задача 1

Фразу на русском языке закодировали 16-битным кодом Unicode:

«Не стыдно чего-нибудь не знать, но стыдно не хотеть учиться» (Сократ)

Каков информационный объем этой фразы (взятой в кавычки) в байтах. В ответе запишите только число.

Задача 2

Текстовый документ, состоящий из 20480 символов, хранился в 8-битной кодировке КОИ-8. Этот документ был преобразован в 16-битную кодировку Unicode. Укажите, какое дополнительное количество Кбайт потребуется для хранения документа. В ответе запишите только число.

Задача 3

Какой объем памяти в килобайтах необходимо выделить под хранение растрового изображения размером 128×128 пикселей, если в палитре изображения 64 цвета? В ответе запишите только число.

Задача 4

Для хранения растрового изображения размером 160×128 пикселей отвели 5 килобайт памяти. Каково максимально возможное количество цветов в палитре изображения? В ответе запишите только число.

Задача 5

Цифровой аудиофайл (моно) занимает 2,7 Мбайт памяти, разрешение 16 бит. С какой частотой дискретизации записан звук, если длительность звучания 1 минута?

Контрольная работа. Вариант 2

Задача 1

Каждый символ в Unicode закодирован двухбайтным словом. Оцените информационный объем следующего предложения в байтах.

«Вкладка – раздел (страница) диалогового окна»

В ответе запишите только число.

Задача 2

Некоторое сообщение первоначально было записано в 16-битном коде Unicode. При его перекодировке в 8-битную кодировку КОИ-8 информационное сообщение уменьшилось на 1040 бит. Укажите длину сообщения в символах. В ответе запишите только число.

Задача 3

Какой объем памяти в килобайтах необходимо выделить под хранение растрового изображения размером 128×128 пикселей, если в палитре изображения 256 цветов? В ответе запишите только число.

Задача 4

Для хранения растрового изображения размером 64×64 пикселей отвели 3 килобайта памяти. Каково максимально возможное количество цветов в палитре изображения? В ответе запишите только число.

Задача 5

Объем свободной памяти на диске 10,1 Мбайт, разрядность звуковой платы – 16 бит. Какой может быть продолжительность звучания аудиофайла (стерео), записанного с частотой дискретизации 44,1 кГц?

Ответы к задачам ЕГЭ:

	1	2	3	4	5	6	7	8	9	10
1	144	26	400	74	16	2	300	156	300	120
2	80	400	440	800	10	40	10	11	320	2048
3	100	50	800	4	2	16	64	90	1,5	900
4	2	4	2	3	1	2	2	3	2	1
Контр. раб. Вариант1	118	20	12	4	3
Контр. раб. Вариант2	90	130	16	64	1

Источник