Поиск
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 76 1–20 | 21–40 | 41–60 | 61–76
Добавить в вариант
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1., ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 301 (C часть).
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.
Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на
Площадь осевого сечения цилиндра равна 7. Найдите площадь боковой поверхности цилиндра, деленную на
Площадь осевого сечения цилиндра равна 9. Найдите площадь боковой поверхности цилиндра, деленную на
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Длина окружности основания цилиндра равна 14. Площадь боковой поверхности равна 182. Найдите высоту цилиндра.
Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 2. Найдите высоту цилиндра.
Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 4. Найдите высоту цилиндра.
Шар вписан в цилиндр. Площадь поверхности шара равна 48. Найдите площадь полной поверхности цилиндра.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 702.
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Длина окружности основания цилиндра равна 3, высота равна 4. Найдите площадь боковой поверхности цилиндра.
Площадь боковой поверхности цилиндра равна
а диаметр основания — 1. Найдите высоту цилиндра.
Площадь боковой поверхности цилиндра равна
а диаметр основания — 8. Найдите высоту цилиндра.
Площадь боковой поверхности цилиндра равна
а диаметр основания — 5. Найдите высоту цилиндра.
Цилиндр и конус имеют общее основание, вершина конуса является центром другого основания цилиндра. Каждая образующая конуса наклонена к плоскости основания под углом 30°.
а) Докажите, что площади боковых поверхностей цилиндра и конуса равны
б) Найдите радиус сферы, касающейся боковых поверхностей цилиндра и конуса, а так
же одного из оснований цилиндра, если известно, что объем конуса равен
Источник: А. Ларин: Тренировочный вариант № 172.
Площадь боковой поверхности цилиндра равна а высота — 1. Найдите диаметр основания.
Площадь боковой поверхности цилиндра равна а высота — 2. Найдите диаметр основания.
Площадь боковой поверхности цилиндра равна а высота — 4. Найдите диаметр основания.
Всего: 76 1–20 | 21–40 | 41–60 | 61–76
10
Сен 2013
Категория: 02 Стереометрия
02. Цилиндр.
2013-09-10
2022-09-11
Задача 1. Радиус основания цилиндра равен высота равна
Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 2. Площадь боковой поверхности цилиндра равна а диаметр основания равен
Найдите высоту цилиндра.
Решение: + показать
Задача 3. Длина окружности основания цилиндра равна высота равна
Найдите площадь боковой поверхности цилиндра.
Решение: + показать
Задача 4. Площадь осевого сечения цилиндра равна Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 5. Объём первого цилиндра равен 48 м У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м
).
Решение: + показать
Задача 6. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Решение: + показать
Задача 7. В цилиндрический сосуд налили см
воды. Уровень воды при этом достигает высоты
см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на
см. Чему равен объем детали? Ответ выразите в см
Решение: + показать
Задача 8. В цилиндрический сосуд налили см
воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в
раза. Найдите объем детали.
Ответ выразите в см
Решение: + показать
Задача 9. В цилиндрическом сосуде уровень жидкости достигает см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в
раза больше первого? Ответ выразите в сантиметрах.
Решение: + показать
Задача 10. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 11. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 12. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 13. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Вы можете пройти тест “Цилиндр”
Автор: egeMax |
комментария 3
Печать страницы
МБОУ Пожарская СОШ Сергачского района Нижегородской области
Учитель математики первой категории Зюляева Л.Ю.
Задания для подготовки к ЕГЭ
11 класс по теме «Цилиндр»
Задачи по готовым чертежам
1 вариант
1. Осевое сечение цилиндра – квадрат со стороной 6 см. Найти сумму высоты и радиуса основания цилиндра.
2. Радиус основания цилиндра равен 2м, высота 3м. Найти диагональ осевого сечения.
3. Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 2. Найдите высоту цилиндра.
Задачи по готовым чертежам
2 вариант
1. Осевое сечение цилиндра – квадрат со стороной 8 см. Найти сумму высоты и радиуса основания цилиндра.
2. Радиус основания цилиндра равен 4м, высота 6м. Найти диагональ осевого сечения.
3. Длина окружности основания цилиндра равна 2. Площадь боковой поверхности равна 1. Найдите высоту цилиндра.
Типы задач на ЕГЭ по теме «Площадь боковой поверхности цилиндра»
1 Диагональ осевого сечения цилиндра равна 48. Угол между этой диагональю и образующей равен 300. Найдите радиус цилиндра.
2. Радиус основания цилиндра равен 6, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
3. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 450 и равна 8√2 см. Найдите площадь боковой поверхности цилиндра, деленную на π .
4.Во сколько раз увеличится площадь боковой поверхности цилиндра, если его высоту и радиус увеличить в три раза?
|
Типы задач |
№ задачи |
|
|
1 тип задач |
Задачи, решаемые в одно действие с помощью т. Пифагора или свойства прямоугольного треугольника |
|
|
2 тип задач |
Задачи, решаемые в одно действие с помощью формулы площади боковой поверхности. |
|
|
3 тип задач |
Задачи, решаемые в два действия с помощью т. Пифагора и формулы площади боковой поверхности. |
Задания по теме «Площадь поверхности цилиндра»
ЕГЭ 2015 Задания из Открытого банка заданий. Математика. Геометрия.
Прототипы заданий №12
Задание №27133
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Задание №245358
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Задание №27058
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
Проверочная тестовая работа Вариант 1
№1. Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности, деленная на π, равна:
40; 10; 20; 4
№2. В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 16π кв.дм. Найдите площадь полной поверхности цилиндра деленную на π.
80; 96; 64; 32
№3. Радиус основания цилиндра в два раза меньше образующей, равной 4, тогда площадь боковой поверхности, деленная на π, равна:
16; 32; 4; 8
№4. Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его большей стороны, деленная на π, равна:
56; 72; 88; 48
№5. Если площадь боковой поверхности цилиндра равна 64π кв.м, а высота – 4 м, тогда радиус равен:
16; 8; 26; 8π
№6. Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра, деленная на π, может быть равна:
256; 100; 24; 64
№7. Осевым сечением цилиндра является прямоугольник со сторонами 12 и 8 см, то площадь боковой поверхности цилиндра, деленная на π, может быть равна:
36; 64; 48; 96
Проверочная тестовая работа
Вариант 2.
№1. Диаметр основания цилиндра равен 4 см, высота – 3 см, тогда площадь боковой поверхности, деленная на π, равна:
40; 10; 12; 4
№2. В цилиндре радиуса осевым сечением является квадрат, а площадь основания равна 9π кв.дм. Найдите площадь полной поверхности цилиндра деленную на π .
40; 54; 60; 32
№3. Радиус основания цилиндра в три раза меньше образующей, равной 6, тогда площадь боковой поверхности, деленная на π, равна:
24; 32; 4; 8
№4. Площадь полной поверхности цилиндра, полученного вращением прямоугольника со сторонами 4 см и 7 см вокруг его меньшей стороны, деленная на π, равна:
56; 105; 154; 48
№5. Если площадь боковой поверхности цилиндра равна 64π кв.м, а радиус – 8м, тогда образующая равна:
16; 4; 26; 8π
№6. Осевым сечением цилиндра является прямоугольник со сторонами 10 и 16 см, то площадь основания цилиндра, деленная на π, может быть равна:
256; 100; 24; 25
№7. Осевым сечением цилиндра является прямоугольник со сторонами 6 и 8 см, то площадь боковой поверхности цилиндра может быть равна:
9; 64; 36; 48
Ключ к тестовой работе (оба варианта)
|
№ задачи |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Ответ |
3 |
2 |
1 |
3 |
2 |
4 |
4 |
ЦИЛИНДР
1. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
2. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 6. Объем параллелепипеда равен 36. Найдите высоту цилиндра.
3. В цилиндрический сосуд налили воды. Уровень жидкости оказался равным 15 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 12 см. Чему равен объем детали? Ответ выразите в
.
4. В цилиндрическом сосуде уровень жидкости достигает 25 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 5 раз больше диаметра первого? Ответ выразите в сантиметрах.
5. В основании прямой призмы лежит прямоугольный треугольник с катетами 4 и 1. Боковые ребра призмы равны . Найдите объём цилиндра, описанного около этой призмы.


6. В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра призмы равны . Найдите объём цилиндра, описанного около этой призмы.
7. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 40. Найдите объём цилиндра.
8. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
9. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
10. Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
11. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2,5. Найдите объем параллелепипеда.
12. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 2. Найдите высоту цилиндра.
13. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 18,5. Объем параллелепипеда равен 5476. Найдите высоту цилиндра.
14. В цилиндрический сосуд налили воды. Уровень жидкости оказался равным 24 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 6 см. Чему равен объем детали? Ответ выразите в
.
15. В цилиндрическом сосуде уровень жидкости достигает 405 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
16. В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые ребра призмы равны . Найдите объём цилиндра, описанного около этой призмы.
17. Дано два цилиндра. Объём первого цилиндра равен 86. У второго цилиндра высота в 3 раза больше, а радиус основания в 2 раза меньше, чем у первого. Найдите объём второго цилиндра.
18. Радиус основания цилиндра равен 7, высота равна 8. Найдите площадь боковой поверхности цилиндра, деленную на .
19. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 7. Найдите площадь боковой поверхности призмы.
20. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 1.
21. Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 111. Найдите площадь поверхности шара.
22. Длина окружности основания цилиндра равна 4, высота равна 4. Найдите площадь боковой поверхности цилиндра.
23. В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
24. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.
25. Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
26. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
27. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
28. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
29. Площадь боковой поверхности цилиндра равна , а диаметр основания — 1. Найдите высоту цилиндра.
30. В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые рёбра призмы равны 2π. Найдите объём цилиндра, описанного около этой призмы.
31. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объём параллелепипеда равен 36. Найдите высоту цилиндра.
32. Площадь боковой поверхности цилиндра равна 12 π, а диаметр основания равен 6. Найдите высоту цилиндра.
33. В цилиндрическом сосуде уровень жидкости достигает 64 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
34. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объём параллелепипеда.
35. В цилиндрический сосуд налили 500 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился
в 1,2 раза. Найдите объём детали. Ответ выразите в куб. см.
36. Площадь боковой поверхности цилиндра равна 24 π,
а диаметр основания равен 8. Найдите высоту цилиндра.
37. В цилиндрическом сосуде уровень жидкости достигает 80 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
38. В цилиндрический сосуд, в котором находится 6 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали? Ответ выразите в дм3.
39. В цилиндрическом сосуде уровень жидкости достигает 32 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
40. Шар вписан в цилиндр. 
41. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). 
42. Цилиндр описан около шара. Объём шара равен 50. 
43. Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.
44. В цилиндрический сосуд налили 2800 см3 воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Найдите объём детали. Ответ выразите
в куб. см.
45. Вода в сосуде цилиндрической формы находится на уровне h= 80 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте
в сантиметрах.
46.
|
Радиус основания цилиндра равен 15, а его образующая |
|
47. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 9, а второго — 9 и 2.
Во сколько раз объём первого цилиндра больше объёма второго?
48. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 14, а второго — 7 и 3.
Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности вт
49.
|
Радиус основания цилиндра равен 15, а его образующая |
|
50. В бак цилиндрической формы, площадь основания которого 60 квадратных сантиметров, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.
51. Даны две кружки цилиндрической формы. Первая кружка в четыре раза ниже второй,
а вторая в полтора раза шире первой.
Во сколько раз объём первой кружки меньше объёма второй?
52. Высота бака цилиндрической формы равна 40 см, а площадь его основания 150 квадратных сантиметров. Чему равен объём этого бака (в литрах)?
В одном литре 1000 кубических сантиметров.
53.
|
54. Даны два цилиндра. Радиус основания и высота первого равны соответственно 9 и 3, а второго — 3 и 6.
Во сколько раз объём первого цилиндра больше объёма второго?
55. Высота бака цилиндрической формы равна 50 см, а площадь его основания 160 квадратных сантиметров. Чему равен объём этого бака (в литрах)?
В одном литре 1000 кубических сантиметров.
56.
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на тему «Цилиндр»
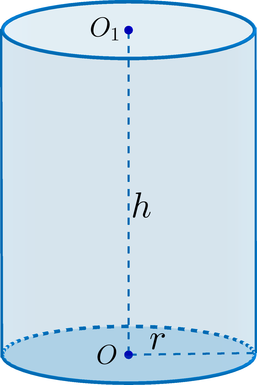
Прямой цилиндр:
(blacktriangleright) Ось цилиндра – прямая, соединяющая центры его оснований.
Отрезок, соединяющий центры оснований – высота.
(blacktriangleright) Образующая цилиндра – перпендикуляр, проведенный из точки границы одного основания к другому основанию.
Заметим, что образующая и высота цилиндра равны друг другу.
(blacktriangleright) Площадь боковой поверхности цилиндра ({Large{S_{text{бок.пов.}}=2pi rh}}), где (r) – радиус основания, (h) – высота (или образующая).
(blacktriangleright) Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований. [{Large{S_{text{полн.пов.}}=2pi rh+2pi r^2}}]
(blacktriangleright) Объем цилиндра ({Large{V=S_{text{осн}}cdot
h=pi r^2h}})
Заметим, что прямой цилиндр имеет некоторое сходство с прямой призмой, только в ее основаниях лежат многоугольники (граница которых – ломаная), а в основаниях цилиндра – круги (граница которых гладкая).
Поэтому можно сказать, что боковая поверхность прямой призмы “ребристая”, а цилиндра – “гладкая”.
Задание
1
#2743
Уровень задания: Равен ЕГЭ
Про прямые круговые цилиндры (C_1) и (C_2) известно, что у (C_1) радиус основания в два раза больше, чем у (C_2), но у (C_2) высота в три раза больше, чем у (C_1). Найдите отношение объёма цилиндра (C_2) к объёму (C_1).
Обозначим высоту цилиндра (C_1) через (h_1), а высоту цилиндра (C_2) через (h_2). Обозначим радиус основания цилиндра (C_1) через (r_1), а радиус основания цилиндра (C_2) через (r_2). Тогда [r_1 = 2r_2,qquad h_2 = 3h_1,.]
Объём цилиндра (C_1) равен (pi {r_1}^2 h_1 = 4pi {r_2}^2 h_1), а объём цилиндра (C_2) равен (3pi {r_2}^2 h_1), тогда [dfrac{V_{C_2}}{V_{C_1}} = dfrac{3pi {r_2}^2 h_1}{4pi {r_2}^2 h_1} = 0,75]
Ответ: 0,75
Задание
2
#1861
Уровень задания: Равен ЕГЭ
Объем цилиндра равен (64pi), а площадь боковой поверхности равна (32pi). Найдите площадь полной поверхности цилиндра, деленную на (pi).
Формулы для нахождения объема и боковой поверхности цилиндра: (V = pi R^2 h), (S_{text{бок}} = 2pi R h). Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: [frac{V}{S_{text{бок}}} = frac{pi R^2 h}{2pi R h} = frac{R}{2} = frac{64pi}{32pi} = 2] (Rightarrow) (R = 4). Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований: [S_{text{полн}} = 2pi R h + 2 pi R^2 = 32pi + 2 cdot 16pi = 64pi.] Осталось разделить полученный объем на (pi), тогда окончательно получаем (64).
Ответ: 64
Задание
3
#1862
Уровень задания: Равен ЕГЭ
Объем цилиндра равен (100pi), а площадь боковой поверхности равна (25pi). Найдите высоту цилиндра.
Формулы для нахождения объема и боковой поверхности цилиндра: (V = pi R^2 h), (S_{text{бок}} = 2pi R h). Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: [frac{V}{S_{text{бок}}} = frac{pi R^2 h}{2pi R h} = frac{R}{2} = frac{100pi}{25pi} = 4] (Rightarrow) (R = 
Ответ: 1,5625
Задание
4
#953
Уровень задания: Равен ЕГЭ
Объём цилиндра [V = dfrac{200}{sqrt{pi}},] а отношение радиуса его основания к его высоте равно (5). Найдите площадь полной поверхности этого цилиндра.
[V_{text{цил}} = pi R^2 H = dfrac{200}{sqrt{pi}},] (dfrac{R}{H} = 5), где (R) – радиус основания цилиндра, (H) – его высота, тогда (R = 5H), следовательно, [pi cdot 25 H^3 = dfrac{200}{sqrt{pi}}qquadRightarrowqquad H^3 = dfrac{8}{pisqrt{pi}},] откуда (H = dfrac{2}{sqrt{pi}}), (R = dfrac{10}{sqrt{pi}}). [S_{text{полн}} = 2pi R H + pi R^2 = 2pi R(H + R) = 2picdotdfrac{10}{sqrt{pi}}cdotdfrac{12}{sqrt{pi}} = 240.]
Ответ: 240
Задание
5
#952
Уровень задания: Сложнее ЕГЭ
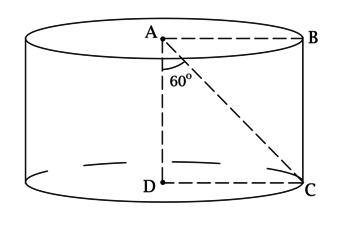
(AD) – ось цилиндра, (BC) – его образующая, (S_{ABCD} = dfrac{16sqrt{3}}{sqrt[3]{pi^2}}), (angle CAD = 60^circ). Найдите объём цилиндра.
Так как (AD) и (BC) – высоты цилиндра, то (ABCD) – прямоугольник, тогда [S_{ABCD} = ADcdot DC = Hcdot R = dfrac{16sqrt{3}}{sqrt[3]{pi^2}}.]
Рассмотрим прямоугольный треугольник (ADC):
Т.к. (angle DAC = 60^circ), то [AD = mathrm{tg}, angle ACDcdot DC = mathrm{tg}, 30^circcdot R = dfrac{R}{sqrt{3}},] т.е. (H = dfrac{R}{sqrt{3}}) или (R = sqrt{3}H).
Подставляя выражение для (R) в (S_{ABCD}), получим: [H^2cdotsqrt{3} = dfrac{16sqrt{3}}{sqrt[3]{pi^2}},] откуда (H = dfrac{4}{sqrt[3]{pi}}), тогда (R = dfrac{4sqrt{3}}{sqrt[3]{pi}}).
[V_{text{цил}} = pi R^2 H = picdot dfrac{16cdot 3}{sqrt[3]{pi^2}}cdotdfrac{4}{sqrt[3]{pi}} = 192.]
Ответ: 192
Повторение базовой теории и формул, в том числе и тех, которые позволяют выполнить расчет объема цилиндра, — один из основных этапов подготовки к ЕГЭ. Несмотря на то, что эта тема достаточно подробно рассматривается на уроках математики в школе, с необходимостью вспомнить основной материал и «прокачать» навык решения задач сталкиваются многие учащиеся. Понимая, как вычислить объем и другие неизвестные параметры цилиндра, старшеклассники смогут получить достаточно высокие баллы по итогам сдачи единого государственного экзамена.
Основные нюансы, которые стоит вспомнить
Чтобы вопрос, как посчитать объем цилиндра и выполнить измерение других неизвестных параметров при решении задач, не ставил ученика в тупик, рекомендуем повторить основные свойства этой фигуры прямо сейчас в режиме онлайн.
Важно помнить, что:
- Цилиндр представляет собой тело, которое ограничено цилиндрической поверхностью и двумя кругами. Цилиндрическая поверхность является боковой. А круги представляют собой основания фигуры.
- Высота цилиндра есть расстояние между плоскостями его оснований.
- Все его образующие являются параллельными и равными между собой.
- Радиус цилиндра есть радиус его основания.
- Фигура называется прямой, если ее образующие перпендикулярны основаниям.
Как подготовиться к экзамену качественно и эффективно?
Занимаясь накануне прохождения аттестационного испытания, многие учащиеся сталкиваются с проблемой поиска необходимой информации. Далеко не всегда школьный учебник оказывается под рукой, когда это требуется. А найти формулы, которые помогут рассчитать площадь и другие неизвестные параметры цилиндра, часто бывает достаточно сложно даже в Интернете в онлайн-режиме.
Занимаясь вместе с математическим порталом «Школково», выпускники смогут избежать типовых ошибок и успешно сдать единый госэкзамен. Мы предлагаем выстроить процесс подготовки по-новому, переходя от простого к сложному. Это позволит учащимся определить непонятные для себя тематики и ликвидировать пробелы в знаниях.
Весь базовый материал, который поможет в решении задач на тему «Цилиндр», выпускники смогут найти в разделе «Теоретическая справка». Специалисты «Школково» изложили с доступной форме все необходимые определения и формулы.
Для закрепления полученных знаний учащиеся могут попрактиковаться в решении задач на тему «Цилиндр» и другие темы, например, нахождение площади или объема конуса. Большая, постоянно обновляющаяся подборка заданий представлена в разделе «Каталог».
Чтобы во время подготовки к ЕГЭ быстро найти конкретную задачу по теме «Цилиндр» и освежить в памяти алгоритм ее решения, выпускники могут предварительно сохранить ее в «Избранное». Отрабатывать собственные навыки на нашем сайте имеют возможность не только столичные школьники, но и учащиеся из других российских городов.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Геометрия 10-11 класс. Цилиндр
Скачать файл в формате pdf.
Геометрия 10-11 класс. Цилиндр
Прямым круговым цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований.
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две его стороны – образующие цилиндра, а две другие – параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это – сечение цилиндра плоскостью, проходящей через его ось.
Площадь боковой поверхности цилиндра находится по формуле: ({S_{{text{б}}{text{.п}}{text{.}}}} = 2,pi ,R,H); площадь полной поверхности цилиндра находится по формуле: (S = 2,pi ,R,H + 2pi ,{R^2}); объем цилиндра находится по формуле: (V = pi ,{R^2},H), где R – радиус основания; H – длина высоты цилиндра.
Задачи для самостоятельного решения
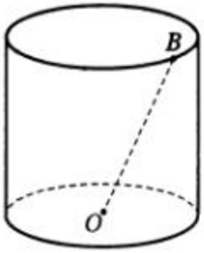
| Задача 1. Образующая цилиндра равна 20, расстояние от точки B до центра нижнего основания равно 29. Найдите диаметр цилиндра.
Ответ
ОТВЕТ: 42. |
 |
| Задача 2. Прямоугольник с диагональю 24 вращают вокруг одной из сторон, другая сторона составляет с этой диагональю угол 60°. Найдите площадь основания полученного тела вращения, деленную на π.
Ответ
ОТВЕТ: 144. |
|
| Задача 3. Высота и диаметр основания цилиндра равны 5. Найдите площадь боковой поверхности цилиндра, деленную на π.
Ответ
ОТВЕТ: 25. |
|
| Задача 4. Площадь боковой поверхности цилиндра равна 81π, а диаметр основания – 9. Найдите высоту цилиндра.
Ответ
ОТВЕТ: 9. |
|
| Задача 5. Длина развертки боковой поверхности цилиндра равна 24π, высота – 5. Найдите расстояние от центра верхнего основания до точки лежащей на окружности нижнего основания.
Ответ
ОТВЕТ: 13. |
|
| Задача 6. Площадь боковой поверхности цилиндра равна площади его основания. Во сколько раз диаметр основания больше высоты цилиндра?
Ответ
ОТВЕТ: 4. |
|
| Задача 7. Высота цилиндра равна 12, площадь боковой поверхности – 240π. Вычислите площадь сечения, параллельного оси цилиндра и отстоящего от него на расстояние 6.
Ответ
ОТВЕТ: 192. |
|
| Задача 8. Площадь боковой поверхности цилиндра равна 100π. Осевым сечением цилиндра является квадрат. Найдите площадь полной поверхности цилиндра, деленную на π.
Ответ
ОТВЕТ: 150. |
|
| Задача 9. Площади сечений параллельных оси цилиндра, находящихся по разные стороны от оси, равны 48 и 36, расстояние между сечениями равно 7. Высота цилиндра равна 6. Найдите радиус основания цилиндра.
Ответ
ОТВЕТ: 5. |
|
| Задача 10. Площади сечений параллельных оси цилиндра, находящихся по одну стороны от оси, равны 120 и 160. Радиус и высота цилиндра равна 10. Найдите расстояние между плоскостями сечений.
Ответ
ОТВЕТ: 2. |
|
| Задача 11. Правильная треугольная призма вписана в цилиндр, радиус основания которого равен (2sqrt 3 ,) а высота цилиндра равна 2. Найдите площадь боковой поверхности призмы.
Ответ
ОТВЕТ: 36. |
|
| Задача 12. Прямоугольник со сторонами (sqrt {frac{5}{pi }} ) и (sqrt {frac{{125}}{pi }} ) вращается вокруг меньшей стороны. Найдите площадь полной поверхности тела вращения.
Ответ
ОТВЕТ: 300. |
|
| Задача 13. Прямоугольник со сторонами (2sqrt {frac{7}{pi }} ) и (2sqrt {frac{1}{{7pi }}} ) вращается вокруг прямой, проходящей через середины больших сторон. Найдите площадь полной поверхности тела вращения.
Ответ
ОТВЕТ: 18. |
|
| Задача 14. Высота цилиндра равна 3. Равнобедренный треугольник ABC с боковой стороной 10 и ∠А = 120° расположен так, что его вершина A лежит на окружности нижнего основания цилиндра, а вершины B и C — на окружности верхнего основания. Найдите синус угла между плоскостью ABC и плоскостью основания цилиндра.
Ответ
ОТВЕТ: 0,6. |
Презентация содержит справочный материал по теме » Поверхность цилиндра», 6 типов задач по 4 варианта на каждый тип.
Задачи на выч.повер.цилиндра.pptx
Задачи на вычисление поверхности цилиндра
Задачи на вычислениеповерхности цилиндра.
Учитель МАОУ школа №12
г. Северодвинск
Шкода Л.И.
Повторение. Основные элементы цилиндра:
Повторение.
Основные элементы цилиндра:
R – радиус основания цилиндра, d – диаметр основания цилиндра, h- высота цилиндра.
d = 2R
C –длина окружности основания C=2πR
S – площадь основания Sосн. = πR2
Sбок. – боковая поверхность цилиндра. Sбок.= 2πRh
Sцил. – полная поверхность цилиндра. Sцил.= Sбок.+2 Sосн., или
Sцил=2πRh+2 πR2 или Sцил=2πR(h+R)
Задача 1 1.1. Радиус основания цилиндра равен 2, высота равна 3
Задача 1
1.1. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π .
1.2. Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на π .
1.3. Радиус основания цилиндра равен 6, высота равна 5. Найдите площадь боковой поверхности цилиндра, деленную на π .
1.4. Радиус основания цилиндра равен 8, высота равна 9. Найдите площадь боковой поверхности цилиндра, деленную на π .
Задача 2. 2.1. Длина окружности основания цилиндра равна 3, высота равна 4
Задача 2.
2.1. Длина окружности основания цилиндра равна 3, высота равна 4. Найдите площадь боковой поверхности цилиндра.
2.2. Длина окружности основания цилиндра равна 5, высота равна 2. Найдите площадь боковой поверхности цилиндра.
2.3. Длина окружности основания цилиндра равна 6, высота равна 6. Найдите площадь боковой поверхности цилиндра.
2.4. Длина окружности основания цилиндра равна 4, высота равна 5. Найдите площадь боковой поверхности цилиндра.
Задача 3. 3.1. Площадь осевого сечения цилиндра равна 28
Задача 3.
3.1. Площадь осевого сечения цилиндра равна 28. Найдите площадь боковой поверхности цилиндра, деленную на π.
3.2. Площадь осевого сечения цилиндра равна 31. Найдите площадь боковой поверхности цилиндра, деленную на π.
3.3. Площадь осевого сечения цилиндра равна 45. Найдите площадь боковой поверхности цилиндра, деленную на π.
3.4. Площадь осевого сечения цилиндра равна 36. Найдите площадь боковой поверхности цилиндра, деленную на π.
Задача 4. 4.1. Длина окружности основания цилиндра равна 14
Задача 4.
4.1. Длина окружности основания цилиндра равна 14. Площадь боковой поверхности равна 182. Найдите высоту цилиндра.
4.2. Длина окружности основания цилиндра равна 13. Площадь боковой поверхности равна 156. Найдите высоту цилиндра.
4.3. Длина окружности основания цилиндра равна 15. Площадь боковой поверхности равна 90. Найдите высоту цилиндра.
4.4. Длина окружности основания цилиндра равна 12. Площадь боковой поверхности равна 180. Найдите высоту цилиндра.
Задача 5. 5.1. Боковая поверхность цилиндра равна 56
Задача 5.
5.1. Боковая поверхность цилиндра равна 56. Образующую цилиндра увеличили в 3 раза, а радиус основания уменьшили в 4 раза. Какой стала боковая поверхность?
5.2. Боковая поверхность цилиндра равна 150. Образующую цилиндра уменьшили в 6 раз, а радиус основания увеличили в 3 раза. Какой стала боковая поверхность?
5.3. Боковая поверхность цилиндра равна 256. Образующую цилиндра уменьшили в 2 раза, а радиус основания уменьшили в 4 раза. Какой стала боковая поверхность?
5.4. Боковая поверхность цилиндра равна 16. Образующую цилиндра увеличили в 3 раза, а радиус основания увеличили в 3 раза. Какой стала боковая поверхность?
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Введите ваш emailВаш email