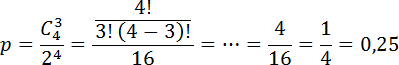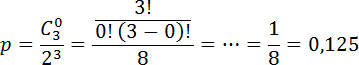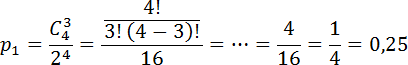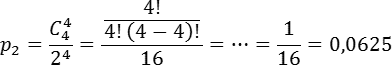Задачи егэ на вероятность с монеткой

Всего: 49    1–20 | 21–40 | 41–49

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 49    1–20 | 21–40 | 41–49

30 мая 2012

Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:

где p — искомая вероятность, k — число устраивающих нас событий, n — общее число возможных событий.

Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k и n. В этом и состоит вся сложность.

Тем не менее, существует как минимум два принципиально различных метода решения:

1. Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
2. Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.

Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!

Метод перебора комбинаций

Этот метод еще называется «решение напролом». Состоит из трех шагов:

1. Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР. Число таких комбинаций — это n;
2. Среди полученных комбинаций отмечаем те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k;
3. Осталось найти вероятность: p = k : n.

К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:

Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.

Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):

OO OP PO PP

Итого n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:

OP PO

Таких вариантов оказалось k = 2. Находим вероятность:

Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем все возможные комбинации орлов и решек:

OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP

Всего получилось n = 16 вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, k = 1. Осталось найти вероятность:

Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.

Специальная формула вероятности

Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:

Теорема. Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:

Где C_n^k — число сочетаний из n элементов по k, которое считается по формуле:

Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.

На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.

Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.

По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу:

С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же.

Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем числа n и k. Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу:

Напомню, что 0! = 1 по определению. Поэтому C₃⁰ = 1.

Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.

Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.

Пусть p₁ — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем:

Теперь найдем p₂ — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем:

Чтобы получить ответ, осталось сложить вероятности p₁ и p₂. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:

p = p₁ + p₂ = 0,25 + 0,0625 = 0,3125

Смотрите также:

1. Правила комбинаторики в задаче B6
2. Комбинаторика в задаче B6: легкий тест
3. Что такое числовая дробь
4. Задачи B12, сводящиеся к линейным уравнениям
5. Сложные задачи на проценты
6. Задача B4 с таблицами: тарифы на интернет

Бросание монет. Решение задач на нахождение вероятности

На этой странице я расскажу об одном популярном классе задач, которые встречаются в любых учебниках и методичках по теории вероятностей — задачах про бросание монет (кстати, они встречаются в части В6 ЕГЭ). Формулировки могут быть разные, например «Симметричную монету бросают дважды…» или «Бросают 3 монеты …», но принцип решения от этого не меняется, вот увидите.

Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать «бросают 3 монеты» или «бросают монету 3 раза», результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).

Для задач о подбрасывании монеты существуют два основных метода решения, один — по формуле классической вероятности (фактически переборный метод, доступный даже школьникам), а также его более сложный вариант с использованием комбинаторики, второй — по формуле Бернулли (на мой взгляд он даже легче первого, нужно только запомнить формулу). Рекомендую по порядку прочитать про оба метода, и потом выбирать при решении подходящий.

1. Классическое определение вероятности

Для начала надо вспомнить саму формулу, по которой будем считать. Итак, вероятность находится как $P=m/n$, где $n$ — число всех равновозможных элементарных исходов нашего случайного эксперимента с подбрасыванием, а $m$ — число тех исходов, которые благоприятствуют событию (то есть тому, что указано в условии задачи). Но как найти эти загадочные исходы? Проще всего пояснить на примерах.

Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Итак, монету бросают дважды. Если обозначить буквой Р выпадение решки (цифры), а буквой О — выпадение орла (герба), то все возможные выпадения можно записать так: РР, ОР, РО и ОО (соответствено, выпали две решки, орел потом решка, решка потом орел и два орла). Подсчитываем число этих комбинаций и получаем $n=4$. Теперь из них надо отобрать только те, что удовлетворяют условию «орел выпадет ровно один раз», это комбинации ОР и РО и их ровно $m=2$. Тогда искомая вероятность равна $P=2/4=1/2=0.5$. Готово!

Пример 2. Дважды бросают симметричную монету. Найти вероятность того, что оба раза выпала одна сторона.

Так как монета снова подбрасывается два раза, множество всех элементарных исходов эксперимента (или комбинаций, как мы их называем здесь для удобства), точно такое же: РР, ОР, РО и ОО, $n=4$. А вот условию «оба раза выпала одна сторона» удовлетворяют другие комбинации: РР и ОО, откуда $m=2$. Нужная вероятность равна $P=2/4=1/2=0.5$.

Как видим, все довольно просто. Перейдем к чуть более сложной задаче.

Пример 3. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.

Снова применим формулу классической вероятности. Шаг первый — выписываем все возможные комбинации уже для 3 бросков! Это будут: ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР. Смотри-ка, бросков всего на один больше, а комбинаций возможных уже $n=8$ (кстати, они находятся по формуле $n=2^k$, где $k$ — число бросков монеты).

Теперь из этого списка надо оставить только те комбинации, где О встречается 2 раза, то есть: ООР, ОРО, РОО, их будет $m=3$. Тогда вероятность события $P=m/n=3/8=0.375$.

Взяли разгон и переходим к 4 монетам.

Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.

Приступаем к вычислению. Шаг первый — выписываем все возможные комбинации для 4 бросков монеты. Чтобы проверить себя, сразу подсчитаем, что их должно получиться $n=2^4=16$ штук! Вот они:

OOOO, OOOP, OOPO, OOPP, OPOO, OPOP, OPPO, OPPP,
POOO, POOP, POPO, POPP, PPOO, PPOP, PPPO, PPPP.

Теперь выбираем те, где герб (он же орел, он же буква О) встречается 2 или 3 раза:
OOOP, OOPO, OOPP, OPOO, OPOP, OPPO, POOO, POOP, POPO, PPOO,

их будет $m=10$. Тогда вероятность равна $P=m/n=10/16=5/8=0.625$.

Думаю, к этому времени вы уже поняли суть метода и сможете сами решить задачи, где бросаются 2-3-4 монеты и орел не выпадает ни разу, или решка ровно один раз и т.п.

2. Комбинаторика + классическая вероятность

Надо заметить, что если действовать исключительно переборным методом (как это делалось выше), с ростом числа монет быстро растет число комбинаций (для 5 монет — 32, для 6 монет — 64 и так далее), так что и вероятность ошибиться при выписывании исходов велика, метод решения теряет свою простоту и привлекательность.

Один из способов решения этой проблемы — остаться в рамках формулы классической вероятности, но использовать комбинаторные методы (см. формулы комбинаторики тут) для подсчета числа исходов. Поясню на примере последней задачи, решив ее другим способом.

Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.

Найдем количество всех равновозможных элементарных исходов эксперимента, заключающегося в бросании 4 монет. Все исходы можно закодировать некоторой последовательностью вида $X_1 X_2 X_3 X_4$, где $X_i=O$ (в $i$-ый раз выпал орел) или $X_i=P$ (в $i$-ый раз выпала решка). Найдем число всех таких последовательностей. Значение $X_1$ (результат первого броска) может быть выбран 2 способами (орел или решка), значение $X_2$ (результат второго броска) может быть выбран 2 способами (орел или решка), и так далее. Итого получим всего $n=2cdot 2cdot 2cdot 2=16$ различных исходов. Или, если использовать формулу комбинаторики для числа размещений с повторениями из 2 объектов по 4 позициям, сразу получим $n=A_4^2=2^4=16$.

Найдем число благоприятствующих исходов с использованием комбинаторики. Сначала найдем число таких последовательностей, где О встречается ровно 2 раза. Выбираем $C_4^2$ способами 2 позиции, где будет стоять О (на остальных тогда ставим решки). Аналогично для последовательностей, где О встречается ровно 3 раза — $C_4^3$ способами выбираем 3 позиции, где будет стоять О (на оставшейся позиции записывается решка). Подсчитывая число сочетаний и складывая, найдем количество благоприятствующих комбинаций:
$$
m=C_4^2+C_4^3=frac{4!}{2!2!}+frac{4!}{3!1!}=frac{3cdot 4}{1cdot 2}+4=6+4=10.
$$
Итого получаем такое же значение вероятности: $P=m/n=10/16=0.625$.

Конечно, этот подход кажется сложнее из-за более формального математического описания решения, но гораздо легче масштабируется.

Например, если рассмотреть подобную задачу:

Пример 5. Монету бросают 8 раз. Найти вероятность того, что герб выпадет ровно 4 раза

Ответ можно получить без выписывания 256 комбинаций (!!!), просто по аналогии с примером выше:
$$
n=2^8=256;\
m=C_8^4=frac{8!}{4!4!}=frac{5cdot 6cdot 7 cdot 8}{1cdot 2 cdot 3 cdot 4}=70;\
P=frac{n}{n}=frac{70}{256}=0.273.
$$

Ради полноты изложения приведу еще пример задачи, решаемой подобным образом (но если хотите, можете сразу переходить к более простому способу 3).

Пример 6. Монету подбрасывают 6 раз. Найти вероятность того, что гербы выпадут два раза и только подряд, а в остальные разы будут только решки.

Найдем количество всех равновозможных элементарных исходов эксперимента, заключающегося в бросании 6 монет. Так как каждый бросок дает 2 возможных исхода (О или Р), всего получим $n=2^6=64$ элементарных исхода (комбинации вида ОРОРОР, ОООРРР и т.д.).

Найдем число благоприятствующих исходов. Мысленно объединим два герба, которые должны появиться рядом, в один объект (ОО). Остается выбрать ему место среди остальных 4 решек (так гербов должно выпасть 2, то решек — 6-2=4). Существует $m=C_5^1=5$ способов выбрать позицию в последовательности из 5 объектов. Для наглядности, если выбрана позиция 2, то есть оба герба стоят на втором месте, это комбинация Р(ОО)РРР, если выбрана позиция 4 — РРР(ОО)Р.
Искомая вероятность: $P=m/n=5/64=0.078$.

Способ 3. Формула Бернулли

Рассмотрим общую задачу о подбрасывании монет.

Пусть бросается $n$ монет (или, что тоже самое, монета бросается $n$ раз). Нужно вычислить вероятность того, что герб появится в точности $k$ раз.

Так как броски монет — события независимые (результат броска одной монеты не влияет на последующие броски), вероятность выпадения герба в каждом броске одинакова (и равна $p=1/2=0.5$), то можно для вычисления вероятности применить формулу Бернулли:
$$
P=P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot left(1/2right)^k cdot left(1-1/2right)^{n-k}=C_n^k cdot left(1/2right)^n.
$$

То есть, мы вывели общую формулу, дающую ответ на вопрос «какова вероятность того, что герб появится в точности $k$ раз из $n$» (запишем в трех эквивалентных видах, выбирайте удобный для себя):
$$
P=C_n^k cdot left(1/2right)^n=frac{C_n^k}{2^n}=C_n^k cdot 0.5^n, quad C_n^k=frac{n!}{k!(n-k)!}.
$$

А теперь все задачи решаются проще простого, вот глядите!

Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Подставляем $n=2, k=1$ и получаем $P=C_2^1 cdot left(1/2right)^2=2 cdot frac{1}{4}=frac{1}{2}=0.5.$

Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.

Это уже третий способ решения задачи!
Подставляем $n=4, k=2$ и $k=3$, получаем
$$P=C_4^2 cdot left(1/2right)^4+C_4^3 cdot left(1/2right)^4=(6+4) cdot frac{1}{16}=frac{10}{16}=0.625.$$

Пример 7. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.

Подставляем $n=3, k=0$ и получаем $P=C_3^0 cdot left(1/2right)^3=1 cdot frac{1}{8}=frac{1}{8}=0.125.$

Пример 8. Пусть бросают 8 монет. Найти вероятность того, что орел не менее 7 раз.

Подставляем $n=8, k=7$ и $k=8$ и получаем
$$P=C_8^8 cdot left(1/2right)^8+ C_8^7 cdot left(1/2right)^8=(1+8) cdot frac{1}{256}=frac{9}{256}=0.035.$$

Таким образом, используя одну простейшую формулу, можно решать множество задач, причем неважно, 3 монеты бросается, или 30, сложность расчетов примерно одинакова. Но, если число бросков становится очень большим, удобнее использовать приближенные формулы Муавра-Лапласа, о которых можно узнать здесь.

Пригодится: онлайн калькулятор для формулы Бернулли

Полезные ссылки

Онлайн калькуляторы Онлайн учебник Более 200 примеров Решенные контрольные

Формулы и таблицы Сдача тестов Решение на заказ Онлайн помощь

Решебник по вероятности

А здесь вы найдете более 200 задач о бросании монет с полными решениями (вводите часть текста для поиска своей задачи):

22 февраля 2022

В закладки

Обсудить

Жалоба

Задачи с монетой по теории вероятностей на профильном ЕГЭ по математике

Задание №2.

1) В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет хотя бы 1 раз.

2) В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.

Теория: zadachi_s_monetoy.pdf

Источник: vk.com/clubinnaleonidovna

Задание 3. Теория вероятностей на ЕГЭ по математике.

Мы начнем с простых задач и основных понятий теории вероятностей.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Вы выиграли в лотерею — случайное событие. Пригласили друзей отпраздновать выигрыш, а они по дороге к вам застряли в лифте — тоже случайное событие. Правда, мастер оказался поблизости и освободил всю компанию через десять минут — и это тоже можно считать счастливой случайностью…

Наша жизнь полна случайных событий. О каждом из них можно сказать, что оно произойдет с некоторой вероятностью. Скорее всего, вы интуитивно знакомы с этим понятием. Теперь мы дадим математическое определение вероятности.

Начнем с самого простого примера. Вы бросаете монетку. Орел или решка?

Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.

Орел и решка — два возможных исхода испытания.

Орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна .

Бросим игральную кость. У кубика шесть граней, поэтому возможных исходов тоже шесть.

Например, вы загадали, что выпадет три очка. Это один исход из шести возможных. В теории вероятностей он будет называться благоприятным исходом.

Вероятность выпадения тройки равна (один благоприятный исход из шести возможных).

Вероятность четверки — тоже .

А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.

Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.

Очевидно, что вероятность не может быть больше единицы.

Вот другой пример. В пакете  яблок, из них  — красные, остальные — зеленые. Ни формой, ни размером яблоки не отличаются. Вы запускаете в пакет руку и наугад вынимаете яблоко. Вероятность вытащить красное яблоко равна , а зеленое — .

Вероятность достать красное или зеленое яблоко равна .
 

БЕСПЛАТНЫЙ МИНИ-КУРС ПО ТЕОРВЕРУ

Определение вероятности. Простые задачи из вариантов ЕГЭ.

Разберем задачи по теории вероятностей, входящие в сборники для подготовки к ЕГЭ.

В фирме такси в данный момент свободно  машин:  красных,  желтых и  зеленых. По вызову выехала одна из машин, случайно оказавшихся ближе всего к заказчице. Найдите вероятность того, что к ней приедет желтое такси.

Всего имеется  машин, то есть к заказчице приедет одна из пятнадцати. Желтых — девять, и значит, вероятность приезда именно желтой машины равна , то есть .

 В сборнике билетов по биологии всего  билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.

Очевидно, вероятность вытащить билет без вопроса о грибах равна , то есть .

Родительский комитет закупил  пазлов для подарков детям на окончание учебного года, из них  с картинами известных художников и  с изображениями животных. Подарки распределяются случайным образом. Найдите вероятность того, что Вовочке достанется пазл с животным.

Задача решается аналогично.

Ответ: .

В чемпионате по гимнастике участвуют  спортсменок: — из России,  — из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая последней, окажется из Китая.

Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется двадцатый номер. Вероятность того, что его вытянет китайская спортсменка, равен (поскольку из Китая —  спортсменок). Ответ: .

Ученика попросили назвать число от  до . Какова вероятность того, что он назовет число кратное пяти?

Каждое пятое число из данного множества делится на . Значит, вероятность равна .

Брошена игральная кость. Найдите вероятность того, что выпадет нечетное число очков.

 — нечетные числа;  — четные. Вероятность нечетного числа очков равна .

Ответ: .

Монета брошена три раза. Какова вероятность двух «орлов» и одной «решки»?

Заметим, что задачу можно сформулировать по-другому: бросили три монеты одновременно. На решение это не повлияет.

Как вы думаете, сколько здесь возможных исходов?

Бросаем монету. У этого действия два возможных исхода: орел и решка.

Две монеты — уже четыре исхода:

орел	орел
орел	решка
решка	орел
решка	решка

Три монеты? Правильно,  исходов, так как .

Вот они:

орел	орел	орел
орел	орел	решка
орел	решка	орел
решка	орел	орел
орел	решка	решка
решка	орел	решка
решка	решка	орел
решка	решка	решка

Два орла и одна решка выпадают в трех случаях из восьми.

Ответ: .

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет  очков. Результат округлите до сотых.

Бросаем первую кость — шесть исходов. И для каждого из них возможны еще шесть — когда мы бросаем вторую кость.

Получаем, что у данного действия — бросания двух игральных костей — всего  возможных исходов, так как .

А теперь — благоприятные исходы:

Вероятность выпадения восьми очков равна .

Стрелок попадает в цель с вероятностью . Найдите вероятность того, что он попадёт в цель четыре выстрела подряд.

Если вероятность попадания равна  — следовательно, вероятность промаха . Рассуждаем так же, как и в предыдущей задаче. Вероятность двух попадания подряд равна . А вероятность четырех попаданий подряд равна .

Лень разбираться самому?
Присоединяйся к мини-курсу по теории вероятностей

ПОДРОБНЕЕ

Вероятность: логика перебора.

 В кармане у Пети было монеты по  рублей и  монеты по  рублей. Петя не глядя переложил какие-то  монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.

Мы знаем, что вероятность события равна отношению числа благоприятных исходов к общему числу исходов. Но как посчитать все эти исходы?

Можно, конечно, обозначить пятирублевые монеты цифрами , а десятирублевые цифрами  — а затем посчитать, сколькими способами можно выбрать три элемента из набора .

Однако есть более простое решение:

Кодируем монеты числами: ,  (это пятирублёвые),  (это десятирублёвые). Условие задачи можно теперь сформулировать так:

Есть шесть фишек с номерами от  до . Сколькими способами можно разложить их по двум карманам поровну, так чтобы фишки с номерами  и  не оказались вместе?

Давайте запишем, что у нас в первом кармане.

Для этого составим все возможные комбинации из набора . Набор из трёх фишек будет трёхзначным числом. Очевидно, что в наших условиях  и  — это один и тот же набор фишек. Чтобы ничего не пропустить и не повториться, располагаем соответствующие трехзначные числа по возрастанию:

…

А дальше? Мы же говорили, что располагаем числа по возрастанию. Значит, следующее — , а затем:

.

Все! Мы перебрали все возможные комбинации, начинающиеся на . Продолжаем:

.

Всего  возможных исходов.

У нас есть условие — фишки с номерами  и  не должны оказаться вместе. Это значит, например, что комбинация нам не подходит — она означает, что фишки  и  обе оказались не в первом, а во втором кармане. Благоприятные для нас исходы — такие, где есть либо только , либо только . Вот они:

134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 – всего  благоприятных исходов.

Тогда искомая вероятность равна .

Ответ: .

Сумма событий, произведение событий и их комбинации

Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Проработав год, чайник может либо сломаться на второй год, либо благополучно служить и после 2 лет работы.
Пусть – вероятность того, что чайник прослужил больше года.

– вероятность того, что он сломается на второй год, – вероятность того, что он прослужит больше двух лет.

Очевидно,

Тогда

Ответ: 0,06.

События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.

Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.

Вероятность суммы несовместных событий равна сумме их вероятностей.

В нашей задаче события «чайник сломался на второй год работы» и «чайник работает больше двух лет» — несовместные. Чайник или сломался, или остается в рабочем состоянии.

На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук выйдет через выход А.

Пронумеруем развилки, на которых паук может случайным образом свернуть в ту или другую сторону.

Он может либо выйти в выход D, и вероятность этого события равна Либо уйти дальше в лабиринт. На второй развилке он может либо свернуть в тупик, либо выйти в выход В (с вероятностью На каждой развилке вероятность свернуть в ту или другую сторону равна а поскольку развилок пять, вероятность выбраться через выход А равна то есть 0,03125.

События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.

В нашей задаче так и есть: неразумный паук сворачивает налево или направо случайным образом, независимо от того, что он делал до этого.

Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.

(А) Два грузовика, работая совместно, вывозят снег с улицы Нижняя Подгорная, причем первый грузовик должен сделать три рейса с грузом снега, а второй — два. Вероятность застрять с грузом снега при подъеме в горку равна 0,2 для первого грузовика и 0,25 — для второго. С какой вероятностью грузовики вывезут снег с улицы Нижняя Подгорная, ни разу не застряв на горке?

Вероятность для первого грузовика благополучно одолеть горку Для второго Поскольку первый грузовик должен сделать 3 рейса, а второй – два, грузовики ни разу не застрянут на горке с вероятностью

Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Нарисуем все возможные исходы ситуации. Покупатель пришел в магазин, который принадлежит агрофирме, и купил яйцо. Надо найти вероятность того, что это яйцо из первого хозяйства.

Яйца могут быть только или из первого домашнего хозяйства, или из второго, причем эти два события несовместны. Других яиц в этот магазин не поступает.

Пусть вероятность того, что купленное яйцо из первого хозяйства, равна . Тогда вероятность того, что яйцо из второго хозяйства (противоположного события), равна .

Яйца могут быть высшей категории и не высшей.
В первом хозяйстве 40% яиц имеют высшую категорию, а 60% — не высшую. Это значит, что случайно выбранное яйцо из первого хозяйства с вероятностью 40% будет высшей категории.

Во втором хозяйстве 20% яиц высшей категории, а 80% — не высшей.

Пусть случайно выбранное в магазине яйцо — из первого хозяйства и высшей категории. Вероятность этого события равна произведению вероятностей:

Вероятность того, что яйцо из второго хозяйства и высшей категории, равна

Если мы сложим эти две вероятности, мы получим вероятность того, что яйцо имеет высшую категорию. По условию, высшую категорию имеют 35% яиц, значит, эта вероятность равна 0,35.

Мы получили уравнение:

Решаем это уравнение и находим, что – вероятность того, что яйцо, купленное у этой агрофирмы, оказалось из первого хозяйства.

Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

С чем пришел пациент в клинику? – С подозрением на гепатит. Возможно, он действительно болен гепатитом, а возможно, у его плохого самочувствия другая причина. Может быть, он просто съел что-нибудь. Вероятность того, что он болен гепатитом, равна 0,05 (то есть 5%). Вероятность того, что он здоров, равна 0,95 (то есть 95%).

Пациенту делают анализ. Покажем на схеме все возможные исходы:

Если он болен гепатитом, анализ дает положительный результат с вероятностью 0,9. То есть анализ покажет: «есть гепатит».
Заметим, что анализ не во всех случаях выявляет гепатит у того, кто действительно им болен. С вероятностью 0,1 анализ не распознает гепатит у больного.

Более того. Анализ может ошибочно дать положительный результат у того, кто не болеет гепатитом. Вероятность такого ложного положительного результата 0,01. Тогда с вероятностью 0,99 анализ даст отрицательный результат, если человек здоров.

Найдем вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

Благоприятные для этой ситуации исходы: человек болен, и анализ положительный (вероятность одновременного наступления этих двух событий равна ), или человек здоров, и анализ ложный положительный (вероятность одновременного наступления этих двух событий равна ). Так как события «человек болен» и «человек не болен» несовместны, то вероятность того, что результат анализа будет положительным, равна

Ответ: 0,0545.

Чтобы поступить в институт на специальность «Лингвистика», абитуриент З. должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.

Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Заметим, что в задаче не спрашивается, будет ли абитуриент по фамилии З. учиться и лингвистике, и коммерции сразу и получать два диплома. Здесь надо найти вероятность того, что З. сможет поступить хотя бы на одну из двух данных специальностей – то есть наберет необходимое количество баллов.
Для того чтобы поступить хотя бы на одну из двух специальностей, З. должен набрать не менее 70 баллов по математике. И по русскому. И еще – обществознание или иностранный.
Вероятность набрать 70 баллов по математике для него равна 0,6.
Вероятность набрать баллы по математике и русскому равна

Разберемся с иностранным и обществознанием. Нам подходят варианты, когда абитуриент набрал баллы по обществознанию, по иностранному или по обоим. Не подходит вариант, когда ни по языку, ни по «обществу» он не набрал баллов. Значит, вероятность сдать обществознание или иностранный не ниже чем на 70 баллов равна

В результате вероятность сдать математику, русский и обществознание или иностранный равна Это ответ.

Чтобы полностью освоить тему, смотрите видеокурс по теории вероятностей. Это бесплатно.

Еще задачи ЕГЭ по теме «Теория вероятностей».

Смотрите также: парадокс Монти Холла.

Сборник задач по теории вероятностей

(с решениями)

Разработка предназначена для   учащихся  9–11  классов для подготовки к ОГЭ и ЕГЭ по математике.

УМК любой

Цель: показать решение типовых задач по данной теме, закрепить умение учащихся решать данные задачи, подготовить учеников к сдаче ОГЭ и ЕГЭ

Методические рекомендации по использованию ресурса:                    Работу можно применить:

• при проведении урока по систематизации и закреплении знаний учащихся
• при проведении консультаций.

Источники информации:                                                       Открытый банк ЕГЭ ФИПИ  http://fipi.ru/                                                       

Теория вероятностей

Классическое определение вероятности
Вероятностью события A называется отношение числа благоприятных для A исходов к числу всех равновозможных исходов: Р (А) =  
где n — общее число равновозможных исходов, m — число исходов, благоприятствующих событию A.
Противоположные события
Событие, противоположное событию A, обозначают Ā. При проведении испытания всегда происходит ровно одно из двух противоположных событий и  
   Объединение несовместных событий
Два события A и B называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию A, так и событию B.
Если события A и B несовместны, то вероятность их объединения равна сумме вероятностей событий  A и B:               P(A U B) =P(A) + P(B)                          

Пересечение независимых событий
Два события A и B называют независимыми, если вероятность каждого из них не зависит от появления или непоявления другого события.
Событие C называют пересечением событий A и B                     (пишут C = A∩B), если событие C означает, что произошли оба события A и B.
Если события A и B независимы, то вероятность их пересечения равна произведению вероятностей  событий A и B:
 P(A∩B) = P(A) • P(B)

Формула сложения вероятностей совместных событий:

                           P(A U B) =P(A) + P(B)  – P(A∩B)

1. Из 1000 собранных на заводе телевизоров 5 штук бракованных. Эксперт проверяет один наугад выбранный телевизор из этой 1000. Найдите вероятность того, что проверяемый телевизор окажется бракованным.
 Решение.  При выборе телевизора наугад возможны 1000 исходов, событию A «выбранный телевизор — бракованный» благоприятны 5 исходов. По определению вероятности                       P(A) = 5÷1000 = 0,005. Ответ: 0,005.

2. В урне 9 красных, 6 жёлтых и 5 зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?                                                                       Решение. Общее число исходов равно числу шаров: 9 + 6 + 5 = 20. Число исходов, благоприятствующих данному событию, равно 6. Искомая вероятность равна 6÷20 = 0,3.  Ответ: 0,3.

 3. Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.

Решение. Вероятность события равна отношению количества благоприятных случаев к количеству всех случаев. Благоприятными случаями являются 3 случая, когда игру начинает Петя, Игорь или Антон, а количество всех случаев 6. Поэтому искомое отношение равно 3:6=0,5. Ответ: 0,5.

4. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

Решение: Обозначим через А событие «команда России во второй группе». Тогда количество благоприятных событий m  = 4 (четыре карточки с номером 2), а общее число равновозможных событий n = 16 (16 карточек) по определению вероятности         Р= 4: 16 = 0,25. Ответ:0,25

5.  В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.

Решение. Всего спортсменов 11 + 6 + 3 = 20 человек. Поэтому вероятность того, что первым будет стартовать спортсмен не из России равна 9:20 = 0,45. Ответ: 0,45.

 6. На каждые 1000 электрических лампочек приходится 5 бракованных. Какова вероятность купить исправную лампочку? 

Решение. На каждые 1000 лампочек приходится 5 бракованных, всего их 1005. Вероятность купить исправную лампочку будет равна доле исправных лампочек на каждые 1005 лампочек, то есть  1000:1005=0,995.Ответ: 0,995.

7. В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт  в магазин? 6 : 8=0,75.

8. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?

Решение. Каждая команда попадет в группу с вероятностью 0,25. Таким образом, вероятность того, что команда не   попадает в группу равна 1-0,25=0,75. Ответ:0,75

9. На турнир по шахматам прибыло 26 участников в том числе Коля и Толя. Для проведения жеребьевки первого тура участников случайным образом разбили на две группы по 13 человек. Найти вероятность того, что Коля и Толя попадут в разные группы.                                                                                               Решение. Всего 26 мест. Пусть Коля займет случайное место в любой группе. Останется 25 мест, из них в другой группе 13. Исходом считаем выбор места для Толи. Благоприятных исходов 13. Р=13/25 = 0,52. Ответ:0,52                                                                     

10. В классе 16 учащихся, среди них два друга —Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе.                                                                    Решение. Если Сергею первому досталось некоторое место, то Олегу остаётся 15 мест. Из них 3 — в той же группе, где Сергей. Искомая вероятность равна 3/15. Ответ:0,2                                                                                                     

11. В классе 21 учащийся, среди них два друга — Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.                                                                                                        Решение. Пусть один из друзей  находится в некоторой группе. Вместе с ним в группе окажутся 6 человек из 20 оставшихся учащихся. Вероятность того, что друг  окажется среди этих 6 человек, равна 6 : 20 = 0,3.          Ответ: 0,3

12. Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 спортсменов, среди которых 7 участников из России, в том числе Платон Карпов. Найдите вероятность того, что в первом туре Платон Карпов будет играть с каким-либо спортсменом из России? 6:15=0,4. Ответ:0,4.                                                                       

13. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 участника из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России?   2: 25=0,08. Ответ: 0,08.

14. В классе 26 учащихся, среди них два друга —   Сергей и Андрей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Сергей и Андрей окажутся в одной группе. Ответ  12 : 25 = 0,48.

15. В классе 21 ученик, среди них 2 друга – Тоша и Гоша. На уроке физкультуры класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Тоша и Гоша попали в одну группу. Ответ 6 : 20 = 0,3.

16. В классе 21 учащийся, среди них две подруги — Аня и Нина. Класс случайным образом делят на семь групп, по 3 человека в каждой. Найдите вероятность того, что Аня и Нина окажутся в одной группе.             Ответ: 2: 20 = 0,1.                                                     

17. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.                                                      Ответ. 6 : 12= 0,5 ( 6 делений между 12 и 7, всего 12 делений)

18. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 6, но не дойдя до отметки 9 часов. 3:12 = 0,25

 При решении задач с монетами число всех возможных исходов можно посчитать по формуле  п=2ª, где α –количество бросков

19.   В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орел выпадет ровно 1 раз.

Решение. Всего возможны четыре исхода: решка-решка, решка-орёл, орёл-решка, орёл-орёл. Орёл выпадает ровно один раз в двух случаях, поэтому вероятность того, что орёл выпадет ровно один раз равна  2:4=0,5.  Ответ: 0,5.

20. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу. Ответ: 1:4=0,25

21. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл не выпадет ни разу.  Решение. 1:8=0,125  Ответ. 0,125                                                                                    

22. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно 2 раза.                                                                           Решение. Составим список возможных вариантов. Бросают 2 раза может выпасть О — Орел, Р — Решка:
ОО, ОР, РО, РР. Всего 4 исхода из них только один случай удовлетворяет условию.   Вероятность (P) = 1 / 4 = 0.25.   Ответ: 0.25

23. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что решка не выпадет ни разу.                                                                            Решение. Всего исходов   = 16, благоприятных  1 ( ОООО).  1:16 = 0,0625. Ответ: 0,0625                                                                                     

При решении задач с кубиками число всех возможных исходов можно посчитать по формуле  п=6ª, где α –количество бросков 

24. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.                                                                                                          Решение. При бросании кубика равновозможных  шесть различных исходов. Событию «выпадет нечётное число очков» удовлетворяют три случая: когда на кубике выпадает 1, 3 или 5 очков. Поэтому вероятность того, что на кубике выпадет нечётное число очков равна 3:6=0,5. Ответ: 0,5.

25.  Определите вероятность того, что при бросании кубика выпало число очков, не большее 3.

Решение. При бросании кубика равновозможны шесть различных исходов. Событию «выпадет не больше трёх очков» удовлетворяют три случая: когда на кубике выпадает 1, 2, или 3 очка. Поэтому вероятность того, что на кубике выпадет не больше трёх очков равна  3:6=0,5 Ответ: 0,5.                                                                  

26. Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.

Решение. При бросании кубика 6²= 36 различных исходов. Событию «выпадет больше трёх очков» удовлетворяют три случая: когда на кубике выпадает 4, 5, или 6 очков , благоприятных исходов 9 (4,4; 4,5; 4,6; 5,4; 5,5; 5,6;  6,4; 6,5; 6,6.)                       Ответ: 9: 36 = 0,25.

27. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.                                      Решение. При бросании кубика 6³= 216  различных исходов, благоприятных  14.  14 : 216 = 0,07.  Ответ: 0,07.     

28.   Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.

Решение. Всего трехзначных чисел 900. На пять делится каждое пятое их них, то есть таких чисел 900:5=180. Вероятность того, что Коля выбрал трехзначное число, делящееся на 5, определяется отношением количества трехзначных чисел, делящихся на 5, ко всему количеству трехзначных чисел: 180:900=0,2.  Ответ: 0,2.

29.Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?

Решение. Всего было подготовлено 50 билетов. Среди них 9 были однозначными. Таким образом, вероятность того, что наугад взятый учеником билет имеет однозначный номер равна 9:50=0,18. Ответ: 0,18.

30. В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?

Решение. Всего в мешке жетонов — 50. Среди них 45 имеют двузначный номер. Таким образом, вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число равна  45 : 50 = 0,9.  Ответ: 0.9. 

31. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на 3?                                           3 : 10 = 0,3.  Ответ: 0,3.

Противоположные события.

32.  Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Решение. Вероятность того, что ручка пишет хорошо, равна 1 − 0,19 = 0,81.  Ответ: 0,81.

  33. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8°C     равна 0,87. Найдите вероятность того, что в случайный момент времени у здорового человека температура тела окажется 36,8°C или выше.  Ответ. 1-0,87=0,13                                    

34. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.

Решение. По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035. Ответ: 0,035.

Несовместные и независимые события.                                                 35. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.                                          Решение. Суммарная вероятность несовместных событий равна сумме вероятностей этих событий: P=0,6+ 0,1 = 0,7.  Ответ: 0,7.

36. Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.

Решение. Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:  P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07. Ответ: 0,07.

                                                                                                                       37. Вероятность того, что на тесте по химии учащийся П. верно решит больше 8 задач, равна 0,48. Вероятность того, что П. верно решит больше 7 задач, равна 0,54. Найдите вероятность того, что П. верно решит ровно 8 задач. Решение. Вероятность решить несколько задач складывается из суммы вероятностей решить каждую из этих задач. Больше 8:  решить 9-ю, 10-ю … Больше 7:  решить 8-ю, 9-ю, 10-ю …Вероятность решить 8-ю = 0,54-0,48=0,06.  Ответ:0.06

38. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет меньше 4?    Ответ: 4 : 10 = 0,4.

 39. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Решение. Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна 0,8•0,8•0,8•0,2•0,2=0,02048.  Ответ:0.02048.

40. Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение. Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09. Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91.   Ответ: 0,91.

41. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

Решение. Вероятность того, что батарейка исправна, равна 0,94. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,94·0,94 = 0,8836.   Ответ: 0,8836.

42.   Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Решение. Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156.   Ответ: 0,156.

43.   В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).

Решение. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что все три продавца заняты равна                       (0,3)³ = 0,027.    Ответ: 0,027.

   44. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.

Решение. Рассмотрим события A = «в автобусе меньше 15 пассажиров» и  В = «в автобусе от 15 до 19 пассажиров». Их сумма — событие A + B = «в автобусе меньше 20 пассажиров». События A и  В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B).

 Тогда, используя данные задачи, получаем: 0,94 = 0,56 + P(В), откуда P(В) = 0,94 − 0,56 = 0,38.Ответ: 0,38.

45. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.

Ответ: 0,35.

 46.Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение. Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года». События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:  P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B)

 откуда, используя данные из условия, получаем     0,97 = P(A) + 0,89.Тем самым, для искомой вероятности имеем: P(A) = 0,97 − 0,89 = 0,08.   Ответ: 0,08.

 

 47. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.

Решение. Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды: P(XXO) = 0,8·0,8·0,2 = 0,128; P(XOO) = 0,8·0,2·0,8 = 0,128; P(OXO) = 0,2·0,2·0,2 = 0,008;  P(OOO) = 0,2·0,8·0,8 = 0,128.Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:

 P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.   Ответ: 0,392.

48. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. 

Решение. Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025. Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975. Ответ: 0,9975.

 49. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение. Рассмотрим событиеА = кофе закончится в первом автомате, В = кофе закончится во втором автомате.

Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятность х = 0,52. Ответ: 0,9975.

50. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение. Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135. Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055.  Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055 = 0,019.                       Ответ: 0,019.

51. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Решение. Джон попадает в муху, если схватит пристрелянный револьвер и попадет из него, или если схватит непристрелянный револьвер и попадает из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·0,9 = 0,36 и 0,6·0,2 = 0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,36 + 0,12 = 0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Его вероятность равна 1 − 0,48 = 0,52. Ответ. 0,52

 

 52. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.

Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.

Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Решение. В силу независимости событий, вероятность успешно сдать экзамены на лингвистику: 0,6·0,8·0,7 = 0,336, вероятность успешно сдать экзамены на коммерцию: 0,6·0,8·0,5 = 0,24, вероятность успешно сдать экзамены и на «Лингвистику», и на «Коммерцию»: 0,6·0,8·0,7·0,5 = 0,168. Успешная сдача экзаменов на «Лингвистику» и на «Коммерцию» — события совместные, поэтому вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Тем самым, поступить на одну из этих специальностей абитуриент может с вероятностью 0,336 + 0,24 − 0,168 = 0,408.  Ответ: 0,408.

53. По отзывам покупателей Иван Иванович оценил надёжность двух интернет- магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.                                                                                          Решение. Вероятность того, что первый магазин не доставит товар равна 1 − 0,9 = 0,1. Вероятность того, что второй магазин не доставит товар равна 1 − 0,8 = 0,2. Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар) равна произведению вероятностей этих событий: 0,1 · 0,2 = 0,02.  Ответ: 0,02.

54.Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры. Решение. Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5·0,5·0,5 = 0,125.   Ответ: 0,125.

  

55. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

Решение.  Анализ пациента может быть положительным по двум причинам: А) пациент болеет гепатитом, его анализ верен; B) пациент не болеет гепатитом, его анализ ложен. Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем: Р(А)=0,9•0.05=0,045;                                         Р(В)= 0,01•0,95=0,0095  ,Р(А+В)=Р(А)(В)=0,045+0,0095=0,0545.

 Ответ:0,0545.

  56. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.

Решение. Ситуация, при которой батарейка будет забракована, может сложиться в результате событий: A = батарейка действительно неисправна и забракована справедливо или В = батарейка исправна, но по ошибке забракована. Это несовместные события, вероятность их суммы равна сумме вероятностей эти событий. Имеем: Р(А+В)=Р(А)+Р(В)=0,02•0,99+0,98•0,01=0,0198+0,0098=0,0296 Ответ: 0,0296.

 57. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).

Решение. Пусть A — событие, состоящее в том, что мишень поражена стрелком с первого выстрела, B — событие, состоящее в том, что мишень поражена со второго выстрела. Вероятность события A равна P(A) = 0,7. Событие B наступает, если, стреляя первый раз, стрелок промахнулся, а, стреляя второй раз, попал. Это независимые события, их вероятность равна произведению вероятностей этих событий: P(B) = 0,3·0,7 = 0,21. События A и B несовместные, вероятность их суммы равна сумме вероятностей этих событий:  P (A + B) = P(A) + P(B) = 0,7 + 0,21 = 0,91.   Ответ: 0,91.

58.Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А.

Решение. Рассмотрим все возможные исходы жеребьёвки.

 · КомандаА в матче в обоих матчах первой владеет мячом.

 · КомандаА в матче в обоих матчах не владеет мячом первой.

 · КомандаА в матче с командой В владеет мячом первой, а в матче с командой С — второй.

 · КомандаА в матче с командой С владеет мячом первой, а в матче с командой В — второй.

Из четырех исходов один является благоприятным, вероятность его наступления равна 1:4=0,25. Ответ: 0,25.

59. Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.

Решение. Вероятность промаха равна 1 − 0,5 = 0,5. Вероятность того, что стрелок первые три раза попал в мишени равна 0,53 = 0,125. Откуда, вероятность события, при котором стрелок сначала три раза попадает в мишени, а четвёртый раз промахивается равна 0,125 · 0,5 = 0,0625.     Ответ: 0,0625.

60. Перед началом матча по футболу судья бросает монету, чтобы определить, какая из команд будет первой владеть мячом. Команда «Байкал» играет по очереди с командами

«Амур», «Енисей», «Иртыш». Найти вероятность того, что команда «Байкал» будет первой  владеть мячом только в игре с «Амуром».

Решение. Монету бросают 3 раза.

Для команды «Байкал» возможные исходы в трех бросках {О О О},{Р О О}, {О Р О}, {О О Р},                  {Р Р О},{Р О Р}, {О Р Р},{Р Р Р}. Всего исходов 8, благоприятныx1(выпадение орла в первой игре)  {О Р Р, 1:8=0,125.Ответ 0,125.

61.У Пети в кармане лежат  шесть монет: четыре монеты по рублю и две монеты по два рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность  того, что теперь две двухрублевые монеты лежат в одном кармане.

 Решение. Пронумеруем монеты: рублевые – 1, 2, 3, 4;  двухрублевые – 5, 6. {123} {124} {125} {126} {134} {135} {136} {145} {146} {156} {234} {235} {236} {245} {246} {256} {345} {346} {356} {456} 

 n = 20     – число всех исходов .Взять три монеты можно так: (числа в порядке возрастания,чтобы не пропустить комбинацию)  m = 8  – число благоприятных  исходов

(комбинации, в которых монеты 5 и 6 (двухрублевые) не взяты или взяты обе. 8:20=0,4