Задачи егэ планиметрия 1 часть - Помощь в подготовке к экзаменам и поступлению

Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.

Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?

Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №1 являются схемами для решения более сложных геометрических задач.

Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №1 Профильного ЕГЭ по математике.

Тригонометрия в прямоугольном треугольнике

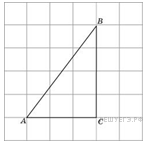
1. B треугольнике ABC угол C равен 90^circ , BC = 15, . Найдите AC.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:

$AC=frac{BC}{tgA}=frac{15}{0,75}=20.$

Ответ: 20.

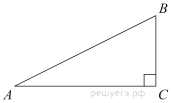
2. B треугольнике ABC угол C равен $90^circ, , tgA=frac{9}{40}, , AC=20$ . Найдите AB.

По определению косинуса угла, $cosA=frac{AC}{AB},AB=frac{AC}{{cos A}}.$

Найдем косинус угла A с помощью формулы:

${tg}^2angle { A+1=}frac{{ 1}}{{cos}^2angle { A}}.$

Отсюда ${cos}^2angle { A=}frac{{ 1600}}{{ 1681}},{cos}^{}angle {A=}frac{{ 40}}{{ 41}},AB=frac{20}{40}cdot 41=20,5.$

Ответ: 20,5.

Треугольники. Формулы площади треугольника.

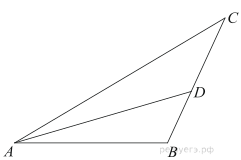
3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен . Найдите угол C. Ответ дайте в градусах.

По условию, угол DBC — внешний угол при вершине B — равен . Тогда угол CBA равен Угол CAB равен углу CBA и тоже равен 58^circ , поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен

4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

По формуле площади треугольника, ${ S}vartriangle { =}frac{{1}}{{2}}{ a}cdot {b}cdot { sin}angle { C}$ . Получим:

$S=frac{1}{2}cdot 10^2 cdot sin30^circ=25$ см2.

Ответ: 25.

Элементы треугольника: высоты, медианы, биссектрисы

5. B треугольнике ABC угол ACB равен 90^circ , угол B равен 58^circ , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда

Углы ACD и DCB в сумме дают 90^circ . Отсюда

6. B остроугольном треугольнике ABC угол равен BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

B треугольниках ACE и OCD угол C — общий, углы A и D равны 90^circ . Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и . Тогда угол DOE — смежный с углом DOC. Он равен

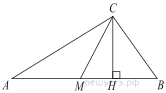
7. Острые углы прямоугольного треугольника равны 24^circ и 66^circ . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.

Тогда

$angle MCH=angle C-angle ACM-angle BCH{ =90^circ -24^circ -}left({ 90^circ -66^circ }right){=42^circ }.$

8. B треугольнике ABC угол A равен 60^circ угол B равен AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Найдем третий угол треугольника ABC — угол C. Он равен

Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть 30^circ и

Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть

9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

По условию, треугольники ADC и ADB — равнобедренные.

Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.

Обозначим угол BAD за х.

Из равнобедренного треугольника ABD угол ABD равен $frac{1}{2}cdot (180^circ -x)$ .

C другой стороны, этот угол равен углу BAC, то есть 2x.

Получим:

$2x=frac{1}{2}cdot (180^circ -x).$
Отсюда ${x }= 36^circ.$

Ответ: 36.

Параллелограмм

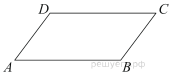
10. B параллелограмме ABCD AB=3, AD=21, $sinA=frac{6}{7}.$ Найдите большую высоту параллелограмма.

Большая высота параллелограмма проведена к его меньшей стороне.

Получим:

$DH=ADsinA=21cdot frac{6}{7}=3cdot 6 =18.$

Ответ: 18.

11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.

Тогда , и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна

Прямоугольник

12. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

Обозначим длины сторон а и b. Тогда периметр равен 2 (a+b) , его площадь равна ab, а квадрат диагонали равен

Получим: , тогда a+b = 4 ,

По формуле квадрата суммы,

Отсюда квадрат диагонали , и длина диагонали AC = 3.

Ответ: 3.

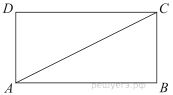
13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит, $HG = EF = frac{5}{2}.$

Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны $frac{5}{2}.$ Тогда HGFE — ромб, и его периметр равен $4cdot frac{5}{2}=10$ .

Трапеция и ее свойства

14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Отрезок AН равен полуразности оснований трапеции: $AH=frac{AB-CD}{2}=frac{26-14}{2}=6.$

Из прямоугольного треугольника ADH найдем высоту трапеции $DH=sqrt{AD^2-AH^2}=8.$

Площадь трапеции равна произведению полусуммы оснований на высоту:

$S=frac{left ( AB+CD right )cdot DH}{2}=160.$

15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим центр окружности и соединим его с точками A, B, C и D.

Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF — высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH — высота трапеции, FH = 7.

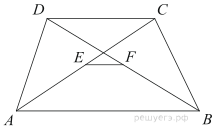
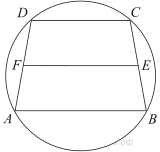
16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем PQ — среднюю линию трапеции,PQ = 2,5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.

PM — средняя линия треугольника ABC, значит, PM = 1.

NQ — средняя линия треугольника BCD, значит, NQ = 1.

Тогда

Ответ: 0,5.

17. Диагонали равнобедренной трапеции перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.

Треугольники AOE и FOC — прямоугольные и равнобедренные,

$OF=FC=frac{1}{2}DC,$

$OE=AE=frac{1}{2}AB.$

Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.

Ответ: 9.

Центральные и вписанные углы

18. Дуга окружности AC, не содержащая точки B, имеет градусную меру , а дуга окружности BC, не содержащая точки A, имеет градусную меру 80^circ . Найдите вписанный угол ACB. Ответ дайте в градусах.

Полный круг — это . Из условия мы получим, что дуга ABC равна Тогда дуга AB, на которую опирается вписанный угол ACB, равна Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть

Ответ: 40.

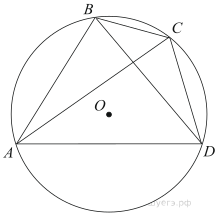
19. Угол ACB равен. 3^circ Градусная величина дуги AB окружности, не содержащей точек D и E, равна . Найдите угол DAE. Ответ дайте в градусах.

Cоединим центр окружности с точками A и B. Угол AОB равен , так как величина дуги AB равна 124 градуса.

Тогда угол ADB равен 62^circ — как вписанный, опирающийся на дугу AB.

Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.

Ответ: 59.

Касательная, хорда, секущая

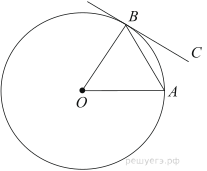
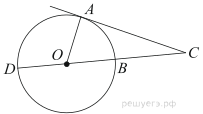
20. Угол между хордой AB и касательной BC к окружности равен Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен 90^circ , и тогда угол ОBA равен Угол ОAB также равен 58^circ , так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен

Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга равна

Ответ: 64.

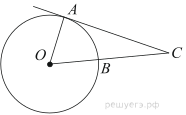
21. Касательные CA и CB к окружности образуют угол ACB, равный . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна , и тогда угол AОB равен

Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна

Bписанные и описанные треугольники

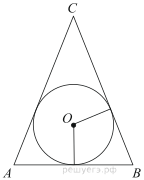
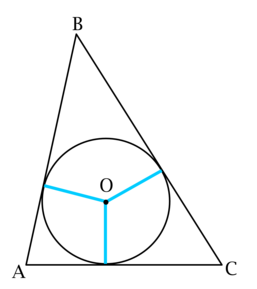
22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Запишем площадь треугольника ABC двумя способами:

, где p — полупериметр, r — радиус вписанной окружности.

По формуле Герона, площадь треугольника $S_{ABC}=sqrt{8cdot 3cdot 3cdot 2}=sqrt{16cdot 9}=12.$

Тогда

$r=frac{2cdot 12}{16}=frac{3}{2}=1,5.$

Ответ: 1,5.

23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.

Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна

Периметр треугольника:

Ответ: 22.

24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

Угол C может быть равен 30^circ или — ведь синусы этих углов равны $frac{1}{2}.$ Однако по рисунку угол C — острый, значит, он равен

Ответ: 30.

25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

По условию, угол C — тупой. Значит, он равен

Ответ: 150.

26. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в прямоугольный треугольник: $r=frac{a+b-c}{2}.$ Гипотенуза равнобедренного прямоугольного треугольника в sqrt{2} раз больше катета. Получим:

$newline r=frac{a+b-c}{2}=frac{2left(82+41sqrt{2}right)-sqrt{2}(82+41sqrt{2})}{2}= newline frac{164+82sqrt{2}-82sqrt{2}-82}{2}=frac{82}{2}=41.$

Ответ: 41.

Bписанные и описанные четырехугольники

27. B четырёхугольник ABCD вписана окружность, AB=10 , CD=16. Найдите периметр четырёхугольника ABCD.

B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,

Тогда периметр четырехугольника равен

Ответ: 52.

28. Cтороны четырехугольника ABCD AB,BC,CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95,49,71,145 градусов.Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен $frac{1}{2}cdot left ( 145^circ + 71^circ right )=108^circ.$

Ответ: 108.

C четырехугольником справились. A с n-угольником?

Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 84^circ . Найдите n.

Рассмотрим треугольник AOB. Он равнобедренный, т.к. AO=OB=R. Значит,

$angle AOB=180^circ -angle ABO - angle BAO = 12^circ, , n=frac{360^circ}{angle AOB}=frac{360^circ}{12^circ}=30.$

Ответ: 30.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 1 Профильного ЕГЭ по математике. Планиметрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Вариант 1 6. Планиметрия

1. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

2. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2.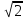

4. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

5. Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

6. Угол между хордой AB и касательной BC к окружности равен 35°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

7. Около трапеции описана окружность. Периметр трапеции равен 24, средняя линия равна 11. Найдите боковую сторону трапеции.

8. Найдите величину угла АВС. Ответ дайте в градусах.

9. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

10. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.

Вариант 2 6. Планиметрия

В 1. Сторона правильного треугольника равна 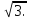Найдите радиус окружности, вписанной в этот треугольник.

2. Две стороны параллелограмма относятся как 9:11, а периметр его равен 40. Найдите большую сторону параллелограмма.

3. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.

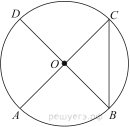
4. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

5. Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.

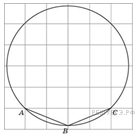
6. Найдите радиус окружности, вписанной в треугольник , считая стороны квадратных клеток равными 1.

7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

8. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

9. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.

10. Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника.

Вариант 3 6. Планиметрия

1. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах.

2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.

3. В треугольнике АВС АС = ВС = 4 , cos ВАС = 0,25. Найдите высоту АН.

4. В ромбе ABCD угол DAB равен 136°. Найдите угол BDC. Ответ дайте в градусах.

5. В треугольнике АВС угол С равен 90°, СН – высота, АС = 3, cos А = . Найдите ВН.

6. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

7. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите

8. Найдите площадь ромба, если его диагонали равны 4 и 12.

9. В треугольнике АВС АС = ВС = 4, угол С равен 30°. Найдите высоту АН.

10. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах

Вариант 4 6. Планиметрия

1. В треугольнике ABC угол C равен 90°, CH — высота, АВ = 15, tg А = . Найдите BH.

2. Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.

3. Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.

4.Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

5. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника.

6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

7. Катеты равнобедренного прямоугольного треугольника равны 82 + 41

Найдите радиус окружности, вписанной в этот треугольник.

8. В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

9. В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4, ВН = 4. Найдите

10. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.

Вариант 5 6. Планиметрия

1. Найдите косинус угла АОВ. В ответе укажите значение косинуса, умноженное на 2.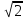

2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

3. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 3, sin А = . Найдите АН.

4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

5. Катеты равнобедренного прямоугольного треугольника равны 2+ Найдите радиус окружности, вписанной в этот треугольник.

6. Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции.

7. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

8.Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.

9. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

10. Стороны параллелограмма равны 38 и 76. Высота, опущенная на первую сторону, равна 57. Найдите высоту, опущенную на вторую сторону параллелограмма.

Вариант 6 6. Планиметрия

1. Сторона АВ треугольника АВС равна 42. Противолежащий ей угол С равен 150° . Найдите радиус окружности, описанной около этого треугольника.

2. Через концы A, B дуги окружности в 114° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

3. В треугольнике АВС АС=ВС, АН – высота, АВ=5, sinВАС= . Найдите

4. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

5. Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.

6. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен Найдите высоту трапеции.

7. В треугольнике ABC угол C равен 90°, АС = 8, cos А = Найдите АВ.

8. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.

9. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

10. В треугольнике ABC угол ACB равен °, угол B равен °, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Вариант 7 6. Планиметрия

1. Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

2. Две стороны параллелограмма относятся как 3:17, а периметр его равен 40. Найдите большую сторону параллелограмма.

3. В треугольнике ABC AC = BC, AB = 22, tg А = . Найдите AC.

4. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.

5. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.

6. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.

7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

8. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

9. Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.

10.Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.

Вариант 8 6. Планиметрия

1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

2. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции.

3. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.

4. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.

5. Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.

6. В треугольнике ABC AC = BC, AB = 8, tg А = . Найдите AC.

7. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.

8. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.

9. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 47.

10. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2

Вариант 9 6. Планиметрия

1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

2. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на

4. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах.

5. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.

6. В треугольнике АВС АС = ВС, АВ = 7 , tg ВАС = , Найдите высоту

7. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 80°. Найдите n.

8. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.

9. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.

10. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла.

Вариант 10 6. Планиметрия

1. Найдите величину угла АВС. Ответ дайте в градусах.

2. В треугольнике ABC угол C равен 76°, AC = BC. Найдите угол A. Ответ дайте в градусах.

3. Площадь треугольника АВС равна 129. ДE – средняя линия, параллельная стороне АВ. Найдите площадь трапеции АВЕД.

4. В треугольнике АВС угол С равен 90°, СН – высота, АН = 12 , cos А = . Найдите АВ.

5. Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника.

6. Основания равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции.

7. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.

8. Хорда AB делит окружность на две части, градусные величины которых относятся как 3:5. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

9. В треугольнике известно, что , , угол равен 90°. Найдите радиус вписанной окружности.

10. В треугольнике АВС АС = ВС = 27 , — высота, sin ВАС = . Найдите

6. Планиметрия

Вариант 1

Вариант 2

Вариант 3

40
2
7,5
22
17,5
160
0,6
24
2
56

Вариант 4

Вариант 5

2
122
17,5
46
1
1,5
2
41
30
28,5

Вариант 6

Вариант 7

150
17
22
0,8
34
10,5
24
55
21
10

Вариант 8

Вариант 9

24
9
1
53
15,5
4
18
141,75
36
1

Вариант 10

45
52
96,75
27
22
26
8
112,5
4
30

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.

а)  докажите, что биссектриса угла С делит отрезок МN пополам

б)  пусть Р  — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.

Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1

Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.

а)  Докажите, что ∠CBE = ∠COE.

б)  Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE  =  24.

Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Известно, что AC  =  3MB.

а)  Докажите, что треугольник ABC прямоугольный.

б)  Найдите сумму квадратов медиан AA₁ и CC₁, если известно, что AC = 12.

На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M  — середина стороны AB.

а)  Докажите, что

б)  Найдите расстояние от точки M до центров квадратов, если AC  =  10, BC  =  32 и ∠ACB  =  30°.

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.

а)  Докажите, что точки A, B, K и E лежат на одной окружности.

б)  Найдите радиус этой окружности, если AB = 12, CH = 5.

Пройти тестирование по этим заданиям

Источник

16. Задачи по планиметрии

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по планиметрии

Задание
1

#2436

Уровень задания: Легче ЕГЭ

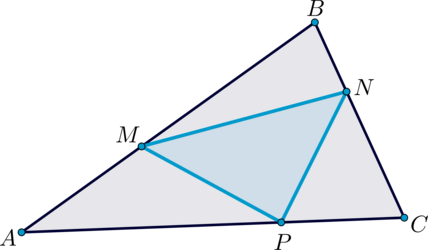
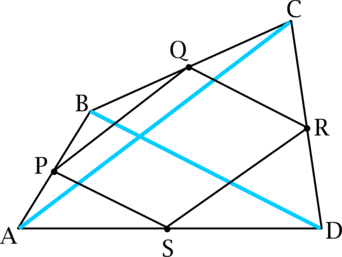
Точки (M, N, P) лежат на сторонах (AB, BC, CA) соответственно треугольника (ABC), причем (AM:AB=BN:BC=CP:CA=1:3). Площадь треугольника (MNP) равна (15). Найдите площадь треугольника (ABC).

(triangle ABC) и (triangle MBN) имеют общий угол (B), при этом (BM=frac23BA), (BN=frac13BC).

Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то

[dfrac{S_{MBN}}{S_{ABC}}=dfrac{frac23BAcdot frac13BC}{BAcdot BC}=
dfrac29 quad Rightarrow quad S_{MBN}=dfrac29S_{ABC}]

Аналогично рассуждая, получаем, что

[S_{MAP}=S_{PCN}=dfrac29S_{ABC}]

Следовательно, [15+3cdot dfrac29S_{ABC}=S_{ABC} quad Rightarrow
quad S_{ABC}=3cdot 15=45.]

Ответ: 45

Задание
2

#2444

Уровень задания: Легче ЕГЭ

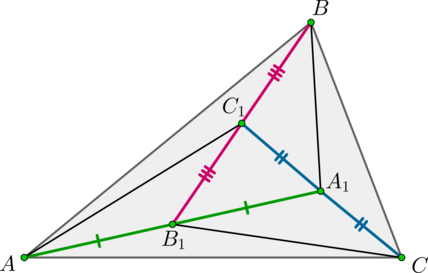
Внутри треугольника (ABC) взяты точки (A_1, B_1, C_1) так, что (B_1) – середина (AA_1), (C_1) – середина (BB_1), (A_1) – середина (CC_1). Найдите отношение площадей треугольников (A_1B_1C_1) и (ABC).

Соединим точки (A) и (C_1), (B) и (A_1), (C) и (B_1).

Т.к. медиана делит треугольник на два равновеликих треугольника, то

[S_{triangle AB_1C}=S_{triangle A_1B_1C}=S_{triangle A_1B_1C_1}.]

Аналогично,

[S_{triangle CA_1B}=S_{triangle C_1A_1B}=S_{triangle AC_1B}=S_{triangle
AC_1B_1}.]

Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,

[S_{triangle A_1B_1C_1}:S_{triangle ABC}=1:7.]

Ответ:

(1:7)

Задание
3

#1760

Уровень задания: Равен ЕГЭ

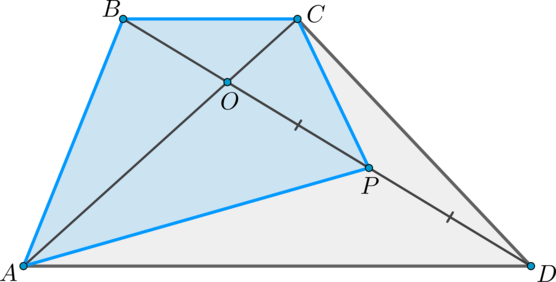
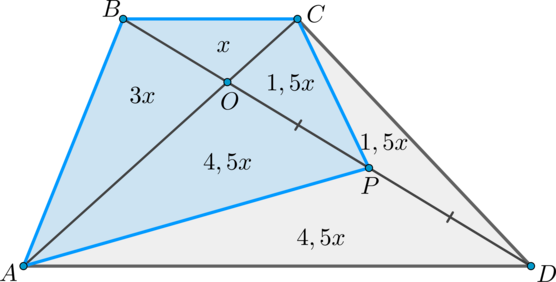
Дана трапеция (ABCD), ее основания (BC) и (AD) равны (2) и (6) соответственно. Диагонали (BD) и (AC) пересекаются в точке (O). Точка (P) – середина (OD). (S_{bigtriangleup ABO}=9). Найдите площадь четырехугольника (ABCP).

Пусть (S_{bigtriangleup BOC}=x). Заметим, что (bigtriangleup BCO
sim bigtriangleup AOD) по двум углам, так как (BCparallel AD), (angle BCA = angle CAD) как накрест лежащие и (angle BOC = angle
AOD) как вертикальные.

Следовательно, [dfrac{BC}{AD} =dfrac{BO}{OD} =dfrac{CO}{OA}
=dfrac{2}{6} =dfrac{1}{3}.]

(dfrac{S_{bigtriangleup ABO}}{S_{bigtriangleup BCO}}
=dfrac{AO}{OC} =dfrac{3}{1} Rightarrow S_{bigtriangleup
ABO}=3x), аналогично, (S_{bigtriangleup CDO}=3x).

(dfrac{S_{bigtriangleup COP}}{S_{bigtriangleup CPD}}
=dfrac{OP}{PD} =dfrac{1}{1} Rightarrow S_{bigtriangleup
COP}=S_{bigtriangleup CPD}=1,5x).

Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, [dfrac{S_{bigtriangleup BOC}}{S_{bigtriangleup AOD}} =left(
dfrac{1}{3} right)^2 =dfrac{1}{9} Rightarrow
S_{bigtriangleup ADO}=9x Rightarrow S_{bigtriangleup APO}=4,5x
Rightarrowqquad S_{ABCP}=10x.] Так как (3x=9), то (x=3) и, следовательно, (S_{ABCP}=30).

Ответ: 30

Задание
4

#2441

Уровень задания: Равен ЕГЭ

Внутри равностороннего треугольника со стороной (m) движется точка. Докажите, что сумма расстояний от этой точки до сторон треугольника не меняется, и найдите эту сумму.

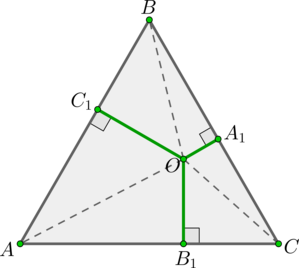
Рассмотрим равносторонний (triangle ABC), (AB=m), (O) – точка внутри треугольника, (OA_1, OB_1, OC_1) — перпендикуляры на стороны (BC, AC, AB) соответственно.

Рассмотрим (triangle AOB, triangle BOC, triangle COA). Их площади равны (0,5mcdot OC_1; 0,5mcdot OA_1; 0,5mcdot OB_1) соответственно. Тогда сумма их площадей равна площади всего (triangle ABC), следовательно:

[0,5mcdot (OC_1+OA_1+OB_1)=S_{triangle ABC}=dfrac{sqrt3}4m^2 quad
Leftrightarrow quad OC_1+OA_1+OB_1=dfrac{sqrt3}2m.]

Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.

Ответ:

(dfrac{sqrt3}2m)

Задание
5

#1287

Уровень задания: Равен ЕГЭ

Радиус вписанной в треугольник (ABC) окружности равен трети одной из его высот.

а) Докажите, что одна из сторон треугольника (ABC) равна среднему арифметическому двух других его сторон.

б) Найдите наибольшее возможное значение периметра такого треугольника, если одна из его сторон равна (4), а две другие имеют целые длины.

а) (S_{ABC} = pcdot r), где (p) – полупериметр, а (r) – радиус вписанной в (ABC) окружности.

Пусть (h) – длина той высоты, которая равна (3r), (a) – длина стороны, высота к которой имеет длину (h), (P) – периметр треугольника (ABC).

В итоге имеем: [dfrac{1}{2}hcdot a = S_{ABC} = pcdot r = pcdotdfrac{h}{3},] откуда (a = dfrac{P}{3}), тогда (b + c = dfrac{2P}{3} = 2a), где (b) и (c) длины других сторон треугольника.

б) Длины сторон треугольника (ABC) образуют арифметическую прогрессию: если обозначить (a — c = d), то (a = c + d), (b = c + 2d).

Пусть (d > 0). Тогда (b) наибольшая сторона треугольника (ABC) и существование треугольника (ABC) с длинами сторон (a), (b) и (c) равносильно выполнению неравенства [b < a + cqquadLeftrightarrowqquad c + 2d < 2c + dqquadLeftrightarrowqquad d < c.] Так как длины всех сторон треугольника (ABC) – целые числа, то (d) – целое, следовательно, (dleq c — 1).

Так как (c) – меньшая из сторон, то (cleq 4), тогда (dleq 3), откуда (aleq 7), (bleq 10), тогда [P_{triangle ABC}leq 4 + 7 + 10 = 21.] При этом случай (c = 4), (a = 7), (b = 10) подходит, следовательно, при (d > 0) максимально возможный периметр равен 21.

При (d = 0) треугольник (ABC) равносторонний и (P_{triangle ABC} = 12 < 21).

Случай (d < 0) рассматривается аналогично (меняется только то, что (c > a > b), следовательно, достаточно в рассуждении из случая (d > 0) всюду поменять местами (b) и (c)).

Таким образом, наибольший возможный периметр треугольника (ABC) равен 21.

Ответ:

б) (21).

Задание
6

#1288

Уровень задания: Равен ЕГЭ

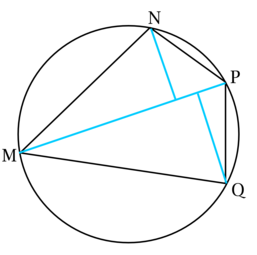
Четырёхугольник (MNPQ) вписан в окружность, причём (dfrac{MN}{PQ} = dfrac{QM}{PN}).

а) Докажите, что точки (N) и (Q) равноудалены от прямой, содержащей (MP).

б) Найдите расстояние от точки (P) до прямой, содержащей (MQ), если (MP = 4), расстояние от (N) до прямой, содержащей (MP) равно (1,5), (MQ = 3).

а) Так как (dfrac{MN}{PQ} = dfrac{QM}{PN}), то (MNcdot PN = QMcdot PQ).

Так как (MNPQ) вписанный, то (angle MNP = 180^circ — angle MQP), следовательно, (sinangle MNP = sinangle MQP).

В итоге [S_{triangle MNP} = 0,5cdot MNcdot PNcdotsinangle MNP = 0,5cdot QMcdot PQcdotsinangle MQP = S_{triangle MQP}.]

С другой стороны, у треугольников (MNP) и (MQP) общее основание, следовательно, их площади относятся как высоты, проведённые к этому основанию, тогда эти высоты равны, значит, точки (N) и (Q) равноудалены от прямой, содержащей (MP).

б) В данном случае (S_{triangle MNP} = 0,5cdot 4cdot 1,5 = 3), но (S_{triangle MNP} = S_{triangle MQP}). Обозначим расстояние от точки (P) до прямой, содержащей (MQ) через (h), тогда [S_{triangle MQP} = 3 = 0,5cdot 3cdot h,] следовательно, (h = 2).

Ответ:

б) (2).

Задание
7

#1289

Уровень задания: Равен ЕГЭ

(ABCD) – выпуклый четырёхугольник, точки (P), (Q), (R) и (S) середины его сторон, причём (PQRS) тоже выпуклый четырёхугольник. (A_1B_1C_1D_1) другой выпуклый четырёхугольник с серединами сторон в точках (P), (Q), (R) и (S).

а) Докажите, что диагонали (PQRS) точкой пересечения делятся пополам.

б) Найдите максимально возможное значение величины (dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}}).

а) Проведём диагонали (AC) и (BD).

Рассмотрим треугольники (APS) и (ABD): (PS) – средняя линия в треугольнике (ABD), тогда треугольники (APS) и (ABD) подобны, причём (dfrac{PS}{BD} = dfrac{1}{2}).

Аналогично (dfrac{QR}{BD} = dfrac{1}{2}), следовательно, (PS = QR).

Аналогично доказывается равенство (PQ = RS). В итоге в выпуклом четырёхугольнике (PQRS) противоположные стороны равны, тогда (PQRS) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.

б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.

Из подобия (APS) и (ABD) получаем: [dfrac{S_{APS}}{S_{ABD}} = left(dfrac{1}{2}right)^2 = dfrac{1}{4}.]

Аналогично (4S_{QCR} = S_{CBD}), (4S_{PBQ} = S_{ABC}), (4S_{SDR} = S_{ACD}). Тогда [S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.] С другой стороны, [S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},] тогда [S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} qquadLeftrightarrow] [S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = dfrac{1}{2}S_{ABCD}.] Но (S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}), откуда окончательно [S_{PQRS} = dfrac{1}{2}S_{ABCD}.]

Таким образом, по взаимному расположению точек (P), (Q), (R), (S) однозначно восстанавливается площадь параллелограмма (PQRS), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках (P), (Q), (R) и (S).

В итоге [dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.]

Ответ:

б) (1).

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задача 3. Начала теории вероятностей

Задача 4. Вероятности сложных событий

Задача 5. Простейшие уравнения

Задача 5. Простейшие уравнения

Задача 6. Вычисления и преобразования

Задача 7. Производная и первообразная

Задача 8. Задачи с прикладным содержанием

Задача 9. Текстовые задачи

Задача 10. Графики функций

Задача 11. Наибольшее и наименьшее значение функций

Источник


3654	В треугольнике ABC угол C равен 90°, CH — высота, BC=5, Cos A=(2sqrt6)/5. Найдите длину отрезка AH Решение	В треугольнике ABC угол C равен 90°, CH — высота, BC=5, Cos A= 2sqrt6 / 5 ! Статград 28-02-2023 11 класс Вариант МА2210309 Задание 1

3636	Четырёхугольник ABCD вписан в окружность. Угол ABC равен 106°, угол CAD равен 69°. Найдите угол ABD. Ответ дайте в градусах Решение	Четырёхугольник ABCD вписан в окружность. Угол ABC равен 106° ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 1

3630	Через концы A и B дуги окружности с центром O проведены касательные CA и CB. Угол CAB равен 39°. Найдите угол AOB. Ответ дайте в градусах Решение	Через концы A и B дуги окружности с центром O проведены касательные CA и CB ! 36 вариантов ФИПИ Ященко 2023 Вариант 24 Задание 1

3624	В четырёхугольник ABCD вписана окружность, AB=13, CD=18. Найдите периметр четырёхугольника ABCD Решение	В четырёхугольник ABCD вписана окружность, AB=13, CD=18 ! 36 вариантов ФИПИ Ященко 2023 Вариант 23 Задание 1

3613	В треугольнике ABC высота CH равна 6, AB=BC, AC=8. Найдите синус угла ACB Решение	Найдите синус угла ACB ! 36 вариантов ФИПИ Ященко 2023 Вариант 22 Задание 1

3602	В треугольнике ABC угол С равен 46°, AD и BE – биссектрисы, пересекающиеся в точке О. Найдите угол AOB. Ответ дайте в градусах Решение	В треугольнике ABC угол С равен 46°, AD и BE – биссектрисы, пересекающиеся в точке О ! 36 вариантов ФИПИ Ященко 2023 Вариант 21 Задание 1 #Задача-аналог 2222

3590	Угол между биссектрисой CD и медианой CM, проведёнными из вершины прямого угла C треугольника ABC равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах Решение	Угол между биссектрисой CD и медианой CM, проведёнными из вершины прямого угла C треугольника ABC равен 10° ! 36 вариантов ФИПИ Ященко 2023 Вариант 18 Задание 1

3584	Острый угол B прямоугольного треугольника равен 50°. Найдите угол между высотой CH и медианой CM, проведёнными из вершины прямого угла. Ответ дайте в градусах Решение	Острый угол B прямоугольного треугольника равен 50°. Найдите угол между высотой CH и медианой CM ! 36 вариантов ФИПИ Ященко 2023 Вариант 17 Задание 1

3576	Площадь параллелограмма ABCD равна 96. Точка E — середина стороны AD. Найдите площадь треугольника ABE Решение	Площадь параллелограмма ABCD равна 96. Точка E — середина стороны AD ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 1 Вариант МА2210209

3567	Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 6. Найдите его большую сторону Решение	Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 1

Источник

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 1.

В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен Найдите центральный угол AOD. Ответ дайте в градусах.

Сторона ромба равна 58, острый угол равен Найдите радиус вписанной окружности этого ромба.

Угол ACB равен Градусная величина дуги AB окружности, не содержащей точек D и E, равна Найдите угол DAE. Ответ дайте в градусах.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 3 угол С равен 135°. Найдите радиус описанной около этого треугольника окружности.

11.

Катеты равнобедренного прямоугольного треугольника равны Найдите радиус окружности, вписанной в этот треугольник.

Хорда AB делит окружность на две части, градусные величины которых относятся как Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

12.

Основания равнобедренной трапеции равны 240 и 70. Радиус описанной окружности равен 125.

Найдите высоту трапеции.

Касательные CA и CB к окружности образуют угол ACB, равный 34°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

13.

Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно , , , Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Угол ACO равен 58°. Его сторона CA касается окружности. Найдите градусную меру дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 48, средняя линия равна 19. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен 8. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 88. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1ЕГЭ «Окружность». ВАРИАНТ – 2.

Сторона ромба равна 100, острый угол равен Найдите радиус вписанной окружности этого ромба.

Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 19 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 4 угол С равен 120°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 72 и 30. Радиус описанной окружности равен 39.

Найдите высоту трапеции.

Касательные CA и CB к окружности образуют угол ACB, равный Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

13.

Угол ACO равен Его сторона CA касается окружности. Найдите градусную величину дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 76, средняя линия равна 6. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 7, описан многоугольник, периметр которого равен 30. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 36. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ –3.

Сторона ромба равна 24, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 20 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 4 угол С равен 135°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 144 и 60. Радиус описанной окружности равен 78.

Найдите высоту трапеции.

13.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник. ОТВЕТ

15.

Около трапеции описана окружность. Периметр трапеции равен 88, средняя линия равна 12. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 29. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 82. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 4.

Сторона ромба равна 46, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 6 угол С равен 120°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 288 и 84. Радиус описанной окружности равен 150.

Найдите высоту трапеции.

13.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 104, средняя линия равна 20. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 4, описан многоугольник, периметр которого равен 63. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 74. Найдите радиус описанной окружности этой трапеции

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 5.

Сторона ромба равна 50, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

11.

12.

Основания равнобедренной трапеции равны 24 и 10. Радиус описанной окружности равен 13.

Найдите высоту трапеции.

13.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 35. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 78. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 6.

Сторона ромба равна 94, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 3 угол С равен 120°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 192 и 56. Радиус описанной окружности равен 100.

13.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 100, средняя линия равна 18. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 62. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 30. Найдите радиус описанной окружности этой трапеции.

Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 7.

Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.

Сторона ромба равна 20, острый угол равен Найдите радиус вписанной окружности этого ромба.

10.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

В треугольнике ABC сторона AB равна 2 угол С равен 120°. Найдите радиус описанной около этого треугольника окружности.

11.

12.

Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20.

Найдите высоту трапеции.

Касательные CA и CB к окружности образуют угол ACB, равный 78°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

13.

Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 76°, 101°, 106°, 77°. Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Угол ACO равен Его сторона CA касается окружности с центром в точке O. Сторона CO пересекает окружность в точках B и D (см. рис.). Найдите градусную меру дуги AD окружности, заключённой внутри этого угла. Ответ дайте в градусах.

14.

Радиус окружности, описанной около правильного треугольника, равен Найдите сторону этого треугольника.

Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.

15.

Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.

Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 50. Найдите его площадь.

16.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 38. Найдите радиус описанной окружности этой трапеции.

Источник