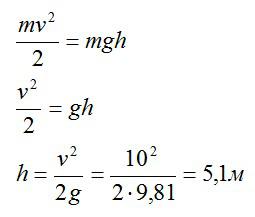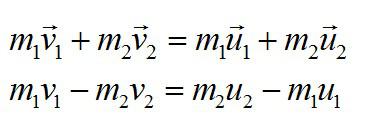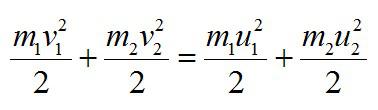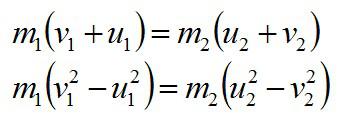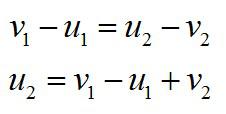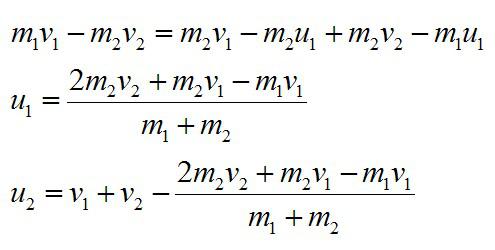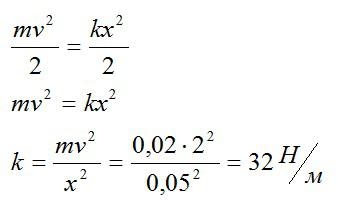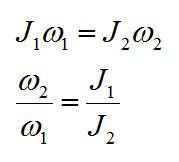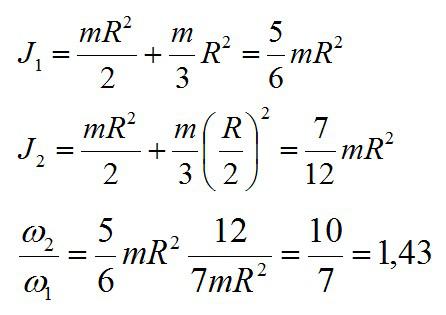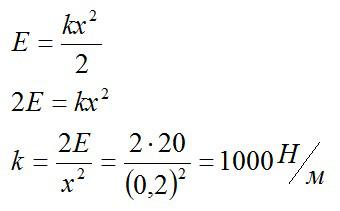Задачи егэ по физике на законы сохранения

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

24 примера с решением.

zakoni-soh.ppt
zakoni-soh.pdf

Мальчик догоняет тележку (бежит навстречу тележке) и запрыгивает на нее. Дальше они двигаются вместе. Масса мальчика m1, масса тележки m2. Скорость мальчика V₁ , скорость тележки V₂.

На вагонетку массой 800 кг, катящуюся по горизонтальному пути со скоростью 0,2 м/с, насыпали сверху 200 кг щебня. На сколько уменьшилась скорость вагонетки?

Рыбак массой 60 кг переходит с носа на корму лодки. На сколько переместится лодка длиной 3 м и массой 120 кг относительно воды?

Охотник стреляет с легкой надувной лодки. Какую скорость приобретает лодка в момент выстрела, если масса охотника с лодкой равна 70 кг, масса дроби 35 г и средняя начальная скорость дроби 320 м/с? Ствол ружья во время выстрела образует угол 60° к горизонту.

Граната, летевшая в горизонтальном направлении со скоростью 10 м/с, разорвалась на два осколка массами 1 кг и 1,5 кг. Скорость большого осколка после разрыва горизонтально возросла до 25 м/с. Определите скорость и направление движения меньшего осколка.

Пуля летит горизонтально со скоростью 400м/с пробивает стоящий на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью ¾ V₀. Масса коробки в 40 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью М= 0,15. На какое расстояние переместилась коробка к моменту, когда ее скорость уменьшится на 20%.

Тело массой 3 кг, свободно падает с высоты 5 м. Найти потенциальную и кинетическую энергию тела на расстоянии 2 м от поверхности земли.

Камень подброшен вертикально вверх с начальной скоростью 10 м/с. На какой высоте h кинетическая энергия камня равна его потенциальной энергии?

Груз массой 25 кг висит на шнуре длиной 2,5 м. На какую наибольшую высоту можно отвести в сторону груз, чтобы при дальнейших свободных качаниях шнур не оборвался? Максимальная сила натяжения, которую выдерживает шнур не обрываясь, равна 550 Н.

Цирковой артист массой 60 кг падает в натянутую сетку с высоты 4 м. С какой силой действует на артиста сетка, если она прогибается при этом на 1 м?

Маятник массой m отклонен на угол α от вертикали. Какова сила натяжения нити при прохождении маятником положения равновесия?

С поверхности земли со скоростью 8 м/с брошено тело под углом 60° к горизонту. Найти величину его скорости на высоте 1,95 м.

Тело скользит без трения по гладкой горизонтальной поверхности со скоростью 5 м/с и въезжает подвижную горку высотой H=1,2 м. На какую высоту поднимается тело по горке, если масса горки в 5 раз больше массы тела?

Два тела массой по 1/18 кг движутся навстречу друг другу. Скорость первого тела 4 м/с, второго — 8 м/с. Какое количество теплоты выделится в результате абсолютно неупругого удара тел?

На некоторой высоте планер имел скорость 10 м/с. Определить величину скорости планера при его снижении на 40 метров. Сопротивлением воздуха пренебречь

Два тела массы m1 и m2 прикреплены к нитям одинаковой длины с общей точкой подвеса и отклонены – одно влево, другое вправо – на один и тот же угол. Тела одновременно отпускают. При ударе друг о друга они слипаются. Определите отношение высоты, на которую тела поднимутся после слипания, к высоте, с которой они начали свое движение вниз.

Тяжелый шарик соскальзывает без трения по наклонному желобу, образующему «мертвую петлю» радиусом R. С какой высоты шарик должен начать движение, чтобы не оторваться от желоба в верхней точке траектории?

На гладком горизонтальном столе лежит шар массой М=240 г, прикрепленный к пружине жесткостью k=40 кН/м. Другой конец пружины закреплен. В шар попадает пуля массой m=10 г, имеющая в момент удара начальная скорость 400 м/с, направленную вдоль оси пружины. Пуля застревает в шаре. Определите амплитуду колебаний шара после удара.

Начальная скорость снаряда, выпущенного вертикально вверх, равна 160 м/с. В точке максимального подъема снаряд разорвался на 2 осколка, массы которых относятся как 1:4. Осколки разлетелись в вертикальных направлениях, причем меньший осколок полетел вниз и упал на землю со скоростью 200 м/с. Определите скорость, которую имел в момент удара о землю больший осколок. Сопротивлением воздуха пренебречь.

Алгоритм решения задач по теме «Законы сохранения»

1) Внимательно изучите условие задачи, поймите физическую сущность явлений и процессов, рассматриваемых в задаче, уясните основной вопрос задачи.

2) Мысленно представьте ситуацию, описанную в задаче, выясните цель решения, четко выделите данные и неизвестные величины.

3) Запишите краткое условие задачи. Одновременно выразите все величины в единицах СИ.

4) Сделайте чертеж, на котором отобразите ситуацию до и после события.

5) Запишите закон сохранения импульса (в проекции на выбранную ось) проверив систему на замкнутость или (и) закон сохранения энергии в соответствии с тем, что отобразили на чертеже (с одной стороны равенства что было «до», с другой что «после»). Выберите нулевой уровень потенциальной энергии.

6) Решите уравнение или систему уравнений относительно неизвестной величины, т.е. решите задачу в общем виде.

7) Если не все величины известны, то для нахождения их можете применить алгоритм решения задач по теме «Динамика».

Найдите искомую величину.

9) Определите единицу величины. Проверьте, подходит ли она по смыслу.

10) Рассчитайте число.

11) Проверьте ответ на «глупость» и запишите его.

Законы сохранения – фундаментальные физические законы. Учитесь решать задачи на эту тему? Отлично! В этой статье мы разберем несколько примеров решений таких задач.

Наш телеграм – это полезная и интересная информация для студентов всех специальностей. Присоединяйтесь!

Задачи на тему «Законы сохранения в механике»

Задача №1. Закон сохранения энергии

Условие

На какую высоту поднимется тело, подброшенное вертикально вверх, с начальной скоростью 10 м/с? При решении задачи не учитывается сопротивление воздуха.

Решение

По закону сохранения энергии, начальная кинетическая энергия брошенного тела будет равна его потенциальной энергии в наивысшей точке подъема.

Ответ: 5,1м

Задача №2. Закон сохранения импульса

Условие

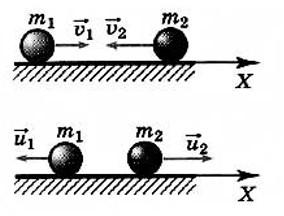
Определите скорости двух шаров массами m1 и m2 после центрального абсолютно упругого удара. Скорости шаров до удара v1 и v2 соответственно

Решение

В задаче применяется закон сохранения импульса. Запишем его в векторном виде и в проекции на горизонтальную ось в соответствии с рисунком:

Теперь запишем закон сохранения энергии:

Преобразуем полученные выражения:

Воспользуемся формулами сокращенного умножения, разделим правые и левые части системы друг на друга и получим:

Подставим выраженное значение u2 в первое уравнение для закона сохранения импульса и получим:

Ответ: см. решение

Задача №3. Закон сохранения энергии

Условие

Спусковую пружину игрушечного пистолета сжали на 5 см, при вылете шарик массой 20 г приобрел скорость 2 м/с. Необходимо рассчитать, какова жесткость пружины

Решение

Потенциальная энергия деформированной пружины переходит в кинетическую энергию шарика

Ответ: 32 Н/м

Задача №4. Закон сохранения момента импульса

Условие

Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определите, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдёт ближе к центру на расстояние, равное половине радиуса платформы.

Решение

Так как в системе человек–платформа сумма моментов сил тяжести и реакции опоры равна нулю, для решения задачи можно применить закон сохранения момента импульса

Запишем моменты инерции системы в начальном и конечном состояниях, затем подставим результат во второе выражение:

Ответ: угловая скорость увеличится в 1,43 раза. 

Задача №5. Закон сохранения энергии

Условие

При растяжении пружины на 20 см она приобрела потенциальную энергию упругодеформированного тела 20 Дж. Какова жесткость пружины?

Решение

Потенциальная энергия пружины вычисляется по формуле

Ответ: 1000 Н/м

Кстати! Для наших читателей действует скидка 10% на любой вид работы

Вопросы на законы сохранения

Вопрос 1. Что такое механическая система тел?

Ответ. Механическая система – это совокупность материальных точек (тел), движения которых взаимосвязаны.

Вопрос 2. Какая механическая система называется замкнутой?

Ответ. Замкнутой называется механическая система, на которую не действуют внешние силы. Такая система не взаимодействует с внешними телами, не входящими в нее.

Вопрос 3. В каких механических системах выполняются законы сохранения импульса, энергии и момента импульса?

Ответ. Законы сохранения импульса, энергии и момента импульса выполняются в замкнутых механических системах.

Вопрос 4. Сформулируйте закон сохранения момента импульса

Ответ. Момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.

Вопрос 5. Каково философское значение законов сохранения?

Ответ. Законы сохранения показывают неуничтожимость и несотворимость движущейся материи со всеми её свойствами в процессах её перехода из одной формы в другую. Другими словами, движение материи вечно и лишь переходит из одной формы в другую. 

Такая точка зрения характерна для диалектического материализма.

Законы сохранения в механике

В физике, точнее в механике, можно выделить три фундаментальных закона сохранения:

1. Закон сохранения импульса.
2. Закон сохранения энергии.
3. Закон сохранения момента импульса.

Формулировка закона момента импульса дана выше, в разделе «Вопросы». Кстати, для понимания физической сути момента импульса рекомендуем сначала почитать о том, что такое момент инерции.

Нужна помощь в решении задач и выполнении любых других заданий? Обращайтесь в профессиональный студенческий сервис.  

Предварительный просмотр:

• Мне нравится 

 

Снова представляю решения задач, которые мы разбирали на групповых занятиях летом с ребятами, желающими участвовать в олимпиадах.

Задача 9.

Два одинаковых маленьких шарика, соединенных невесомым твердым стержнем длиной , падают на гладкую, абсолютно упругую горизонтальную плоскость. Непосредственно перед ударом нижнего шарика о плоскость скорости шариков оказались взаимно перпендикулярны. Каковы величина скорости центра масс гантели и угловая скорость вращения стержня сразу после удара? Под каким углом к вертикали был наклонен стержень перед ударом?

Решение. Стержень в момент удара движется поступательно со скоростью и вращательно. Центр масс стержня посередине (он симметричный), и скорости вращения шариков относительно центра равны по модулю и противоположны по направлению.

Пусть шарик 1 – нижний, который ударился о плоскость. Шарик 2 – верхний.

Скорость первого шарика складывается из скорости поступательного движения и вращательной.

А для второго шарика

Так как скорости перпендикулярны, то их скалярное произведение равно нулю:

Где

Закон сохранения энергии:

Складываем (1) и (2):

Возведем в квадрат правую и левую части, при этом удвоенное произведение равно нулю, так как скорости и перпендикулярны.

Следовательно,

Теперь ищем угол. На второй шарик действует сила, направленная вдоль стержня. А сил, действующих перпендикулярно стержню, нет. Так как сумма сил на это направление равна нулю, то скорость, спроецированная на данное направление, сохраняется. Она была равна . А стала равна проекции скорости на эту ось, да еще вращательной скорости, проекция которой на эту ось будет равна ей самой.

Мы выяснили модуль скорости , но не знаем ее направления.

В момент удара на гантель действует сила реакции опоры, направленная вверх, и сила тяжести (вертикально вниз). Это внешние силы. По теореме о центре масс ускорение центра масс направлено по вертикальной оси. Скорость центра масс до удара была равна и направлена вертикально вниз. Значит, скорость центра масс после удара может быть направлена только по вертикальной оси. Вероятно, вверх. Тогда проекция этой скорости на ось равна

Ответ: , , .

Задача 10.

На неподвижное, ориентированное в вертикальной плоскости гладкое кольцо радиусом надета бусинка. К бусинке, находящейся в нижней точке кольца, крепится невесомая пружина, другим концом скрепленная с верхней точкой кольца. Пружина растянута так, что бусинка давит на кольцо с силой, вдвое превышающей силу тяжести, действующую на бусинку. Из-за неустойчивости бусинка начинает скользить по кольцу, и ее скорость достигает максимума в тот момент, когда пройдена треть кольца. Чему равна длина недеформированной пружины? Чему равна максимальная скорость бусинки?

Решение. Для положения бусинки в самой нижней точке кольца составим уравнение по второму закону Ньютона.

По условию, , следовательно,

Пусть длина пружины в нерастянутом состоянии равна . Тогда растяжение пружины будет равно , и можно записать с учетом предыдущего уравнения, что

Когда бусинка пройдет треть окружности (что соответствует ), ей останется пройти до наивысшего положения . То есть треугольник — правильный.

Значит, длина пружины равна в этом случае (вместе с удлинением).

Если скорость бусинки достигла максимума, значит, производная скорости равна нулю. Таким образом, равно нулю тангенциальное ускорение бусинки, направленное по касательной. А значит, сумма сил в проекции на касательную равна нулю.

Получаем второе уравнение:

Но

То есть

Получили систему уравнений:

Выражаем и подставляем во второе уравнение:

Тогда

Следовательно, в первом случае растяжение пружины

Составим уравнение по закону сохранения энергии. В конечном положении бусинка находится на высоте по отношению к первоначальному:

Так как , а, то

Ответ: , .