По теме: методические разработки, презентации и конспекты
Решение задач по теме: «Тела вращения
Цели урока:
• систематизировать знания учащихся;
• обобщить изученный материал;
• рассмотреть задачи на комбинацию тел;
• проверить умения и навыки при решении задач на нахождение объемов тел …
Задачи к уроку по теме «Тела вращения»
При обучении геометрии большое значение имеет умение решать задачи, требующее установление соотношений между данными и искомыми. При решении таких задач проявляется уровень математического развит…
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
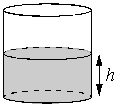
В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
2
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.
3
В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.
4
В сосуде, имеющем форму конуса, уровень жидкости достигает
высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Источник: Пробный экзамен Санкт-Петербург 2014. Вариант 1.
5
Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй кружки больше объёма первой?
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 120911., ЕГЭ по базовой математике 26.03.2015. Досрочная волна
Пройти тестирование по этим заданиям
Данный файл по геометрии для учащихся 10-11 классов содержит задачи по теме » Тела вращения. Площадь поверхности». ( Взяты из материалов по подгот овки к ЕГЭ ( базовая часть)
Просмотр содержимого документа
«Задачи по теме » Тела вращения»( в формате ЕГЭ)»
-
Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на пи.
-
Площадь осевого сечения цилиндра равна 23. Найдите площадь боковой поверхности цилиндра, деленную на пи .
-
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
-
Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на пи.
-
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
-
Площадь боковой поверхности цилиндра равна 2 пи, а диаметр основания — 1. Найдите высоту цилиндра.
-
Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 6. Найдите его объем, деленный на пи.
-
Длина окружности основания конуса равна 5, образующая равна 8. Найдите площадь боковой поверхности конуса.
-
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
-
Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
-
Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
Зачет «Тела вращения»
1 вариант
№13
ЕГЭ, база
1)
Радиус основания
цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности
цилиндра, деленную на π.
2)
Площадь боковой поверхности цилиндра
равна 2π, а диаметр основания равен 1. Найдите высоту цилиндра.
3)
Площадь боковой поверхности цилиндра
равна 2π, а высота равна 1. Найдите диаметр основания.
4)
Во сколько раз увеличится площадь боковой
поверхности конуса, если его образующую увеличить в 3 раза?
5)
Высота конуса равна 4, а диаметр
основания — 6. Найдите образующую конуса.
6)
Площадь большого круга шара равна 3. Найдите
площадь поверхности шара.
7)
Даны два шара с радиусами 3 и 1. Во
сколько раз площадь поверхности первого шара больше площади поверхности
второго?
№16
ЕГЭ, база

Площадь осевого сечения цилиндра равна 4.
Найдите площадь боковой поверхности цилиндра, деленную на π.
9)
Длина окружности основания конуса равна 3,
образующая равна 2. Найдите площадь боковой поверхности конуса.
10) Куб
вписан в шар радиуса . Найдите объем куба.
11) Около
шара описан цилиндр, площадь поверхности которого равна 18. Найдите
площадь поверхности шара.
12) Около
конуса описана сфера (сфера содержит окружность основания конуса и его
вершину). Центр сферы находится в центре основания конуса. Радиус сферы
равен . Найдите образующую
конуса.
Дополнительно: (№13 ЕГЭ, профиль)
13)
В цилиндре
образующая перпендикулярна плоскости основания. На окружности одного из
оснований цилиндра выбраны точки А и В, а на
окружности другого основания — точки В1 и С1,
причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает
ось цилиндра.
а)
Докажите, что угол АВС1 прямой.
б)
Найдите угол между прямыми ВВ1 и АС1,
если АВ = 6, ВВ1 = 15, В1С1 = 8.
Зачет «Тела вращения»
2 вариант
№13
ЕГЭ, база
1)
Радиус основания цилиндра
равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра,
деленную на π .
2)
Длина
окружности основания цилиндра равна 3. Площадь боковой поверхности
равна 6. Найдите высоту цилиндра.
3) Площадь
боковой поверхности цилиндра равна 40π а диаметр основания равен
5. Найдите высоту цилиндра.
4) Во сколько
раз уменьшится площадь боковой поверхности конуса, если радиус его основания
уменьшится в 1,5 раза, а образующая останется прежней?
5)
Высота конуса равна 4, а
длина образующей — 5. Найдите диаметр основания конуса.
6)
Во сколько раз увеличится
площадь поверхности шара, если радиус шара увеличить в 2 раза?
7)
Даны два
шара. Диаметр первого шара в 8 раз больше диаметра второго. Во сколько
раз площадь поверхности первого шара больше площади поверхности
второго?
№16
ЕГЭ, база

Радиус основания
цилиндра равен 26, а его образующая равна 9. Сечение, параллельное оси
цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого
сечения.
9)
Длина окружности основания
конуса равна 8, образующая равна 8. Найдите площадь боковой поверхности конуса.
10) Куб вписан в шар радиуса .
Найдите объем куба.
11)
Около шара описан цилиндр,
площадь поверхности которого равна 45. Найдите площадь поверхности шара.
12) Около
конуса описана сфера (сфера содержит окружность основания конуса и его
вершину). Центр сферы находится в центре основания конуса. Радиус сферы
равен . Найдите образующую
конуса.
Дополнительно: (№13 ЕГЭ, профиль)
13) В цилиндре образующая перпендикулярна плоскости основания.
На окружности одного из оснований цилиндра выбраны точки А и В,
а на окружности другого основания — точки В1 и С1,
причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает
ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите площадь боковой
поверхности цилиндра, если AB = 20, BB1 = 15, B1C1 = 21.
В БЛОГАХ…
еще…
еще…
Спасибо, Зоя Андреевна, за Ваш труд и помощь учителям! Ваши ресурсы всегда выпол…
Прекрасный материал о кошках! Спасибо за интересную викторину, Раиса Поликарповна!
Шаблон, действительно, прелестный! А идея и использование этого шаблона Вами, На…
Благодарю Вас,Зоя Андреевна! Изучу это хорошее дело.
Благодарю Вас, Наталья Александровна! Ваши добрые слова, действительно, согреваю…
Ну и ну, так стильно вписали цифру восемь к Международному женскому дню! Такое к…
Такой подарочек приятный, Любовь Николаевна! Первоцветы и весна — это прелесть! …
Задачи для подготовки к ЕГЭ «Тела вращения»ЕГЭ по математике
|
||||||||||||||||||||||||||||
|
Презентация «Задачи для подготовки к ГИА и ЕГЭ» содержит задания на тему «Тела вращения» (треугольник, конус, усечённый конус, шар). Подходит для любых УМК. Может быть использована при систематизации знаний и на занятиях по подготовке к ЕГЭ в 11 классе. Цели урока: Образовательные: повторить и закрепить знания телах вращения, научиться применять эти знания при решении конкретных задач. Развивающие: развивать умение анализировать условие задачи. Воспитательные: воспитание аккуратности, внимательности, быстроты мышления. © Коломина Наталья Николаевна Коломина Наталья Николаевна Понравилось? Сохраните и поделитесь: Неограниченная бесплатная загрука материала «Задачи для подготовки к ЕГЭ «Тела вращения»» доступна всем пользователям. Разработка находится в разделе «ЕГЭ по математике» и представляет собой: «проверка знаний, повторение, систематизация».
Загрузка началась… Понравился сайт? Получайте ссылки Подарок каждому подписчику!
|
||||||||||||||||||||||||||||
|
Порядок вывода комментариев:
|
Разноуровневые задачи по теме «Тела вращения»
Работу подготовила:
Бушмелева Любовь Петровна
Должность:
учитель математики
Место работы:
ГБОУ Центр образования №170 Санкт-Петербурга
20 декабря 2017 г.
Санкт-Петербург
Изучение геометрии позволяет формировать и развивать пространственное воображение, критичность мышления на уровне, необходимом затем для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности; а также умения и навыки умственного труда — планирование своей работы, поиск рациональных путей её выполнения, критическая оценка результатов. В процессе изучения геометрии школьники должны научиться не только решать геометрические задачи, но и излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобрести навыки чёткого, аккуратного и грамотного выполнения математических записей.
Тема «Многогранники и тела вращения» одна из основных в традиционном курсе школьной геометрии. Они составляют, можно сказать, центральный предмет стереометрии. Сознательное овладение учащимися системой геометрических знаний и умений необходимо также в повседневной жизни для изучения смежных дисциплин и продолжения образования. Практические умения и навыки геометрического характера необходимы для трудовой и профессиональной подготовки школьников, а активное использование задач на всех этапах учебного процесса развивает творческие способности школьников и умение логически мыслить. Предлагаю для подготовки к ГИА и для проведения проверочных работ учащимися задания по геометрии из открытого банка задач.
Все задания я разбила на III уровня по степени возрастания сложности, в каждом из них по десять заданий. Ответы прилагаются.
I уровень.
-
Площадь боковой поверхности цилиндра равна 64π, а диаметр основания 8. Найдите высоту цилиндра.
-
Площадь боковой поверхности цилиндра равна 72π. А высота цилиндра 9. Найдите радиус основания.
-
Высота конуса равна 16, а длина образующей — 20. Найдите диаметр основания конуса.
-
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую и радиус увеличить в 3 раза?
-
Даны два шара. Диаметр первого шара в 8 раз больше диаметра второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
-
Даны два цилиндра. Радиус основания и высота первого равны соответственно 9 и 8, а второго — 12 и 3.
Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго? -
Осевое сечение конуса равносторонний треугольник, сторона которого равна 12 см. Найдите площадь основания конуса. Ответ дайте в S/π.
-
Объем шара равен 36 π см3 . Найдите его радиус
II уровень
-
Осевым сечением цилиндра является квадрат. Площадь основания цилиндра равна 36π см2. Вычислите высоту цилиндра
-
В цилиндрическом сосуде уровень жидкости равен 45 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше, чем диаметр первого?
-
В цилиндрическом сосуде уровень жидкости равен 50 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 5 раз больше, чем диаметр первого?
-
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 3 и 6, а второго — 4 и 9. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
-
Даны два шара с радиусами 8 и 2. Во сколько раз площадь поверхности большего шара больше площади поверхности другого?
-
Даны два цилиндра. Радиус основания и высота первого равны соответственно 9 и 8, а второго — 4 и 9. Во сколько раз объём первого цилиндра больше объёма второго?
-
Объем конуса равен 176. Через середину высоты параллельно основанию проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
-
Даны два шара с диаметрами 14 и 2. Во сколько раз объем первого шара больше объема второго шара?
III уровень
-
Радиус основания цилиндра равен 13, а его образующая
равна 18. Сечение, параллельное оси цилиндра, удалено
от неё на расстояние, равное 12. Найдите площадь этого сечения.
-
Объём конуса равен 27. Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
-
Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
-
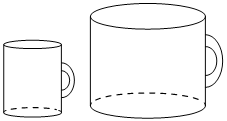
Даны две кружки цилиндрической формы. Первая кружка в четыре раза ниже второй, а вторая в полтора раза шире первой.
Во сколько раз объём первой кружки меньше объёма второй?
-
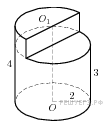
Найдите объем
части цилиндра, изображенной на рисунке. В ответе укажите V/π.
-
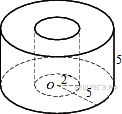
Найдите объем
части цилиндра, изображенной на рисунке. В ответе укажите V/π.
-
Объем шара равен 288
. Найдите площадь его поверхности, деленную на π.
-
Площадь сечения сферы, проходящего через центр равна 15π . Найдите площадь сферы, деленную на π.
Ответы.
|
Уровень |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
I |
8 |
4 |
24 |
9 |
64 |
1,5 |
36 |
3 |
|
II |
12 |
5 |
2 |
2 |
16 |
4,5 |
22 |
343 |
|
III |
180 |
1 |
48 |
9 |
14 |
105 |
144 |
36 |
Цилиндры, сферы и конусы: будем вписывать их в другие объекты, будем рассекать их различными плоскостями, отыскивать углы наклона этих сечений к основанию или их площади.
Задача 1.
В правильную шестиугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Сфера вписана в пирамиду
Так как сфера касается всех граней, то точки касания обязательно лежат на апофемах граней. Нарисуем пирамиду в разрезе, причем разрез пройдет по апофемам противолежащих граней. Тогда сечение – треугольник MSN, а сечение сферы – вписанная в этот треугольник окружность. Разберемся, отрезки каких длин в этом сечении присутствуют. Так как высота пирамиды 6, а боковое ребро 10, найдем длину отрезка :
Так как основание пирамиды составлено из правильных треугольников, то длина равна ребру основания. Теперь можем определить длину апофемы:
Основание треугольника сечения составлено из двух одинаковых отрезков, которые равны высоте треугольника , например. Так как это правильный треугольник со стороной 8, то высота этого треугольника равна
, а длина MN тогда
.
Сечение пирамиды
Итак, теперь мы знаем стороны треугольника сечения :
,
.
Определим радиус вписанной в него окружности.
Вписанная в сечение пирамиды окружность (сечение сферы)
Как известно, радиус вписанной окружности можно определить через площадь:
Теперь, зная радиус, можно найти и площадь поверхности сферы:
Ответ:
Задача 2.
Радиус основания конуса равен 6, а его высота равна 8. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 4. Найдите расстояние от центра основания конуса до плоскости сечения.
Сечение конуса
Образующую конуса можно найти из осевого сечения по теореме Пифагора.
Отрезок OP – высота треугольника . В треугольнике MON стороны равны 4, 6 и 6, определим его площадь по формуле Герона и затем найдем высоту:
Полупериметр треугольника MON равен 8, площадь:
Искомое расстояние – высота треугольника , проведенная к SP.
Определим высоту сечения SP.
Дополнительные построения к задаче
По теореме Пифагора
Площадь треугольника SOP:
Наконец, искомое расстояние:
Ответ:
Задача 3.
В правильную четырёхугольную пирамиду, боковое ребро которой равно 10, а высота равна 6, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Пирамида, в которую надо вписать сферу
Так как сфера касается всех граней, то точки касания обязательно лежат на апофемах граней. Нарисуем пирамиду в разрезе, причем разрез пройдет по апофемам противолежащих граней. Тогда сечение – треугольник SQP, а сечение сферы – вписанная в этот треугольник окружность. Разберемся, отрезки каких длин в этом сечении присутствуют. Так как высота пирамиды 6, а боковое ребро 10, найдем длину отрезка :
Тогда равна
, так как треугольник
— равнобедренный и прямоугольный, имеет острые углы по
, тригонометрические функции которых хорошо известны:
Определим длину апофемы грани:
В треугольнике SQP стороны: ,
Определим радиус вписанной в него окружности.
Как известно, радиус вписанной окружности можно определить через площадь:
Теперь, зная радиус, можно найти и площадь поверхности сферы:
Ответ:
Задача 4.
Радиус основания конуса с вершиной равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки
и
, делящие окружность на две дуги, длины которых относятся как 1:5. Найдите площадь сечения конуса плоскостью
.
Дуги окружности основания конуса и сечение
Длины дуг окружности пропорциональны центральным углам, поэтому ,
. Таким образом, поскольку радиус основания конуса равен 6, то треугольник MON правильный и длина хорды
. Далее просто пользуемся формулой Герона для определения площади сечения:
Ответ:
Задача 5.
Две параллельные плоскости, расстояние между которыми 2, пересекают шар. Одна из плоскостей проходит через центр шара. Отношение площадей сечений шара этими плоскостями равно 0,84. Найдите радиус шара.
Сфера и ее сечения
Площадь сечения шара плоскостью – окружность. Площадь окружности
Большая окружность проходит через центр сферы, поэтому ее радиус – радиус сферы R.
Тогда отношение площадей:
Рассмотрим треугольник . В нем
,
,
.
Это прямоугольный треугольник, поэтому
Или
Тогда:
Получили уравнение:
Ответ:












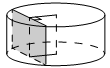
 части цилиндра, изображенной на рисунке. В ответе укажите V/π.
части цилиндра, изображенной на рисунке. В ответе укажите V/π.