Каталог заданий.
Шар
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 2 № 27059
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Аналоги к заданию № 27059: 5049 27185 72765 72719 72721 72723 72725 72727 72729 72731 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 2 № 27072
Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27072: 5075 73287 520653 520694 26551 73243 73245 73247 73249 73251 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 2 № 27097
Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
Аналоги к заданию № 27097: 74403 74405 74407 74409 74411 74413 74415 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 2 № 27125
Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Аналоги к заданию № 27125: 75307 75309 75311 75313 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор стереометрии: Объём цилиндра, конуса, шара
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 2 № 27162
Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Аналоги к заданию № 27162: 76349 76355 505443 76351 76353 76357 76359 Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.6 Площадь поверхности конуса, цилиндра, сферы
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Классификатор стереометрии: Объём цилиндра, конуса, шара, Площадь сферы
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
Тема 2.
Геометрия в пространстве (стереометрия)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
геометрия в пространстве (стереометрия)
2.01Теорема о трех перпендикулярах
2.02Угол между прямыми
2.03Угол между прямой и плоскостью
2.04Угол между плоскостями и двугранный угол
2.05Пирамида
2.06Правильная и прямоугольная пирамиды
2.07Призма
2.08Правильная и прямая призмы
2.09Параллелепипед как частный случай призмы
2.10Прямоугольный параллелепипед
2.11Куб как частный случай прямоугольного параллелепипеда
2.12Конус
2.13Цилиндр
2.14Сфера и шар
2.15Комбинированные тела: их объемы и площади поверхностей
2.16Отношение площадей поверхностей и отношение объемов тел
2.17Вписанные и описанные тела
Решаем задачи
Площадь поверхности шара равна 24. Найдите площадь большого круга шара.
Показать ответ и решение
Площадь поверхности шара вычисляется по площади где
— радиус шара.
Площадь большого круга шара вычисляется по формуле где
— радиус шара.
Тогда искомая площадь равна
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Показать ответ и решение
Пусть — радиус шара, тогда площадь большого круга равна
Площадь поверхности шара вычисляется по формуле
Тогда окончательно имеем:
Объем шара равен Чему будет равна площадь поверхности шара, если его радиус увеличить на
Показать ответ и решение
По формуле объема шара с радиусом имеем:
Радиус нового шара равен
Тогда найдем площадь поверхности:
Показать ответ и решение
Так как точка
– центр круга
— центр сферы, то
и
Тогда
— прямоугольная
трапеция, площадь которой равна
Здесь — радиус сферы,
— радиус
Далее, зная площадь круга, найдем его радиус:
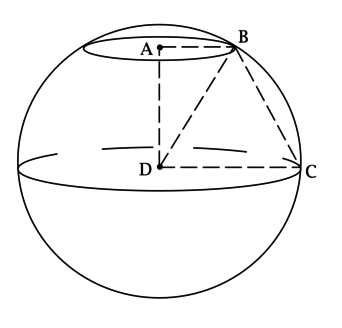
Рассмотрим прямоугольный треугольник Так как
то
то есть
Тогда имеем:
Тогда искомая площадь равна
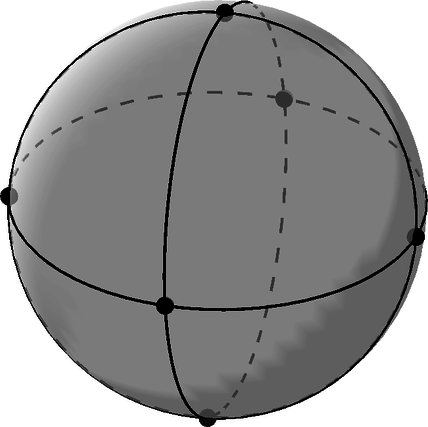
Евгений изучает сферу. Он решил расположить её так, чтобы её центр совпал с началом прямоугольной
системы координат . Плоскости
,
и
пересекли рассматриваемую сферу по
большим окружностям. Евгений заметил, что если разрезать сферу по этим окружностям, то она
распадётся на несколько криволинейных треугольников. Количество треугольников, на которые
распадётся сфера, он обозначил через . Но сферу он разрезать не стал.
Затем Евгений посчитал число точек на сфере, через которые прошли хотя бы две из этих
окружностей, он назвал эти точки вершинами, а полученное число обозначил через . Напоследок он
посчитал число криволинейных отрезков на сфере, соединяющих соседние вершины (каждый такой
отрезок представляет собой четверть дуги одной из полученных больших окружностей) и обозначил его
через . Найдите
.
Показать ответ и решение
При разрезании сфера распалась бы на треугольников, то есть
.
Назовём отрезки, соединяющие соседние вершины, рёбрами. Число вершин равно , то есть
.
При этом каждая из трёх полученных больших окружностей состоит из четырёх рёбер (и вершин, но их
мы уже посчитали), следовательно, , тогда
Замечание
Полученное в данной задаче число называется эйлеровой характеристикой двумерной
сферы. По аналогии можно рассматривать эйлеровы характеристики и у других поверхностей.
Площадь поверхности шара равна . На расстоянии
от центра шара проведена плоскость.
Найдите длину полученной в сечении окружности.
Показать ответ и решение
Т.к. площадь поверхности сферы ищется по формуле , то
По условию задачи . Рассмотрим
: он прямоугольный (
), гипотенуза
, катет
равен радиусу
окружности сечения.
Таким образом, по теореме Пифагора
Таким образом, длина окружности сечения равна
Площадь поверхности шара равна . На расстоянии
от центра шара проведена плоскость.
Найдите площадь полученного сечения.
Показать ответ и решение
Т.к. площадь поверхности сферы ищется по формуле , то
По условию задачи . Рассмотрим
: он прямоугольный (
), гипотенуза
, катет
равен радиусу
окружности сечения.
Таким образом, по теореме Пифагора
Таким образом, площадь сечения равна
Во сколько раз объем шара больше объема сегмента, высота которого равна половине радиуса?
Показать ответ и решение
Необходимо объем шара разделить на объем соответствующего сегмента, высота которого равна
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Сфера и шар»
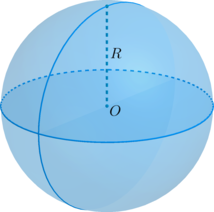
(blacktriangleright) Сфера – это множество точек пространства, находящихся на одинаковом расстоянии от заданной точки (O) (называемой центром сферы).
(blacktriangleright) Шар – это сфера вместе со своей внутренностью.
Основные формулы (где (R) – радиус сферы или шара):
(blacktriangleright) площадь сферы ({large{S=4pi R^2}})
(blacktriangleright) объем шара ({large{V=dfrac{4}{3}pi R^3}})
Задание
1
#1878
Уровень задания: Равен ЕГЭ
Объем шара равен (displaystyle frac{36}{sqrtpi}). Чему будет равна площадь поверхности шара, если его радиус увеличить на (displaystyle frac{6}{sqrtpi})?
(displaystyle V_{text{шара}} = frac{4}{3}pi R^3 = frac{36}{sqrtpi}) (Rightarrow) (displaystyle R = frac{3}{sqrtpi}). Радиус нового шара равен: (displaystyle R_{text{нов.}} = R + frac{6}{sqrtpi} = frac{9}{sqrtpi}). Тогда найдем площадь поверхности: (displaystyle {S_{text{пов.}} = 4pi R_{text{нов.}}^2 = 4pi left(frac{9}{sqrtpi}right)^2 = 4pifrac{81}{pi} = 324}.)
Ответ: 324
Задание
2
#1877
Уровень задания: Равен ЕГЭ
Во сколько раз объем шара больше объема сегмента, высота которого равна половине радиуса?
Необходимо объем шара разделить на объем соответствующего сегмента, высота которого равна (H = frac{1}{2}R)
[frac{V_{text{шара}}}{V_{text{сегм.}}} = frac{frac{4}{3}pi R^3}{pi left(frac{1}{2}Rright)^2left(R — frac{1}{3}left(frac{1}{2}Rright)right)} = frac{frac{4}{3}pi R^3}{frac{5}{24}pi R^3} = frac{4}{3} cdot frac{24}{5} = frac{32}{5} = 6,4.]
Ответ: 6,4
Задание
3
#2674
Уровень задания: Сложнее ЕГЭ
Имеются две сферы (S_1) и (S_2), про которые известно, что радиус первой сферы в (2) раза больше, чем радиус второй сферы. Кроме того, сфера (S_2) целиком находится внутри сферы (S_1). Пусть объём шара, ограниченного второй сферой, равен (V_2), а объём тела, заключённого между сферами, равен (V). Найдите (V : V_2).
Пусть (V_1) – объём шара, ограниченного первой сферой. Так как радиус (S_1) в два раза больше, чем радиус (S_2), то (V_1 : V_2 = 
[V = V_1 — V_2 = 8V_2 — V_2 = 7V_2,,] следовательно, (V : V_2 = 7).
Ответ: 7
Задание
4
#2306
Уровень задания: Сложнее ЕГЭ
Площадь поверхности шара равна (frac{37}{pi}). На расстоянии (frac1{2pi}) от центра шара проведена плоскость. Найдите длину полученной в сечении окружности.
Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то
[4pi R^2=dfrac{37}{pi} quad Rightarrow quad R^2=dfrac{37}{4pi^2}]
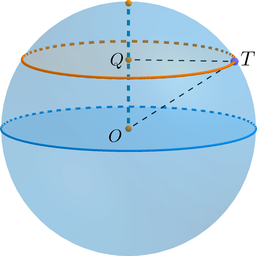
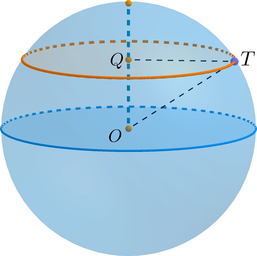
По условию задачи (OQ=frac1{2pi}). Рассмотрим (triangle OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.
Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{37}{4pi^2}-dfrac1{4pi^2}=dfrac{9}{pi^2}
quad Rightarrow quad r=dfrac3{pi}]
Таким образом, длина окружности сечения равна [C=2pi
r=2picdotfrac3{pi}=6.]
Ответ: 6
Задание
5
#2307
Уровень задания: Сложнее ЕГЭ
Площадь поверхности шара равна (64). На расстоянии (frac3{2sqrt{pi}}) от центра шара проведена плоскость. Найдите площадь полученного сечения.
Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то
[4pi R^2=64 quad Rightarrow quad R^2=dfrac{64}{4pi}]
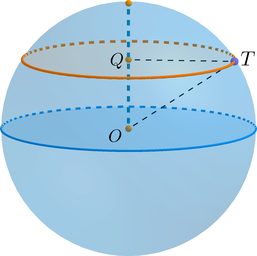
По условию задачи (OQ=frac3{2sqrt{pi}}). Рассмотрим (triangle
OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.
Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{64}{4pi}-dfrac9{4pi}=dfrac{55}{4pi}]
Таким образом, площадь сечения равна
[S=picdot r^2=picdot dfrac{55}{4pi}=dfrac{55}4=13,75.]
Ответ: 13,75
Задание
6
#951
Уровень задания: Сложнее ЕГЭ
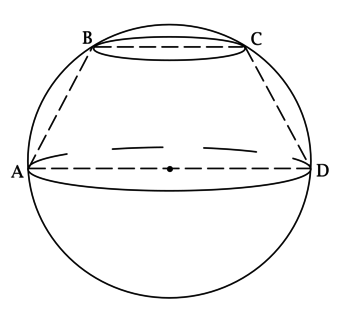
Центр большего основания усечённого конуса совпадает с центром сферы, а окружность его меньшего основания лежит на сфере. Отрезки (BC) и (AD) – диаметры меньшего и большего оснований этого усечённого конуса соответственно, (BCparallel AD), [S_{ABCD} = dfrac{210}{sqrt[3]{pi^2}},qquadqquad dfrac{r}{R} = dfrac{1}{sqrt{15}},] где (R) и (r) – радиусы большего и меньшего оснований усечённого конуса соответственно, (angle ADC = 45^circ). Найдите объём шара, ограниченного данной сферой.
Рассмотрим (ABCD): т.к. (BCparallel AD), то (ABCD) – трапеция. Так как (AB) и (CD) – образующие усечённого конуса, то (AB = CD) и трапеция (ABCD) – равнобедренная.
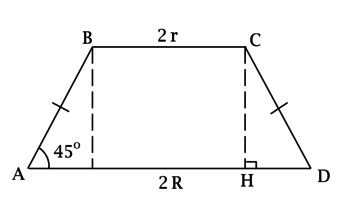
Построим (CHperp AD). Так как (angle ADC = 45^circ), то (triangle CHD) – равнобедренный и (CH = HD).
[HD = dfrac{AD — BC}{2} = R — r,qquadqquad S_{ABCD} = dfrac{BC + AD}{2}cdot CH = (R + r)(R — r) = R^2 — r^2 = dfrac{210}{sqrt[3]{pi^2}},] но (r = dfrac{R}{sqrt{15}}), тогда [R^2left(1-dfrac{1}{15}right) = dfrac{210}{sqrt[3]{pi^2}}qquadRightarrowqquad R = dfrac{15}{sqrt[3]{pi}}qquadRightarrowqquad V_{text{шара}} = dfrac{4}{3}pi R^3 = dfrac{4}{3}cdotpicdotdfrac{15^3}{pi} = 4500.]
Ответ: 4500
Задание
7
#3114
Уровень задания: Сложнее ЕГЭ
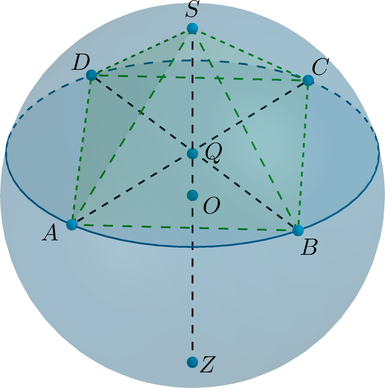
Дан шар, диаметр которого равен (9). Плоскость (alpha) пересекает диаметр (SZ) шара под углом (90^circ) и делит его точкой пересечения в отношении (1:2), считая от вершины (S). Найдите объем пирамиды с вершиной в точке (S), в основании которой лежит квадрат, вписанный в сечение шара плоскостью (alpha).
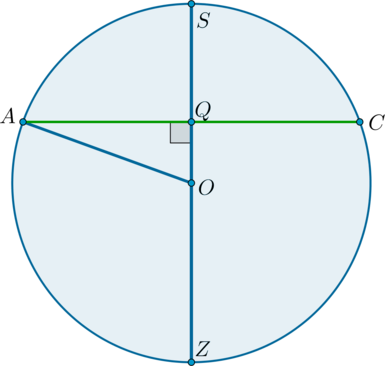
Пусть (O) – центр шара, (Q) – точка пересечения (SZ) и плоскости (alpha). Пусть (SABCD) – пирамида, объем которой нужно найти.
Рассмотрим сечение шара плоскостью (ASC).
Так как (SQ:QZ=1:2), то (SQ:SZ=1:3), следовательно, (SQ:SO=2:3), следовательно, (OQ:SO=1:3). Тогда [AQ=sqrt{AO^2-OQ^2}=sqrt{AO^2-left(dfrac13AOright)^2}=dfrac{2sqrt2}3AO
=dfrac{2sqrt2}3cdot dfrac92=3sqrt2] Следовательно, (AC=6sqrt2). Следовательно, (AB=AC:sqrt2=6).
Также [SQ=dfrac23SO=dfrac23cdot dfrac92=3] Заметим, что (SQ) – высота пирамиды, так как (SQperp alpha). Следовательно, [V=dfrac13cdot SQcdot AB^2=36.]
Ответ: 36
Задачи по стереометрии, в которых требуется произвести расчет объема сферы и измерение других неизвестных параметров, встречаются в ЕГЭ каждый год. Это означает, что знать основные формулы и уметь оперативно находить правильный ответ должны выпускники с разным уровнем подготовки. Понимая принцип решения задач ЕГЭ, в которых требуется вычислить объем или, к примеру, площадь сферы, старшеклассники смогут выполнять упражнения с любым количеством действий и при этом получить достаточно высокие баллы по итогам прохождения экзаменационного испытания.
Базовая информация
- Сферой называется поверхность, которая состоит из множества точек пространства. Все они располагаются на одинаковом расстоянии от точки О. Она является центром сферы.
- Геометрическое тело, которое ограничено сферой, называется шаром. Его осевое сечение представляет собой круг. Радиус последнего равен радиусу шара.
- Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в n2 раз, а объем — в n3 раз.
Занимайтесь с образовательным порталом «Школково» для качественной подготовки к экзамену!
Проблема поиска необходимой информации встает перед старшеклассниками достаточно остро. Не всегда школьный учебник оказывается под рукой. А поиск базовых формул для вычисления площади, объема шара и других неизвестных параметров бывает достаточно трудоемким даже в онлайн-режиме.
Наш образовательный проект поможет сэкономить время и эффективно подготовиться к сдаче экзаменационного испытания. Мы предлагаем учащимся и их преподавателям выстроить процесс подготовки к ЕГЭ от простого к сложному. Такой подход позволит старшеклассникам понять, какие темы требуют более детального изучения, и улучшить имеющиеся знания.
Базовая информация, которую стоит повторить еще до выполнения задач на нахождение объема шара, представлена в разделе «Теоретическая справка». Материал, подготовленный опытными преподавателями «Школково», поможет вам восполнить пробелы в знаниях без помощи репетитора.
Чтобы задачи ЕГЭ по теме «Шар» или, например, по теме «Цилиндр», не вызывали затруднений, мы предлагаем также потренироваться в выполнении соответствующих упражнений. Множество заданий разной степени сложности вы найдете в разделе «Каталог». Каждое упражнение содержит подробный алгоритм решения. Попрактиковавшись в режиме онлайн и поняв принцип нахождения правильного ответа, школьники смогут без труда вычислить объем сферы.
При необходимости любое задание можно сохранить в разделе «Избранное». Это позволит в дальнейшем вернуться к нему.
Выполнять онлайн-задания на нахождение площади боковой сферы могут не только школьники из столицы, но и выпускники из других российских городов.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
08
Сен 2013
Категория: 02 Стереометрия
02. Шар
2013-09-08
2022-09-11
Задача 1. Объем шара равен 12348. Найдите площадь его поверхности, деленную на
Решение: + показать
Задача 2. Площадь большого круга шара равна Найдите площадь поверхности шара.
Решение: + показать
Задача 3. Площадь поверхности шара равна Найдите площадь большого круга шара.
Решение: + показать
Задача 4. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в раз?
Решение: + показать
Задача 5. Во сколько раз увеличится объем шара, если его радиус увеличить в пять раз?
Решение: + показать
Задача 6. Объем первого шара в раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Решение: + показать
Задача 7. Радиусы двух шаров равны и
Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Решение: + показать
Задача 8. Радиусы трех шаров равны ,
и
Найдите радиус шара, объем которого равен сумме их объемов.
Решение: + показать
Вы можете пройти тест
Автор: egeMax |
комментариев 7
Задачи
для подготовки к ЕГЭ
«Шар.
Площадь поверхности шара»
№1 Площадь большого круга шара равна 3. Найдите
площадь поверхности шара.
№2 Дано два
шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз
площадь поверхности первого шара больше площади поверхности второго?
№3 Радиусы
двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого
равна сумме площадей поверхностей двух данных шаров.
№4Площадь поверхности
шара равна 24. Найдите площадь большого круга шара.
№5 Даны два
шара с радиусами 5 и 1. Во сколько раз площадь поверхности первого
шара больше площади поверхности второго?
№6 Шар вписан
в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь
поверхности шара.
№7 Около конуса
описана сфера (сфера содержит окружность основания конуса и его вершину).
Центр сферы совпадает с центром основания конуса. Образующая конуса
равна 7 Найдите радиус сферы.
№8 Шар вписан
в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной
поверхности цилиндра.
Домашнее
задание
№1
Площадь большого круга шара равна
1. Найдите площадь поверхности шара.
№2 Дано два шара. Радиус первого шара в 60 раз
больше радиуса второго. Во сколько раз площадь поверхности первого шара больше
площади поверхности второго?
№3Радиусы двух шаров равны 32 и 60. Найдите
радиус шара, площадь поверхности которого равна сумме площадей поверхностей
двух данных шаров.
№4 Площадь поверхности шара равна 12. Найдите
площадь большого круга шара.
№5 Даны два шара с радиусами 8 и 4. Во сколько
раз площадь поверхности первого шара больше площади поверхности
второго?
№6 Шар вписан в цилиндр. Площадь полной
поверхности цилиндра равна 6. Найдите площадь поверхности шара.
№7 Около конуса описана сфера (сфера содержит
окружность основания конуса и его вершину). Центр сферы совпадает с
центром основания конуса. Образующая конуса равна Найдите
радиус сферы.
№8 Шар вписан в цилиндр.
Площадь поверхности шара равна 30. Найдите площадь полной поверхности
цилиндра.
По теме: методические разработки, презентации и конспекты
мини-сборник для подготовки ГИА: «Уравнение с одной переменной»
сборник составлен для подготовки к ГИА по теме «Уравнения с одной переменной»…
Сборник заданий части С для подготовки к ЕГЭ по химии
Здесь собраны задания части С из материалов ЕГЭ по химии….
Сборник по подготовке к ЕГЭ авт.Щеголева Л.М. и Тимченко И.В. издан в журнале «Французский язык»
Сборник содержит различные виды заданий по подготовке к ЕГЭ….
Сборник по подготовке к ЕГЭ, ГИА по темам «Сказуемое и его основные виды», «Тире между подлежащим и сказуемым», «Односоставное предложение».
В связи с переходом образовательных учреждений РФ и в частности школ на новую форму итоговой аттестации в 9 классе возникает необходимость и в новом подходе к планировани…
Сборник по подготовке к ЕГЭ, ГИА по темам «Сказуемое и его основные виды», «Тире между подлежащим и сказуемым», «Односоставное предложение».
В связи с переходом образовательных учреждений РФ и в частности школ на новую форму итоговой аттестации в 9 классе возникает необходимость и в новом подходе к планировани…
Задания из сборника.Часть В 14 (по старому В 13)
Этот документ содержит основные задания из части.В-13.Для успешной сдачи экзамена рекомендую решить самим или с помощью учителя! Успехов!…
Устная часть ОГЭ. Задание 2. Сборник вопросов
Во втором задании устной части ученику предлагается принять участие в телефонном опросе, где у него есть 40 секунд, чтобы ответить на каждый из 6 вопросов….
Шар
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. В куб вписан шар радиуса 1. Найдите объем куба.
-
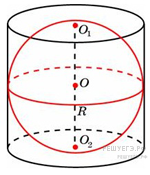
Около шара описан цилиндр, площадь поверхности которого равна 6. Найдите площадь поверхности шара.
-
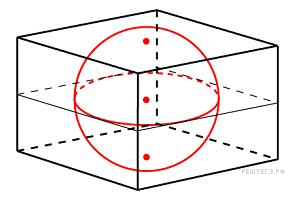
Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
-
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
-
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна
. Найдите радиус сферы.
-
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен
. Найдите образующую конуса.
-
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.









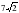 . Найдите радиус сферы.
. Найдите радиус сферы.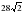 . Найдите образующую конуса.
. Найдите образующую конуса.