в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 205 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
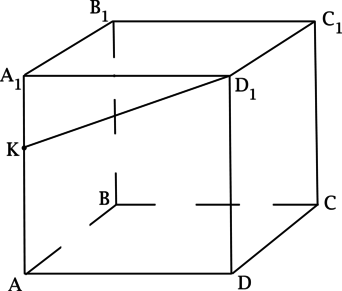
Плоскость α проходит через середину ребра AD прямоугольного параллелепипеда ABCDA1B1C1D1 перпендикулярно прямой BD1.
а) Докажите, что угол между плоскостью α и плоскостью ABC равен углу между прямыми BB1 и B1D.
б) Найдите угол между плоскостью α и плоскостью ABC, если объём параллелепипеда ABCDA1B1C1D1 равен
и
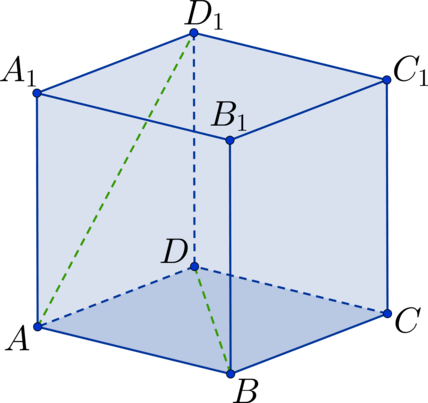
Плоскость α проходит через середину ребра AD прямоугольного параллелепипеда ABCDA1B1C1D1 перпендикулярно прямой BD1.
а) Докажите, что угол между плоскостью α и плоскостью ABC равен углу между прямыми BB1 и B1D.
б) Найдите угол между плоскостью α и плоскостью ABC, если объём параллелепипеда ABCDA1B1C1D1 равен
и
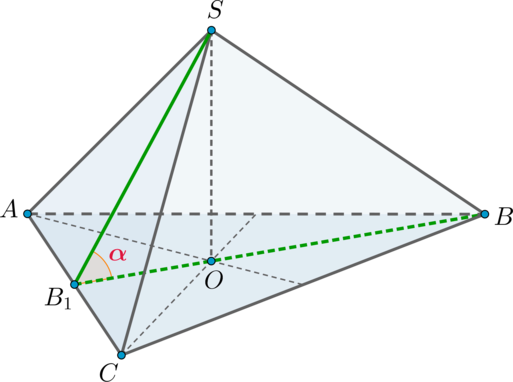
Боковое ребро правильной треугольной пирамиды SABC равно 6, а косинус угла ASB при вершине боковой грани равен Точка M — середина ребра SC, точка N — середина ребра AC.
а) Докажите, что угол между прямыми BM и SA либо равен углу BMN, либо дополняет его до 180°.
б) Найдите косинус угла между прямыми BM и SA.
Основанием пирамиды АВСD является равносторонний треугольник АВС, длина стороны которого равна 4. Боковое ребро CD перпендикулярно плоскости основания и имеет длину Пусть М — середина ребра ВС, а N — середина ребра АВ.
А) Докажите, что угол между прямыми DM и СN равен 45°.
Б) Найдите расстояние между прямыми DM и СN.
Источник: А. Ларин. Тренировочный вариант № 346.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 5, найдите угол между прямыми FA и D1E1. Ответ дайте в градусах.
Источник: ЕГЭ по математике 23.04.2013. Досрочная волна. Восток. Вариант 1.
В правильной треугольной призме ABCA1B1C1 известны рёбра: AB AA1 = 4. Точка M — середина ребра BC.
а) Докажите, что прямые B1C и C1M перпендикулярны.
б) Найдите угол между прямой C1M и плоскостью грани ABB1A1.
Источник: ЕГЭ — 2017.Вариант 511 (C часть).
Точки A, B и C лежат на окружности основания конуса с вершиной S, причем A и C диаметрально противоположны. Точка M — середина BC.
а) Докажите, что прямая SM образует с плоскостью ABC такой же угол, как и прямая AB с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если AB = 6, BC = 8 и AS =
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2019.
Точка O — центр грани ABCD куба ABCDA1B1C1D1. На рёбрах AD и C1D1 отмечены соответственно точки M и N так, что DM = D1N = AO.
а) Докажите, что прямая MN образует с плоскостью DCC1 угол 30°.
б) Найдите угол между плоскостями MNO и DCC1.
Точка O — центр грани ABB1A1 куба ABCDA1B1C1D1. На рёбрах AA1 и C1D1 отмечены соответственно точки M и N так, что A1M = D1N = AO.
а) Докажите, что прямая MN образует с плоскостью A1B1C1 угол 30°.
б) Найдите угол между плоскостями MNO и A1B1C1.
На ребре CC1 куба ABCDA1B1C1D1 отмечена точка E так, что CE : EC1 = 1 : 2.
а) Пусть точка F делит ребро BB1 в отношении 1 : 2, считая от вершины B1. Докажите, что угол между прямыми BE и AC1 равен углу AC1F.
б) Найдите угол между прямыми BE и AC1.
Источник: ЕГЭ 10.07.2012 по математике. Вторая волна. Вариант 501.
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите угол между прямыми ВВ1 и АС1, если АВ = 8, ВВ1 = 6, В1С1 = 15.
Источник: ЕГЭ — 2018. Основная волна 01.06.2018. Вариант 302 (C часть)., Задания 14 (С2) ЕГЭ 2018
В конусе с вершиной S и центром основания O радиус основания равен 13, а высота равна Точки A и B — концы образующих, M — середина SA, N — точка в плоскости основания такая, что прямая MN параллельна прямой SB.
а) Докажите что ANO — прямой угол.
б) Найдите угол между MB и плоскостью основания, если дополнительно известно что AB = 10.
Источник: ЕГЭ по математике 10.04.2019. Досрочная волна, резервная волна, Задания 14 (С2) ЕГЭ 2019
Точки A, B и C лежат на окружности основания конуса с вершиной S, причем A и C диаметрально противоположны. Точка M — середина BC.
а) Докажите, что прямая SM образует с плоскостью ABC такой же угол, как и прямая AB с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если AB = 4, BC = 6 и AS =
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2019.
Диагональ основания ABCD правильной пирамиды SABCD равна 8, высота пирамиды SO равна 1. Точка M — середина ребра SC, точка K — середина ребра CD.
а) Найдите угол между прямыми BM и SK.
б) Найдите расстояние между прямыми BM и SK.
Источник: А. Ларин. Тренировочный вариант № 257.
В правильном тетраэдре ABCD точка К — середина ребра АВ, точка Е лежит на ребре CD и EC : ED = 1 : 2.
а) Найдите угол между прямыми ВС и КЕ.
б) Найдите расстояние между прямыми ВС и КЕ, если ребро тетраэдра равно
Источник: А. Ларин. Тренировочный вариант № 298.
Точки A, B и C лежат на окружности основания конуса с вершиной S, причём A и C диаметрально противоположны. Точка M — середина BC.
а) Докажите, что прямая SM образует с плоскостью ABC такой же угол, как и прямая AB с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если AB = 6, BC = 8 и
Источник: Избранные задания по математике из последних сборников ФИПИ
Точки A, B и C лежат на окружности основания конуса с вершиной S, причём A и C диаметрально противоположны. Точка M — середина BC.
а) Докажите, что прямая SM образует с плоскостью ABC такой же угол, как и прямая AB с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если AB = 4, BC = 6 и
Источник: Избранные задания по математике из последних сборников ФИПИ
Всего: 205 1–20 | 21–40 | 41–60 | 61–80 …
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между прямыми
(blacktriangleright) Угол между прямыми – это такой угол (alpha), что (0leqslant alphaleqslant 90^circ).
(blacktriangleright) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
(blacktriangleright) Порядок нахождения угла между скрещивающимися прямыми:
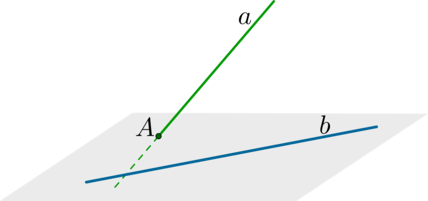
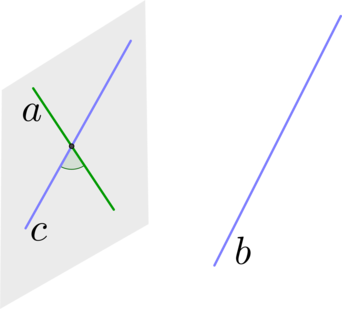
Шаг 1: через одну из двух прямых (a) провести плоскость, параллельную второй прямой (b) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую (c), параллельную прямой (b);
Шаг 3: тогда угол между прямыми (a) и (b) будет равен углу между прямыми (a) и (c).
Задание
1
#934
Уровень задания: Равен ЕГЭ
(ABCDA_1B_1C_1D_1) – куб. Найдите угол между прямыми, содержащими отрезки (AC) и (B_1D_1). Ответ дайте в градусах.
Прямая (BD) параллельна прямой (B_1D_1), тогда угол между (AC) и (B_1D_1) равен углу между (AC) и (BD), но (AC) и (BD) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ (90^{circ}).
Ответ: 90
Задание
2
#2847
Уровень задания: Равен ЕГЭ
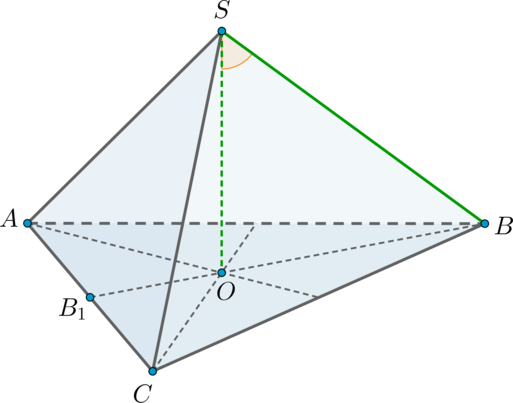
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите угол между высотой пирамиды и ребром (SB), если высота пирамиды равна (2sqrt3), а сторона основания пирамиды равна (6). Ответ дайте в градусах.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота (SO) падает в точку пересечения медиан основания.
Пусть (BB_1) – медиана, а значит, и высота. По теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=3sqrt3 quadRightarrowquad BO=dfrac23BB_1=2sqrt3,] так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Следовательно, прямоугольный (triangle SOB) является равнобедренным ((SO=BO=2sqrt3)), значит, острые углы равны по (45^circ).
Ответ: 45
Задание
3
#933
Уровень задания: Равен ЕГЭ
(ABCDA_1B_1C_1D_1) – куб. Точка (K) лежит на ребре (AA_1). Найдите угол между прямыми, содержащими отрезки (D_1K) и (AB). Ответ дайте в градусах.
Так как (ABCDA_1B_1C_1D_1) – куб, то (AB) перпендикулярен плоскости ((ADD_1)), тогда (AB) перпендикулярен любой прямой, лежащей в плоскости ((ADD_1)), следовательно, угол между прямыми, содержащими отрезки (D_1K) и (AB) равен (90^{circ}).
Ответ: 90
Задание
4
#2845
Уровень задания: Равен ЕГЭ
Дан правильный тетраэдр (SABC). Найдите квадрат тангенса угла между высотой грани (SAC), опущенной из вершины (S), и высотой грани (ABC), опущенной из вершины (B).
Пусть (SB_1) – высота грани (SAC). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть (SB_1) также является и медианой, значит, (AB_1=B_1C). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если (SO) – высота, то (O) – точка пересечения медиан треугольника (ABC), а значит и высот, так как (triangle ABC) правильный. Следовательно, (BB_1) — медиана и высота.
Таким образом, необходимо найти (mathrm{tg}^2angle (SB_1,
BB_1)).
Пусть (a) – ребро тетраэдра. Тогда (BC=a, B_1C=0,5a), следовательно, по теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=dfrac{sqrt3}2a] Так как (O) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB_1=frac13BB_1=frac{sqrt3}6a).
Так как (triangle ABC=triangle SAC), то (SB_1=BB_1). Следовательно, из прямоугольного (triangle SB_1O): [cos
alpha=dfrac{OB_1}{SB_1}=dfrac13 quadRightarrowquad sin alpha
=sqrt{1-cos^2alpha}=dfrac{2sqrt2}3 quadRightarrowquad
mathrm{tg}^2alpha=(2sqrt2)^2=8.]
Ответ: 8
Задание
5
#1846
Уровень задания: Равен ЕГЭ
Дан куб (ABCDA_1B_1C_1D_1). Найдите угол между прямыми (AD_1) и (BD). Ответ дайте в градусах.
Заметим, что (BC_1 || AD_1), тогда рассмотрим треугольник (triangle BDC_1), в котором необходимо определить (angle DBC_1). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали (Rightarrow) (triangle BDC_1) – равносторонний треугольник (Rightarrow) (angle DBC_1 = 60^circ).
Ответ: 60
Задание
6
#1847
Уровень задания: Равен ЕГЭ
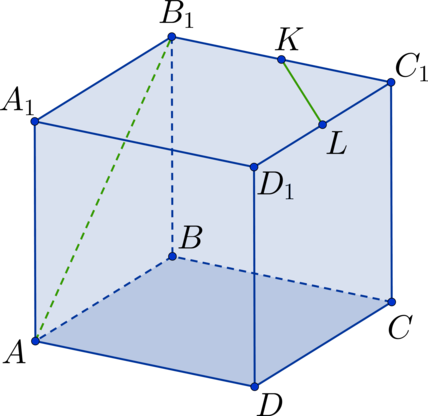
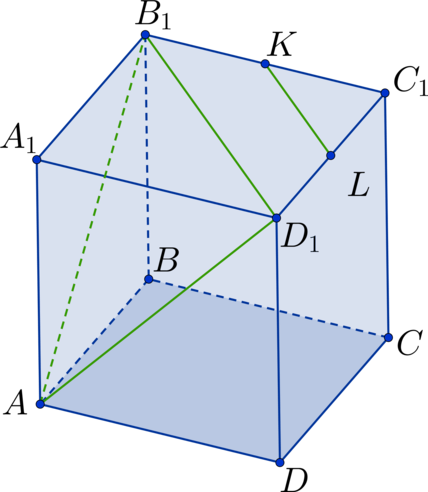
Дан куб (ABCDA_1B_1C_1D_1). Точка (K) – середина стороны (B_1C_1), а точка (L) – середина стороны (C_1D_1). Найдите угол между прямыми (AB_1) и (KL). Ответ дайте в градусах.
Проведем диагональ (B_1D_1) в квадрате (A_1B_1C_1D_1). Тогда (KL) – средняя линия в (triangle B_1C_1D_1) (Rightarrow) (KL || B_1D_1) (Rightarrow) (angle AB_1D_1) – искомый угол. Рассмотрим (triangle AB_1D_1). Он состоит из диагоналей соответствующих квадратов (Rightarrow) треугольник является равносторонним (Rightarrow) (angle AB_1D_1 = 60^circ).
Ответ: 60
Задание
7
#2846
Уровень задания: Сложнее ЕГЭ
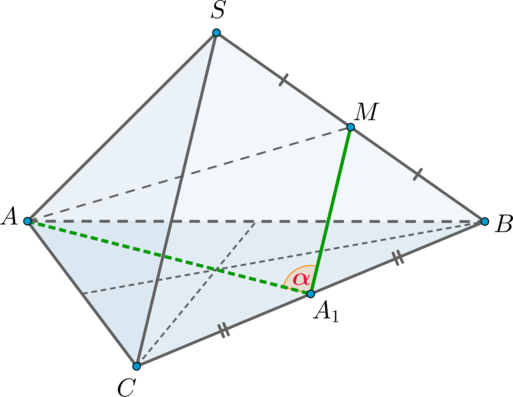
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите косинус угла между высотой основания (AA_1) и ребром (SC), если сторона основания равна (sqrt3), а боковое ребро равно (2).
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, (AA_1) также является и медианой.
Заметим, что прямые (AA_1) и (SC) скрещиваются. Проведем (A_1Mparallel SC), следовательно, (angle (AA_1, SC)=angle (AA_1,
A_1M)).
Так как (A_1Mparallel SC) и (A_1) – середина (BC), то (M) – середина (SB). Следовательно, (A_1M) – средняя линия и [A_1M=frac12SC=1.] По теореме Пифагора из (triangle ABA_1): [AA_1=sqrt{AB^2-A_1B^2}=dfrac32.] Медиану (AM) из (triangle SAB) можно найти по формуле медианы: [AM^2=dfrac{2AS^2+2AB^2-SB^2}4=dfrac52.] Следовательно, по теореме косинусов из (triangle AA_1M): [cos alpha=dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1cdot A_1M}=dfrac14=0,25.]
Ответ: 0,25
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
Основные моменты
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
ЕГЭ Профиль №13. Угол между прямыми
Скачать файл в формате pdf.
ЕГЭ Профиль №13. Угол между прямыми
Угол между двумя прямыми. Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых. Очевидно, ({0^ circ } < alpha leqslant {90^ circ }). Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся. Для нахождения этого угла, как правило, используют теорему косинусов. Две прямые называются перпендикулярными, если угол между ними равен ({90^ circ }). Угол между параллельными прямыми считается равным нулю.
Нахождение угла между прямыми координатным методом.
1) Находим координаты двух точек на каждой из прямых.
2) Находим координаты векторов (для этого из координат конца вычитаем соответствующие координаты начала).
3) Используя скалярное произведение векторов, находим косинус угла между эти векторами, который и будет являться косинусом угла между прямыми, (cos left( {overrightarrow a {,^ wedge }{kern 1pt} overrightarrow b } right) = frac{{overrightarrow a {kern 1pt} {kern 1pt} overrightarrow b }}{{left| {,overrightarrow a ,} right|{kern 1pt} left| {{kern 1pt} overrightarrow b {kern 1pt} } right|}} = frac{{{x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}}}{{sqrt {x_1^2 + y_1^2 + z_1^2} ,sqrt {x_2^2 + y_2^2 + z_2^2} }}), где x1, y1, z1 координаты вектора (vec a), а x2, y2, z2 координаты вектора (vec b).
4) Если косинус получился равен отрицательному значению, то берем это значение по модулю.
1В. Дана треугольная пирамида ABCD.
а) Постройте её сечение плоскостью, проходящей через середину ребра AB параллельно рёбрам AD и BC.
б) Найдите угол между прямыми AD и BC, если AD = 24, BC = 10, а расстояние между серединами рёбер BD и AC равно 13.
2В. Точка K лежит на ребре AD треугольной пирамиды ABCD.
а) Постройте сечение пирамиды плоскостью α, проходящей через точку K параллельно рёбрам AB и CD.
б) Пусть M — точка пересечения плоскости α с ребром BC. Найдите угол между прямыми AB и CD, если K — середина ребра AD, AB = 8, CD = 6, KM = 5.
3В. В правильной шестиугольной пирамиде SABCDEF с вершиной S точка M — середина бокового ребра SC.
а) Постройте точку пересечения прямой BM с плоскостью грани ESF.
б) Найдите угол между прямыми BM и DE.
4В. Точка G лежит на боковом ребре SC правильной шестиугольной пирамиды SABCDEF с вершиной S.
а) Постройте точку пересечения прямой BG с плоскостью боковой грани ESF.
б) Найдите угол между прямыми BG и AD, если стороны основания пирамиды равны 6, боковые рёбра равны (3sqrt {13} ), а SG : GC = 1 : 2.
5В. Основания призмы ABCA1B1C1 — равносторонние треугольники. Точки M и M1 — центры оснований ABC и A1B1C1 соответственно.
а) Докажите, что угол между прямыми BM и C1M1 равен ({60^circ }).
б) Найдите угол между прямыми BM1 и C1M, если призма прямая и AB : AA1 = 3 : 2.
ОТВЕТ: (arccos frac{{11}}{{14}}).
6В. Основание прямой призмы ABCA1B1C1 — равнобедренный прямоугольный треугольник ABC с прямым углом при вершине C. Точка M —середина ребра AB. Известно, что AB = 2AA1.
а) Докажите, что прямые A1C и MB1 перпендикулярны.
б) Найдите угол между прямыми AC1 и MB1.
ОТВЕТ: (arccos frac{{sqrt 6 }}{3}).
7В. Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1 со стороной основания (sqrt 3 ) и боковым ребром 1.
а) Докажите, что плоскости ACA1 и B1CE1 перпендикулярны.
б) Найдите угол между прямыми BF1 и CD1.
ОТВЕТ: (arccos frac{{11sqrt {10} }}{{40}}).
8В. Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1.
а) Докажите, что плоскости AB1F и ACC1 перпендикулярны.
б) Найдите угол между прямыми AB1 и CF1, если (A{A_1} = ABsqrt 2 ).
9В. Основание пирамиды SABCD — параллелограмм ABCD. Точка K —середина ребра SD.
а) Плоскость проходит через точку K параллельно медианам BM и SN граней BSC и ASD. Постройте прямую пересечения этой плоскости с плоскостью основания пирамиды.
б) Найдите угол между прямыми BM и SN, если пирамида SABCD правильная, причём все её рёбра равны.
ОТВЕТ: (arccos frac{1}{6}).
10В. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Точки K и L —центры граней BB1C1C и A1B1C1D1 соответственно.
а) Докажите, что точка пересечения прямой KL с плоскостью основания ABCD равноудалена от вершин B и C.
б) Пусть M — середина ребра CD. Найдите котангенс угла между прямыми MD1 и KL, если известно, что AB = 2AA1.
11В. Дан параллелепипед ABCDA1B1C1D1. Точка M — середина ребра A1B1.
а) Докажите, что любая плоскость, проведённая через точку M параллельно диагонали CA1 параллелепипеда, проходит через центр грани BB1C1C.
б) Найдите угол между прямыми BM и CB1, если параллелепипед прямоугольный, AB = 2BC и CC1 : BC = 4 : 3.
ОТВЕТ: (arccos frac{{16}}{{25}}).
12В. Основание пирамиды SABCD — квадрат ABCD, высота пирамиды проходит через точку D.
а) Докажите, что все боковые грани пирамиды — прямоугольные треугольники.
б) Пусть M — середина бокового ребра SC. Найдите угол между прямыми AM и BC, если известно, что отношение высоты пирамиды к стороне её основания равно (sqrt {11} ).
13В. Дана правильная четырёхугольная пирамида SABCD с вершиной S. Точки M и N — середины рёбер AB и SC.
а) Постройте сечение пирамиды плоскостью, проходящей через прямую MN параллельно SA.
б) Найдите угол между прямыми SA и MN, если боковое ребро пирамиды равно стороне основания.
14В. В основании пирамиды DABC лежит прямоугольный треугольник ABC с прямым углом при вершине C. Высота пирамиды проходит через точку B.
а) Докажите, что отрезок, соединяющий середины рёбер BC и AD, равен отрезку, соединяющему середины рёбер AB и CD.
б) Найдите угол между прямой BD и прямой, проходящей через середины рёбер BC и AD, если известно, что BD = AC.
15В. Дана правильная треугольная призма ABCA1B1C1. На ребре BC взята точка M, причём BM : CM = 1 : 2.
а) Докажите, что плоскость, проходящая через центры граней A1B1C1 и BB1C1C параллельно ребру AC, проходит через точку M.
б) Пусть K — середина ребра A1C1, N — центр грани BB1C1C. Найдите угол между прямыми B1K и MN, если (AC = 18sqrt 3 ,;;A{A_1} = sqrt {13} ).
ОТВЕТ: (arccos frac{9}{{11}}).
16В. Основание призмы ABCDEFA1B1C1D1E1F1 — правильный шестиугольник ABCDEF.
а) Постройте точку пересечения прямой B1E с плоскостью ACD1.
б) Найдите угол между прямыми AB1 и BD1, если призма правильная, а (A{A_1}:AB = sqrt 3 :1).
ОТВЕТ: (arccos frac{{sqrt 6 }}{4}).
17В. Дана прямая призма ABCA1B1C1. Плоскость, проходящая через центр основания A1B1C1 и середину K ребра BC, параллельна прямой AB. Эта плоскость пересекает прямую CC1 в точке L.
а) Докажите, что CL = 3CC1.
б) Найдите угол между прямыми KL и AC1, если ∠ACB = ({90^circ }) и (A{A_1} = AC = frac{1}{4}BC).
ОТВЕТ: (arccos frac{{3sqrt {26} }}{{26}}).
18В. В основании пирамиды SABCD лежит трапеция ABCD с основаниями AD и BC и прямым углом при вершине A, причём BC = 2AD. Высота пирамиды проходит через точку A.
а) Докажите, что сечение пирамиды плоскостью, проходящей через прямую AD и середину M ребра SC, — прямоугольник.
б) Найдите косинус угла между прямыми AM и CD, если известно, что AD = AB и (SA = sqrt 3 AB).
19В. В основании пирамиды SABCD лежит равнобедренная трапеция ABCD с основаниями AD и BC. Высота пирамиды проходит через точку A, SH — высота треугольника BSC. Известно, что BC = 2AD, AB = AD = 2SA.
а) Докажите, что SH = CD.
б) Найдите косинус угла между прямыми CD и SH.
20В. Основание ABCD прямой призмы ABCDA1B1C1D1 — ромб с острым углом ({60^circ }) при вершине A. Точка M — середина ребра CD, точка H лежит на стороне AB, причём DH — высота ромба ABCD.
а) Докажите, что D1M ⊥DH.
б) Найдите угол между прямыми MD1 и BC1, если ∠ABA1 = ({60^circ }).
ОТВЕТ: (arccos frac{{11sqrt {13} }}{{52}}).
21В. Основание прямой призмы ABCDA1B1C1D1 — равнобедренная трапеция ABCD с основаниями AD = 2BC и боковой стороной AB = BC.
а) Докажите, что AB ⊥ DB1.
б) Найдите угол между прямыми CD1 и DB1, если боковая грань AA1D1D — квадрат.
ОТВЕТ: (arccos frac{{sqrt {35} }}{{14}}).
22В. Две правильные пирамиды DABC и FABC имеют общее основание ABC и расположены по разные стороны от него. Все плоские углы при вершинах D и F прямые.
а) Докажите, что угол между плоскостями ADB и AFB равен углу между прямыми CD и CF.
б) Найдите угол между прямыми AD и BF, если боковые рёбра каждой пирамиды равны 1.
ОТВЕТ: (arccos frac{2}{3}).
23В. Две правильные четырёхугольные пирамиды EABCD и FABCD имеют общее основание ABCD и расположены по разные стороны от него. Точки M и N — середины рёбер BC и AB соответственно. Все рёбра пирамид равны.
а) Докажите, что угол между прямыми AE и BF равен ({60^circ }).
б) Найдите угол между прямыми EM и FN.
ОТВЕТ: (arccos frac{2}{3}).
24В. Основание пирамиды DABC — прямоугольный треугольник АВС с прямым углом при вершине С. Высота пирамиды проходит через точку В. Точки М и N — середины рёбер АD и BC соответственно.
а) Докажите, что MN является биссектрисой угла ВМС.
б) Найдите угол между прямыми BD и MN, если (BD = 6sqrt 2 ), AC = 16.
ОТВЕТ: ({mathop{rm arctg}nolimits} frac{{4sqrt 2 }}{3}).
Координаты вектора
Вектор – отрезок, имеющий длину и указывающий направление.
На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.
Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$
Скрещивающиеся прямые
И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$
Уравнение плоскости
В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.
Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.
Например, пусть даны три точки:
$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$
Подставим координаты точек в общее уравнение плоскости:
$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$
Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.
Теперь у нас есть три уравнения и три неизвестные – можем решить систему:
Пример 3
Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$
Расстояние от точки до плоскости
Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$
Пример 4
Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$
Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$
Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.
Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).
Пример 5
Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.
Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) — середина ребра (CE).
- Докажите, что прямые (AD) и (BG) перпендикулярны.
- Найдите расстояние между прямыми (AD) и (BG).
Решение:
Решим задачу полностью методом координат.
Нарисуем рисунок и выберем декартову систему координат. (Рис 5).
Предлагаемый материал предназначен как для подготовки выпускников 11-х классов общеобразовательных учреждений к государственной итоговой аттестации по математике, так и при изучении темы «Угол между прямыми в пространстве». Материал состоит из комплекта: теория по теме, задания на выбор верного утверждения, задачи на готовых чертежах, опорные задачи и задачи для самостоятельного решения. все наборы задач снабжены ответами и могут быть использованы при различных видах работы с обучающимися: в индивидуальных консультациях, при самостоятельной подготовке или поэтапно при изучении темы.
Работа составлена с использованием следующих источников:
- Геометрия: Учеб. для 10-11 кл. общеобразоват. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. — М.: Просвещение, 2016
- Задачи и упражнения на готовых чертежах. 10-11 классы. Геометрия. / Рабинович Е.М. — М.: ИЛЕКСА, 2014
- Сборник задач по геометрии в рисунках и тестах. 10-11 кл. / Смирнова И.М. — М. — «Аквариум», 1999
- Геометрия: Задачи на готовых чертежах для подготовки к ЕГЭ: 10-11 классы / Э.Н.Балаян. — Ростов-н/Д: Феникс, 2013
- ЕГЭ 2019. 100 баллов. Математика. Профильный уровень. Опорные задачи по геометрии. Планиметрия. Стереометрия. / Е.В.Потоскуев. — М.: «Экзамен», 2019
- ЕГЭ 2019. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень) / под ред. И.В.Ященко — М. : МЦМНО, 2019
Просмотр содержимого документа
«БУКЛЕТ угол между прямыми»
Просмотр содержимого документа
«ВЕРНО — НЕВЕРНО Угол между прямыми в пространстве»
Просмотр содержимого документа
«ГОТОВЫЕ ЧЕРТЕЖИ Угол между прямыми в пространстве»
Просмотр содержимого документа
«ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ Угол между прямыми в пространстве»
Просмотр содержимого документа
«ИСТОЧНИКИ Угол между прямыми в пространстве»
Просмотр содержимого документа
«ОПОРНЫЕ ЗАДАЧИ Угол между прямыми в пространстве»
Просмотр содержимого документа
«ТЕОРИЯ Угол между прямыми в пространстве»
Просмотр содержимого документа
«описание разработки»
Описание презентации по отдельным слайдам:
-
1 слайд
(1;1;0)
В кубе ABCDA1B1C1D1 точки E и K середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
y
z
x
D1
B
A
D
C
B1
C1
A1
E
K
(1;0;0)
Найдем координаты точек A, Е, В, K.
AE
1.
BK
2.
(0; ; 1)
2
1
(- ; 0; 1)
2
1
1
1
1
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому можно взять ребро куба, например, a или х. А можно рассмотреть единичный куб, все ребра которого равны 1.
(1; ;1)
2
1
( ;1;1)
2
1
Найдем координатывекторов АЕ и ВК.
?
?
?
?
Чтобы найти координаты вектора вычтем из координат конца вектора соответствующие координаты начала вектора.
-
2 слайд
3.
AE
(0; ; 1)
2
1
BK
(- ; 0; 1)
2
1 -
3 слайд
Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.
D
А
В
С
А1
D1
С1
В1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Куб отлично вписывается в систему координат.
К
1
2
1
2
х
y
z
?
(1;0; )
1
2
?
(1;1;0)
?
(0;1;0)
?
(1;0;1)
1
1
1
1
2 способ
1 способ -
4 слайд
Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.
D
А
В
С
А1
D1
С1
В1
1
1
1
2
К
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Заменим BA1 на параллельную прямую CD1. Угол между прямыми А1В и СК будет равен углу между CD1 и СК.
a
1
2
1
2
1
5
2
5
2
2 способ -
5 слайд
Точка К – середина ребра АА1 куба АВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.
D
А
В
С
А1
D1
С1
В1
1
1
1
2
К
a
1
2
1
2
1
5
2
5
2
3
2
Применим теорему косинусов для треугольника CKD1. Я хочу найти косинус угла KCD1, значит, составляем теорему косинусов для стороны KD1: -
6 слайд
A
D
C
A1
B1
C1
D1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Куб отлично вписывается в систему координат.
х
y
z
?
?
(0;0;1)
?
(0;1;0)
?
(0;1;1)
1
1
1
1 способ
Точка M – середина ребра АD куба АВСDA1B1C1D1. Найдите угол между прямыми C1M и B1С.M
B
1
2
1
2
(1; ; 0) -
7 слайд
1
1
A
D
C
A1
B1
C1
D1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Рассмотрев это трудоёмкое решение, метод координат показался мне «конфеткой».
2 способ
Точка M – середина ребра АD куба АВСDA1B1C1D1. Найдите угол между прямыми C1M и B1С.M
1
2
1
2
a
1
1
1
2
2
1
2
1
13
2
3
2
Применим теорему Пифагора к трем треугольникам.
К
К1
L
L1
Закончи решение самостоятельно.
Ответ:
Составим теорему косинусов для стороны MK. -
8 слайд
B
A
D
B1
C1
D1
A1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Куб отлично вписывается в систему координат.
х
y
z
?
?
(0;0;1)
?
1
1
1
1 способ
C
(0;1; )
1
2
(1;1;0)
Точка Е – середина ребра DD1 куба ABCDA1B1C1D1 найдите угол между прямыми СЕ и АС1.
E -
9 слайд
B
A
D
B1
C1
D1
A1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
Куб отлично вписывается в систему координат.
х
y
z
?
?
(0;0;1)
?
1
1
1
1 способ
C
(1;0;0)
(0;0; )
1
3
(1;1;0)
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что
СЕ : ЕС1 = 1 : 2. Найдите угол между прямыми ВЕ и АС1.
E -
10 слайд
B
A
B1
C1
D1
A1
Если в кубе не дано ребро, то можно обозначить его буквой или взять за «1»
1
1
1
C
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что
СЕ : ЕС1 = 1 : 2.
Найдите угол между прямыми
ВЕ и АС1.
E
1
3
2
3
K
3
13
3
D
a
10
3
Чтобы найти угол составим теорему косинусов для стороны KC1 в AKC1.
3
12
4
2 способ -
11 слайд
Точка Е – середина ребра DD1 куба ABCDA1B1C1D1 найдите угол между прямыми СЕ и АС1.
C
A
D1
C1
B
B1
1
D
A1
1
E
2
K
K1
N
N1
L
1
1
2
1
2
3
2
5
1
5
21
2
a
Чтобы найти угол составим теорему косинусов для стороны KL в KLD1.
Отрицательное значение косинуса говорит о том, что угол KD1L тупой. Но в стереометрии угол между прямыми не может быть тупым. Поэтому нам нужен смежный острый угол с углом KD1L. Строить его на чертеже не обязательно.
Если косинус тупого угла – ,то косинус смежного с ним
острого равен .
Ответ: = arccos
15
15
15
15
15
15