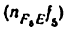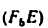ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Уфа 2008
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Уфимский государственный авиационный технический университет
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Допущено редакционно—издательским советом УГАТУ в качестве учебного пособия для студентов всех форм обучения, обучающихся по направлению 150200 «Машиностроительные технологии и оборудование»
Уфа 2008
УДК 621.833 (07) ББК 34.444 (я7)
Т33
Рецензенты: доктор техн. наук, проф. Ковган С.Г. доктор техн. наук, проф. Набиев Т.С.
Т33 Теория механизмов и машин: Учебное пособие / Уфимск. гос. авиац. техн. ун—т. Б.И.Гурьев, Л.С.Кутушева, Л.Л.Русак, А.Я.Садыкова, Р.Ш.Хабибуллина. – Уфа, 2008. –114 с.
ISBN 978-5-86911-757-1
Пособие соответствует дисциплине (курсу) Теория механизмов и машин.
Работа содержит достаточно подробное изложение курса лекций по теории механизмов и машин, по разделам: структурный анализ меха— низмов, кинематический анализ рычажных и зубчатых механизмов, си— ловой анализ рычажных механизмов, геометрия зубчатых передач. Кро— ме того, в каждом из разделов приведены типовые задачи, которые сту— денты могут использовать при подготовке к экзамену.
Учебное пособие предназначено для студентов механических спе— циальностей.
Ил. 149. Библ.: 6 назв.
ISBN 978-5-86911-757-1
©Уфимский государственный авиационный технический университет, 2008
|
Содержание |
|
|
Введение |
5 |
|
1. Структурный анализ механизмов. Строение и классификация |
|
|
плоских механизмов |
6 |
|
1.1. Классификация кинематических пар |
6 |
|
1.2. Классификация кинематических цепей |
8 |
|
1.3. Структурная формула плоского механизма |
9 |
|
1.4. Замена высших кинематических пар низшими |
12 |
|
1.5. Классификация плоских механизмов по Л. В. Ассуру |
12 |
|
1.6. Порядок структурного исследования плоского механизма |
14 |
|
Вопросы для самопроверки |
15 |
|
Задачи |
16 |
|
2. Кинематический анализ плоских рычажных механизмов |
21 |
|
Теоретические основы метода планов скоростей и ускорений |
21 |
|
Вопросы для самопроверки |
27 |
|
Задачи |
28 |
|
3. Кинематический анализ зубчатых механизмов |
34 |
|
3.1. Кинематика рядовых механизмов |
35 |
|
3.2. Кинематика планетарных и дифференциальных |
|
|
механизмов |
36 |
|
3.3. Кинематика комбинированных механизмов |
|
|
с последовательным соединением ступеней |
39 |
|
3.4. Кинематика замкнутых механизмов |
40 |
|
3.5. Синтез зубчатых механизмов. Особенности синтеза |
|
|
соосных механизмов |
41 |
|
Вопросы для самопроверки |
45 |
|
Задачи |
46 |
|
4. Силовой анализ плоских рычажных механизмов |
56 |
|
4.1. Характеристики реакций в кинематических парах |
57 |
|
4.2. Условие разрешимости задачи силового анализа плоского |
|
|
механизма |
58 |
|
4.3. Порядок силового анализа механизма |
58 |
|
4.4. Методы силового анализа |
59 |
|
4.5. Кинетостатика структурных групп II класса |
59 |
|
4.6. Кинетостатика начального звена |
65 |
|
4.7. Определение уравновешивающих сил и моментов |
|
|
методом Н. Е. Жуковского |
67 |
|
4.8. Определение уравновешивающих сил и моментов |
|
|
методом, основанным на применении принципа |
|
|
возможных перемещений |
69 |
|
Вопросы для самопроверки |
70 |
|
Задачи |
71 |
3
|
5. Геометрия зубчатых колес и передач |
76 |
|
5.1. Основной закон зацепления. Сопряженные профили |
76 |
|
5.2. Эвольвента окружности, ее уравнение и свойства |
77 |
|
5.3. Свойства эвольвентного зацепления |
78 |
|
5.4. Исходный контур. Исходный производящий контур |
81 |
|
5.5. Параметры зубчатого колеса, получаемые при нарезании |
|
|
зубьев |
82 |
|
5.6. Параметры зацепления, составленного из эвольвентных |
|
|
колес, нарезанных со смещением исходного контура |
87 |
|
5.7. Последовательность проектирования эвольвентной |
|
|
зубчатой передачи, составленной из колес, нарезанных |
|
|
стандартным реечным инструментом |
94 |
|
5.8. Проверка качества зацепления по геометрическим |
|
|
показателям |
97 |
|
5.9. Выбор коэффициентов смещения с помощью |
|
|
блокирующих контуров |
98 |
|
5.10. Размеры для контроля взаимного положения |
|
|
разноименных профилей зубьев (измерительные |
|
|
размеры) |
103 |
|
Вопросы для самопроверки |
107 |
|
Задачи |
108 |
|
Список литературы |
113 |
4
ВВЕДЕНИЕ
Дисциплина «Теория механизмов и машин» относится к циклу об— щепрофессиональных дисциплин.
При изучении курса «Теория механизмов и машин» (ТММ) студент получает основополагающие сведения о механизмах – об их многообра— зии, основных типах и о возможности их использования в различных машинах; изучает основные методы анализа и синтеза механизмов, применяемых в разнообразных машинах и устройствах; учится привле— кать ЭВМ для рационального проектирования механизмов и оптимиза— ции их параметров.
Этот курс лежит в основе конструкторских разделов большинства специальных дисциплин, освоение которых без знания основ теории ме— ханизмов и машин невозможно или затруднительно.
Умение самостоятельно и грамотно решать задачи – это важней— шие навыки, приобретаемые студентами, изучающими ту или иную тех— ническую дисциплину.
Настоящее пособие является одновременно конспектом лекций и сборником типовых задач, используемых кафедрой ОКМиМ УГАТУ в те— чение ряда последних лет при письменных экзаменах по ТММ.
Сборник содержит задачи по следующим разделам курса:
•структурный анализ механизмов; строение и классификация пло— ских механизмов;
•кинематический анализ плоских рычажных механизмов;
•кинематический анализ зубчатых механизмов;
•силовой анализ плоских рычажных механизмов;
•геометрия зубчатых колес и передач.
Основная масса задач составлена авторами настоящего пособия, кинематические схемы некоторых механизмов и содержание отдельных задач позаимствованы из других подобных источников.
В начале каждого раздела приведены достаточно полные теорети— ческие сведения, используемые при решении соответствующих задач и представляющие собой конспект лекций.
Авторы решили воздержаться от приведения примеров решений задач, поскольку достаточно большое их количество опубликовано в из— данных ранее задачниках и методических указаниях.
5
1. СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМОВ. СТРОЕНИЕ И КЛАССИФИКАЦИЯ ПЛОСКИХ МЕХАНИЗМОВ
Механизм – система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемые движения других твердых тел (в теории механизмов и машин под твердыми тела— ми понимают как абсолютно твердые, так и деформируемые, и гибкие тела).
Звено – твердое тело, входящее в состав механизма; звено может состоять из нескольких деталей, не имеющих между собой относитель—
ного движения.
Кинематическая пара – соединение двух соприкасающихся
звеньев, допускающее их относительное движение.
Элемент кинематическая пары – совокупность поверхностей, ли— ний и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару.
1.1. Классификация кинематических пар
Кинематические пары различают и классифицируют по различным признакам.
1) По числу связей, налагаемых на относительное движение звеньев.
Всякое свободно движущееся в пространстве абсолютно твердое тело обладает шестью степенями свободы или шестью видами незави— симых возможных движений. Вхождение двух звеньев в кинематическую пару налагает на их относительное движение некоторые ограничения или условия связи; класс кинематической пары (номер класса совпадает с числом условий связи S) всегда находится в пределах от 1 до 5, число оставшихся подвижностей H дополняет число связей до шести, т.е. H = 6 − S , поэтому пару пятого класса называют одноподвижной, чет— вертого – двухподвижной и т.д.
На рис. 1.1 представлены примеры кинематических пар 1 – 5 клас—
сов.
2) По характеру контакта звеньев различают пары низшие (тре—
буемое относительное движение звеньев можно получить постоянным соприкасанием их элементов по поверхности) и высшие (требуемое от— носительное движение можно получить только соприкасанием их эле— ментов по линиям и в точках). Например, трехподвижная пара по
рис. 1.1, в – низшая, а четырехподвижная по рис. 1.1, б – высшая.
3) По области относительного движения звеньев пары могут быть плоскими (траектории всех точек в относительном движении звеньев – плоские кривые, расположенные в параллельных плоскостях) и пространственными.
Плоская одноподвижная пара может быть либо вращательной
6

(шарниром – рис. 1.1, д), либо поступательной (рис. 1.1, е); пространст— венная пара может быть, например, винтовой (одноподвижная), цилинд— рической (двухподвижная), сферической (двух— и трехподвижная) и т.д.
Механизм, звенья которого образуют только вращательные, посту— пательные, цилиндрические и сферические пары, называют рычажным.
|
а – пятиподвижная пара |
б – четырехподвижная пара |
|
(1 класс) |
(2 класс) |
|
в – трехподвижная пара |
г – двухподвижная пара |
|
(3 класс) |
(4 класс) |
|
д – одноподвижная |
е – одноподвижная |
|
вращательная пара (5 класс) |
поступательная пара (5 класс) |
|
Рис. 1.1 |
7
Сборник задач 1 (Прорешенные задачи к экзамену по курсу ТММ)
PDF-файл Сборник задач 1 (Прорешенные задачи к экзамену по курсу ТММ) Теория механизмов и машин (ТММ) (135023): Ответы (шпаргалки) — 4 семестрСборник задач 1 (Прорешенные задачи к экзамену по курсу ТММ) — PDF (135023) — СтудИзба2021-06-122021-06-12guts_officialСтудИзба
Описание файла
PDF-файл из архива «Прорешенные задачи к экзамену по курсу ТММ»,
который расположен в категории «».
Всё это находится в предмете «теория механизмов и машин (тмм)» из 4 семестр, которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана.
Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. .
Просмотр PDF-файла онлайн
Текст из PDF
Свежие статьи
Популярно сейчас
Здравствуйте на этой странице я собрала теорию и практику с примерами решения задач по предмету теория машин и механизмов с решением по каждой теме, чтобы вы смогли освежить знания!
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Теория механизмов и машин
Теория механизмов и машин (ТММ) является одним из разделов механики, в котором изучается строение, кинематика и динамика механизмов и машин в связи с их анализом и синтезом.
Механизмом называется система материальных тел, предназначенных для преобразования движения одного или нескольких тел в требуемые движения остальных.
Состав механизмов – разнообразен и включает механические, гидравлические, электрические и др. устройства.
Несмотря на разницу в назначении механизмов их строение, кинематика и динамика имеет много общего, поэтому исследование механизмов проводится на базе основных принципов современной механики. Всякий механизм состоит из отдельных тел (деталей), соединенных между собой.
Структура механизмов. Основные определения
Механизмом называется искусственно созданная система тел, предназначенная для преобразования движения одного нлн нескольких тел в требуемые движения других тел.
Одно или несколько жестко соединенных твердых тел, входящих в состав механизма, называется звеном. Звено, принимаемое за неподвижное, называется стойкой. Звенья механизма, положения которых назначаются непосредственно значением выбранных независимых параметров — обобщенных координат, называются ведущими, а звенья механизма, положения и перемещения которых однозначно зависят от положений и перемещений ведущих звеньев, называются ведомыми.
Возможно эта страница вам будет полезна:
Кинематической парой называется соединение двух соприкасающихся звеньев, допускающее их относительное движение. Поверхности, линии, точки звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару, называются элементами кинематической пары.
Кинематической цепью называется связанная система звеньев, образующих между собою кинематические пары. Кинематические цепи подразделяются на простые и сложные, замкнутые и незамкнутые.
Простой кинематической цепью называется цепь, у которой каждое звено входит не более чем в две кинематические пары.
Сложной кинематической цепью называется цепь, у которой имеется хотя бы одно звено, входящее более чем в две кинематические пары.
Замкнутой кинематической цепью называется цепь, каждое звено которой входит по крайней мере в две кинематические пары.
Незамкнутой кинематической цепью называется цепь, у которой есть звенья, входящие только в одну кинематическую пару.
Подавляющее большинство механизмов, применяющихся в инженерной практике, образованы замкнутыми кинематическими цепями. Поэтому механизм (состоящий только из твердых тел) может быть определен также следующим образом.
Механизмом называется кинематическая цепь, в которой при заданном движении одного или нескольких звеньев (ведущих) относительно любого из них (стойки) все остальные звенья (ведомые) совершают однозначно определяемые движения.
Число степеней свободы механизма относительно стоики назыоают степенью подвижности и обычно обозначают буквой 
В сборнике принята классификация кинематических пар по Артоболевскому. Все кинематические пары разделяются на пять классов. Номер класса кинематической пары определяется числом условий связи, которые наложены на движение одного звена пары относительно другого. Отсюда следует, что пара 1 класса может быть названа пяпиподвижной, пара II класса — четырёхподвижной и т. д.
Для решения вопроса, к какому классу относится та или иная кинематическая пара, следует поступать так. Одно из звеньев, входящих в кинематическую пару, представить неподвижным. Связать с ним систему координат 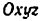
На рис. 1 изображена низшая (сферическая) кинематическая пара. Элементом кинематической пары на первом звене является сферическая поверхность радиуса R,
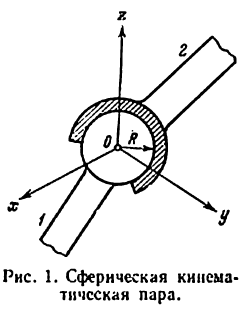
а на звене 2 — сферическая поверхность того же радиуса R, охватывающая сферическую поверхность на звене 1. Проведя через центр О сферы прямоугольную систему координат Oxyz связанную со звеном 1, замечаем, что звено 2 не может перемещаться поступательно вдоль осей Ох, Оу и Oz, но может свободно вращаться вокруг этих же осей. Следовательно, эту кинематическую пару надо отнести к третьему классу (невозможны три из шести движений).
Рассмотрим еще один пример. Пусть (рис. 1) на движение звеньев, входящих в сферическую пару, наложено условие, что они совершают плоскопараллельное движение относительно плоскости Oyz. В данном случае, помимо ранее наложенных связей, появились еще две общие связи — невозможность вращения вокруг осей Оу и Oz. Эту кинематическую пару надо отнести к пятому классу.
Классификация механизмов
1. Все механизмы можно разделить на плоские и пространственные. У плоского механизма точки его звеньев описывают траектории, лежащие в параллельных плоскостях. У пространственного механизма точки его звеньев описывают плоские траектории или траектории, лежащие и пересекающихся плоскостях.
На (рис. 2 )изображен плоский шарнирный четырехзвенный механизм, а на( рис. 3 )— плоский механизм двухступенчатого редуктора. На (рис. 4) показан пространственный механизм. На (рис. 5) изображена пространственная зубчатая передача, образованная коническими колесами.
(Рис, 4.) Пространственный механизм зажима: а) полуконструктивная схема, б) кинематическая схема.
(Рис. 5.) Зубчатая передача с коническими колесами: а) полукоиструктнвная схема, б) кинематическая схема.
2. Механизмы различаются еще по семействам, которых существует пять — от нулевого до четвертого.
Номер семейства равен числу общих условий связи, которые наложены на все звенья механизма. Поэтому, например, плоские механизмы следует отнести к третьему семейству.
3. Число степеней подвижности замкнутой кинематической цепи с одним неподвижным звеном можно найти, воспользовавшись структурными формулами, которые для механизмов различных семейств имеют следующий вид: для механизмов нулевого семейства (формула Сомова— Малышева):
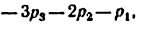
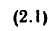
для механизмов первого семейства
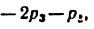
механизмов второго семейства:
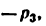
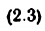
для механизмов третьего семейства — плоских и сферических (формула Чебышева)
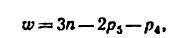
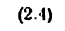
для механизмов четвертого семейства (формула Добровольского)
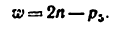
В этих формулах и» —степень подвижности механизма, л —число подвижных звеньев, 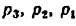
Так, например, 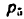
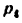
Прежде чем применять структурные формулы, следует установить, сколько общих условий связи наложено на движение звеньев исследуемого механизма. Число этих связей будет соответствовать номеру семейства.
После установления номера семейства следует выяснить, нет ли в данном механизме звеньев, которые накладывают пассивные связи или вносят лишние степени свободы, не влияющие на кинематику основных звеньев механизма.
Па (рис. 6 и 7 )показаны два механизма, которые надо отнести к плоским, так как на движения их звеньев наложены по три общих условия связи: звенья не могут перемешаться поступательно вдоль оси Ох и вращаться вокруг осей Оу и Оz. Следовательно, оба эти механизма принадлежат к третьему семейству.
В механизме на (рис. 6) длины звеньев (расстояния между осями шарниров) подобраны так, что изменяемая фигура 
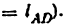
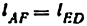
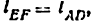
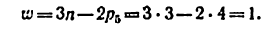
Это означает, что для придания определенности движения звеньям механизма достаточно задать движение одному звену.
Если бы не была отброшена пассивная связь (звено 5 и кинематические пары пятого класса F и Е), то при подсчете степени подвижности был бы получен неверный результат, так как в этом случае степень подвижности 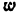
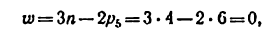
т. е. вместо механизма должна бы быть жесткая неизменяемая система, являющаяся формой.
На (рис. 7) представлен плоский кулачковый механизм, у которого на конце толкателя 3 имеется круглый ролик 2,»поворачивающийся вокруг своей осн. Если ролик жестко связать с толкателем, то от этого закон движения толкателя, очевидно, не изменится. Круглый ролик, свободно поворачивающийся вокруг своей оси, вносит в механизм лишнюю степень свободы, и при подсчете степени подвижности механизма это вращательное движение приниматься во внимание не должно. Считая, что ролик жестко связан с толкателем, подсчитываем степень подвижности механизма по формуле (2.4):
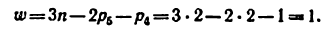
Формальный же подсчет привел бы нас к такому результату:
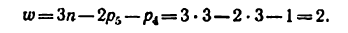
Составление кинематических схем механизмов
1. Кинематическая схема механизма дает полное представление о структуре механизма и определяет его кинематические свойства. Она является графическим изображением механизма посредством условных обозначений звеньев и кинематических пар с указанием размеров, которые необходимы для кинематического анализа механизма.
На кинематических схемах механизмов звенья, как правило, изображаются отрезками прямых и нумеруются арабскими цифрами. Кинематические пары в пространственных механизмах обозначаются большими буквами латинского
алфавита и схематически изображаются так, как это сделано на (рис. 8.) Схематическое изображение кинематических пар плоских механизмов показано на (рис. 9). Элементы высшей пары очерчиваются кривыми, которыми они характеризуются в натуре. Стойку (неподвижное звено) принято выделять штриховкой (рис. 10).
2. Для построения кинематической схемы механизма рекомендуется следующая последовательность действий.
- Установить основное кинематическое назиачепие механизма. Например, механизм на( рис. 7) предназначен для преобразования вращательного движения кулачка 1 в поступательное движение толкателя 3.
- Подсчитать общее число звеньев k, включая стойку. Число n подвижных звеньев будет равно
- Выяснить, сколько наложено на подвижные звенья механизма общих условий связи, и по их числу установить номер семейства механизма.
- Подсчитать и установить класс кинематических пар, а также найти степень подвижности механизма.
- Вычертить схему механизма. Начинать ее надо с нанесения на чертеж неподвижных элементов кинематических пар, т. е. элементов, принадлежащих стойке. Далее следует вычертить ведущие звенья, входящие в кинематические пары со стойкой. (Число этих звеньев соответствует найденной ранее степени подвижности.) Затем надо нанести на чертеж кинематическую цепь, образующую ведомую часть механизма
При составлении схемы плоских механизмов чертеж должен совпадать с плоскостью, параллельно которой движутся точки звеньев механизма. Исключение составляют передачи
с цилиндрическими зубчатыми колесами, когда для наглядности схема вычерчивается в плоскости, перпендикулярной плоскости вращения колес. На (рис. 11, а)показана схема зубчатой передачи, вычерченная по общим правилам для схем плоских механизмов, а на(рис. 11, б) — та же передача, вычерченная по правилам для схем передач с цилиндрическими зубчатыми колесами.
Классификация плоских механизмов
1. В сборнике принята классификация плоских механизмов Ассура — Артоболепского.
К механизмам, отнесенным по этой классификации к одному и тому же классу, применяется методика кинематического и силового анализа, специально разработанная для этого класса.
Согласно идеям Л. В. Ассура, любой механизм образуется последовательным присоединением к механической системе с определенным движением (ведущим звеньям и стойке) кинематических цепей, удовлетворяющих условию, что степень их подвижности 
Группы Ассура подразделяются на классы в зависимости от их строения. Класс же механизма определяется наивысшим классом группы Ассура, образовавшей его ведомую часть.
Определить класс плоского механизма по Ассуру — Артоболевскому можно только тогда, когда предварительно выявлена структура механизма, определена
Рис. 12. Замена кинематической пары IV класса одним звеном, входящим в две кинематические пары V класса: а) элементы кинематической пары — две кривые линии 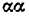
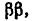
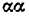
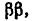
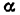
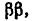
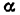
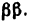
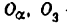
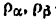
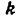
Его степень подвижности, число ведущих звеньев, входящих в кинематические пары V класса со стойкой, и когда все кинематические пары в механизме являются только парами V класса. Если же исследуемый механизм имеет кинематические пары IV класса, то они предварительно должны быть заменены одним звеном, входящим в две кинематические пары V класса. Получившийся после такой замены механизм называется заменяющим. Такая замена для двух смежных бесконечно малых перемещений не меняет значений перемещений, скоростей и ускорений основного механизма.
На (рис. 12) показан способ замены кинематической пары IV класса (высшей) одним звеном, входящим в две пары V класса.
2. Ведущее звено, входящее в кинематическую пару V класса со стойкой, образует механизм первого класса. Иногда в литературе это же звено называется начальным, а совместно со стойкой — начальным механизмом.
3. Степень подвижности группы Ассура будет

где 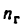
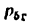
Из условия (4.1) получим, что 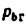

Так как число кинематических пар V класса 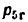
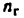
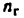
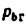
Согласно соотношению (4.2) в группах Ассура могут быть следующие числа звеньев и кинематических пар V класса:

Первый столбец таблицы (4.3) относится к группам Ассура второго класса следующих пяти видов (рис. 13): а) первого, б) второго, в) третьего, г) четвертого, и) пятого.
В группах Ассура различают кинематические пары внутренние (кинематическая пара С) и внешние (кинематические пары В и D на рис. 13). Число внешних кинематических пар или, точнее, их элементов, которыми группа присоединяется к не относящимся к ней звеньям механизма (например, к ведущему звену и стойке), называют порядком группы. Все группы второго класса являются группами второго порядка.
Второй столбец таблицы (4.3) позволяет образовать три варианта кинематических цепей, формально удовлетворяющих условию (4.2) (рис. 14). Кинематическая цепь, показанная на( рис. 14, а), не является группой: она распадается на две группы Ассура второго класса BCD и EFG.
Кинематическая цепь, показанная на (рис. 14, б), образует группу Ассура третьего класса третьего порядка. В этой группе кинематические пары В, С, D будут внешними, и пары Е, F, G — внутренними.
Кинематическая цепь, изображенная на(рис. 14, в), называется группой Ассура четвертого класса второго порядка. В этой группе кинематические пары В и С будут внешними, а пары D, E , F , G — внутренними.
Класс группы Ассура выше второго определяется числом внутренних кинематических пар, образующих так называемый исходный контур.
Группы Ассура третьего и более высоких классов по видам не различаются.
Класс механизма определяется наивысшим классом группы Ассура, которая входит в его состав. Следует иметь в виду, что изменением ведущего звена можно либо повысить, либо понизить класс механизма. Поэтому при всех прочих равных условиях класс механизма зависит и от выбора ведущего звена. Кинематический и силовой анализы механизма усложняются с повышением класса механизма, следовательно, всегда надо стремиться выбирать ведущее звено так, чтобы класс
механизма оказался наинизшим из всех возможных для данной кинематической схемы механизма.
Пример задачи №1.
(На рис 18) показана схема механизма конхоидографа с ведущим звеном в двух вариантах: на (рис. 18, а) — это звено 1, на (рис. 18, б) — звено 4.
четвертое.
Решение:
1) Определяется степень подвижности механизма по формуле Чебышева. Так как 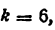
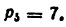
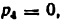
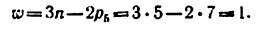
2) Так как 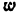
3) Разложение на группы Ассура. По первому варианту (ведущее звено 1) от механизма можно отделить только кинематическую цепь, состоящую из звеньев 2, 3, 4 и 5. Эта цепь представляет собой группу Ассура третьего класса третьего порядка ,так как в ней три внутренних кинематических пары (вращательные пары D, C и поступательная E) и три внешних ( вращательные пары B,G и F) По второму варианту (рис. 18, б) от механизма последовательно отделяются группы Ассура второго класса, состоящие из звеньев 1 и 2, 3 и 5.
4) Формула строения механизма запишется так. При ведущем звене 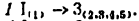
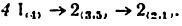
Аналитическое определение положений, скоростей и ускорений звеньев механизмов
1. Функцией положения ведомого звена (или точки на нем) называется зависимость его (или ее) перемещения от перемещения ведущего звена (или точки на нем).
На (рис. 19) показано ведущее звено n с точкой N на нем и ведомое звено 
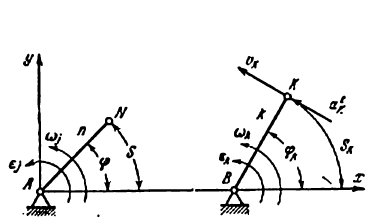
координатой 
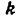
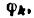
Функция положения звена 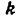

Функция положения точки К :

Вид функции положения зависит от схемы механизма, а значения постоянных, которые входят в нее, —от размерных параметров механизма.
Для того чтобы составить функцию положении механизма, следует рассмотреть фигуру, которую образуют оси его звеньев. Из геометрических свойств этой фигуры находят искомую зависимость (подробнее об этом см. книгу В. Л. Зиновьева «Теория механизмов и машин», Физматгиз, 1972).
Пример задачи №2.
В синусном механизме (рис. 20) ведущим является звено 1, а ведомым — звено 3. Положение ведущего звена определяется углом 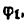
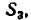
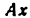
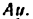
Решение:
Опускаем из точки В ил линию Ах перпендикуляр ВК, где точка В —проекция оси вращательной кинематической пары В на плоскость движения точек звеньев плоского механизма.
В последующем изложении аналогично будут обозначаться проекции осей вращательных кинематических пар на плоскость движения точек звеньев плоских механизмов, например, для некоторой вращательной пары С—точка С.
Из треугольника АВК имеем 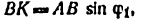

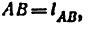
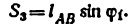
Единственным размерным параметром в этом механизме будет размер 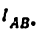
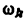
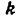
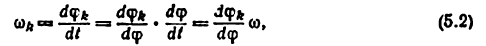
где 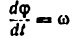
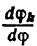
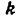
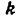
аналог угловой скорости

передаточное отношение

Скорость 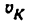
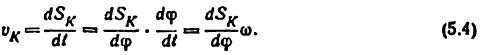
Производная 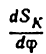

передаточное отношение

Из формул (5.2)—(5.5) следует, что
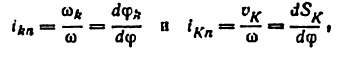
т. е. передаточное отношение от звена 
Таким образом, соотношения скоростей в механизме зависят только от кинематической схемы механизма и его размерных параметров, причем значения скоростей определяются значением скорости ведущего звена.
Пример задачи №3.
Найти скорость звена 3 синусного механизма (рис. 20), если скорость звена 1 равна
Решение:
Находим аналог скорости звена 3 по формуле (5.5а):
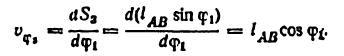
Скорость звена 3 находим по формуле (5.4):
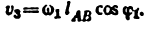
3. Угловое ускорение 
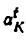
Угловое ускорение 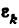
Здесь 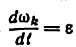
Касательное ускорение равно
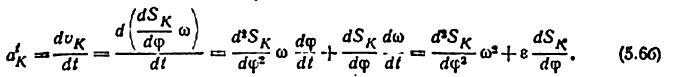
Производные 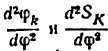
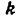
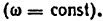
аналог углового ускорения

аналог касательного ускорения

Из формул (5.6а) и (5.6б) следует, что ускорения ведомых звеньев механизма полностью определяются аналогами их скоростей и ускорений и законом движения ведущего звена.
Пример задачи №4.
Для синусного механизма (рис. 20) найти ускорение звена 3, если угловая скорость звена 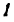
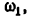
Решение:
Аналогом ускорения звена 3 является
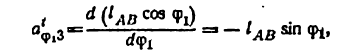
а ранее найденный аналог скорости его есть 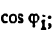
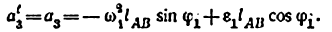
Планы положений, скоростей и ускорений механизмов
1. Задачи о положениях, скоростях и ускорениях решаются применительно к группам Ассура, которыми образован механизм.
Эти задачи решаются в такой последовательности:
- Проводится структурный анализ и классификация механизма по Ассуру.
- Выбирается ведущее звено (при
=1). За ведущее звено обычно выбирают звено, которое совершает вращательное движение и может совершить полный оборот вокруг неподвижной оси. Задается закон движения этого звена (как правило, задается равномерное вращение этого звена).
- Выбирается масштаб чертежа и на чертеже наносятся неподвижные элементы кинематических пар механизма. По заданной обобщенной координате строится положение ведущею звена.
- Строятся планы положений каждой группы Ассура в соответствии с последовательностью образования ими механизма.
- Строятся планы скоростей.
- Строятся планы ускорений.
Масштабы для планов положений, скоростей и ускорений подбирают так, чтобы планы получились достаточно точными и лучше использовалось поле чертежа.
В курсе теории механизмов и машин принято понимать под масштабом той или иной величины отношение этой величины к отрезку, который ее изображает на чертеже.
Размерности масштабов для кинематических величин таковы: масштаба длин — 
2. Покажем решение задачи о положениях на конкретном примере.
Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.
Пример задачи №5.
Требуется построить план положения механизма
двигателя внутреннего сгорания (рис. 21, а), у которого ведущее звено А В (первое) составляет с осью Ах угол 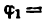
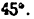
Решение:
1) Число звеньев механизма 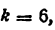
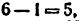
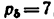
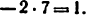
2) Ведущее звено задано в условии примера, это звено АВ.
3) Отмечаем на чертеже положения неподвижных элементов кинематических пар: шарнира А и направляющих Аy и Аz (рис. 21, б).
Длину отрезка АВ, изображающего на чертеже размер ведущего звена, принимаем равной 25 мм. Тогда масштаб схемы механизма будет
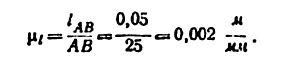
Строим положение ведущего звена под заданным углом 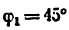
4) Вычисляем длины отрезков ВС, BD, CD, DE:
Строим положение группы, состоящей из звеньев 2, 3. Из точки В проводим окружность радиуса ВС до пересечения с линией Ау, тем самым найдем положение точки С. Положение группы, состоящей из звеньев 2. 3, построено. На стороне ВС строим засечками треугольник BDC.
Положение группы, состоящей из звеньев 4,5, строится аналогично положениию группы, состоящей из звеньев 2, 3.
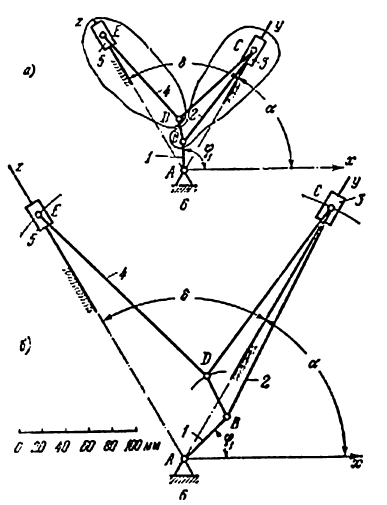
Если построить ряд последовательных положений ведущего звена и на одном и том же чертеже изобразить планы положений остальных звеньев механизма, то можно построить траекторию любой точки механизма.
Траектории точек звена, не входящего в кинематические пары со стойкой, т. е. шатуна, называются шатунными кривыми. На ( рис. 22 )построена шатунная кривая, описываемая точкой Е ламбдообразного механизма Чебышева (построение сделано для 12 равноотстоящих положений ведущего звена). Принятые размеры звеньев: 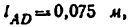
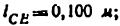
3. Планы скоростей и ускорений механизма строятся после решения задачи о его положении, причем построение планов проводится для отдельных групп Ассура, которые образовали механизм.
Вначале строится план скоростей (ускорений) группы, которая присоединена элементами своих внешних кинематических пар к ведущему звену и стойке, затем строятся планы скоростей (ускорений) второй и. т. д. групп, взятых в той же последовательности, в какой они присоединяются при образовании механизма. Эта последовательность обозначена в формуле строения механизма.
В дальнейшем не будет делаться различия между планами скоростей или ускорений и планами аналогов скоростей и ускорении, так как эти планы отличаются только своими масштабами. На (рис. 23, а) показано ведущее звено АВ, вычерченное в масштабе 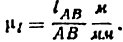
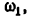
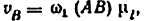
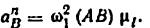
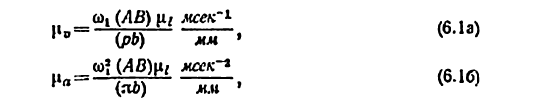
а масштабами планов аналогов скоростей и ускорений будут
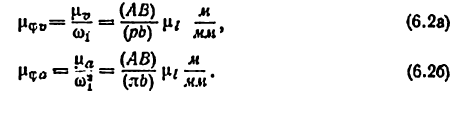
Планы скоростей и ускорений, у которых отрезки (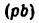
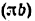

Соответственно масштабами планов аналогов скоростей и ускорений будут

Когда длины звеньев механизма соизмеримы с длиной ведущего звена (не превосходят се более чем в 6—8 раз), тогда планы скоростей и ускорений желательно строить в масштабе радиуса, так как это значительно сокращает вычисления.
В некоторых случаях полезно строить повернутые планы скоростей, т. е. такие, у которых все векторы скоростей повернуты в одну и ту же сторону на 90″ относительно их действительных направлений. Эти планы отличаются от обычных (не повернутых) большей точностью построения и. кроме того, удобны в качестве рычага Жуковского для определения уравновешивающей или приведенной силы (см. § 13).
Последовательность решения задачи на построение планов скоростей и ускорений (предполагается, что задача о положении решена и, следовательно, предварительно выяснено строение механизма и назначено ведущее звено).
- Задают закон движения ведущего звена. Обычно принимают, что оно вращается равномерно. Если же нельзя считать, что оно врашается равномерно, то надо указать отношение его углового ускорения к его угловой скорости. Числовое значение угловой скорости задавать не обязательно, оно отражается только п масштабах планов скоростей и ускорений и никак не сказывается на вычислении масштабов аналогов этих планов.
- Строят план скоростей группы Ассура, непосредственно присоединенной к ведущему звену и стойке.
- Строит план ускорений этой же группы.
- Переходят к построению планов скоростей и ускорений следующей присоединенной группы Ассура и так продолжают до тех пор, пока не будут построены планы скоростей и ускорений всех групп механизма.
Задачу кинематического анализа следует считать решенной, если для каждого звена механизма будут известны положения, скорости и ускорения двух его точек или станут известными положение, скорость и ускорение одной точки и угловая координата, угловая скорость и угловое ускорение самого звена.
4*. Решим несколько примеров на построение планов скоростей и ускорений
Пример задачи №6.
Построить планы скоростей и ускорений кривошипно ползунного механизма компрессора (рис. 24, а). Найти скорость и ускорение точки С, угловую скорость и угловое ускорение шатуна ВС, а также определить длину радиуса кривизны 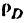
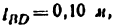
Решение:
I) Проводим структурный анализ и устанавливаем класс за данного механизма. Число звеньев 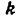
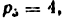
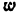
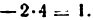
2) Строим план положения механизма (рис. 24, б). Задаемся длиной отрезка (АВ) = 25 мм, вычисляем масштаб схемы механизма:
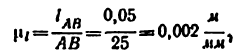
и по нему находим длины отрезков (ВС) и (BD):
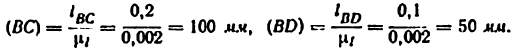
По полученным размерам и заданному углу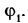
3) Строим план скоростей для группы 2, 3. Построение ведем по следующим двум векторным уравнениям:
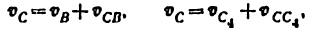
где 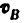
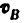
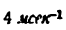
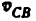
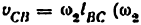
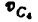
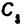
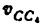
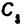
Построение плана скоростей ведем в такой последовательности (рис. 24, в). Строим решение первого векторного уравнения, указанного выше: от полюса р откладываем отрезок (pb), изображающий скорость точки В, перпендикулярно линии А В и в соответствии с направлением вращения звена А В, причем длину отрезка (pb) выбираем равной (АВ) = 25 мм, т. е. строим план в масштабе кривошипа; из точки b проводим направление скорости 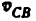
Переходим к построению решения второго векторного уравнения, указанного выше: из точки р надо было бы отложить скорость 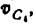
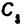
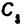
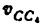
Скорость точки D находим по правилу подобия: конец вектора этой скорости должен лежать па линии (bс) и делить отрезок (bc) в том же отношении, в каком точка D делит отрезок ВС, т. е.
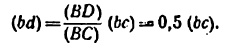
Вычисляем масштаб плана скоростей:
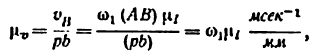
масштабом плана аналогов скоростей будет
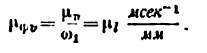
Скорость 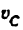
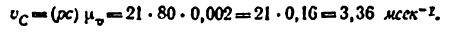
Угловая скорость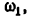
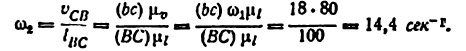
На (рис. 24, б) построен повернутый план скоростей непосредственно на схеме механизма. В этом плане полюс р совмещен с точкой А. Направление вектора скорости точки В совпадает с направлением АВ, направление скорости 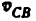
4) Строим план ускорений для группы 2, 3. Этот план строится по таким двум векторным уравнениям:
где 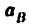
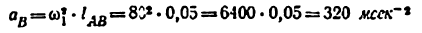
и направленное параллельно линии АВ от точки В к точке А; — нормальное ускорение точки С во вращательном движении звена ВС относительно точки В, но модулю равное
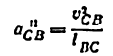
и направленное параллельно линия ВС от точки С к точке В; 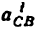
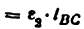
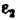
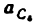
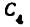
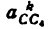
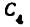
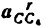
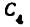
Построение плана ускорений ведем в такой последовательности (рис. 24, г). Строим решение первого векторного уравнения, указанного выше, для чего от полюса плана 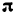
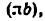
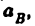
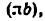
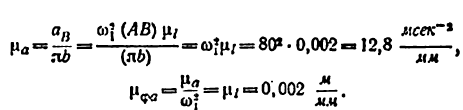
От точки b откладываем отрезок 
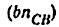
Через точку 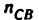
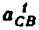
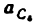
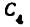
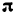
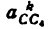
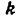
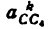
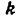
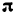
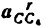
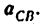
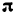
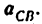
Соединив точку d с полюсом плана 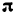
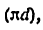
Величина ускорения точки С найдется так:
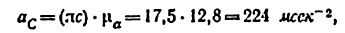
а величина углового ускорения звена ВС
5) Находим радиус кривизны траектории точки D. Через точку D (рис. 24, б) проводим линию 
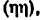
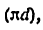
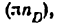
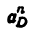
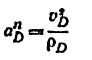
получим, что искомый радиус кривизны будет равен
Решение задач по всем темам теории машин и механизмов (ТММ)
Теория механизмов и машин (ТММ) – наука об общих методах исследования свойств механизмов и машин (анализ) и проектирования их схем (синтез). Излагаемые в ТММ методы являются общими и не зависят от целевого назначения механизмов и машин.
Теория механизмов и машин (ТММ) является первой общетехнической дисциплиной.
В ТММ изучаются свойства отдельных типовых механизмов, широко применяемых в самых различных машинах, приборах и устройствах. При этом анализ и синтез механизмов осуществляется независимо от его конкретного назначения, т.е. однотипные механизмы (рычажные, кулачковые, зубчатые и др.) исследуются одними и теми же приемами для двигателей, насосов, компрессоров и других типов машин.
В основе ТММ — методы математического анализа, векторной и линейной алгебры, дифференциальной геометрии и других разделов математики, теоремы и положения теоретической механики.
Решая задачи геометро-кинематического и динамического синтеза механических систем, ТММ является основой курсов «Детали машин», «Детали приборов» и других спецкурсов по проектированию и расчету механизмов и машин (специального назначения). В этих дисциплинах широко используются общие методы, разработанные ТММ в приложении к конкретным механизмам.
Сейчас, как и прежде, перед учеными, инженерами и конструкторами стоят задачи дальнейшего совершенствования всех видов современной техники, и в первую очередь создание новых высокопроизводительных машин и систем машин, освобождающих человека от трудоемких и утомительных процессов.
Несколько слов о методологии проектирования машин
Процесс проектирования сложен и трудоемок не только в том случае, когда создается новая машина, не имеющая близких аналогов, но и тогда, когда необходимо получить более высокий качественный уровень одного или нескольких параметров машины с уже существующей кинематической схемой. Последовательность проектирования показана на рис. 1.1.
При проектировании машины должен быть осуществлен выбор ее оптимальных параметров (структурных, кинематических, точностных, динамических, эксплутационных), наилучшим образом соответствующих предъявляемым к ней требованиям. Решения, принимаемые на стадии проектирования, могут корректироваться несколько позднее, на стадии разработки технологии изготовления машины. Однако следует помнить, что качество новой машины определяется в первую очередь качеством проектирования.
Поэтому неудачные решения на этом этапе не всегда могут быть компенсированы на последующих стадиях. Затраты на качественное проектирование окупятся за счет экономии, получаемой впоследствии, включая и эксплуатацию машины.
Любая машина выполняет свой рабочий процесс посредством механического движения, поэтому она должна иметь носителя этого движения, каковым является механизм или система механизмов. Следовательно, составной частью общего процесса проектирования машины является ‘проектирование ее механизмов. Оно включает разработку и анализ возможных вариантов схем машины и ее механизмов и оценку полученных решений методами оптимизации (рис. 1.2). Поиск оптимального, т.е. наилучшего решения для каждого варианта ведется, как правило, с использованием итерационных алгоритмов, которые поддаются формализации и должны быть реализованы на ЭВМ.
Процесс проектирования состоит из нескольких итерационных (повторяющихся) циклов (рис. 1.3). Первый цикл имеет сравнительно небольшой набор исходных данных, необходимых для расчета, и заканчивается совокупностью результатов, именуемых начальными. Эти результаты расчета первого цикла позволяют, во-первых, произвести в составе исходных данных, необходимых для расчета второго цикла, нужные уточнения и, во-вторых, пополнить исходные данные новыми, неизвестными ранее параметрами. Затем следует расчет второго цикла.
Второй итерационный цикл реализуется в результате определения масс и моментов инерции звеньев и уточнения размеров сочленений звеньев. По этим данным проводится силовой расчет с учетом ускоренного движения звеньев механизма и наличия трения в кинематических парах.
Третий итерационный цикл позволяет корректировать конструкцию привода. Исходные данные, необходимые для
выбора двигателя, определяются в блоке «Динамический синтез, определение закона движения, управление движением» (см. рис. 1.3).
Проектирование нового механизма начинается с создания схемы механизма со структурно-кинематическими свойствами, соответствующими заданным с требуемой точностью. Структурные свойства механизма подразделяются на внешние — количество степеней свободы и число обеспечиваемых механизмом связанных друг с другом перемещений рабочих органов машины; и внутренние — состав механизма, т.е. его внутренняя структура (состав звеньев и способ их соединения друг с другом). С точки зрения внутренней структуры можно выделить два типа механизмов — структурно-элементарные и структурно-сложные.
Структурно-элементарные механизмы, осуществляющие преобразование и передачу движения по определенному закону, объединены в группы по способу соединения звеньев друг с другом. Такими элементарными механизмами являются рычажные, зубчатые передаточные, планетарные, кулачковые и др., которые будут рассматриваться в последующих лекциях. В состав структурно-сложных механизмов могут входить несколько элементарных механизмов с различными кинематическими свойствами.
Кинематические свойства проектируемого механизма определяются его геометро-кинематическими характеристиками, связывающими параметры движения на входе механизма и на выходе из него. Основные геометро-кинематические характеристики механизмов: функция положения, определяющая связь координат выходного и входного звеньев, и кинематическая передаточная функция, являющаяся первой производной от функции положения.
Известно очень большое количество разновидностей как структурно-элементарных, так и структурно-сложных механизмов, обладающих разнообразными структурно-кинематическими характеристиками. Поэтому при проектировании нового механизма следует проанализировать возможности использования уже существующих механизмов для осуществления заданной функции. Для этого необходимо использовать систематизацию существующих схем механизмов [7, 9, 19, 14] по структурно-кинематическим признакам с определением их кинематических характеристик. Во многих случаях геометро-кинематические характер.
Механизм и его элементы
Механизмом называется система твердых тел, объединенных геометрическими или динамическими связями, и предназначенных для преобразования движения входного звена в требуемое движение выходных звеньев.
Твердые тела, входящие в состав механизма, не являются абсолютно твердыми, однако их деформации обычно весьма малы.
Главное назначение создаваемого механизма — осуществление технической операции в результате движения его элементов.
Звено — это твердое тело, входящее в состав механизма.
Кинематическая пара — это соединение двух соприкасающихся звеньев, допускающее их относительное движение.
Звено, относительно которого рассматривается движение остальных звеньев, считается условно-неподвижным и называется стойкой.
Входное звено — это звено, которому сообщается движение, преобразуемое механизмом в требуемое движение других звеньев.
Выходное звено — это звено, совершающее движение, для выполнения которого предназначен данный механизм.
Рассмотрим простейший кривошипно-ползунный механизм на рис. 1.6, основные элементы которого: кривошип (1); шатун (2); ползун (3); стойка (4), составляющие кинематические пары A, B, C, D.
Несколько звеньев, связанных между собой кинематическими парами, образуют кинематическую цепь, которая может быть: а) замкнутой, у которой звенья образуют один или несколько замкнутых контуров; б) незамкнутой, звенья которой не образуют замкнутых контуров (рис. 1.7, цифровые и буквенные обозначения такие же, как на рис 1.6).
В современном машиностроении применяются машины и механизмы с абсолютно твердыми (жесткими), упругими (гибкими), жидкими и газообразными телами (звеньями).
Преобладающее большинство используемых в механизмах звеньев являются абсолютно твердыми. К упругим звеньям относят пружины, мембраны и другие элементы, упругая деформация которых вносит существенные изменения в работу механизма; к гибким — ремни, цепи, канаты; к жидким и газообразным — масло, воду, газ, воздух и т.п. вещества.
Основные виды звеньев механизмов показаны в табл. 1.1
Классификация кинематических пар
Каким бы ни был механизм машины, он всегда состоит только из звеньев и кинематических пар.
Условия связи, налагаемые в механизмах на подвижные звенья, в теории машин и механизмов принято называть кинематическими парами.
Кинематической парой называется подвижное соединение двух соприкасающихся звеньев, обеспечивающее их определенное относительное движение.
В табл. 2.1 представлена классификация кинематических пар, приведены названия, рисунки, условные обозначения наиболее распространенных на практике способов подвижных соединений звеньев.
Звенья при объединении их в кинематическую пару могут соприкасаться между собой по поверхностям, линиям и точкам.
Элементами кинематической пары называют совокупность поверхностей, линий или точек, по которым происходит подвижное соединение двух звеньев, и которые образуют кинематическую пару. В зависимости от вида контакта элементов кинематических пар различают высшие и низшие кинематические пары.
Кинематические пары, образованные элементами в виде линии или точки, называются высшими.
Кинематические пары, образованные элементами в виде поверхностей, называются низипши.
Чтобы пара существовала, элементы входящих в нее звеньев должны находиться в постоянном контакте, т.е. быть замкнутыми. Замыкание кинематических пар может быть геометрическим или силовым, осуществляемым, например, с помощью собственной массы, пружин и т.п.
Примечания. Вилы кинематических пар: 111 — поступательная; 1В — вращательная: 1 ВТ — вращательная точечная; 2Ц — цилиндрическая: ЗСФ — сферическая; ЗИЛ — плоскостная: 411 — четырехподвижная с линейным контактом; 5Т — пятиподвижная с точечным контактом.
Прочность, износостойкость и долговечность кинематических пар зависят от их вида и конструктивного исполнения. Низшие пары более износостойкие, чем высшие. Это объясняется тем, что в низших парах контакт элементов пар происходит по поверхности, а следовательно, при одинаковой нагрузке в них возникают меньшие удельные давления, чем в высших. Износ, при прочих равных условиях, пропорционален удельному давлению, поэтому низшие пары изнашиваются медленнее, чем высшие. Использование низших пар с целью уменьшения износа в машинах предпочтительнее, однако применение высших кинематических пар часто позволяет значительно упростить структурные схемы машин, что снижает их габариты и упрощает конструкцию. Поэтому правильный выбор кинематических пар является сложной инженерной задачей.
Кинематические пары разделяют также по числу степеней свободы (подвижности), которые она предоставляет соединенным посредством нее звеньям, или по числу условий связей (класс пары), налагаемых парой на относительное движение соединяемых звеньев. При использовании такой классификации разработчики машин получают сведения о возможных относительных движениях звеньев и о характере взаимодействия силовых факторов между элементами пары.
Свободное звено, находящееся в общем случае в М-мерном пространстве, допускающем П видов простейших движений, обладает числом степеней свободы Я или W-подвижно.
Так, если звено находится в трехмерном пространстве, допускающем шесть видов простейших движений — три вращательных и три поступательных вокруг и вдоль осей X, Y, Z, то говорят, что оно обладает шестью степенями свободы, или имеет шесть обобщенных координат, или шести-подвижно. Если звено находится в двухмерном пространстве, допускающем три вида простейших движений — одно вращательное вокруг Z и два поступательных вдоль осей X и У, то говорят, что оно имеет три степени свободы, или три обобщенные координаты, или оно трехподвижно и т.д.
При объединении звеньев с помощью кинематических пар они лишаются степеней свободы, значит S — число связей, которые кинематические пары налагают на соединяемые ими звенья.
В зависимости от числа степеней свободы, которым обладают в относительном движении звенья, объединенные в кинематическую пару, определяют подвижность пары (W= Н). Если Н — число степеней свободы звеньев кинематической пары в относительном движении, то подвижность пары определится следующим образом:
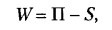
где П — подвижность пространства, в котором существует рассматриваемая пара; S — число налагаемых парой связей.
Следует заметить, что подвижность пары W, определенная по табл. 2.1, зависит не от вида пространства, в котором она реализуется, а только от конструкции.
Например, вращательная (поступательная) пара (см. табл. 2.1) как в шести-, так и в трехподвижном пространстве все равно останется одноподвижной. В первом случае на нее будет наложено 5 связей, а во втором случае — 2 связи, соответственно, будем иметь:
для шестиподвижного пространства:
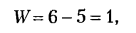
для трехподвижного пространства:
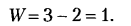
Как видим, подвижность кинематических пар не зависит от характеристик пространства, что является преимуществом данной классификации. Напротив, часто встречающееся деление кинематических пар на классы страдает тем, что класс пары зависит от характеристик пространства, а значит, одна и та же пара в разных пространствах имеет разный класс. Это неудобно для практических целей, следовательно, такая классификация кинематических пар нерациональна, поэтому ее лучше не применять.
Можно подобрать такую форму элементов пары, чтобы при одном независимом простейшем движении возникало второе — зависимое (производное). Примером такой кинематической пары является винтовая (см. табл. 2.1). В этой паре вращательное движение винта (гайки) вызывает поступательное его (ее) перемещение вдоль оси. Такую пару следует отнести к одноподвижной, так как в ней реализуется всего одно независимое простейшее движение.
Кинематические соединения
Кинематические пары, приведенные в табл. 2.1, просты и компактны. Они реализуют практически все необходимые при создании механизмов простейшие относительные перемещения звеньев. Однако при создании машин и механизмов они применяются редко. Это обусловлено тем, что в точках соприкосновения звеньев, образующих пару, обычно возникают большие силы трения. Это приводит к значительному износу элементов пары и ее разрушению. Поэтому простейшую двухзвенную кинематическую цепь кинематической пары часто заменяют более длинными кинематическими цепями, которые в совокупности реализуют то же самое относительное движение звеньев, что и заменяемая кинематическая пара.
Кинематическая цепь, предназначенная для замены кинематической пары, называется кинематическим соединением.
Приведем примеры кинематических цепей для наиболее распространенных на практике кинематических пар: вращательной, поступательной, винтовой, сферической и плоскость-плоскость.
В табл. 2.1 показано, что простейшим аналогом вращательной кинематической пары является подшипник с телами качения. Аналогично роликовые направляющие заменяют поступательную пару и т.д.
Кинематические соединения удобнее и надежнее в эксплуатации, выдерживают значительно большие силы (моменты) и позволяют механизмам работать при высоких относительных скоростях звеньев.
Основные виды механизмов
Механизм можно рассматривать как частный случай кинематической цепи, у которой, как минимум, одно звено обращено в стойку, а движение остальных определено заданным движением входных звеньев.
Отличительными особенностями кинематической цепи, представляющей механизм, являются подвижность и определенность движения се звеньев относительно стойки.
Механизм может иметь несколько входных и одно выходное звено, в этом случае он называется суммирующим механизмом и, наоборот, одно входное и несколько выходных, тогда он называется дифференцирующим механизмом.
По своему назначению механизмы разделяются на передаточные и направляющие.
Передаточным называется механизм, предназначенный для воспроизведения заданной функциональной зависимости между перемещениями входного и выходного звеньев.
Направляющим называется механизм, у которого траектория определенной точки звена, образующего кинематические пары только с подвижными звеньями, совпадает с заданной кривой.
Рассмотрим основные виды механизмов, нашедших широкое применение в технике.
Механизмы, звенья которых образуют только низшие кинематические пары, называют шарнирно-рычажными. Эти механизмы нашли широкое применение благодаря тому, что они долговечны, надежны и просты в эксплуатации. Основным представителем таких механизмов является шарнирный четырехзвенник (рис. 2.1), состоящий из кривошипа (1), шатуна (2), коромысла (3).
Названия механизмов обычно определяются по названиям их входного и выходного звеньев или характерного звена, входящего в их состав.
В зависимости от законов движения входного и выходного звеньев, этот механизм может называться кривошип-но-коромысловым, двойным кривошипным, двойным коро-мысловым, коромыслово-кривошипным.
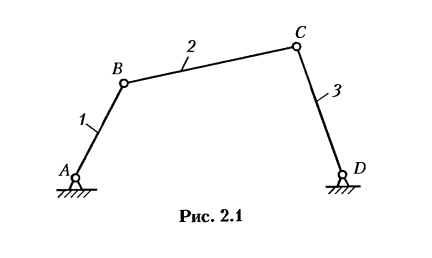
Шарнирный четырехзвенник применяется в станкостроении, приборостроении, а также в сельскохозяйственных, пищевых, снегоуборочных и других машинах.
Если заменить в шарнирном четырехзвеннике вращательную пару, например D, на поступательную, то получим широко известный кривошипно-ползунный механизм, различные виды которого представлены на рис. 2.2, а, б.
Главными составляющими кривошигшо-ползунных механизмов являются: кривошип (1); шатун (2); ползун (3).
Кривошипно-ползунный (ползунно-кривошипный) механизм нашел широкое применение в компрессорах, насосах, двигателях внутреннего сгорания и других машинах.
Заменив в шарнирном четырехзвеннике вращательную пару С на поступательную, получим кулисный механизм (различные виды механизмов на рис. 2.3, а, б, в). Составляющие кулисного механизма: кривошип (1); камень (2); кулиса (3). Кулисный механизм на рис. 2.3, в получен из шарнирного четырехзвенника путем замены в нем вращательных пар С и D на поступательные.
Кулисные механизмы нашли широкое применение в строгальных станках благодаря присущему им свойству асимметрии рабочего и холостого хода: у них длительный рабочий ход и быстрый, обеспечивающий возврат резца в исходное положение, холостой ход.
Большое применение шарнирно-рычажные механизмы нашли в робототехнике. В изображенном на рис. 2.4 устройстве механизма манипулятора 1, 2, 3, 4 — звенья; А, В, C,D ~ кинематические пары.
Особенностью этих механизмов является то, что они обладают большим числом степеней свободы, а значит, имеют много приводов. Согласованная работа приводов входных звеньев обеспечивает перемещение схвата по рациональной траектории и в заданное место окружающего пространства.
Широкое применение в технике получили кулачковые механизмы. При помощи кулачковых механизмов конструктивно наиболее просто можно получить практически любое движение ведомого звена по заданному закону.
В настоящее время существует большое число разновидностей кулачковых механизмов, некоторые из них представлены на рис. 2.5. Устройство кулачкового механизма: кулачок (1) плоский толкатель (2); коромысло (2); острый толкатель (2); ролик (3).
Необходимый закон движения выходного звена кулачкового механизма достигается за счет придания входному звену (кулачку) соответствующей формы. Кулачок может совершать вращательное (рис. 2.5, а, б), поступательное
(рис. 2.5, в, г) или сложное движение. Выходное звено, если оно совершает поступательное движение (рис. 2.5, а, в), называют толкателем, а если качательное (рис. 2.5, г) — коромыслом. Для снижения потерь на трение в высшей кинематической паре В применяют дополнительное звено-ролик (рис. 2.5, г).
Кулачковые механизмы применяются как в рабочих машинах, так и в разного рода командоаппаратах.
Очень часто в металлорежущих станках, прессах, различных приборах и измерительных устройствах применяются винтовые механизмы, простейший из которых представлен на рис. 2.6. Он состоит из винта (1); гайки (2) и кинематических пар А, В, С.
Винтовые механизмы обычно применяются там, где необходимо преобразовать вращательное движение во взаимозависимое поступательное или наоборот
Взаимозависимость движений устанавливается правильным подбором геометрических параметров винтовой пары В.
Клиновые механизмы (рис. 2.7) применяются в различного вида зажимных устройствах и приспособлениях, в которых требуется создать большое усилие на выходе при ограниченных силах, действующих на входе. Отличительной особенностью этих механизмов являются простота и надежность конструкции: 1,2 — звенья; Л, Я, С — кинематические пары (см. рис. 2.7).
Механизмы, в которых передача движения между соприкасающимися телами осуществляется за счет сил трения, называются фрикционными. Простейшие трехзвен-ные фрикционные механизмы представлены на рис. 2.8: фрикционный механизм с параллельными осями (а); фрикционный механизм с пересекающимися осями (б); реечный фрикционный механизм (в). Основные составляющие механизмов: входной ролик 1; выходной ролик (колесо) 2; рейка 2 (см. рис. 2.8).
Вследствие того, что звенья 1 и 2 прижаты друг к другу, по линии касания между ними возникает сила трения, которая увлекает за собой ведомое звено 2.
Широкое применение фрикционные передачи получили в приборах, лентопротяжных механизмах, вариаторах (механизмах с плавной регулировкой числа оборотов).
Для передачи вращательного движения по заданному закону между валами с параллельными, пересекающимися и перекрещивающимися осями применяются различного вида зубчатые механизмы. При помощи зубчатых колес можно осуществлять передачу движения как между валами с неподвижными осями, так и с осями, перемеищаюищимися в пространстве.
Зубчатые механизмы применяют для изменения частоты и направления вращения выходного звена, суммирования или разделения движений.
На рис. 2.9 показаны основные представители зубчатых передач с неподвижными осями: цилиндрическая (а), коническая (б); торцовая (в); реечная (г), состоящие из шестерни 1, зубчатого колеса 2 и рейки 2*.
Меньшее из двух зацепляющихся зубчатых колес называют шестерней, а большее — зубчатым колесом.
Рейка является частным случаем зубчатого колеса, у которого радиус кривизны равен бесконечности.
Если в зубчатой передаче имеются зубчатые колеса с подвижными осями, то их называют планетарными (рис. 2.10). Планетарная зубчатая передача состоит из: 0 — стойки, представляющей зубчатое колесо 3 с внутренним зацеплением; солнечного зубчатого колеса 1, сателлита 2; водила Н; низших кинематических пар A, D, Е; высших кинематических пар В, С.
Планетарные зубчатые передачи позволяют передавать большие мощности и передаточные числа при меньшем числе зубчатых колес, чем передачи с неподвижными осями. Они также широко применяются при создании суммирующих и дифференциальных механизмов.
Передача движений между перекрещивающимися осями осуществляется с помощью червячной передачи (рис. 2.11), состоящей из червяка 1 и червячного колеса 2.
Червячная передача получается из передачи винт-гайка путем продольной разрезки гайки и ее двукратного сворачивания во взаимно перпендикулярных плоскостях. Червячная передача обладает свойством самоторможения и позволяет в одной ступени реализовывать большие передаточные отношения.
К зубчатым механизмам прерывистого движения относят также механизм «мальтийского креста», или мальтийский механизм. На рис. 2.12 показан механизм четырех-лопастного «мальтийского креста».
Механизм «мальтийского креста» преобразует непрерывное вращение ведущего звена — кривошипа 1 с цевкой 3 в прерывистое вращение креста 2; цевка 3 без удара входит в радиальный паз креста 2 и поворачивает его на угол —, 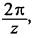
Для осуществления движения только в одном направлении применяют храповые механизмы. На рис. 2.13 показан храповый механизм, состоящий из коромысла 1, храпового колеса 3, стойки 4, собачек 2, 5 и пружины 6.
При качаниях коромысла 1 качающаяся собачка 2 сообщает вращение храповому колесу 3 только при движении коромысла против часовой стрелки. Для удержания колеса 3 от самопроизвольного поворота по часовой стрелке при движении коромысла против хода часов служит стопорная собачка 5 с пружиной 6 .
Мальтийские и храповые механизмы широко применяются в станках и приборах.
Если необходимо передать на относительно большое расстояние механическую энергию из одной точки пространства в другую, то применяют механизмы с гибкими звеньями.
В качестве гибких звеньев, передающих движение от одного звена механизма к другому, используются ремни, канаты, цепи, нити, ленты, шарики и т.п.
На рис. 2.14 приведена структурная схема простейшего механизма с гибким звеном, состоящего из малого шкифа 1, гибкого элемента 2 и большого шкифа 3
Передачи с гибкими звеньями широко применяются в машиностроении, приборостроении и других отраслях промышленности.
Выше были рассмотрены наиболее типичные простейшие механизмы. Большое количество механизмов приводится в специальной литературе, патентах и справочниках, например таких, как [7, 9, 14].
Структурные формулы механизмов
Существуют общие закономерности в структуре (строении) самых различных механизмов, связывающие число степеней свободы W механизма с числом звеньев и числом и видом его кинематических пар. Эти закономерности носят название структурных формул механизмов.
Для пространственных механизмов в настоящее время наиболее распространена формула Малышева, вывод которой производится следующим образом.
Пусть в механизме, имеющем m звеньев (включая стойку), 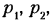
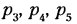
где i = Н — подвижность кинематической пары; 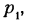
или в краткой записи
при q = 0 механизм — статически определимая система, при q > 0 — статически неопределимая система.
В общем случае решение уравнения (2.2) — трудная задача, поскольку неизвестны W и q; имеющиеся способы решений сложны и не рассматриваются в данной лекции. В частном случае, если W, равное числу обобщенных координат механизма, найдено геометрическим способом, из этой формулы можно найти число избыточных связей1
и решить вопрос о статической определимости механизма; или же, зная, что механизм статически определимый, найти (или проверить) W.
Важно заметить, что в структурные формулы не входят размеры звеньев, поэтому при структурном анализе механизмов можно предполагать их любыми (в некоторых пределах). Если избыточных связей нет (q = 0), сборка механизма происходит без деформирования звеньев, последние как бы самоустанавливаются; поэтому такие механизмы называют самоустанавливающимися [12]. Если избыточные связи есть (q > 0), то сборка механизма и движение его звеньев становятся возможными только при деформировании последних.
Для плоских механизмов без избыточных связей структурная формула носит имя П. Л. Чебышева, впервые предложившего ее в 1869 г. для рычажных механизмов с вращательными парами и одной степенью свободы. В настоящее время формула Чебышева распространяется на любые плоские механизмы и выводится с учетом избыточных связей следующим образом.
Пусть в плоском механизме, имеющем т звеньев (включая стойку), 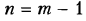
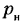
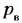
В число наложенных связей может войти некоторое число 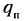
Если 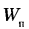
Индекс «п» напоминает о том, что речь идет об идеально плоском механизме, или, точнее, о его плоской схеме, поскольку за счет неточностей изготовления плоский механизм в какой-то мере является пространственным.
По формулам (2.2)—(2.5) проводят структурный анализ имеющихся механизмов и синтез структурных схем новых механизмов.
Структурный анализ и синтез механизмов. Влияние избыточных связей на работоспособность и надежность машин
Как было сказано выше, при произвольных (в некоторых пределах) размерах звеньев механизм с избыточными связями (q > 0) нельзя собрать без деформирования звеньев. Поэтому такие механизмы требуют повышенной точности изготовления, в противном случае в процессе сборки звенья механизма деформируются, что вызывает нагружение кинематических пар и звеньев значительными дополнительными силами (сверх тех основных внешних сил, для передачи которых механизм пред назначен). При недостаточной точности изготовления механизма с избыточными связями трение в кинематических парах может сильно увеличиться и привести к заклиниванию звеньев, поэтому с этой точки зрения избыточные связи в механизмах нежелательны.
Что касается избыточных связей в кинематических цепях механизма, то при конструировании машин их следует стремиться устранять или же оставлять минимальное количество, если полное их устранение оказывается невыгодным из-за усложнения конструкции или по каким-либо другим соображениям. В общем случае оптимальное решение следует искать, учитывая наличие необходимого технологического оборудования, стоимость изготовления, требуемые ресурс работы и надежность машины. Следовательно, это весьма сложная задача для каждого конкретного случая.
Методику определения и устранения избыточных связей в кинематических цепях механизмов рассмотрим на примерах.
Пусть плоский четырехзвенный механизм с четырьмя одноподвижными вращательными парами 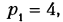
точки В’ звена 2 вдоль оси х и угловые деформации звена 2 вокруг осей x и z (показаны стрелками). Это означает наличие в механизме трех избыточных связей, что подтверждается и по формуле (2.3): q = 1 -6-3 + 5-4 = 3. Для того чтобы данный пространственный механизм был статически определимым, нужна другая структурная схема, например изображенная на рис. 2.15, б, где W=1, 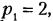
Возможен вариант механизма (рис. 2.15, в) с двумя сферическими парами (р, = 2, р3 = 2); в этом случае, помимо основной подвижности механизма 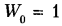
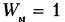
Формула Малышева подтверждает, что такой механизм будет статически определимым:
Наиболее простой и эффективный способ устранения избыточных связей в механизмах приборов — применение высшей пары с точечным контактом взамен звена с двумя низшими парами; степень подвижности плоского механизма в этом случае не меняется, поскольку по формуле Чебышева (при 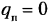
На рис. 2.16, а, б, в дан пример устранения избыточных связей в кулачковом механизме с поступательно движущимся роликовым толкателем. Механизм (см. рис. 2.16, а) — четырехзвенный (n = 3); кроме основной подвижности (вращение кулачка 1) имеется местная подвижность (независимое вращение круглого цилиндрического ролика 3 вокруг своей оси); следовательно, 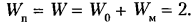
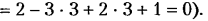
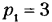
Снижая класс высшей пары путем применения бочкообразного ролика (пятиподвижная пара с точечным контактом, см. рис. 2.16,в), получим при 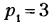
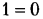
На (рис. 2.16, г, д) дан другой пример устранения избыточных связей в зубчатой четырехзвенной передаче 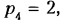
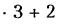
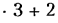
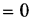
связей не имеет; по формуле Малышева, q = 1 — 6 • 3 + 5- 3 + 2- 2 = 2 — механизм статически неопределимый, следовательно, потребуется высокая точность изготовления, в частности для обеспечения параллельности геометрических осей всех трех колес.
Заменив зубья промежуточного колеса 2 на бочкообразные (см. рис. 2.16, д), получим q =1-6-3 + 5- 3+1-2 = 0 — статически определимый механизм.
Кинематические характеристики механизмов
Основным назначением механизма является выполнение им требуемых движений. Эти движения могут быть описаны посредствам его кинематических характеристик. К ним относят координаты точек и звеньев, их траектории, скорости и ускорения. К числу кинематических характеристик относятся и такие характеристики, которые не зависят от закона движения начальных звеньев, определяются только строением механизма и размерами его звеньев и в общем случае зависят от обобщенных координат. Это функции положения, кинематические передаточные функции скорости и ускорения.
Для создания механизмов, наилучшим образом отвечающих поставленным требованиям, надо знать методы определения кинематических характеристик механизмов.
Различают следующие методы определения кинематических характеристик механизмов:
- Геометрический метод — основанный на анализе векторных контуров кинематических цепей механизмов, представленных в аналитическом или графическом виде.
- Метод преобразования координат точек механизма, решаемый в матричной или тензорной форме (обычно применяется для исследования кинематических цепей манипуляторов промышленных роботов с использованием ЭВМ).
- Метод кинематических диаграмм — метод численного интегрирования и дифференцирования (решаемый с помощью ЭВМ или графически).
- Метод планов положений, скоростей и ускорений, основанный на решении векторных уравнений, связывающих кинематические параметры, в графическом виде или аналитической форме.
- Экспериментальный метод.
Кинематика входных и выходных звеньев
Число независимых друг от друга кинематических параметров механизма с заданными размерами звеньев и структурной схемой равно числу степеней свободы механизма или числу обобщенных координат механизма.
Звено, которому приписывается одна или несколько обобщенных координат, называют начальным звеном. Например, звено 1, вращающееся вокруг неподвижной точки, т.е. образующее со стойкой 2 сферическую кинематическую пару (рис. 5.1, а), имеет три степени свободы и его положение определяется тремя параметрами — тремя углами Эйлера: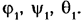
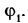
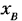
движения звеньев, для выполнения которых предназначен механизм. Входному звену механизма с одной степенью свободы обычно присваивают номер 1, а выходному звену — номер 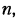
Во многих случаях при проектировании машин и механизмов закон изменения обобщенных координат в функции времени удается определить только на последующих стадиях проектирования, обычно после динамического исследования движения агрегата с учетом характеристик сил, приложенных к звеньям механизма масс и моментов инерции звеньев. В таких случаях движение выходных и промежуточных звеньев определяется в два этапа: на первом устанавливаются зависимости кинематических параметров звеньев и точек от обобщенной координаты, т.е. определяются относительные функции (функции положения и передаточные функции механизма), а на втором — определяется закон изменения обобщенной координаты от времени и зависимости кинематических параметров, выходных и промежуточных звеньев от времени.
Функцией положения механизма называется зависимость углового или линейного перемещения точки или звена механизма от времени или обобщенной координаты.
Кинематическими передаточными функциями механизма называются производные от функции положения но обобщенной координате. Первая производная называется первой передаточной функцией или аналогом скорости (обозначаются 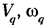
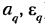
Кинематическими характеристиками механизма называются производные от функции положения по времени. Первая производная называется скоростью (обозначают V, о), вторая — ускорением (обозначают 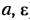
Связь между скоростью 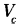
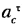
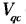
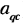
Определение кинематических характеристик плоского рычажного механизма геометрическим методом в аналитической форме
Рассмотрим пример с кривошипно-ползунным механизмом.
К основным размерам, характеризующим кинематическую схему механизма, относятся:
- длина кривошипа —
,
- относительная длина шатуна —
- относительная внеосиость —
- угол наклона направляющей ползуна —
- начальная угловая координата звена 1 —
Изобразим кинематическую схему механизма (рис. 5.3)
Условие замкнутости векторного контура АВСС’А для любого положения механизма выражается уравнением
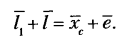
Проецируя этот векторный контур на оси координат 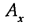
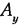
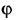
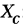
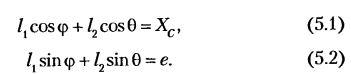
Из уравнения (5.2) угловая координата 0 вектора 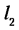
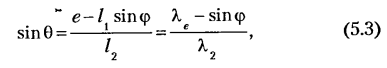
где
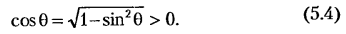
Дифференцируя (5.2) по обобщенной координате 
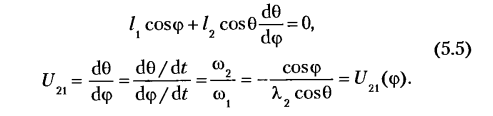
Дифференцируя (5.1) по 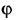
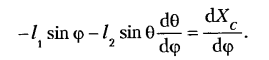
Передаточная функция скорости точки С:
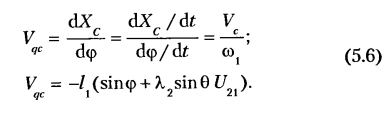
Из векторного контура 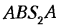
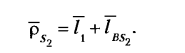
Проецируя этот векторный контур на оси координат АХ и 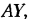
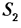
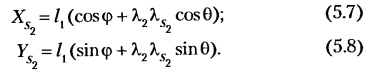
Дифференцируя (5.7) и (5.8) по 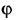
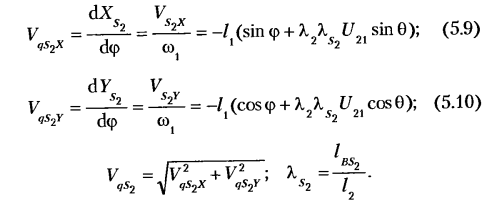
Дифференцируя по 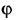
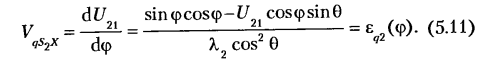
Дифференцируя по 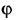
Аналогично можно получить кинематические передаточные функции ускорения точки 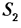
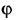
Для общего случая движения механизма, когда 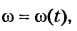
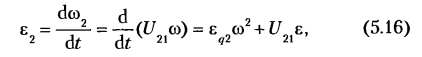
ускорение ползуна:
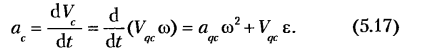
Блок-схема программы определения кинематических передаточных функций скорости кривошипио-ползуиного механизма (AR210) изображена на рис. 5.4
Метод планов положений, скоростей и ускорений
Кинематические характеристики кривошипно-ползунного (и любого другого) механизма могут быть определены и с помощью графоаналитического метода, или, как его чаще называют, метода планов положений, скоростей и ускорений.
Планом механизма называется масштабное графическое изображение кинематической схемы механизма соответствующее заданному положению входного звена.
Планом скоростей механизма называется чертеж, на котором изображены в виде отрезков векторы, равные по модулю и направлению скоростям различных точек механизма в данный момент.
Чертеж, на котором изображены в виде отрезков векторы, равные по модулю и направлению ускорениям различных точек звеньев механизма в данный момент, называют планом ускорений механизма.
Для иллюстрации этого метода построим план скоростей (рис. 5.5) для той же угловой координаты 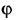
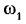
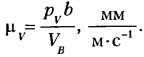
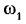
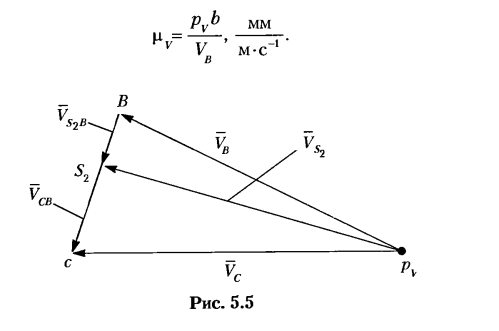
Определение скоростей. Векторные уравнения для определения скоростей точек В, С и 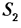
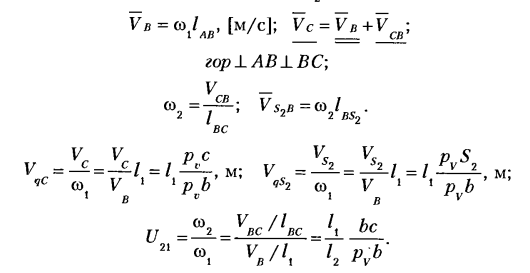
Определение ускорений. Для определения ускорений точек В и С записываем уравнения в следующем виде:
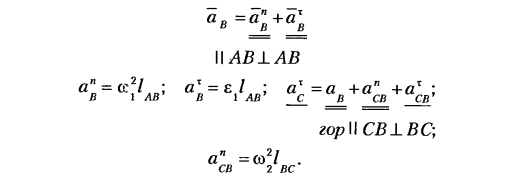
Далее строим план ускорений (рис. 5.6) в масштабе 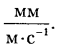
Решение задач по теории машин и механизмов (ТММ)
Задача №1.
На рис. 15 показана схема механизма автомата-перекоса вертолета.Ведущее звено АВ отмечено круговой стрелкой.
Решение:
1) Подсчитывается степень подвижности механизма но формуле Чебышева (2.4). Для эюго определяются общее число звеньев к = 8, число под-
вижных звеньев 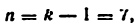
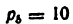
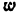
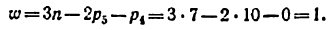
2) Ведущее звено задано в условии примера, и оно должно быть одно, так как 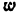
3) Механизм расчленяется на группы Ассура. Вначале отделяется группа Ассура второго класса, образованная звеньями 7 и 6 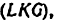
класса, состоящая из звеньев 5 и 4 (HEF), и, наконец, группа второго класса составленная звеньями 3 и 2 (DCB).
На этом расчленение механизма заканчивается, так как остались ведущее звено 1 и стойка 8 (на рисунке отделяемые группы обведены замкнутыми контурами).
4) Записывается формула строения механизма:
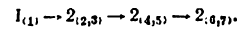
В этой формуле римская цифра I обозначает ведущее звено, арабские — классы присоединяемых групп (2), а индексы при арабских цифрах указывают, какие звенья образовали ведущее звено и присоединяемые группы.
Из формулы строения механизма видно, что наивысший класс присоединенных групп — второй, поэтому механизм автомата-перекоса вертолета при ведущем звене 1 следует отнести ко второму классу.
Задача №2.
На( рис. 16, а) показана схема механизма приемника давления электрического диетаЛционного манометра.
Решение:
1) Подсчитывается степень подвижности механизма по формуле Чебышева (рис. 16, а). Имеем 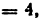
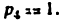
Строится заменяющий механизм (рис. 16, б) (кинематическая пара IV класса В заменяется в соответствии с рис. 12, б одним звеном, входящим в две кинематические пары V класса). Для этого механизма имеем 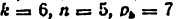
2) Ведущее звено задано в условии примера п должно быть одно, так как
3) Механизм расчленяется на группы Ассура (рис. 16, б). Вначале отделяется группа Ассура второго класса, образованная звеньями 3 и 4 (DEF), затем группа второго класса, состоящая из звеньев 2 и 6 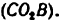
4) Записывается формула строения механизма:
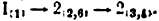
Наивысший класс присоединенных групп — второй, поэтому механизм надо отнести ко второму классу (при ведущем звене 1).
Задача №3.
На (рис. 17, а )показана схема механизма газораспределения двигателя внутреннего сгорания с ведущим звеном (кулачок)
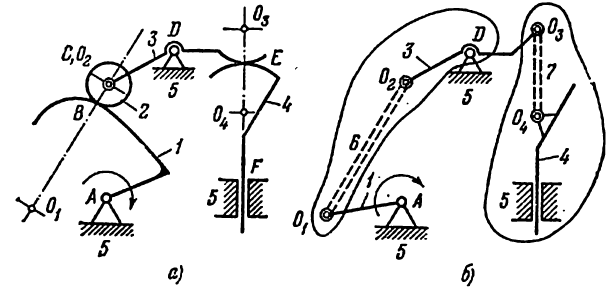
Рис. 17. Механизм газораспределения двигателя внутреннего сгорания: а) основной механизм, б) заменяющий механизм.
Решение:
1) Подсчитывается степень подвижности 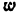
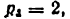
Круглый ролик 2, свободно вращающийся вокруг своей оси, вносит лишнюю степень свободы, поэтому при подсчете числа звеньев он не учитывается. Также в числе 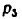
Строим заменяющий механизм (рис. 17, б). Каждую кинематическую пару IV класса В и Е заменяем, согласно (рис. 12, а), одним звеном, входящим в две кинематические пары V класса. У заменяющего механизма степень подвижности 
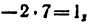
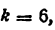
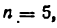
2) Так как 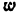
3) Расчленение на группы Ассура (рис. 17, б). Вначале отделяется группа второго класса, образованная звеньями 4 и 7, затем группа второго класса, состоящая из звеньев 3 и 6; на этом разложение заканчивается, так как остались ведущее звено 1 и стойка 5.
4) Записывается формула строения механизма:
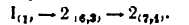
Наивысший класс присоединенных групп — второй, поэтому механизм следует отнести ко второму классу (при ведущем звене 1).
Задача №4.
На (рис. 18) показана схема механизма конхоидографа с ведущим звеном в двух вариантах: на (рис. 18, а )— это звено 1,на (рис. 18, б) — звено 4.
Рис. 18. Механизм конхоидографа: а) ведущее звено первое, б) ведущее звено четвертое.
Решение:
I) Определяется степень подвижности механизма по формуле Чебышева. Так как 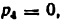
2) Так как 
3) Разложение на группы Ассура. По первому варианту (ведущее звено 1) ог механизма можно отделить только кинематическую цепь, состоящую из звеньев 2, 3, 4 и 5. Эта цепь представляет собой группу Ассура третьего класса третьего порядка, так как в ней три внутренних кинематических пары (вращательной пары D, C и поступательная Е ) и три внешних ( вращательных пары 
4) Формула строения механизма запишется так. При ведущем звене 
При ведущем звене 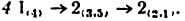
Готовые задачи по теории машин и механизмов
Теория механизмов и машин — научная дисциплина (или раздел науки), которая изучает строение (структуру), кинематику и динамику механизмов в связи с их анализом и синтезом.
Цель ТММ — анализ и синтез типовых механизмов и их систем.
Задачи ТММ: разработка общих методов исследования структуры, геометрии, кинематики и динамики типовых механизмов и их систем.
Типовыми механизмами будем называть простые механизмы, имеющие при различном функциональном назначении широкое применение в машинах, для которых разработаны типовые методы и алгоритмы синтеза и анализа.
Задача №1
Построить планы скоростей и ускорений механизма строгального станка (рис. 25, а). Найти скорость и ускорение звена 5. Дано: 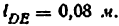
Решение:
1) Проводим структурный анализ и устанавливаем класс механизма. Число звеньев k = 6, число подвижных звеньев n = 5, число кинематических пар V класса 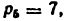
2) Строим план положения механизма. Длину отрезка (AB) выбираем равной 25 мм поэтому масштаб схемы будет
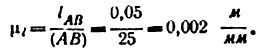
Длины остальных отрезков на чертеже:
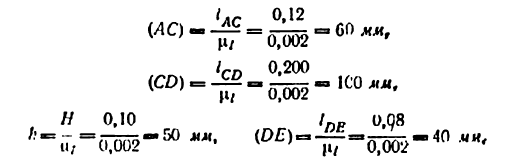
По полученным размерам строим план положения механизма (рис. 25, б)
3) Строим план скоростей механизма. Начинаем с группы, состоящей из звеньев 2 и 3, так как она непосредственно присоединена к ведущему звену и стойке. Построение ведем по следующим векторным уравнениям:
где 
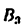
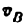
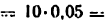
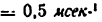
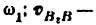
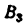
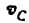
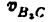
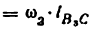
Строим решение первого векторного уравнения, указанного выше. От полюса р плана (рис. 25, а) откладываем отрезок (pb), изображающий скорость 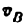
Длину этого отрезка принимаем равной (pb) = (АВ) 25 мм, т. е. план строим в масштабе кривошипа. Через точку b проводим направление скорости —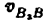
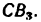
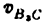
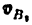
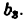
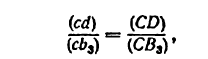
откуда
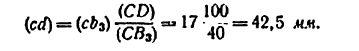
Переходим к построению плана скоростей группы 4, 5. Этот план строим по уравнениям
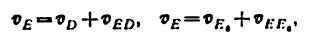
где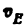
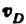
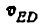
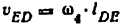
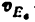
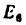
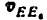
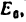
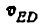
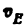
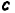
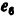
Масштаб плана скоростей равен
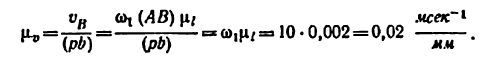
Масштаб плана аналогов скоростей равен
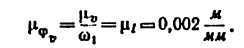
Искомая скорость суппорта (скорость точки Е) равна
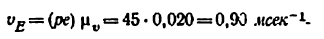
4) Строим план ускорений группы 2, 3. Построение ведем по следующим двум векторным уравнениям
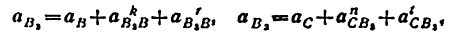
где 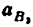
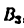
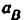

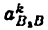
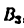
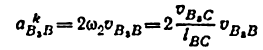
так как 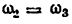
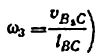
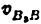
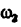
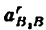
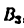
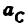
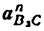
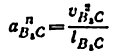
и направленное параллельно линии 
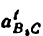
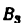
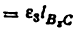
Строим решение первого векторного уравнения, указанного выше (рис. 25, г). Задаемся отрезком 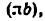
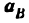
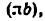
Масштаб плана ускорений равен
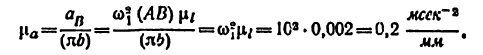
Масштаб плана аналогов ускорений равен
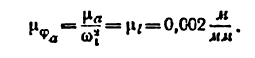
Выбранный отрезок 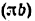
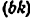
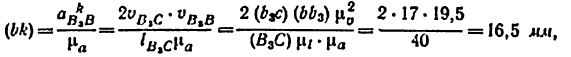
отрезки 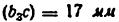
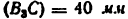
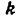
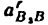
Переходим к построению второго векторного уравнения. Точку с совмещаем с точкой 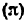
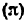
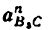
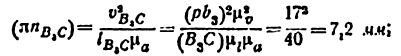
далее через точку 
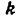
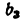
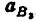
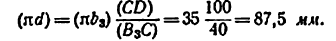
Переходим к построению плана ускорений группы 4 , 5 по уравнениям
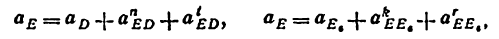
где аЕ — ускорение точки 
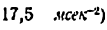
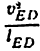
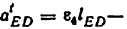
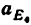
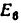
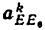
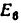
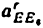
В соответствии с первым векторным уравнением от точки d откладываем отрезок (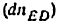
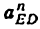
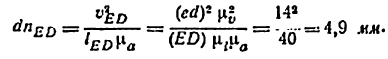
Далее через точку 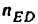
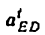
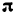
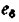
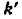
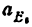
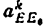
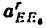
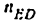
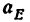
Искомое ускорение суппорта (точки Е) будет равно
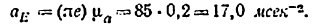
Задача №2
Методом планов найти угловые скорость и ускорение лепестка (звена 5) в механизме привода лепестков фотозатвора (рис. 26, а). Дано: 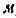
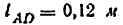
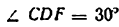
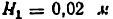
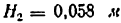
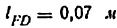
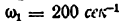
Решение:
1) Проводим структурный анализ и устанавливаем класс механизма. Число звеньев равно k = 6, число подвижных звеньев разно n = 5, число кинематических пар V класса 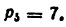
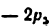
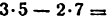
2) Строим план положения механизма. Длину отрезка (АВ) назначаем равной (АВ) = 10 мм, поэтому масштабом чертежа будет
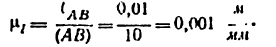
Вычисляем длины остальных отрезков на чертеже:
По полученным размерам строим план положения механизма (рис. 26, б).
3) Строим план скоростей механизма. Начинаем с группы Ассура, состоящей из звеньев 2, 3, так как она непосредственно присоединена к ведущему звену и стойке. План строим по векторным уравнениям

где 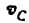
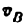
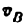
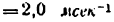
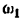
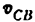
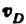
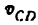
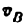
(отрезок (pb) взят равным (рb) = 50 мм). Переходим к построению решения второго векторного уравнения, указанного выше. Скорость 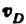
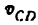
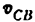
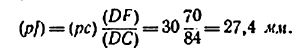
Этот отрезок составит с отрезком (рс) угол
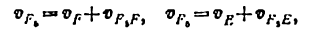
где 
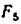
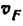
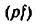
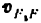
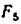
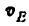
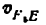
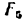
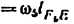
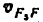
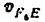
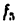
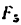
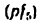
Масштаб плана скоростей равен
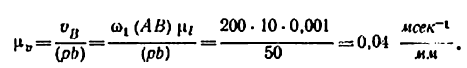
Масштаб плана аналогов скоростей равен
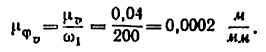
Угловая скорость звена 5 равна
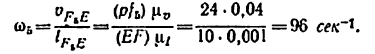
Ее направление определяется вектором скорости 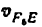
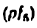
4) Строим план ускорений группы, состоящей из звеньев 2, 3. Он должен соответствовать таким векторным уравнениям:
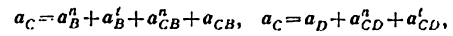
где 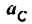
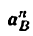

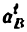
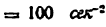
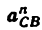
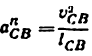
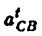
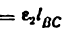
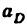
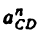
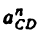
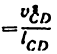
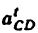
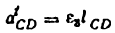
5) Приступаем к построению плана ускорений (рис. 26, г). Строим решение первого векторного уравнения, указанного выше. От полюса 
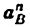
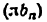
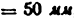
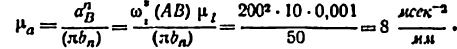
От точки 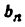
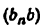
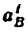
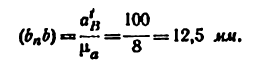
Далее от точки b откладываем отрезок 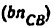
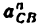
(в нашем случае дробь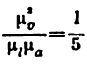
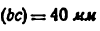
через точку 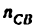
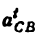
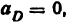
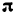
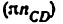
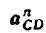
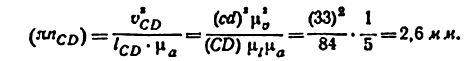
Далее через точку 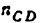
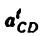
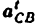
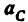
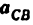
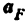
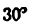
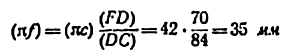
(отрезок 
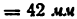
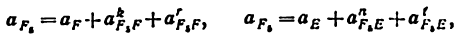
где 
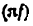
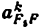
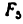
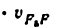
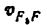
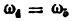
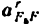
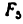
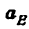
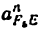
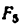
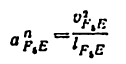
и направленное параллельно лннни EF; 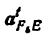
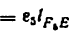
Строим решение первого векторного уравнения, указанного выше (рис. 26, г). Oт точки 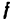
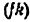
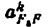
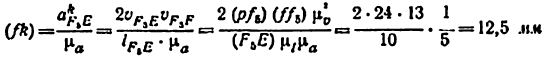
(дробь 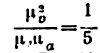
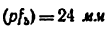
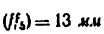
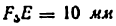
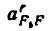
Переходим к построению решения второго векторного уравнения, указанного выше.
Конец ускорения
точки Е (точку е) совмещаем с полюсом плана
и от нее откладываем отрезок
ускорение
.
Этот отрезок равен
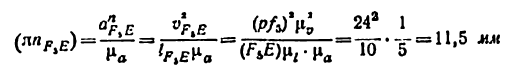
(отрезок 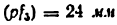
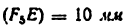
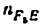
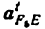
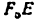
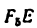
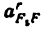
Точка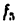
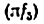
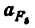
Угловое ускорение звена 5 находится по формуле
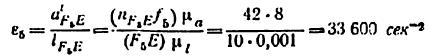
(отрезок 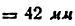
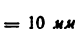
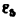
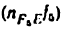
Примерный перечень экзаменационных вопросов по курсу «Теория механизмов и машин» с ответами, для студентов очной и заочной форм обучения.
Решение курсовых работ >
Онлайн помощь на экзамене >
Сохранить и поделиться с друзьями
Ответы на другие вопросы к экзамену можно найти воспользовавшись поиском на нашем сайте.
Структура
- Понятие механизма, детали, звена.
- Название звеньев механизма в зависимости от характера их движения.
- Классификация кинематических пар.
- Условные изображения кинематических пар.
- Кинематические цепи (простые, сложные, замкнутые, незамкнутые).
- Определение числа степеней свободы кинематической цепи.
- Обосновать формулу подвижности для пространственного и плоского механизма.
- Пассивные и избыточные связи в кинематической цепи.
- Лишние степени свободы кинематической цепи.
- Высшие и низшие пары. Понятие заменяющего механизма. Примеры замены высших пар низшими.
- Структурная классификация плоских механизмов.
- Определение класса и порядка групп Ассура.
- Виды групп Ассура второго класса.
- Начальные звенья при кинематическом анализе механизмов.
Кинематика
- Задачи кинематического анализа (цели и методы).
- Графический метод кинематического исследования.
- Графическое дифференцирование методом касательных и хорд.
- Кинематический анализ методом планов групп Ассура 1вида.
- Кинематический анализ методом планов групп Ассура 2вида.
- Кинематический анализ методом планов групп Ассура 3вида.
- Кинематический анализ методом планов групп Ассура 4вида.
- Кинематический анализ методом планов групп Ассура 5вида.
- Аналитический метод кинематического исследования.
- Аналоги скоростей и ускорений.
Динамика
- Задачи динамики механизмов.
- Классификация сил при силовом расчете механизмов.
- Метод кинетостатики при силовом расчете механизмов.
- Главный вектор и главный момент сил инерции.
- Коэффициент трения скольжения, Коэффициент трения качения, конус трения.
- Коэффициент трения в паре с клиновидным профилем.
- Трение в цапфах вращательных пар.
- Трение в пятах.
- Формула Эйлера для расчета сил трения между шкивом и гибкой лентой.
- Определение уравновешивающей силы (момента) с помощью теоремы Жуковского.
- Уравнение энергетического баланса машины.
- Механический коэффициент полезного действия машины, коэффициент потерь.
- Коэффициент полезного действия системы механизмов при их параллельном и последовательном соединении.
- Кинетическая энергия механизма.
- Приведенная масса и приведенный момент инерции механизма.
- Уравнение движения машинного агрегата.
- Коэффициент неравномерного хода. Регулирование хода машины.
- Уравновешивание сил инерции вращающихся звеньев.
- Задачи и этапы синтеза механизмов. Методы оптимизации.
- Условия существования кривошипа в четырехзвенных механизмах.
- Построение схемы четырехзвенного механизма по заданному коэффициенту изменений средней скорости ведомого звена.
- Проектирование механизма по заданному ходу выходного звена.
- Приводы, принципы их работы.
Зубчатые механизмы
- Признаки классификации зубчатых передач.
- Кинематика рядного зубчатого механизма. Передаточное отношение многоступенчатых механизмов.
- Планетарные и дифференциальные передачи. Формула Виллиса для расчета передаточного отношения.
- Зубчатые механизмы: основной закон зацепления.
- Эвольвента и ее свойства.
- Геометрические элементы зубчатых колес.
- Модуль зубчатого колеса.
- Зубчатая рейка, исходный контур, его основные параметры.
- Методы изготовления зубчатых колес.
- Геометрические показатели качества зацепления.
Кулачковые механизмы
- Кулачковые механизмы, схемы плоских механизмов.
- Определение угла передачи движения для кулачкового механизма со смещенным толкателем.
- Методика построения профиля кулачка с роликовым толкателем.
- Силовое замыкание пары кулачок-толкатель.
- Учебная литература по ТММ
- Помощь на экзамене и защите курсовых по ТММ
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее


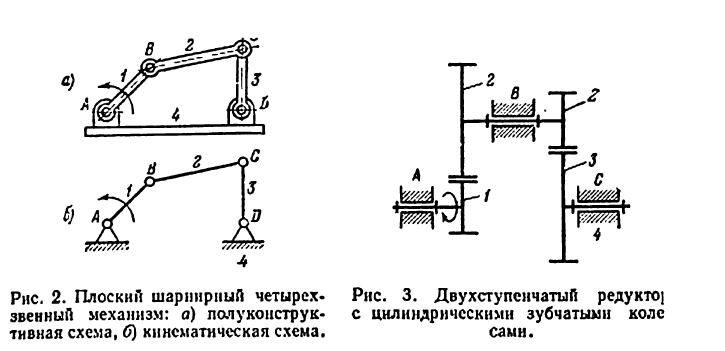
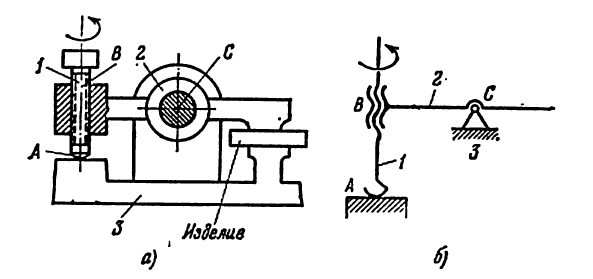
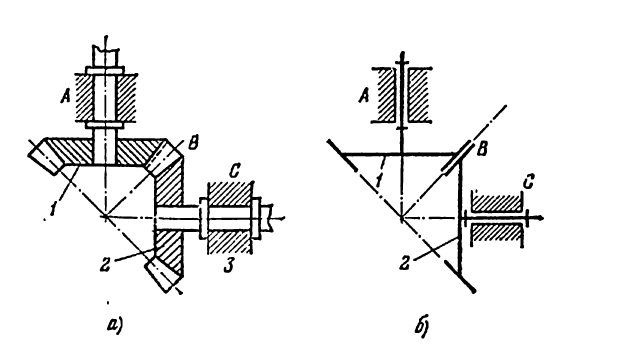
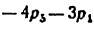
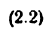
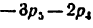
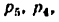
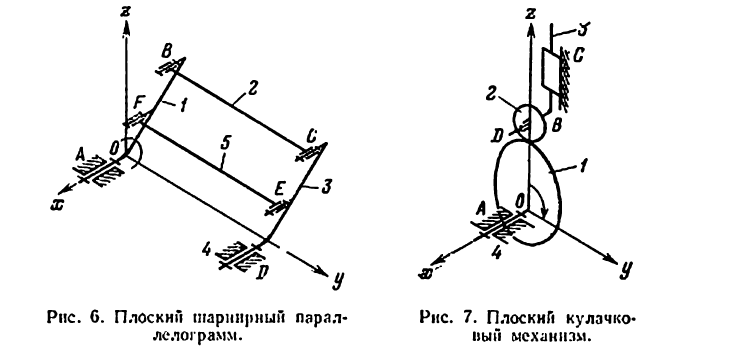
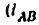
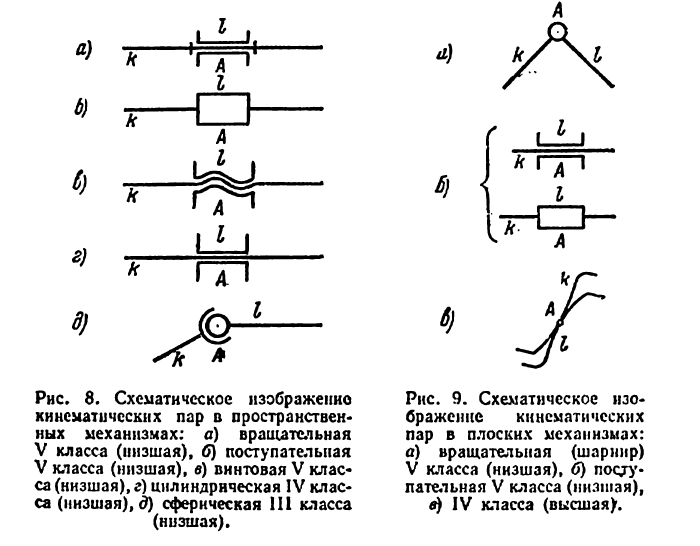
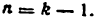
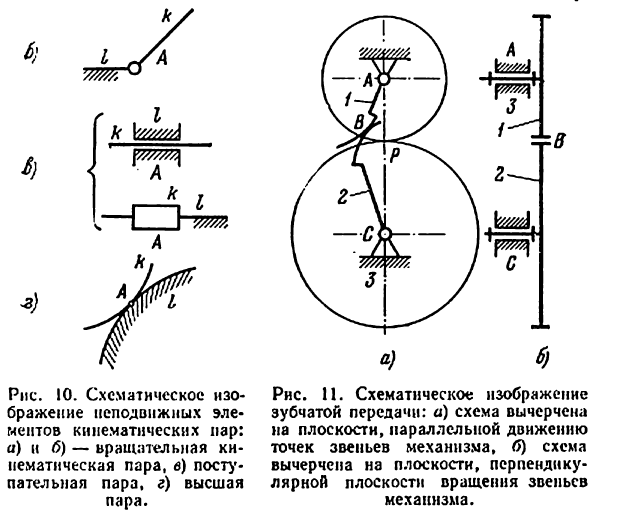
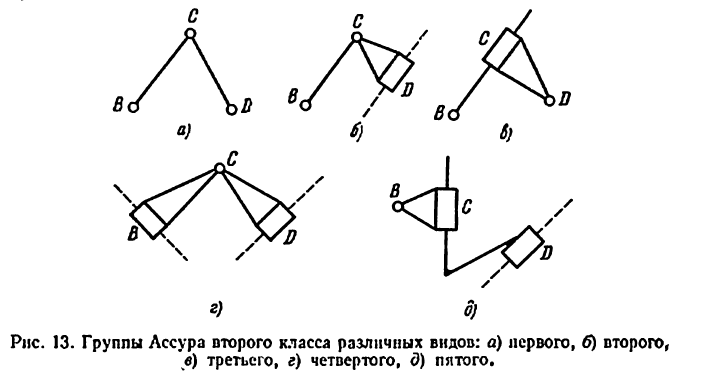
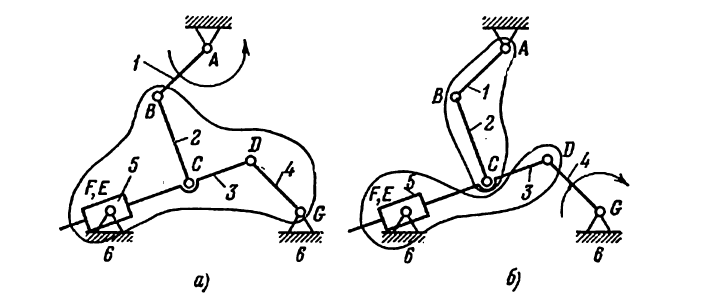
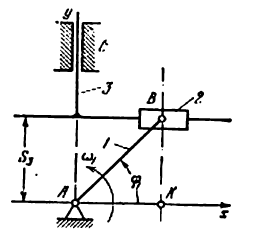
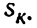
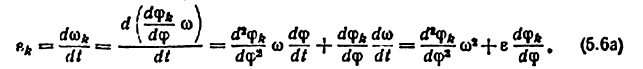
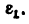
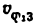
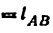
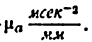
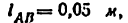
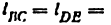
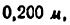
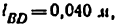
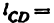
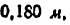
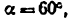
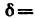
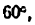
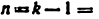

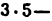
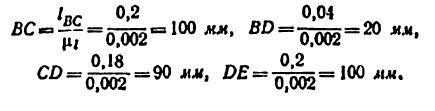
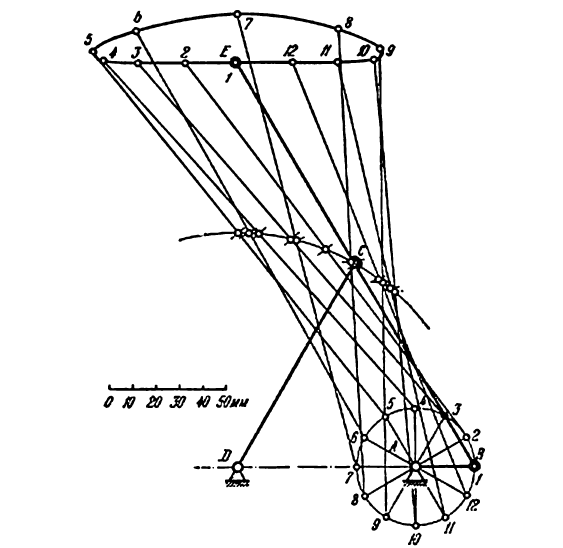
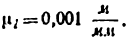
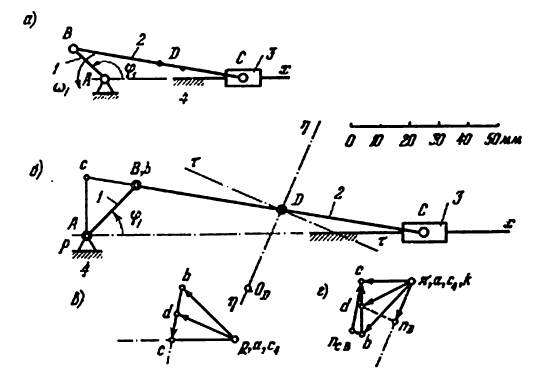
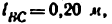
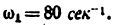
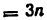
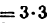
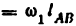
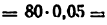
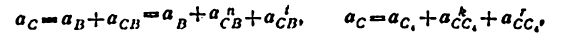
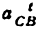
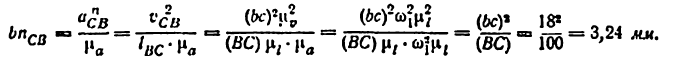
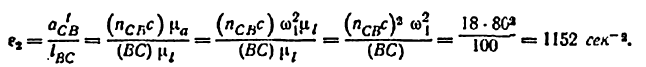
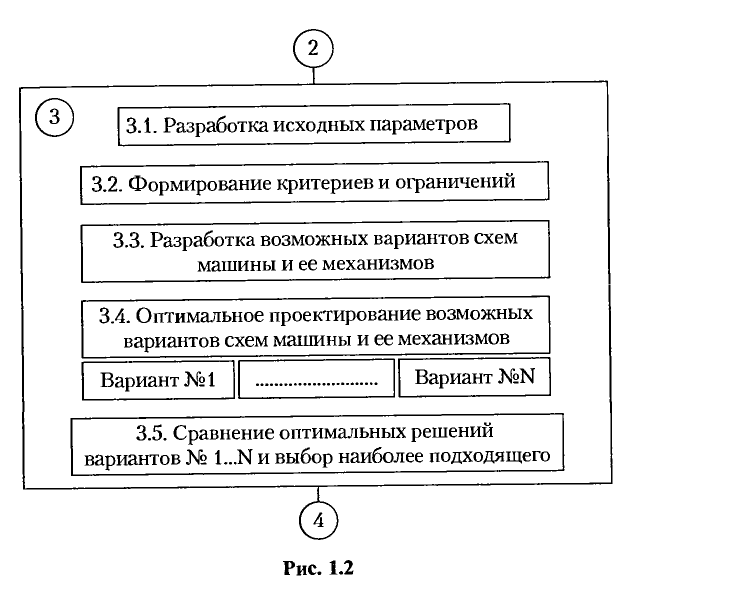
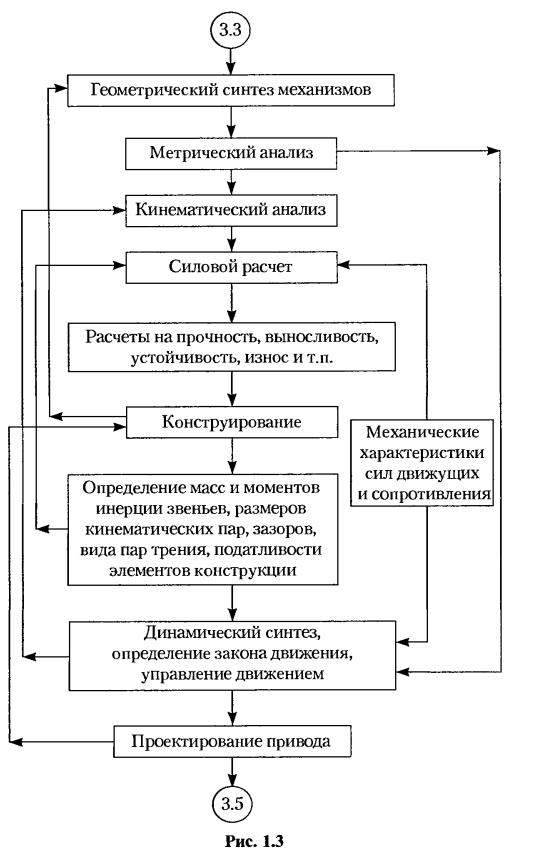
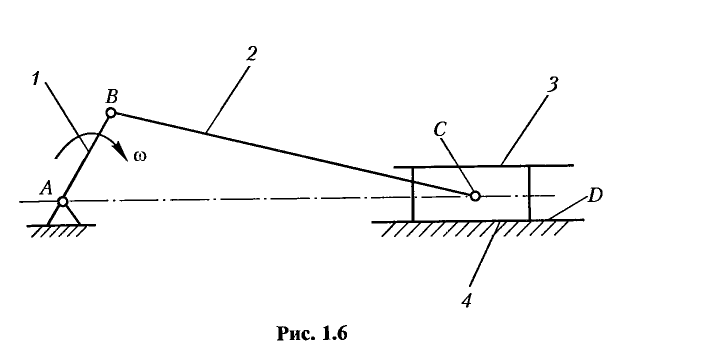
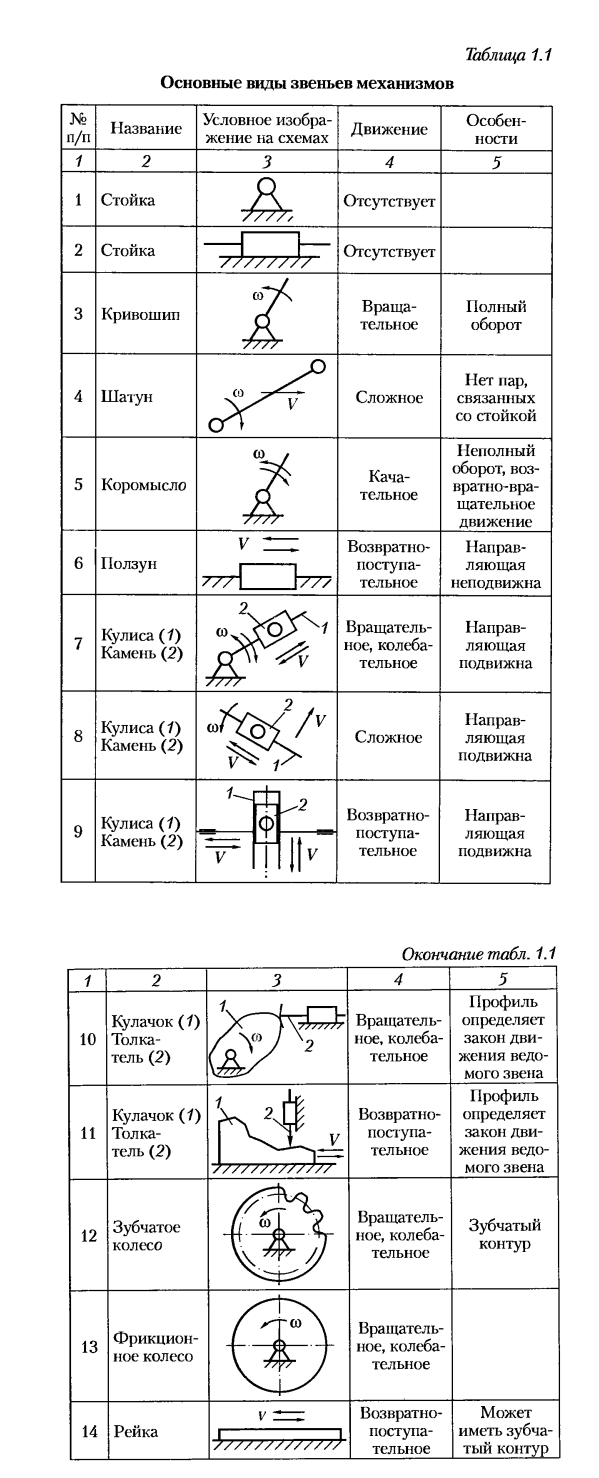
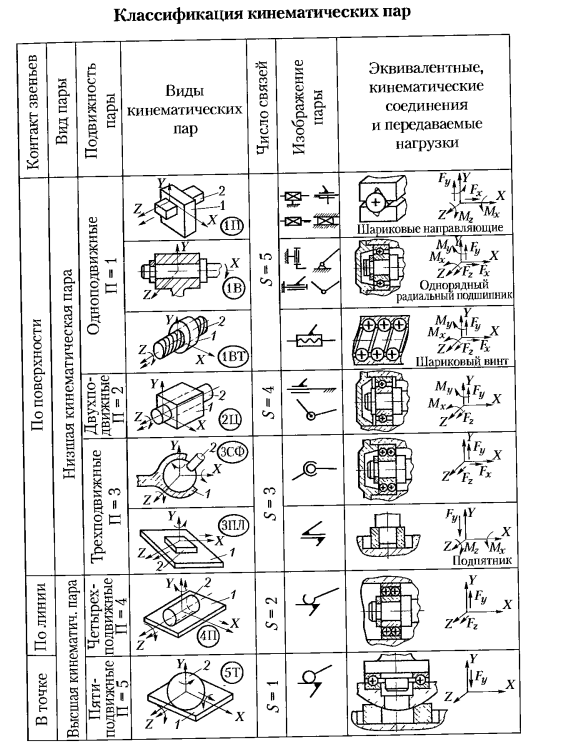
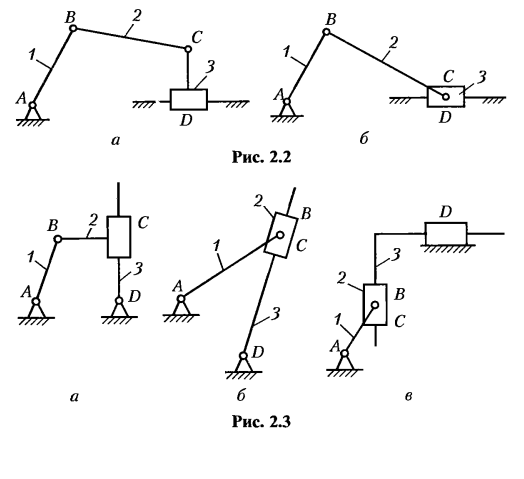
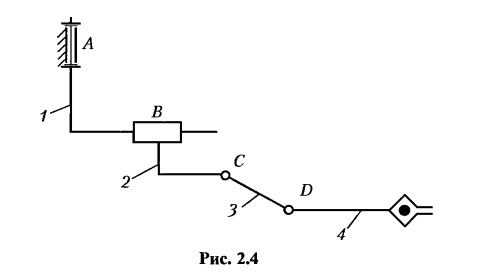
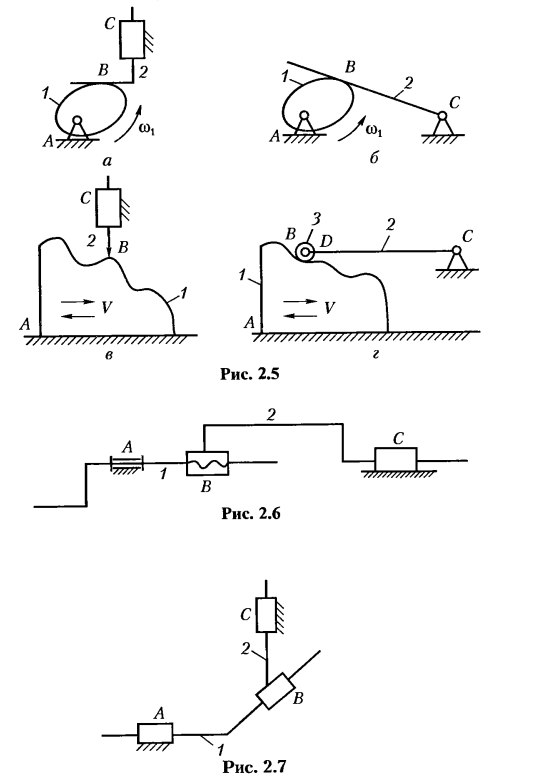
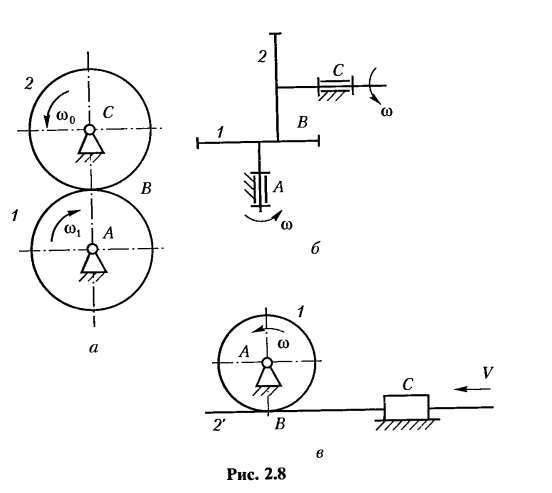
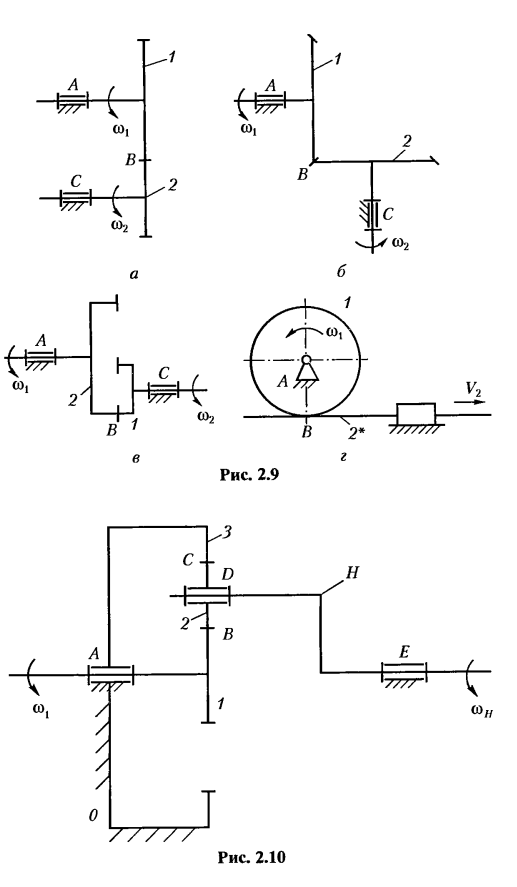
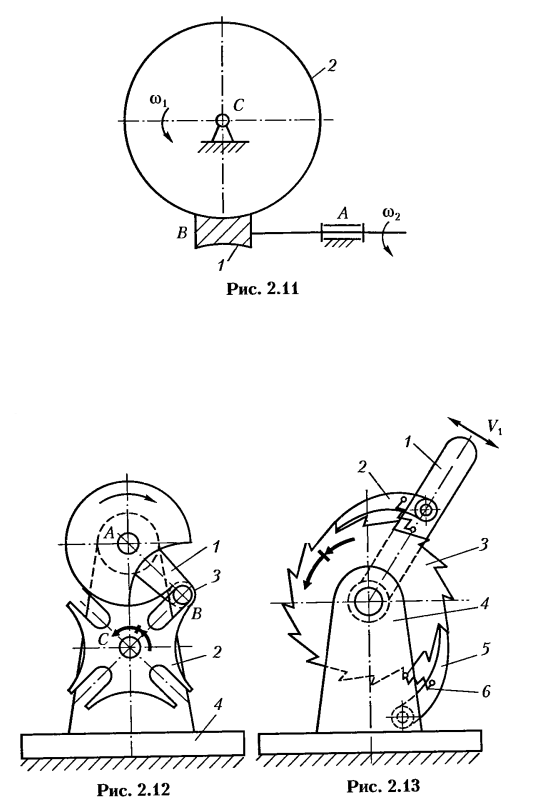
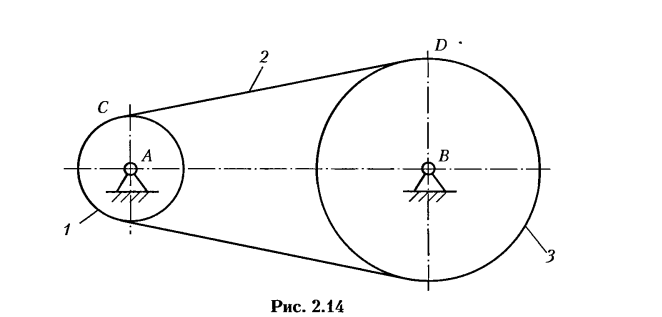
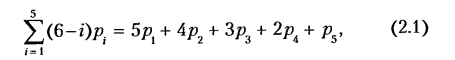
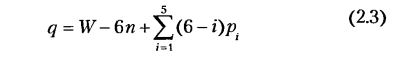
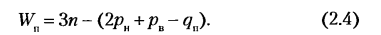
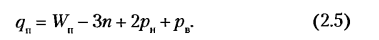
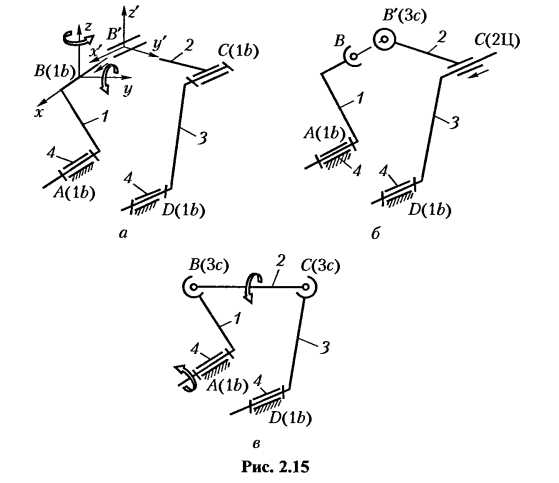
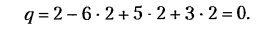
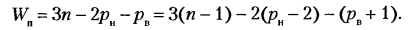
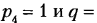
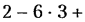
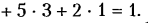
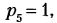
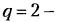
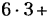
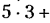
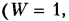
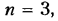
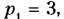
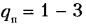
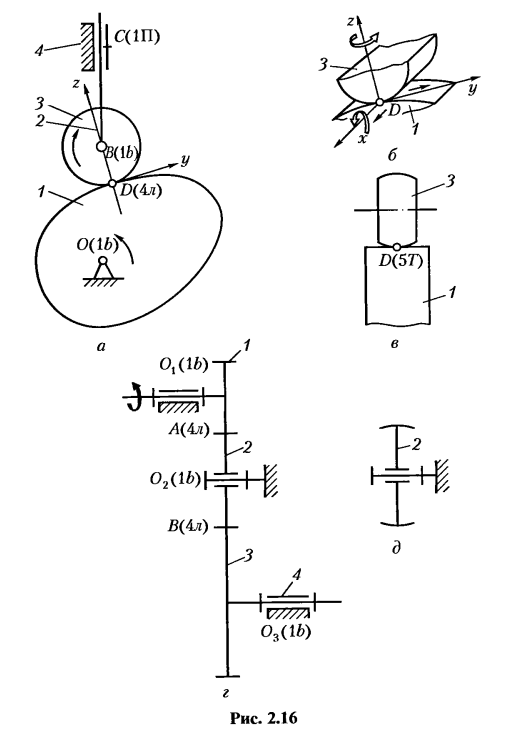
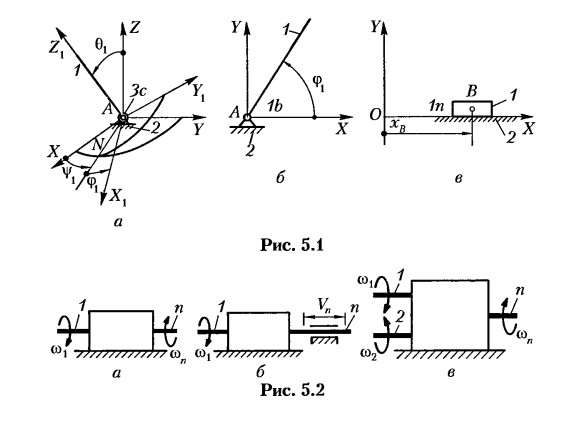
 ,
,
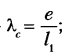
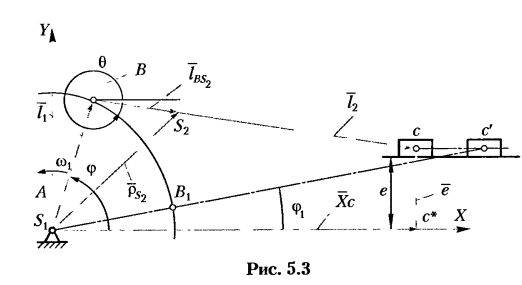
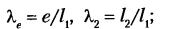
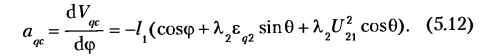
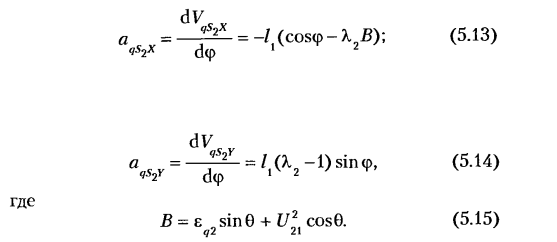
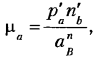
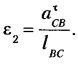
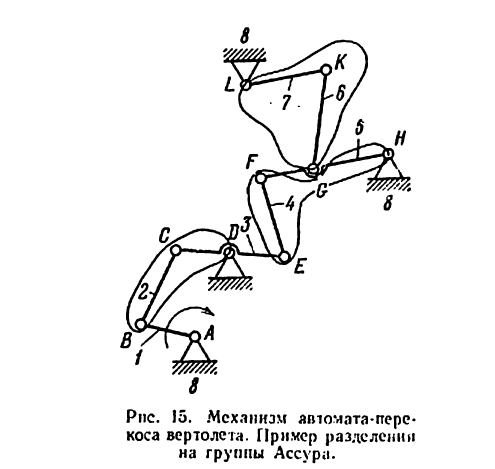
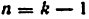
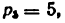
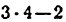
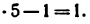
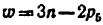
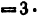
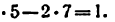
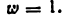
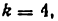
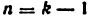
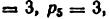
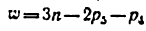
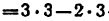
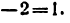
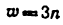
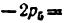
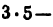
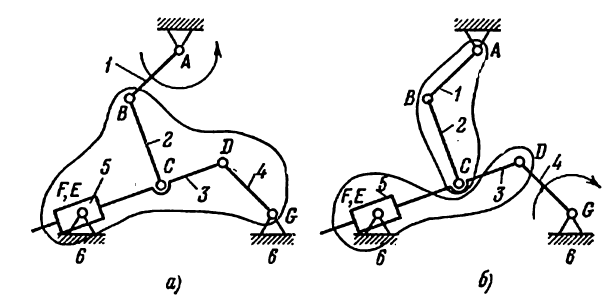
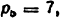
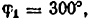
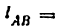
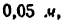
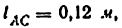
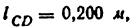
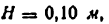
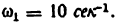
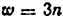
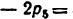
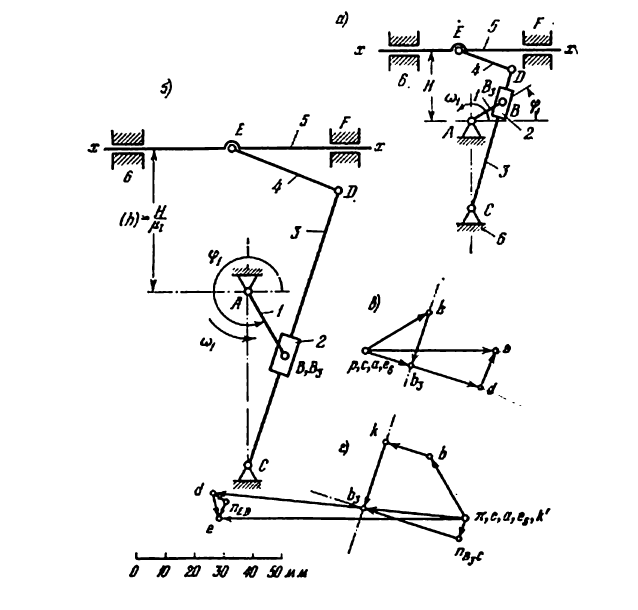
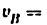
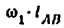
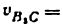
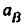
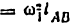
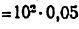
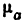
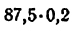
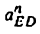
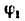
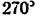
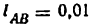
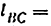
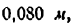
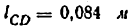
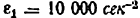
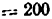
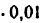
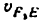
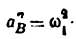
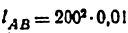
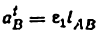

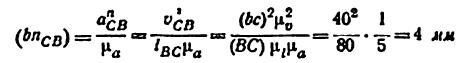
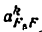
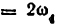
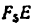
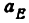 точки Е (точку е) совмещаем с полюсом плана
точки Е (точку е) совмещаем с полюсом плана 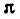 и от нее откладываем отрезок
и от нее откладываем отрезок 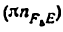 ускорение
ускорение 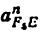 .
.