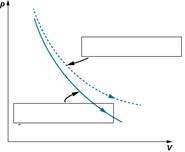
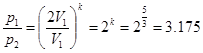Задачи на адиабатный процесс егэ - Помощь в подготовке к экзаменам и поступлению

1.На рисунке ниже, показаны графики двух
процессов адиабатного и изотермического. Подпишите на рисунке название каждого
процесса.

2. При адиабатическом сжатии газа
была совершена работа 400Дж. Как и насколько изменилась при этом
внутренняя энергия газа?

(Ответ: согласно
первому закону термодинамики работа ,совершенная над газом равна изменению
внутренней энергии, следовательно внутренняя энергия увеличится на 400Дж.

Ответ: увеличится на 400 Дж)

3. В процессе адиабатического
расширения газ совершил работу равную 5 кДж. Чему равно изменение внутренней
энергии газа?

(Ответ:: согласно
первому закону термодинамики газ совершает работу за счет внутренней энергии,
тогда внутренняя энергия уменьшится на 5·10³Дж.

Ответ: уменьшится на 5 кДж)

4.Одноатомный идеальный газ, взятый
в количестве двух молей, расширился без теплообмена с окружающей средой.
Температура газа в ходе расширения уменьшилась на 10^оС. Определить
работу, совершённую газом. (249Дж)

Решение:

Поскольку известно, что газ
одноатомный, количество вещества и изменение внутренней энергии можно
рассчитать по формуле

Поскольку работа совершается за
счет изменения внутренней энергии то она равна 249 Дж.

5.
Одноатомный идеальный газ адиабатически сжали так, что его объем увеличился в 2
раза. Как изменится давление газа?

Ответ
:

Представим
состояние газа в начале и конце адиабатного процесса через уравнение Пуассона:

Учтем изменение объема

Выразим отношение давлений

Источник

Рубрика Задание 10, Решаем ЕГЭ по математике Комментарии (0)

Задание. При адиабатическом процессе для нагревания идеального газа выполняется закон pV^k = 7,776·10⁶ Па·м⁴, где p – давление в газе в паскалях, V – объём газа в кубических метрах, k = 4/3. Найдите какой объём V (в куб. м) будет занимать газ при давлении p, равном 3,75·10⁶ Па.

Решение:

Понравилось? Нажмите

Источник

Молекулярная физика. Расчетная задача

В. З. Шапиро

Это задание также относится к высокому уровню сложности. Как правило, тематика этого задания «МКТ» и «Термодинамика». Какие-то задачи требуют только формульного решения, какие-то необходимо сопровождать графическими пояснениями термодинамических процессов. В любом случае, теоретический материал полностью соответствует кодификатору элементов содержания и спецификации контрольных измерительных материалов.

1. В вертикальном цилиндре, закрытом лёгким поршнем, находится бензол $(C_{6}H_{6}),$ при температуре кипения При сообщении бензолу некоторого количества теплоты часть его превращается в пар, который при изобарном расширении совершает работу, поднимая поршень. Удельная теплота парообразования бензола $L = 396 cdot 10^{3}$ Дж/кг, а его молярная масса $M = 78cdot 10^{-3}$ кг/моль. Какая часть подводимого к бензолу количества теплоты идёт на увеличение внутренней энергии системы? Объёмом жидкого бензола и трением между поршнем и цилиндром пренебречь.

Необходимая теория:

Первый закон термодинамики

Внутренняя энергия

Дано: «СИ»

$L= 396 cdot 10^{3}$ Дж/кг;

$M = 78cdot 10^{3}$ кг/моль.

Найти: $displaystyle frac{Delta U}{Q}$ — ?

Решение:

Запишем первый закон термодинамики для изобарного процесса:

Выразим из этого равенства изменение внутренней энергии:

Для $displaystyle frac{Delta U}{Q}$ запишем:

$displaystyle frac{Delta U}{Q}=frac{Q - A$ (1).

Работу газа в изобарном процессе можно рассчитать по формуле:

с учетом уравнения Менделеева-Клапейрона получим:
(2).
При совершении работы давление бензола не изменяется, так как поршень в цилиндре легкоподвижный. Давление бензола все время остается равным атмосферному.

При этом
Delta m – масса бензола, превратившегося в газообразное состояние.

Количество теплоты, которое идет на превращение бензола в это состояние можно рассчитать по формуле:

Выражение для работы бензола (2) и количества теплоты (3) подставим в уравнение (1).

$displaystyle frac{Delta U}{Q}=1 - frac{frac{Delta m}{M}RT}{Delta mcdot L} .$

После сокращения на получим искомую формулу:
$displaystyle frac{Delta U}{Q}=1 - frac{RT}{Mcdot L}.$

Подставим численные значения и проведем расчет:

$displaystyle frac{Delta U}{Q}=1 - frac{8,31cdot 353}{78cdot {10}^{-3 }cdot 396cdot {10}^{-3 }}approx 0,905.$

Ответ: 0,905.

Секрет решения. На первый взгляд задача кажется несложной, но в ней «спрятаны» несколько искусственных приемов, до которых додуматься достаточно сложно. Первый прием – выражение $displaystyle frac{Delta U}{Q}=frac{Q-A$ Это математический ход, который сразу подсказывает, что конкретно надо находить в этой задаче.

Второй прием – получение равенства, используя уравнения Менделеева-Клапейрона Здесь надо придерживаться следующих рассуждений: если в левой части уравнения есть переменная величина (в этой задаче Delta V ), то и в правой части должна изменяться какая-то физическая величина (в этой задаче Delta m ). Можно сказать еще проще: если в левой части равенства есть знак дельта « Delta «, то и в правой части он должен обязательно появиться. В крайнем случае, можно «перебрать» все величины из правой части: температура не может изменяться, так как при парообразовании она всегда постоянна; молярная масса также неизменна, потому что речь идет об одном и том же газе; R – табличная величина. Остается только Эти рассуждения помогут понять ситуацию, описанную в задаче и правильно ее решить.

2. Одно и то же постоянное количество одноатомного идеального газа расширяется из одного и того же начального состояния $p_{1}, V_{1}$ до одного и того же конечного объёма $V_{2}$ первый раз по изобаре 1–2, а второй по адиабате 1–3 (см. рисунок). Отношение работы газа в процессе 1–2 к работе газа в процессе 1–3 равно $displaystyle frac{A$ =к=2. Чему равно отношение х количества теплоты $Q_{12},$ полученного газом от нагревателя в ходе процесса 1–2, к модулю изменения внутренней энергии газа $left|U_{3} - U_{1} right|$ в ходе процесса 1–3?

Необходимая теория:

Первый закон термодинамики

Внутренняя энергия

Изопроцессы

Дано:

1–2 р=const;

2–3 Q=const;
$displaystyle frac{A$ =к=2.
Найти: $displaystyle frac{Q_{12}}{left| U_3 - U_1right|}?$

Решение:

Для участка 1–2 применим первый закон термодинамики с учетом изобарного процесса.

$Q_{12}=A$

Работу газа при расширении найдем как площадь прямоугольника под графиком.

Изменение внутренней энергии одноатомного идеального газа запишем в виде формулы:

$displaystyle {Delta U}_{12}=frac{3}{2}vartheta Rleft(T_2 - T_1right) (3).$
Применим уравнение Менделеева-Клапейрона:

Тогда (3) примет вид:

$displaystyle {Delta U}_{12}=frac{3}{2}left(vartheta RT_2 - vartheta RT_1right)=frac{3}{2}left(p_1V_2 - p_1V_1right)=frac{3}{2}p_1left(V_2 - V_1right)$ (4).

Таким образом количество теплоты на участке 12 равно:

$displaystyle Q_{12}=p_1left(V_2 - V_1right)+frac{3}{2}p_1left(V_2 - V_1right)=frac{5}{2}p_1left(V_2 - V_1right)$ (5).

Для участка 1–3 применим первый закон термодинамики с учетом адиабатного процесса.

$Q_{13}=A$ но так как $Q_{13}=0,$ запишем:

0=A или Это выражение означает, что газ на участке 13 совершает работу за счет уменьшения своей внутренней энергии.

Учтем, что по условию $displaystyle frac{A$ =к=2, тогда:

$- displaystyle {Delta U}_{13}=A$

Используя (5) и (6) получим искомую формулу:

$displaystyle frac{Q_{12}}{left| U_3 - U_1right|}=frac{Q_{12}}{| - {Delta U}_{13}|}=frac{frac{5}{2}p_1left(V_2 - V_1right)}{frac{p_1left(V_2 - V_1right)}{2}}=frac{5}{2}:frac{1}{2}=5.$

Ответ: 5.

Секрет решения. Несмотря на громоздкие расчеты и обилие разных индексов в уравнениях, задача является среднего уровня сложности. Надо знать:

— первый закон термодинамики;

— его применение к изопроцессам;

— формулы, выражающие работу газа и его внутреннюю энергию (только для одноатомного идеального газа);

— уметь «читать» графики;

— понимать, что при расширении газ совершает положительную работу, при сжатии – отрицательную работу;

— проводить рассуждения о том, откуда газ берет энергию для совершения работы (за счет своей внутренней энергии или за счет поступления энергии извне);

— указанные пункты описывать соответствующими уравнениями.

Суть любой задачи по физике – описание физических процессов математическими уравнениями, которые надо решить удобным (рациональным) способом.

3. В тепловом двигателе 1 моль одноатомного разряженного газа совершает цикл 1–2–3–4–1, показанный на графике в координатах p–T, где p – давление газа, Т – абсолютная температура. Температуры в точках 2 и 4 равны и превышают температуру в точке 1 в 2 раза. Определите КПД цикла.

Дано:

$T_{2} =T_{4} = 2T_{1}.$

Найти: eta – ?

Решение:

КПД теплового двигателя определяется формулой:

– полезная работа, совершенная газом за цикл, Q – полученное за цикл количество теплоты. Можно графически рассчитать работу, если перерисовать данный цикл в координатах рV. Проведем анализ каждого процесса.

12: V=const, p↑, T↑;

23: p=const, T↑, V↑;

34: V=const, p↓, T↓;

41: p=const, T↓, V↓.

В координатах рV график будет иметь вид:

Работа газа за цикл будет определяться площадью прямоугольника 1-2-3-4.

Учтем, что $T_{2} =T_{4} = 2T_{1}.$

Поэтому (на основании закона Шарля).

$V_3=V_4={2V}_2={2V}_1$ (на основании закона Гей-Люссака).

Таким образом, можно выразить полезную работу через p_1 и V_1.

Газ получает положительное количество теплоты на участках 1–2 и 2–3.
$Q=Q_{12}+Q_{23}.$

Применим к этим участкам первый закон термодинамики.
$Q_{12}=Delta U_{12}+A$

Но работа газа на этом участке равна нулю, так как процесс изохорный.
$displaystyle Q_{12}=Delta U_{12}=frac{3}{2}vartheta Rleft(T_2 - T_1right)=frac{3}{2}(vartheta RT_2 - vartheta RT_1).$

С учетом уравнения Менделеева-Клапейрона и получим:

$displaystyle Q_{12}=frac{3}{2}left(p_2V_2 - p_1V_1right)=frac{3}{2}left(2p_1V_1 - p_1V_1right)=frac{3}{2}p_1V_1=1,5p_1V_1$ (2).

Для участка 23 первый закон термодинамики примет вид:

$Q_{23}=Delta U_{23}+A$
Работа определяется площадью прямоугольника под участком 23.

$displaystyle Delta U_{23}=frac{3}{2} vartheta Rleft(T_3 - T_2right)=frac{3}{2}(vartheta RT_3 - vartheta RT_2)$ (4).

С учетом уравнения Менделеева-Клапейрона (4) примет вид:

$displaystyle Delta U_{23}=frac{3}{2}left(p_3V_3 - p_2V_2right)=frac{3}{2}left(2p_1cdot 2V_1 - 2p_1cdot V_1right)=frac{3}{2}cdot 2p_1cdot V_1=3p_1V_1$ (5).

Таким образом, полученное количество теплоты на участке 23 равно:
$Q_{23}=2p_1V_1+3p_1V_1=5p_1V_1.$

Общее количество теплоты, полученное за цикл:

(6).

Полученные выражения из (1) и (6) подставим в формулу КПД.

Ответ: 15,3%.

Секрет решения. За задачи на определение КПД тепловой машины по графику надо получать максимальные 3 балла. Эти задания сопровождаются большими расчетами, поэтому на первое место надо ставить внимательность их выполнения.

Необходимо выделить следующие моменты в решении:

— определять работу графически можно только в координатах рV;

— если в условии дан график в других координатах, то его надо перечертить в рV;

— поэтапно применять первый закон термодинамики и газовые законы для всех процессов;

— свести в единую формулу полученные данные для расчета КПД.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 30 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.03.2023

Источник