Задачи на алгебру логики егэ - Помощь в подготовке к экзаменам и поступлению

На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи

Содержание:

Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки

2-е задание: «Таблицы истинности»

Уровень сложности

— базовый,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 3 минуты.

Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы

Типичные ошибки и рекомендации по их предотвращению:

«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»

ФГБНУ «Федеральный институт педагогических измерений»

Таблицы истинности и порядок выполнения логических операций

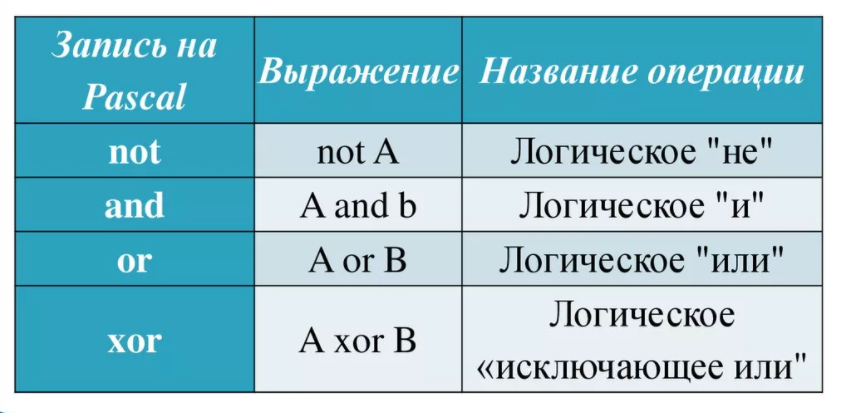
Для логических операций приняты следующие обозначения:

операция	пояснение	в программировании
¬ A, A	не A (отрицание, инверсия)	not(A)
A ∧ B, A ⋅ B	A и B (логическое умножение, конъюнкция)	A and B
A ∨ B, A + B	A или B (логическое сложение, дизъюнкция)	A or B
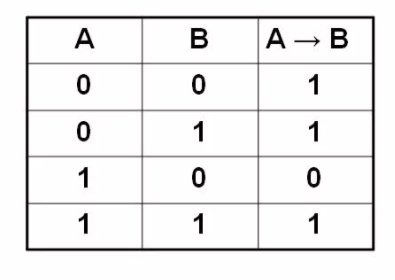
A → B	импликация (следование)	A <= B
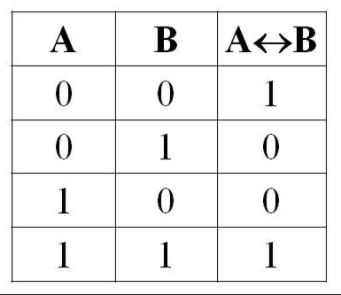
A ↔ B, A ≡ B, A ∼ B	эквиваленция (эквивалентность, равносильность)	A==B (python) A=B(pascal)
A ⊕ B	строгая дизъюнкция	A != B (python) A <> B (pascal)

Егифка ©:

Отрицание (НЕ):

Таблица истинности операции НЕ

Конъюнкция (И):

Таблица истинности операции И (конъюнкция)

Дизъюнкция (ИЛИ):

Таблица истинности операции ИЛИ (дизъюнкция)

Импликация (если…, то…):

Таблица истинности операции Импликация (если…, то…)

Эквивалентность (тогда и только тогда, …):

Таблица истинности операции Эквивалентность (тогда и только тогда, …)

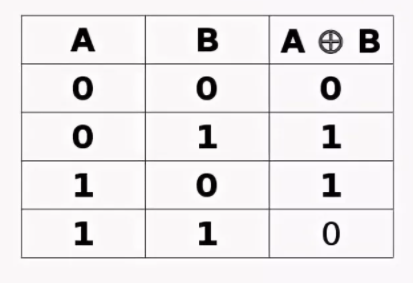
Сложение по модулю 2 (XOR):

A	B	A ⊕ B
0	0	0
0	1	1
1	0	1
1	1	0

Порядок выполнения операций:

если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность

Еще о логических операциях:

логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)

О преобразованиях логических операций читайте здесь.

Егифка ©:

Решение заданий 2 ЕГЭ по информатике

Задание 2_11: Решение 2 задания ЕГЭ по информатике:

Логическая функция F задается выражением

(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

Перем.1	Перем.2	Перем.3	Перем.4	F
???	???	???	???	F
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

✍ Решение:

✎ Способ 1. Электронные таблицы Excel + Логические размышления:

Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 2⁴=16:

Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

Выделите таблицу и отсортируйте строки по столбцу с результатом функции. Для этого в меню Главная => Настраиваемая сортировка =>:

Получили верхние строки таблицы — с которыми сравним исходную таблицу и найдем результат:

Получаем следующий порядок переменных:

xwzy

✎ Способ 2. Программирование:

Язык python:

print('x y z w')
for x in 0, 1:
  for y in 0, 1:
    for z in 0, 1:
      for w in 0, 1:
        F = (not(x) or y or z) and (x or not(z) or not(w))
        if not(F):
          print(x, y, z, w)

В результате будут выведены значения для F=0:

Сопоставив их с исходной таблицей, получим результат:

xwzy

Язык pascalAbc.net:

begin
  writeln('x':7, 'y':7, 'z':7,'w':7);
  for var x:=false to true do
    for var y:=false to true do
      for var z:=false to true do
        for var w:=false to true do
          if not((not x or y or z) and (x or not z or not w)) then
            writeln(x:7, y:7, z:7,w:7);
end.

В результате будут выведены значения для F=0:

      x      y      z      w
  False  False   True   True
  False   True   True   True
   True  False  False  False
   True  False  False   True

Где false = 0, True = 1
Сопоставив их с исходной таблицей, получим результат:

Ответ:

xwzy

✎ Способ 3. Логические размышления:

Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:

(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда:
1. (¬x ∨ y ∨ z) = 1 
И 
2. (x ∨ ¬z ∨ ¬w) = 1

Общая идея дальнейшего решения такова: поскольку внешняя операция — конъюнкция, и результат ее истинен, когда оба сомножителя в скобках будут истинны (=1), то нам необходимо сначала составить все наборы таблицы истинности для обоих сомножителей в скобках. Затем, так как конъюнкция подразумевает пересечение, необходимо сопоставить обе таблицы истинности и выбрать для каждого подходящего набора первого сомножителя подходящий (подходящие) набор (наборы) второго сомножителя. НО! так как у нас в задании известны только наборы для F = 0, то мы сопоставлять будем наборы, которые возвращают ложь. Теперь подробно.
Разобьём исходное выражение на две части и составим таблицу истинности отдельно для двух частей.
Для сомножителя (¬x ∨ y ∨ z):

x	y	z	результат
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Получили ложь в одном наборе, так как дизъюнкция (∨) ложна только тогда, когда ложны все операнды.
Для сомножителя (x ∨ ¬z ∨ ¬w):

x	z	w	результат
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

Соответственно, опять получили ложь в одном наборе, когда ложны все операнды.
Учтем, что нам нужно выбрать и «пересечь» (так как внешняя операция ∧) из всех наборов только те, которые возвращают ложь (так как по заданию известны только строки, где F = 0):

Выпишем только пересеченные наборы:

x	y	z	w	F
0	0	1	1	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0

Сравнив вторую строку заданной таблицы и вторую строку получившейся таблицы, находим, что x находится в первом столбце.

x	y	z	w	F
0	0	1	1	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0

x	???	???	???	F
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

Сравнив первую и четвертую одинаковые строки получившейся таблицы, находим, что y в обоих случаях равен 0. Значит он находится в 4-м столбце.

x	y	z	w	F
0	0	1	1	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0

x	???	???	y	F
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

Сравнив предпоследнюю и последнюю строки получившейся таблицы, там где x = 1, находим, что z в обоих случаях равен 0, тогда как w принимает значение и 1 и 0. Значит z находится в 3-м столбце.

x	y	z	w	F
0	0	1	1	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0

Для w остается второй столбец:

x	w	z	y	F
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	1	0	0	0

Результат: xwzy

🎦 Видеорешение (бескомпьютерный вариант):

📹 здесь
📹 Видеорешение на RuTube здесь

Задание 2_12: Разбор 2 задания ЕГЭ:

Миша заполнял таблицу истинности функции:

(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)

но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:

Перем.1	Перем.2	Перем.3	Перем.4	F
???	???	???	???	F
1	1			0
1		0		0
	1	1	0	0

Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.

Подобные задания для тренировки

✍ Решение:

✎ Способ 1. Логические размышления (бескомпьютерный вариант):

Решим задание методом построения полной таблицы истинности.
Посчитаем общее количество строк в таблице истинности и построим ее:

4 переменных -> 2⁴ = 16 строк

Для начала упростим выражение и выделим в нем две основные части относительно внешней операции (операция, которая выполняется последней).

(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
1. Избавимся от импликации:
¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w)
2. Внесем знак отрицания в скобки (закон Де Моргана):
(z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0
   ^{1 часть = 0     2 часть = 0}

* Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.

Разбили исходное выражение на две части, теперь добавим столбцы для двух частей в таблицу истинности:

Поясним: в первой части внешняя операция — дизъюнкция (ложна, когда оба операнда ложны). Во второй части внешняя операция — конъюнкция — ложна во всех случаях кроме того, когда оба операнда истинны:

(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0

¬y ∧ ¬w = 0 когда:
1. ¬y = 0  ¬w = 0
2. ¬y = 1  ¬w = 0
3. ¬y = 0  ¬w = 1

В результирующей таблице истинности получили только три набора значений переменных при которых выражение возвратит ложь.

x	y	w	z	F
0	1	0	0	0
0	1	1	0	0
1	0	1	0	0

Сравнив их с исходной таблицей истинности, имеем:

y	w	x	z	F
1	1	0	0	0
1	0	0	0	0
0	1	1	0	0

Таким образом, ответ: ywxz

Результат: ywxz

✎ Способ 2. Программирование:

Язык PascalAbc.net:

begin
  writeln('x':7, 'y':7, 'z':7,'w':7);
  for var x:=false to true do
    for var y:=false to true do
      for var z:=false to true do
        for var w:=false to true do
          if not((not z and (x xor y)) <= not(y or w)) then
            writeln(x:7, y:7, z:7,w:7);
end.

В результате будут выведены значения для F=0:

      x      y      z      w
  False   True  False  False
  False   True  False   True
   True  False  False   True

Где false = 0, True = 1

Сопоставив их с исходной таблицей, получим результат: ywxz

Язык Python:

print ('x y z w')
for x in 0,1:
    for y in 0,1:
        for z in 0,1:
            for w in 0,1:
                F=(not z and not(x==y))<=(not(y or w))
                if not F:
                    print (x,y,z,w)

В результате будут выведены значения для F=0:

Сопоставив их с исходной таблицей, получим результат:

Результат: ywxz

🎦 Доступно видео решения этого задания (бескомпьютерный вариант):

📹 здесь
📹 Видеорешение на RuTube здесь

🎦 Видео (решение 2 ЕГЭ в Excel):

📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)

Задание 2_10: Решение 2 задания ЕГЭ по информатике:

Логическая функция F задается выражением

¬a ∧ b ∧ (c ∨ ¬d)

Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.

Перем.1	Перем.2	Перем.3	Перем.4	F
???	???	???	???	F
0	1	0	0	1
1	1	0	0	1
1	1	0	1	1

В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.

✍ Решение:

🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:

📹 здесь
📹 Видеорешение на RuTube здесь

Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:

Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.

Перем. 1	Перем. 2	Перем. 3	Перем. 4	F
???	???	???	???	F
1	0	0	0	0
1	1	0	0	0
1	1	1	0	0

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Подобные задания для тренировки

✍ Решение:

✎ Логические размышления (бескомпьютерный вариант):

Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:

¬x ∨ y ∨ (¬z ∧ w)

Вспомним таб. ист-ти для дизъюнкции (логическое сложение):

x1	x2	F
0	0	0
0	1	1
1	0	1
1	1	1

Чтобы исходное выражение было истинным, нужно, чтобы хотя бы один из операндов равнялся единице. Т.е. нельзя наверняка сказать, где будет 1, а где 0 (¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).
Функция же ложна только в одном случае, — когда все операнды ложны. Поэтому будем искать по признаку лжи.
В исходной таблице истинности во всех строках функция ложна. Чтобы понять в каком столбце должна находиться та или иная переменная, возьмем за основу строку, в которой только одна единица или только один нуль.
Строка №1: в ней одна единица — первый столбец. В исходной формуле, чтобы функция была ложна, необходимо, чтобы ¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x.

Перем. 1	Перем. 2	Перем. 3	Перем. 4	F
x	???	???	???	F
1	0	0	0	0

Строка №3: в ней один нуль — четвертый столбец. В исходной формуле, чтобы функция была ложна, необходимо, чтобы y = 0. Значит четвертый столбец соответствует переменной y.

Перем. 1	Перем. 2	Перем. 3	Перем. 4	F
x	???	???	y	F
1	1	1	0	0

Строка №2: в ней второй столбец равен единице, а третий — нулю. В исходном выражении ¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w.

x	z	w	y	F
1	0	0	0	0
1	1	0	0	0
1	1	1	0	0

Результат: xzwy

✎ Способ 2. Программирование:
Язык pascalABC.NET:

begin
  writeln('x  ','y  ','z  ','w  ');
  for var x:=false to true do
    for var y:=false to true do
      for var z:=false to true do
        for var w:=false to true do
          if not(not x or y or(not z and w)) then
            writeln(x:7,y:7,z:7,w:7);
end.

🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:

📹 здесь
📹 Видеорешение на RuTube здесь

Задание 2_13: Разбор досрочного егэ по информатике 2019

Логическая функция F задаётся выражением

(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.

Перем.1	Перем.2	Перем.3	Перем.4	F
???	???	???	???	F
0			0	0
0	1	0	1	0
	1	0		0

✍ Решение:

🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь

Задания для тренировки

Задание 2_2: Задание 2 ЕГЭ по информатике:

Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.

Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?

Подобные задания для тренировки

✍ Решение:

Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 2⁵=32, т.е. 32 строки.
Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:

№	F	G	F ∨ G
1	0	0	0
2	0	1	1
…	…	…	1
32	…	…	1

Соответственно, истинными будут все остальные строки:

32 - 1 = 31

Результат: 31

Подробное объяснение данного задания смотрите на видео:

📹 здесь

Задание 2_6: Решение 2 задания ЕГЭ по информатике:

Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.

Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?

✍ Решение:

Полная таблица истинности для каждого из выражений A и B состоит из 2⁷ = 128 строк.
В четырех из них результат равен единице, значит в остальных — 0.
A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:

A	B
1	0
1	0
1	0
1	0
0	1
0	1
0	1
0	1
0	0
…	…

Итого получаем 8 строк.
Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.

Результат: 8

Задание 2_7: Решение 2 задания ЕГЭ по информатике:

Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.

Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?

✍ Решение:

Полная таблица истинности для каждого из выражений A и B состоит из 2⁸ = 256 строк.
В шести из них результат равен единице, значит в остальных — 0.

A ∧ B ложно в том случае, когда:

A ∧ B = 0 если:

1. A = 0, B = 1 
2. B = 0, A = 1
3. A = 0 и B = 0

Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0

A	B	F
1	0	0
1	0	0
1	0	0
1	0	0
0	1	0
0	1	0
0	1	0
0	1	0
0	0	0
…	…	…

Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0

Результат: 256

Задание 2_4: 2 задание:

Дан фрагмент таблицы истинности выражения F.

x1	x2	x3	x4	x5	x6	x7	F
1	0	0	1	1	1	1	0
0	1	0	0	1	0	1	1
0	1	0	1	1	0	1	0

Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7

✍ Решение:

В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:

Но проверим на всякий случай остальные.
Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:

Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:

Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:

Таким образом, ответ равен 1.

Результат: 1

Решение 2 задания ГВЭ по информатике смотрите на видео:

📹 здесь

Задание 2_8: Решение 2 задания ЕГЭ по информатике:

Дано логическое выражение, зависящее от 5 логических переменных:

(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)

Сколько существует различных наборов значений переменных, при которых выражение истинно?

1) 0
2) 30
3) 31
4) 32

Подобные задания для тренировки

✍ Решение:

Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 2⁵ = 32 строк.
Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
Найдем сколько нулей существует для таб. истинности:

Теперь рассмотрим каждый случай отдельно:

1 случай. 0 0 : A = 0 и B = 0, то есть:

¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.

Обратим внимание, что во вторых скобках везде стоит инверсия переменных, которые находятся в первых скобках. Таким образом, это невозможно, так как дизъюнкция равна нулю, когда все операнды равны нулю. А если в первых скобках все 0, то из-за инверсий во вторых скобках все 1. То есть этот случай нам не подходит.
2 случай. 0 1 : нам он подходит, так как если первая скобка возвратит 0, то вторая вернет 1.
3 случай. 1 0 : нам он подходит, так как если вторая скобка возвратит 0, то первая вернет 1.
Итого получаем два случая, когда исходное выражение вернет 0, т.е. две строки таблицы истинности.
Тогда получим количество строк, с результатом равным 1:

32 - 2 = 30, что соответствует номеру 2

Результат: 2

Подробное решение задания смотрите в видеоуроке:

📹 здесь

Задание 2_5: Решение 2 задания ЕГЭ по информатике:

Дан фрагмент таблицы истинности для выражения F:

x1	x2	x3	x4	x5	x6	F
0	0	1	1	0	0	1
0	0	0	0	1	1	1
1	0	1	0	1	1	1
0	1	1	1	0	1	0

Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.

Подобные задания для тренировки

✍ Решение:

Полная таблица истинности будет иметь 2⁶ = 64 строк (т.к. 6 переменных).
4 из них нам известны: в них x3 два раза не совпадает с F.
Неизвестных строк:

 
64 - 4 = 60

В неизвестных x3 может не совпадать с F, кроме того, в двух известных x3 не совпадает с F. Соответственно максимально возможное число строк с несовпадающими x3 и F, будет:

60 + 2 = 62

Результат: 62

Задание 2_9: Решение 2 задания ЕГЭ по информатике:

Дан фрагмент таблицы истинности для выражения F:

x1	x2	x3	x4	x5	x6	x7	F
			0		0		0
			0			0	1
1			1				1

Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7

✍ Решение:

Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).

1 пункт:

(((x1 ∧ (x2 → x3) ∧  ¬x4) ∧ x5) ∧ x6)  ∧ ¬x7

Внешняя операция — конъюнкция. Ее проще проверять по строке, в которой F = 1 (значит все сомножители должны быть равны 1).
Возьмем 3-ю строку, в ней x4=1. В нашем выражении х4 с отрицанием, т.е. = 0. Для конъюнкции, когда хоть один из сомножителей равен нулю, выражение вернет в результате 0, а у нас в строке 1. Т.е. этот пункт не подходит:

2 пункт:

(((x1 ∨ (¬x2 → x3) ∨  ¬x4) ∨ ¬x5) ∨ x6)  ∨ ¬x7

Последняя выполняющаяся операция (внешняя) — дизъюнкция. Ее легче проверять по строке, в которой F = 0 (значит все слагаемые должны быть равны 0).
Смотрим по первой строке: х4 = 0, в рассматриваемом пункте он с отрицанием, т.е. = 1. Соответственно все выражение вернет единицу, а в таблице в строке 0. Т.е. этот пункт не подходит:

3 пункт:

(((¬x1 ∧ (x2 → ¬x3) ∧  x4) ∧ ¬x5) ∧ x6) ∧ x7

Последняя операция — конъюнкция. Ее проще проверять по строке, в которой F = 1 (значит все сомножители должны быть равны 1).
Возьмем 2-ю строку: в ней х7 = 0, в рассматриваем пункте х7 без отрицания, т.е. так и остается равным нулю. При умножении выражение вернет в результате 0. В таблице — 1. Т.е. пункт тоже не подходит:

Единственным подходящим вариантом остался пункт под номером 4 (на всякий случай всегда стоит проверить и его).

Результат: 4

В видеоуроке рассмотрено подробное решение 2 задания:

📹 здесь

Задание 2_1: Задание 2 ЕГЭ по информатике:

Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

№	Перем. 1	Перем. 2	Перем. 3	F
	???	???	???	F
1	0	0	0	0
2	0	0	1	0
3	0	1	0	1
4	0	1	1	1
5	1	0	0	0
6	1	0	1	0
7	1	1	0	0
8	1	1	1	1

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.

✍ Решение:

Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:

(y → x) ∧ (y → z) ∧ z

Конъюнкцию легче рассматривать по тем строкам таб. ист-ти, в которых F = 1, т.е. №3, №4, и №8
Поскольку для конъюнкции функция истинна только тогда, когда все переменные истинны, то необходимо чтобы отдельно каждая скобка была истинна ((y → x) = 1 и (y → z)=1) и переменная z тоже была истинной (=1)

(y → x) ∧ (y → z) ∧ z = 1
   если: 
1. (y → x) = 1
2. (y → z) = 1
3. z = 1

Поскольку с выражениями в скобках сложней работать, определим сначала какому столбцу соответствует z. Для этого выберем строку (№3), где F = 1, а в остальных ячейках только одна единица, остальные — нули.

№	Перем. 1	Перем. 2	Перем. 3	F
3	0	1	0	1

Таким образом, делаем вывод, что z находится во втором столбце (отсчет ведем слева):

№	Перем. 1	Перем. 2	Перем. 3	F
_	???	z	???	F

Дальше нам необходимо рассмотреть две скобки, в которых находится операция импликации: (y → x) и (y → z). Обе эти скобки должны возвращать истину (=1). В таб. истинности для импликации, функция возвращает в результате 1 тогда, когда:
вторая переменная (заключение) равна 1 (первая при этом может быть любой),
вторая переменная (заключение) равна 0, а первая обязательно должна быть равна тоже 0.
Рассмотрим скобку (y → x) и строку 4 таблицы:

№	Перем. 1	z	Перем. 3	F
4	0	1	1	1

Для этой строки только y может быть равен 0, т.к. если x = 0, тогда y=1, и скобка в результате возвратит ложь (1 → 0 = 0). Соответственно, y находится в первом столбце. А x значит должен стоять в третьем:

Результат: yzx

Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:

📹 здесь

Источник

Муниципальное общеобразовательное учреждение

«Семигорская средняя общеобразовательная школа»

Проект по математике

«Решение логических задач

для подготовки к ЕГЭ»

Выполнил работу ученик 10 класса

Муранцев Егор Александрович

Руководитель Кухарчук Людмила Владимировна

Семигорск, 2022

СОДЕРЖАНИЕ

Введение

Основная часть

Что такое «логика», «логическая задача».

Основные Методы решения логических задач:

1.Метод рассуждения;

2. Метод таблиц;

3. Метод алгебры высказываний;

4. Метод решения с помощью полупрямой;

5. Метод решения с помощью кругов Эйлера;

6. Задачи на смекалку.

Заключение

Список литературы

Паспорт проекта

Название проекта: Решение логических задач для подготовки к ЕГЭ

Описание проблемы: Не все школьники умеют решать логические задачи, электронный сборник помог бы разобраться в решении часто встречающихся задач из сборников ЕГЭ по математике базового уровня.

Проблемные вопросы: Как успешно научиться решать логические задачи, при подготовке к ЕГЭ по математике?

Аннотация: Наша жизнь — это постоянное решение больших и маленьких логических задач или проблем. Жуть будет сложно без умения правильно, логически рассуждать, поступать разумно.

Довольно часто мы, сами того не замечая, решаем логические задачи. Логические задачи развивают умение делать анализ, обобщать данные, искать различные пути решения, формировать стратегию, проверять данные на достоверность. Логические задачи сейчас очень популярны и они должны входить в наше развитие и образование с самых ранних лет.

Чтобы успешно логические задачи, нужно уметь выделять их общие признаки, подмечать закономерности, выдвигать гипотезы, проверять их, строить цепочки рассуждений, делать выводы. Знание различных методов решения логических задач поможет развить логическое мышление, успешно подготовиться к ЕГЭ по математике базового уровня.

Характеристика проекта

Признаки	Характеристика проекта
Количество учащихся	Индивидуальный
Привязка к учебным дисциплинам	Монопредметный — математика Межпредметный — информатика, геометрия
Продолжительность	Краткосрочный
Тип проекта	Информационный
Характер контактов	Внутриклассный
Ценностно — ориентированные признаки	Математический проект
Возрастная категория	Учащиеся 10-11 классов

Цель проекта: Научиться успешно решать логические задачи.

Задачи проекта:

1) изучить литературу по данной теме, познакомиться с понятием «логика», «логическая задача»;

2) изучить основные методы решения логических задач;

3) создать электронный сборник логических задач с решениями для учащихся 10-11 классов для подготовки к ЕГЭ по математике базового уровня.

Планируемые результаты: овладение способами решения логических задач базового уровня, успешная сдача ЕГЭ по математике.

Продукт проекта: Создание электронного сборника логических задач с решениями для учащихся 10-11 классов для подготовки к ЕГЭ по математике базового уровня.

Необходимое оборудование: компьютер, мультимедиапроектор.

ВВЕДЕНИЕ

При подготовке к ЕГЭ по математике умения решать логические задачи очень важно, это возможность получить дополнительные баллы, найти подход к решению задач через логику. Логическое мышление и знание основ математики поможет справиться со многими заданиями из ЕГЭ по математике.

Логические задачи отличаются от других математических задач тем, что не имеют определенного алгоритма действий для отыскания их решения, не задаются формулами, не требуют сложных вычислений, а требуют умения логически рассуждать.

Все мы когда-то пытались решать логические задачи, но сталкивались с этим редко, так как на уроках математики эта тема затрагивается мало. Хотя это очень увлекательно и интересно.

При составлении школьных математических олимпиад используют много различных задач, где надо применять логическое мышление. Умение решать логические задачи часто встречается и в разных жизненных ситуациях, например на отдыхе, в спорте, да и просто в разговоре с собеседником.

Проблема: Как успешно научиться решать логические задачи, при подготовке к ЕГЭ по математике? Не все школьники умеют решать логические задачи, электронный сборник помог бы разобраться в решении часто встречающихся задач из сборников ЕГЭ по математике базового уровня.

Актуальность: Наша жизнь — это постоянное решение больших и маленьких логических задач или проблем. Жить будет сложно без умения правильно, логически рассуждать, поступать разумно.

Гипотеза: Чтобы успешно решать логические задачи, нужно уметь выделять их общие признаки, подмечать закономерности, выдвигать гипотезы, проверять их, строить цепочки рассуждений, делать выводы. Знание различных методов решения логических задач поможет развить логическое мышление, успешно подготовиться к ЕГЭ по математике базового уровня.

Цель: Научиться успешно решать логические задачи.

Задачи:

1) изучить литературу по данной теме, познакомиться с понятием «логика», «логическая задача»;

2) изучить основные методы решения логических задач;

Методы исследования:

1. Поисковый метод (сбор и изучение информации).

2. Обобщение теоретического материала.

Продукт проекта: электронный сборник логических задач с решениями для учащихся 10-11 классов для подготовки к ЕГЭ по математике базового уровня.

ОСНОВНАЯ ЧАСТЬ

Что такое «логика», «логическая задача»

Ло́гика — «наука о правильном мышлении», «способность к рассуждению» от др.-греч. λόγος — «логос», «рассуждение», «мысль», «разум», «смысл») — нормативная наука о законах, формах и приёмах интеллектуальной деятельности.

Логика, как наука, возникла в недрах древнегреческой философии. Далее в течение почти двух с половиной тысячелетий до второй половины XIX века логика изучалась как часть философии и риторики. Начало современной логики, построенной в форме исчисления, положил Г. Фреге в сочинении «Begriffsschrift» .

Основная сущность логики, её цель и функция всегда оставались неизменными: исследование того, как из одних утверждений можно выводить другие. При этом рассматриваются только такие выводы, которые зависят только от способа связи и строения входящих в вывод утверждений, а не их конкретного содержания. Изучая, как одни мысли следуют из других, логика выявляет наиболее общие формальные условия правильного мышления. При этом сфера конкретных интересов логики в выявлении условий формального вывода на протяжении её истории существенно менялась.

Что же представляют собой логические задачи? Логические задачи или, как их еще иногда называют, нечисловые, представляют собой текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений задачи может выступать с различной истинностной оценкой (быть истинной или ложной). А любые вычисления и построения играют вспомогательную роль или вообще отсутствуют. То есть – логические задачи отличаются от обычных тем, что в них чаще не требуется умение вычислять, а требуется умение рассуждать.

Чтобы научиться решать типовые логические задачи, простые и нестандартные математические задачи, важно знать основные приемы и методы их решения. Ведь решить одну и ту же задачу и прийти к правильному ответу во многих случаях можно разными способами.

Существуют разные типы логических задач и разные способы их решения: Каждый из этих способов обладает своими достоинствами.

Основные Методы решения логических задач

1. Метод рассуждения.

Самый примитивный способ решения простых логических задач — метод рассуждения. Его суть заключается в последовательных рассуждениях с использованием всех известных условий задачи. Таким образом, мы постепенно приходим к выводу, который и будет являться ответом задачи.

Например:

1.1 В корзине лежат 30 грибов – рыжиков и груздей. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов – хотя бы один груздь. Сколько рыжиков и сколько груздей в корзине?

Решение:

Так как среди любых 12 грибов хотя бы один – рыжик, то груздей не больше 11. Так как среди любых 20 грибов хотя бы один – груздь, то рыжиков не больше 19. А так как всего в корзине 30 грибов, то груздей ровно 11, а рыжиков ровно 19.

1.2. Взяли несколько досок и распилили их (за один распил можно распилить только одну доску). Всего сделали 11 поперечных распилов, в итоге получилось 16 кусков. Сколько досок взяли?

Решение.

Каждый поперечный распил добавляет один кусок к уже имеющимся, следовательно, изначально было 16 − 11 =  5 досок.

1.3. Восемь столбов соединены между собой проводами так, что от каждого столба отходит ровно 5 проводов. Сколько всего проводов протянуто между этими восемью столбами?

Решение.

Если от каждых из 8 столбов отходит по 5 проводов, то между каждыми парами таких столбов ровно 5 проводов. Всего имеем 8:2 = 4 пар и

4∙5 = 20 проводов

2. Метод таблиц.

Суть метода состоит в оформлении условий задачи и полученных результатов логических рассуждений в виде таблицы. В зависимости от того, является высказывание истинным или ложным, соответствующие ячейки таблицы заполняются знаками + и -.

2.1 В одном дворе живут четыре друга. Вадим и шофёр старше Сергея; Николай и слесарь занимаются боксом; электрик – младший из друзей; по вечерам Антон и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей.

	Вадим	Сергей	Николай	Антон
Шофер	0	0	0	1
Слесарь	0	1	0	0
Токарь	1	0	0	0
Электрик	0	0	1	0

2.2 В семье четверо детей. Им 5,8,13 и 15 лет. Их зовут Аня, Боря, Вера и Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори и сумма лет Ани и Веры делится на три?

	Аня	Боря	Вера	Галя
5	0	0	1	0
8	0	1	0	0
13	1	0	0	0
15	0	0	0	1

2.3 Коля, Боря, Вова и Юра заняли первые четыре места в соревновании, причём никакие два мальчика не делили между собой какие-нибудь места. На вопрос, кто какое место занял, Коля ответил: «Ни первое, ни четвёртое»; Борис сказал : «Второе», а Вова заметил, что он был не последним. Какое место занял каждый из мальчиков?

	Коля	Боря	Вова	Юра
Первый	0	0	1	0
Второй	0	1	0	0
Третий	1	0	0	0
Последний	0	0	0	1

3. Метод алгебры высказываний.

Алгебра высказываний изучает способы построения и закономерности высказываний. Но её цель ― не всестороннее изучение, а их истинностная оценка. Именно это и является определяющим свойством высказывания. Оно не может быть одновременно и истинным, и ложным. Пусть имеется несколько простейших высказываний, о каждом из которых точно известно, истинно оно или ложно. Причем имеются как истинные высказывания, так и ложные.

3.1 Когда учитель физики Николай Дмитриевич ведёт урок, он обязательно отключает свой телефон. Выберите утверждения, которые верны при приведённом условии.

1) Если телефон Николая Дмитриевича включён, значит, он не ведёт урок.

2) Если телефон Николая Дмитриевича включён, значит, он ведёт урок.

3) Если Николай Дмитриевич проводит на уроке лабораторную работу по физике, значит, его телефон выключен.

4) Если Николай Дмитриевич ведёт урок физики, значит, его телефон включён.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Решение.

1) Утверждение следует из приведённых данных.

2) Утверждение не следует из приведённых данных, оно противоречит поставленному условию.

3) Утверждение следует, так как лабораторная работа это тоже урок, следовательно, телефон Николая Дмитриевича обязательно будет выключен.

4) Утверждение не следует из приведённых данных, так как при проведении урока Николай Дмитриевич обязательно выключает телефон.

Ответ: 13

3.2 Двадцать выпускников одного из 11 классов сдавали ЕГЭ по математике. Самый низкий балл, полученный среди них, был равен 36, а самый высокий — 75.

Выберите утверждения, которые следуют из данной информации.

1) Среди этих выпускников есть человек, который получил 75 баллов за ЕГЭ по математике.

2) Среди этих выпускников есть два человека с равными баллами за ЕГЭ по математике.

3) Среди этих выпускников нет человека, получившего 72 балла за ЕГЭ по математике.

4) Баллы за ЕГЭ по математике любого из этих двадцати человек не ниже 35.

В ответе запишите номера выбранных утверждений без пробелов, запятых и

других дополнительных символов.

Решение.

1) Это так, иначе это не был бы самый высокий балл в классе. 2) Учеников 20, а различных результатов за ЕГЭ, которые могли бы быть Таким образом, необязательно у каких-то двух учеников есть одинаковый балл.

3) Такой человек мог быть, нам об этом ничего не известно.

4) Баллы всех двадцати учеников не меньше 36, значит, они также не меньше 35.

Ответ: 14

3.3 Некоторые сотрудники фирмы летом 2021 года отдыхали на даче, а некоторые — на море. Все сотрудники, которые не отдыхали на море, отдыхали на даче.

Выберите утверждения, которые верны при указанных условиях.

1) Сотрудник этой фирмы, который летом 2021 года не отдыхал на даче, не отдыхал и на море.

2) Каждый сотрудник этой фирмы отдыхал летом 2021 года или на даче, или на море, или и там, и там.

3) Если Галина летом 2021 года не отдыхала ни на даче, ни на море, то она является сотрудником этой фирмы.

4) Если сотрудник этой фирмы летом 2021 года не отдыхал на даче, то он отдыхал на море.

Решение.

1) Нет, так как если сотрудник отдыхал на море, то он обязательно отдыхал и на даче.

2) Да, так как все сотрудники, не отдыхавшие на море, отдыхали на даче, то есть, нет таких, которые нигде не отдыхали.

3) Да, так как все сотрудники фирмы отдыхали на даче, а некоторые из них отдыхали еще и на море.

4) Нет, см. п. 1.

Ответ: 23

4. Метод решения с помощью полупрямой

Если в задаче имеется множество объектов и требуется установить взаимоотношение между элементами этого множества, то задачу можно решать на полупрямой.

4.1. Виктор старше Дениса, но младше Егора. Андрей не старше Виктора. Выберете утверждения, которые верны при указанных условиях.

Егор самый старший из указанных четверых человек.

Андрей и Егор одного возраста.

Виктор и Денис одного возраста.

Денис младше Егора.

Решение. Построим модель описанной ситуации, отмечая на прямой правее старшего мальчика.

Ответ: 14.

4.2. В очереди в школьный буфет стоят Вика, Соня, Боря, Денис и Алла. Вика стоит впереди Сони, но после Аллы; Боря и Алла не стоят рядом; Денис не находится рядом ни с Аллой, ни с Викой, ни с Борей. В каком порядке стоят ребята? [3]

Решение. Построим модель описанной ситуации, считая обычный луч «линией времени».

а ) Вика стоит впереди Сони, но после Аллы

б) Денис не находится рядом ни с Аллой, ни с Викой, значит он – крайний слева

в) Боря и Алла не стоят рядом, Борис не находится рядом с Денисом, значит место Бориса – после Вики

Ответ: Алла, Вика, Борис, Соня, Денис.

4.3. При взвешивании животных в зоопарке выяснилось, что жираф тяжелее верблюда, верблюд тяжелее тигра, а леопард легче верблюда. Выберите утверждения, которые верны при указанных условиях.

1) Леопард тяжелее верблюда

2) Жираф тяжелее леопарда.

3) Жираф легче тигра.

4) Жираф самый тяжелый из всех этих животных.

Решение. Отметим данные задачи на полупрямой, причем тех животных, которые тяжелее, будем отмечать правее.

ЖЖ

ВЛ

ЛЛ

Ответ: 24

5. Метод решения с помощью кругов Эйлера

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным. Ценность задач, решаемых с помощью кругов Эйлера, состоит в том, что решения задач с громоздкими условиями и со многими данными, просты и не вызывают особых умозаключений. Эйлер наглядно изображал операции над множествами при помощи особых чертежей, называемых кругами Эйлера. Для этого множества, сколько бы элементов они не содержали, представляют при помощи кругов, овалов или любых других геометрических фигур.

Данный метод позволяет графически решать математические задачи на основе применения теории множеств.

5.1. В фирме N работает 50 сотрудников, из них 40 человек знают английский язык, а 20 -немецкий. Выберете утверждения, которые верны при указанных условиях.

1).В фирме N хотя бы три сотрудника знают и английский, и немецкий языки.

2).В этой фирме нет ни одного сотрудника, знающего и английский, и немецкий языки.

3).Если сотрудник этой фирмы знает английский язык, то он знает и немецкий

4).Не более 20 сотрудников этой фирмы знают и английский, и немецкий языки.

Р ешение: построим диаграмму, используя условия. Получается, что английский и немецкий языки знают 10 человек.

Ответ: 14.

5 .2. В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение. Изобразим множества следующим образом:

70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом занимаются 5 человек.

Ответ. 5 человек занимаются только спортом.

5.3. В 7-А учится 38 человек. Ученики увлекаются разными спортивными играми: 16 – баскетболом, 17 – хоккеем, 18 – футболом. Одновременно баскетбол и хоккей любят 4 человека, баскетбол и футбол – 3, хоккей и футбол – 5, а 3 ученика не интересуются спортом. Есть ли ученики, увлекающиеся всеми спортивными играми?

Решение. Все ученики класса – наибольшая окружность. Круг «Б» — баскетболисты, «Х» — хоккеисты, «Ф» — футболисты, «x» — универсальные спортсмены. Трое неспортивных учеников просто находятся в общем круге. Баскетболисты, входящие в множество «Б», но не входящие в зоны пересечения со множествами «Х» и «Ф»:16 – (4 + x + 3) = 9 – x

П о аналогии, находим количество хоккеистов:17 – (4 + x + 5) = 8 – x.

Футболисты: 18 – (3 + x + 5) = 10 – x.

Чтобы определить значение x, нужно суммировать множества учеников.

3 + (9 – x) + (8 – x) + (10 – x) + 3 + 4 + 5 + x = 38;

42 – 2 x = 38;

x = 2.

Соответственно, Б = 7, Ф = 8, Х = 6.

Ответ: 2 человека увлекаются всеми спортивными играми.
6. Задачи на смекалку

Существуют такие задания, решение которых зависит только от здравого смысла, сообразительности и смекалки того, кому они заданы. Решение задач на смекалку помогает развивать нестандартность мышления и внимание.
Так как же их решать?

Во-первых – внимательно прочитайте задание. Проанализируйте каждое условие и утверждение – верны они или нет. Часто ответ задачи на смекалку лежит на поверхности и становится очевиден, если найдено несоответствие условия задачи с реальностью.
Во-вторых – будьте внимательны, когда визуально представляете картинку, описанную в задаче. Задание зачастую нарочно запутывает отгадывающего.
В-третьих – не сдерживайте свое мышление в определенных рамках, отпустите его. Именно нестандартность мышления часто помогает найти выход в запутанной ситуации.
6.1. Квартира Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
Решение: 462 : 7 = 66 квартир, на каждом из 7 этажей в подъезде не меньше 9 квартир. Пусть на каждой лестничной площадке по 9 квартир. Тогда в первых семи подъездах всего 9 · 7 · 7 = 441 квартира, и квартира 462 окажется в восьмом подъезде, что противоречит условию. Пусть на каждой площадке по 10 квартир. Тогда в первых семи подъездах 10 · 7 · 7 = 490 квартир, а в первых шести — 420. Следовательно, квартира 462 находится в седьмом подъезде. Она в нем 42-ая по счету, поскольку на этаже по 10 квартир, она расположена на пятом этаже. Если бы на каждой площадке было по 11 квартир, то в первых шести подъездах оказалось бы 11 · 7 · 6 = 462 квартиры, то есть 462 квартира в шестом подъезде, что противоречит условию. Тем самым, Саша живёт на пятом этаже.
6.2 Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 2 м. Высота дерева 14 м. За сколько дней улитка доползёт от основания до вершины дерева?

Решение: Улитка за день поднимается вверх на 4 м, а опускается вниз на 2 м. Итого за сутки она продвигается на 2 м. За 5 суток она поднимется на 10 м. За 6 день улитка поднимется ещё на 4 м и окажется на высоте 14 м, то есть она достигнет вершины дерева.

Ответ: 6.

6.3 Каждую секунду бактерия делится на две новые бактерии. Известно, что весь объём одного стакана бактерии заполняют за 1 час. За сколько секунд стакан будет заполнен бактериями наполовину?

Решение: Заметим, что каждую секунду в стакане становится в два раза больше бактерий. То есть если в какой-то момент бактериями заполнена половина стакана, то через секунду будет заполнен весь стакан. Таким образом, полстакана будет заполнено через 59 минут и 59 секунд то есть через 3599 секунд.

Ответ: 3599 секунд

ЗАКЛЮЧЕНИЕ

Таким образом, на основе изученного материала можно с уверенностью сделать вывод о том, что умение решать логические задачи является необходимым в повседневной жизни для того, чтобы справляться не только с учебой, но и с жизненными ситуациями. Чтобы успешно решать логические задачи, нужно уметь выделять их общие признаки, подмечать закономерности, выдвигать гипотезы, проверять их, строить цепочки рассуждений, делать выводы. Знание различных методов решения логических задач поможет развить логическое мышление, успешно подготовиться к ЕГЭ по математике базового уровня, эту гипотезу полностью подтверждаю. Были изучены материалы учебно-методической литературы, материалы из интернета. Решено множество задач.

Моя работа направлена на изучение способов решения логических задач, встречающимся в КИМах ЕГЭ базового уровня по математике, итогом работы является созданный электронный сборник логических задач с разборами решений.

Чтобы успешно их решать, нужно знать способы решения, иметь развитое логическое мышление, обладать графической культурой. Задачи на логическое мышление, как правило, требуют не столько большого объема знаний, сколько умения эти знания применить. С уверенностью могу сказать, что логические задачи на едином государственном экзамене по математике базового уровня решу верно. Моя гипотеза подтвердилась.

СПИСОК ЛИТЕРАТУРЫ:

Интернет источники

1. https://ru.wikipedia.org/wiki/

2. https://pandia.ru/text/80/398/205.php

3. https:// infourok.ru/zadachi-na-smekalku-podgotovka-k-ege-bazoviy-uroven-2105271.html

4. https://www.kakprosto.ru/kak-38069-kak-reshit-zadachu-na-smekalku

5. http://xn—-etbbfc5ae1a3k.xn--p1ai/?base=zadachi-na-smekalku

6.https://www.google.com/search?q=%D1%80%D0%B5%D1%88%D1%83+%D0%B5%D0%B3%D1%8D+2022

7. ЕГЭ 2022. Математика. Базовый уровень: типовые экзаменационные варианты: 30 вариантов / под ред. И.В. Ященко. – М.: Издательство «Национальное образование», 2022 – 190 с.

8. ЕГЭ 2022. Математика. Базовый уровень: типовые экзаменационные варианты: 12 вариантов / под ред. И.В. Ященко. – М.: Издательство «Национальное образование», 2022 – 72 с.

9. ЕГЭ 2022. Математика. Базовый уровень: типовые экзаменационные варианты: 50 вариантов / под ред. И.В. Ященко. – М.: Издательство «Национальное образование», 2022 – 350 с.

Автор материала: Е. Муранцев (10 класс)

Источник

ЕГЭ по информатике выбирают будущие работники ИТ-сферы. Но для сдачи экзамена нужно не только уметь программировать. Многие задачи связаны с математикой, анализом данных, логикой. Чтобы без проблем решить их на экзамене, необходимо много практиковаться. Вы можете учиться самостоятельно, а можете записаться на курсы подготовки к ЕГЭ и ОГЭ, где преподаватели будут объяснять все сложные моменты. В статье мы разберем тему «Логические выражения». Она встречается в 23 номере ЕГЭ по информатике.

Алгебра логики

Прежде чем приступить к разбору заданий, нужно изучить теорию. Алгеброй логики называют один из разделов математической логики. Его особенность в том, что логические выражения анализируются с использованием алгебраических законов и правил. Создание науки связано с именем Дж. Буля (1815-1864). Ученый разработал собственный математический язык, записывал с его помощью уравнений. Истинность и ложность выражений доказывал с помощью алгебраических операций. Несмотря на то, что алгебра логики продолжает развиваться, принцип остается прежним.

Основой алгебры логики (и 23 задания ЕГЭ) являются логические высказывания — не вопросительные предложения, по поводу которых можно однозначно сказать, являются они истинными или ложными. Например, высказывание «снег белый» истинно, «солнце светит ночью» — ложно. Предложение «мороженое вкусное» не является логическим высказыванием, нельзя однозначно сказать о его правдивости. Если заменить его на «я люблю мороженое», то оно может принимать как истинное, так и ложное значение, это зависит от предпочтений человека.

В 23 задании по информатике встречаются двузначные высказывания, принимающие значения «правда» и «неправда». Но алгебра логики рассматривает также многозначные, имеющие значения «вероятно», «невозможно», «возможно». Элементарные высказывания обозначают латинскими буквами (например, A = «осенью деревья сбрасывают листву»). Сложные высказывания составляются из элементарных с использованием частиц «и», «или», «тогда и только тогда», «если.. то» (например, А и В = «осенью деревья сбрасывают листву и некоторые птицы улетают на юг»). В цифровом представлении истине соответствует число 1, а лжи число 0. Для вычисления примеров обычно используются таблицы истинности.

Основные операции алгебры логики

Для решения номера 23 по информатике нужно знать основные операции:

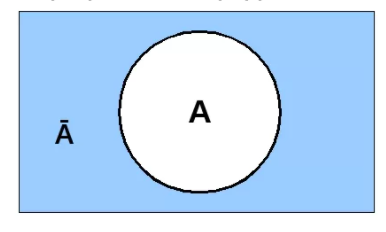
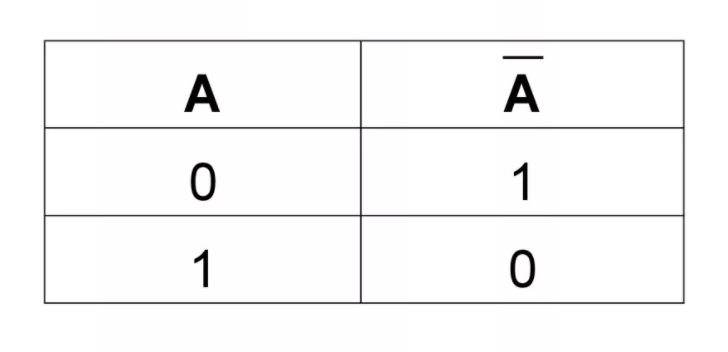
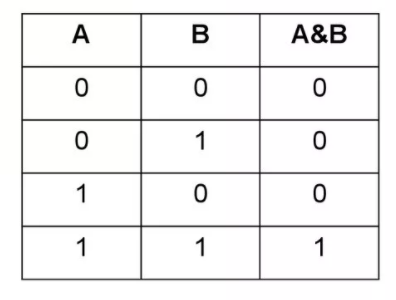
инверсия (отрицание). Операция называется унарной, так как преобразует одну величину: «переворачивает» выражение, меняет истину на ложь и наоборот. Обозначается чертой над буквой, символом ᆨ, словом «not». В результате преобразования числа A получается высказывание ᆨA. Читается «не А», «отрицание А», «А ложно». Пример: A = 1 больше 0; Ā = 1 не больше 0. На рисунке А — множество точек, Ā — все точки, не принадлежащие множеству;

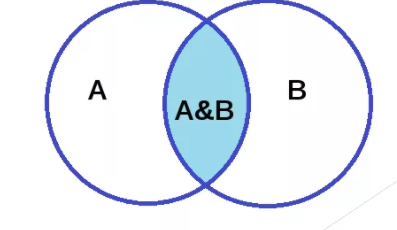
конъюнкция (умножение). Обозначает величины (2 или больше), объединенные союзом И. Для математической записи используются знаки ∧, •, &, and. Иногда знак опускают, по аналогии с математикой. Высказывание истинно, когда все его части правдивы, например, A∧B = «химия изучает вещества и молекулы». На рисунке изображается множествами, их пересечение соответствует A∧B;

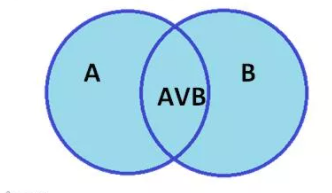
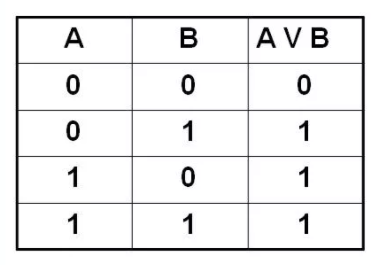
дизъюнкция (сложение). Связывает 2 и более выражения союзом ИЛИ. Обозначается знаками ∨, +, |, or. Выражение истинно, если правдива одна часть или сразу обе. Пример: А∨В = «звезды состоят из газа или плазмы». На рисунке изображается объединением множеств;

строго-разделительная (исключающая) дизъюнкция. Связывает высказывания союзом ИЛИ. Особенность в том, что союз является исключающим, то есть выражение истинно, когда правдива одна из его частей. Обозначают через ∨∨, ⊕, а читают «либо А, либо В». Пример: А⊕В = «валентность серы II или IV»;

импликация. Соединяет выражения, указывающие на причину и следствие. Обозначается ⟶, ⊃, читается «из А следует В», «если А, то В», «А влечет В». Пример является ложью, когда причина правдива, а следствие — неправда. Пример: А⟶В = «если число делится только на себя и на 1, то оно сложное».

эквивалентность. Операция объединяет высказывания связками ТОГДА И ТОЛЬКО ТОГДА, РАВНОСИЛЬНО, НЕОБХОДИМО И ДОСТАТОЧНО. Обозначается ~, ↔️, читается «А эквивалентно В». Выражение истинно, когда обе части одинаковы. Например: А~В = «число делится на 5 тогда, когда его последняя цифра 0 или 5». Эквивалентность противоположна строго-разделительной дизъюнкции.

На самом деле, для решения номеров достаточно трех операций: сложения, умножения, отрицания. Строго-разделительную дизъюнкцию можно представить как (ᆨА∧B)∧(А∧ᆨВ), импликацию — ᆨА∨B, эквивалентность (ᆨA∧ᆨB)∨(A∧B). Порядок выполнения действий при вычислении:

инверсия;
конъюнкция;
дизъюнкция;
остальные.

Примеры решения задач

Переходим к разбору 23 задания по информатике. Решим несколько задач.

Задача 1. Вычислите логическое значение: (ᆨ(15 < 3))∧(10 > 20).

Решение: Составим таблицу.

15 < 3	10 > 20	ᆨ(15 < 3)	ᆨ(15 < 3)∧(10 > 20)
0	1	1	0

Ответ: ложь.

Задача 2. Запишите высказывание с помощью логических операций, определите его значение: «если часы неправильно показывают время, то вы не успеете на занятия».

Решение: Пусть «часы неправильно показывают время» = А, «успеете на занятия» = В, а «не успеете на занятия» = ᆨВ. Логическое выражение: А⟶ᆨВ. Из причины сделал верный вывод, поэтому выражение является истинным.

Ответ: истина.

Задача 3. Определить значение ((х > 10) ∨ (х < 15)) → (х < 5) для 1) x = 9 и 2) х = 4.

Решение: Для х = 9: ((9 > 10) ∨ (9 < 15)) → (9 < 5) = ложь ∨ истина → ложь = истина → ложь = ложь.

Для х = 4: ((4 > 10) ∨ (4 < 15)) → (4 < 5) = ложь ∨ истина → истина = истина → истина = истина.

Ответ: 1) ложь; 2) истина.

Мы изучили основную теорию алгебры логики и разобрались, как решать 23 номер в ЕГЭ. Эта тема очень важна, поэтому не забывайте ее и постоянно практикуйтесь, чтобы подготовиться к экзамену лучше. Желаем вам легких вариантов и высоких баллов!

Источник