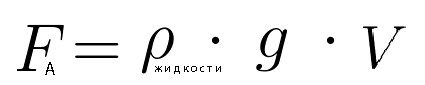Сила Архимеда
Из кодификатора по физике, 2020.
«1.3.5. … если тело и жидкость покоятся в ИСО, то
Теория
Архимедова (выталкивающая) сила равна:
где – плотность жидкости (кг/м3), g — ускорение свободного падения (м/с2),
— объем погруженной части тела (м3).
— Объем жидкости , вытесненной телом, равен объему
погруженной части тела в жидкость
— Если тело находится полностью в жидкости, то объем жидкости , вытесненной телом, равен объему тела
Задачи
Задача 1. Груз массой 3 кг, подвешенный на тонкой нити, целиком по-гружен в воду и не касается дна сосуда (рис. 1). Модуль силы натяжения нити 10 Н. Найдите объём груза (в литрах).
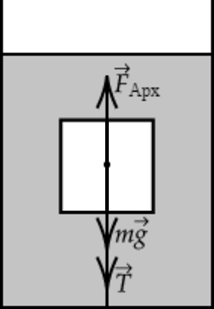
Решение. На груз в воде действуют сила тяжести (), архимедова сила (FA) и сила натяжения нити (Т). Ось OY направим вверх (рис. 2). Запишем второй закон Ньютона:
где — плотность воды, которую находим из таблицы «Плотность» (см. «Справочные данные»). Тогда
Задача 2. Предмет из алюминия объемом 100 см3 подвесили к пружине и опустили в бензин. Определите силу натяжения пружины.
Решение. На тело в керосине действуют сила тяжести (), архимедова сила (FA) и сила упругости (Fупр) пружины. Ось OY направим вверх (рис. 3). Запишем второй закон Ньютона:
где — объем тела,
— масса тела,
=700 кг/м3 — плотность бензина, ρ = 2700 кг/м3 — плотность алюминия, которые находим из таблицы «Плотность» (см. «Справочные данные»). Тогда
Задача 3. Стальной шарик висит на нити, привязанной к штативу. Шарик целиком погружен в керосин (рис. 4). Затем стакан с керосином заменили на стакан с водой, и шарик оказался целиком в воде (рис. 5). Как изменились при этом сила натяжения нити и сила Архимеда, действующая на шарик?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась; 2) уменьшилась; 3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Сила натяжения нити | Сила Архимеда, действующая на шарик |
Решение. На тело в жидкости действуют сила тяжести (), архимедова сила (FA) и сила натяжения нити (T). Ось OY направим вверх (рис. 6). Запишем второй закон Ньютона:
Архимедова сила равна
где — объем тела. Тогда
Масса бруска m и его объем V не меняются, плотность жидкости ρж увеличивается (ρ1ж = 800 кг/м3 — плотность керосина, ρ2ж = 1000 кг/м3 — плотность воды, которые находим из таблицы «Плотность» (см. «Справочные данные»)).
Из уравнения (2) следует, что так как масса бруска m не меняется, а плотность жидкости ρж увеличивается, то сила натяжения нити уменьшается. Это соответствует изменению № 2.
Из уравнения (1) следует, что так как масса бруска m и его объем V не меняются, а плотность жидкости ρж увеличивается, то сила Архимеда так же увеличивается. Это соответствует изменению № 1.
Ответ: 21.
Задача 4. К динамометру подвесили тело. Показания динамометра в воздухе 12 Н, в воде — 7 Н. Определите плотность тела.
Решение. Показания динамометра — это значение силы упругости Fупр его пружины. На тело в воздухе действуют сила тяжести () и сила упругости (Fупр1) (рис. 7, а). На тело в воде действуют сила тяжести (
), архимедова сила (FA) и сила упругости (Fупр2) (рис. 7, б). Ось 0Y направим вверх. Запишем второй закон Ньютона для двух случаев:
где — объем тела, ρж = 1000 кг/м3 — плотность воды, которую находим из таблицы «Плотность» (см. «Справочные данные»), ρ — плотность тела. Тогда
Автор Сакович А.Л.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Сила Архимеда» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Гидростатика. Сила Архимеда
Закон Архимеда
На погружённое в жидкость или газ тело действует выталкивающая сила, и равная весу среды, объём которой равен объёму тела.
Выталкивающая сила (сила Архимеда) равна
[F_A=rho_text{ж} g V_text{пчт}] где (displaystyle V_text{пчт}) — объём погружённой части тела, (displaystyle rho_text{ж}) — плотность жидкости.
Плавание тел
Рассмотрим тело плотности (rho) и жидкость плотности (rho_0). Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести (mg) и архимедова сила (F_A). Если объём тела равен V, то
[mg=rho g V,] [F_A=rho_0 g V]
Имеются три возможности дальнейшего движения тела.
Сила тяжести больше архимедовой силы: (displaystyle mg > F_A), или (displaystyle rho>rho_0). В этом случае тело тонет.
Сила тяжести равна архимедовой силе: (displaystyle mg = F_A), или (displaystyle rho=rho_0). В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
Сила тяжести меньше архимедовой силы: (displaystyle mg < F_A), или (displaystyle rho<rho_0). В этом случае тело всплывает, достигая поверхности жидкости.
Таким образом, условие плавания тела можно записать в виде неравенства (displaystyle rholeq rho_0).
Два жестко связанные друг с другом одинаковых бруска, имеющие толщину (h=5) см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.)
Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
(displaystylerho_1) – плотность материала, из которого изготовлены бруски, а (displaystyle V) – объем двух брусков. Тогда масса этих брусков будет равна [displaystyle m=rho_1V] Сила, с которой льдинки действуют на воду, равна силе тяжести [displaystyle F=mg=rho_1Vg] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда [F_text{Арх}=rho gfrac{V}2,] где (displaystyle rho) – плотность воды, (displaystyle frac{V}2) – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: [rho_1Vg=rho gfrac{V}2,] откуда (displaystyle rho_1=dfrac{rho}2,) то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину [frac72h=3,5cdot5text{ см}=17,5 text{ см}.] Глубина увеличится на (displaystyle 17,5 -5=12,5) см.
Ответ: 12,5
Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна (displaystyle rho_text{ ал}=2700 text{ кг}/text{м}^3. ) Какова длина ребра куба, если выталкивающая сила равна (displaystyle F_text{Арх}=33,75text{ Н}?) (Ответ дайте в сантиметрах.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV,] где (displaystyle rho_text{в}) – плотность жидкости, в которую погружен кубик, (displaystyle V) – объем погруженной части тела. Так как куб погружен целиком, то (displaystyle V=a^3), получим: [F_text{Арх}=rho_text{в} ga^3] Выразив из этой формулы сторону (displaystyle a), получаем [a=sqrt[3]{frac{F_text{Арх}}{rho_text{в}g }}] Подставив значения в формулу, получим: [a=sqrt[3]{frac{33,75text{ Н}}{10text{ м}/{c^2}cdot1000text{ кг}/text{м}^3}}=0,15text{ м}=15text{ cм }]
Ответ: 15
Однородный цилиндр, изготовленный из материала плотностью (displaystyle rho=600) кг/м(^3), с радиусом основания (displaystyle R=25) см и высотой (displaystyle H=20) см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)
Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: [vec T+vec F_text{Арх}+mvec g=mvec a,] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [T- F_text{Арх}+mg=0, quad(1)] массу цилиндра можно рассчитать, исходя из формулы (displaystyle rho=frac {m}{V} Rightarrow m=rho V,) где V – объем цилиндра, который можно вычислить по формуле [V=pi R^2 H] Из формулы (1) выразим силу натяжения нити T:[T=F_text{Арх}-mg=rho_text{в}gV-rho gV=Vg(rho_text{в}-rho)=pi R^2 Hg(rho_text{в}-rho),] где (displaystyle rho_text{в}) – плотность воды, подставим в получившееся выражение численные значения:[T=3,14cdot0,25^2text{ м}cdot0,2text{ м}cdot 10text{ м}/text{с}^2 cdot (1000text{ кг}/text{м}^3-600text{ кг}/text{м}^3)=157text{ Н }]
Ответ: 157
Однородный кубический предмет с ребром (displaystyle a=18) см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна (displaystyle rho_text{др}=340) кг/м(^3), плотность эфира (displaystyle rho_text{э}=720) кг/м(^3). (Ответ дайте в сантиметрах.)
Запишем условие равновесия кубика на поверхности эфира: [F_text{ Арх}=mg, quad(1)] где (F_text{ Арх}) – выталкивающая сила, действующая на брусок, (displaystyle m) – масса кубика, которую можно рассчитать, исходя из формулы (displaystyle rho_text{др}=frac {m}{V} Rightarrow m=rho_text{др} V,) где V – объем кубика, который можно вычислить по формуле [V=a^3.] Выталкивающая сила равна: [F_text{ Арх}=rho_text{э}gV_text{пчт},] где (displaystyle V_text{пчт}) – объем погруженной части кубика,[V_text{пчт}=xa^2,] где (displaystyle x) – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: [rho_text{э}gxa^2=rho_text{др}a^3] [rho_text{э}x=rho_text{др}a, text{ выразим } x=frac{rho_text{др}a}{rho_text{э}}.] Пусть (displaystyle y) – длина части стороны, находящейся над эфиром, можем записать: [y=a-x,] искомая разница длин (displaystyle delta=y-x=a-2x=a-2cdot dfrac{rho_text{др}a}{rho_text{э}}=a(1-2cdot dfrac{rho_text{др}}{rho_text{э}})) подставим в получившееся выражение численные значения: [displaystyle delta=0,18text{ м}(1-2cdot dfrac{340text{ кг}/text{м}^3}{720text{ кг}/text{м}^3})=0,01text{ м}=1text{ см}]
Ответ: 1
В некий резервуар было налито 1000 литров жидкости плотностью (displaystyle rho_1=1500) кг/м(^3). В этой жидкости в равновесии плавает кубик, погруженный в воду на (displaystyle x=130) см. Длина стороны кубика равна (displaystyle a=200) см. В сосуд доливают ещё 1000 литров жидкости плотностью (displaystyle rho_2=1100) кг/м(^3) и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)
В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. [rho_text{нов}=dfrac{rho_1+rho_2}{2}] Так как кубик плавает на поверхности, то можно записать: [mg=F_text{Арх},] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна:[F_text{Арх1}=rho_1 g V_text{пчт1},] где (displaystyle V_text{пчт1}=a^2x) – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: [F_text{Арх2}=rho_text{нов} g V_text{пчт2}=dfrac{rho_1+rho_2}{2}g V_text{пчт2},]где (displaystyle V_text{пчт2}=a^2y) – объем погруженной части куба до смешивания, (displaystyle y) – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим [rho_1 g a^2x=dfrac{rho_1+rho_2}{2} g a^2y] [rho_1x=dfrac{rho_1+rho_2}{2}y,] выразим отсюда y: [y=frac{2rho_1 x}{rho_1+rho_2},] подставим в получившееся выражение численные значения: [y=frac{2cdot1500text{ кг}/text{м}^3 cdot1,3text{ м}}{1500text{ кг}/text{м}^3+1100text{ кг}/text{м}^3}=1,5text{ м}]
Ответ: 1,5
Стеклянный шарик опускается в воде с ускорением (displaystyle a=6) м/с(^2). Найти плотность стекла. Плотность воды (displaystyle rho_text{в}=1000) кг/м(^3). Силами вязкого трения пренебречь. (Ответ дайте в кг/м(^3).)
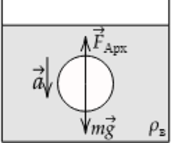
При движении шарика в воде на него действует сила тяжести (displaystyle mvec g) и сила Архимеда (displaystyle F_text{Арх}). Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: [vec F_text{Арх}+mvec g=mvec a,] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [mg- F_text{Арх}=ma,] Отсюда с учетом выражения для силы Архимеда (displaystyle F_text{Арх}=rho_text{в} g V), где V – объем шарика, а
(displaystyle rho_text{в}) – плотность воды, получим: [mg- rho_text{в} g V=ma,] Выразим массу шарика:[m=frac{rho_text{в} g V}{g-a}.] Исходя из формулы, плотность стекла равна [displaystyle rho_text{ст}=frac {m}{V}=frac{rho_text{в} g V}{(g-a)V}=frac{rho_text{в} g }{g-a},] подставим в получившееся выражение численные значения: [rho_text{ст}=frac{1000 text{ кг}/text{м}^3cdot 10text{ м}/text{с}^2 }{10text{ м}/text{с}^2-6text{ м}/text{с}^2}=2500text{ кг}/text{м}^3]
Ответ: 2500
Однородный шарик, изготовленный из материала плотностью (displaystyle rho=2000) кг/м(^3) погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
(displaystyle F_text{Арх}=100) Н? (Ответ дайте в сантиметрах и округлите до целых.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV_text{пчт},] где (displaystyle rho_text{в}) – плотность воды, (displaystyle V_text{пчт}) – объем погруженной части тела. Так как шар полностью опущен в воду, то [V_text{пчт}=frac43pi R^3,] где (displaystyle R) – радиус шара, получим: [F_text{Арх}=rho_text{в} gfrac43pi R^3, (1)] выразим из формулы R: [R=sqrt[3]{frac{3F_text{Арх}}{4rho_text{в}gpi}}] Подставив значения в формулу, получим: [R=sqrt[3]{frac{3 cdot100text{ Н}} {4 cdot1000 text{ кг}/text{м}^3cdot10text{ м}/{c^2}cdot3,14}} approx0,13text{ м}=13text{ см }]
Ответ: 13

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Закон Архимеда (задачи)
Задачи на закон Архимеда чаще всего связаны с самой силой Архимеда:
(1)
- где
— искомая сила Архимеда
— плотность жидкости (среды), в которую погружено тело
— ускорение свободного падения
— объём погружённой части тела
Кроме того, т.к. мы работаем с силами, то часто необходим второй закон Ньютона:
(2)
- где
— векторная сумма сил, действующих на тело
— масса тела
— ускорение тела
Иногда тело покоится (задача на статику), тогда ускорение тела равно нулю (), тогда, исходя из (2):
(3)
- Определите силу Архимеда, действующую на мальчика…
- На гайку, погружённую в керосин, действует выталкивающая сила…
- Динамометр с висящим телом в воздухе показывает…
- Пенопластовый буй объёмом удерживается леской так…
- Определите плотность вещества, частично погруженного под воду…
- При полном погружении в воду алюминиевой детали массой…
- После посадки рыбака в воду с вертикальными бортами и площадью…
Сила Архимеда .
На тело, погруженное в жидкость действует вверх сила, равная весу вытесненной жидкости.
(rho) это плотность жидкости или газа, то есть той среды, в которой находится тело
Силу Архимеда еще называют выталкивающей силой.
0. Аня уронила в речку мячик объёмом 0,8 л какая сила архимеда действует на мячик,если он погружен в воду только наполовину?
Показать ответ
Показать решение
Видеорешение
Репетитор по физике
8 916 478 10 32
1. Найти силу Архимеда, действующую на тело объемом (V=150 см^3), целиком погруженное в воду .Плотность воды: (rho=1000dfrac{кг}{м^3}).
Показать ответ
Показать решение
Видеорешение
2. Найти силу Архимеда, действующую на тело объемом (V=850 см^3), целиком погруженное в керосин .Плотность керосина (rho=800dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
3. Найти силу Архимеда, действующую на тело объемом (V=2 м^3), половина объема которого погружено в воду .Плотность воды: (rho=1000dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
4. Найти силу Архимеда, действующую на тело объемом (V=2 м^3), четверть объема которого погружено в воду .Плотность воды: (rho=1000dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
5. Найти объем тела, полностью погруженного в воду, если действующая на него сила Архимеда (F_A=20) Н , а плотность воды (rho=1000 ) (dfrac{КГ}{М^3})
Показать ответ
Показать решение
Видеорешение
6. На тело, объемом (V=0,5м^3) полностью погруженное в жидкость, действуюет сила Архимеда (F_A=5000Н). Найти плотность этой жидкости.
Показать ответ
Показать решение
Видеорешение
7. Стальной шар объемом (V=50см^3), полностью погружен в воду. Какая сила Архимеда действует на шар? Плотность воды (rho=1000dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
8. Чему равна выталкивающая сила (сила Архимеда), действующая в воде на полностью погруженный железный шар массой 0,78 кг? Плотность воды (rho_в=1000dfrac{кг}{м^3})
, Плотность железа (rho_ж=7800dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
9. Чему равна выталкивающая сила, действующая в воде на полностью погруженный деревянный брусок размером 60x10x15см? Плотность воды (rho_в=1000dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
10. Чему равна сила Архимеда, действующая в бензине на полностью погруженный медный брусок размером 6x1x2см? Плотность бензина (rho_в=710dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
11. Чему равна архимедова сила, действующая в воздухе на шарик объемом (V=3000 см^3)? Плотность воздуха (rho_в=1,29dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
12. Какую силу нужно приложить к камню, находящемуся под водой, чтобы не дать ему пойти ко дну, если на него действует сила тяжести
(F_Т=10Н) и сила Архимеда (F_A=4Н)?
Куда направлена эта сила?
Показать ответ
Показать решение
Видеорешение
13. Какую силу нужно приложить к стальному предмету, находящемуся под водой, чтобы не дать ему пойти ко дну, если на него действует сила тяжести
(F_Т=780Н) и сила Архимеда (F_A=100Н)?
Куда направлена эта сила?
Показать ответ
Показать решение
Видеорешение
14. Какую силу нужно приложить к деревянному предмету, находящемуся под водой, чтобы не дать ему всплывать, если на него действует сила тяжести
(F_Т=50Н) и сила Архимеда (F_A=125Н)?
Куда направлена эта сила?
Показать ответ
Показать решение
Видеорешение
15. Какую силу нужно приложить к деревянному бруску, объемом (V= 0,1 м^3), находящемуся под водой, чтобы не давать ему всплывать ?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Плотность дерева (rho_д=400dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
16. Какую силу нужно приложить к деревянной доске, объемом (V= 300 см^3), находящейся под водой, чтобы не давать ей всплывать ?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Плотность дерева (rho_д=400dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
17. Какую силу нужно приложить к стальному листу, массой (m= 780 г), находящемуся под водой, чтобы не давать ему утонуть ?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Плотность стали (rho_с=7800dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
19. Какую силу нужно приложить к сплошному деревянному кубу, массой (m= 3 кг), находящемуся под водой, чтобы не давать ему всплывать ?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Плотность дерева (rho_д=400dfrac{кг}{м^3})
Показать ответ
Показать решение
Видеорешение
20. Полый алюминиевый куб, массой (m= 3 кг) и объемом (V= 0,01 м^3) бросили в воду.
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Куб утонет или будет плавать на поверхности?
Показать ответ
Показать решение
Видеорешение
21. Полый алюминиевый куб, массой (m_к= 3 кг) и объемом (V= 0,01 м^3) бросили в воду, но едва он коснулся поверхности воды, как на него села птичка массой (m_п= 2 кг).
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Удастся ли птичке поплавать на нем?
Показать ответ
Показать решение
Видеорешение
22. Каким должен быть минимальный объем надувной лодки массой 50 кг, чтобы взять на борт груз массой 500 кг?
Плотность воды (rho_в=1000dfrac{кг}{м^3}). Удастся ли птичке поплавать на нем?
Показать ответ
Показать решение
Видеорешение
23. какая сила архимеда действует шар объемом (1 м^3 ) и массой 0,5 кг плавающего на поверхности воды ?
Показать ответ
Показать решение
Видеорешение