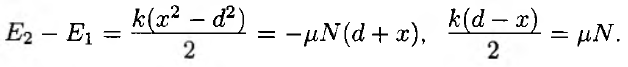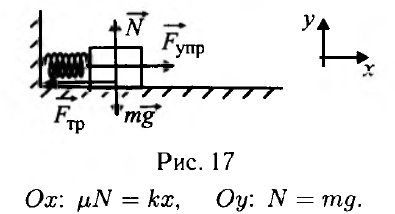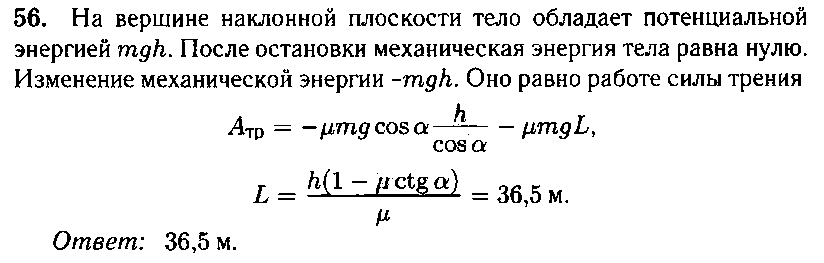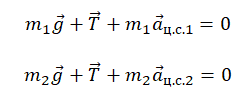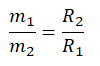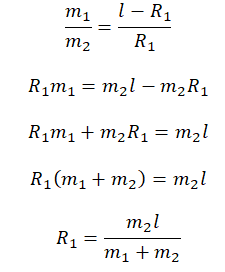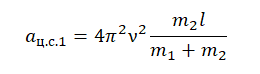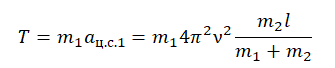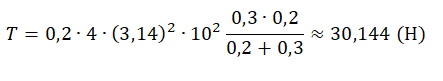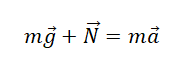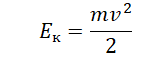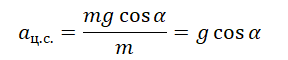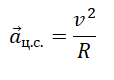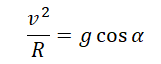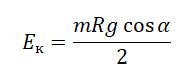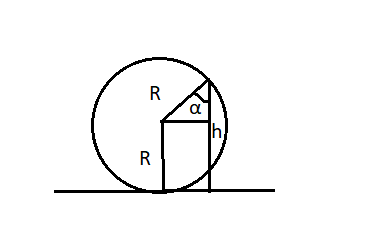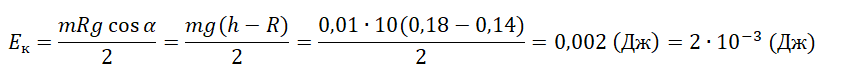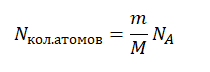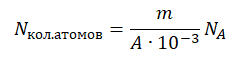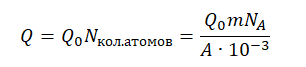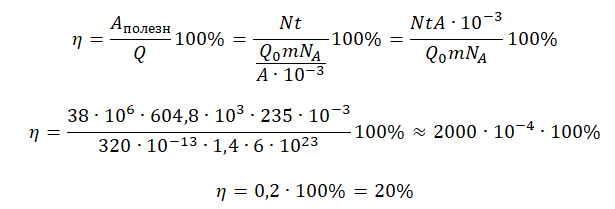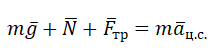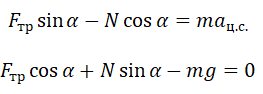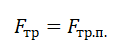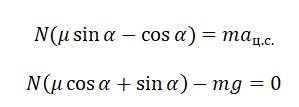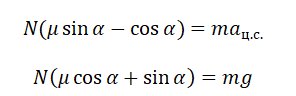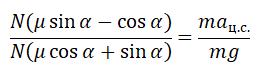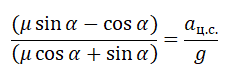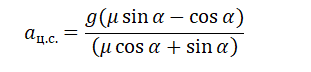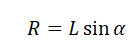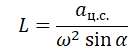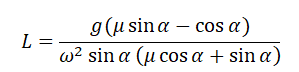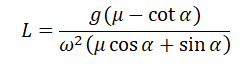в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 126 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
С горизонтальной плоскости вначале бросают маленький мячик под углом
к горизонту со скоростью υ = 20 м/с. В момент, когда мячик достигает наивысшего положения на своей траектории, стреляют пулей из ружья со скоростью V = 120 м/с в направлении мячика, причём пуля вылетает из той же точки, из которой был брошен мячик (см. рис.). Под каким углом
к горизонту надо стрелять, чтобы пуля из ружья попала в мячик? Трением мячика и пули о воздух можно пренебречь. Указание: для численного решения уравнений используйте микрокалькулятор.
Какие законы Вы использовали для описания движения тел? Обоснуйте их применение к данному случаю.
Человек ростом h = 1,6 м, стоя на земле, кидает мяч из-за головы и хочет перебросить его через забор высотой H = 4,8 м, находящийся на расстоянии l = 6,4 м от него. Определите модуль скорости, с которой необходимо бросить мяч, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории? Сопротивлением воздуха пренебречь.
Какие законы Вы использовали для описания движения мяча? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 11.06.2021. Основная волна. Москва
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рис.).
На краю трамплина скорость гонщика направлена под углом к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Какие законы Вы используете для описания гонщика по трамплину? Обоснуйте их применение к данному случаю.
Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и высоту
м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии
м от места его обнаружения. Известно, что снаряды данного типа вылетают из ствола пушки со скоростью 800 м/с. Какова была максимальная высота Н траектории снаряда, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.
Какие законы Вы использовали для описания движения снаряда? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 6.
В длинном и широком спортивном зале с высотой потолка H = 10 м баскетболист бросает мяч товарищу по команде с начальной скоростью V = 20 м/с. Какова может быть максимальная дальность его передачи по горизонтали? Сопротивлением воздуха и размерами мяча можно пренебречь, бросок делается и принимается руками на уровне h = 2 м от горизонтального пола.
Какие законы Вы использовали для описания движения мяча? Обоснуйте их применение к данному случаю.
Источник: Тренировочная работа по физике 27.04.2018, вариант ФИ10503
Пружинное ружье наклонено под углом к горизонту. Энергия сжатой пружины равна 0,41 Дж. При выстреле шарик массой
проходит по стволу ружья расстояние b, вылетает и падает на расстоянии
от дула ружья в точку M, находящуюся с ним на одной высоте с дулом. (см. рис.). Найдите расстояние b. Трением в стволе и сопротивлением воздуха пренебречь.
Какие законы Вы использовали для описания движения шарика? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания
Задания Д29 C2 № 3070
Наклонная плоскость пересекается с горизонтальной плоскостью по прямой AB. Угол между плоскостями Маленькая шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью
под углом
к прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной плоскостью, найдите расстояние AB.
Небольшое тело бросили под углом α = 30º к горизонтальной плоскости с начальной скоростью V0 = 40 м/c. В верхней точке траектории в него попало другое тело такой же массы, брошенное с той же плоскости вертикально вверх с начальной скоростью u0 = 25 м/c, и оба тела в результате абсолютно неупругого удара слиплись и полетели дальше вместе (см. рис.). На каком расстоянии l от места броска второго тела слипшиеся тела упадут на горизонтальную плоскость? Сопротивлением воздуха можно пренебречь.
Какие законы Вы используете для описания взаимодействия тел? Обоснуйте их применение к данному случаю.
Человек ростом h, стоя на Земле, бросает из-за головы камень и хочет перебросить его через забор высотой H, находящийся на расстоянии L от человека. Найдите угол, под которым нужно бросить камень, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории.
Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рис.).
На краю трамплина скорость гонщика направлена под углом к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова дальность полета L на этом трамплине? Cопротивлением воздуха и трением пренебречь.
Какие законы Вы используете для описания движения гонщика по трамплину? Обоснуйте их применение к данному случаю.
Первый камень бросают с горизонтальной поверхности под углом 45° к горизонту. Второй камень бросают с той же по модулю начальной скоростью, но угол, под которым она направлена к горизонту, уменьшают в 2 раза. Как для второго камня по сравнению с первым изменятся время полёта и дальность полёта, если сопротивление воздуха пренебрежимо мало?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Время полёта камня | Дальность полёта камня |
Человек ростом h = 1,6 м, стоя на земле, кидает мяч из-за головы и хочет перебросить его через забор высотой H = 4,8 м, находящийся на расстоянии l = 6,4 м от него. Определите модуль скорости, с которой необходимо бросить мяч, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории? Сопротивлением воздуха пренебречь.
Источник: ЕГЭ по физике 11.06.2021. Основная волна. Москва
Тело, брошенное с горизонтальной поверхности со скоростью под углом
к горизонту, поднимается над горизонтом на максимальную высоту h, а затем падает на расстоянии S от точки броска. Сопротивление воздуха пренебрежимо мало.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Максимальная высота h над горизонтом
Б) Расстояние S от точки броска до точки падения
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 6.
Тело бросили с одинаковой начальной скоростью сначала под углом к горизонту 20°, а затем под углом 30°. Как изменились максимальная высота подъема и время полета тела? Сопротивлением воздуха пренебречь.
Для каждой величины определите соответствующий характер изменения:
1) увеличилась;
2) уменьшилась;
3) не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Максимальная высота подъема, Н | Время полета, t |
Источник: ЕГЭ по физике 11.06.2021. Основная волна. Москва
Небольшой камень бросили под углом α к горизонту с высоты h от поверхности земли с начальной скоростью Сопротивление воздуха пренебрежимо мало. Через время t после броска камень ещё не упал на землю.
Установите соответствие между физическими величинами, характеризующими движение камня, и формулами, выражающими их в рассматриваемой задаче.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) тангенс угла, который составляет вектор скорости камня с горизонтом через время t после броска
Б) модуль скорости камня в момент его падения на землю
Ответ:
Первый камень бросают с горизонтальной поверхности под углом 45° к горизонту. Второй камень бросают с той же по модулю начальной скоростью, но угол, под которым она направлена к горизонту, увеличивают в 1,5 раза. Как для второго камня по сравнению с первым изменятся время полёта и дальность полёта, если сопротивление воздуха пренебрежимо мало?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Время полёта камня | Дальность полёта камня |
Тело, брошенное с горизонтальной поверхности со скоростью под углом
к горизонту, в течение t секунд поднимается над горизонтом, а затем снижается и падает на расстоянии S от точки броска. Сопротивление воздуха пренебрежимо мало.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Время подъёма t на максимальную высоту
Б) Расстояние S от точки броска до точки падения
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 1., ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 5.
Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания
Всего: 126 1–20 | 21–40 | 41–60 | 61–80 …
Опубликовано сб, 06/29/2019 — 14:28 пользователем fizportal.ru


КИНЕМАТИКА 3. Баллистика
1.3.1. а) Камень бросают со скоростью $v$ под углом $alpha$ к горизонту. Определите время полёта камня. б) Решите задачу a) в случае, когда камень бросают с высоты $h$.
Ответ
а) $T = frac{2vsinalpha}{g}$; б) $T = frac{sqrt{v^2sin^2alpha + 2gh} + vsinalpha}{g}$
1.3.2. Пушка стреляет под углом $alpha$ к горизонту. Скорость снаряда в момент выстрела $v_0$. Как зависит от времени скорость и расстояние снаряда от пушки?
1.3.3. Баскетболист бросает мяч в кольцо. Скорость броска $8$ м/с, и направлена под углом $60^0$ к горизонту. С какой скоростью мяч влетел в кольцо, если он долетел до него за $1$ с?
1.3.4. С высоты $h$ бросают камень под углом к горизонту. После прохождения точки наивысшего подъёма, находящейся на высоте $H$ от поверхности земли, за оставшееся время падения он переместился по горизонтали на расстояние $l$. Найти величину начальной скорости камня.
Ответ
$v = sqrt{2g(H — h + frac{S^2}{4H}}$
1.3.5. Спортсмен толкает ядро под углом $45^0$ к горизонту со скоростью $20$ м/с. Через какое время после толчка угол наклона скорости к горизонту уменьшится до $30^0$?
1.3.6. Камень бросили с крутого берега вверх под углом $30^0$ к горизонту со скоростью $10$ м/с. С какой скоростью он упал в воду, если время полёта камня $2$ с?
1.3.7. С балкона, находящегося на высоте $20$ м, бросают мяч со скоростью $20$ м/с (см. рисунок). Мяч упруго ударяется о стену соседнего дома и падает на землю под балконом. Определите расстояние до соседнего дома, если время полёта мяча $1,4$ с.
1.3.8. а) Зенитный снаряд, взлетающий вертикально, через время $tau$ достигает максимальной высоты и взрывается. Скорость осколков в момент взрыва равна $v$. Какой участок земли засыпят осколки через время $tau$ после взрыва? б)* На каком участке окажутся осколки (см. задачу а), когда все они упадут на землю?
Ответ
а) Круг радиуса $vtau$, б) $r_0 = vtau sqrt{1 + (v/gtau)^2}$
1.3.9. а) Со склона с углом $alpha$ к горизонту бросают камень в горизонтальном направлении, со скоростью $v$. Через какое время камень упадёт на склон? На каком расстоянии от места броска будет место падения камня? б) Из миномёта, расположенного на склоне горы, ведут стрельбу вниз по склону, образующему угол $beta$ с горизонтом (см. рисунок). На каком расстоянии от миномёта будут падать мины, если их начальная скорость v направлена под углом $alpha$ к горизонту?
Ответ
a) $t = frac{2v}{g}tgalpha, l = frac{2v^2}{g}frac{sinalpha}{cos^2alpha}$, б) $l = frac{2v^2}{g}sin(alpha + beta)frac{cosalpha}{cos^2beta}$
1.3.10. Самолёт пролетает над зенитной пушкой на высоте $h$, со скоростью $v$, которая направлена горизонтально. Под каким углом к горизонту должна в этот момент выстрелить пушка, и какова должна быть скорость снаряда, чтобы поразить самолёт?
Ответ
$cosalpha = frac{v}{u}$, где $u$ — скорость снаряда должна быть больше $sqrt{v^2 + 2gh}$
1.3.11. С какой скоростью в момент старта ракеты должен вылететь из пушки снаряд, чтобы поразить ракету, стартующую вертикально с ускорением $а$, если расстояние от пушки до места старта ракеты равно $l$ и пушка стреляет под углом $alpha$ к горизонту?
Ответ
$v = sqrt{frac{2(g + a)l}{sin2alpha}}$
1.3.12. На расстоянии $L$ друг от друга находятся две одинаковые пушки, направленные в одну сторону под углом $alpha$ к горизонту. Начальная скорость снаряда $v$ (см. рисунок). На какой высоте можно поразить снаряд одной пушки снарядом другой?
Ответ
$h = frac{(vsinalpha)^2}{2g} — frac{gL^2}{8(vcosalpha)^2}$
1.3.13. В прямоугольной коробке, упруго ударяясь о дно и правую стенку, по одной траектории туда и обратно прыгает шарик (см. рисунок). Промежуток времени между ударами о дно и стенку равен $T$. Дно коробки образует угол $alpha$ с горизонтом. Определить минимальную скорость шарика.
Ответ
$v = frac{1}{2}gTsin2alpha$
1.3.14.* В сферической лунке радиуса $R$, упруго отражаясь от стенок лунки, по одной траектории туда и обратно движется шарик. Места ударов находятся на одной горизонтали. Время от удара до удара $Т$. Определить скорость шарика в момент удара.
1.3.15.* Из миномёта выстреливают под углом $alpha$ к горизонту. Скорость вылетающей мины $v$. Через какое время мина будет на максимальном расстоянии от миномёта?
Ответ
$t = (frac{3}{2} — sqrt{frac{1}{4}sin^2alpha — 2cos^2alpha})frac{v}{g}$, если $tgalpha geq 2sqrt{2}$, $t = frac{2vsinalpha}{g}$, если $tgalpha leq 2sqrt{2}$
1.3.16.* а) После взрыва снаряда, лежащего в центре дна прочного стакана, осколки снаряда, вылетевшие из стакана, усеяли область вокруг него в радиусе $R$ (см. рисунок). Высота стакана $h$, радиус $r$, осколки разлетелись в момент взрыва во все стороны с одинаковой скоростью. Определите эту скорость.
б) После взрыва снаряда, лежащего в центре дна цилиндрического колодца глубины $h$ и радиуса $r$, осколки снаряда, вылетевшие из колодца, усеяли область вокруг него в радиусе $R$ (см рисунок). Осколки в момент взрыва разлетелись во все стороны с одинаковой скоростью. Определите эту скорость.
Ответ
а) $v = sqrt{gR}$, если $frac{hR}{r(R — r)} < 1$ и $v = sqrt{frac{1}{2}gR(frac{hR}{r(R — r)} + frac{r(R — r)}{hR})}$, если $frac{hR}{r(R — r)} > 1$, б) $v = sqrt{(sqrt{R^2 + h^2} + h)g}$, если $frac{hR}{r(R — r)} < 1$ и $v = sqrt{(frac{1}{2}R(frac{hR}{r(R — r)} + frac{r(R — r)}{hR}) + 2h)g}$, если $frac{hR}{r(R — r)} > 1$
1.3.17.* С какой минимальной скоростью можно бросить камень через здание высоты $Н$ с куполообразной крышей радиуса $R_1$.
Ответ
1.3.18.* а) С какой скоростью должен скользить шарик радиуса $r$ по горизонтальной доске, чтобы, достигнув края доски, оторваться от неё? б) Горизонтальная доска имеет на конце закругление радиуса $R$, С какой скоростью должен скользить по доске шарик радиуса $r$, чтобы, достигнув начала округления доски, оторваться от неё?
Ответ
а) $v = sqrt{rg}$, б) $v = sqrt{(R + r)g}$
1.3.19. Какое дополнительное ускорение в горизонтальном направлении должен развить реактивный снаряд, выстреливаемый горизонтально с высоты $h$ (см. рисунок), чтобы удвоить дальность полёта в сравнении с дальностью $l$, которая была при выключенном двигателе.
1.3.20. Ракета на старте развивает дополнительное ускорение $а$ под углом $alpha$ к горизонту, $asinalpha > g$. Через время $tau$ после старта тяга выключается. Определите длительность и дальность полёта ракеты.
Ответ
$t = (frac{a}{g}sinalpha — 1 + sqrt{(frac{a}{g}sinalpha — 1)frac{a}{g}sinalpha})tau$, $l = atau (t + frac{1}{2}tau)cosalpha$
1.3.21. Из орудия под углом $alpha$ к горизонту произведён выстрел реактивным снарядом (см. рисунок). Начальная скорость снаряда $v$, и сразу же после выстрела развивает постоянное дополнительное ускорение $а$ в направлении выстрела. Определите время полёта, дальность полёта и максимальную высоту подъёма снаряда.
Ответ
$t = frac{2vsinalpha}{g — asinalpha}, l = frac{gv^2sin2alpha}{(g — asinalpha)^2}$
Геометрический подход к баллистическим задачам
В серии статей на эту тему предложен интересный подход к решению задач кинематики, позволяющий решать их значительно проще. Некоторые задачи с помощью данного метода можно решить в одну строчку, в то время как другие можно решить только с его помощью. Конспект занятий, проводимых Пенкиным М.А.
Сначала немного теории.
Так как статья посвящена равноускоренному движению, то мы с вами будем использовать следующие формулы.
Здесь — перепад высот, «минус» соответствует движению вверх, «плюс» — движению вниз. Формула хороша тем, что в ней отсутствует время
. В общем виде формула записывается так:
Так как скалярное произведение равно , а в нашем случае
.
Рисунок 1
Последнюю формулу можно вывести из энергетических соображений:
Наконец, нам понадобится еще формула
При решении будем пользоваться векторными треугольниками. Выделяют два векторных треугольника: треугольник скоростей и треугольник перемещений.
Изобразим первый.
Рисунок 2
Вектор направлен вниз. Сумма векторов
и
в сумме дают вектор
. Проведем высоту в этом треугольнике. Тогда угол
— угол, под которым произведен бросок. Угол при вершине треугольника тогда будет равен
. Достроим наш треугольник до параллелограмма. В параллелограмме диагонали делятся пополам точкой пересечения. Половина диагонали параллелограмма, таким образом, будет медианой треугольника. А длина этого вектора будет равна
. Этот вектор будет направлен вниз, если тело приземляется ниже точки броска. В случае же, если тело падает на тот же горизонтальный уровень, он будет направлен горизонтально и треугольник в этом случае равнобедренный,
. Если мы закидываем тело вверх, указанный вектор будет направлен вверх.
Представим себе, что вектор перпендикулярен
. Тогда указанный вектор (
) равен радиусу описанной окружности (из геометрии). Кроме того, в этом случае вектор
направлен по биссектрисе угла между вектором перемещения и вертикалью. Это очень важный факт, который позволяет существенно упростить решение некоторых задач. Доказательство будет приведено ниже.
Если говорить о площади этого треугольника, то она пропорциональна перемещению (дальности полета).
Теперь нарисуем второй треугольник -треугольник перемещений. Высота этого треугольника – не что иное, как дальность полета .
Рисунок 3
Задача 1.
С поверхности земли под углом к горизонту выстрелила пушка. Через время
она поразила наземную цель. Определите дальность полета снаряда. Пушка и ее цель неподвижны и расположены на одном горизонтальном уровне. Сопротивлением воздуха пренебречь. Размеры пушки, снаряда и цели не учитывать.
Первый способ решения. Введем систему координат, ось направим горизонтально,
— вертикально.
Рисунок 4
Запишем уравнения по осям:
Минус этого способа – два уравнения. Плюс – привычные нам оси.
Выражаем :
Подставим скорость в первое уравнение:
Второй способ. Метод тоже аналитический. Выберем другие оси: выберем ось , совпадающую с направлением скорости
, а ось
— перпендикулярно ей.
Рисунок 5
Тогда в проекциях на эту ось (проекция
равна нулю):
Третий способ. Нарисуем векторный треугольник перемещений.
Рисунок 6
Тогда в этом треугольнике
Ответ: .
Задача 2.
Мячик бросили со скоростью под углом к горизонту. В полете он находился время
. Чему равна дальность полета мячика, если точки бросания и приземления находятся на одном горизонтальном уровне? Сопротивлением воздуха пренебречь.
Снова рисуем векторный треугольник перемещений.
Рисунок 7
По теореме Пифагора
Ответ: .
Задача 3.
С поверхности земли под углом к горизонту бросают камень со скоростью . Какова максимальная дальность полета камня, если точки бросания и приземления находятся на одном горизонтальном уровне? Сопротивлением воздуха пренебречь.
По аналогии с задачей 2 запишем
Проанализируем выражение под корнем. . Так как выражение под корнем – парабола, то
Тогда
Ответ: .
Задача 4.
С обрыва под углом к горизонту бросили камушек со скоростью
м/с. Сколько времени камушек находился в полете, если его конечная скорость составила
м/с и была направлена под углом
к горизонту? Сопротивлением воздуха пренебречь.
Рисунок 8
Из того, что дано, заключаем, что конечная и начальная скорость перпендикулярны друг другу. Поэтому можно записать из треугольника скоростей
Ответ:
Задача 5.
С обрыва под углом к горизонту бросили камушек со скоростью
м/с. Сколько времени камушек находился в полете, если его конечная скорость была направлена под углом
к горизонту? Сопротивлением воздуха пренебречь.
Эта задача – вариант предыдущей. Из данных понимаем, что конечная и начальная скорость перпендикулярны друг другу. Мы в этой задаче не знаем конечную скорость, но знаем угол.
Поэтому можно записать из треугольника скоростей
Откуда
Ответ: .
Задача 6.
Камень бросили со скоростью под углом
к горизонту. Чему равен модуль перемещения, если до места падения он летел время
? Сопротивление воздуха не учитывать.
Заметим, что нам не известно, на каком уровне упал камень: на том же самом или ниже.
Рисунок 9
Рассмотрим треугольник перемещений и применим для него теорему косинусов. Тогда
Это готовый ответ.
Задача 7.
С крутого берега реки со скоростью бросили камень под углом
к горизонту. С какой скоростью он упал в воду, если до места падения он летел время
? Сопротивление воздуха не учитывать.
В этой задаче мы также применим теорему косинусов для треугольника скоростей.
Рисунок 10
Ответ: .
Автор: Дроздова Елена Дмитриевна
Место работы/учебы (аффилиация): МБОУ «Новониколаевская СШ №1», Волгоградская область, 11 класс
Актуальность темы. На сегодняшний день в ЕГЭ содержатся задачи на движение тел, брошенных под углом к горизонту и частный случай данного движения: начальная скорость направлена горизонтально. Немаловажно знать, что науку о движении тел, брошенных в пространстве, называют баллистикой. Данный раздел физики связан с военным делом и включает в себя теоретические расчеты, а уже после практическое применение в различны сферах. Например, она нашла отражение в криминалистике, где важно знание движения тел в пространстве и огнестрельных повреждений, а также в ракетостроении, для создания нужной траектории и последующем поражении цели. Естественно, такая важная наука изучается в школе, но вот достаточно ли этого для ясного представления законов баллистического движения и решения задач по этой теме? Согласно статистике типичных ошибок участников ЕГЭ 2020 года, размещенные на сайте ФИПИ, можно сказать, что результаты решения задач повышенного уровня сложности, включающие задания на баллистику, составляют в среднем 18%. Большинство учеников не берутся за выполнение заданий данный темы, так как вывод формул и математические преобразования вызывают боязнь, и их решение остается без внимания.
Таким образом, актуальность исследования объясняется непониманием учащихся, как решать данные виды задач. Мы же попробуем найти алгоритм для выполнения заданий на баллистическое движение, не требующий использования знаний сложных формул, чтобы те не вызывали трудностей.
Выдвинем гипотезу: создание четкого алгоритма выполнения заданий на баллистическое движение увеличит процент учащихся, способных выполнить задачи по данной теме.
Объектом исследования являются задачи по теме «Движение тел, брошенных под углом к горизонту».
Предметом исследований — решение задач по теме «Движение тел, брошенных под углом к горизонту».
Цель исследования: изучение характерных закономерностей баллистического движения, создание алгоритма выполнения задач по данной теме.
Цель и предмет исследования обусловили необходимость решения следующий задач:
- Выяснить, какие существуют виды задач по баллистике.
- Подобрать и решить задачи по каждому виду, используемых в КИМах ЕГЭ.
- Сформулировать четкий план действий для решения данного типа задач.
В ходе написания исследовательской работы будут использованы такие методы научного познания как: эксперимент, анализ и синтез полученных данных. Поставленные задачи обусловили использование в работе следующих методов: изучение справочной литературы, анализ КИМ.
12 февраля 2023
В закладки
Обсудить
Жалоба
50 задач с ответами.
Задание №1 посвящено кинематике. Чаще всего в этих заданиях приведены графики равномерного или равнопеременного движения. Но есть также задания на исследование уравнений vx(t) и x(t), на равномерное движение по окружности и на относительность движения. Задачи на свободное падение и баллистику тут не встречаются. За верное выполнение этого задания Вы получите 1 балл.
1fiz.pdf
Автор: Суслов А.А.
Источник: vk.com/suslov_ege
Подготовка к ЕГЭ по физике. Задания высокого уровня сложности с развернутыми ответами. ЗАДАНИЕ № 29 (с решениями). Расчетная задача. Максимальная оценка 3 балла.
Задания 29 — 32 представляют собой расчётные задачи. В текстах заданий нет указаний на требования к полноте решения, эту функцию выполняет общая инструкция. В каждом варианте экзаменационной работы перед заданиями 29 — 32 приведена инструкция, которая в целом отражает требования к полному правильному решению расчётных задач.
ЕГЭ по физике. ЗАДАНИЕ № 29
К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно. Коэффициент трения груза по плоскости μ = 0,2. Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.
Один из вариантов решения
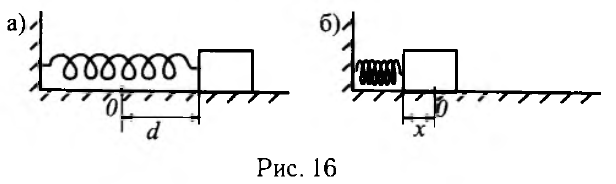
Сделаем поясняющий чертёж.
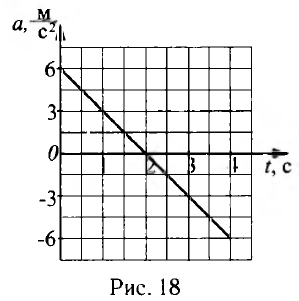
В начальный момент времени (см. рис. 16а) пружина была растянута на величину d, следовательно, её потенциальная энергия была равна E1 = kd2/2 (k — коэффициент жёсткости пружины). Когда груз отпустили, пружина начала сжиматься, а сам груз — двигаться в сторону закреплённого конца пружины. В некоторый момент движение груза прекратилось, пружина при этом сжалась на величину х (см. рис. 16б). Соответственно в момент остановки груза потенциальная энергия пружины была равна Е2 = kx2/2.
Изменение механической энергии системы равно работе сил трения.
А = –Fтр • S = –Fтр • (d + х) = – μN • (d + x).
Здесь S — пройденный грузом путь, μ — коэффициент трения, N — сила реакции опоры.
Кинетические энергии груза и в начальном положении, и в конечном равны нулю, следовательно:
Рассмотрим силы, действующие на груз в момент остановки — силу трения, силу упругости со стороны пружины, силу тяжести и силу реакции опоры (см. рис. 17). Груз покоится, значит, равнодействующая этих сил равна нулю. Запишем проекции сил на оси Ох и Оу:
Выразим из этих двух уравнений величину сжатия пружины х: х = μN/k = μmg/k
Отсюда k/2 • (d – μmg/k) = μN. Выразим массу тела: m = kd/2μg = 2,5 (кг).
Ответ: m = 2,5 кг.
Решение № 1 (на 3 балла)
Комментарий: Здесь в полном соответствии с пунктом 2 в критериях оценки указана на рисунке вновь введённая автором решения величина d1.
Решение № 2 (на 2 балла)
Комментарий: К недостаткам работы следует отнести отсутствие рисунка с указанием вновь вводимых обозначений. Кроме того, замечены ошибки в математических преобразованиях; однако недостатки решения, каждый из которых приводит к снижению оценки на 1 балл, не суммируются. Оценка 2 балла.
Решение № 3 (на 2 балла)
Комментарий: Такие же замечания, как и в предыдущей работе, и та же оценка.
Решение № 4 (на 2 балла)
Комментарий: Здесь получен правильный ответ, т.к. как ошибки в расчётах сил сопротивления компенсировались ошибками в математических преобразованиях. Оценка 2 балла.
Решение № 5 (на 0 баллов)
Комментарий: Оценка 0 баллов, т.к. неверно записаны исходные формулы.
Образцы заданий № 29 (с решениями)
Часть 1. Кинематика
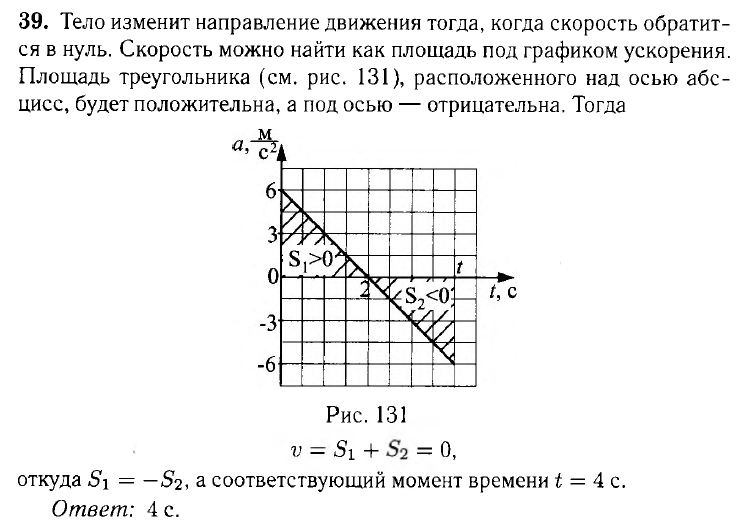
1.1. На рисунке 18 представлена зависимость ускорения материальной точки от времени. Начальная скорость точки равна 0. В какой момент времени точка изменит направление движения?
Смотреть решение и ответ
1.2. Тело брошено под углом α к горизонту с начальной скоростью υ0. При этом на тело действует попутный горизонтальный ветер, сообщая ему постоянное ускорение а. Найдите время полёта, наибольшую высоту и наибольшую дальность полёта.
Смотреть решение и ответ
1.3. Тело брошено с высоты 20 м. Какой путь пройдёт тело за последние 0,1 с своего движения? Начальная скорость тела равна нулю.
Смотреть решение и ответ
1.4. Из некоторой точки одновременно бросают два тела с одинаковой скоростью 25 м/с: одно — вертикально верх, другое — вертикально вниз. На каком расстоянии друг от друга будут эти тела через 2 с?
Смотреть решение и ответ
1.5. Из поднимающегося вертикально вверх вертолёта со скоростью υ на высоте Н вылетает тело. Через сколько времени оно упадёт на Землю? Какой будет скорость у тела? Сопротивления воздуха нет.
Смотреть решение и ответ
1.6. Жонглёр бросает вертикально вверх шарики с одинаковой скоростью через равные промежутки времени. При этом пятый шарик жонглёр бросает в тот момент, когда первый шарик возвращается в точку бросания. Найдите максимальное расстояние Smax между первым и вторым шариками, если начальная скорость шариков υ0 = 5 м/с. Ускорение свободного падения принять равным g = 10 м/с2. Сопротивлением воздуха пренебречь.
Смотреть решение и ответ
Часть 2. Динамика
2.1. Диск вращается в горизонтальной плоскости с угловой скоростью 3 рад/с. На расстоянии 30 см от центра диска лежит небольшое тело. При каком минимальном значении коэффициента трения тело будет удерживаться на диске?
Смотреть решение и ответ
2.2. С наклонной плоскости длиной 4 м и углом наклона 30° соскальзывает тело массой 2 кг, после чего проходит некоторое расстояние по горизонтали. Коэффициент трения на всём пути 0,05. Найдите расстояние, пройденное телом по горизонтали.
Смотреть решение и ответ
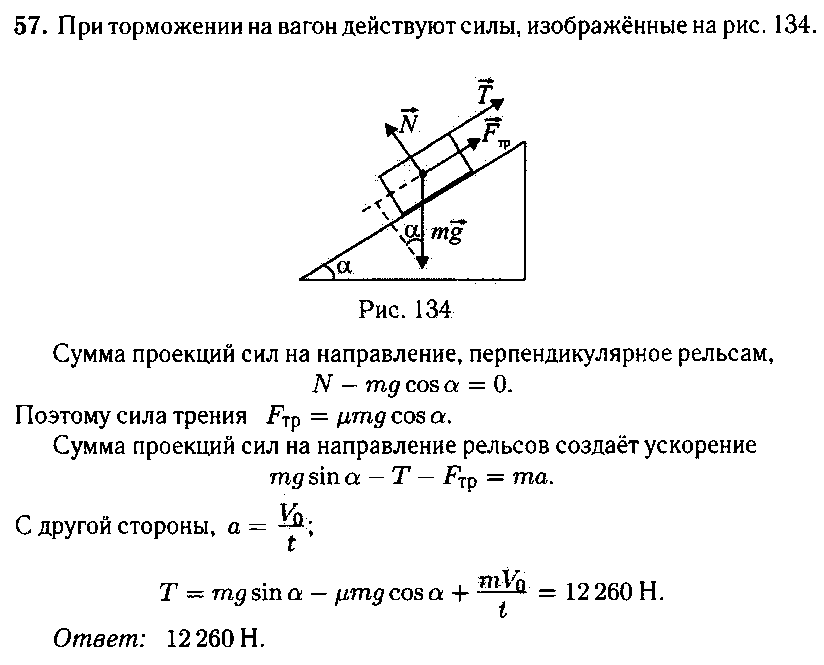
2.3. По рельсам фуникулёра, проложенным под углом 30° к горизонту, спускается вагон массой 2 т. Скорость вагона на всём пути рана 10 м/с, время торможения перед остановкой 5 с. Найдите силу натяжения каната при торможении. Коэффициент трения между колёсами и рельсами 0,1.
Смотреть решение и ответ
2.4. Лётчик массой 70 кг совершает мёртвую петлю в вертикальной плоскости с включённым двигателем, поддерживая постоянную по модулю скорость. Насколько вес лётчика в верхней точке траектории меньше, чем в нижней?
Смотреть решение и ответ
2.5. Катер массой 1 т плывёт под действием трёх сил: силы тяги двигателя 1,5 кН, силы ветра 1 кН и силы сопротивления 0,5 кН, причём сила тяги и сила ветра перпендикулярны друг другу. Каково ускорение катера?
Смотреть решение и ответ
2.6. На расстоянии r = 25 см от центра шероховатого диска покоится тело. Диск начали раскручивать, увеличивая его угловую скорость вращения. Чему равен коэффициент трения тела о диск, если тело начинает скользить по диску при угловой скорости ω = 4,5 рад/с?
Смотреть решение и ответ
Подготовка к ЕГЭ по физике. Задания высокого уровня сложности с развернутыми ответами. ЗАДАНИЕ № 29 (с решениями). Задания 29 — 32 представляют собой расчётные задачи. В текстах заданий нет указаний на требования к полноте решения, эту функцию выполняет общая инструкция. В каждом варианте экзаменационной работы перед заданиями 29 — 32 приведена инструкция, которая в целом отражает требования к полному правильному решению расчётных задач.
Просмотров:
15 491
Особенность задания № 29 заключается в том, что в нем требуется использование материалов не менее чем из двух-трех разделов механики. Актуальные сведения, необходимые для решения задания, приведены в разделе теории. Законы сохранения, силы, действующие в макромире, и другая нужная информация содержится в разделах теории соответствующих типовых заданий по механике.
Задание EF18920
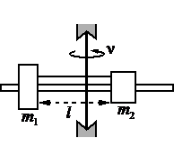
Алгоритм решения
1.Записать исходные данные. Перевести их в СИ.
2.Сделать чертеж, обозначив все силы, действующие на систему тел, их направления. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме для каждого из тел.
4.Записать второй закон Ньютона для каждого из грузов в виде проекций на ось ОХ.
5.Вывести формулу для радиуса окружности, по которой движется любой из грузов.
6.Вывести формулу для вычисления силы натяжения нити, подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные, сразу переведя их в СИ:
• Масса первого груза m1 = 200 г = 0,2 кг.
• Масса первого груза m2 = 300 г = 0,3 кг.
• Длина нити l = 20 см = 0,2 м.
• Натяжение нити с обеих сторон одинаково, следовательно: T1 = T2 = T.
• Частота вращения штанги ν = 600 об./мин. = 10 об./с.
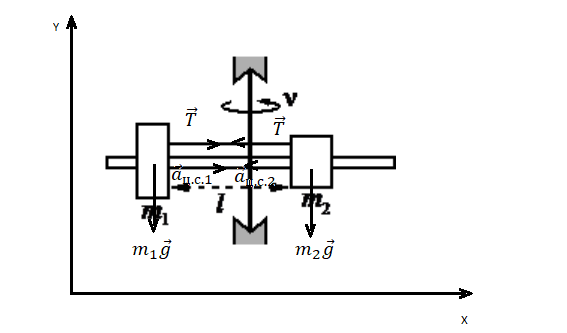
Сделаем чертеж, обозначив все силы. Учтем, что сила натяжения нити равна с обеих сторон. Выберем систему координат, в которой ось ОУ параллельна оси вращения.
Запишем второй закон Ньютона для первого и второго груза соответственно:
Запишем проекции на ось ОХ для каждого из тел:
T = m1aц.с.1
T = m2aц.с.2
Центростремительное ускорение также определяется формулой:
aц.с. = ω2R
Угловая скорость определяется формулой:
ω = 2πν
Следовательно, центростремительное ускорение равно:
aц.с. = 4π2ν2R
Применим эту формулу для обоих грузов:
aц.с.1 = 4π2ν2R1
aц.с.2 = 4π2ν2R2
Сумма радиусов окружностей, по которым вращаются грузы, есть длина нити:
R1 + R2 = l
Выразим радиус окружности, по которой вращается второй груз:
R2 = l – R1
Так как грузы связаны между собой, и ни один из них не перевешивает другой:
m1gR1 = m2gR2
Ускорение свободного падения взаимоуничтожается. Получаем:
Подставим радиус второй окружности и выразим радиус первой окружности:
Следовательно, центростремительное ускорение первого груза равно:
Теперь возьмем проекцию на ось ОХ для первого тела и вставим в формулу найденное центростремительное ускорение для первого тела:
Подставим известные данные и вычислим силу натяжения нити:
pазбирался: Алиса Никитина | обсудить разбор | оценить
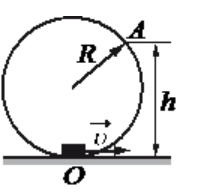
Задание EF18982
Алгоритм решения
1.Записать исходные данные. Перевести единицы измерения величин в СИ.
2.Сделать чертеж и указать все силы, действующие на шайбу в точке А. Указать их направление и выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на ось ОХ.
5.Записать формулу, определяющую кинетическую энергию тела.
6.Применить геометрические законы для нахождения величины радиуса кольца и формулу центростремительного ускорения для нахождения скорости тела.
7.Записать решение в общем виде, подставить исходные данные и произвести вычисления.
Решение
Запишем исходные данные:
• Масса шайбы m = 10 г = 0,01 кг.
• Радиус кольца, по которому перемещалась шайба, составляет R = 0,14 м.
• Высота, с которой шайба упала, равна h = 0,18 м.
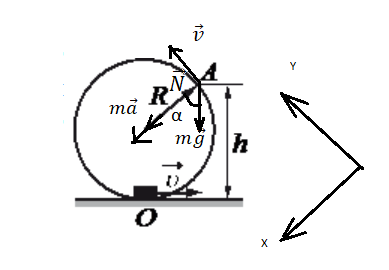
Сделаем чертеж. Выберем систему координат такую, чтобы направление линейной скорости шайбы в точке совпадала с направлением оси ОУ.
Запишем второй закон Ньютона в векторной форме:
Под ускорением в этой записи понимается полное ускорение, составляющими которого является центростремительное и тангенциальное ускорение, направленное касательно к окружности (на рисунке мы его не обозначили, так как оно нам не понадобится).
Запишем проекцию на ось ОХ. Учтем, что в точке А шайба отрывается от кольца и падает. Следовательно, нормальная реакции опоры равна нулю:
mg cosα = maц.с.
Кинетическая энергия тела определяется формулой:
Выразим центростремительное ускорение из проекции на ось ОХ:
Но центростремительное ускорение также определяется формулой:
Приравняем правые части уравнений и получим:
Квадрат скорости будет равен:
Следовательно, кинетическая энергия равна:
Чтобы избавиться от неизвестных величин, обратимся к геометрии:
Из рисунка видно, что высота h есть сумма радиуса окружности и произведения радиуса на косинус угла α:
h = R + Rcosα
Отсюда следует, что:
Rcosα = h – R
Подставим это выражение в формулу кинетической энергии и выполним вычисления:
Отсюда следует, что кинетическая энергия шарика в начале движения равна 2 мДж.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
Энергия, выделенная всеми атомами, равна:
Теперь можем вычислить КПД:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18127
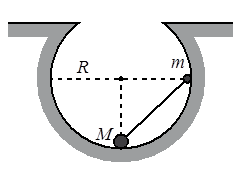
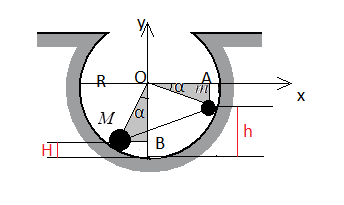
В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Максимальная высота подъёма шарика массой М относительно нижней точки выемки оказалась равной 12 см. Каков радиус выемки R?
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж конечного положения шариков. Обозначить их высоты, выбрать нулевой уровень отсчета потенциальной энергии. Выбрать систему координат.
3.Записать закон сохранения энергии.
4.Выполнить общее решение задачи.
5.Подставить известные данные и выполнить вычисление искомой величины.
Решение
Запишем исходные величины:
• Масса первого шарика: m = 30 г.
• Масса второго шарика: M = 60 г.
• Максимальная высота подъема шарика М: H = 12 см.
Переведем единицы измерения величин в СИ:
30 г = 0,03 кг
60 г = 0,06 кг
12 см = 0,12 м
Выполним чертеж:
Нулевой уровень — нижняя точка выемки.
Запишем закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep = const
В начальном положении кинетическая энергия обоих шариков равна 0. Потенциальная энергия шарика М тоже равна нулю, так как он находится на нулевом уровне. Потенциальная энергия шарика m равна:
Ep0m = mgR
Кинетическая энергия шариков после установления равновесия тоже будет равна нулю. Но b[ потенциальная энергия будет отличной от нуля:
Epm = mgh
EpM = MgH
Поэтому закон сохранения энергии применительно к задаче примет вид:
mgR = mgh + MgH
Преобразуем выражение и получим:
mgR−mgh=MgH
R−h=MgHmg=MHm
При движении гантели по поверхности выемки высоты подъема большого и малого шаров связаны. Рассмотрим прямоугольные треугольники OmA и OMB. Для них справедливы следующие равенства:
MB = mA = R – h
OA = OB = R – H
OM = Om = R
Это дает нам право воспользоваться теоремой Пифагора:
(R−h)2=R2−OA2=R2−(R−H)2
Следовательно:
(R−h)2=R2−(R2−2RH+H2)=2RH−H2
Подставим в это выражение правую часть ранее полученного выражения:
R−h=MHm
(MHm)2=2RH−H2
Теперь можем выразить и вычислить радиус:
2RH=(MHm)2+H2
R=(MHm)2+H22H
R=(Mm)2H2+H2=(0,060,03)20,122+0,122=0,3 (м)
Ответ: 0,3
pазбирался: Алиса Никитина | обсудить разбор | оценить
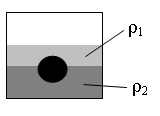
Задание EF18057
Алгоритм решения
1.Записать исходные данные.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в проекции на ось ординат.
5.Выполнить общее решение.
6.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
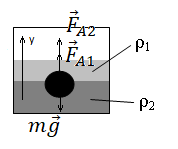
• Плотность первой жидкости: ρ1 = 400 кг/м3.
• Плотность второй жидкости: ρ2 = 2ρ1.
• Объем шарика выше границы раздела двух жидкостей: V1 = V/4.
• Объем шарика выше границы раздела двух жидкостей: V2 = 3V/4.
Построим рисунок и укажем все силы, действующие на шарик:
Запишем второй закон Ньютона в векторном виде:
m→g+→FA1+→FA2=0
Запишем второй закон Ньютона в виде проекции на ось ординат:
mg=FA1+FA2
Выразим массу тела через его объем и плотность, выразим выталкивающие силы через закон Архимеда и получим:
ρVg=ρ1gV1+ρ2gV2
Преобразуем выражение, сократив ускорение свободного падения и подставив выражения для объемов погруженных в жидкости частей тела, а также выражение для плотности второй жидкости:
ρV=ρ1V4+2ρ13V4
Объемы сокращаются. Остается:
ρ=ρ14+2ρ134=7ρ14=7·4004=700 (кгм3)
Ответ: 700
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17513
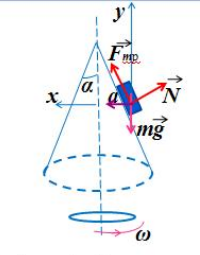
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
Второй закон Ньютона в векторном виде выглядит следующим образом:
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
Максимальное значение силы трения равно:
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
Запишем систему уравнение в следующем виде:
Поделим первое уравнение на второе и получим:
Сделаем сокращения и получим:
Отсюда центростремительное ускорение равно:
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
Отсюда центростремительное ускорение равно:
Выразим искомую величину L:
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
pазбирался: Алиса Никитина | обсудить разбор | оценить