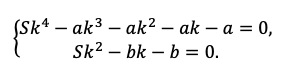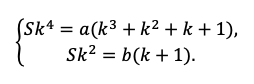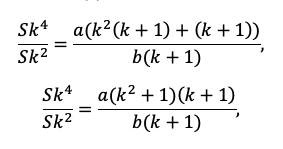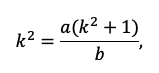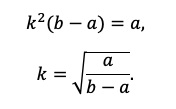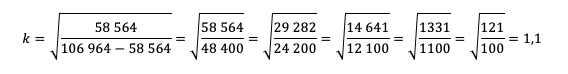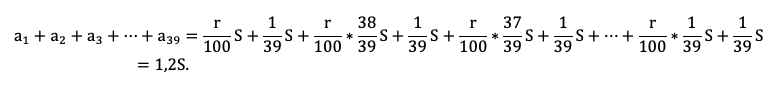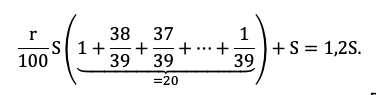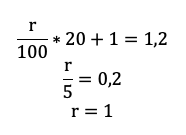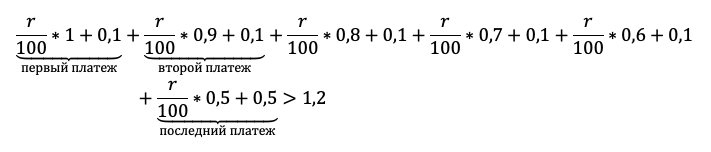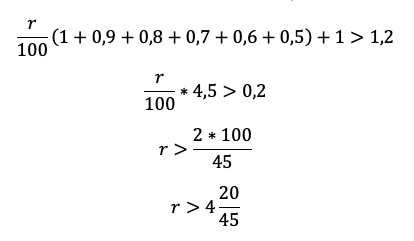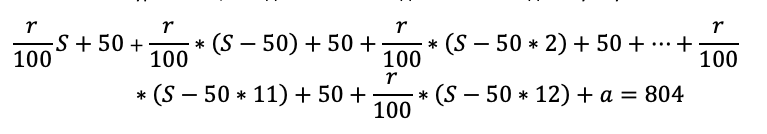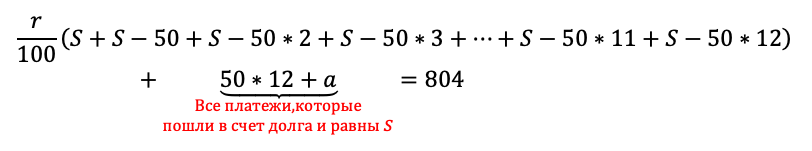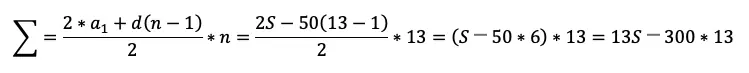Баба Валя, накопив часть своей пенсии, решила улучшить свое материальное положение. Она узнала, что в Спёрбанке от пенсионеров принимают вклады под определенный процент годовых и на этих условиях внесла свои сбережения в ближайшее отделение Спёрбанка. Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры, есть коммерческий банк, в котором процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в Спёрбанке. Баба Валя не доверяла коммерческим банкам, но стремление улучшить свое материальное положение взяло верх. После долгих колебаний и ровно через год после открытия счета в Спёрбанке Баба Валя сняла половину образовавшейся суммы от ее вклада, заявив: «Такой навар меня не устраивает!» и открыла счет в том коммерческом банке, о котором говорила ее соседка, не теряя надежды на значительное улучшение своего материального благосостояния.
Надежды оправдались: через год сумма Бабы Вали в коммерческом банке превысила ее первоначальные кровные сбережения на 65%. Сожалела Баба Валя, что год назад в Спёрбанке сняла не всю сумму, а лишь половину, однако, подумала: «А где же мы не теряли?..» Гендиректор коммерческого банка оказался хорошим: не оставил Бабу Валю без денег.
А каков в Спёрбанке процент годовых для пенсионеров?
В части с развернутым ответом в ЕГЭ по профильной математике есть уникальный номер, к которому школьник почти готов сразу после освоения материала для первых 12-ти заданий. Речь об экономической задаче под номером 17 в ЕГЭ по математике. Конечно, поготовиться придется, но, если повезет с прототипом, баллы можно урвать почти даром!
Прототипы для 17-го номера делятся на три большие группы:
- банковские задачи,
- на ценные бумаги,
- задачи на оптимальный выбор.
В этой статье мы расскажем, как научить ученика структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение. Расскажем, на что обратить внимание ученика, чтобы школьник не потерял баллы из-за неверного оформления.
Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.
- Как работает процент по кредиту?
- На какую сумму начисляется?
- Из каких частей состоит платеж?
- Как уменьшается долг?
На все эти вопросы вам придется ответить. Это отличная возможность показать пользу уроков математики, ведь 17-ый номер — едва ли не самая прикладная задача за весь школьный курс!
Например, можно рассказать о том, какие бывают образовательные кредиты. Вы в курсе, что их дают с 14 лет, а платеж первые годы может быть ничтожным? Школьник об этом точно не знает.
С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике
Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность рассказать школьнику что-то из реальности! Если у вас есть опыт с кредитованием, самое время им поделиться. Если нет, то воспользуйтесь нашим:
- Например, расскажите, что клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Ваши ученики знают, как работает страховка?
- Расскажите о механизме аннуитетного платежа: как часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
- Например, по нашему опыту, в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.
Хорошая новость в том, что в экзаменационных задачах подобной вакханалии не бывает. Долг и проценты или гасятся равномерно, или по заранее известному алгоритму, достаточно просто внимательно прочитать условие.
Еще одно частое упрощение в ЕГЭ — процент там обычно не годовой, а ежемесячный! То есть своим платежом заемщик гасит набежавший за этот месяц процент и уменьшает долг на заданную величину. Удобно.
Мы предлагаем научить школьника упорядочивать данные банковской задачи в ЕГЭ по математике с помощью таблицы. Табличка — не единственный способ решить 17-ый номер, кто-то использует последовательности, кто-то — считает прикладным методом как заправский бухгалтер. Однако наш метод универсален, а значит вы дадите школьнику один алгоритм на все типы банковских задач. Согласитесь, работать с одним алгоритмом проще, чем подбирать разные по ситуации.
Тип 1. Равные платежи
Особенность этого типа заданий в том, что заемщик всегда вносит одинаковые суммы.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
Очевидно, что эта схема должна оказаться у школьника в тетради. Ведь вы же знаете: того, чего нет в тетради, и на уроке-то не было!
Заполняем всю табличку. Учитываем обе ситуации из условия. Для наглядности каждую выделим жирной рамкой.
Теперь остался еще один непростой шаг — перейти от структурированных данных к математической модели. Дайте ученику возможность увидеть, что уже почти составил ее.
Мы получили два уравнения, которые подсветили в табличке оранжевым. Объединим их в систему и решим!
Напомните выпускнику о культуре вычислений! Порой эти задачи составлены так, что неудачная последовательность действий сделает их нерешаемыми без калькулятора. Потому не надо спешить делать первое попавшееся действие, пусть школьник тренируется думать на пару ходов вперед.
Например, разделим одно уравнение на другое, ведь так мы избавимся от одной неизвестной S:
Наше решение не зависит от суммы кредита, S сокращается.
По сути, мы получили уравнение с одной неизвестной, ведь платежи a и b знаем из условия. Выразим k:
Пожалуй, все, проще уже некуда. Подставляем значения!
Тут можно обратить внимание ученика на то, как составители экзамена на самом деле заботятся о нем! Ведь будь задачка хоть чуть-чуть другой, посчитать без калькулятора было бы невозможно.
Вспоминаем, что k=1+r/100, а найти нам надо r.
Ответ: 10%.
Не забудьте после решения расставить акценты в задаче:
Чтобы решить задачу и получить 3 балла, мы:
— Воспользовались простым алгоритмом упорядочивания данных,
— Составили математическую модель,
— Нашли удобный способ решить ее, ВСЕ!
Это и есть алгоритм решения банковской задачи.
Тип 2. Равномерно убывающий долг
В прошлой задаче заемщик платил одинаковую сумму каждый месяц. Тут ему нужно уменьшать долг на одну и ту же величину. То есть за месяц пользования деньгами банк начислил на них процент, клиент теперь должен чуть больше. Своим платежом он оплатит банку проценты, чтобы заем стал таким, как ДО их начисления. А сверху внесет сумму, которая как раз и пойдет на то самое РАВНОМЕРНОЕ уменьшение долга.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
(Считайте, что округления при вычислении платежей не производятся.)
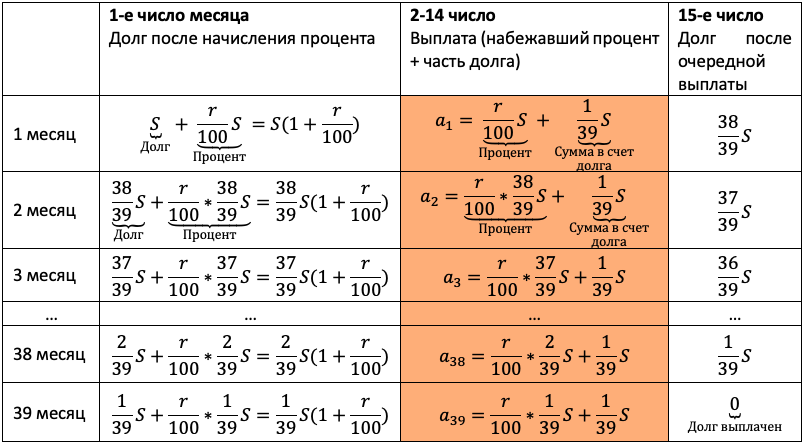
Тут главный элемент в задаче — равномерно убывающий долг. Если мы взяли сумму S на 39 месяцев, и каждый месяц долг должен быть меньше на одинаковую величину, то что это за величина? Пусть правильный ответ 1/39 S даст ученик.
Проиллюстрируйте школьнику, как здорово работает наш алгоритм. Пусть выпускник проговаривает пункты вслух, а вы их выполняйте. Следите, чтобы каждый шаг подопечный фиксировал в тетради:
Продолжаем заполнять табличку. Пусть дальше пробует выпускник, ведь пока сам не попробуешь, не научишься:
Осталось увязать добытую информацию в уравнение или неравенство. Обратите внимание подопечного на то, что ненужных подробностей в задачах ЕГЭ не бывает! Единственная информация в задаче, которую мы до сих пор не использовали — общая сумма выплат. По условию она на 20% больше суммы кредита, то есть равна 1,2S:
Приведем подобные, вынесем общий множитель за скобку:
Решение в итоге снова не зависит от того, какую сумму взяли в долг. Разделим обе части на S и упростим выражение:
Ответ: 1%.
И снова все по нашему алгоритму, ничего нового, кроме него, мы не используем! Не забудьте излучать восторг, иначе школьник не проникнется мощью вашего метода решения.
Тип 3. Долг, убывающий согласно табличке
Задача похожа на прошлую. Разница лишь в том, что кроме процентов нам каждый месяц придется гасить не равную долю долга, а долю согласно таблице.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг(в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн рублей.
Протестируем нашу универсальную табличку в третий раз, доверьте это непростое занятие школьнику. Пусть процессом командует он! По ответам будет ясно, ловит ли он суть.
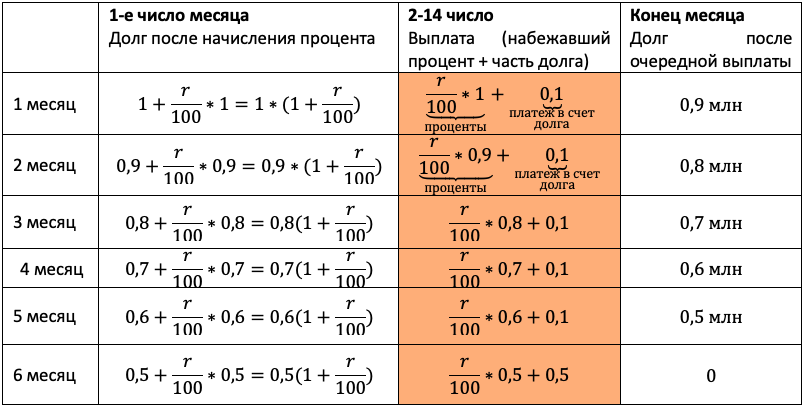
Отличие от прошлого типа будет лишь в том, что в третий столбец мы будем записывать не равномерно убывающий долг, а перенесем остаток долга из таблицы условия. Чтобы не таскать по решению нули, считать будем в миллионах:
Чтобы долг убывал согласно табличке, нам снова каждый раз придется гасить набежавшие проценты и первые 5 месяцев добавлять сверху 0,1 млн. После останется погасить весь остаток.
Акцентируйте внимание на механизме погашения, для школьника он не всегда очевиден.
«По условию нам снова дана общая сумма выплат, значит достаточно просуммировать оранжевый столбец, и уравнение готово», — вероятно, подумает школьник. Подловите его! Уравнение в этой задаче — прямой путь потерять балл! Сумма выплат должна быть БОЛЬШЕ 1,2 млн. Отразим это в модели с помощью неравенства:
Подопечный должен быть уверен в каждом символе в бланке ответа. Даже не пригодившиеся промежуточные вычисления с ошибкой приведут к катастрофе.
Приведем подобные и вынесем общие множители за скобку:
Последний шаг – не забыть, что по условию процент должен быть целым и округлить в верную сторону.
Ответ: 5%.
Правильная математическая модель — это суперважно! К ней проверяющие обязательно придерутся.
Тип 4. Погашение кредита в два этапа.
По сути, это та же прошлая задача, но месяцев больше
В 2017-2018 учебном году составителей экзамена посетило вдохновение, на свет родился вот этот тип банковских задач. Школьники были в шоке, и от страха завалили 17-ый номер. Хотя всего-то нужно было догадаться воспользоваться знаниями об арифметической прогрессии и достать из условия одно немного неочевидное дано!
15-го декабря планируется взять кредит в банке на 13 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 12-й долг должен быть на 50 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 13-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 804 тысячи рублей?
И снова пусть по возможности командует школьник. По крайней мере он уже точно в курсе, что происходит первые 13 месяцев.
Последовательно начисляем процент на остаток долга – считаем выплату – фиксируем остаток долга после выплаты. Сумму кредита возьмем за S.
Научите школьника не спешить с вычислениями. Например, вместо того чтобы написать S-600, мы пишем S-50*12, потому что так удобнее: нам сразу ясно, что речь идет о двенадцатом месяце. Да и потом вычисления будут проще, если мы оставим маленькие числа.
Осталось составить уравнение, и модель готова. В задаче нам снова дали сумму всех выплат:
Как обычно, сгруппируем отдельно слагаемые с r/100, отдельно слагаемые без них:
Вот именно последняя группировка всех платежей в счет долга и оказалась неочевидной. Без нее в задаче остается одна лишняя неизвестная величина, которая рушит все решение.
Осталось привести уравнение к решаемому виду. Для этого надо просуммировать то, что получилось в скобках. Если внимательно приглядеться, то видно, что это сумма арифметической прогрессии:
Посчитаем эту сумму:
Подставляем выражение для суммы в уравнение, заметим, что по условию r=2:

Мы сокращали дробь, пока это было возможно, и в итоге довольно просто получили ответ даже без калькулятора. Ваш подопечный должен научиться также!
Ответ: 700 тысяч.
Зачем использовать формулу суммы прогрессии, если можно посчитать вручную? Все верно, можно. Но это только в данном случае кредит взяли всего на 13 месяцев. А бывают прототипы, когда срок – 21 и больше месяцев. В какой-то момент считать вручную станет совсем долго и неудобно, потому воспользоваться формулой суммы – более универсальный метод.
Чем закончить разбор экономической (банковской) задачи № 17 в ЕГЭ по математике
Чтобы у ученика окончательно сложилась картинка занятия, пробегитесь еще раз по основным выводам:
- Повторите алгоритм заполнения таблицы и решения задачи (да, пятый раз);
- Повторите типы задач и механизм распределения платежа на проценты и долг;
- Напомните, как важно считать культурно и быть уверенным в каждой циферке в бланке;
- Проговорите, что математическая модель должна точно отражать условие задачи.
Как показывает практика, чем больше повторяешь, тем больше шансов, что в голове выпускника останется хоть что-то.
За что дают баллы?
Знание критериев оценивания экономической (банковской) задачи № 17 в ЕГЭ по математике поможетученику чувствовать себя увереннее, ведь выставление баллов — это не какая-то магия и не вредность экспертов. Все правила игры прописаны в нормативных документах.
17-ый номер стоит 3 балла. Чтобы узнать, как их присуждают, мы залезли в методические рекомендации для членов предметных комиссий.
Согласно пояснениям из документа, для получения одного балла мало просто обоснованно составить математическую модель по задаче, надо предложить правильный метод ее анализа.
Два балла получит школьник, который ошибся в вычислениях или не обосновал появление математической модели в решении. Например, согласно методическим рекомендациям, решение на 2 балла выглядит так:
А вот отсутствие промежуточных вычислений хоть и усложняет проверку, но баллы не снимает.
Идеально выполненная первая часть ЕГЭ по профильной математике принесет школьнику всего 62 тестовых балла. Добавим сюда пару ошибок по невнимательности, и останутся совсем крохи — баллов 50, не больше. Для поступления на бюджет мало, а значит необходимо планировать делать вторую часть! Чем раньше школьник это осознает, тем проще будет с ним работать. А банковская задача поможет получить дополнительные баллы с минимальными усилиями.
Однако кредиты – не единственный прототип 17-го номера, и в следующий раз мы расскажем, как научить школьника решать задачи на оптимальный выбор и ценные бумаги.
В 2018 году на ЕГЭ по математике появились задачи, напугавшие многих выпускников. «Это страшно, — говорили они после экзамена. — Никогда такого не было. Решить невозможно».
Конечно же, я сочувствую абитуриентам, для которых ЕГЭ – все-таки большой стресс. Экзамен – это испытание не только знаний, но и хладнокровия, и способности действовать в сложной ситуации. И может быть, сказать себе: «Да, задача необычная, но я знаю общий подход к решению таких задач – справлюсь и на этот раз».
Действительно ли настолько страшны были «банковские» задачи на ЕГЭ по математике 2018 года? Они своеобразны. Их невозможно решить без подготовки, без знания того, как вообще устроены задачи ЕГЭ на кредиты.
Запомним: есть всего два характерных типа «банковских» задач, или задач на кредиты.
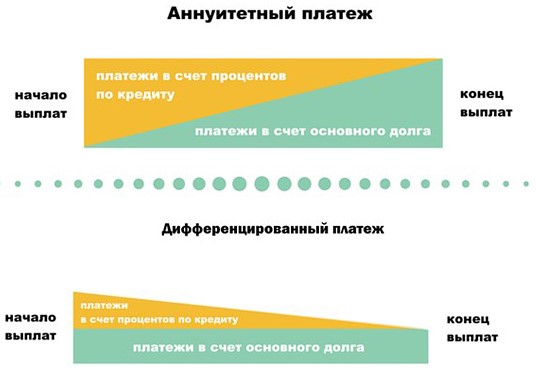
1 тип. Выплаты кредита производятся равными платежами. Эта схема еще называется «аннуитет». К первому типу относятся также все задачи, где известны платежи (или дана закономерность именно для платежей).
2 тип. Выплаты кредита подбираются так, что сумма долга уменьшается равномерно. Это так называемая «схема с дифференцированными платежами». Ко второму типу относятся также задачи, где известна закономерность уменьшения суммы долга.
О двух схемах решения задач на кредиты – мой краткий теоретический материал.
Более подробно я рассказываю теорию и решаю такие задачи на своих мастер-классах и интенсивах. Чтобы узнать о них, подпишись на нашу рассылку.
Посмотрим с этой точки зрения на «банковские» задачи ЕГЭ-2018.
1.
15-го декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1604 тысяч рублей?
Прежде всего, введем переменные. Расчеты будем вести в тысячах рублей.
Пусть S – сумма, которую планируется взять в кредит,
Z – общая сумма выплат, Z = 1604 (тыс. рублей),
Х — ежемесячное уменьшение суммы долга, Х = 30 (тысяч рублей),
p=3% — процент, начисляемый банком ежемесячно.
После первого начисления процентов сумма долга равна После каждого начисления процентов сумма долга увеличивается в
раза. В нашей задаче k = 1,03.
Определим, к какому типу относится задача. Долг уменьшается равномерно (по условию, 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше долга на 15-е число предыдущего месяца). Значит, это задача второго типа. А в задачах второго типа мы рисуем следующую схему:
После первого начисления процентов сумма долга равна kS. Затем, после первой выплаты, сумма долга равна S – X, где Х = 30 (тысяч рублей).
Значит, первая выплата равна kS – (S – X) (смотри схему).
Вторая выплата: k (S – X ) – ( S – 2X).
…
Последняя выплата: k ( S – 20 X).
Найдем общую сумму выплат Z:
Z = kS – (S – X) + k (S – X ) – ( S – 2X) + … + k ( S – 20X) =
= k ( S + S – X + S – 2X + … + S – 20 X) – ( S – X + S – 2X + … + S – 20X).
Мы сгруппировали слагаемые, содержащие множитель k, и те, в которых нет k.
Упростим выражения в скобках:
k (21S – X (1 + 2 + 3+ … + 20)) – (20S – X (1 + 2 + 3+ … + 20)) = Z.
В задачах этого типа (когда сумма долга уменьшается равномерно) применяется формула для суммы арифметической прогрессии:
В этой задаче мы тоже ее используем:
Получим:
k (21 S – 210X ) – 20 S + 210 k = S (21k – 20) – 210 X (k-1) = Z.
Осталось подставить числовые значения:
S ( 21⋅ 1,03 – 20) – 210 ⋅ 30 ⋅ 0,03 = 1604.
Отсюда S = 1100 тысяч рублей = 1 100 000 рублей.
Следующая задача относится к тому же типу. Математическая модель та же самая. Только найти нужно другую величину – процент, начисляемый банком. К тому же количество месяцев, на которое взят кредит, неизвестно.
2.
15-го декабря планируется взять кредит в банке на 1 000 000 рублей на (n+1) месяц. Условия его возврата таковы:
—1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— 15-го числа n-го месяца долг составит 200 тысяч рублей;
— к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.
Как всегда, введем обозначения. Для удобства ведем расчеты в тысячах рублей.
S = 1000000 рублей = 1000 (тыс. рублей) – сумма кредита,
Х = 40 (тыс. рублей) – ежемесячное уменьшение суммы долга,
Z = 1378 (тыс. рублей) – общая сумма выплат,
— коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов.
Рисуем уже знакомую схему погашения кредита.
Первая выплата: kS – (S – X).
Вторая выплата: k (S – X ) – ( S – 2X).
…
Последняя выплата: k ( S – n X).
По условию, 15-го числа n-го месяца долг составит 200 тысяч рублей.
Значит, S – nX = 200. Подставим числовые данные:
1000 – 40 n = 200; тогда n = 20, n + 1 = 21, то есть кредит был взят на 21 месяц. Очень удобно – количество месяцев в этой задаче оказалось таким же, как в предыдущей. Поэтому очень кратко повторим основные моменты решения
Общая сумма выплат Z:
Z = kS – (S – X) + k (S – X ) – ( S – 2X) + … + k ( S – X) =
= k ( S + S – X + S – 2X + … + S – 20 X) – ( S – X + S – 2X + … + S – 20X) =
= k (21S – X (1 + 2 + 3+ … + 20)) – (20S – X (1 + 2 + 3+ … + 20)) =
= k (21 S – 210X ) – 20 S + 210 k = S (21k – 20) – 210 X (k-1).
Мы снова использовали ту же формулу для суммы арифметической прогрессии:
По условию, Z = 1378 (тыс. рублей).
Выразим k из формулы S (21k – 20) – 210 X (k-1) = Z:
Подставим данные из условия задачи.
Ответ: r = 3%.
Третья задача из числа «кошмаров» ЕГЭ-2018 по математике. Та же схема!
3.
15-го декабря планируется взять кредит в банке на сумму 300 тысяч рублей на 21 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 20-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15-го числа 20-го месяца долг составит 100 тысяч рублей;
— к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Тоже задача второго типа – есть информация об уменьшении суммы долга. Точно также будем вести расчеты в тысячах рублей.
Как всегда, введем обозначения. Для удобства ведем расчеты в тысячах рублей.
S = 300 (тыс. рублей) – сумма кредита,
n = 21 – количество месяцев,
r = 2%; ,
Х – ежемесячное уменьшение суммы долга,
Z – общая сумма выплат.
Рисуем ту же схему, что и в предыдущей задаче. По условию, 15-го числа 20-го месяца долг составит 100 тысяч рублей.
Значит, S – 20 X = 100. Подставив данные из условия, найдем, что Х = 10.
Точно так же считаем сумму выплат (смотри задачи 1 и 2).
Z = S (21k – 20) – 210 X (k-1).
Подставляем данные из условия: Z = 300 (21 ⋅ 1,02 – 20) – 210 ⋅ 10 ⋅ 0,02 = 384 (тыс. рублей).
Ответ: 384000 рублей.
Хочешь узнать решения всех сложных задач ЕГЭ? Подпишись на нашу рассылку.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Разбор задачи №17 («Банковская», или «Экономическая») на ЕГЭ по математике 2018 года.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Задачи на проценты»
Открытый банк заданий по теме задачи на проценты. Задания B11 из ЕГЭ по математике (профильный уровень)
Задание №1099
Тип задания: 11
Тема:
Задачи на проценты
Условие
Елена сделала вклад в банк в размере 5500 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Спустя год Наталья положила такую же сумму в этот же банк и на тех же условиях. Ещё через год Елена и Наталья одновременно закрыли вклады и забрали деньги. В результате Елена получила на 739,2 рубля больше, чем получила Наталья. Найдите, какой процент годовых начислял банк по вкладам?
Показать решение
Решение
Пусть процент годовых будет x, тогда через год вклад Елены составил:
5500 + 0, 01x cdot 5500 = 5500(1 + 0,01x) рублей, а ещё через год — 5500(1 + 0,01x)^2 рублей. Вклад Натальи лежал в банке только год, потому он равен 5500(1 + 0,01x) рублей. А разность между получившимися вкладами Елены и Натальи составила 739,2 рубля.
Составим и решим уравнение:
5500(1+ 0,01x)^2-5500(1+0,01x)= 739,2,
(1+0,01x)^2-(1+0,01x)=0,1344,
x^2+100x-1344=0,
x_1=-112,enspace x_2=12.
Банк начислял 12% годовых.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1098
Тип задания: 11
Тема:
Задачи на проценты
Условие
Предприниматель Петров получил в 2005 году прибыль в размере 12,000 рублей. Каждый следующий год его прибыль увеличивалась на 110% по сравнению с предыдущим годом. Сколько рублей заработал Петров за 2008 год?
Показать решение
Решение
В 2005 году прибыль составляла 12,000 рублей, каждый следующий год она увеличивалась на 110%, то есть становилась 210% = 2,1 от предыдущего года. Через три года она будет равна 12,000 cdot 2,1^3 = 111,132 рубля.
Ответ
111132
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1097
Тип задания: 11
Тема:
Задачи на проценты
Условие
Имеется два сплава. Первый сплав содержит 12% железа, второй — 28% железа. Масса второго сплава больше массы первого на 2 кг. Из этих двух сплавов изготовили третий сплав с содержанием железа 21%. Найдите массу третьего сплава. Ответ дайте в килограммах.
Показать решение
Решение
Обозначим массу первого сплава через x кг. Тогда масса второго сплава (x + 2) кг. Содержание железа в первом сплаве равно 0,12x кг, во втором сплаве — 0,28(x + 2) кг. Третий сплав имеет массу x + x + 2 = 2x + 2 (кг), и в нём содержание железа равно 2(x + 1) cdot 0,21 = 0,42(x + 1) кг.
Составим и решим уравнение:
0,12x+ 0,28(x + 2) = 0,42(x+1),
6x + 14(x + 2) = 21(x + 1),
x = 7.
Третий сплав имеет массу 2 cdot 7 + 2 = 16 (кг).
Ответ
16
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №942
Тип задания: 11
Тема:
Задачи на проценты
Условие
Цена телевизора в магазине ежеквартально (в квартале — три месяца) уменьшается на одно и то же число процентов от предыдущей цены. Известно, что телевизор, стоимостью 50 000 рублей был продан спустя два квартала за 41 405 рублей. Найдите, на сколько процентов ежеквартально уменьшалась стоимость телевизора.
Показать решение
Решение
Цена телевизора первоначально была 50 000 руб. Через квартал она стала 50,000-50,000cdot0,01x = 50,000(1-0,01x) рублей, где x — количество процентов, на которые уменьшается ежеквартально цена телевизора. Через два квартала его цена стала
50,000(1-0,01x)(1-0,01x)=50,000(1-0,01x)^2.
Составим и решим уравнение:
50,000(1-0,01x)^2=41,405,
(1-0,01x)^2=0,8281,
1-0,01x=0,91,
x=9.
Итак, на 9 процентов уменьшалась цена телевизора ежеквартально.
Ответ
9
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №941
Тип задания: 11
Тема:
Задачи на проценты
Условие
В 2005 году в посёлке проживало 55 000 человек. В 2006 году, в результате строительства новых домов, число жителей увеличилось на 6%, а в 2007 году — на 10% по отношению к 2006 году. Найдите, число жителей посёлка в 2007 году.
Показать решение
Решение
В 2006 году число жителей посёлка выросло на 6%, т.е. стало 106%, что равно 55,000 cdot 1,06 = 58,300 (жителей). В 2007 году число жителей посёлка выросло на 10% (стало 110%) по сравнению с 2006 годом, т.е. число жителей посёлка стало 58,300 cdot 1,1 = 64,130 человек.
Ответ
64130
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №940
Тип задания: 11
Тема:
Задачи на проценты
Условие
В сосуд, содержащий 3 литра 14-процентного водного раствора некоторого вещества, добавили 4 литра воды. Найдите концентрацию (в процентах) получившегося после смешивания раствора.
Показать решение
Решение
В 3 литрах 14%-ного водного раствора содержится 3cdot0,14=0,42 л. некоторого вещества. Добавили 4 литра воды, стало 7 литров раствора. В этих 7 литрах нового раствора — 0,42 л некоторого вещества. Найдём концентрацию нового раствора: 0,42:7cdot100=6%.
Ответ
6
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №329
Тип задания: 11
Тема:
Задачи на проценты
Условие
Строительные фирмы учредили компанию с уставным капиталом 150 млн рублей. Первая фирма внесла 20% уставного капитала, вторая фирма — 22,5 млн рублей, третья — 0,3 уставного капитала, четвертая фирма внесла оставшуюся часть.
По договоренности ежегодная прибыль между фирмами будет расформирована пропорционально внесенным в уставный капитал вкладам. Какую сумму получит четвертая фирма, если прибыль составила 100 млн рублей? Ответ дайте в млн рублей.
Показать решение
Решение
Первая форма — 150cdot20:100=30 (млн руб.).
Вторая фирма — 22,5 (млн руб.).
Третья фирма — 0,3cdot150=45 (млн руб.).
Четвертая фирма — 150-(30+22,5+45)=52,5 (млн руб.).
Часть уставного капитала, который составляет взнос четвертой фирмы: frac{52,5}{150}=0,35.
Найдем сумму от прибыли, причитающуюся четвертой фирме: 100cdot0,35=35 (млн руб.).
Ответ
35
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №327
Тип задания: 11
Тема:
Задачи на проценты
Условие
В результате смешивания 25%-го и 15%-го растворов серной кислоты было получено 750 г 20%-го раствора. Сколько граммов 15%-го раствора было использовано?
Показать решение
Решение
Пусть x г было взято 15%-го раствора, тогда (750-x) г было взято 25%-го раствора.
frac{xcdot15}{100}=(0,15x) г кислоты содержал 15%-й раствор.
frac{(750-x)cdot25}{100}=(187,5-0,25x) г кислоты содержал 25%-й раствор.
В результате смешивания получили 20%-й раствор, который содержал frac{750cdot20}{100}=150 г кислоты.
Составим и решим уравнение.
0,15x+187,5-0,25x=150,
0,1x=37,5,
x=375.
375 г — масса 15%-го раствора.
Ответ
375
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №87
Тип задания: 11
Тема:
Задачи на проценты
Условие
Имеются два куска металла массой 80 г и 70 г, которые содержат различную концентрацию серебра. Если сплавить эти два металла, то на выходе получится металл, который будет содержать 63% серебра. Если же сплавить одинаковые массы этих металлов, то результатом будет сплав, содержащий 65% серебра. Найдите, сколько граммов серебра находится в первом куске металла.
Показать решение
Решение
Пусть в первом сплаве концентрация серебра составляет x1%, во втором – x2%. Соответственно в первом сплаве находится 80x1 г серебра, а во втором – 70x2 г.
При сплавлении металлов образуется третий сплав массой 150 г, который содержит x1 + x2 г серебра. По условию задачи, концентрация серебра в нем составляет 63%, т.е. масса серебра равна 0,63·150. Составим уравнение:
80x1 + 70x2 = 0,63·150
При сплавлении равных масс металлов, концентрация серебра в новом металле составляет 65%. Т.е.:
x1 + x2 = 2·0,65
Составляем и решаем систему уравнений:
begin{cases} 80 x_1 + 70 x_2 = 0,63 cdot 150\ x_1 + x_2=2 cdot 0,65end{cases}
begin{cases} 80x_1+70x_2=94,5\ x_1 + x_2= 1,3 end{cases}
Из второго уравнения выразим x2:
x2 = 1,3 − x1
Подставим это значение в первое уравнение системы:
80x1 + 70x2 = 94,5
80x1 + 70(1,3 − x1) = 94,5
80x1 + 91 − 70x1 = 94,5
10x1 = 3,5
x1 = 0,35
Как указывалось выше, в первом сплаве содержится 80x1 г серебра. Вычисляем:
80·x1 = 80·0,35 = 28 г серебра содержится в 80 г сплава.
Ответ
28
Задание №56
Тип задания: 11
Тема:
Задачи на проценты
Условие
В двух сплавах имеется различное содержание кобальта. В первом – 25%, во втором – 30% кобальта. На производстве из них был получен третий сплав общей массой 150 кг, в котором содержится 28% кобальта. Определите разницу в весе двух сплавов. Ответ дайте в килограммах.
Показать решение
Решение
Пусть x – масса первого сплава. Тогда масса второго сплава равна 150 − x. В первом сплаве содержится 25% никеля, т.е 0,25·x, а во втором 30% никеля, т.е. 0,3 cdot (150 — x). Третий сплав имеет массу 150 кг и содержит массы двух сплавов с содержанием никеля 28%, т.е. 0,28 cdot 150. Зная эти значения, можем составить уравнение:
0,25x+0,3cdot (150-x)=0,28cdot 150
0,25x+45-0,3x=42
0,3x-0,25x=45-42
0,05x=3
x=60
Масса первого сплава равна 60 кг. Масса второго равна 150 − 60 = 90 кг. Разница в весе сплавов составляет 90 − 60 = 30 кг.
Ответ
30
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
17. Сложные задачи прикладного характера
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи про банковский вклад
Банковский вклад — это сумма денег, переданная банку на хранение с целью получить доход в виде начисленных процентов.
Раз в какой-то промежуток времени (в задачах это, как правило, месяц или год) банк начисляет на текущую сумму некоторое количество (r%) процентов.
Раз в год после начисления процентов клиент, как правило, имеет право доложить на счет любую сумму денег. Также клиент имеет право снимать со счета любую сумму (естественно, не превышающую имеющуюся). Время, когда он может это сделать, указывается в задаче.
Пример: В январе (2014) года клиент положил в банк (30,000) рублей под (10%) годовых, которые банк начисляет раз в год в декабре. Сколько рублей будет на счете у клиента в январе (2017) года?
То, что банк начисляет на текущую сумму (10%), значит, что после начисления процентов сумма будет составлять (110%) от суммы, находящейся на счете до начисления процентов.
Составим таблицу: [begin{array}{|l|c|c|}
hline text{Год}&text{Сумма на счете до начисления} %&text{Сумма на счете после начисления} %\
&text{(январь)}&text{(декабрь)}\
hline 2014&30,000&1,1cdot 30,000\
hline 2015&1,1cdot 30,000&1,1^2cdot 30,000\
hline 2016&1,1^2cdot 30,000&1,1^3cdot 30,000\
hline
end{array}]
Таким образом, в декабре (2016) года после начисления процентов на счете у клиента будет (1,1^3cdot 30,000) рублей. Эта же сумма будет у него на счете и в январе (2017) года (т.к. проценты начисляются только в декабре).
Значит, ответом будет (39,930) рублей.
Задание
1
#2934
Уровень задания: Равен ЕГЭ
Клиент вложил некоторую сумму под (10%) годовых, начисляемых на вклад раз в год. Известно, что в конце первого года (после начисления процентов) он снял со своего счета (10%) от имеющейся на тот момент суммы, а в конце второго года (также после начисления процентов) он доложил на счет (10%) от имеющейся суммы. Определите, в конце третьего года (после начисления процентов) увеличилась или уменьшилась сумма на счете после таких манипуляций по сравнению с первоначальным вкладом и на сколько процентов.
Пусть клиент сделал вклад в размере (A) рублей. Тогда после начисления процентов в первый год на счете у него уже будет (1,1A) рублей. Так как он снял (10%) от этой суммы, то у него осталось (90%) или (0,9cdot 1,1A) рублей.
Тогда в конце второго года банк снова начислил проценты и сумма на счете стала равна (1,1cdot (0,9cdot 1,1A)) рублей. Далее он доложил (10%), следовательно, на счете у него стало (110%) или (1,1cdot (1,1cdot (0,9cdot 1,1A))) рублей.
На третьем году после начисления процентов у него стало (1,1cdot
1,1cdot (1,1cdot (0,9cdot 1,1A))) рублей.
Удобно следить за данными операциями, составив таблицу: [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& 1,1A& -,0,1cdot (1,1A)\
hline 2&0,9cdot (1,1A)& 1,1cdot (0,9cdot 1,1A)& +,0,1cdot (1,1cdot 0,9cdot 1,1A)\
hline 3& 1,1cdot (1,1cdot 0,9cdot 1,1A)& 1,1cdot (1,1cdot 1,1cdot 0,9cdot 1,1A)&\
hline
end{array}]
Следовательно, на счете у него стало [1,1^4cdot 0,9A=1,31769A,] что больше первоначального вклада (A) на (31,769%).
Ответ: 31,769
Задание
2
#2841
Уровень задания: Равен ЕГЭ
Владелец автосалона решил разделить свой капитал на (3) части и вложить их в (3) различных банка, причем годовые процентные ставки в этих банках относятся как (2:3:5). В каком отношении он должен поделить свой капитал, чтобы через год чистая прибыль от вкладов во всех трех банках была одинакова?
Обозначим за (2y) процентную ставку в первом банке, тогда в остальных банках ставки будут (3y%) и (5y%). Пусть вклад в первый банк составил (A_{1}), во второй – (A_{2}), в третий – (A_{3}). Составим таблицу:
[begin{array}{|l|c|c|c|}
hline text{Банк}&text{Размер вклада до} &text{Размер вклада после} &text{Чистая прибыль}\
&text{начисления }%&text{начисления }%&\
hline &&&\
1&A_{1} &dfrac{100+2y}{100}cdot A_{1}&A_{1}cdot left(dfrac{100+2y}{100}-1right)\
&&&\
hline &&&\
2&A_{2} &dfrac{100+3y}{100}cdot A_{2}&A_{2}cdot left(dfrac{100+3y}{100}-1right)\
&&&\
hline &&&\
3&A_{3} &dfrac{100+5y}{100}cdot A_{3}&A_{3}cdot left(dfrac{100+5y}{100}-1right)\
&&&\
hline
end{array}]
Т.к. чистая прибыль во всех банках должна быть одинакова, то
(A_{1}cdot left(dfrac{100+2y}{100}-1right)=A_{2}cdot
left(dfrac{100+3y}{100}-1right)=A_{3}cdot
left(dfrac{100+5y}{100}-1right)
Leftrightarrow )
(2A_{1}=3A_{2}=5A_{3} Rightarrow A_{1}:A_{2}:A_{3}=15:10:6).
Ответ:
(15:10:6).
Задание
3
#2840
Уровень задания: Равен ЕГЭ
Алексей решил внести некоторую сумму (A) рублей в банк под целое число (y) процентов годовых. Каждый год после начисления процентов он дополнительно вносит на счет сумму, равную половине от той, которая находилась на счете у Алексея в начале текущего года. Какая наименьшая процентная ставка (y) должна быть у банка, чтобы к концу третьего года (после внесения третьей дополнительной суммы) сумма на счете была не менее (8A) рублей?
Составим таблицу, обозначив за (t=dfrac{100+y}{100}): [begin{array}{|l|c|c|c|}
hline text{Год} & text{Сумма на счете} & text{Сумма на счете} & text{Сумма на счете}\
& text{до начисления }% & text{после начисления }% & text{после дополнительного взноса} \
hline &&&\
1 & A & tA & tA+frac{1}{2}A\
&&&\
hline &&&\
2 & tA+frac{1}{2}A & t(tA+frac{1}{2}A) & t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A) \
&&&\
hline &&&\
3 & t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A) & t(t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A)) & t(t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A))+\
&&&\
&&& +frac{1}{2}(t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A))\
&&&\
hline
end{array}]
По условию итоговая сумма на счете должна быть не менее (8A
Rightarrow)
(t(t(tA+frac{A}{2})+frac{1}{2}(tA+frac{1}{2}A))+frac{1}{2}(t(tA+frac{1}{2}A)+frac{1}{2}(tA+frac{1}{2}A))
geqslant 8A)
Преобразовав левую часть неравенства, получим:
(t^3A+dfrac{3t^2A}{2}+dfrac{3tA}{4}+dfrac{A}{8} geqslant 8A
Longleftrightarrow dfrac{A(2t+1)^3}{8} geqslant 8A)
Решив данное неравенство, получим: (t geqslant 1,5 Rightarrow y
geqslant
50)
Таким образом, наименьшее целое значение (y=50%).
Ответ:
(50%).
Задание
4
#2936
Уровень задания: Равен ЕГЭ
В банке оформили два одинаковых вклада под один и тот же процент годовых на 3 года. По первому вкладу были проделаны следующие манипуляции: в конце первого года (после начисления процентов) со счета было снято (20%) от имеющейся там суммы, а в конце второго (после начисления процентов) доложено (30%) от имеющейся там суммы. По второму вкладу: в конце первого года (после начисления процентов) на счет было доложено (20%) от имеющейся там суммы, а в конце второго (после начисления процентов) снято (30%) от имеющейся там суммы.
Определите, на каком из двух счетов в конце третьего года после проделанных действий оказалось больше денег? Найдите отношение суммы, находящейся на первом счете, к сумме, находящейся на втором счете.
Пусть оба вклада были размером (A) рублей. Пусть после начисления процентов вклад увеличивался в (t) раз.
Составим таблицу для первого вклада: [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& tA
& -,0,2cdot (tA)\
hline 2&0,8cdot (tA)& tcdot (0,8cdot tA)
& +,0,3cdot (tcdot 0,8cdot tA)\
hline 3& 1,3cdot (tcdot 0,8cdot tA)& tcdot (1,3cdot tcdot 0,8cdot tA)&\
hline
end{array}]
Следовательно, в конце третьего года на счете было [1,3cdot
0,8cdot t^3A=1,04t^3A quad {small{text{рублей.}}}]
Составим таблицу для второго вклада: [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& tA
& +,0,2cdot (tA)\
hline 2&1,2cdot (tA)& tcdot (1,2cdot tA)
& -,0,3cdot (tcdot 1,2cdot tA)\
hline 3& 0,7cdot (tcdot 1,2cdot tA)& tcdot (0,7cdot tcdot 1,2cdot tA)&\
hline
end{array}]
Следовательно, в конце третьего года на счете было [1,2cdot
0,7cdot t^3A=0,84t^3A quad {small{text{рублей.}}}]
Заметим, что по первому вкладу на счете оказалась большая сумма. Отношение равно [1,04:0,84=26:21.]
Ответ:
26:21
Задание
5
#2935
Уровень задания: Равен ЕГЭ
Ваня сделал вклад в банке на 3 года. Раз в год банк начисляет на сумму, находящуюся на счете, некоторое количество процентов. У Вани есть возможность в один из первых двух лет (после начисления процентов) снять со счета (20%) от имеющейся там суммы, а в другой год (из первых двух лет) — доложить также (20%) от имеющейся там суммы. Или сделать наоборот. Определите, какое из этих действий спустя 3 года принесет Ване большую выгоду и сколько процентов составит эта выгода?
Пусть Ваня положил в банк (A) рублей. Пусть каждый год банк увеличивает сумму, находящуюся на счете, в (t) раз. Рассмотрим два случая:
1) сначала он снял (20%), затем доложил. [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& tA
& -,0,2cdot (tA)\
hline 2&0,8cdot (tA)& tcdot (0,8cdot tA)
& +,0,2cdot (tcdot 0,8cdot tA)\
hline 3& 1,2cdot (tcdot 0,8cdot tA)& tcdot (1,2cdot tcdot 0,8cdot tA)&\
hline
end{array}]
2) сначала он доложил (20%), затем снял. [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма до начисления }%
&text{Сумма после начисления }%&text{Манипуляции}\
hline 1& A& tA
& +,0,2cdot (tA)\
hline 2&1,2cdot (tA)& tcdot (1,2cdot tA)
& -,0,2cdot (tcdot 1,2cdot tA)\
hline 3& 0,8cdot (tcdot 1,2cdot tA)& tcdot (0,8cdot tcdot 1,2cdot tA)&\
hline
end{array}]
Таким образом, мы видим, что в обоих случаях в конце третьего года на счете у Вани будет [0,8cdot 1,2cdot t^3A quad {small{text{рублей.}}}]
Следовательно, выгода составляет (0%).
Ответ: 0
Задание
6
#2937
Уровень задания: Равен ЕГЭ
В феврале женщина оформила в банке вклад на 4 года. Каждый год в ноябре банк начисляет на вклад (8%). В декабре первого года пользования услугами данного банка женщина решила купить квартиру и сняла для этой цели со своего счета (8) млн. рублей. Ровно через два года она продала эту квартиру и сразу же вернула на счет в банке те же (8) млн. рублей. Определить, сколько рублей потеряла по истечении срока действия вклада из-за подобных действий эта женщина.
Пусть размер вклада составил (A) млн. рублей. Составим таблицу, описывающую действия, происходившие со вкладом: [begin{array}{|l|c|c|c|}
hline text{Номер года}&text{Сумма в феврале}
&text{Сумма в ноябре}&text{Манипуляции}\
hline 1& A & 1,08A & -,8\
hline 2& 1,08A-8 & 1,08 (1,08A-8) & \
hline 3& 1,08 (1,08A-8) & 1,08^2 (1,08A-8) & +,8\
hline 4&1,08^2 (1,08A-8)+8 & 1,08(1,08^2 (1,08A-8)+8)&\
hline
end{array}]
Таким образом, спустя четыре года на счете у женщины было [1,08(1,08^2 (1,08A-8)+8)=1,08^4A-8cdot 1,08(1,08-1)(1,08+1) quad {small{text{млн. рублей}}}]
Если бы она не совершала данные манипуляции, то каждый год ее вклад увеличивался бы в (1,08) раз и к концу четвертого года составил бы (1,08^4A) млн. рублей. Следовательно, из-за подобных действий ее вклад уменьшился на [8cdot 1,08(1,08-1)(1,08+1)=8cdot 1,08cdot 0,08cdot 2,08=1,437696quad {small{text{млн. рублей}}}]
Ответ:
(1,437,696) рублей
Задание
7
#2932
Уровень задания: Равен ЕГЭ
В январе 2014 года Андрей сделал вклад в размере (6,640,000) рублей под (y) процентов годовых. В феврале 2014 года он захотел купить квартиру стоимостью (9) млн. рублей, но решил для этого взять кредит под (21%) годовых на 15 лет, который необходимо выплачивать дифференцированными платежами. Найдите наименьшее число (y), чтобы процентов, начисляемых на его вклад каждый год, было достаточно для того, чтобы вносить платежи в счет погашения кредита.
Заметим, что так как кредит должен выплачиваться дифференцированными платежами, то из их определения следует, что первый платеж по кредиту будет наибольшим среди всех платежей.
Так как каждый платеж по такому кредиту состоит из двух частей: (frac1{15}) часть от (9) млн. рублей плюс проценты, “набежавшие” на долг за текущий год, то первый платеж будет равен [dfrac1{15}cdot 9000+0,21cdot 9000 {small{text{тыс. рублей.}}}] (так как в первый год пользования кредитом долг равен (9) млн. рублей или, что то же самое, (9000) тыс. рублей)
Рассмотрим вклад. В первый год на вклад “набегут” проценты в размере (0,01ycdot 6640) тыс. рублей. Этой суммы должно хватить для того, чтобы сделать первый платеж. Следовательно, [0,01ycdot 6640geqslant dfrac1{15}cdot 9000+0,21cdot 9000 qquad (*)]
Заметим, что таким образом, если он снимет в первый год со счета не более (0,01ycdot 6640) тыс. рублей, то на счете у него останется как минимум (6640) тыс. рублей, то есть точно не меньше, чем было в начале первого года. Следовательно, “набежавших” процентов во второй год также хватит на то, чтобы сделать второй платеж (ведь он меньше первого платежа!). Такое же рассуждение относится и к всем следующим годам.
Следовательно, нам важно, чтобы именно первых “набежавших” процентов хватило на то, чтобы сделать первый платеж.
[ygeqslant dfrac{83}3cdot dfrac{9000}{6640} quadRightarrowquad
ygeqslant dfrac{3000}{80}=37frac12]
Следовательно, наименьшее подходящее (y) равно (37,5%).
Ответ: 37,5
Во время сдачи ЕГЭ по математике многие выпускники сталкиваются с проблемой решения задач по банковским вкладам и кредитам. Данная тематика встречается в тестовых заданиях довольно редко, поэтому ей уделяется недостаточно внимания при подготовке. Чтобы легко справляться с упражнениями, обращайтесь к нашему онлайн-порталу. Вы научитесь быстро находить правильные ответы и сможете решать примеры различной сложности.
«Школково» — залог успешной сдачи заключительного аттестационного тестирования!
На нашем сайте представлены все материалы, которые необходимы для подготовки к Единому государственному экзамену по математике. Наши преподаватели собрали и подали информацию по теме в наиболее простой и понятной форме. Благодаря такому подходу занятия проходят быстро и легко.
Чтобы подготовка к итоговому тестированию проходила максимально результативно, советуем воспользоваться предложенным нами алгоритмом действий.
Зайдите в раздел «Теоретическая справка», где размещены самые необходимые правила, формулы и простейшие примеры решения типовых экономических задач. Внимательно ознакомьтесь с материалами.
После этого переходите в раздел «Каталоги». Там собрано множество упражнений различного уровня сложности. Советуем начать с простых задач и постепенно переходить к более трудным. Так вы сможете определить свои слабые стороны и сделать упор на решении определенных упражнений.
Если у вас возникли проблемы с каким-либо примером на тему «Решение задач по банковским вкладам и кредитам», его можно добавить в «Избранное». Задание не потеряется, и вы сможете вернуться к его выполнению самостоятельно или вместе с преподавателем.
База упражнений на нашем портале постоянно обновляется и дополняется. Поэтому школьники каждый день получают совершенно новые задания, соответствующие уровню их текущих навыков. Такой подход значительно отличается от стандартных занятий с использованием школьных пособий. Выпускники совершенствуют свои знания, а не просто заучивают, как решать типовые примеры, предложенные в учебниках.
Начните подготовку на портале «Школково» уже сегодня, и результат не заставит себя ждать! Всего через несколько дней регулярных занятий вы заметите, что с легкостью справляетесь с теми упражнениями, которые ранее вызывали сложности.
Обратите внимание, что на нашем портале могут заниматься все желающие. Для того чтобы сохранить и отслеживать прогресс, зарегистрируйтесь на официальном сайте shkolkovo.net. Желаем приятной подготовки к Единому государственному экзамену!

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Вклады и кредиты
Задание № 17 КИМ ЕГЭ по математике профильного уровня
Текстовая задача с экономическим содержанием – относительно новый вид заданий, появившихся в КИМ ЕГЭ профильного уровня, хотя задачи «на проценты» в вариантах вступительных экзаменов в вузы встречались в «доегэшную пору» достаточно часто, особенно если речь шла об экономических специальностях.
Решение таких задач связано со знанием некоторых специфических математических моделей из области экономики, умением переводить сформулированные в виде текста условия в уравнения и неравенства и пониманием того, как решения полученных уравнений и неравенств соотносятся с тем, что написано в условии задачи, – то есть какой смысл имеют полученные результаты.
С чего начать подготовку к решению экономической задачи? Прежде всего, стоит вспомнить основные правила решения текстовых задач вообще (они пригодятся и для решения более простой текстовой задачи № 11 варианта КИМ).
Решение любой текстовой задачи складывается из нескольких основных моментов:
• чтение условия задачи; читайте его до тех пор, покуда сможете, не подглядывая в текст, объяснять суть описанного в задаче процесса (без конкретных числовых данных, конечно, – зазубривать ничего не нужно);
• выбор переменных; для каждого типа задач существуют рекомендации, какие величины лучше всего обозначать как переменные (и это не всегда те величины, о которых идет речь в вопросе задачи); переменных при решении текстовой задачи нужно вводить столько, сколько их нужно для того, чтобы просто и логично составить уравнения и неравенства (не бойтесь, если переменных оказалось слишком много – например, больше, чем число уравнений: если вы все делаете правильно, то «лишние» переменные взаимно уничтожатся или сократятся; еще один вариант – в процессе решения надо будет найти не сами переменные по отдельности, а какую-либо их комбинацию);
• составление уравнений и неравенств, формализация того, что необходимо найти в процессе решения задачи; при составлении уравнений обращайте внимание на единицы измерения – они должны быть одинаковыми для всех одноименных величин;
• решение полученного уравнения, неравенства или системы;
• исследование полученного результата и нахождение ответа на вопрос задачи.
Рекомендую вам «держать в голове» эти основные шаги решения текстовой задачи.
На следующем этапе нужно выяснить, насколько хорошо учащиеся владеют таким понятием как «процент». Начать надо с темы «Вычисление “простых” процентов». Для этого можно порешать задачи на проценты прототипа 11 ЕГЭ.
Далее переходим к изучению «Сложных процентов».
Пропускать данный раздел нельзя, т.к. в дальнейшем формулы сложных процентов мы будем использовать при решении задач с аннуитетными платежами.
Сложные проценты — эффект часто встречающийся в экономике и финансах, когда проценты прибыли в конце каждого периода прибавляются к основной сумме и полученная величина в дальнейшем становится исходной для начисления новых процентов.
Формула вычисления сложных процентов:

или 
Где S— размер первоначального вклада;

r — процентная ставка за расчетный период (день, месяц, год, …);
n — количество расчетных периодов.
Вывод формулы вычисления сложных процентов выполнить несложно и лучше вместе с учениками вывести данное соотношение.
Решение экономической задачи целесообразно начинать:
1) с анализа данных в задаче и структурирования их в виде таблицы; ( самое важное!)
2) с представления решения задачи в виде понятного, а значит простого алгоритма действий. Алгоритм – запоминаем!
Выполнив первые 2 пункта, вы и построите математическую модель.
Далее решение сводится к исследованию этой модели и получению результата.
И, помните, что каждый тип задачи вы разбираете вместе с учениками, а потом они самостоятельно решают парные задачи каждого типа!
1. Задачи на «сложные» проценты.
1-1. Вкладчик внес в банк 500000 рублей под 20% годовых. В конце каждого года из первых трех лет после начисления процентов он дополнительно вносил одну и ту же сумму. К концу четвёртого года его вклад стал равным 1364400 рублей. Какую сумму в рублях дополнительно вносил вкладчик в течение каждого из первых трех лет?
Решение.
S– вклад, S= 500 000 рублей,
r=20% — процент годовых по вкладу,

|
Год |
Сумма на счете в начале года |
Сумма на счете после начисления % |
Платеж |
Остаток на счете в конце года |
|
1 |
S |
Sm |
x |
Sm+x |
|
2 |
Sm+x |
Sm2+xm |
x |
Sm2+xm+x |
|
3 |
Sm2+xm+x |
Sm3+xm2+xm |
x |
Sm3+xm2+xm+x |
|
4 |
Sm3+xm2+xm+x |
Sm4+xm3+xm2+xm |
— |
Sm4+xm3+xm2+xm |
Можно использовать формулы:
Парная задача
1-2. Вкладчик внёс в банк 500000 рублей под 20% годовых. В конце каждого из первых трёх лет после начисления процентов он снимал одну и ту же сумму. К концу четвертого года его вклад стал равным 927600 рублей. Какую сумму вкладчик снимал в течение каждого из первых трёх лет?
Ответ: 25000 рублей.
2. Задачи на кредиты (платеж равными взносами), аннуитетные платежи.
Аннуитетный платёж отличает специфика расчёта и выплат – равные части в течение всего срока кредитования, состоящие из кредитного процента и суммы основного долга. Современные банки практикуют преимущественно аннуитетные платежи при кредитовании, ввиду высокой прибыли по процентам.
2. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
– в январе каждого года долг увеличивается на 20% по сравнению с предыдущим годом;
– с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, какую сумму взяли в кредит, если известно, что кредит был выплачен четырьмя равными платежами (то есть за четыре года) и общая сумма выплат составила 311040 рублей.
Решение.
S–сумма кредита, Sk-общая сумма выплат,
r=20% — процент годовых по вкладу,

x рублей- ежегодная выплата,
|
Год |
Сумма на счете в начале года |
Сумма на счете после начисления % |
Платеж |
Остаток на счете в конце года |
|
1 |
S |
Sm |
x |
Sm-x |
|
2 |
Sm—x |
Sm2—xm |
x |
Sm2-xm-x |
|
3 |
Sm2—xm—x |
Sm3—xm2—xm |
x |
Sm3-xm2-xm-x |
|
4 |
Sm3—xm2—xm—x |
Sm4—xm3—xm2—xm |
x |
Sm4-xm3—xm2-xm-x |
Sk=4x;
Кредит был погашен за 4 года, значит:
Ответ: 201 300 рублей.
3. Задачи на кредиты (уменьшение долга каждый год или месяц на одну и ту же величину), дифференцированные платежи.
Основные характеристики дифференцированного платежа
1. Долг уменьшается равномерно (убывающая арифметическая прогрессия);
2. Платежи уменьшаются равномерно (убывающая арифметическая прогрессия);
3. Дифференцированный платеж равен 
4. Первый платеж самый большой;
5. Последний платеж самый маленький.
При расчете дифференцированного платежа общая сумма основного долга делится на равные части пропорционально сроку кредитования. Ежемесячно в течение всего срока погашения кредита заемщик выплачивает банку часть основного долга плюс начисленные на его остаток проценты.
3. 15–го января планируется взять кредит в банке на 24 месяцев. Условия его возврата таковы:
– 1–го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2–го по 14–е число каждого месяца необходимо выплатить часть долга;
– 15–го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15–е число предыдущего месяца. Известно, что в течение второго года кредитования нужно вернуть банку 958.5тыс. рублей. Какую сумму нужно выплатить банку за первые 12 месяцев?
Решение.
S–сумма кредита,
r=1% — ежемесячный процент по вкладу,
n=24 – срок кредитования
|
Месяц |
Сумма на счете в начале месяца |
Погашение % по вкладу |
Погашение тела кредита |
Общие ежемесячные выплаты |
Остаток на счете в конце месяца |
|
1 год |
|||||
|
1 |
S |
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
… |
… |
… |
…. |
… |
… |
|
12 |
|
|
|
|
|
|
2 год |
|||||
|
13 |
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
|
24 |
|
|
|
|
|
Выплаты за 2 год
Выплаты за 1 год
Ответ:1 066 500 рублей.
4. Задачи на вклады (выплата долга в соответствии с данной таблицей или разные платежи каждый год).
4. 15 января планируется взять кредит в банке на сумму 1 млн рублей на 6 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн. рублей) |
1 |
0.6 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1.2 млн. рублей.
Решение.
r% — ежемесячный процент по вкладу,

|
Месяц |
Сумма на счете в начале месяца |
Сумма на счете после начисления % |
Платеж |
Остаток на счете в конце месяца |
|
1 |
1 |
1m |
m-0.6 |
0.6 |
|
2 |
0,6 |
0.6m |
0.6m-0.4 |
0.4 |
|
3 |
0,4 |
0.4m |
0.4m-0.3 |
0.3 |
|
4 |
0,3 |
0.3m |
0.3m-0.2 |
0.2 |
|
5 |
0,2 |
0.2m |
0.2m-0.1 |
0.1 |
|
6 |
0,1 |
0.1m |
0.1m |
0 |
Общая сумма выплат равна
Sk= m-0.6+0.6m-0.4+0.4m-0.3+0.3m-0.2+0.2m-0.1+0.1m=2.6m-1.6;
2.6m<1.2; m<
Ответ: 7%.
Разобранными в данной работе примерами, конечно, не исчерпываются все возможные вариации задач о вкладах и кредитах.
Сложность таких задач в том, что здесь нет готовых методов решения, каждая задача уникальна и требует своего подхода. Поэтому посоветовать можно только одно: чтобы научиться решать такие задачи, надо их решать.
Использованная литература
1. ЕГЭ 2020. Математика. Профильный уровень. 36 типовых вариантов заданий.
М.: 2020. — 168 с.
2. ЕГЭ. Математика. Задача с экономическим содержанием. 220 задач в формате ЕГЭ с ответами.
4-е изд., перераб. и доп. — М.: 2018. — 128 с.
3
4. ЕГЭ 2018. Математика. Задачи с экономическим содержанием. Задача 17 (профильный уровень) Шестаков С.А.
М.: 2018. — 208 с.