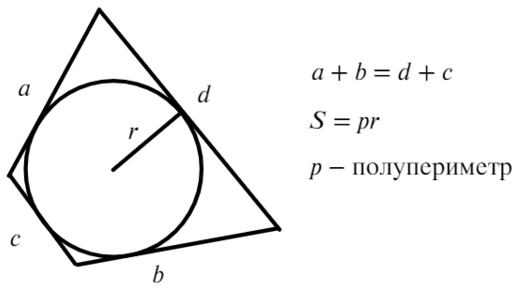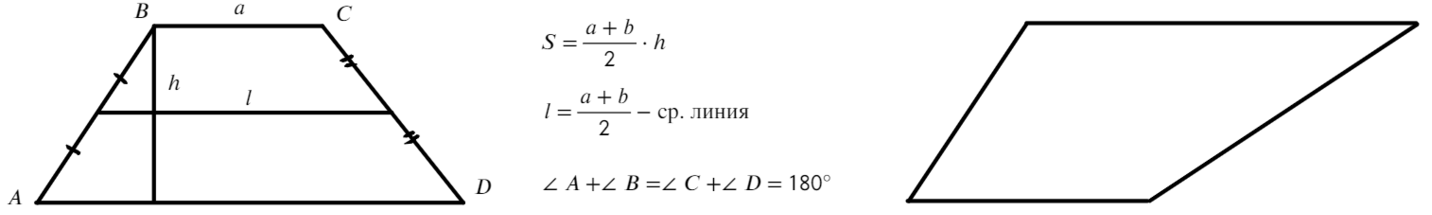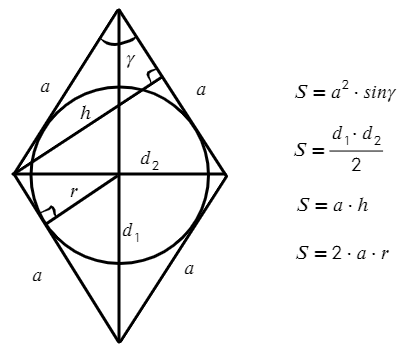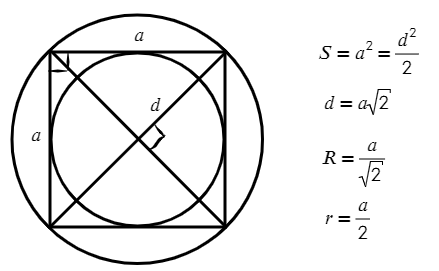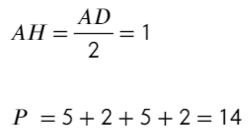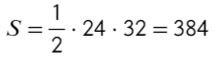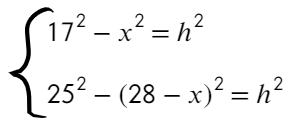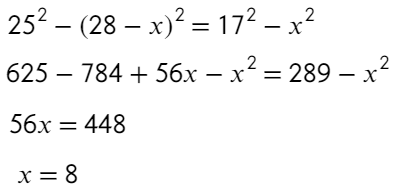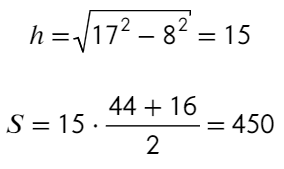Каталог заданий
Задания 12. Планиметрия . Четырёхугольники и их элементы
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла трапеции.
2
Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
Источник: Пробный экзамен Санкт-Петербург 2014. Вариант 1.
3
В параллелограмме ABCD АВ = 8, АС = ВD =17. Найдите площадь параллелограмма.
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166082.
4
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 137752., Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166704.
5
Источник: Апробация базового ЕГЭ по математике, 13—17 октября: вариант 152741.
Пройти тестирование по этим заданиям
ЕГЭ Профиль №16. Четырехугольники
Четырёхугольники и их элементы
1. 
Высота трапеции равна 14. Найдите тангенс острого угла.
2. 
боковая сторона, равная 7, образует с одним из оснований трапеции
угол 150°. Найдите площадь трапеции.
3. В параллелограмме ABCD АВ = 8, АС = ВD =17. Найдите площадь параллелограмма.
4. 
боковая сторона, равная 6, образует с одним из оснований трапеции угол 150°.
Найдите площадь трапеции.
5. 
Найдите угол ABD. Ответ дайте в градусах.
6. 
Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 64.
7. 
8. Основания равнобедренной трапеции равны 11 и 21, боковая сторона равна 13. Найдите высоту трапеции.
9.
Сумма двух углов ромба равна 120°, а его меньшая диагональ равна 25. Найдите периметр ромба.
10. В параллелограмме ABCD диагонали являются биссектрисами его углов, AB = 26, AC = 20. Найдите BD.
11. 
12. 
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Четырехугольники»
Открытый банк заданий по теме четырехугольники. Задания B3 из ЕГЭ по математике (профильный уровень)
Задание №861
Тип задания: 3
Тема:
Четырехугольники
Условие
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (-2; 1), (-2; 4), (-6; 1), (-6; 4).
Показать решение
Решение
Диагонали прямоугольника равны. Диагональ AC найдём как гипотенузу прямоугольного треугольника ADC с катетами AD=4, CD=3:
AC=sqrt{AD^2+CD^2}=sqrt{4^2+3^2}=5
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №268
Тип задания: 3
Тема:
Четырехугольники
Условие
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (3; 7), (3; 11), (6; 7), (6; 11).
Показать решение
Решение
У точек (3; 7) и (6; 7) одинаковые ординаты, поэтому длина основания прямоугольника равна 6-3=3. Аналогично, высота прямоугольника равна 11-7=4. Значит, диагональ равна sqrt{3^2+4^2}=5.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №264
Тип задания: 3
Тема:
Четырехугольники
Условие
Диагонали AC и BD равнобедренной трапеции ABCD перпендикулярны. Найдите среднюю линию трапеции, если ее высота равна 47.
Показать решение
Решение
Так как трапеция ABCD равнобедренная, то triangle AOB = triangle DOC по стороне и двум прилегающим углам. Тогда triangle AOD равнобедренный. Так как он еще и прямоугольный, то angle ADO = 45^{circ}. Пусть ВН — высота трапеции ABCD. Тогда в прямоугольном triangle BHD углы при гипотенузе BD равны по 45^{circ}. Значит, triangle BHD также равнобедренный, то есть DH=BH=47.
В равнобедренной трапеции DH= BC+AH= BC+frac{AD-BC}{2}= frac{2BC+AD-BC}{2}= frac{BC+AD}{2}. Но DH=47, значит, средняя линия трапеции равна frac{BC+AD}{2}=47.
Ответ
47
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Четырехугольники
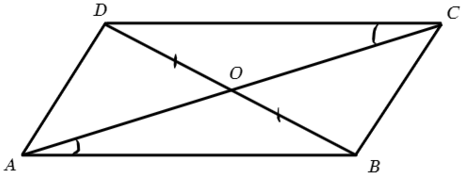
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны.
$АВ││CD;BC││AD.$
Свойства параллелограмма:
1. В параллелограмме противоположные стороны и углы попарно равны.
$АВ=CD;BC=AD$
$∠А=∠С; ∠В=∠D$.
2. Диагональ делит параллелограмм на два равных треугольника.
$∆ABD=∆BCD.$
3. Диагонали точкой пересечения делятся пополам.
$BO=OD; AO=OC.$
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
$BD^2+AC^2=2(AB^2+AD^2)$
5. Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
$∆АВК$ — равнобедренный.
6. В параллелограмме биссектрисы углов, прилежащих к одной стороне (соседних углов), пересекаются под углом в $90°$.
Площадь параллелограмма:
- Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними. $S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
- Площадь параллелограмма равна произведению основания на высоту. $S=h_a·a$, где $a$ — сторона параллелограмма, $h_a$ — высота, проведенная к стороне $a$.
Пример:
Определите синус острого угла параллелограмма, если его большая высота равна $7$, а стороны $10$ и $14$.
Решение:
Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
$S=a·b·sinα$, из этой формулы можем выразить синус угла.
$sinα={S}/{a·b}$
Стороны параллелограмма нам известны, осталось вычислить площадь. Площадь параллелограмма можно вычислить как произведение высоты на основание. Нам известна большая высота параллелограмма, а большая высота опускается к меньшей стороне параллелограмма, следовательно, $S=7·10=70$.
Подставим все известные данные в формулу синуса:
$sinα={S}/{a·b}={70}/{14·10}=0.5$
Ответ: $0.5$
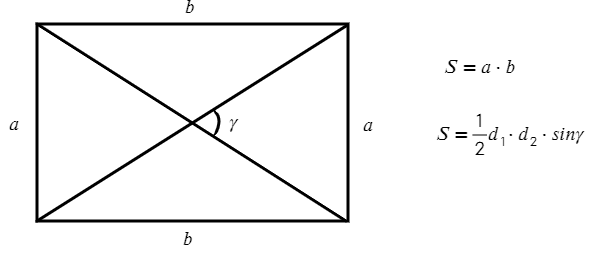
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
- Все свойства параллелограмма (Так как прямоугольник – это тот же параллелограмм, только особенный, поэтму у него присутствуют все свойства параллелограмма).
- Диагонали прямоугольника равны. $BD=AC$.
Площадь прямоугольника равна половине произведения смежных (соседних) сторон.
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб — это параллелограмм, у которого все стороны равны.
Свойства ромба:
- Все свойства параллелограмма.
- Диагонали ромба пересекаются под прямым углом. $BD⊥AC$.
- Диагонали ромба являются биссектрисами углов.
Площадь ромба:
- Площадь ромба равна половине произведения его диагоналей. $S={d_1·d_2}/2$, где $d_1$ и $d_2$ — диагонали ромба
- Площадь ромба равна произведению квадрата стороны на синус острого угла ромба. $S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Все свойства прямоугольника.
- Все свойства ромба.
Площадь квадрата:
- $S=a^2$, где $а$ — сторона квадрата.
- $S={d^2}/{2}$, где $d$ — диагональ квадрата.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие нет.
Параллельные стороны называются основаниями: $ВС$ и $AD$ — основания.
Непараллельные стороны называются боковыми сторонами: $АВ$ и $CD$ – боковые стороны.
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Свойства средней линии трапеции:
1. Средняя линия параллельна основаниям трапеции.
$MN││BC; MN││AD.$
2. Средняя линия равна полусумме оснований.
$MN={BC+AD}/{2}$
3. Диагональ делит среднюю линию на две части, каждая из которых является средней линией получившихся треугольников.
$МК$ — средняя линия треугольника $ABD; MK={AD}/{2}$.
$KN$ — средняя линия треугольника $BCD; KN={BC}/{2}$.
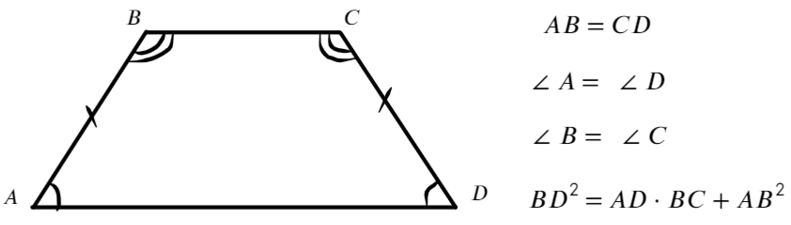
Трапеция, у которой боковые стороны равны, называется равнобедренной.
Свойства равнобедренной трапеции:
1. Углы при основаниях равны.
$∠А=∠D; ∠B=∠C.$
2. Диагонали в равнобедренной трапеции равны.
$BD=AC.$
3. Основание высоты равнобедренной трапеции, опущенной из меньшего основания, делит другое основание на отрезки, больший из которых равен полусумме оснований.
$АС_1={BC+AD}/{2}.$
4. Основания высот равнобедренной трапеции, опущенных из меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований.
$BC=B_1C_1;$
$AB_1=C_1 D={AD-BC}/{2}.$
5. Если трапеция является равнобедренной, то около неё можно описать окружность.
6. Если в равнобедренной трапеции диагонали пересекаются под прямым углом, то высота рана длине средней линии данной трапеции.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
Около четырехугольника не всегда можно описать окружность. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Биссектриса – это линия, которая делит угол пополам.
Свойства биссектрисы:
1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
$AD=DC$
3. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$
Четырехугольники
и их свойства.
Разобрать решенные задачи и выполнить
самостоятельную работу.
Трапеция.
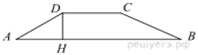
Задача 1. Основания трапеции равны 18 и 6, боковая
сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите
площадь трапеции.
Решение.
Введём обозначения, как показано на
рисунке. Площадь трапеции — произведение полусуммы оснований на высоту:
Ответ: 42.
Задача
2. В прямоугольной трапеции с основаниями
и
угол
прямой,
,
. Найдите
среднюю линию трапеции.
Решение.
Для того, чтобы найти среднюю линию
трапеции необходимо знать длину оснований, найдём AD.
Проведём высоту СH к AD.
Найдём АD:
Средняя линия трапеции равна
полусумме оснований:
Ответ: 6,5.
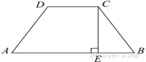
Задача 3. Основания трапеции равны 8 и 16, боковая сторона, равная 6, образует
с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
Решение.
Угол в 150° образует боковая
сторона и меньшее основание, тогда с большим основанием эта сторона образует
угол 30°. Проведем высоту трапеции и рассмотрим прямоугольный треугольник. Из
определения синуса острого угла прямоугольного треугольника получаем:
По формуле площади трапеции находим
Ответ: 36.
Задача 4. Основания равнобедренной трапеции равны 56 и 104, боковая сторона
равна 30. Найдите длину диагонали трапеции.
Решение.
Найдем разницу между двумя
основаниями:
Поскольку трапеция равнобедренная,
то высотой, проведенной из точки С, а также высотой проведенной из точки D, от
нижнего основания «отрезается» 2 равные части. Найдем длину одной из
таких частей:
Рассмотрим треугольник СЕВ. Из него
(по теореме Пифагора) найдем высоту СЕ:
Рассмотрим, наконец, треугольник
АСЕ. В нем мы знаем высоту, а также . Теперь, также по
теореме Пифагора найдем искомую диагональ АС, которая является гипотенузой
прямоугольного треугольника:
Ответ: 82.
Решить самостоятельно.
1. Основания равнобедренной трапеции равны 17 и 87. Высота
трапеции равна 14. Найдите тангенс острого угла.
2. трапеции ABCD известно, что AB = CD,
∠BDA = 54° и ∠BDC = 23°.
Найдите угол ABD. Ответ дайте в градусах.
3.
Основания равнобедренной трапеции
равны 11 и 21, боковая сторона равна 13. Найдите высоту трапеции.
4.
В прямоугольной трапеции основания
равны 4 и 7, а один из углов равен 135°. Найдите меньшую боковую сторону.
Параллелограмм.
Задача 1. В параллелограмме отмечена точка
— середина стороны
. Отрезки
и
пересекаются в точке
. Найдите
если
.
Решение.
Обозначим О точку
пересечения диагоналей параллелограмма. Диагонали параллелограмма точкой
пересечения делятся пополам, поэтому ВО — медиана треугольника АВС.
Отрезок АМтакже является медианой треугольника АВС, точкой
пересечнния медианы делятся в отношении 2 : 1, считая от вершины.
Поэтому
Ответ: 4.
Решить самостоятельно.
5.
В параллелограмме ABCD АВ
= 8, АС = ВD =17. Найдите площадь параллелограмма.
6.
В параллелограмме диагональ
в
два раза больше стороны и
.
Найдите тупой угол между диагоналями параллелограмма. Ответ дайте в градусах.
План решения задачи №6.
1)
Рассмотреть ∆ COD —
равнобедренный с углом при вершине С =104°.
2)
Найти <COD = <CDO.
3)
Найти величину угла, смежного с <COD.
7.
В параллелограмме ABCD
диагонали являются биссектрисами его углов, AB = 26, AC = 20.
Найдите BD.
8.
Стороны параллелограмма равны 9 и
12. Высота, опущенная на меньшую сторону, равна 8. Найдите высоту, опущенную на
большую сторону параллелограмма.
Ромб. Квадрат.Прямоугольник.
Задача 1. Сумма двух углов ромба равна 120°, а его
меньшая диагональ равна 25. Найдите периметр ромба.
Решение.
Сумма двух углов ромба равна 120°,
значит, каждый угол равен 120° : 2 = 60°. Сумма двух остальных углов ромба
равна 360° − 120° = 240°, значит, каждый из них равен 240° : 2 = 120°.
Меньшая диагональ ромба лежит напротив меньшего угла ромба 60°, поэтому
получаем равносторонний треугольник, основанием которого является данная
диагональ. Таким образом, периметр ромба равен 25 · 4 = 100.
Ответ:
100.
Задача 2. Ромб и
квадрат имеют одинаковые стороны. Найдите площадь ромба, если его острый угол
равен 30°, а площадь квадрата равна 64.
Решение.
Площадь квадрата вычисляется по
формуле: . Площадь ромба
вычисляется по формуле: Таким образом:
Ответ: 32. Решить самостоятельно.
9.
В ромбе Найдите
синус угла .
10.
Сумма двух углов ромба равна 120°,
а его периметр равен 84. Найдите длину меньшей диагонали ромба.
ромба равна 240°, а его периметр равен 68. 
Одна из сторон прямоугольника на 2 см меньше стороны квадрата. Найти периметр
прямоугольника.
Ответы
на задачи.
|
Трапеция. |
|
|
№1 |
0,4 |
|
№2 |
49 |
|
№3 |
12 |
|
№4 |
3 |
|
Параллелограмм. |
|
|
№5 |
120 |
|
№6 |
142 |
|
№7 |
48 |
|
№8 |
6 |
|
Ромб. Квадрат. |
|
|
№9 |
0,75 |
|
№10 |
21 |
|
№11 |
17 |
|
№12 |
26 |

Основные формулы и свойства трапеции.
Основные формулы и свойства параллелограмма.
Основные формулы и свойства ромба.
Основные формулы и свойства прямоугольника.
Основные формулы и свойства квадрата.
Примеры и решения задач.
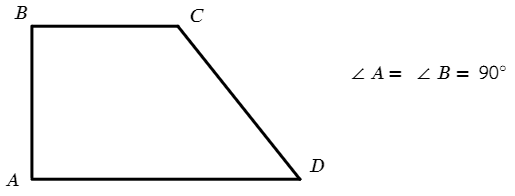
Разберем по сторонам каждый четырехугольник. А начнем с самой негармоничной фигуры — четырехугольника:
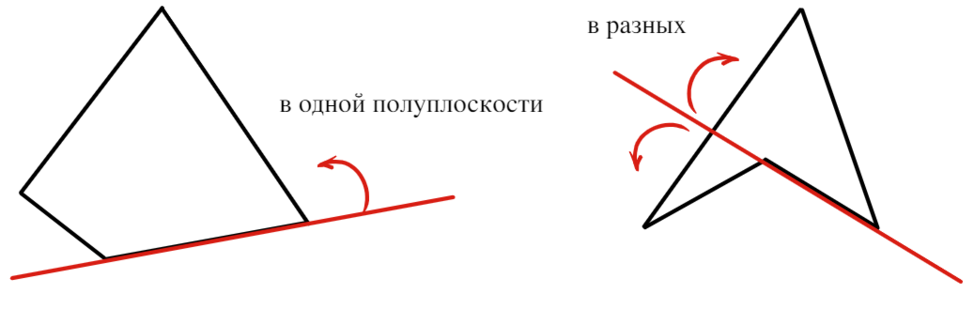
Выпуклым называется четырехугольник, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
В ЕГЭ встречается только выпуклый, поэтому его брата оставим без внимания.
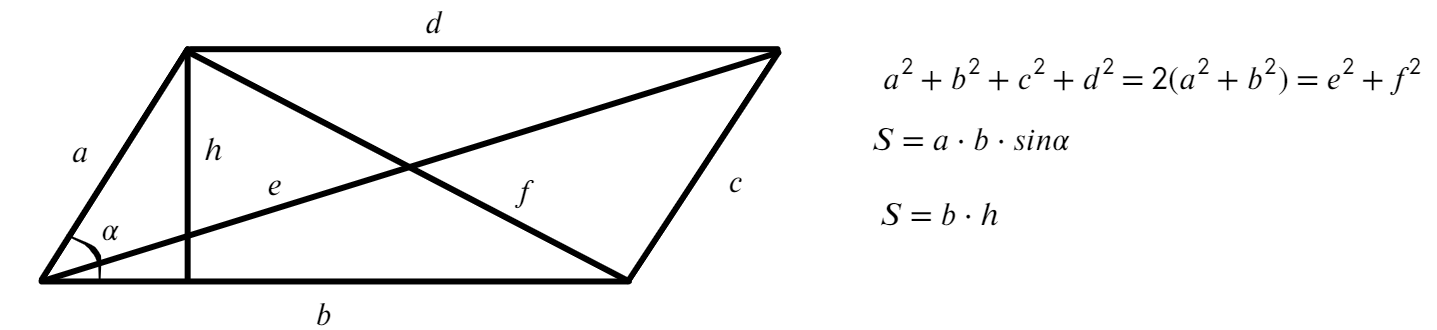
Если четырехугольник произвольный:
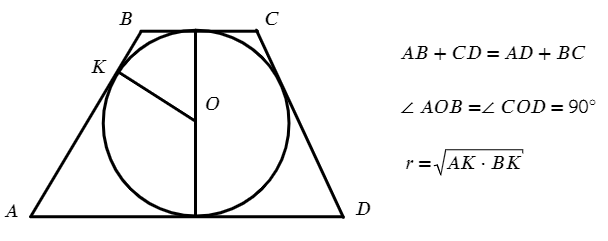
Если в четырехугольник можно вписать окружность, то помимо выше описанных свойств добавляются эти:
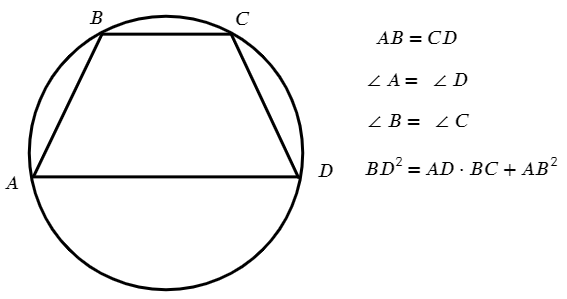
Если вокруг четырехугольника можно описать окружность, то добавляются такие свойства:
Две теоремы Птолемея можно встретить в №16 ЕГЭ, планиметрии повышенного уровня сложности.
Если поставить условие, что две противоположные стороны должны быть параллельны, то четырехугольник становится трапецией.
Всем привычна такая трапеция, но та, что справа, также существует!
В равнобедренной трапеции:
Прямоугольная трапеция:
В трапецию можно вписать окружность, когда? Когда сумма противоположных сторон одинакова!
Да точно также, как и в четырехугольник, все свойства четырехугольника работают и в трапеции!
— И площадь через диагонали?
— Конечно!
А описать окружность вокруг трапеции? Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая!
Свойства остаются те же.
Следующий на очереди параллелограмм:
Если сказать, что в трапеции две попарно противоположные стороны параллельны, то трапеция станет параллелограммом.
Если сказать, что в трапеции две противоположные стороны параллельны и равны, то трапеция станет параллелограммом.
Еще добавляются 2 формулы площади:
Свойства параллелограмма:
- Если у четырёхугольника противолежащие стороны попарно равны, то это параллелограмм.
- Если у четырёхугольника две противолежащие стороны равны и параллельны, то это параллелограмм.
- Четырёхугольник, диагонали которого в точке пересечения делятся пополам, – параллелограмм.
- Если у четырёхугольника противолежащие углы попарно равны, то это параллелограмм.
Дальше, чтобы из параллелограмма получить следующую фигуру, есть два пути:
1) Если у параллелограмма один угол 90°, то это прямоугольник.
2) Если у параллелограмма две прилежащие стороны равны, то это ромб.
Ромб — параллелограмм, у которого все стороны равны:
Свойства ромба:
- Диагонали ромба взаимно перпендикулярны.
- Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).
- Диагонали делят ромб на четыре равных прямоугольных треугольника.
- В ромб можно всегда вписать окружность.
Прямоугольник — параллелограмм, у которого все углы прямые:
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Вокруг прямоугольника всегда можно описать окружность.
Правильный четырехугольник — квадрат. Папа был прямоугольником, а мама ромбом. Квадрат объединяет свойства и формулы этих фигур и добавляет свои:
Свойства квадрата:
- Все углы квадрата прямые, все стороны квадрата равны.
- Диагонали квадрата равны и пересекаются под прямым углом.
- Диагонали квадрата делят его углы пополам.
- В квадрат можно всегда вписать окружность.
- Вокруг квадрата можно всегда описать окружность.
Задача №1 Докажите, что ABCD параллелограмм, если известно, что ∠CAD = ∠CAB и DO = OB.
Что нужно, чтобы сказать, что четырехугольник является параллелограммом?
- Две противоположные стороны параллельны и равны.
- Две попарно противоположные стороны параллельны.
Скажем, что DC II AB, т.к. ∠CAD = ∠CAB — накрест лежащие углы. Если не знаешь, что такое накрест лежащие углы — читай!
Но раз DC II AB, то и ∠CDB = ∠DBA (как накрест лежащие), а ∠AOB и ∠DOC — рыжие что ли? Нет, они вертикальные, значит, тоже равны: ∠AOB = ∠DOC.
Тогда ΔAOB = ΔDOC (по стороне и двум прилежащим углам) => DC = AB.
Получается, что DC = AB и DC II AB, свойство №1 доказано.
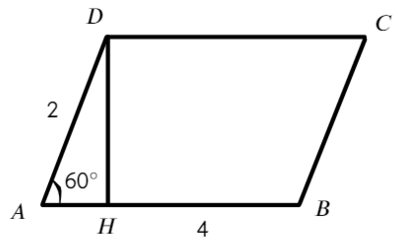
Задача №2 Найдите периметр параллелограмма.
Вспомним, что в прямоугольном треугольнике находится против угла в 30°. Да-да, катет в два раза меньший гипотенузы. Следовательно AB = AH + HB = 1+4 = 5.
Тогда периметр:
Ответ: 14.
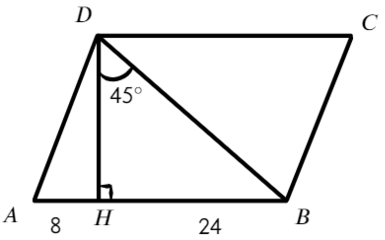
Задача №3 Найдите площадь параллелограмма.
В ΔDHB ∠DBH = 180 – 90° – 45° = 45°=> ΔDHB — равнобедренный => DH = HB = 24
Ответ: 384
Задача №4 Найдите площадь ABCD.
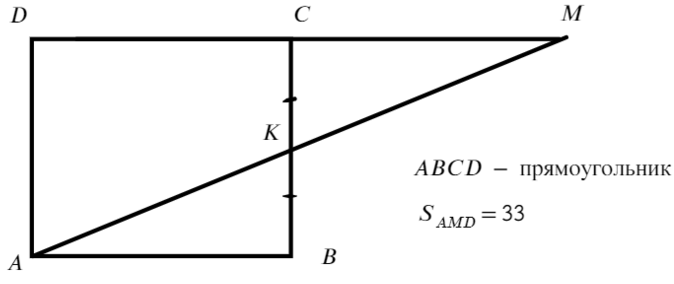
ABCD — прямоугольник. Чтобы найти его площадь, нужно знать две стороны, но мы знаем только площадь треугольника.
Площадь AKCD общая у ABCD и ADM, а вот отличаются они площадью ΔABK и ΔKCM, но мы только что доказали, что они равны, значит, площади ABCD и ADM тоже равны!
Ответ: 33
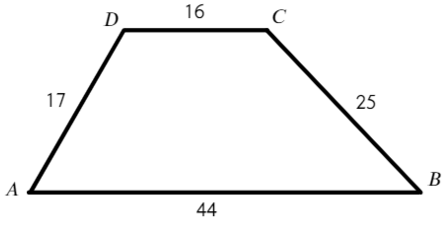
Задача №5 Найдите площадь трапеции, параллельные стороны которой равны 15 и 44, а непараллельные 17 и 25.
Площадь трапеции можно найти так:
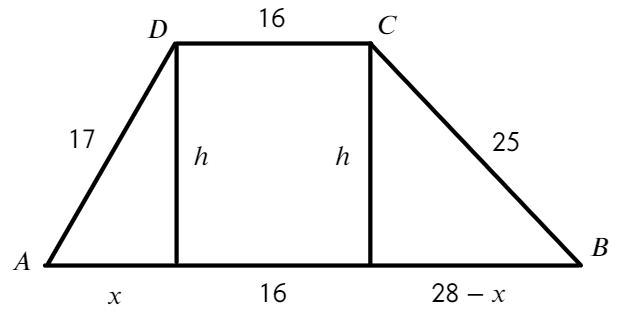
Не хватает высоты, попробуем разбить трапецию на треугольники и прямоугольник:
Запишем теорему Пифагора для двух треугольников:
Решим уравнение:
Зная, как разделится основание найдем высоту:
Если нашел опечатку, или что-то непонятно − напиши.
Первая и вторая часть по треугольникам.
Статья по окружностям.