Всего: 339 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
В обменном пункте 1 гривна стоит 3 рубля 70 копеек. Отдыхающие обменяли рубли на гривны и купили 3 кг помидоров по цене 4 гривны за 1 кг. Во сколько рублей обошлась им эта покупка? Ответ округлите до целого числа.
В обменном пункте 1 гривна стоит 3 рубля 90 копеек. Отдыхающие обменяли рубли на гривны и купили арбуз весом 7 кг по цене 2 гривны за 1 кг. Во сколько рублей обошлась им эта покупка? Ответ округлите до целого числа.
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Источник: Досрочный ЕГЭ по математике (Центр) 30.03.2018
Диагональ экрана телевизора равна 113 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Ананасы стоят 85 руб. за штуку. Какое максимальное число ананасов можно купить на 500 руб., если их цена снизится на 20%?
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
Диагональ экрана телевизора 21 дюйм. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1.
Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 2.
Диагональ экрана телевизора равна 60 дюймам. Выразите диагональ экрана в сантиметрах. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
Диагональ экрана телевизора равна 40 дюймам. Выразите диагональ экрана в сантиметрах. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Какова скорость автомобиля в километрах в час, если спидометр показывает 65 миль в час? Считайте, что 1 миля равна 1609 м. Ответ округлите до целого числа.
Маша отправила SMS-сообщения с новогодними поздравлениями своим 16 друзьям. Стоимость одного SMS-сообщения 1 рубль 30 копеек. Перед отправкой сообщения на счету у Маши было 30 рублей. Сколько рублей останется у Маши после отправки всех сообщений?
Рост человека 5 футов 11 дюйм. Выразите его рост в сантиметрах, если 1 фут равен 12 дюймам. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
Рост человека — 6 футов 11 дюймов. Выразите его рост в сантиметрах, если 1 фут равен 12 дюймам. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
Рост человека — 5 футов 8 дюймов. Выразите его рост в сантиметрах, если 1 фут равен 12 дюймам. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
Для покраски потолка требуется 280 г краски на 1 м2. Краска продаётся в банках по 2,5 кг. Какое наименьшее количество банок краски нужно купить для покраски потолка площадью 61 м2?
Рост человека 6 футов 1 дюйм. Выразите его рост в сантиметрах, если 1 фут равен 12 дюймам. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 35 рублей за штуку. У Вани есть 160 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?
На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?
Студент получил свой первый гонорар в размере 700 рублей за выполненный перевод. Он решил на все полученные деньги купить букет тюльпанов для своей учительницы английского языка. Какое наибольшее количество тюльпанов сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, тюльпаны стоят 60 рублей за штуку и букет должен состоять из нечетного числа цветов?
Всего: 339 1–20 | 21–40 | 41–60 | 61–80 …
14 марта 2020
В закладки
Обсудить
Жалоба
В данной работе рассмотрены примеры решения задачи №19 ЕГЭ по профильной математике.
chisla19.docx
Задание №19 может быть 4 типов:
1) Числа и их свойства.
2) Числовые наборы на карточках и досках.
3) Последовательности и прогрессии.
4) Сюжетные задачи: кино, театр, мотки верёвки и тому подобное.
Числа и их свойства
В зависимости от задачи можно использовать следующие методы:
1) Свойства делимости целых чисел (в частности, делимость на 2, 3, 4, 5, 7, 9, 11).
2) Работа с простыми и составными числами.
3) Работа с каноническим разложением натурального числа, количество делителей натурального числа.
4) Работа с НОД и НОК.
Автор: Бурмистрова Анна Владимировна, учитель математики.
Муниципальное автономное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М.Кузьмина»
Методическая разработка по теме:
«Решение задачи №19 ЕГЭ по профильной математике»
Бурмистрова А.В.,
учитель математики
ТАМБОВ 2020
Оглавление
Введение и актуальность 3
Виды задания №19 4
Числа и их свойства 4
Свойства делимости целых чисел 4
Работа с простыми и составными числами 7
Работа с каноническим разложением натурального числа, количество делителей натурального числа 8
Работа с НОД и НОК 9
Числовые наборы на карточках и досках 11
Последовательности и прогрессии 16
Сюжетные задачи 19
Вывод 21
Используемая литература 22
Введение и актуальность
ЕГЭ в наше время является логическим завершением среднего образования большинства и от того, как вы сдадите эти экзамены в некоторой степени зависит дальнейшая жизнь и возможное высшее образование. И математика является обязательным предметом для всех без исключения выпускников. Несмотря на то, что большинство выбирают и сдают базовый уровень математики, профильный уровень всё равно востребован (в 2018 году 421 тысяча выпускников сдавала профильный уровень, а 567 тысяч человек – базовый уровень). 19 задача при правильном и полном решении даёт 4 первичных балла из 32, и вопреки распространённому мнению, получить 2 гарантированных балла за эту задачу может почти каждый ученик со средней успеваемостью по математике, а при должной подготовке решить и последний пункт этой задачи, дающий целых 2 первичных балла.
Задание №19 может быть 4 типов:
-
Числа и их свойства
-
Числовые наборы на карточках и досках
-
Последовательности и прогрессии
-
Сюжетные задачи: кино, театр, мотки верёвки и тому подобное
Рассмотрим каждый из типов поподробнее.
Числа и их свойства
Как можно было понять из названия, работа в этом типе будет идти с целыми числами и их свойствами, такими как: делимость с остатком и без, вид этих чисел в различных системах счисления и другое.
В зависимости от задачи можно использовать следующие методы:
-
Свойства делимости целых чисел (в частности, делимость на 2, 3, 4, 5, 7, 9, 11)
-
Работа с простыми и составными числами
-
Работа с каноническим разложением натурального числа, количество делителей натурального числа
-
Работа с НОД и НОК
Свойства делимости целых чисел
Для решения таких задач надо вспомнить признаки делимости на различные числа, также не лишним будет напомнить основные свойства делимости целых чисел.
Делимость на 2, 4, 8, 2^n:
Числом кратным двум (чётным числом) является число, оканчивающееся на чётную цифру: 2, 4, 6, 8, 0.
Число кратно 4 если последние две цифры образуют число кратное 4. Например 144 оканчивается на 44, 44 делится на 4, значит и 144 делится на 4.
Число кратно 8 если последние три цифры образуют число кратное 8. Например 2864 оканчивается на 864, 864 делится на 8, значит и 2864 делится на 8.
Проанализировав эти три признака можно вывести признак делимости на 2^n. Число кратно 2^n если его последние n цифр образуют число, кратное 2^n. Докажем это утверждение. Пусть у нас есть число 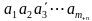
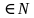
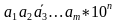
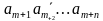
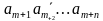
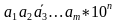
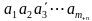
Делимость на 3, 9:
Число кратно 3 сумма цифр этого числа кратна 3. Например сумма цифр 141 равна 6, 6 делится на 3, значит и 141 делится на 3.
Число кратно 9 сумма цифр этого числа кратна 9. Например сумма цифр 981 равна 18, 18 делится на 9, значит и 981 делится на 3.
Но в отличие от 2, свойство делимости на остальные степени тройки не распространяется. Например, 54 кратно 27, но сумма цифр равна 9.
Делимость на 5^n:
Число кратно 5^n если его последние n цифр образуют число, кратное 5^n. Доказательство аналогично доказательству кратности 2^n.
Делимость на 7:
Пусть у нас есть число 10 * а + b, где, а — какое-то натуральное число, а b – цифра. Тогда если |а – 2 * b| кратно 7, то и 10 * а + b кратно 7. Например 343: 34 – 6 = 28, 28 кратно 7, значит и 343 кратно 7.
Делимость на 11:
Число кратно 11 если модуль разности сумм цифр, стоящих на чётных и нечётных местах кратен 11. Например число 482735: | (4+2+3) – (8+7+5) | = 11 кратно 11, значит и 482735 кратно 11.
Конечно, существуют и другие признаки делимости, но они встречаются редко в ЕГЭ, поэтому их можно не рассматривать. Также можно вспомнить различные свойства делимости в общем:
-
Если a и b делятся на m, то числа a +b и a -b также делятся на m.
-
Если a и b делятся на m, то при любых целых числах k и l число a*k
b*l также делится на m.
-
Если a делится на m, а b не делится на m, то числа a
b также не делятся на m.
-
Если a делится на m, а m делится на k
N , то число a также делится на k .
-
Если a делится на m, а b не делится на m, то число a*b делится на m.
-
Если a делится на каждое из чисел m и k, причем НОД(m, k) =1, то a делится на произведение m*k .
-
Если a делится на m, то a*k делится на m*k при любом k
N .
-
Если a*b делится на m и b взаимно просто с m, то a делится на m.
Доказывать эти свойства не будем, так как они рассматриваются и доказываются в школьной программе.
Примеры
Пример 1. Натуральное число 3n+2 и 8n +3 делятся на натуральное число
p 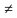
Решение. Так как числа 3n 2 и 8n 3 делятся p , то и число 8 (3n 2) 3(8n 3) 7 должно делиться на p . Но единственное натуральное число p 1, на которое делится 7, равно 7. Значит p 7 . Например, при n 4 получаем числа 14 и 35, которые делятся на 7. (В данной ситуации следует, используя свойства делимости найти выражение, не содержащее переменные)
Ответ: p 7
Пример 2. («Сборник задач по алгебре. М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич. М: Просвещение». №3.6)
Докажите, что сумма квадрата целого числа и самого числа есть число четное.
Решение. Пусть n- целое число. n²+n=n(n+1)- произведение 2-х последовательных чисел. Значит одно из них четное, а другое нечетное. Произведение четного и нечетного чисел есть число нечетное. Что и требовалось доказать.
Работа с простыми и составными числами
Для начала вспомним определения простых и составных чисел.
Простое число – это число, у которого ровно два положительных делителя: единица и само число.
Составное число – это число, у которого более двух положительных делителей.
Как мы можем заметить из этих определений, единица не является ни составным, ни простым числом.
Примеры.
Пример1.Доказать, что число a 41612 240 делится на 33.
Решение. Так как 41612 22 448 250, то a 250 240 240 (210 1) 240 (25 1) (25 1) 240 3133, откуда следует, что a делится на 33.
Пример 2. Доказать, что число a 8n2 10n3 является составным при любом натуральном n.
Решение. Число a является составным при любом натуральном n, поскольку a =8n2 10n 3 (2n 1) (4n 3), где числа 2n 1 и 4n3 натуральные, большие единицы.
Работа с каноническим разложением натурального числа, количество делителей натурального числа
Каноническим разложением целого числа n 1 называется представление n в виде
n p1k1 p2k2 …ps ks
где p1, p2, …, ps – попарно различные простые числа, а k1, k2, …, ks – натуральные числа. Для отрицательных целых чисел n 1 каноническим разложением считается представление в виде
n p1k1 p2k2 …ps ks
Количество делителей натурального числа можно посчитать по формуле (n) (k1 1)(k2 1)…(ks 1), где k1, k2, …, ks – коэффициенты каноничного разложения этого числа.
Примеры.
Пример 1. Найти число различных делителей числа 1440, включая единицу и само число.
Решение. Запишем каноническое разложение числа 1440. Так как 1440 5288 5932, то 1440 25 32 51. Следовательно, (n) (51)(21)(11) 36. Ответ: 36.
Пример 2. Найти количество и сумму всех натуральных чисел, не превосходящих 1000 и имеющих нечетное число делителей.
Решение. Натуральное число, имеющее нечетное число делителей, является полным квадратом. Следовательно, чтобы ответить на первый вопрос задачи, нужно сосчитать количество чисел, являющихся квадратами и не превосходящими 1000. Наибольшим таким числом является 961312. Значит имеется 31 такое число.
Искомая сумма равна S 12 22 …312. Используя формулу

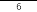
Ответ: 31 и 10416.
Пример 3. Найти число различных делителей числа 1440, включая единицу и само число.
Решение. Запишем каноническое разложение числа 1440. Так как 1440 5288 5932, то 1440 25 32 51. Следовательно, (n) (51)(21)(11) 36. Ответ: 36.
Работа с НОД и НОК
Наибольшим общим делителем(НОД) натуральных чисел a1, a2, …, an называется наибольшее натуральное число, на которое делятся данные числа.
Наименьшим общим кратным(НОК) – наименьшее натуральное число, делящееся на каждое из этих чисел.
Свойства:
-
НОД a; b = НОД a; a b;
-
НОД a; b = НОД a; a — b;
-
a, b – взаимно простые числа, если НОД a; b = 1, верно и обратное;
-
a * b = НОД a; b * НОК a; b
Также стоит вспомнить алгоритм Евклида.
Алгоритм Евклида — Для нахождения НОД двух чисел делят большее число на меньшее, и если получается ненулевой остаток, то делят меньшее число на остаток; если снова получается ненулевой остаток, то делят первый остаток на второй. Так продолжают делить до тех пор, пока в остатке не получится нуль. Последний делитель и есть НОД данных чисел.
Существует также вариация этого метода, где вместо деления используется вычитание, но он более занимает больше времени и шанс ошибки увеличивается.
Примеры
Пример 1. Найти все пары натуральных чисел, наименьшее общее кратное которых равно 78, а наибольший общий делитель равен 13.
Решение. Пусть a и b искомые числа. По условию (a, b) 13. Значитa 13a1 и b 13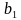
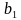
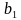
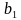
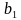
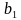
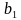
Ответ: (13, 78), (26, 39).
Пример 2. (МИОО, 2010). Найти наибольший общий делитель всех чисел вида 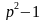
Решение. Запишем 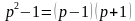
, то 24 – наибольший общий делитель всех чисел вида
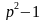
Ответ: 24.
Практика
Задание 1 Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100.
а) Может ли частное этого числа и суммы его цифр быть равным 90?
б) Может ли частное этого числа и суммы его цифр быть равным 88?
в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
Решение
Пусть данное число равно 100a +10b +c, где a, b и c — цифры сотен, десятков и единиц соответственно. Если частное этого числа и суммы его цифр равно k, то выполнено 100a + 10b + c = ka + kb +kc.
а) Если частное равно 90, то 100a + 10b + c = 90a + 90b +90c; 10a = 80b + 89 c, что верно, например, при c = 0, b =1, a =8: частное числа 810 и суммы его цифр равно 90
б) Если частное равно 88, то 100a + 10b + c = 88a + 88b +88c; 12a = 78b + 87 c. Получаем: a a b + 87 c . Значит, b = 0, c =1 или b = 1, c =0. Но ни 78, ни 87 не делятся на 12. Значит, частное трёхзначного числа и суммы его цифр не может быть равным 88.
в) Пусть k — наибольшее натуральное значение частного числа, не кратного 100, и суммы его цифр. Тогда 100a+10b+c = ka + kb +kc; (100-k)a=(k-10)b + (k-1)c. Учитывая, что b+c0, получаем: 9(100-k) = (100-k)a = (k-10)b +(k-1)c=(k-10)(b+c)=k-10, откуда 9(100-k)=k-10 10kk
Ответ: а) да; б) нет; в)91.
Числовые наборы на карточках и досках
Задачи такого вида довольно редки и довольно-таки однотипны. Для их решения понадобится та теория, что связана с целыми числами и их свойствами, часть которой мы вспомнили в прошлом разделе. Кроме-того будет не лишним вспомнить определения и понятия, связанные с числовыми рядами.
Медиана ряда чисел – это число, которое стоит строго посередине ряда нечётного количества чисел, упорядоченного от наименьшего к наибольшему.
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Модой ряда чисел называется число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Так как каких-то конкретных приёмов для такого типа задач нет, можно сразу перейти к практике и разбору конкретных случаев.
Практика
Задание 1 Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т. д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 4, 6, 8, 10.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 8, 10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.
Решение.
а) Задуманные числа 2, 2, 2, 2, 2 дают требуемый набор, записанный на доске.
б) Поскольку задуманные числа натуральные, то наименьшее число в наборе — это наименьшее из задуманных чисел, а наибольшее число в наборе — это сумма всех задуманных чисел. Среди чисел записанного набора должна быть сумма всех чисел, кроме наименьшего, то есть 22 − 1 = 21. Но этого числа нет в наборе, поэтому не существует примера таких задуманных чисел, для которого на доске будет выписан набор из условия.
в) Число 7 — наименьшее число в наборе — является наименьшим из задуманных чисел, а наибольшее число в наборе — это сумма всех задуманных чисел. Поэтому количество задуманных чисел не превосходит целой части, то есть 5. Кроме того, числа 8 и 10 меньше, чем сумма двух чисел 7, поэтому они также являются задуманными. Значит, сумма оставшихся задуманных чисел равна 41 − 7 − 8 − 10 = 16. Таким образом, так как наименьшее задуманное число равно 7, оставшиеся задуманные числа — это 8 и 8 или 16. Для задуманных чисел 7, 8, 8, 8, 10 и 7, 8, 10, 16 на доске будет записан набор, данный в условии.
Ответ: а) 2, 2, 2, 2, 2; б) нет; в) 7, 8, 8, 8, 10 или 7, 8, 10, 16.
Задание 2 На доске написано число 2015 и еще несколько (не менее двух) натуральных чисел, не превосходящих 5000. Все написанные на доске числа различны. Сумма любых двух из написанных чисел делится на какое-нибудь из остальных.
а) Может ли на доске быть написано ровно 1009 чисел?
б) Может ли на доске быть написано ровно пять чисел?
в) Какое наименьшее количество чисел может быть написано на доске?
Решение.
Заметим, что если среди выписанных чисел есть число 1, то попарные суммы всех остальных чисел будут делиться на 1.
а) Может. Например, числа 1, 2, 3, 5, 7, …, 2015 (выписано 1008 нечётных чисел от 1 до 2015 и число 2). Сумма 1 и любого нечётного числа делится на 2, сумма 1 и 2 делится на 3, сумма любых двух чисел, отличных от 1, делится на 1. Другой пример: 1, 2, 3, … , 1007, 2014, 2015. Если среди двух чисел нет 1, то их сумма делится на 1. Если вместе с 1 выписаны числа k и k + 1, то сумма первых двух делится на третье; оставшиеся суммы 1 + 1007 и 1 + 2015 делятся на 2. Третий пример: 1, 2, 3, 5, 6, … , 1009, 2015 (в группе подряд идущих чисел пропущено 4).
б) Может. Например, числа 1, 2, 3, 5, 2015. Другой пример — числа a, 2a, 3a, 4a, 5a, где a = 403.
в) Пример для четырёх чисел: 1, 2, 3, 2015. Другой пример — числа a, 2a, 3a, 5a, где a = 403. Покажем, что трёх чисел быть не может. Действительно, пусть три различных числа таковы, что a 5000. Противоречие. Приведём другое доказательство. Пусть даны числа a, b, c, и сумма любых двух из них делится на третье. Если они все имеют отличный от 1 наибольший общий делитель d, то на него можно сократить, и свойство делимости сохранится. Будем считать, что все три числа взаимно простые. Поскольку сумма двух чисел делится на третье, то сумма всех чисел делится на каждое. Числа попарно взаимно просты, поэтому их сумма должна делиться на произведение. В частности, a + b + c ≥ abc. Полагая a 5000.
Ответ: а) Может. Например, числа 1, 2, 3, 5, 7, …, 2015; б) Может. Например, числа 1, 2, 3, 5, 2015; в) 4, например, 1, 2, 3, 2015.
Задание 3 Саша берёт пять различных натуральных чисел и проделывает с ними следующие операции: сначала вычисляет среднее арифметическое первых двух чисел, затем среднее арифметическое результата и третьего числа, потом среднее арифметическое полученного результата и четвёртого числа, потом среднее арифметическое полученного результата и пятого числа — число A.
а) Может ли число A равняться среднему арифметическому начальных пяти чисел?
б) Может ли число A быть больше среднего арифметического начальных чисел в пять раз?
в) Какое наибольшее целое число раз число A может быть больше среднего арифметического начальных пяти чисел?
a) Пусть начальные числа: a, b, c, d и e, тогда . Поскольку равенство 4d — 11(a + b)+6(4e — c)=0 Равенство 4 * 11 – 11 * 4 + 6(4 * 2 – 
б) Равенство приводит к равенству , что невозможно для натуральных слагаемых.
Вывод: нет.
в) Пусть число A в k раз больше среднего арифметического. Тогда: (16k-5)a + (16k-5)b + (16k-10)c + (16k-20)d + (16k-40)e = 0, что невозможно при k 3. Пример для k = 2: 1, 3, 4, 7, 35.
Ответ: а) да, например: 1, 3, 8, 11, 2; б) нет; в) 2.
Последовательности и прогрессии
В таком виде задач могут встречаться любые последовательности и прогрессии, но зачастую это либо арифметическая, либо геометрическая прогрессии. Также стоит отдельно вспомнить последовательность чисел Фибоначчи.
Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:
-
для каждого натурального числа существует элемент данного множества;
-
это число является номером элемента и обозначает позицию данного элемента в последовательности;
-
для любого элемента последовательности можно указать следующий за ним элемент.
Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией. an+1 = an + d , n є N
Сумма n членов арифметической прогрессии:
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число. Таким образом, геометрическая прогрессия – это числовая последовательность, заданная соотношениями bn+1 =bn · q, где bn ≠ 0, q ≠ 0, q – знаменатель прогрессии.
Сумма n первых членов геометрической прогрессии равна
Сумма n первых членов, бесконечно убывающей геометрической прогрессии равна
Чи́сла Фибона́ччи — элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …, в которой первые два числа равны 1 и 1, а каждое последующее число равно сумме двух предыдущих чисел.
Практика
Задание 1 В строку подряд написано 1000 чисел. Под каждым числом a первой строки напишем число, указывающее, сколько раз число a встречается в первой строке. Из полученной таким образом второй строки аналогично получаем третью: под каждым числом второй строки пишем, сколько раз оно встречается во второй строке. Затем из третьей строки так же получаем четвёртую, из четвёртой — пятую, и так далее.
а) Докажите, что некоторая строчка совпадает со следующей.
б) Докажите, что 11‐я строка совпадает с 12‐й.
в) Приведите пример такой первоначальной строчки, для которой 10‐я строка не совпадает с 11‐й.
Решение.
а) Очевидно, что начиная со второй строчки, все числа в таблице не больше 1000. Кроме того, каждое число не больше написанного под ним. Поэтому сумма чисел в третьей строчке не меньше, чем во второй и т.д., и каждая из этих сумм не больше миллиона. Следовательно, поскольку все время суммы возрастать не могут, в каких-то соседних строчках суммы совпадут, а тогда совпадут и сами строчки.
б) Докажем, что если в m-ой строчке при m=2, число отлично от написанного над ним, то оно не меньше, чем . Действительно, для m = 2 это очевидно, так как все числа второй строки натуральные. Пусть это уже проверено для всех строк с номерами, меньшими m. Пусть в m-1-ой строчке написано число a, а под ним написано число b, большее a. Тогда в m-2-ой строчке написано b чисел, равных a. Ясно, что в m-2-ой строчке будет написано несколько групп одинаковых чисел, по a в каждой группе, причем числа из разных групп различны. Отсюда вытекает, что b делится на a, то есть b=2a. Кроме того, по крайней мере одно из чисел в этих группах отличается от a а значит, по предположению индукции
. Итак,
. Наше утверждение доказано по индукции для всех m=2. Если предположить, что 11-я строчка отлична от 12-й, то какое-то число в 12-й строчке будет больше, чем
в) Приведем такой пример:
0, 1, 2, 2, 4, 4, 4, 4, …, 256, …, 256, 488, …, 488
1, 1, 2, 2, 4, 4, 4, 4, …, 256, …, 256, 488, …, 488
2, 2, 2, 2, 4, 4, 4, 4, …, 256, …, 256, 488, …, 1488
4, 4, 4, 4, 4, 4, 4, 4, …, 256, …, 256, 488, …, 488
…………………………………………………………….
256, ……………………………., 256, 488, …, 488
1 512, ……………………………., 512, 488, …, 488
В первой строчке 0 и 1 встречаются по одному разу, 2 — два раза, 4 — четыре раза, 8 — восемь раз, …., 256 — 256 раз, 488 — встречается 488 раз, в 11 строчке встречается 512 раз число 512 и 488 раз число 488.
Задание 2 Можно ли из последовательности 1, 1/2, 1/3, 1/4,… выделить арифметическую прогрессию
а) длиной 4
б) длиной 5
в) длиной k, где k — любое натуральное число?
Решение
а) Например, годится такая прогрессия: 1/6, 1/8, 1/12, 1/24;
б) Например, годится такая прогрессия: 1/24, 1/30, 1/40, 1/60, 1/120;
в) Ясно, что последовательность является арифметической прогрессией с разностью . Кроме того, каждый член такой последовательности можно сократить так, чтобы в числителе была единица. Значит, все они являются членами исходной последовательности.
Сюжетные задачи
Как можно было понять из названия, в таком типе задач описывается какая-то особая ситуация кино, театр, мотки верёвки и тому подобное. Четкое определение всему виду дать трудно и зачастую приходится подбирать нужную теорию и формулы к каждой задаче в частном порядке. Отдельно можно отметить два подвида: работа с дробями и теория игр. В теории игр нет какой-либо особой теории, там надо последовательно разбирать случаи и варианты ходов игроков. А для задач с дробями, нужны лишь основные принципы и знания, которые проходят в школе.
Практика
Задание 1 Два игрока ходят по очереди. Перед началом игры у них есть поровну горошин. Ход состоит в передаче сопернику любого числа горошин. Не разрешается передавать такое количество горошин, которое до этого уже кто‐то в этой партии передавал. Ноль горошин тоже передавать нельзя. Тот, кто не может сделать очередной ход по правилам, — считается проигравшим. Начинающий или его соперник победит в этой игре, как бы ни играл партнёр?
Рассмотрите случаи:
а) у каждого по две горошины;
б) у каждого по три горошины;
в) у каждого по N горошин.
Решение.
а) Первый игрок либо отдаст второму две горошины (на это второй даст ему одну, и у первого не будет ходов), либо отдаст одну. В этом случае второй игрок может отдать ему две горошины, назад получит три, отдаст четыре и победит. Так или иначе выигрывает второй игрок.
б) Если первый игрок отдаст три или две, назад получит одну и сразу проиграет. Если же отдаст одну, то назад получит две. Далее у первого два варианта хода, но оба плохи: отдав 4, он получит назад 3 и проиграет, а отдав 3, получит 4, будет вынужден отдать 5, получит 6 и всё равно проиграет.
в) Победит второй игрок, придерживаясь правила: «всякий раз отдавай минимально возможное число горошин». Докажем, что это действительно выигрышная стратегия. Достаточно показать, что у второго игрока всегда будет ход. Начинает игру у нас первый игрок, но мы схитрим и сделаем так, чтобы игру начинал второй: предположим, что второй (условно) передаёт сначала первому 0 горошин. Теперь можно видеть, что всякий раз в ответ на ход второго первый игрок вынужден будет отдать ему больше, чем сам получил. Поэтому количество горошин у второго с каждым парным ходом будет увеличиваться хотя бы на одну. Перед K-ом ходом у него будет не менее N + K горошин. А отдать на K-ом ходу он в соответствии со своей стратегией должен не более 2K горошин. Это осуществимо, поскольку более чем N ходов игра длиться не может, а значит N + K ≥ 2K.
Задание 2 Трое друзей играли в шашки. Один из них сыграл 25 игр, а другой — 17 игр. Мог ли третий участник сыграть
а) 34;
б) 35;
в) 56 игр?
Решение.
а) Да, мог. Например, если первый с третьим сыграли 21 игру, второй с третьим — 13 игр, а первый со вторым — 4 игры.
б) Нет, не мог. Действительно, в таком случае общее число сыгранных партий было бы равно (25 + 17 + 35)/2 = 38,5 игр — не целое число.
в) Нет, не мог. Пусть такое возможно, тогда третий игрок сыграл больше партий, чем первый и второй вместе взятые (25 + 17
Задание 3 Леша задумал двузначное число (от 10 до 99). Гриша пытается его отгадать, называя двузначные числа. Если Гриша правильно называет число, или же одну цифру называет правильно, а в другой ошибается не более чем на единицу, то Леша отвечает «тепло»; в остальных случаях Леша отвечает «холодно». (Например, если задумано число 65, то назвав 65, 64, 66, 55 или 75, Гриша услышит в ответ «тепло», а в остальных случаях услышит «холодно».)
а) Покажите, что нет способа, при котором Гриша гарантированно узнает число, истратив 18 попыток.
б) Придумайте способ, при котором Гриша гарантированно узнает число, истратив 24 попытки (какое бы число ни задумал Леша).
в) А за 22 попытки получится?
Решение.
а) Расположим двузначные числа в клетках прямоугольника высоты 9 и ширины 10 (по горизонтали откладываем единицы, по вертикали – десятки). Каждой попытке Гриши соответствует крестик из пяти клеток: в центре названное им число, а по бокам четыре числа, отличающиеся в одной цифре на единицу (если названное число содержит цифру 0 или 9, некоторые клетки крестика выходят за края прямоугольника; таким клеткам никакие числа не соответствуют). Задача Гриши – покрыть прямоугольник 9 × 10 такими крестиками. Убедимся, что 18 крестиков ему не хватит. Суммарная площадь крестиков равна 18 × 5 = 90, т. е. равна площади прямоугольника. Но, покрывая угловую клетку, мы неизбежно выйдем за пределы прямоугольника, и эта потеря помешает покрыть весь прямоугольник.
в) Решим сразу пункт в) — убедимся, что 22 попыток хватит. Покрытие из 22 крестиков легко найти, если заметить, что крестиками можно выложить плоскость без перекрытий (правда, придётся ещё добавить несколько крестиков по краям прямоугольника). Например, Гриша может назвать числа 11, 13, 17, 25, 29, 30, 32, 37, 44, 49, 51, 56, 63, 68, 70, 75, 82, 87, 89, 90, 94, 97.
Вывод
Были изучены основные виды 19 задачи из ЕГЭ по профильной математике, рассмотрена необходимая теория и решены типичные для каждого из видов задачи.
Используемая литература
-
https://infourok.ru/podgotovka-uchaschihsya-k-resheniyu-olimpiadnih-zadach-na-delimost-klassi-1154972.html
-
https://math-ege.sdamgia.ru/
-
https://mirurokov.ru/
-
https://calcs.su/html/math/grade7/srednee-arifmeticheskoe.html
-
https://mathlesson.ru/ege2020fipi-yashenko36var-1var
-
https://alexlarin.net/
-
Корянов А.Г., Прокофьев А.А. Задачи на целые числа (от учебных задач до олимпиадных)
Главная » ЕГЭ » ЕГЭ. Математика. Задачи на целые числа. Типовые задания 19.
Пособие посвящено одному из самых трудных заданий ЕГЭ по математике — заданию 19 профильного уровня (бывшее задание С6). В большом количестве представлены и примеры выполнения заданий, и упражнения для самостоятельной работы. Ко всем заданиям даны ответы, а в некоторых случаях приведены указания. Издание адресовано выпускникам, сдающим ЕГЭ по математике профильного уровня, а также учителям и методистам. Книга дополняет учебно-методический комплекс «Математика. Подготовка к ЕГЭ».
- Рубрика: ЕГЭ / ЕГЭ по математике
- Автор: неизвестно
- Год: 2016
- Для учеников: 11 класс
- Язык учебника: Русский
- Формат: PDF
- Страниц: 272
1
Задачи с целыми числами
Первая часть.
Дихтярь М. Б.
Простые и составные числа
Натуральные числа – это числа 1, 2, 3,… . Множество всех
натуральных чисел обозначается через N.
Целые числа – это числа
. Множество всех целых
чисел обозначается через Z.
Натуральное число b называется делителем целого числа a, если
существует целое число с такое, что
называется простым, если его
натуральными делителями являются только числа 1 и р.
Наименьшим простым числом является число 2. Число 2 –
единственное простое чётное число.
Всякое простое число
Натуральные числа называются взаимно простыми, если они не
имеют общих делителей, кроме единицы.
Например, числа
взаимно простые.
Если число делится на каждое взаимно простое число, то оно
делится на их произведение.
Если произведение
и с взаимно простые
числа, то
делится на с.
Если произведение
– простые числа,
делится на простое число
совпадает с одним из чисел
.
Натуральное число называется составным числом, если оно имеет
не менее трёх натуральных делителей, включая единицу и само число.
Если произведение
– простые числа,
делится на составное число
равно произведению из нескольких
сомножителей чисел
всегда является составным, если оно чётное (кроме
)
или, если оно кратно 5 (кроме
) или, если сумма цифр этого числа
делится на 3 (кроме
).
Для того чтобы показать, что данное число составное, достаточно
2
представить его в виде произведения двух натуральных чисел, ни одно
из которых не равно 1.
Единица – единственное натуральное число, которое не является ни
простым, ни составным.
Чтобы определить, что число р является простым (если не
очевидно, что оно составное), надо:
1) найти корень квадратный этого числа (найти
);
2) проверить делимость числа р на все простые числа, которые
меньше
Пример. Проверить являются ли числа 151, 161, 171 простыми.
Решение. Так как числа 151, 161 не являются чётными, не делятся
на 5, не делятся на 3, то они могут быть простыми числами.
1. Проверяем число 151.
1) Находим
2) Проверим делимость числа 151 на простые числа: 7, 11 (простые
числа меньше 12, но не равные 2, 3 и 5).
Так как число 151 не делится ни на одно из рассматриваемых
чисел, то оно является простым числом.
2. Проверяем число 161.
1) Находим
2) Проверим делимость числа 161 на простые числа: 7, 11.
Так как число 161 делится на 7, то оно не является простым числом.
3. Проверяем число 171.
Так как сумма цифр числа 171 равна 9, то это число делится на 9.
Это означает, что число 171 не является простым числом.
Ответ. Число 151 является простым числом.
Каждое натуральное число
можно единственным способом
представить в виде произведения степеней простых чисел:
– простые делители числа n, числа
является числом повторений числа
). Такое представление числа n называется каноническим
разложением числа n. Число делителей числа n, включая единицу и
число n, равно произведению
( ) ( ) ( )
12
1 1 1
m
k k k+ + +
.
Деление с остатком.
Разделить натуральное число a на натуральное число b – значит
найти такие числа q и r, что
3
называется делимым, число b называется делителем, число q называется
частным, число r называется остатком.
Отметим:
1) любое целое число n можно представить в виде
где k
– натуральное число, q – целое число, r – целое число (остаток), который
принимает k значений, при этом
2) если при делении натурального числа a на натуральное число b
остаток равен нулю, то число a делится на b без остатка (нацело) и
(в этом случае говорят, что число a делится на число b или а
кратно b);
3) из
целых чисел найдутся хотя бы два числа, которые при
делении на n имеют равные остатки (разность чисел с равными
остатками делится на n);
4) из n последовательных натуральных чисел одно и только одно
делится на n;
5) число
не делится ни на какое натуральное число
получаем в остатке 1 (остаток не равен нулю);
6) числа
! 2; ! 3; ; !n n n n+ + +
являются составными идущими
подряд натуральными числами. Количество этих чисел равно
7) остаток от деления суммы (разности, произведения) двух чисел
на третье равен остатку от деления суммы (разности, произведения) их
остатков;
8) остаток от деления числа на 9 (на 3) равен остатку отделения
суммы цифр этого числа на 9 (на 3);
9) если целое число делится на произведение натуральных чисел, то
оно делится на каждый сомножитель.
Сравнение чисел по модулю
Определение. Целые числа a и b называются сравнимыми по
модулю
, если при делении на число n они дают одинаковый
остаток. Обозначение
7 1 5 2, 2 0 5 2;= + = +
делится на 5.
Некоторые свойства сравнений чисел по модулю.
( ) ( ) ( )
mod , mod mod .a b n b c n а c n
( )( )
mod ,a c b d n+ +
( )( )
mod .a c b d n
Признаки делимости
В десятичной системе счисления натуральное число n записывается
в виде
12
1 2 1
10 10 10 ,
nn
nn
n a a a a
−−
−
= + + + +
11
1 9, 0 9, , 0 9.
nn
a a a
−
1 1 1 1 1 1
10 .
k
n n k k n n k k
aa а а а a a а а а
− + − +
= +
3
24657843 10 24657 843; 24657843 10 2465784 3.= + = +
1. Натуральное число делится на 4 тогда и только тогда, когда две
последние цифры этого числа, образуют число, которое делится на 4.
2. Натуральное число делится на 8 тогда и только тогда, когда три
последние цифры этого числа, образуют число, которое делится на 8.
3. Натуральное число делится на 11 тогда и только тогда, когда
разность суммы цифр, стоящих на нечетных местах и суммы цифр
стоящих на четных местах, делится на 11.
Например,
а) число 63976 делится на 11, так как число
( ) ( )
6 9 6 3 7 11+ + − + =
делится на 11;
б) число 282754 на 11 не делится, так как
( ) ( )
2 2 5 8 7 4 10+ + − + + = −
не делится на 11.
Наибольший общий делитель. Наименьшее общее кратное.
Общим делителем нескольких целых чисел, не равных
одновременно нулю, называется число являющееся делителем каждого
из этих чисел.
Наибольший из общих делителей называется наибольшим общим
делителем и обозначается НОД.
Обозначение:
наибольший общий делитель
чисел
.
Если НОД(m, n)=d, то существуют взаимно простые натуральные
числа х и у таковы, что
Отметим: число х является
делителем
а у является делителем числа
5
Общим кратным нескольких целых чисел, не равных
одновременно нулю, называется число, которое делится на каждое из
этих чисел.
Наименьшие из общих кратных называется наименьшим общим
кратным и обозначается НОК.
Обозначение:
наименьшее общее кратное чисел
( ; ) ( ; ) .НОД a b НОК a b а b =
Способы нахождения НОД
Первый способ.
Чтобы найти НОД нескольких чисел надо:
1) найти каноническое разложение каждого числа на простые
множители;
2) найти произведение их общих множителей в наименьших
степенях;
3) полученное число является НОД этих чисел.
Второй способ.
Чтобы найти НОД двух чисел, делят большее число на меньшее, и
если получается остаток, не равный нулю, то делят меньшее число на
остаток; если снова получается остаток, не равный нулю, то делят
первый остаток на второй и так продолжают до тех пор, пока в остатке
не получится ноль.
Последний делитель будет НОД этих чисел.
Для того чтобы найти НОД трёх и более чисел, то находят НОД
каких—нибудь двух чисел из данных. Затем находят НОД найденного
делителя и какого—нибудь третьего числа из данных чисел и так
продолжают до тех пор, пока не будут взяты все данные числа.
НОД последней пары и будет НОД данных чисел.
Способы нахождения НОК.
Чтобы найти НОК нескольких чисел надо:
1) найти каноническое разложение каждого числа на простые
множители;
2) найти произведение всех множителей, входящих хотя бы в одно
из разложений, при этом множители, входящие в каждое разложение,
надо брать в наибольших степенях;
3) полученное число является НОК.
6
Замечание. Если числа не имеют общих множителей, то их НОК
равен произведений этих чисел.
Пример. Найдите НОД чисел 726, 660, 504 двумя способами и
НОК этих чисел.
Найдём НОК и НОД первым способом.
Так как
2 2 3 2
726 2 3 11 , 660 2 3 5 11, 504 2 3 7,= = =
3 2 2
(726;660;504) 2 3 5 7 11 304920,
(726;660;504) 2 3 6.
НОК
НОД
= =
= =
Второй способ.
1) Сначала найдём НОД чисел 726, 660.
Разделим число 726 на 660 и получим
Разделим число 660 на 66 и получим
Так как 660 делится на 66 без остатка, то НОД(726; 660)=66.
2) Найдём НОД чисел 504, 66.
Разделим число 504 на 66 и получим
Разделим число 66 на 42 и получим
Разделим число 42 на 24 и получим
Разделим число 24 на 18 и получим
Разделим число 18 на 6 и получим
3) Так как 18 делится на 6 без остатка, то НОД(726; 660; 504)=6.
Основные алгебраические формулы
1. Для произвольных чисел a и b и произвольного натурального
числа n справедлива формула бинома Ньютона
0 1 1 1 1
()
n n n i n i i n n n n
n n n n n
a b C a C a b C a b C ab C b
− − − −
+ = + + + + + +
.
Если a и b целые числа, то
( )
1 1 2 1
( ) ( ) .
n n n n n n n
n
k целое число
ab а a C a b nb b a b kа b
− − −
−
+ = + + + + + = +
Таким образом, существует целое число k такое, что для
произвольных целых чисел a и b и произвольного натурального числа n,
выполняется равенство
2. Для произвольных чисел a и b и произвольного натурального
числа n справедлива формула
( )
( )
2 1 2 1 2 2 1 2 2 2 2 1 2n n n n n n n
a b a b a a b a b ab b
+ + − − −
+ = + − + − − +
Если a и b целые числа, не равные нулю, то
( )
( )
( )
2 1 2 1 2 2 1 2 2 2 2 1 2n n n n n n n
k целое число
a b a b a a b a b ab b k a b
+ + − − −
−
+ = + − + − − + = +
7
Таким образом, существует целое число k такое, что для
произвольных целых чисел a и b, которые не равны нулю, и
произвольного натурального числа n, выполняется равенство
( )
2 1 2 1
.
nn
a b k аb
++
+ = +
3. Для произвольных чисел a и b и произвольного натурального
числа n справедлива формула
( )
( )
1 2 3 2 2 1n n n n n n n
a b a b a a b a b ab b
− − − − −
− = − + + + + +
Если a и b целые числа, если
( )
( )
( )
1 2 3 2 2 1
.
n n n n n n n
k целое число
a b a b a a b a b ab b k a b
− − − − −
−
− = − + + + + + = −
Таким образом, существует целое число k такое, что для
произвольных целых чисел a и b таких, что
, и произвольного
натурального числа n, выполняется равенство
Задачи на простые числа
1. Докажите: если
простое число, то оно представимо в виде
может быть простым.
2. Найдите простое число p, если
простое число.
Решение. 1. Если
22
14 1 57 14 1 3 19pp+ = + = −
( ) ( )
2 2 2
14 1 14 36 12 1 1 3 168 56 5 .р k k k k+ = + + = +
( )
( )
22
14 1 3 168 56 5 . 1р k k+ = +
( )
2
168 56 5 56 3 1 5 1,k k k k + = +
не является простым числом.
Ответ.
8
3. Найдите все простые числа p и q, для которых число
точный квадрат.
Решение. Если
то при любом простом числе p
число
то простое число q является нечётным числом, тогда
будет точным квадратом, если
точный квадрат, то найдётся число
( )( )
22
4 4 2 2 .p k p k p k k+ = = − = − +
Так как p является простым числом, то равенство
возможно только в случае когда
и p любое простое число;
простое число
простое число, при
делении на 9 даёт остаток, равный 1, если
Рассмотрим два случая.
1) Если
2 1 6 1 2 6
nn
kk− = − = −
этот случай невозможен, так как
1
2 1 6 1 2 6 2 2 3 1.
n n n
k k k
−
− = + = + = +
( )
( )( )
( ) ( )
1 1 2
2 2 1 3 1 6 1 2 2 1 9 2 1.
n n n n
k k k k
−−
− = + + − = + +
( ) ( )
12
2 2 1 9 2 1,
nn
kk
−
− = + +
простое число, при делении на 9 даёт остаток, равный 1.
5. Найдите все тройки последовательных простых чисел, сумма
квадратов которых также является простым числом.
Решение. Пусть
последовательные простые числа.
1. Пусть одно из простых чисел равно 2. Так как
последовательные простые числа, то
Найдём сумму квадратов последовательности 2, 3, 5:
не простое число (последовательность 2, 3, 5 не
удовлетворяет условию задачи).
последовательные простые
числа, то
Найдём сумму квадратов последовательности 3, 5, 7:
простое число (последовательность 3, 5, 7
удовлетворяет условию задачи).
3. Пусть
простые числа, которые больше
3, то
1 1 2 2 3 3
6 1, 6 1, 6 1,р k р k р k= = =
( ) ( ) ( )
( )
( )
( )
( )
( )
2 2 2
2 2 2 2 2 2
1 2 3 1 2 3 1 2 3
222
1 2 3 1 2 3 1 2 3
6 1 6 1 6 1 36
12 3 3 12 4 1 .
р р р k k k k k k
k k k k k k k k k
+ + = + + = + +
+ + + = + + + + +
( )
( )
( )
2 2 2 2 2 2
1 2 3 1 2 3 1 2 3
3 12 4 1 .р р р k k k k k k+ + = + + + + +
( )
( )
222
1 2 3 1 2 3
12 4 1 1.k k k k k k+ + + + +
Тогда
из (1) следует, что
составное число.
Ответ. 3, 5, 7
6. Найдите все простые числа, которые одновременно являются
суммами и разностями двух простых чисел.
Решение. Пусть
1 2 3 4
, , , ,р р р р р −
простые числа, удовлетворяющие
уравнениям
1 2 3 4
,.р р р р р р= + = −
нечётные числа
(алгебраическая сумма двух нечётных чисел чётное число), а тогда
( )
13
6 1 2, 6 1 2. 1k р k р = + = −
Рассмотрим два случая.
1) Если
( )
3 3 3
6 1 2 6 3 3 2 1 .k р р k р k+ = − = + = +
будет
простым числом, если
Этот случай невозможен, так как
( )
1 1 1
6 1 2 6 3 3 2 1 .k р р k р k− = + = − = −
будет
простым числом, если
удовлетворяет условию задачи.
10
Ответ. 5.
7. Докажите, что не существуют наибольшего простого числа.
Решение. Пусть
наибольшее простое число.
Рассмотрим число
( )
2 3 5 1,n р= +
все простые
числа не больше р. Очевидно,
делится на любое простое число, так как по
предположению
наибольшее простое число. Тогда остаток при
делении числа
на любое простое равен 1. Значит, n
не делится ни на одно простое число.
Так как любое составное число
делится хотя бы на одно простое
число, которое меньше
, то число n является простым числом. Число n
не может быть простым числом, так как
наибольшее простое число.
Из предположения, что существует наибольшее простое число,
получили противоречие. Тогда не существует наибольшего простого
числа.
8.
Докажите, что ни одно из чисел
произведение первых т простых чисел, не является квадратом.
Решение. Так как
произведение первых т простых чисел, то р
делится на 2 (является чётным числом) и не делится на 4.
1. Пусть
является квадратом целого числа п. Тогда
( ) ( )
22
4 4 2 2 .р п р п р п п+ = = − = − +
Так как р – чётное число, то из равенства
следует, что п
– чётное число, а тогда
делится на 4. Так как р не делится
на 4, а
( ) ( )
2
2 2 4 .р п п р п − + +
является квадратом целого числа п. Тогда
Так как р – чётное число, то
чётное число. Тогда
существует число
( )
2 2 2
4 2 2 4 2 2 .п т п т п т+ = = − = −
делятся на 4. Так как р не
делится на 4, а
Из 1. и 2. следует: ни одно из чисел
не является
квадратом.
9. Найдите все натуральные числа n такие, что числа
4, 6, 10, 30n n n n− + + + −
простые.
Решение. Так как
не являются
простыми.
2. Если
6 13, 10 17, 30 37n n n+ = + = + =
являются простыми. Значит,
удовлетворяет условию задачи.
2. Пусть
.
Рассмотрим два случая.
1) Если
4 6 1 6 3,n k n k− = − = +
не
будет простым числом, так как
( )
30 6 33 30 3 2 11n k n k+ = + + = + −
4 6 1 6 5,n k n k− = + = +
не
будет простым числом, так как
( )
10 6 15 10 3 2 5n k n k+ = + + = + −
).
Ответ. 7.
10. Найдите все простые числа p для которых число
тоже
простое число.
Решение. 1. Если
не является простым числом
2.
Если
является простым числом
3. Пусть
( ) ( ) ( ) ( )( )
4 4 2 2
2 2 1 1 2 1 1 1 .
p p p
p p p p+ = + + − = + + − +
( ) ( )( )
( )
4 2 2
2 2 1 1 1 . 1
pp
p p p+ = + + − +
1) Докажем, что делится на 3. Так как
нечётное число, то
найдётся число
( )
( ) ( )
21
11
2 1 2 1 2 4 1 2 3 1 1
2 3 3 1 1 2 3 2 3 3 .
k
p k k
k k k k
kk
+
−−
+ = + = + = + + =
= + + + + = + + +
( )
1
2 1 2 3 2 3 3
p k k
k
−
+ = + + +
делится на 3.
2) Докажем, что
, то его можно представить в
виде
( ) ( )( )
2
2
1 6 1 6 1 6 1 .p k k k
− = + − = + − + +
( )( )
2
1 6 1 6 1p k k
− = + − + +
делится на 3.
Итак, доказали:
( ) ( )( )
4 2 2
2 2 1 1 1 ,
pp
p p p+ = + + − +
то из 1) и 2) следует,
что
делится на 3. Тогда, так как
, не является простым числом.
Ответ.
то существует натуральное
число n
такое, что
( )
( )
32
1 1 1q q q q− = − + +
делится только одно из чисел
Тогда существует натуральное
число т
такое, что
Тогда существует
натуральное число
( ) ( ) ( )
22
1 1 1 1 1 .qq рk q q рk k k q q р k k+ + = + = − + − + = − + −
( ) ( ) ( )
1 1 1 .qq р k k+ = − + −
( ) ( ) ( )
1 1 1 ,qq р k k+ = − + −
( )
2
22
1 1 1qq рk q q q+ + = + + + −
это невозможно. Предположение, что
12.
Докажите, что для любого простого числа
( )( )
4 2 2 2
85 324 81 4 .q р р q р р= − + = − −
простое число то оно может оканчиваться на одно из
следующих цифр: 1, 3, 7, 9. Тогда
может оканчиваться на 1 или 9. В
этом случае
делится на 5.
2. Докажем, что число
делится на 24.
а) Так как
, то его можно представить в
виде
( ) ( ) ( ) ( )
( )
2 2 2 2
81 4 12 9 3 20 12 4 1 . 1q p p q k k k k= − − = − −
делится на 12.
б) Докажем, что
чётное число
(алгебраическая сумма двух нечётных чисел является чётным числом), а
тогда число
является чётным числом, а значит, оно делится
на 2.
Так как
делится на 24.
Было доказано, что
делится на 120.
13. Какое наибольшее количество простых чисел, больших трёх,
встречается среди 13 последовательных натуральных чисел?
Решение. Любое натуральное число n можно представить в виде
где k – натуральное число, r – остаток
может быть простым только, если
Пусть n – первый член последовательности 13 натуральных чисел.
Рассмотрим следующие случаи.
1. Пусть
Заданными числами являются числа:
( )
( )
6 2, 6 1, 6 , 6 1, 6 2, 6 3, 6 4, 6 5 6 1 1,
6 6, 6 7 6 1 1, 6 8, 6 9, 6 10.
k k k k k k k k k
k k k k k k
− − + + + + + = + −
+ + = + + + + +
В этом случае может быть не более 4 простых чисел:
( ) ( )
6 1, 6 1, 6 5 6 1 1, 6 7 6 1 1.k k k k k k− + + = + − + = + +
Заданными числами являются числа:
( )
( ) ( )
6 1, 6 , 6 1, 6 2, 6 3, 6 4, 6 5 6 1 1, 6 6,
6 7 6 1 1, 6 8, 6 9, 6 10, 6 11 6 2 1.
k k k k k k k k k
k k k k k k k
− + + + + + = + − +
+ = + + + + + + = + −
В этом случае может быть не более 5 простых чисел:
( ) ( ) ( )
6 1, 6 1, 6 5 6 1 1, 6 7 6 1 1, 6 11 6 2 1.k k k k k k k k− + + = + − + = + + + = + −
Заданными числами являются числа:
( )
( ) ( )
6 , 6 1, 6 2, 6 3, 6 4, 6 5 6 1 1, 6 6,
6 7 6 1 1, 6 8, 6 9, 6 10, 6 11 6 2 1, 6 12.
k k k k k k k k
k k k k k k k k
+ + + + + = + − +
+ = + + + + + + = + − +
В этом случае может быть не более 4 простых чисел:
( ) ( ) ( )
6 1, 6 5 6 1 1, 6 7 6 1 1, 6 11 6 2 1.k k k k k k k+ + = + − + = + + + = + −
Заданными числами являются числа:
( ) ( )
( ) ( )
6 1, 6 2, 6 3, 6 4, 6 5 6 1 1, 6 6, 6 7 6 1 1,
6 8, 6 9, 6 10, 6 11 6 2 1, 6 12, 6 13 6 2 1,
k k k k k k k k k
k k k k k k k k
+ + + + + = + − + + = + +
+ + + + = + − + + = + +
В этом случае может быть не более 5 простых чисел:
( ) ( ) ( ) ( )
6 1, 6 5 6 1 1, 6 7 6 1 1, 6 11 6 2 1, 6 13 6 2 1.k k k k k k k k k+ + = + − + = + + + = + − + = + +
Заданными числами являются числа:
( ) ( )
( ) ( )
6 2, 6 3, 6 4, 6 5 6 1 1, 6 6, 6 7 6 1 1, 6 8,
6 9, 6 10, 6 11 6 2 1, 6 12, 6 13 6 2 1, 6 14.
k k k k k k k k k
k k k k k k k k
+ + + + = + − + + = + + +
+ + + = + − + + = + + +
В этом случае может быть не более 4 простых чисел:
( ) ( ) ( ) ( )
6 5 6 1 1, 6 7 6 1 1, 6 11 6 2 1, 6 13 6 2 1.k k k k k k k k+ = + − + = + + + = + − + = + +
Заданными числами являются числа:
( ) ( )
( ) ( )
6 3, 6 4, 6 5 6 1 1, 6 6, 6 7 6 1 1, 6 8, 6 9,
6 10, 6 11 6 2 1, 6 12, 6 13 6 2 1, 6 14, 6 15.
k k k k k k k k k
k k k k k k k k
+ + + = + − + + = + + + +
+ + = + − + + = + + + +
В этом случае может быть не более 4 простых чисел среди 13
последовательных натуральных чисел:
( ) ( ) ( ) ( )
6 5 6 1 1, 6 7 6 1 1, 6 11 6 2 1, 6 13 6 2 1.k k k k k k k k+ = + − + = + + + = + − + = + +
Например, 5 простых чисел будет среди следующих 13
последовательных натуральных чисел: 11, 12, 13, 14, 15, 16, 17, 18, 19,
20, 21, 22, 23.
Ответ. 5.
14. Найдите число
простые числа
и каждое из чисел
является делителем натурального
числа, то
4 , 1; 2, ,
ii
p mp i m N− = =
( )
1 4, 1; 2, ,
i
p m i m N− = =
4 , 1; 2, .
ii
p mp i m N− =
равно хотя бы одному нечётному делителю
числа
( )
1
4 1; 7;11; 77 .p −
22
154 5 770n p n p= =
22
154 11 1694 .n p n p= =
22
770 1 2 5 7 11 .n p n p= =
равно хотя бы одному
нечётному делителю числа
которые не принадлежат
множеству
( )
2
4 5; 5 7;11 7;11 7 5 .p −
22
4 11 7 5 389pp− = = −
2
22
1694 1 2 7 11 .n p n p= =
равно хотя бы одному
нечётному делителю числа
которые не принадлежат
множеству
( )
22
2
4 11 ; 7 11 .p −
2 2 2
4 7 121 851 23 37p p p− = = = −
15. Какое наибольшее количество чисел можно выбрать из отрезка
натурального ряда чисел 1 до 3125 так, чтобы разность любых двух из
них не была простым числом?
16
Решение. 1. Если из исходного натурального ряда берутся числа
вида
то в этой последовательности
разность между двумя соседним числами равна 2 – простое число.
2. Если из исходного натурального ряда берутся числа вида
, то в этой последовательности
разность между двумя соседними числами равна 3 – простое число.
3. Пусть из исходного натурального ряда берутся числа
то из исходного ряда чисел берётся
последовательность чисел
Рассматриваемая последовательность состоит из 781
чисел, разность между любыми двумя числами этой последовательности
кратна 4 (не является простым числом).
б) Если
то из исходного ряда чисел берётся
последовательность
Рассматриваемая последовательность состоит из 782
чисел, разность между любыми двумя числами этой последовательности
кратна 4.
в) Если
то из исходного ряда чисел берётся
последовательность
Рассматриваемая последовательность состоит из 781
чисел, разность между любыми двумя числами этой последовательности
кратна 4 (не является простым числом).
г) Если
то из исходного ряда чисел берётся
последовательность
Рассматриваемая последовательность состоит из 781
чисел, разность между любыми двумя числами этой последовательности
кратна 4.
4. Если из исходного натурального ряда берутся числа вида
, , , 5, 0,1,2,3, , 1т k n N т т
= −
, то наибольшее
количество чисел, которое можно выбрать из отрезка натурального ряда
чисел 1 до 3125, меньше 782.
Ответ. 782.
Задачи на основные алгебраические формулы
В задачах 16.– 21. Используется следующее:
17
1. Для произвольных целых чисел a и b и произвольного
натурального числа n, существует целое число k такое, что
2. Для произвольных целых чисел a и b, которые не равны нулю, и
произвольного натурального числа n существует целое число k такое,
что
( )
2 1 2 1
.
nn
a b k аb
++
+ = +
3. Для произвольных целых чисел a и b, где
и
произвольного натурального числа n существует целое число k такое,
что
16. Найдите три последние цифры суммы
999 999 999 999
999 1999 2999 999999 .S = + + + +
( ) ( ) ( ) ( ) ( )
999 999 999 999
1000 0 999 1000 1 999 1000 2 999 1000 999 999 . 1S = + + + + + + + +
Так как для произвольных чисел a и b и произвольного
натурального числа n, существует целое число k такое, что
то каждое слагаемое суммы представим в виде
( )
999
999
1000 999 1000 999 , , .k k n k n N + = +
Так как число слагаемых в сумме (1) равно 1 000, то
( )
999
999
1000 1000 999 1000 999 , .S m S m m N= + = +
Так как сумма S делится на 1 000, то три последние цифры: 0, 0, 0.
Ответ. 0, 0, 0.
17. Докажите, что число
делится на 97.
Решение. Имеем
( ) ( )
( ) ( )
99 99
99 99
396 396 4 4
3 2 3 2 81 16 .+ = + = +
Существует натуральное число m такое, что
( ) ( ) ( ) ( ) ( )
99 99 99 99
81 16 81 16 81 16 97 .тт+ = + + =
делится на 97.
18. Докажите, что число
делится на 5.
Решение. Так как
, то существует целое число k такое,
что
( )
57
57 57 57
55 2 55 2 57 55 2 .kk+ = + = +
, то существует целое число m такое, что
( ) ( )
23 23
57 23
25 2 25 2 23 25 2 .mm− = + − = −
( )
( )
( )
57 23 57 23 23 34
57 23 55 2 25 2 5 11 5 2 2 1 .
целое число
А k m k m= − = + − − = − + +
Число
А делится на 5, если число
то существует целое число n такое, что
( )
17
4 1 4 1 5 .nn+ = + =
делится на 5,
а тогда и число А делится на 5.
19. Докажите, что
N делится на 37.
Решение. Так как
( )
( ) ( )
44
2 3 2 3 2 81 162
n
nn
n n n
= = =
( ) ( )
( ) ( ) ( )
5 4 3 1 5 4 3 5
555
5 5 5
( ) 2 3 5 2 2 3 5 5 2 162 5 125
2 162 2 125 2 125 5 125
2 162 125 2 5 125 2 162 125 37 125 .
n
n n n n n n n
n n n n
n n n n n n
An
++
= + = + = + =
= − + + =
= − + + = − +
Существует натуральное число m такое, что
( ) ( ) ( ) ( ) ( )
162 125 162 125 162 125 37 .
n n n n
тт− = − − =
5
( ) 2 37 37 125 , .
n
An т m N= +
делится на 37.
20. Докажите, что
N делится на 31.
Решение. Так как
2 2 1 2 2 1
5 6 5 5 6 5 6 6 ,
n n n n n n+ + + +
+ = + − +
( )
( ) ( )
( )
( )
2 2 1 2 2 1 2
5 6 5 5 6 6 5 6 5 25 6 6 6 5 .
n n n n n n n n n
Аn
+ + + +
= + = + + − = + + −
( ) ( )
2
6 5 36 5 ,
n n n n
− = −
то существует целое
число m такое, что
( )
( )
36 5 36 5 31
nn
mm− = − =
( )
21
2 1 2 1 2 1
1 2 3 2 , , ,
n
n n n
Smгде m n N
+
+ + +
= + + + +
Решение. Представим данную сумму в виде
( ) ( ) ( ) ( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
2 1 2 1 2 1 2 1
2 1 2 1
2 1 2 1 2 1
2 1 2 1 2 1
1 2 2 1 2 2 1 2 1 1 2 1
1 2 1 2 1 2
1 2 2 2 1 1 .
n n n n
nn
n n n
n n n
делится на m m делится на m m делится на m m m
S m m m m
S m m m m
+ + + +
++
+ + +
+ + +
+ = + + − = + + + = +
= + + + + + + + − +
= + + + − + + + +
19
Так как каждое слагаемое суммы делится на
Задачи на делимость
22. Натуральное число n такое, что числа
являются
квадратами натуральных чисел. Докажите, что число n делится на 8.
Решение. Так как по условию числа
являются
квадратами натуральных чисел, то существуют натуральные числа
( )( ) ( ) ( )
22
10 1 10 1 10 1 1 10 4 1 5 2 1 .n k n k n k k n p p n p p+ = = − = − + = + = +
( ) ( ) ( ) ( ) ( ) ( )
22
10 1 3 1 4 1 .n n m k m k m k q p q p+ − + = − = − + = − + +
( ) ( ) ( ) ( ) ( ) ( )
10 1 3 1 4 1 7 4 1 .n n q p q p n q p q p+ − + = − + + = − + +
( ) ( ) ( )
7 4 1 . 1n q p q p= − + +
Возможны следующие случаи.
1) Если
является чётным числом и
делится на 2. Тогда из (1) следует, что
является чётным
числом и делится на 2. Тогда из (1) следует, что
делится на 8.
Доказали, что
делится на 8.
23. Найдите цифры х, у, z, при которых число
делится на 7,
11, 13.
Решение. Искомое число запишем в виде
( ) ( ) ( ) ( )( )
5 4 3 2
5 2 4 3 3 2
10 10 10 10 10
10 10 10 10 10 1 10 1 10 10 .
nxу z x y z
x у z х у z
= + + + + + =
= + + + + + = + + +
( )( )
32
10 1 10 10 .n х у z= + + +
делится на 7, 11, 13 при
любых значениях х, у, z (
цифры числа), удовлетворяющих
условиям
1 9, 0 9, 0 9.x y z
20
24. Найдите цифры х, у при которых число
делится на 88.
Решение. Натуральное число
делится на 88 тогда и
только тогда, когда оно делится на 8 и на 11.
1. Число а делится на 8 тогда и только тогда, когда число
делится на 8. Перебирая все значения у, если
делится 8, если у принимает одно из значений: 1, 5, 9.
2. Число а делится на 11 тогда и только тогда, когда делится на 11
число
( )
7 8 6 21 .c x y c x y= + + − − = − +
Так как х, у цифры числа, то
Ответ. 79 816, 75 856, 71 896.
25. Найдите цифры х, у при которых число
делится на 31.
Решение. 1. Искомое число запишем в виде
6 5 4 3 2
10 10 10 10 2 10 3 10 4 5nx у= + + + + + +
6 5 4 3 2
10 ,10 ,10 ,10 ,10
разделить на 31, то получим
соответственно остатки 2; 25; 18; 8; 7. Тогда найдутся числа
1 2 3 4 5
, , , ,m m m m m N
6 5 4
1 2 3
32
45
10 31 2 ; 10 31 25; 10 31 18 ;
10 2 31 8 2; 10 3 31 7 3.
x m x m у m у
mm
= + = + = +
= + = +
( ) ( )
( ) ( ) ( )
1 2 3 4 5
1 2 3 4 5
31 2 31 25 31 18 31 8 2 31 7 3 40 5
31 2 25 18 16 21 45
31 2 18 31 3 14 31 3 2 9 7 .
mN
n m x m m у m m
m m m m m x у
mxу m x у
= + + + + + + + + + + + =
= + + + + + + + + + + =
= + + + + = + + + +
( ) ( )
31 3 2 9 7 .n m x y= + + + +
2. Число n делится на 31, тогда и только тогда, когда число
делится на 31.
Оценим число k.
Так как
1 9 0 7 9 7 9 9 9 7 8 9 7 97 8 97.x y x y k+ + + + + + + +
следует: так как число k кратно
31, то оно принимает хотя бы одно из значений: 31, 62, 93.
21
3. Найдём значения х и у из уравнения
9 7 31 24 9 .x y x у+ + = = −
Решение последнего
уравнения – это
9 7 62 55 9 .x y x у+ + = = −
Решение последнего
уравнения – это
9 7 93 86 9 .x y x у+ + = = −
Решение последнего
уравнения – это
.
26. Докажите, что число
делится на 37.
Решение. Имеем
( )
1251 1251
1251 1251 1251 1251 1251
11 1144 44 11 11 10 44 44 11 11 10 4 .= + = +
( )
1248 1245 3
1251
1248 1245 3
1251
11 11 111 10 111 10 111 10 111
11 11 3 37 10 10 10 1 .
= + + + +
= + + + +
( )
1248 1245 3
1251 1251
11 1144 44 3 37 10 10 10 1 .= + + + +
Из последнего равенства следует, что данное число делится на 37.
27. Найдите наименьшее натуральное число
делится на В=9 999 999.
Решение. 1. Имеем
( )
( ) ( )
( ) ( )
( )
3 2 1 3 2
3 2 1 3 2 1 3 2
3 2 1 3 2 1 3 2
2 1 1
1122 211 10 10 2 10 10 10 10 10 1
10 10 10 10 10 10 10 10 10 10 10 1
10 10 10 10 10 10 10 10 10 10 10 1
10 10 10 10 10 1 10
n n n n
n
n n n n n n
n n n n n n
n n n
A
+ + +
+ + + +
+ + + +
+−
= = + + + + + + + + =
= + + + + + + + + + + + + + =
= + + + + + + + + + + + + + =
= + + + + + +
( )
( )
1 3 2
11
2
10 10 10 10 1
101 10 10 10 10 1 101 11 1.
nn
n n n
n
+
+−
+
+ + + + + + =
= + + + + + =
22
2. Легко проверить, что число
не делится на 101. Тогда
число
делится на В. Так как В
делится на 9, то а должно делится на 9 и делится на 1 111 111.
Если
делится на 9, то число цифр (единиц) в числе а
кратно 9. Тогда существуют натуральное число
Так как а делится на 1 111 111, то перепишем число а в виде
9 7 9 14 9 7
29
11 11 1111111 10 1111111 10 1111111 10 .
k k k т
nk
а
− − −
+=
= = + + + + +
Наименьшее значение числа а, при котором число а делится на
1 111 111, находим из уравнения
9 7 0 9 7 .k т k т− = =
Наименьшим значением т, которое удовлетворяет уравнению
28. Докажите, что существует натуральное число, записанное
одними единицами, которое делится на 271.
Решение. Рассмотрим 272 числа:
272
1, 11, 111, , 11 11.
единицы
Число
остатков при делении на 271, равно 271, а чисел 272. Тогда хотя бы два
числа при делении на 271 имеют равные остатки. Это означает, что
разность чисел с одинаковыми остатками делится на 271.
Пусть числа
имеют одинаковые остатки.
Рассмотрим разность
11 11 11 11 11 1100 00 11 11 10 .
k
n единиц k единиц n k единиц n k единиц
k нулей
а а а
−−
= − = =
делится на число 271, а число
не
делится на 271, то число
удовлетворяет условию задачи. Отметим:
29. Если числа 4 118 и 3 469 разделить на одно и то же число, то
получим соответственно остатки 14 и 11. Найдите этот делитель.
Решение. Пусть d искомый делитель. Так как остатки равны 14 и
11, то
Если d делитель чисел 4 118 и 3 469, то существуют целые
числа х и у такие, что
33
4118 14 4104 2 3 19 38 9 12 ;
3469 11 3458 2 7 13 19 38 7 13 .
d x d x d x d x
d x d y d y d y
= + = = =
= + = = =
38 9 12 38 7 13,dx и d y = =
30. Число при делении на 1970 и 1971 даёт остаток, равный 69.
Найдите остаток, который даёт при делении на 15 это число.
Решение. 1) Если число х при делении на 1970 даёт остаток, равный
69, то
делится на 5.
2) Если число х при делении на 1971 даёт остаток, равный 69, то
делится на 3.
Так как 5 и 3 простые числа, то из 1) и 2) следует, что
( ) ( )
69 9 60 9 69 15 4.х х х х− = − − − = − +
делится
на 15. Тогда число х при делении на 15 даёт остаток, равный 9.
Ответ. 9.
31. Докажите, что натуральное число имеет нечётное число
делителей тогда и только тогда, когда оно является точным квадратом.
Решение. Если d делитель числа х, то
также делитель числа х.
Делители числа х, разбиваем на пары
делители совпадают, это означает, что в
этом случае число делителей нечётно.
Обратно, если число делителей числа х нечётно, то в одной паре
делителей
делители совпадают, то есть
.
Доказали: натуральное число имеет нечётное число делителей
тогда и только тогда, когда оно является точным квадратом.
32. Натуральные числа а и b имеют ровно по 57 натуральных
делителей (считая 1 и само число). Может ли произведение этих чисел
иметь 300 делителей.
Решение. Так как числа а и b имеют по нечётному числу
натуральных делителей, то они являются точными квадратами. Тогда их
произведение аb тоже точный квадрат, а это означает, что число
делителей аb должно быть нечётным. Поэтому аb не может иметь 300
делителей.
33. Докажите, что
24
Решение. По определению
это произведение чисел от 1 до
1500, то есть
1500! 1 2 3 1499 1500.=
.х целая часть числа х−
1500! 1 2 3 1499 1500=
число чисел, делящихся
на 11, равно
где целое число l
удовлетворяет условию
34. Найдите наибольшее натуральное число n, для которого число
1111! делится на
( )
1110 30 37 1111 36 31 1116. 1= =
1. Докажем, что число
1111! не делится на
Так как число 37 простое, то среди чисел
(2)
всего 30 чисел кратных 37. Это числа:
(следует из
(1)). Поэтому число
1111! делится на
2. Докажем, что число
1111! делится на
1) Среди чисел
(2) имеется 30 чисел вида
1 36, 2 36, , 30 36 1080. =
2) Из чисел
(2) можно получить более 6 чисел, которые делятся на
36, например, такие 7 чисел:
2 18, 3 12, 4 9, 6 24, 8 72, 14 54, 16 27.
. можно получить более 36
чисел, которые делятся на 36, поэтому число
1111! делится на
Так как число
1111! не делится на
Ответ 36.
35. Сумма квадратов двух целых чисел делится на 7, тогда и только
тогда когда каждое число делится на 7.
Решение. Каждое из чисел
при делении на 7 может давать
остатки
( ) ( )
( ) ( )
22
2 2 2 2 2 2
7 7 7 7 2 7 2 .
kN
a b n m n n m m
+ = + + + = + + + + +
22
7 2 7 2 ,n n m m k
+ + + =
( )
( )
2 2 2 2
7 . 1a b k
+ = + +
Тогда из (1) следует, что
делится на 7.
Итак, если оба числа делятся на 7, то сумма квадратов двух целых
чисел делится на 7.
2. Из (1) следует, если
( )
22
0,
02
0.
=
+ =
=
делится на 7, то из (2) следует, что
делятся на 7.
36.
Докажите, что если сумма натуральных чисел делится на 6, то
и сумма пятых степеней этих же чисел делится на 6.
Решение. Пусть при делении числа а на 6 остаток равен
Существует натуральное число m такое, что
( )
5
5
6 6 ,а k а m
= + = +
при делении на 6 имеют одинаковые
остатки. Имеем
( )
5 5 5
5 5 5
0 6 0 0, 1 6 0 1, 2 6 5 2,
3 6 40 3, 4 6 170 4, 5 6 520 5. 1
= + = + = +
= + = + = +
Из (1) следует: если при делении на 6 число
делении на 6 имеют остаток,
равный
( )
1 2 1
,
nn
а a а а
−
+ + + +
делится на 6, то и сумма пятых степеней этих же
чисел делится на 6, так как сумма остатков в обоих случаях равна нулю.
Таким образом, доказали: если сумма натуральных чисел делится
на 6, то и сумма пятых степеней этих же чисел делится на 6.
37. Докажите, что число
N делится на 64.
Решение. Воспользуемся формулой
( )
( )
( )
1 2 3
1 1 1 . 1
n n n n
a a a a a a
− − −
− = − + + + + +
( ) ( ) ( )
( )
( ) ( ) ( )
( )
2 1 2 1 0
1 2 1 1 2 1
3 1 8 9 1 8 (9 1) 9 9 9 9 8
8 9 9 9 1 1 1 1 1 8 9 1 9 1 9 1 .
n n n n n
n n n n
n слагаемых
n слагаемых
А n n n
−−
− − − −
= − − = − − = − + + + + − =
= + + + + − + + + + = − + − + + −
Так как каждое слагаемое последней суммы при любом
N делится на 64.
38. Найдите значение
делится на 56.
Решение. 1. Пусть
Замечание. Для произвольных чисел a и b, где
и
произвольного натурального числа n существует целое число k такое,
что
а) Докажем, что А делится на 7. Имеем
( ) ( )
2 2 2 2 2 2 2 2
10 5 2 3 10 3 5 2 .
k k k k k k k k
А = + − − = − + −
Из замечания следует: число
, число А делится на 7.
б) Докажем, что А делится на 8. Имеем
( ) ( )
2 2 2 2
10 2 5 3 .
k k k k
А = − + −
Из замечания следует: число
, число А делится на 8.
Так как при
, число А делится на 7 и на 8, то при
, число А делится на 56.
2. Пусть
( ) ( )
2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1
10 5 2 3 10 3 5 2 .
k k k k k k k k
А
+ + + + + + + +
= + − − = − + −
а) Из замечания следует: число
( )
2 1 2 1 2 2 2 2 2 2 2
5 2 5 5 2 2 3 2 3 2 5 5 2 3 2 .
k k k k k k k k k++
− = − − + = − +
( )
2 1 2 1 2 2 2
5 2 5 5 2 3 2 .
k k k k k++
− = − +
27
Выше было доказано, что
( ) ( )
2 1 2 1 2 2 2
10 3 5 5 2 3 2
k k k k k
А
++
= − + − +
не делится на 7, а значит
и не делится на 56, если
.
39. Докажите: если натуральное число
( )
12 8 4
99А n n n n= − − +
делится на 256.
Решение. Разложим
( ) ( ) ( ) ( )
( )( ) ( )( )( )( )( )
12 8 4 12 8 4 8 4 4
4 8 2 2 2 2 4
9 9 9 9 9 9
9 1 3 3 1 1 1 .
А n n n n n n n n n
n n n n n n n
= − − + = − − − = − − − =
= − − = − + − + +
( )
( )( )( )( )( )
2 2 2 2 4
3 3 1 1 1 .А n n n n n n= − + − + +
– нечётное натуральное число, то
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )( )( )( )
( )
( )
( )( )
( )
( )
( )
( )
2 2 2 2 4
4
2 2 2 2
4
6 2 2 2
2 1 3 2 1 3 2 1 1 2 1 1 2 1 1
4 4 2 4 4 4 4 4 4 4 2 2 1 1
2 2 2 1 1 1 2 2 1 2 1 1 .
А k k k k k
k k k k k k k k k
k k k k k k k k k
= + − + + + − + + + + =
= + − + + + + + + + =
= + − + + + + + + +
являются последовательными натуральными
числами, поэтому их произведение делится на 2. Число
является чётным числом, поэтому оно делится на 2.
Итак, если
6 5 4 3 2
3 5 15 4 12А n n n n n n= − − + + −
N делится на 720.
Решение. Разложим число А на множители:
( ) ( ) ( )
( )
( )
( )
( )
( )( )
( )( )( ) ( )( )
6 5 4 3 2 4 2
4 2 2 2
3 5 15 4 12 3 5 3 4 3
3 5 4 3 1 4
3 2 1 1 2 .
А n n n n n n n n n n n n
n n n n n n n
n n n n n n
= − − + + − = − − − + − =
= − − + = − − − =
= − − − + +
( )( )( ) ( )( )
3 2 1 1 2 .А n n n n n n= − − − + +
Число А является произведением шести последовательных
натуральных чисел. Поэтому число А делится на
41.
Докажите, что при любом
( ) ( )
29 20 21 30 50
nn
− + −
( ) ( ) ( )
29 20 21 30 50.
nn
fn= − + −
( ) ( ) ( )
1.n f n f n
= + −
( ) ( ) ( ) ( ) ( )
( )
( ) ( )
( )
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
11
11
1 29 20 20 21 30 30
29 20 1 20 1 21 30 30 1 10 29 21 2 1 3 .
n n n n
n n n n n
nn
n f n f n
++
++
= + − = − − − + − =
= − + + − = − +
( ) ( ) ( )
( )
( )
1
10 29 21 2 1 3 . 1
nn
nn
n
+
= − +
( ) ( ) ( )
1,n f n f n
= + −
( ) ( ) ( )
1.f n n f n
+ = +
( ) ( ) ( )
( )
( )
1
1 10 29 21 2 1 3 .
nn
nn
f n f n
+
+ = − + +
( ) ( ) ( )
29 20 21 30 50,
nn
fn= − + −
( ) ( ) ( )
1f n n f n
+ = +
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
2 1 , 3 1 2 , , 1 2 1 , 2.f f f n n где n
= = + = + + + −
( ) ( ) ( )
( )
1
10 29 21 2 1 3 , ,
nn
nn
n где n N
+
= − +
( ) ( ) ( ) ( )
1 2 1 ,f n n
= + + + −
( ) ( ) ( )
( )
1
10 29 21 2 1 3 , 1,
nn
nn
n где n
+
= − +
( ) ( )
1
2 1 3
n
nn
gn
+
= − +
( ) ( ) ( )
( ) ( )
( ) ( ) ( )
21
2 2 2 2
2 2 1 3 2 3 2 2 9 4 .
kk
k k k
kk
g k g k g k
+
= − + = − = −
Так как существует натуральное число m такое, что
( )
9 4 9 4 5 ,
kk
тт− = − =
( ) ( ) ( )
22
2 1 2 1 2 1 2 1
2 1 2 1 3 2 1 3 2 .
k
k k k k
g k g k
+
+ + + +
+ = − + + = +
Так как существует натуральное число m такое, что
( )
2 1 2 1
3 2 3 2 5 ,
kk
тт
++
+ = + =
( )
2 1 2 1
2 1 3 2
kk
gk
++
+ = +
делится на 5.
Доказали, что число
( ) ( )
1
2 1 3
n
nn
gn
+
= − +
Тогда исходное число делится на
42. Найдите натуральные значения n, при которых число
( ) ( )
1
( ) 1 1
n
n
а n n n
+
= + +
29
Решение. Любое натуральном число
( ) ( )
3 1 3
3 3 1 ,
kk
kk
+
++
одно слагаемое, которого делится на 3, а другое слагаемое не делится на
3, поэтому сумма не делится на три.
2. Если
( ) ( ) ( ) ( )
( )
31
3 2 3 1 3 2
3 1 3 2 3 1 3 1 1 .
k
k k k
k k k k
+
+ + +
+ + + = + + + −
( ) ( ) ( )
( )
( ) ( )
31
3 2 3 2 3 1
12
3 1 3 1 , 3 1 1 3 1 1 .
k
k k k
kkт k k т
+
+ + +
+ = + + − = + + −
( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
( )
( )
( )
31
3 2 3 1 3 2
3 2 3 1 3 1
12
3 1 3 2 3 1 3 1 1
3 1 3 1 1 3 1 1 1 .
k
k k k
k k k
k k k k
k т k n k m k m
+
+ + +
+ + +
+ + + = + + + − =
= + + + + − = + + + + −
( )
3 1 2
31т k т k т= + + −
( ) ( ) ( )
( )
3 2 3 1 3 1
3
3 1 3 2 3 1 1 ,
k k k
kkт
+ + +
+ + + = + + −
( ) ( )
3 2 3 1
3 1 3 2
kk
kk
++
+ + +
( )
( )
( )
3 1 3 1
1 1 0 1 1 2 , .
kk
k m m N
++
+ − = − = − =
2
3 1 6 1.
km
n k n m
=
= + = +
( ) ( )
3 3 3 2
3 2 3 3 ,
kk
kk
++
+ + +
одно слагаемое, которого делится на 3, а другое слагаемое не делится на
3, поэтому сумма не делится на три.
Ответ.
Задачи на НОД и НОК
43. Найдите два натуральных числа, сумма которых равна 344, а
общий наибольший делитель равен 43.
Решение. Пусть a и b являются искомыми числами. Так как, по
условию задачи, НОД (а; b)=43, то существуют взаимно простые
натуральные числа х и у такие, что
( )
344 43 344 8.ab х у х у+ = + = + =
удовлетворяют пары взаимно простых чисел
( ) ( ) ( ) ( )
1; 7 , 3; 5 , 5; 3 , 7;1
. Тогда искомыми числами являются числа: 43 и
301, 129 и 215.
Ответ. 43 и 301, 129 и 215.
30
44. Найдите наибольший общий делитель натуральных чисел m и n,
если он увеличивается в 15 раз при увеличении числа m на 10.
Решение. Пусть НОД(m , n)=d. Тогда НОД(m+10, n)=15d.
Воспользуемся следующим: если целое число делится на
произведение натуральных чисел, то оно делится на каждый
сомножитель.
Отметим:
1.Так как НОД(m+10, n)=15d, то 5 и
являются делителями чисел
m+10 и n. Так как НОД(m , n)=d, то
является делителем чисел m и n.
Тогда
а) m+10 делится на 5 и так как 10 делится на 5, то m
делится на 5;
б) n делится на 5.
Из а) и б) следует, что 5 делитель чисел m и n. Так как
наибольший общий делитель чисел m и n, то 5 делитель
кратно 5.
в) m+10 делится на
то НОД(m, n)=5 и НОД(m+10, n)=75. Тогда, например,
удовлетворяет условию задачи.
2) Если
то НОД(m, n)=10 и НОД(m+10, n)=150. Тогда,
например,
удовлетворяет
условию задачи.
Ответ.
5 или 10.
45. Различные натуральные числа m и n таковы, что
НОД (m, n)+НОК (m, n) =m+n.
Докажите, что одно из чисел является делителем другого.
Решение. Пусть НОД (m, n)=d. Тогда существуют взаимно простые
натуральные числа х и у таковы, что
( ) ( )
, , ,НОД m n НОК m n m n =
( ) ( )
( ) ( ) ( ) ( )( )
0
,,
1 1 1 1 1 1 0.
d
НОД m n НОК m n m n d dxy dx dy
d xy d x y xy x y х у х х у
+ = + + = +
+ = + + = + − = − − − =
следует, что m является делителем числа n.
следует, что n является делителем числа m.
46. Пусть
натуральные числа, сумма которых равна
2 737. Какое наибольшее значение может принимать их наибольший
общий делитель?
Решение. Если
( )
1 2 15
, , , ,d НОД а а а=
то существуют взаимно
простые натуральные числа
( )
( )
1 2 15
1 2 15 1 2 15
1 2 15
1
2737
182,4 6 .
15
i
n
а а а
а а а d n n n d
n n n
dd
+ + +
+ + + = + + + =
+ + +
( )
1 2 15 1 2 15
а а а d n n n+ + + = + + +
1 2 15
2737 7 17 23.а а а+ + + = =
является наибольшим общим делителем чисел:
1 13 14 15
161, , 161, 322, 322,а а а а= = = =
сумма которых равна 2 737.
Ответ. 161.
47. Пусть НОК(a, b)=504 и НОК(a, с)=378, где a, b, c натуральные
числа. Найдите НОК(b, с).
Решение. Разложим числа 504 и 378 на простые множители:
3 2 3
504 2 3 7, 378 2 3 7.= =
( )
32
, 2 3 7НОК a b =
( )
3
, 2 3 7,НОК a с =
то найдутся
целые неотрицательные числа
3 3 3
1 1 1 2 2 2
2 3 7 , 2 3 7 , 2 3 7 .
n m k
n m k n m k
a b c= = =
Из определения наименьшего общего кратного следует:
( )
1 2 1 2 1 2
max , max , max ,
, 2 3 7 ,
n n m m k k
НОК a b =
( )
( )
1 3 1 3 1 3
2 3 2 3 2 3
max , max , max ,
max , max , max ,
, 2 3 7 ,
, 2 3 7 .
n n m m k k
n n m m k k
НОК a c
НОК b c
=
=
Для того чтобы найти НОК(b, с) надо найти
2 3 2 3 2 3
max , , max , , max , .n n m m k k
( )
( )
1 2 1 2 1 2
12
max , max , max ,
12
32
12
max , 3,
, 2 3 7 ,
max , 2,
, 2 3 7;
max , 1.
n n m m k k
nn
НОК a b
mm
НОК a b
kk
=
=
=
=
=
( )
( )
1 3 1 3 1 3
13
max , max , max ,
13
3
13
max , 1,
, 2 3 7 ,
max , 3,
, 2 3 7;
max , 1.
n n m m k k
nn
НОК a с
mm
НОК a с
kk
=
=
=
=
=
Тогда имеется две возможности для значения
1) Если хотя бы одно из значений
( )
2 3 2 3 2 3
max , max , max ,
, 2 3 7 .
n n m m k k
НОК b c =
( ) ( )
33
, 2 3 7 , 1512;НОК b c НОК b c= =
( ) ( )
3 3 0
, 2 3 7 , 216.НОК b c НОК b c= =
Ответ.
1 512, 216.
48. Пусть наибольший общий делитель натуральных чисел
равен единице. Какое наибольшее значение может принимать НОД
чисел
1000 , 990 990 990 1000 , 990 989999 ,
990 ; 990 ; 990 ;
990 989999 ,
989 999 989999 989999 990 ;
990 989999 ,
989 999 990 989999 990 ;
990 989999 ,
99000
а m n а m n а b n
b n m b n m b n m
а b n
b n m
а b n
bb аm
а b n
= + = + − =
= + = + = +
−=
= +
−=
+ − =
−=
990 989999 ,
0 990 989999 990 ; 1000 989999 .
а b n
b а m b а m
−=
− = − =
( )
990 989999 , 1000 989999 . 1а b n b а m− = − =
является наибольшим общим делителем чисел a и b,
то
и n (следует из (1)). Так как числа
и
n взаимно простые числа, то
является делителем числа 989 999.
Покажем, что найдутся взаимно простые числа
999 27 37, 989 23 43.mn= = = =
и
n взаимно простые числа. Тогда
999 1000 989 989999аа= + =
989 990 999 989999.bb= + =
Ответ.
989 999.
49. Пусть НОД(m, n)=d и НОК (m, n) =q, где
m и n
натуральные числа. Найдите наименьшее значение числа
Решение. Так как НОД(m, n)=d, то существуют взаимно простые
натуральные числа х и у такие, что
( ) ( )
, , ,НОД m n НОК m n m n =
( )
0
, : .
d
НОК m n dxy q dxy q d xy
= = =
Надо найти значения х и у, при которых
принимает
наименьшее значение, если
( )
0
5 8 14 5 8 14 5 8 14 5 8 14 .
d
m n dx dy d x y x y d
− = − = − = − =
Так как
х и у натуральные числа, то из уравнения
, если х и у взаимно простые натуральные числа
и они являются решением уравнения
5 8 14 8 5 14 5 ,x y d x y d− = = +
.
Отметим: наименьшее значение
является искомым значением.
Так как
не являются решением уравнения
(в
этом случае, левая часть уравнения меньше нуля, а правая часть больше
нуля), то
то уравнение (1) принимает вид
( )
81
8 5 1 5 5
5
y
x y x
+
= + =
. Уравнение (5) имеет целые решения,
если
является наименьшим значением,
при котором х принимает целое число, равное 5
.
Итак, если
то уравнение (1) принимает вид
( )
41
8 5 2 5 2 4
5
y
x y x
+
= + =
. Уравнение (4) имеет целые решения,
если
является наименьшим значением,
при котором х принимает целое число, равное 2. Итак, если
взаимно простые натуральные числа). Тогда
является найденное
значение
Задачи на сравнение чисел по модулю
Воспользуемся следующим: Если
где k целое число,
то k является остатком от деления числа а на n.
Если
( )( )
mod ,a c b d n+ +
( )( )
mod ;a c b d n
50. Найдите остаток от деления числа
( ) ( )
81 81
36 2 mod17 36 2 mod17
( )
( )
( ) ( )
10
8 8 10 81
2 1 mod17 2 1 mod17 2 2 mod17 .
на 17 равен 2.
Ответ. Равен 2.
2. Найдите остатки от деления числа
на 5, 11, 13.
Решение. 1) Так как
( )
44
2 16 2 1 mod5 1930 4 482 2,и= = +
( )
( ) ( ) ( ) ( )
482
485
1930 4 2
2 2 2 mod5 1 4 mod5 4 mod5 .
то остаток от деления числа а на 5 равен 4.
2) Так как
( )
55
2 32 2 3 11 1= = −
( )( )
( )
( ) ( ) ( )
1930 5 386
386
386
5 5 1930
2 1 mod11 2 1 mod11 2 1 mod11 .
=
− −
то остаток от деления числа а на 11 равен 1.
3) Так как
( )
66
2 64 2 5 13 1= = −
( )( )
( )
( ) ( )
( )( ) ( )
1930 6321 4
321
321
6 6 4
1930 1930
2 1 mod11 2 2 1 16 mod13
2 1 13 2 10 mod13 2 10 mod13 .
= +
− −
− −
то остаток от деления а на 13 равен 10.
Ответ. 4, 1, 10.
51. Найдите последнею цифру числа
Решение. Последняя цифра числа а совпадает с остатком от деления
числа а на 10. Поэтому надо найти наименьшее целое число k такое, что
( )
( )
( ) ( ) ( )
1969 4 492 1
492
492
4 4 1 1969
3 1 mod10 3 3 1 3 mod10 3 3 mod10 .
= +
( )
( )
( ) ( ) ( )
1537 2 768 1
768
768
2 2 1537
19 1 mod10 19 19 1 19 mod10 19 9 mod10 .
= +
( )
( )( )
( )
( )
1969 1537 1969 1537
3 19 3 9 mod10 3 19 2 mod10 .+ + +
Последняя цифра числа а равна 2, так как
( )
( )
1969 1537
3 19 2 mod10 .+
Ответ. 2.
52. Найдите две последние цифры числа
36
Решение. Две последние цифры числа а совпадает с остатком от
деления числа а на 100. Поэтому надо найти наименьшее целое число k
такое, что
( ) ( )
( )
( ) ( )
( )
1971 4 492 3
492
492
4 4 4 3
1971
7 301 mod100 7 1 mod100 7 7 1 343 mod100
7 43 mod100 .
= +
то две последние цифры числа а равны 43.
Ответ. 43.
53. Найдите наименьшее натуральное число, представимое в виде
суммы 1892 натуральных слагаемых с одинаковыми суммами цифр и в
виде суммы 1987 натуральных слагаемых с одинаковыми суммами цифр.
Решение. Если искомое натуральное число n является суммой 1892
натуральных чисел, сумма цифр каждого из которых равна k, то сумма
цифр числа n, равна
Если искомое натуральное число n является суммой 1987
натуральных чисел, сумма цифр каждого из которых равна m, то сумма
цифр числа n, равна
Воспользуемся следующим: остаток от деления числа на 9 равен
остатку отделения суммы цифр этого числа на 9.
Так как остатки от деления чисел n,
( )
( )
( )
( ) ( ) ( ) ( )
1892 mod9 ,
1892 1987 mod9
1987 mod9 ;
210 9 2 220 9 7 mod9 2 7 mod9 .
nk
km
nm
k m k m
+ +
Числа 2k и 7m сравнимы по модулю 9, если k кратно 7, а m кратно 2.
Так как надо найти наименьшее натуральное число n, то рассмотрим
случай когда
.
Отметим: если сумма цифр числа равна 7, то числами могут быть,
например, такие: 7, 16, 25; если сумма цифр числа равна 2, то числами
могут быть, например, такие: 2, 11, 20.
Так как, любое натуральное число не меньше суммы своих цифр, то
7
2
1892 , 13244,
13244.
1897 ; 3794;
k
m
n k n
n
n m n
=
=
представимо в виде суммы 1892
натуральных слагаемых, каждое из которых равно 7.
Имеем
1892
13244 7 1892 13244 7 7 7.
семёрка
= = + + +
представимо в виде суммы 1892 натуральных
слагаемых, если сумма цифр каждого слагаемого равна 7.
2). Докажем, что число
представимо в виде суммы 1987
натуральных слагаемых, сумма цифр каждого слагаемого равна 2.
Пусть а – число слагаемых, каждое из которых равно 2 и b– число
слагаемых, каждое из которых равно 11. Тогда имеем
( )
13244 2 1987 11 ,
13244 2 11 , 9 9270, 1030,
1987; 1987; 957.
1987;
bb
a b b b
a b a b a
ab
= − +
= + = =
+ = + = =
+=
957 1030
13244 2 957 11 1030 13244 2 2 2 11 11 11.= + = + + + + + + +
представимо в виде суммы 1987 натуральных
слагаемых, если сумма цифр каждого слагаемого равна 2.
Таким образом, искомым числом является число
Математушка
- Наши выпускники
- Оставить заявку
- ЕГЭ
- Статьи
- Контакты
- Цены
- Заочное обучение
- Войти
Задачи ЕГЭ по математике
Задача № 1
Показать ответ
Показать решение
Задача № 2
Показать ответ
Показать решение
Задача № 3
Показать ответ
Показать решение
Задача № 4
Показать ответ
Показать решение
240 руб.
300 руб.
Цена действительна только для интернет-магазина
и может отличаться от цен в розничных магазинах
Скидка 15% при заказе от 3 000 до 7 000 рублей
Скидка 20% при заказе от 7 000 рублей
Бесплатная доставка при заказе от 2000 рублей до пункта выдачи Boxberry
Описание:
Полистать (.pdf)
Пособие предназначено для отработки навыков выполнения одного из самых трудных заданий ЕГЭ по математике профильного уровня — задания на целые числа.
Книга содержит:
- более 300 задач для самостоятельного решения;
- алгоритмы решения задач и методические рекомендации по их выполнению;
- ответы ко всем задачам.
Пособие адресовано выпускникам, сдающим ЕГЭ по математике профильного уровня, и учителям. Оно может быть использовано и при дистанционном обучении.
Информация о авторе:

Прокофьев Александр Александрович
Отзывы:
|
Анна Смирнова 20.01.2023 12:23:16 |
|
Наконец-то нашла этот сборник.. Ещё купила и социально-экономические задачи. Спасибо! |
|
Имя |
Добавить отзыв

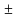 b*l также делится на m.
b*l также делится на m.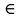 N , то число a также делится на k .
N , то число a также делится на k .