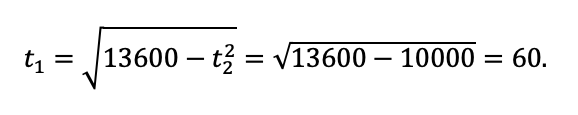Задачи на ценные бумаги с решением егэ математика

Цена ценной бумаги на конец года вычисляется по формуле S = 1,1S₀ + 2000, где S₀ — цена этой ценной бумаги на начало года в рублях. Максим может приобрести ценную бумагу а может положить деньги на банковский счет, на котором сумма увеличивается за год на 12%. В начале любого года Максим может продать бумагу и положить все вырученные деньги на банковский счет, а также снять деньги с банковского счета и купить ценную бумагу. В начале 2021 года у Максима было 80 тысяч рублей, которые он может положить на банковский счет или может приобрести на них ценную бумагу. Какая наибольшая сумма может быть у Максима через четыре года? Ответ дайте в рублях.

Решение:

По условию задачи S₀ = 80 тысяч руб = 80000 руб

2021 год:

Если Максим в начале года приобретет ценную бумагу, то в конце года цена ценной бумаги будет равна 1,1⋅80000 + 2000 = 88000+2000 = 90000 руб
Если Максим в начале года положит деньги на банковский счет, тогда в конце года сумма на банковском счете будет 1,12⋅80000 = 89600 руб
Отсюда мы делаем вывод о том, что Максиму в начале 2021 года выгоднее будет приобрести ценную бумагу, так как ее цена на конец года будет больше. Тогда в конце 2021 года у Максима будет 90000 руб

2022 год

:
Если Максим не будет продавать ценную бумагу, то в конце года цена ценной бумаги будет равна 1,1⋅90000 + 2000 = 101000 руб
Если Максим продаст бумагу, то в конце года сумма на банковском счете будет 1,12⋅90000 = 100800 руб
Получаем, что в начале года Максиму выгоднее не продавать ценную бумагу, тогда в конце года ее цена составит 101000 руб

2023 год:

Если Максим не будет продавать ценную бумагу, то в конце года цена ценной бумаги будет равна 1,1⋅101000 + 2000 = 113100 руб
Если Максим продаст бумагу, то в конце года сумма на банковском счете будет 1,12⋅101000 = 113120 руб
Получаем, что в начале года Максиму необходимо продать ценные бумаги и положить деньги на банковский счет, тогда в конце года сумма на банковском счете будет 113120 руб

2024 год:

Если Максим не будет продавать ценную бумагу, то в конце года цена ценной бумаги составит 1,1⋅113120 + 2000 = 126432 руб
Если Максим продаст бумагу, то в конце года сумма на банковском счете будет 1,12⋅113120 = 126694,4 руб
Получаем, что в начале года Максиму нужно оставить деньги на банковском счете, тогда в конце года у него будет 126694,4 руб

Наибольшая сумма, которая может быть у Максима через четыре года, — 126694,4 руб

Ответ: 126694,4 руб

Ученик, который сдает профильную математику наверняка рассчитывает поступить с ней в вуз, иначе зачем так напрягаться? Только весь масштаб катастрофы школьник средней руки осознает, когда доберется до части с развернутым ответом, ведь без нее баллов, скорее всего, не хватит. На наш взгляд, самые «дешевые» 3 балла можно получить за задачу на финансовую математику в ЕГЭ.

Напомним, что прототипы для 17-го номера делятся на три большие группы: 

• банковские задачи, 
• задачи на ценные бумаги,
• задачи на оптимальный выбор. 

Мы уже рассказали, как научить школьника решать любую задачу на кредиты. Прелесть этих прототипов в том, что любой подобный номер решается по единому алгоритму. Однако никто не отменял менее удачливых школьников, которым попадется другой вид задач. Потому в этой статье мы покажем, как научить выпускника решать задачи на ценные бумаги и, самое страшное, оптимальный выбор. Поехали!

Финансовая математика в ЕГЭ: задачи на вклады и ценные бумаги

На самом деле это еще один «подарочный» прототип. Обычно это довольно простая задача на проценты, но нюансы, конечно, есть. Преподавателю придется сконцентрировать снимание школьника на трех вещах:

• Механизм работы вкладов и ценных бумаг. Даже если школьник может представить себе, как работает вклад, то ценные бумаги, вероятно, вообще темный лес. Как показывает, практика, каждое незнакомое слово в условии дает +50 к панике и увеличивает шансы того, что к задаче не приступят вовсе.

Предложите школьнику воспользоваться демо-режимом в каком-нибудь брокерском приложении. Например, «Сбербанк Инвестор» позволяет целый месяц торговать на виртуальном брокерском счете и дает на это 400 тысяч виртуальных рублей. Может, именно ваш ученик станет следующим Уорреном Баффетом! 

• Оформление. Каждый символ в бланке ответа должен быть выверен. Например, частая ошибка оформлять математическую модель уравнением, когда в условии стоит формулировка «не больше» или «не меньше». За такие погрешности школьник лишится баллов за 17 номер.
• Вычисления. Преподаватель должен демонстрировать культуру вычислений с самой первой встречи с учеником. Какой смысл в выверенных алгоритмах решения, если подопечный закопается в цифрах? Научите школьника не спешить, продумывать расчеты на пару ходов вперед. Зачем умножать, если в следующем действии придется делить, и все лишнее сократится? Зачем считать дискриминант до конца, если из получившегося огромного числа придется извлекать нетабличный корень?

Задача 1

Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Самый, на наш взгляд, изящный способ решить эту задачу — понять, в какой момент станет выгодно хранить деньги в банке? Покажите школьнику, как меняется стоимость каждый год:

• 1 год: если оставим бумагу, то заработаем 2000. А если продадим и положим в банк, то только 10% от 7000, то есть 700 рублей;
• 2 год: бумага все еще принесет 2000, а вот депозит уже принес бы 900;
• 3 год: 2000 против 1100…

То есть прибыль от ценной бумаги сохраняется, а депозит с ростом ее стоимости может приносить все больше. Когда же он станет выгодным? Когда 10% от стоимости бумаги перевалят за 2000:

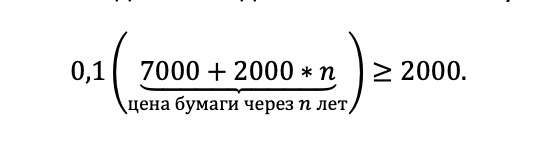
Осталось решить неравенство и не забыть, что n – целое число лет.

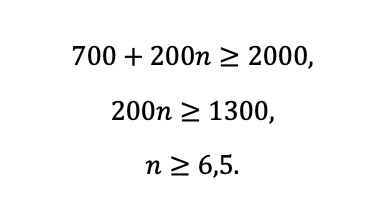
То есть, когда срок будет равен 6-ти годам, неравенство еще не выполнится. Когда пройдет 7 лет, и бумага подорожает еще на 2000, сумма станет достаточной, чтобы проценты на депозите давали больше. Значит, на восьмой год можно ее продавать.

Ответ: в течение 8-го года.

Финансовая математика в ЕГЭ: задачи на оптимальный выбор

Ну вот мы и добрались до самого неприятного варианта. Во-первых, тут надо уметь работать с условием текстовых задач. Во-вторых, бегло владеть методом исследования функций с помощью производной. И если второе укладывается в алгоритм, то первое далеко не всегда.

Если в задачах с кредитами набор прототипов очень ограничен, и там трудно придумать что-то новое, то на задачах на оптимальный выбор народ разгулялся. Тут может происходить всё что угодно: 

• Покупка и продажа ценных бумаг;
• Движение двух объектов по перпендикулярным траекториям;
• Строительство заводов и оплата труда рабочим;
• Деление огорода под посадки…

Хорошая новость в том, что далеко не все задачки, которые вам попадутся, могут встретиться на экзамене. Большинство самых страшных номеров — это усложненные варианты от Александра Ларина. Ими вполне можно развлечь сильного ученика, но не стоит пугать ими того, кто «плавает». Каждый прототип, который к вам принес школьник с квадратными от испуга глазами, стоит проверить на принадлежность к авторам ФИПИ.

Мы рассмотрим 2 самых распространенных прототипа:

• Первый — из демонстрационного варианта ЕГЭ по математике 2021 года,
• Второй — более древний, но зато математическая модель из него встречается в задачах ФИПИ чаще всего.

Задача 2.1

Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5x² + x + 7 млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу,то прибыль фирмы (в млн рублей) за один год составит px – (0,5x² + x + 7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?

Первым делом убедитесь, что школьник понимает условие задачи: предложите ему пересказать ситуацию своими словами.

Если выкинуть из задачи все «лишнее», то получится, что завод хочет заработать как можно больше, и может добиться этого, выпустив больше единиц товара. То есть нам надо узнать, при каком значении x функция прибыли примет максимальное значение, цена тут будет считаться уже зафиксированной:

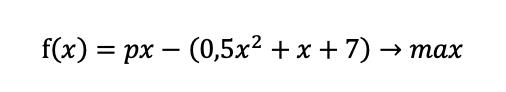
Перед нами функция, которую необходимо исследовать на максимум. Дайте школьнику подумать, вдруг он осознает, что уже владеет инструментом для такого исследования? Если не осознает, проведите аналогию с 12-ым номером.

Ищем производную, учитываем, что p – константа:

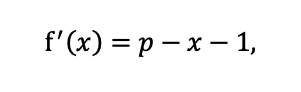
Приравниваем к нулю:

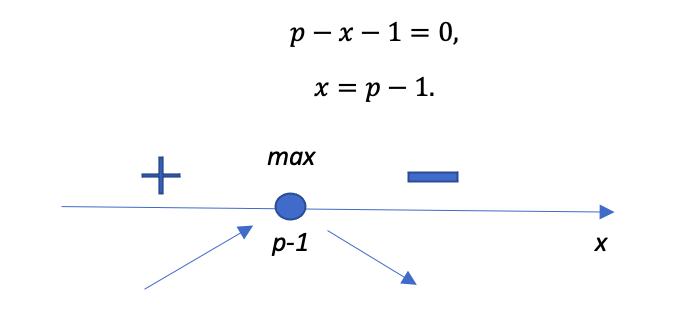
Словом, пока ничего нового, за исключением наверняка очень пугающей школьника второй переменной. Главное — чтобы подопечный не расставлял знаки интервалом по инерции, как это часто происходит в неравенствах. Напомните, что тут всегда проверяем знак подстановкой в исследуемую функцию. Например, правее точки экстремума будет точка p, а левее – p-2.

Мы выяснили, что прибыль будет максимальная, если выпускать p-1 единицу товара. Школьнику следует хорошо подумать, и понять, что дальше.От нас хотят узнать, за какую цену следует продавать товар, чтобы прибыль окупила вложенные в завод 75 млн за 3 года. Будем очень аккуратными с моделью:

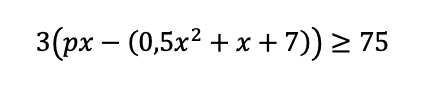
Подставим подсчитанное количество единиц товара x=p-1:

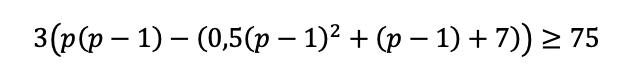
Ясно, что отрицательная цена нас не устраивает, а вот первое положительное значение, при котором неравенство выполняется — это 9. Заставляйте школьника рассуждать, иначе самостоятельно справиться с подобной задачей у него не выйдет.

Ответ: 9 тысяч.

Прошлая задача, можно сказать, уже содержала математическую модель в готовом виде. Давайте теперь посмотрим, как выглядит номер без единого выражения в условии.

Задача 2.2

Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование.
В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t² часов в неделю, то за эту неделю они производят 3 t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t² часов в неделю, то за эту неделю они производят 5 t единиц товара.
За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
Григорий готов выделять 6 800 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Пожалуй, школьнику может быть трудно осознать, что время работы в этой задаче — это не просто t, а t². Еще, вероятно, ему захочется вспомнить формулу работы, но тут она совершенно ни к чему:

Предприниматель хочет заработать побольше, а для этого надо произвести и продать больше товара. Но при этом и заплатить рабочим хочется меньше. Из-за того, что производительность на одном заводе выше, и товары производятся быстрее, а оплата труда та же, имеет смысл нагрузить его чуть больше. Надо посчитать, как именно следует распределить производство между заводами.

С одной стороны, нам интересно максимально много товара:

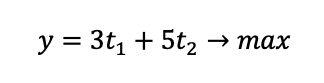
Если для ученика индексы при t станут неожиданностью, объясните, что работать на заводах будут разное количество времени.

С другой — у Григория есть ограничения по бюджету:

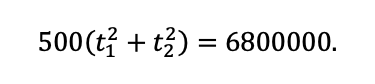
До сих пор мы не могли исследовать функцию производства товара на максимум, ведь переменных там было две, и ни одну из них зафиксировать мы не могли. Но теперь мы можем выразить, к примеру, t₁ из второго уравнения, и тогда анализ станет возможным.

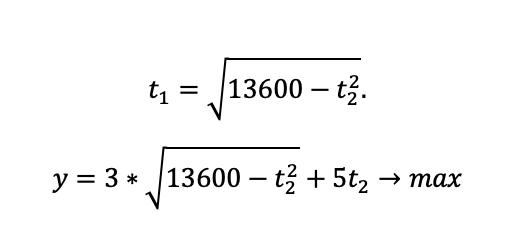
Ура! С этого момента школьник точно в курсе, что делать, дайте ему поработать самостоятельно.Ищем производную и приравниваем к нулю:

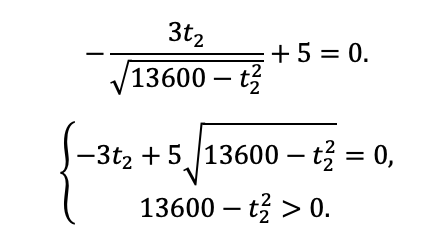
Ваш подопечный помнит, как правильно оформляется дробно-рациональное уравнение? Несмотря на то, что ОДЗ в данном случае никак на ответ не повлияет, не стоит рисковать и забывать про него.

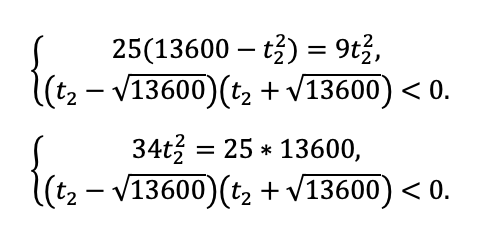
Обратите внимание школьника: мы не стали перемножать большие числа. Потому что знаем: скоро придется делить.

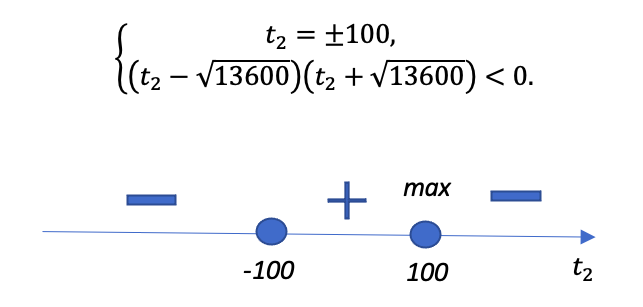
И снова повод убедиться, не забывает ли подопечный проверять тут знаки интервалов подстановкой.

Мы нашли количество рабочих часов на втором заводе. Дайте выпускнику сориентироваться в решении. Что делать дальше?

Осталось ответить на вопрос задачи:

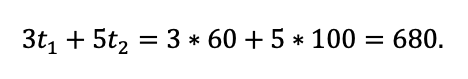
Ответ: 680 единиц товара.

Подведём итог

Мы рассмотрели 2 оставшихся прототипа 17 номера ЕГЭ по математике.

В первом случае выпускник будет работать с задачкой на проценты, где для него мало нового. Во втором ему придется вытащить из условия функцию для анализа с помощью производной.

Учитывайте, что текстовые задачи — довольно трудный для подростков формат работы, потому сопротивление ожидаемо. Однако, только экономическую задачу можно уместить всего в пару уроков разбора, все остальные номера займут гораздо больше времени! Нельзя упускать такую возможность подготовиться и урвать пару дополнительных драгоценных баллов. Донесите это до ученика, и…

Пусть удача всегда будет с вами!

(с) Голодные игры

Всего: 149    … 21–40 | 41–60 | 61–80 | 81–100 | 101–120 | 121–140 | 141–149

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 149    … 21–40 | 41–60 | 61–80 | 81–100 | 101–120 | 121–140 | 141–149

Для решения таких задач необходимо понимать алгоритм решения экономических задач

За задание №17 по математике ЕГЭ профильный уровень можно получить 3 балла. Мы рассмотрим как решать экономические задачи ЕГЭ по математике, которые в каждом варианте профильного уровня по математике идут под номером 17.

Решение №17 включает в себя обязательное построение математической модели, то есть это обычная текстовая задача, но с экономическим (финансовым) уклоном и чаще всего с большим количеством вычислений.

Можно выделить несколько блоков заданий:

1. Вклады и кредиты

2. Акции и другие ценные бумаги

3. Методы оптимальных решений

Рассмотрим каждый из вышеперечисленных блоков.

Вклады и кредиты

Вклады и кредиты – самый обширный блок. Здесь вы можете встретить различные схемы возврата кредита или увеличения суммы вклада, и ваша задача – упорядочить данные таким образом, чтобы большой массив текста превратился в удобную математическую схему.

Чтобы правильно решать такие задачи, необходимо владеть формулой сложных процентов. Начисление по этой формуле предполагает, что каждый последующий год процент начисляется не на исходную сумму, а на исходную сумму, увеличенную предыдущим начислением процентов.

Формула выглядит следующим образом:

где FV – будущая сумма.

PV – текущая сумма.

p – процент, в соответствии с которым происходит начисление

n – количество лет начисления процента.

Если начисления происходят не ежегодно, а чаще, например, ежеквартально, формула модифицируется в следующий вид:

,

где

FV – будущая сумма

PV – текущая сумма

p – процент, в соответствии с которым происходит начисление

n – количество лет начисления процента

m – количество начислений в год (например, m=4, если начисления ежеквартальные).

Давайте отработаем эту формулу на подготовительной задаче.

Задача 1

Алексей положил 100 000 рублей в банк под 6% годовых на 3 года. Какая сумма будет у Алексея через год? Через 2 года? Через 3 года?

Решение:

Рассчитаем по формуле сложного процента сумму через год:

Теперь сумму через 2 года:

Теперь сумму через 3 года:

Более того, вам придётся работать со схемами кредитов/вкладов, поэтому решим более сложную задачу, в которой нужно будет переводить текст в таблицы и уравнения/неравенства.

Задача 2

Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего года и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при котором через четыре года вклад станет не меньше 28 млн рублей.

Решение:

Пусть искомая сумма составит a млн рублей.

Составим таблицу, чтобы упорядочить данные и построить математическую модель.

По условию, нужно найти наименьшее целое x, для которого выполнено неравенство

14,641 + 2,31a ≥ 28

a ≥ 

Наименьшее целое число, при котором знак неравенства выполняется, это число 6.

Значит, искомая сумма — 6 млн рублей.

Ответ: 6 млн рублей.

Акции и другие ценные бумаги

Следующий блок, который мы рассмотрим, затрагивает относительно новое понятие ценной бумаги. Что вам нужно знать о ценной бумаге, чтобы решать подобные задания, не вдаваясь в экономические особенности, это то, как она может приносить доход.

Тип 1: когда вы получаете доход от того, что ценная бумага, которую вы купили ранее, растет в цене. Например, сначала ценная бумага стоила 3 000, а через год стала стоить 4 000. Непосредственно этих 4 000 у вас нет, но вы можете продать ценную бумагу за 4 000 и получите больше, чем потратили за год до этого.

Тип 2: когда вы получаете некий процент от прибыли компании за то, что ранее приобрели ценную бумагу этой компании. Если вы являетесь владельцем акции, то доход данного типа вы получаете в форме дивидендов.

Помимо этого дохода вы также можете продать эту ценную бумагу и, если она теперь стоит больше, чем когда вы ее покупали, вы также получите прибыль. Это не все пути получения дохода от ценных бумаг, но других особенностей вам знать не нужно. При необходимости все дополнительные условия будут описаны в самой задаче.

Рассмотрим следующую задачу, в которой как раз фигурирует понятие ценной бумаги.

Задача 3.

Григорий приобрёл ценную бумагу компании за 9000 рублей в начале 2016 года. Компания находится на стадии активного роста, поэтому цена данной бумаги каждый год возрастает на 2000 рублей. В любой момент Григорий может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 12 %. В начале какого года Григорий должен продать ценную бумагу, чтобы через 15 лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Решение:

Продать бумагу нужно тогда, когда прирост стоимости ценной бумаги станет меньше, чем банковский процент. Пусть это случится в год n.

К этому моменту n к изначальной цене акции 9000 прибавится n раз по 2000, тогда на текущий момент её цена составит:

9000 + 2000n

Чтобы получить прирост, который Григорий получит, если хранить деньги в форме акции, необходимо ежегодный прирост (в данной задаче – 2000 рублей) поделить на накопленную к данному моменту сумму.

Прирост денежной суммы в банке всегда одинаков и равен предложенному проценту, то есть 0,12.

Либо можем составить уравнение, которое объединит все строчки нашей таблицы:

По прошествии четырёх лет Григорий должен продать бумагу, то есть в начале 2020 года.

Ответ: 2020

Методы оптимальных решений

Это особый блок, позволяющий максимизировать одну целевую функцию при учёте данных в условии ограничений.

Основные типы заданий в этом блоке:

1. Оптимизация работы на производстве с учётом цен на рынке товара и факторов производства;

2. Многозаводское производство (включая разные заводы/ отели/ другие рабочие пространства);

3. Транспортная задача.

Разберём несколько задач с основными методами решения.

Задача.

У фермера есть 2 поля, площадь каждого из которых составляет 10 гектаров. На каждом поле можно выращивать пшеницу и ячмень. Урожайность пшеницы на первом поле составляет 500 ц/га, а на втором поле – 300 ц/га. Урожайность ячменя, наоборот, на первом поле составляет 300 ц/га, а на втором поле – 500 ц/га. При этом известно, что между данными злаками поля можно делить в любом соотношении.

Если известно, что на рынке установилась цена на пшеницу 7000 рублей за центнер, а цена на ячмень 9000 рублей за центнер, то какой наибольший доход фермер может получить?

Решение:

Имеем 2 поля с различными характеристиками.

В целом, продавать ячмень выгоднее, чем продавать пшеницу, так как 9000 > 7000 рублей.

Более того, известно, что на втором поле урожайность ячменя выше, чем урожайность пшеницы (500 ц/га против 300 ц/га). Тогда очевидно, что второе поле полностью фермер займёт ячменём, откуда получит:

10·500· 9000= 45000000 рублей

Ситуация с первым полем не так очевидна.

Продавать ячмень, как и прежде, выгоднее, чем продавать пшеницу. Однако на первом поле урожайность ячменя ниже, чем урожайность пшеницы (300 ц/га против 500 ц/га).

Поэтому необходимо сравнить соотношения этих величин:

Тогда получается, что засеять первое поле пшеницей выгоднее, так как низкая цена компенсируется высокой урожайностью.

Доход с первого поля:

10 · 500 ·7000 = 35000000 рублей

Суммарный доход составит:

35000000 рублей + 45000000 рублей = 80000000 рублей

Ответ: 80000000 рублей

Есть и другие типы заданий, в которых необходимо будет применить не житейские знания, а навыки составления уравнений и нахождения наименьшего/ наибольшего значений функций.

Задача.

На двух заводах есть по 360 рабочих, каждый из которых готов трудиться по 5 часов в сутки для обработки чёрных или цветных металлов. На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов. На втором заводе для обработки x кг чёрных металлов в день требуется x2 человеко-часов труда, а для обработки у кг цветных металлов в день требуется у2 человеко-часов труда.

Владельцу заводов поступил заказ на обработку металлов, причём 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов. Какую наибольшую массу обработанных металлов может за сутки суммарно получить заказчик?

Решение:

Как и дано в условии, 1 кг чёрных металлов ценится заказчиком так же, как 1 кг цветных металлов, что означает, что металлы взаимозаменяемы в пропорции 1:1.

Пусть на втором заводе t рабочих обрабатывают чёрные металлы, тогда (360-t) рабочих обрабатывают цветные металлы.

Знаем, что x2 человеко-часов труда требуется обработки x кг чёрных металлов, а у2 человеко-часов труда требуется в день для обработки у кг цветных металлов.

На первом заводе один рабочий за час обрабатывает 0,3 кг чёрных металлов или 0,1 кг цветных металлов, однако чёрные и цветные металлы для заказчика равнозначны, из чего сделаем вывод, что все 360 рабочих обрабатывают чёрные металлы, то есть 108*5 = 540 кг в день.

Имея соотношение на втором заводе и производительность рабочих на первом заводе, составим функцию возможного количества обработанных металлов:

Необходимо найти наибольшее значение этой функций. Последовательность действий мы уже знаем из темы «Анализ функций». Необходимо:

1. Найти производную функции;

2. Приравнять производную к 0, получить точки, подозрительные на экстремум;

3. Определить знаки производной на полученных промежутках и проверить, какие точки являются точкой максимума, а какие – точкой минимума.

Проведём такую последовательность действий с нашей производственной функцией.

1. 
2.      Приведём к общему знаменателю.  Приравняем числитель к 0.Возведём в квадрат.Получили единственную точку экстремума.
3. Проверим, является ли она точкой максимума.Видим, что в точке t=180 производная меняет знак с + на -, тогда, по определению, это точка максимума.Итак, на втором заводе 180 рабочих обрабатывают чёрные металлы, тогда 180 рабочих обрабатывают цветные металлы.Поставим данные значения в изначальную целевую функцию.Ответ: 600 кг

Видим, что экономическая задача достаточно разнообразна, но и решать вы её можете абсолютно разными способами – через производные, составление таблиц, схем, выведение формул и простой перебор вариантов.

Самое главное – внимательно прочитать и понять условие.

Примеры решения задач

Задача 1. В 2019 году клиент планирует открыть вклад в банке 1 ноября сроком на 1 месяц под 11% годовых. Какая сумма денег окажется на счёте вклада 1 декабря того же года, если планируемая сумма вклада равна 100 000 рублей? Ответ округлите до двух знаков после запятой.

Решение: При однократном начислении процентов через дней на вклад под годовых в невисокосный год получим сумму  

Воспользуемся этой формулой, считаяS₀= 100 000, r = 11 , m = 30 (так как в ноябре 30 дней).

Получим:

Число в скобках с точностью до 7 знаков после запятой равно 1,0090411, значит, S=100 904,11Таким образом, на счёте вклада будет 100 904 рубля 11 копеек.

Задача 2. Через сколько полных лет у клиента на счету будет не менее 950 000 рублей, если он намерен открыть вклад 31 декабря и планирует каждый год класть на счет 260 000 рублей при условии, что банк раз в год (начиная со следующего года) 31 декабря будет начислять 10% на имеющуюся сумму?

Решение:

Будем последовательно вычислять сумму на счете и упорядочивать данные с помощью таблицы.

Задача 3. По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» увеличивает эту сумму на 11% в течение каждого из первых двух лет, а на третий год начисляемые проценты изменяются. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором по истечении трёх лет этот вклад всё ещё будет выгоднее вклада «А».

Решение:

Пусть на каждый тип вклада была внесена сумма По вкладу «А» сумма каждый год увеличивается на 

умножается на коэффициент 1,1.

Тогда по вкладу «А» после первого года сумма станет равна ;

после второго года: 1,21S;

после третьего года: 1,331S.

По вкладу «Б» после первого года сумма станет равна1,11S;

после второго года 1,2321S.

Пусть на третий год по вкладу «Б» банк увеличивает сумму на r%. Тогда после третьего года по вкладу «Б» сумма станет равна

, где r— натуральное число,

коэффициент повышения в третий год.

По условию требуется найти наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А», то есть сумма через три года на вкладе «Б» должна быть больше суммы на вкладе «А». Составим неравенство:

Так как r— натуральное число, то наименьший процент равен 9%.

Задача 4. Сергей планирует приобрести ценную бумагу за 7 тысяч рублей. Цена бумаги каждый год будет возрастать на 2 тысячи рублей. В любой момент Сергей сможет продать ценную бумагу и вырученные деньги положить на банковский счет. Каждый год сумма на счете будет увеличиваться на 10%. В течение какого года после покупки Сергей должен продать ценную бумагу, чтобы через 30 лет после покупки этой бумаги сумма на счете стала наибольшей?

Решение.

Во второй год цена ценной бумаги составит: (7+2) тысячи рублей

В третий год (7+2)+2= 7+2∙2 тысячи рублей

В четвертый год (7+2)+2)+2= 7+2∙3 тысячи рублей

.

Сопоставим 10% банковский рост цены бумаги ее ежегодному росту на 2000 рублей.

10% от цены бумаги на 

Ценную бумагу стоит продать тогда, когда 10% от цены бумаги станут больше, чем 2 тысячи рублей.

Получаем неравенство:

Наименьшее натуральное n, удовлетворяющее этому неравенству, равно 8.

Задача 5.

Пенсионный фонд владеет ценными бумагами, которые стоят t² тыс. рублей в конце года t (t=1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 20%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце тридцатого года сумма на его счёте была наибольшей?

Материал опубликовала

Рощина Оксана Юрьевна858 Педагогический стаж — 19 лет, высшая квалификационная категория. Россия, Рязанская обл., Рыбное

ЕГЭ(профиль)
Задание №17
Задачи о кредитовании и банковских процентах: задачи на ценные бумаги
Подготовила учитель математики
МБОУ «Рыбновская СШ №2»
Рощина Оксана Юрьевна

Задача №1
В начале 2001 года Алексей приобрёл ценную бумагу за 7000 рублей. В конце каждого года цена бумаги возрастает на 2000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?

Решение задачи №1
Пусть в начале 2001 г. стоимость ценной бумаги составляет a1 = 7000 руб.
в начале 2002 г. – a2 = 7000 руб + 2000 руб. = 9000 руб.
в начале 2003 г. – a3 = 9000 руб + 2000 руб. = 11000 руб.
….
в начале 200n г. – an = (an -1 + 2000 )руб.
a1, a2, a3, … , аn — арифметическая прогрессия
a1 = 7000, d = 2000
Нужно выяснить в начале какого года Алексей должен продать ценную бумагу и положить деньги в банк. Это нужно сделать тогда, когда 10% от an будут превышать 2000 рублей(d).
0,1an > d
0,1an > 2000
an = a1 + d(n-1) – формула n -го члена арифметической прогрессии
0,1 (a1 + d(n-1) ) > 2000
0,1 (7000 + 2000(n-1) ) > 2000
700 + 200(n-1) > 2000
200(n-1) > 1300
n-1> 6,5
n > 7,5
Так как n – натуральное число, то ближайшее натуральное число, удовлетворяющее неравенству равно 8.
ОТВЕТ: 2008 ГОД

Задача №2
Пенсионный фонд владеет ценными бумагами, которые стоят 10t тыс. рублей в конце года t (t = 1; 2;…). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 24%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцатого года сумма на его счёте была наибольшей?

Решение задачи №2

Задача №3
Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t = 1; 2;…). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в (1 + r) раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчеты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?

Решение задачи №3
Если пенсионный фонд продаст ценные бумаги в конце года t , то в конце 25 –го на
его счете будет S(t) = t2 ∙ (1+r)25-t тыс. рублей.
Рассмотрим функцию
S(x) = x2 ∙ (1+r)25-x
зависящую от действительной переменной x , на отрезке [0;25].
Функция S(x) непрерывна на отрезке [0;25] и S(0) = 0, S(25) = 625.
Найдем производную этой функции
S’(x) = (x2 ∙ (1+r)25-x )’ = 2x(1+r)25-x — x2 ∙ (1+r)25-x ∙ ln(1+r) = x(1+r)25-x (2 – x ln(1+r) ).
Далее находим критические точки функции
S’(x) = 0
x(1+r)25-x (2 – x ln(1+r) ) =0
X = 0 или 2 – x ln(1+r) =0
x = 2/ ln(1+r)
Поэтому, функция S(x) имеет единственную точку максимума
xmax = 2/ ln(1+r) , в которой и достигается наибольшее на отрезке [0;25] значение.
0
25
2/ ln(1+r)
S’(x)
+
—
S(x)

Решение задачи №3
В условии сказано, что ценные бумаги выгоднее продать в конце 21-го года. Значит, максимум функции S(x) находится на интервале (20;22) и, следовательно, достаточно решить систему
S(21) > S(20) ;
S(21) > S(22) ,
212 ∙ (1+r)25-21 > 202 ∙ (1+r)25-20 ;
212 ∙ (1+r)25-21 > 222 ∙ (1+r)25-22 ,
212 > 202 ∙ (1+r);
212 > 222 ∙ (1+r).
r < 41/400;
r > 43/441,
Ответ: 43/441 < r < 41/400.

Задача №4

Решение задачи №4
Если пенсионный фонд продаст ценные бумаги в конце года t , то в конце 25 –го на
его счете будет f(t) = t2 ∙ r25-t тыс. рублей.
Рассмотрим функцию
f(t) = t2 ∙r25-t
зависящую от действительной переменной t , на отрезке [0;25].
Функция f(t) непрерывна на отрезке [0;25] и f(0) = 0, f(25) = 625.
Найдем производную этой функции
f’(t) = (t2 ∙r25-t )’ = 2t ∙r25-t — t2 ∙r25-t ∙ lnr = t ∙r25-t (2 – t ∙ lnr).
Далее находим критические точки функции
f’(t) = 0
t ∙r25-t (2 – t ∙ lnr) =0
t = 0 или 2 – t ∙ lnr =0
x = 2/ lnr
Поэтому, функция f(t) имеет единственную точку максимума
tmax = 2/ lnr , в которой и достигается наибольшее на отрезке [0;25] значение.
0
25
2/ lnr
f’(t)
+
—
f(t)

Решение задачи №4
В условии сказано, что ценные бумаги выгоднее продать в конце 21-го года. Значит, максимум функции f(t) находится на интервале (20;22) и, следовательно, достаточно решить систему
f(21) > f(20) ;
f(21) > f(22) ,
212 ∙ r25-21 > 202 ∙ r25-20 ;
212 ∙ r25-21 > 222 ∙r25-22 ,
212 > 202 ∙ r;
212 > 222 ∙ r.
r < 441/400;
r > 484/441,
Именно при таких значениях r нужно продать акции в конце 21 года, чтобы получить наибольшую прибыль в конце 25 года.
Ответ: 484/441 < r < 441/400.

Задача №5
Пенсионный фонд владеет акциями, цена которых к концу года t становится равной t2 тыс. руб. (т. е. к концу первого года они стоят 1 тыс. руб., к концу второго — 4 тыс. руб. и т. д.), в течение 20 лет. В конце любого года можно продать акции по их рыночной цене на конец года и положить вырученные деньги в банк под 25% годовых. В конце какого года нужно продать акции, чтобы прибыль была максимальной?

Решение задачи №5

Цена ценной бумаги на конец года вычисляется по формуле S = 1,1S₀ + 2000, где S₀ – цена этой ценной бумаги на начало года в рублях. Максим может приобрести ценную бумагу а может положить деньги на банковский счет, на котором сумма увеличивается за год на 12%. В начале любого года Максим может продать бумагу и положить все вырученные деньги на банковский счет, а также снять деньги с банковского счета и купить ценную бумагу. В начале 2021 года у Максима было 80 тысяч рублей, которые он может положить на банковский счет или может приобрести на них ценную бумагу. Какая наибольшая сумма может быть у Максима через четыре года? Ответ дайте в рублях.

Решение:

По условию задачи S₀ = 80 тысяч руб = 80000 руб

2021 год:

Если Максим в начале года приобретет ценную бумагу, то в конце года цена ценной бумаги будет равна 1,1⋅80000 + 2000 = 88000+2000 = 90000 руб

Если Максим в начале года положит деньги на банковский счет, тогда в конце года сумма на банковском счете будет 1,12⋅80000 = 89600 руб

Отсюда мы делаем вывод о том, что Максиму в начале 2021 года выгоднее будет приобрести ценную бумагу, так как ее цена на конец года будет больше. Тогда в конце 2021 года у Максима будет 90000 руб

2022 год:

Если Максим не будет продавать ценную бумагу, то в конце года цена ценной бумаги будет равна 1,1⋅90000 + 2000 = 101000 руб

Если Максим продаст бумагу, то в конце года сумма на банковском счете будет 1,12⋅90000 = 100800 руб

Получаем, что в начале года Максиму выгоднее не продавать ценную бумагу, тогда в конце года ее цена составит 101000 руб

2023 год:

Если Максим не будет продавать ценную бумагу, то в конце года цена ценной бумаги будет равна 1,1⋅101000 + 2000 = 113100 руб

Если Максим продаст бумагу, то в конце года сумма на банковском счете будет 1,12⋅101000 = 113120 руб

Получаем, что в начале года Максиму необходимо продать ценные бумаги и положить деньги на банковский счет, тогда в конце года сумма на банковском счете будет 113120 руб

2024 год:

Если Максим не будет продавать ценную бумагу, то в конце года цена ценной бумаги составит 1,1⋅113120 + 2000 = 126432 руб

Если Максим продаст бумагу, то в конце года сумма на банковском счете будет 1,12⋅113120 = 126694,4 руб

Получаем, что в начале года Максиму нужно оставить деньги на банковском счете, тогда в конце года у него будет 126694,4 руб

Наибольшая сумма, которая может быть у Максима через четыре года, – 126694,4 руб

Ответ: 126694,4 руб