Инфоурок
›
Геометрия
›Другие методич. материалы›Набор задач по теме «Цилиндр, конус, шар, комбинированные тела» из текстов ЕГЭ
Набор задач по теме «Цилиндр, конус, шар, комбинированные тела» из текстов ЕГЭ
Скачать материал
Скачать материал


- Сейчас обучается 1079 человек из 83 регионов


- Сейчас обучается 28 человек из 12 регионов


- Сейчас обучается 140 человек из 45 регионов


Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 784 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Организация деятельности секретаря руководителя со знанием английского языка»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
-
Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
-
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
-
Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»
-
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
-
Скачать материал
-
08.10.2021
4393
-
PDF
858.1 кбайт -
680
скачиваний -
Рейтинг:
4 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Михалева Татьяна Александровна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 8 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 67028
-
Всего материалов:
29
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
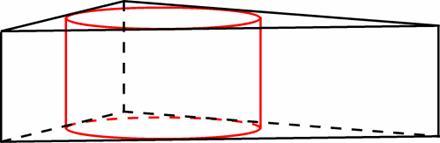
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 114.
Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 138.
Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 2.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Цилиндр описан около шара. Объем шара равен 38. Найдите объем цилиндра.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 116. Найдите объем конуса.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Сибирь
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 42. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 156. Найдите объём конуса.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 36. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 63. Найдите объём цилиндра.
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Источник: Основная волна ЕГЭ по математике 29.05.2019. Центр
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 2. Найдите объем шара.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.
Источник: ЕГЭ по математике 28.03.2016. Досрочная волна, вариант 3
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
Всего: 129 1–20 | 21–40 | 41–60 | 61–80 …
ЕГЭ Профиль №8. Цилиндр, конус, шар
данный материал поможет учителям при проверке усвоенного материала
Скачать:
Предварительный просмотр:
Задачи для самопроверки по теме: «Цилиндр, конус, сфера»
- Высота конуса равна 15, а диаметр основания – 16. Найти образующую конуса.
- Площадь боковой поверхности конуса равна 16 см2. Радиус основания конуса уменьшили в 4 раза, а образующую увеличили в 2 раза. Найти площадь боковой поверхности получившегося конуса.
- Площадь боковой поверхности конуса равна 10 см2. Радиус основания конуса увеличили в 6 раз, а образующую уменьшили в 4 раза. Найти площадь боковой поверхности получившегося конуса.
- Площадь боковой поверхности цилиндра равна 16П, а высота – 2. Найти диаметр основания цилиндра.
- Площадь боковой поверхности цилиндра равна 21П, а диаметр основания равен 7. Найти высоту цилиндра.
- Радиус основания конуса равен 3, высота равна 4. Найти площадь поверхности конуса, деленную на П.
- Площадь боковой поверхности цилиндра равна 40П, а высота – 4. Найти площадь поверхности цилиндра, деленную на П.
- Площадь большого круга шара равна 3. Найти площадь поверхности шара.
- Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
- Дано два шара с радиусами 8 и 4. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
- Сечение шара площадью 64П находится на расстоянии 6 см от центра шара. Найти площадь поверхности шара, деленную на П.
- Расстояние от центра шара радиуса 12 см до секущей плоскости равно 8 см. Найти площадь сечения, деленную на П.
- Радиусы двух шаров равны 14 и 48. Найти радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
- Около шара описан цилиндр, площадь поверхности которого равна 162. Найти площадь поверхности шара.
- Около конуса описана сфера. Центр сферы совпадает с центром основания конуса. Найти радиус сферы, если образующая конуса равна 40√2.
- Около конуса описана сфера. Центр сферы совпадает с центром основания конуса. Найти образующую конуса, если радиус сферы 5√2.
По теме: методические разработки, презентации и конспекты
- Мне нравится
Теория
| 1. | Параллелепипед, призма, пирамида | |
| 2. | Цилиндр, конус, шар | |
| 3. | Как решать задание ЕГЭ |
Задания
| 1. |
Высота треугольной призмы
Сложность: |
1 |
| 2. |
Объём по площади боковой грани
Сложность: |
1 |
| 3. |
Найти радиус основания цилиндра
Сложность: |
1 |
| 4. |
Радиус основания бочки
Сложность: |
1 |
| 5. |
Уровень жидкости в сосуде
Сложность: |
1 |
| 6. |
Боковая поверхность конуса
Сложность: |
1 |
| 7. |
Радиус основания цилиндра
Сложность: |
1 |
| 8. |
Боковая поверхность конуса (вписан в цилиндр)
Сложность: |
2 |
| 9. |
Объём куба
Сложность: |
2 |
| 10. |
Площадь полной поверхности параллелепипеда
Сложность: |
2 |
| 11. |
Объём параллелепипеда
Сложность: |
2 |
| 12. |
Вычисление высоты параллелепипеда
Сложность: |
2 |
| 13. |
Площадь основания призмы
Сложность: |
2 |
| 14. |
Боковое ребро пирамиды
Сложность: |
2 |
| 15. |
Радиус цилиндра, описанного около призмы
Сложность: |
2 |
| 16. |
Объём правильной четырёхугольной пирамиды
Сложность: |
1 |
| 17. |
Площадь поверхности тетраэдра
Сложность: |
2 |
| 18. |
Поверхность и объём куба, описанного около шара
Сложность: |
2 |
| 19. |
Площадь диагонального сечения
Сложность: |
3 |
| 20. |
Площадь основания и высота треугольной призмы
Сложность: |
3 |
| 21. |
Площадь основания пирамиды
Сложность: |
3 |
| 22. |
Высота правильной треугольной пирамиды
Сложность: |
3 |
| 23. |
Диагонали диагонального сечения
Сложность: |
3 |
| 24. |
Радиус шара, описанного около куба
Сложность: |
3 |
| 25. |
Цилиндр вписан в призму
Сложность: |
3 |
| 26. |
Площадь боковой поверхности пирамиды
Сложность: |
3 |
| 27. |
Высота и площадь боковой поверхности пирамиды
Сложность: |
3 |
| 28. |
Площадь сечения
Сложность: |
3 |
| 29. |
Угол между диагональю основания и стороной основания
Сложность: |
2 |
| 30. |
Высота пирамиды
Сложность: |
3 |
Экзаменационные задания (подписка)
| 1. |
Как на ЕГЭ (1). Призма, пирамида, цилиндр, конус, шар
Сложность: |
1 |
| 2. |
Как на ЕГЭ (2). Призма, пирамида, цилиндр, конус, шар
Сложность: |
1 |
| 3. |
Как на ЕГЭ (3). Призма, пирамида, цилиндр, конус, шар
Сложность: |
1 |
| 4. |
Как на ЕГЭ (4). Призма, пирамида, цилиндр, конус, шар
Сложность: |
1 |
Тесты
| 1. |
Тренировка по теме Призма, пирамида, цилиндр, конус, шар
Сложность: среднее |
12 |
Материалы для учителей
| 1. | Методическое описание |
Подборка задач по стереометрии «Цилиндр, конус шар».
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен
, а высота равна 2.
Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна 3.
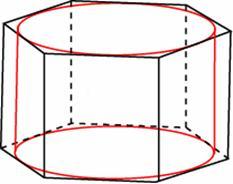
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2.
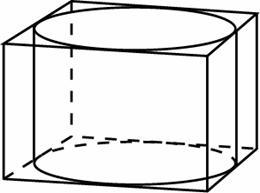
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем
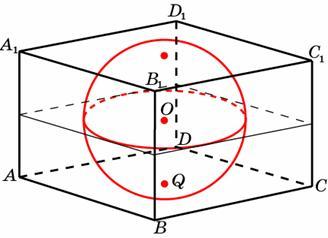
В куб с ребром 21 вписан шар Найдите объем этого шара, деленный на .
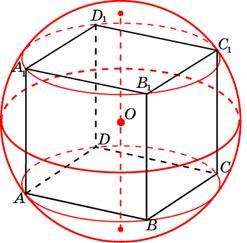
Около куба с ребром описан шар. Найдите объем этого шара, деленный на
.
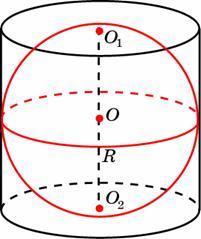
Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда
. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
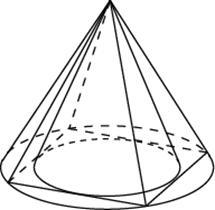
Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 5. Найдите его объем, деленный на .
Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
В цилиндрический сосуд налили воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в
.
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса
. Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,9 раза. Чему равен объем детали? Ответ выразите в литрах.
Найдите объем V конуса, образующая которого равна 3 и наклонена к плоскости основания под углом 30. В ответе укажите
.
Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 18,5 раза?
Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 22 раза?
Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 114.
Во сколько раз увеличится объем шара, если его радиус увеличить в десять раз?
Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Источники :
Открытый банк заданий ЕГЭ по математике
Цилиндр, конус, шар
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.
Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Основания цилиндра равны и лежат в параллельных плоскостях.
- Все образующие цилиндра параллельны и равны.
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
- Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
- Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
- Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
- Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
- Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.
$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$
Площадь поверхности и объем цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
$S_{бок.пов.}=2πR·h$
Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.
$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$
Объем цилиндра равен произведению площади основания на высоту.
$V=πR^2·h$
Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Пример:
Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.
Решение:
Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.
$R_{цилиндр}=R_{шар}; h_{цилиндр}=2R_{шар}$
Распишем формулы объема цилиндра и шара.
$V_{цилиндра}=πR_{цилиндр}^2·h_{цилиндр}=πR_{шар}^2·2R_{шар}=2πR_{шар}^3$
$V_{шара}={4π·R_{шар}^3}/{3}$
Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.
${V_{цилиндра}}/{V_{шара}}={2πR_{шар}^3·3}/{4π·R_{шар}^3}={3}/{2}=1.5$
Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.
$V_{шара}=30:1.5=20$
Ответ: $20$
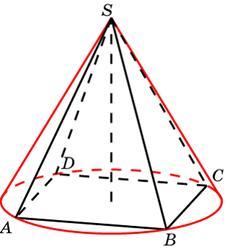
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).
$l=SA$
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.
$SО$ — высота и ось конуса.
Свойства конуса:
- Все образующие конуса равны.
- Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
- Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
- Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
- Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.
Площадь поверхности и объем конуса.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
$S_{бок.пов.}=πR·l$
Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.
$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$
Объем конуса равен трети произведения площади основания на высоту.
$V={πR^2·h}/{3}$
Объем части конуса, в основании которого лежит сектор: $V={πR^2·n°·h}/{360·3}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).
Тело, ограниченное сферой, называется шаром.
Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.
Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы
Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.
Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.