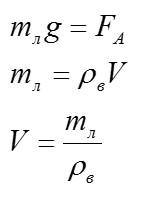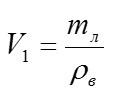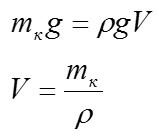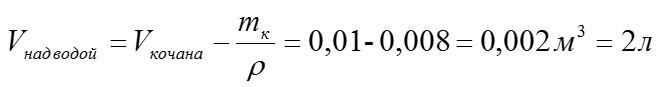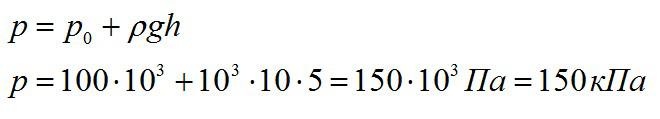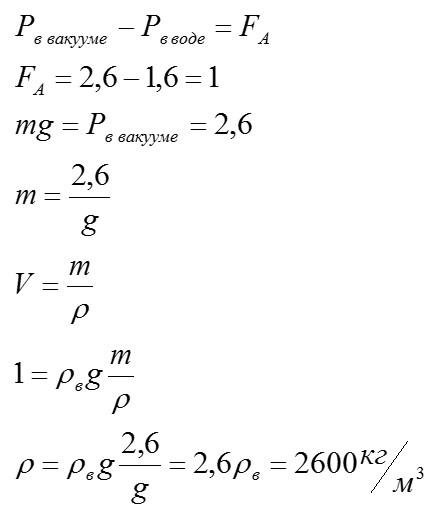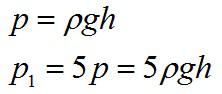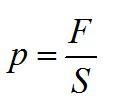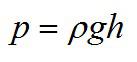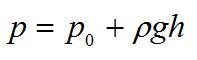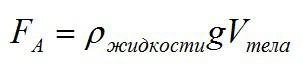Задачи на давление жидкости егэ

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

В последнее время мы разбирали решения многих простейших физических задач по разным темам: законы Ньютона, сила трения, свободное падение и т.д. Пришла пора взяться за что-то посложнее. Сегодня решаем задачи по теме «гидростатика». 

За полезными лайфхаками и новостями студенческой жизни добро пожаловать на наш телеграм-канал.

Задачи по гидростатике с решениями

Задача №1 на гидростатику

Условие

B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает? 

Решение

По условию плавания тел:

V – объем погруженной в воду части льда. После таяния льда образуется объем воды:

Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.

Ответ: уровень не изменится.

Задача №2 на гидростатику

Условие

Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?

Решение

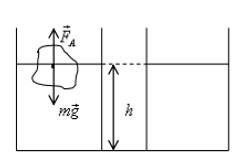
Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:

Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:

В одном кубическом метре – тысяча литров.

Ответ: 2 литра.

Задача №3 на гидростатику

Условие

Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.

Решение

Вспоминаем основное уравнение гидростатики и записываем:

Ответ: 150 кПа.

Задача №4 на гидростатику

Условие

Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.

Решение

Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.

Ответ: 2600 кг/м3.

Задача №5 на гидростатику

Условие

Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?

Решение

Формула для гидростатического давления:

Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.

Ответ: высота увеличилась в 5 раз.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Вопросы по гидростатике

Вопрос 1. Что такое гидростатический парадокс?

Ответ. Гидростатический парадокс – явление, когда вес жидкости в сосуде не совпадает с весовым давлением, которое она оказывает на стенки сосуда. Возникает в сосудах конусообразной формы.

Вопрос 2. Какие есть внесистемные единицы изменения давления:

Ответ. Внесистемные единицы давления:

• миллиметр ртутного столба;
• бар;
• атмосфера.

Вопрос 3. В условиях физических задач часто можно встретить формулировку «нормальные условия». Что этот значить?

Ответ. Это значит, что давление нужно брать равным 101325 Па (или 760 мм рт. ст.), а температуру – 0 градусов Цельсия (или 273 Кельвина).

Вопрос 4. Что такое сообщающиеся сосуды?

Ответ. Сообщающиеся сосуды – это емкости, соединенные между собой. Жидкость может свободно перетекать из одного сосуда в другой. Уровень жидкости с одной плотностью в сообщающихся сосудах всегда одинаков. Простейший пример сообщающихся сосудов: обычный чайник. Если мы нальем в него воду, уровень будет одинаковым как в носике, так и в основном объеме. Если же плотности жидкостей разные, то выше будет уровень той, у которой плотность меньше.

Вопрос 5. Что такое гидравлический пресс?

Ответ. Гидравлический пресс – устройство, в основе действия которого лежит закон Паскаля и принцип сообщающихся сосудов. Пресс состоит из двух соединённых и заполненных маслом цилиндров: узкого и широкого. При нажатии на поршень узкого цилиндра, широкий цилиндр получает во столько раз большее давление, во сколько раз площадь большего поршня больше площади меньшего поршня.

Гидростатика: немного теории

Гидростатика – раздел физики, изучающий равновесие жидкостей.

Равновесие жидкостей – очень важный раздел. Например, если вы выпили много пива, просто необходимо, чтобы оно находилось в равновесии. Но шутки в сторону! Какие фундаментальные понятия нужно знать, чтобы решать задачи по гидростатике? 

Давление и плотность

Давление – физическая величина, равная отношению модуля силы, перпендикулярно действующей на поверхность, к площади этой поверхности. 

Давление столба жидкости называют гидростатическим, а измеряется оно в Паскалях. Гидростатическое давление столба жидкости высотой h на дно сосуда рассчитывается по формуле:

Греческое «ро» — плотность жидкости. Плотность измеряется в килограммах на кубический метр и равна отношению массы тела к его объему.

Жидкость – изотропная среда. Это значит, что ее свойства одинаковы в любой ее точке.

Закон Паскаля и основное уравнение гидростатики

Давление, оказываемое на жидкость или газ передается в любую точку этой жидкости одинаково и во всех направлениях.

Это и есть закон Паскаля. Согласно ему, давление жидкости зависит только от плотности жидкости и высоты ее столба. На глубине h жидкость оказывает одинаковое давление как на дно, так и на стенки сосуда.

В данном случае р нулевое – давление столба воздуха (атмосферы), которое действует на жидкость.

В своей другой формулировке основное уравнение гидростатики показывает, что гидростатический напор является постоянной величиной для всего объема неподвижной жидкости. Здесь мы не будем останавливаться на этом понятии, так как оно изучается в курсе гидравлики.

Закон Архимеда и условия плавания тел

Закон Архимеда – еще одна важнейшая часть гидростатики. Он гласит:

На тело, погруженное в газ или жидкость действует выталкивающая сила, равная весу жидкости (газа) в объеме погруженной части тела. Эта сила называется силой Архимеда.

Тело плавает, если выталкивающая сила Архимеда больше действующей на него силы тяжести. Это же условие можно переписать, используя понятие плотности: тело будет плавать, если плотность жидкости больше, чем плотность тела.

Подробнее о законе Архимеда и фактах из жизни этого выдающегося античного инженера читайте в нашем отдельном материале.

Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис за качественным и быстрым объяснением.

В этой статье представляю задачи, связанные с плаванием тел и силой Архимеда. Как обычно, сначала пытаемся решить задачи простые, а затем перейдем к более сложным, которые вы найдете в следующей статье.

Задача 1. В воду погружен стеклянный кубик с ребром 10 см. Нижняя его грань находится на глубине 30 см. Рассчитайте силу давления жидкости, действующую: а) на верхнюю грань кубика; б) на нижнюю грань кубика; в) на правую грань; г) на левую грань; д) на переднюю и заднюю грани. Найдите равнодействующую всех этих сил.

---

Давление столба жидкости может быть вычислено по формуле , а сила давления может быть найдена из формулы , из которой находим: .

Не забываем, что очень важно помнить про перевод всех данных задачи в систему СИ, поэтому все расстояния и глубины из сантиметров переводим в метры.

Тогда сила давления на грань: , где — длина ребра кубика в метрах, — глубина, причем для боковых граней возьмем среднее значение () так как давление у верхнего края боковых граней и у нижнего – разное.

Сила давления на верхнюю грань, Н:

Сила давления на нижнюю грань, Н:

Сила давления на боковые грани, заднюю и переднюю, Н:

Понятно, что все силы, действующие на боковые, заднюю и переднюю грани друг друга компенсируют, а равнодействующая всех сил будет в итоге суммой сил давления на нижнюю и верхнюю грани:

Так как сила давления на нижнюю грань больше, чем на верхнюю, то равнодействующая направлена вверх.

Задача 2. Определите объем куска алюминия, на который в керосине действует архимедова сила величиной 120 Н.

---

Сила Архимеда может быть вычислена как , где — плотность жидкости, а — объем самого тела. То есть сила Архимеда не зависит  от того, из чего сделано тело, а только от его объема. Вы спросите: почему тогда одинаковые по объему тела, например, шарики равных радиусов, сделанные из дерева и какого-либо металла, по-разному себя ведут в воде: один плавает, второй – тонет? Да просто есть ведь и сила тяжести, которая зависит как раз от массы тела, и в случае деревянного шарика сила Архимеда достаточна, чтобы компенсировать силу тяжести, а в случае с металлическим шариком – нет.

Рассчитаем объем: м

Задача 3. Плавающий деревянный брусок вытесняет 0,5 л воды. Сколько весит брусок?

---

Так как брусок плавает, то сила Архимеда равна силе тяжести. Нас спрашивают в задаче про вес бруска. Так как система в покое и ускорения нет, то вес бруска равен силе тяжести:

Можно эту задачу решить иначе: вес тела равен весу воды, вытесняемой им. Брусок вытеснил 0,5 литра воды. Воспользовавшись формулой  плотности вещества, определяем, что масса такого количества воды равна 0,5 кг, а вес, значит, 5Н.

Задача 4. Тела изготовлены из дерева, пробки и стали. Они имеют объем 100 см каждое. Найдите архимедову силу, действующую на каждое тело, если его погрузить в воду.

---

Как было показано в одной из предыдущих задач, неважно, из чего изготовлено тело, а важен его объем, поэтому, раз тела обладают одним и тем же объемом, то и сила Архимеда на них действует одинаковая:

Ответ: 1 Н

Задача 5.Тело при погружении в воду становится легче в 5 раз, чем в воздухе. Определите плотность этого тела.

---

Мы с вами помним, конечно, что на всякое тело, погруженное как в жидкость, так и в газ, действует сила Архимеда. Поэтому в воздухе она также будет действовать на тело. Однако плотность воздуха так мала по сравнению с плотностью воды, что, я думаю, мы этой силой пренебрежем, и примем вес тела в воздухе равным силе тяжести.

Тогда вес тела — на воздухе, а вес тела в воде . А уменьшился вес этого тела в воде благодаря силе Архимеда: , откуда получаем, что

Масса тела равна произведению его плотности на объем:

Подставим:

Откуда и найдем плотность тела:

Ответ: плотность тела 1250 кг/м

Задача 6. На предмет, целиком погруженный в керосин, действует выталкивающая сила величиной 2 кН. Какой будет архимедова сила, действующая на него в воде? А в спирте?

---

Чтобы узнать, какой будет Архимедова сила, нужно знать объем предмета. Определим его, зная Архимедову силу в керосине:  , откуда получаем, что .

Зная объем, определяем Архимедову силу в воде, Н:

Так как плотность спирта равна плотности керосина, то и Архимедовы силы в этих жидкостях будут одинаковы.

Задача 7.Цинковый шар имеет массу 360 г. При погружении в воду его вес становится равным 2,8 Н. Сплошной этот шар или полый?

---

Определим объем шара в предположении, что полости в нем нет, по формуле плотности (то есть найдем объем куска цинка массой 360 г):

Плотность цинка равна кг/м, объем получается м

Теперь определим реальный объем шара, то есть  тот, который он вытесняет, по известному весу в жидкости. Вес шара Н, вес в жидкости равен , откуда объем вытесняемой жидкости (и объем шара)

мы получили больший объем, чем в первом случае, то есть шар имеет полость внутри, которая и влияет на его внешний объем.

Задача 8. Камень имеет объем 7,5 дм и массу 18,7 кг. Какую силу придется приложить, чтобы удерживать его в воздухе и в воде?

---

Чтобы удержать такой камень в воздухе, нужно преодолеть силу тяжести, то есть Н.

Теперь определим, какую силу достаточно будет приложить в воде, ведь там нам поможет сила Архимеда!

Тогда сила, которую нужно приложить в воде для удержания камня (или, проще, вес этого камня в воде) равна Н

Задача 9. Сплошное однородное тело, будучи погруженным в воду, весит 170 мН, а в глицерин – 144 мН. Каким будет вес этого тела, если его погрузить в четыреххлористый углерод?

---

Запишем систему уравнений по тем условиям, что описаны в задаче. Вес тела в воде равен весу тела на воздухе, уменьшенному на силу Архимеда:

Вес тела в глицерине равен весу тела на воздухе, уменьшенному на силу Архимеда – только в глицерине сила Архимеда отличается от той, что действовала на тело в воде:

Из этих двух уравнений, объединив их в систему, можно найти объем тела. Вычтем второе уравнение из первого:

Подставляем числа:

Теперь, когда мы знаем объем тела и плотность четыреххлористого  углерода, можно найти силу Архимеда в нем:

Ответ: 110 мН

Задача 10. Кусок парафина толщиной 5 см плавает в воде. Он имеет форму прямоугольного параллелепипеда. Какая часть куска выступает над водой?

---

Если кусок парафина плавает, а не тонет, значит, сила Архимеда достаточна для того, чтобы компенсировать силу тяжести. Тогда можно записать:

Представим массу куска через его объем и плотность:

Здесь — объем всего куска, а — объем погруженной части.

Тогда:

Так как объем – это произведение площади основания на высоту, то можно сократить площадь:

Откуда делаем вывод, что , то есть из пяти см выступает 0,5 см.

Задача 11. Прямоугольная баржа после приема груза осела на 0,5 м. Принимая длину баржи 5 м, а ширину – 3 м, рассчитать вес принятого ею груза.

---

Рассчитаем объем воды, который был вытеснен баржей после осадки:

м

Такой объем воды весит 7,5 тонн – это легко понять, помня величину плотности воды.

То есть вес груза, принятого баржей, равен , или 75 кН.

Задача 12. Плот состоит из 12 бревен, каждое из которых имеет объем 0,8 м. Бревна сосновые. Можно ли на этом плоту переправить на другой берег автомобиль массой 1,5 тонны?

---

Рассчитаем вес плота: Н

К этому весу будет еще добавлен вес автомобиля: Н

Определим силу Архимеда. Если она окажется больше, чем суммарный вес плота и автомобиля, то плот выдержит (не будет затоплен при переправе), а если меньше, то переправлять автомобиль нельзя. Предположим, весь объем плота оказывается в воде при погрузке автомобиля. Тогда сила Архимеда: Н.

Так как , то делаем вывод, что плот может переправить автомобиль и даже не  погрузится при переправе целиком в воду, то есть колеса не намокнут.

Задача 13. Теплоход, вес которого вместе с оборудованием составляет 20 МН, имеет объем подводной части при погружении до ватерлинии 6000 м. Как велика грузоподъемность теплохода?

---

Сразу вычислим силу Архимеда, так как знаем водоизмещение судна:

Н.

Часть этой силы пойдет на компенсацию веса самого судна с оборудованием:

, или 40 МН – такого веса груз можно нагрузить на теплоход.

Задача 14. В сообщающиеся сосуды диаметром каждый налита жидкость плотностью . В один сосуд опустили тело массой , которое стало плавать в жидкости. Как и на сколько изменится уровень жидкости в сосудах?

---

Так как тело плавает, то заключаем, что сила Архимеда достаточна, чтобы скомпенсировать вес тела. Тогда запишем это формулой:

Так как сосудов два, и по закону уровень воды в них одинаков, то, если общий объем воды увеличивается на благодаря телу, то в каждом сосуде он поднимется на .

Высота подъема воды равна

Или

Давление жидкости .

(h) это глубина.
(rho) это плотность жидкости

  

---

1. Определить давление воды на глубине 7 м.Плотность воды: (rho=1000dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
    Показать решение
    Видеорешение

---

2. Найти давление на дно цистерны с нефтью, если ее глубина (h=5м), а плотность нефти (rho=800dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
    Показать решение
    Видеорешение

---

---

3. На какой глубине давление воды (p= 250 кПа) ? Плотность воды (rho=1000dfrac{кг}{м^3}).Атмосферное давление не учитывать.
Показать ответ
    Показать решение
    Видеорешение

---

---

5. Давление жидкости на глубине (h=2м) равно 16 кПа. Найти плотность этой жидкости. Атмосферное давление не учитывать.

Показать ответ
    Показать решение
    Видеорешение

---

6. Определить силу, действующую снаружи на иллюминатор подводной лодки, если она находится на глубине (h=) 20 м, а его площадь (s=500 см^2) .Плотность воды (rho=1000dfrac{кг}{м^3}). Атмосферное давление не учитывать.

Показать ответ
    Показать решение
    Видеорешение

---

Данная тема посвящена решению задач на давление твердых тел,
жидкостей и газов, а также задач с применением закона Паскаля.

Задача 1. В четыре сосуда, вертикальные сечения
которых показаны на рисунке, налита вода. Одна клеточка на рисунке
соответствует 10 см. В каком из этих сосудов гидростатическое давление на дно
максимально и чему оно равно?

РЕШЕНИЕ

Гидростатическое давление — это давление
неподвижной жидкости, обусловленное ее весом.

Как видно из формулы, давление жидкости на дно сосуда не
зависит от его формы, а определяется только высотой уровня жидкости и ее
плотностью.

Так как во всех четырех сосудах находится вода, то
гидростатическое давление будет определяться только высотой ее столба в сосуде.
Как видно из рисунка, самый высокий уровень воды в третьем сосуде — 5 клеточек,
то есть пятьдесят сантиметров. Следовательно, в этом сосуде давление на дно
будет максимальным.

ОТВЕТ: гидростатическое давление максимальное в сосуде
№3 и равно 5 кПа.

Задача 2. Однородный кубик с ребром 10 см и плотностью
2500 кг/м³ лежит на дне сосуда с водой, высота уровня которой над
верхней гранью кубика равна 20 см. Атмосферное давление равно 100 кПа.
Определите силу давления кубика на дно сосуда. Считать, что вода под кубик не
подтекает.

Задача 3. Самолет совершает «мертвую петлю» радиусом
500 м со скоростью 792 км/ч. Определите давление бензина на дно бака,
заполненного до высоты 1 м, в верхней точке «мертвой петли».

Задача 4. В двух сообщающихся сосудах разного диаметра
находится вода. В широкий сосуд налили слой масла высотой 7 см, а в узкий
— слой бензина высотой 15 см. Определите разность уровней воды в сосудах.

Задача 5. Резиновая камера заполнена ртутью и
соединена со стеклянной трубкой так, как показано на рисунке. На камеру
положили доску массой 0,5 кг и гирю массой 12 кг. Определите высоту столба
ртути в трубке, если площадь доски равна 50 см².

Задача 6. Малый поршень гидравлического пресса за один
ход опускается на 0,9 м, а большой поршень поднимается на 0,01 м. С какой силой
действуют на малый поршень пресса, если пресс действует на зажатое в нем тело с
силой 100 кН?

«Доводы, до которых человек
додумывается сам,

обычно убеждают его больше, нежели те,

которые пришли в голову другим»

Блез Паскаль

Закон Паскаля

Гидростатика (от греч. hydor — вода и statos — стоящий) — один из подразделов механики, изучающий равновесие жидкости, а также равновесие твердых тел, частично или полностью погруженных в жидкость.

Закон Паскаля — основной закон гидростатики, согласно которому давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях.

Этот закон был открыт французским ученым Б. Паскалем в 1653 г. и опубликован в 1663 г.

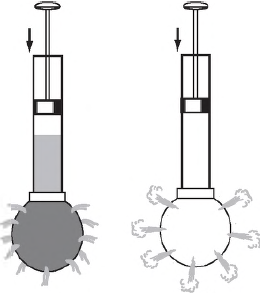
Чтобы убедиться в справедливости закона Паскаля, достаточно проделать простой опыт. Присоединим к трубке с поршнем полый шар со множеством маленьких отверстий. Наполнив шар водой, нажмем на поршень, чтобы увеличить в нем давление. Вода начнет выливаться, но не только через то отверстие, которое находится на линии действия прилагаемой нами силы, а и через все остальные тоже. Причем напор воды, обусловленный внешним давлением, во всех появившихся струйках будет одинаковым.

Аналогичный результат мы получим в том случае, если вместо воды будем использовать дым. Таким образом, закон Паскаля справедлив не только для жидкостей, но и для газов.

Жидкости и газы передают оказываемое на них давление по всем направлениям одинаково.

Передача давления жидкостями и газами во всех направлениях одновременно объясняется достаточно высокой подвижностью частиц, из которых они состоят.

Давление покоящейся жидкости на дно и стенки сосуда (гидростатическое давление)

Жидкости (и газы) передают по всем направлениям не только внешнее давление, но и то давление, которое существует внутри них благодаря весу собственных частей.

Давление, оказываемое покоящейся жидкостью, называется гидростатическим.

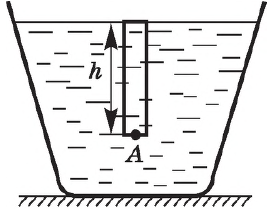
Получим формулу для расчета гидростатического давления жидкости на произвольной глубине $h$ (в окрестности точки А на рисунке).

Сила давления, действующая со стороны вышележащего узкого столба жидкости, может быть выражена двумя способами:

1) как произведение давления $р$ в основании этого столба на площадь его сечения $S$:

$F=pS;$

2) как вес того же столба жидкости, т. е. произведение массы $m$ жидкости на ускорение свободного падения:

$F=mg$

Масса жидкости может быть выражена через ее плотность $р$ и объем $V$:

$m=pV,$

а объем — через высоту столба и площадь его поперечного сечения:

$V=Sh$

Подставляя в формулу $F=mg$ значение массы из $m=pV$ и объема из $V=Sh$, получим:

$F=pVg=pShg$

Приравнивая выражения $F=pS$ и $F=pVg=pShg$ для силы давления, получим:

$pS=pShg$

Разделив обе части последнего равенства на площадь $S$, найдем давление жидкости на глубине $h$:

$p=phg$

Это и есть формула гидростатического давления.

Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой определяется давление.

Важно еще раз подчеркнуть, что по формуле гидростатического давления можно рассчитывать давление жидкости, налитой в сосуд любой формы, в том числе давление на стенки сосуда, а также давление в любой точке жидкости, направленное снизу вверх, поскольку давление на одной и той же глубине одинаково по всем направлениям.

С учетом атмосферного давления $р_0$, формула для давления покоящейся в ИСО жидкости на глубине $h$ запишется следующим образом:

$p=p_0+pgh$

Гидростатический парадокс

Гидростатический парадокс — явление, заключающееся в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда.

В данном случае под словом «парадокс» понимают неожиданное явление, не соответствующее обычным представлениям.

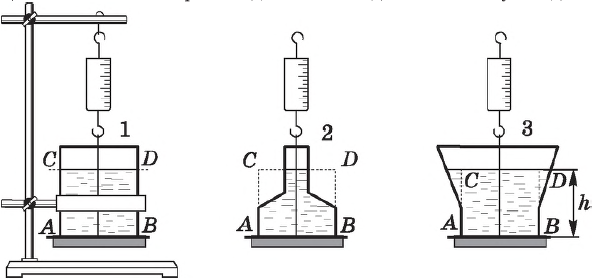
Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в сужающихся — больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на разный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде.

Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости: $p=pgh$ (формула гидростатического давления). А так как площадь дна у всех сосудов одинакова, то и сила, с которой жидкость давит на дно этих сосудов, одна и та же. Она равна весу вертикального столба $АВСD$ жидкости: $P=pghS$, здесь $S$ — площадь дна (хотя масса, а следовательно, и вес в этих сосудах различны).

Гидростатический парадокс объясняется законом Паскаля — способностью жидкости передавать давление одинаково во всех направлениях.

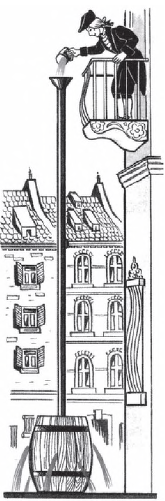
Из формулы гидростатического давления следует, что одно и то же количество воды, находясь в разных сосудах, может оказывать разное давление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создавать очень большое давление. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Закон Архимеда

Закон Архимеда — закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.

Этот закон был открыт древнегреческим ученым Архимедом в III в. до н. э. Свои исследования Архимед описал в трактате «О плавающих телах», который считается одним из последних его научных трудов.

Ниже приведены выводы, следующие из закона Архимеда.

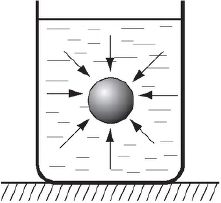
Действие жидкости и газа на погруженное в них тело

Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?

На тело, погруженное в воду, со всех сторон действуют силы давления воды. В каждой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростатическое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих на тело сверху.

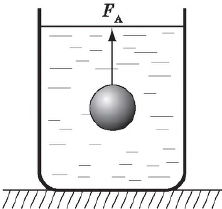
Если заменить все силы давления, приложенные к погруженному в воду телу, одной (результирующей или равнодействующей) силой, оказывающей на тело то же самое действие, что и все эти отдельные силы вместе, то результирующая сила будет направлена вверх. Это и заставляет тело всплывать. Эта сила называется выталкивающей силой, или архимедовой силой (по имени Архимеда, который впервые указал на ее существование и установил, от чего она зависит). На рисунке она обозначена как $F_A$.

Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глубинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.

Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном пространстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.

Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).

Если вес тела в вакууме (например, в сосуде, из которого откачан воздух) равен $Р_0$, то его вес в воздухе равен:

$P{возд}=P_0-F’A,$

где $F’A$ — архимедова сила, действующая на данное тело в воздухе. Для большинства тел эта сила ничтожно мала и ею можно пренебречь, т. е. можно считать, что $P{возд}=P_0=mg$.

Вес тела в жидкости уменьшается значительно сильнее, чем в воздухе. Если вес тела в воздухе $P{возд}=P_0$, то вес тела в жидкости равен $Р{жидк}= Р_0 — F_A$. Здесь $F_A$ — архимедова сила, действующая в жидкости. Отсюда следует, что

$F_A=P_0-P{жидк}$

Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.

Другими словами, учитывая формулу $F_A=P_0-P_{жидк}$, можно сказать:

Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.

Определить архимедову силу можно также теоретически. Для этого предположим, что тело, погруженное в жидкость, состоит из той же жидкости, в которую оно погружено. Мы имеем право это предположить, так как силы давления, действующие на тело, погруженное в жидкость, не зависят от вещества, из которого оно сделано. Тогда приложенная к такому телу архимедова сила $F_A$ будет уравновешена действующей вниз силой тяжести $m_{ж}g$ (где $m_{ж}$ — масса жидкости в объеме данного тела):

$F_{a}=m_{ж}g$

Но сила тяжести $m_{ж}g$ равна весу вытесненной жидкости $Р_ж$, Таким образом,

$F_A=P_ж$

Учитывая, что масса жидкости равна произведению ее плотности $р_ж$ на объем, формулу $F_{A}=m_{ж}g$ можно записать в виде:

$F_A=p_{ж}V_{ж}g$

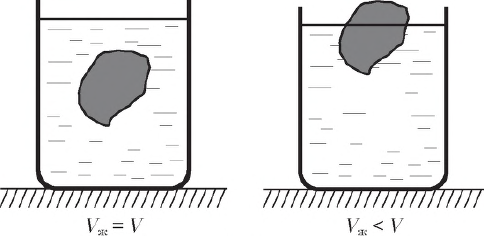
где $V_ж$ — объем вытесненной жидкости. Этот объем равен объему той части тела, которая погружена в жидкость. Если тело погружено в жидкость целиком, то он совпадает с объемом $V$ всего тела; если же тело погружено в жидкость частично, то объем $V_ж$ вытесненной жидкости меньше объема $V$ тела.

Формула $F_{A}=m_{ж}g$ справедлива и для архимедовой силы, действующей в газе. Только в этом случае в нее следует подставлять плотность газа и объем вытесненного газа, а не жидкости.

С учетом вышеизложенного закон Архимеда можно сформулировать так:

На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или газа), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).