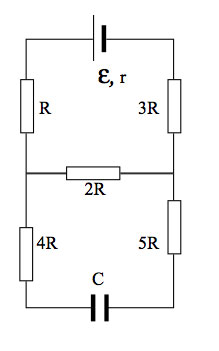
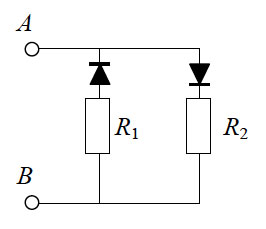
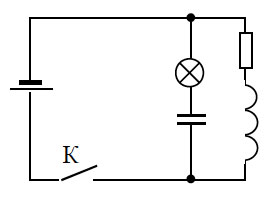
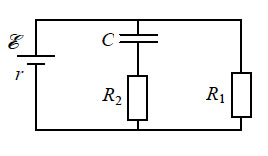
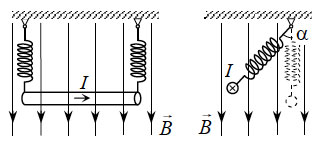
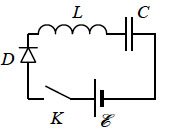
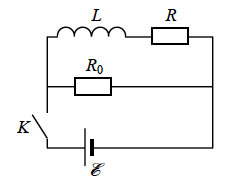
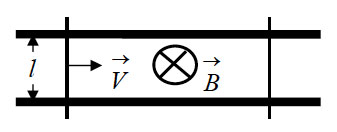В цепи, изображённой на рисунке, сопротивление диода в прямом направлении пренебрежимо мало, а в обратном многократно превышает сопротивление резисторов. При подключении к точке А положительного полюса, а к точке В отрицательного полюса батареи с ЭДС 12 В и пренебрежимо малым внутренним сопротивлением потребляемая мощность равна 14,4 Вт. При изменении полярности подключения батареи потребляемая мощность оказалась равной 21,6 Вт. Укажите, как течёт ток через диод и резисторы в обоих случаях, и определите сопротивления резисторов в этой цепи.
Спрятать решение
Решение.
Токи будут течь, как показано на рисунке.
В первом случае мощность равна откуда
Через диод и резистор ток не течёт, через резистор
течёт ток
Во втором случае мощность равна откуда
Через диод и резистор течёт ток
через резистор течёт ток
Ответ: направления токов изображены на рисунках, R1 = 20 Ом, R2 = 10 Ом
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| I) Приведено полное решение, включающее следующие элементы: записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом;
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ. |
3 |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.). И (ИЛИ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И (ИЛИ) Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины). |
2 |
| Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. ИЛИ В решении отсутствует одна из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В одной из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла. | 0 |
| Максимальный балл | 3 |
Источник: ЕГЭ по физике 02.04.2016. Досрочная волна
3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: использованы свойства диоа,
сказано в каком направлении он открыт, а в каком закрыт. Записана формула мощности, сказано как
находится общее сопротивление цепи в обоих случаях)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов. (введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
Задачи из ДЕМОВАРИАНТОВ (с решениями)
1. Две параллельные
неподвижные диэлектрические пластины расположены вертикально
и заряжены разноименно. Пластины находятся на расстоянии d
= 2 см друг от друга. Напряженность поля в пространстве внутри
пластин равна Е = 4•105 В/м. Между
пластинами на равном расстоянии от них помещен шарик с зарядом
q = 10-10 Кл и массой m = 20 мг.
После того как шарик отпустили, он начинает падать и ударяется
об одну из пластин. Насколько уменьшится высота местонахождения
шарика Δh к моменту его удара об одну из пластин?
Образец возможного решения
2. Конденсатор
состоит из двух неподвижных, вертикально расположенных, параллельных,
разноименно заряженных пластин. Пластины расположены на расстоянии
d = 5 см друг от друга. Напряженность поля внутри конденсатора
равна Е = 104 В/м. Между пластинами, на
равном расстоянии от них, помещен шарик с зарядом q
= 10-5 Кл и массой m = 20 г. После того
как шарик отпустили, он начинает падать и через некоторое время
ударяется об одну из пластин. Оцените время падения Δt
шарика.
Образец возможного решения
3. Конденсаторы,
электрическая емкость которых 2 мкФ и 10 мкФ, заряжают до напряжения
5 В каждый, а затем «плюс» одного из них подключают к «минусу»
другого и соединяют свободные выводы резистором 1000 Ом. Какое
количество теплоты выделится в резисторе?
Образец возможного решения
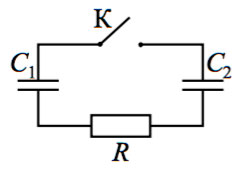
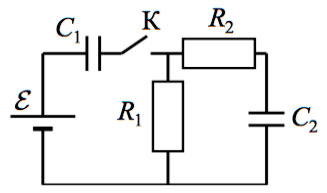
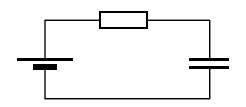
3*. Заряженный конденсатор C1 = 1 мкФ включён в последовательную цепь из резистора R = 300 Ом, незаряженного конденсатора C2 = 2 мкФ и разомкнутого ключа К (см. рисунок). После замыкания ключа в цепи выделяется количество теплоты Q = 30 мДж. Чему равно первоначальное напряжение на конденсаторе С1?
Образец возможного решения
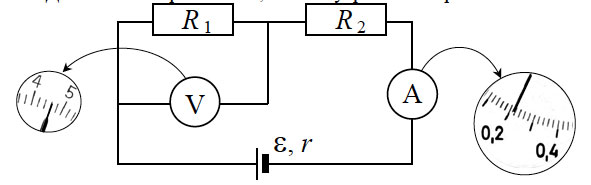
4. При проведении лабораторной
работы ученик собрал электрическую цепь по схеме на рисунке.
Сопротивления R1 и R2
равны 20 Ом и 150 Ом соответственно. Сопротивление вольтметра
равно 10 кОм, а амперметра – 0,4 Ом. ЭДС источника равна 36
В, а его внутреннее сопротивление – 1 Ом. На рисунке показаны
шкалы приборов с показаниями, которые получил ученик. Исправны
ли приборы или же какой-то из них даёт неверные показания?
Образец возможного решения
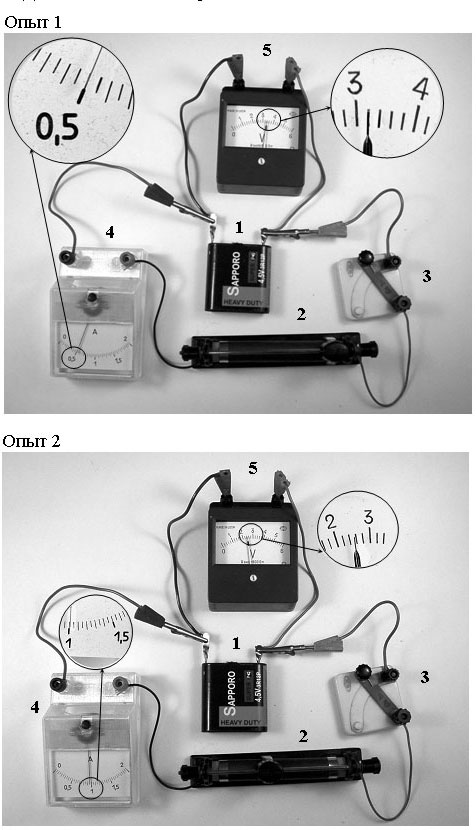
5. Ученик собрал электрическую цепь, состоящую
из батарейки (1), реостата (2), ключа (3), амперметра (4) и
вольтметра (5). После этого он провел измерения напряжения на
полюсах и силы тока в цепи при различных сопротивлениях внешней
цепи (см. фотографии). Определите ЭДС и внутреннее сопротивление
батарейки.
Образец возможного решения
6. Ученик собрал электрическую цепь, состоящую
из батарейки (1), реостата (2), ключа (3), амперметра (4) и
вольтметра (5) (см. фотографии: опыт 1, опыт 2). После этого
он измерил напряжение на полюсах источника тока и силу тока
в цепи при двух положениях ползунка реостата. Определите КПД
источника тока в первом опыте.
Образец возможного решения
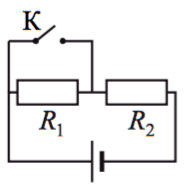
6*. Источник тока, два резистора и ключ включены в цепь, как показано на рисунке. При разомкнутом ключе на резисторе R1 выделяется мощность P1 = 2 Вт, а на резисторе R2 − мощность P2 = 1 Вт. Какая мощность будет выделяться на резисторе R2 после замыкания ключа К? Внутренним сопротивлением источника пренебречь.
Образец возможного решения
7. Электрическая цепь состоит из источника
тока и реостата. ЭДС источника ε = 6 В, его внутреннее
сопротивление r = 2 Ом. Сопротивление реостата можно
изменять в пределах от 1 Ом до 5 Ом. Чему равна максимальная
мощность тока, выделяемая на реостате?
Образец возможного решения
8. К однородному
медному цилиндрическому проводнику длиной 10 м приложили разность
потенциалов 1 В. Определите промежуток времени, в течение которого
температура проводника повысится на 10 К. Изменением сопротивления
проводника и рассеянием тепла при его нагревании пренебречь.
(Удельное сопротивление меди 1,7•10-8 Ом•м.)
Образец возможного решения
9. К источнику тока с ЭДС ε = 9 В и
внутренним сопротивлением r = 1 Ом подключили параллельно
соединенные резистор с сопротивлением R = 8 Ом и
плоский конденсатор, расстояние между пластинами которого
d = 0,002 м. Какова напряженность электрического
поля между пластинами конденсатора?
Образец возможного решения
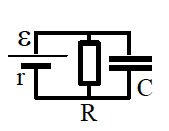
10. Чему равна энергия
конденсатора емкости С, подключенного по электрической схеме,
представленной на рисунке? Величины ε, R и r
считать известными.
Образец возможного решения
10*. В цепи, изображённой на рисунке, ЭДС батареи равна 100 В; сопротивления резисторов R1 = 10 Ом и R2 = 6 Ом, а ёмкости конденсаторов: C1 = 60 мкФ и C2 = 100 мкФ. В начальном состоянии ключ К разомкнут, а конденсаторы не заряжены. Через некоторое время после замыкания ключа в системе установится равновесие. Какое количество теплоты выделится в цепи к моменту установления равновесия?.
Образец возможного решения
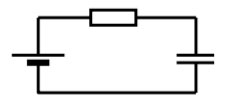
10**. Источник постоянного напряжения с ЭДС 100 В подключён через резистор к конденсатору, расстояние между пластинами которого можно изменять (см. рисунок). Пластины раздвинули, совершив при этом работу 90 мкДж против сил притяжения пластин. На какую величину изменилась ёмкость конденсатора, если за время движения пластин на резисторе выделилось количество теплоты 40 мкДж? Потерями на излучение пренебречь.
Образец возможного решения
11. В цепи, изображённой на рисунке, сопротивление
диодов в прямом направлении пренебрежимо мало, а в обратном
многократно превышает сопротивление резисторов. При подключении
к точке А положительного полюса, а к точке В
отрицательного полюса батареи с ЭДС 12 В и пренебрежимо малым
внутренним сопротивлением, потребляемая мощность равна 7,2
Вт. При изменении полярности подключения батареи потребляемая
мощность оказалась равной 14,4 Вт. Укажите условия протекания
тока через диоды и резисторы в обоих случаях и определите
сопротивление резисторов в этой цепи.
Образец возможного решения
12. С какой
скоростью вылетает α-частица из радиоактивного ядра, если
она, попадая в однородное магнитное поле с индукцией 1 Тл перпендикулярно
его силовым линиям, движется по дуге окружности радиуса 0,5
м (α-частица – ядро атома гелия, молярная масса гелия 0,004
кг/моль).
Образец возможного решения
13. Электрон
влетает в область однородного магнитного поля индукцией В
= 0,01 Тл со скоростью v = 1000 км/с перпендикулярно линиям
магнитной индукции. Какой путь он пройдет к тому моменту, когда
вектор его скорости повернется на 1о?
Образец возможного решения
14. В кинескопе
телевизора разность потенциалов между катодом и анодом 16 кВ.
Отклонение электронного луча при горизонтальной развертке осуществляется
магнитным полем, создаваемым двумя катушками. Ширина области,
в которой электроны пролетают через магнитное поле, равна 10
см. Какова индукция отклоняющего магнитного поля при значении
угла отклонения электронного луча 30°?
Образец возможного решения
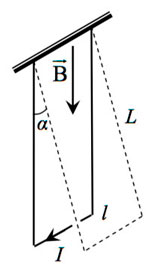
14*. Металлический стержень длиной l = 0,1 м и массой m = 10 г, подвешенный на двух параллельных проводящих нитях длиной L = 1 м, располагается горизонтально в однородном магнитном поле с индукцией B = 0,1 Тл, как показано на рисунке. Вектор магнитной индукции направлен вертикально. На какой максимальный угол отклонятся от вертикали нити подвеса, если по стержню пропустить ток силой 10 А в течение 0,1 с? Угол α отклонения нитей от вертикали за время протекания тока мал.
Образец возможного решения
15. Два параллельных друг
другу рельса, лежащих в горизонтальной плоскости, находятся
в однородном магнитном поле, индукция B которого направлена
вертикально вниз (см. рисунок). Левый проводник движется вправо
со скоростью V, а правый покоится. С какой скоростью v надо
перемещать правый проводник (такой же), чтобы в три раза уменьшить
силу Ампера, действующую на левый проводник? (Сопротивлением
рельсов пренебречь.)
Образец возможного решения
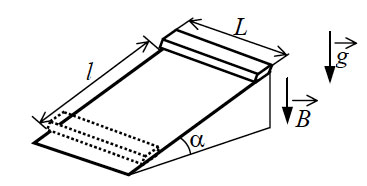
16. Тонкий алюминиевый
брусок прямоугольного сечения, имеющий длину L = 0,5
м, соскальзывает из состояния покоя по гладкой наклонной плоскости
из диэлектрика в вертикальном магнитном поле с индукцией В
= 0,1 Тл (см. рисунок). Плоскость наклонена к горизонту под
углом α = 30°. Продольная ось бруска при движении сохраняет
горизонтальное направление. Найдите величину ЭДС индукции на
концах бруска в момент, когда брусок пройдет по наклонной плоскости
расстояние l = 1,6 м.
Образец возможного решения
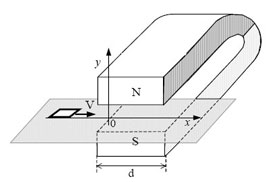
17. Квадратная рамка со
стороной b = 5 см изготовлена из медной проволоки сопротивлением
R = 0,1 Ом. Рамку перемещают по гладкой горизонтальной
поверхности с постоянной скоростью V вдоль оси Ох.
Начальное положение рамки изображено на рисунке. За время движения
рамка проходит между полюсами магнита и вновь оказывается в
области, где магнитное поле отсутствует. Индукционные токи,
возникающие в рамке, оказывают тормозящее действие, поэтому
для поддержания постоянной скорости движения к ней прикладывают
внешнюю силу F, направленную вдоль оси Ох.
С какой скоростью движется рамка, если суммарная работа внешней
силы за время движения равна А = 2,5·10-3 Дж?
Ширина полюсов магнита d = 20 см, магнитное поле имеет
резкую границу, однородно между полюсами, а его индукция В
= 1 Тл.
Образец возможного решения
17*. Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos(bt), где а = 6·10–3 Тл, b = 3500 с–1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?
Образец возможного решения
18. В идеальном
колебательном контуре амплитуда колебаний силы тока в катушке
индуктивности 5 мА, а амплитуда колебаний заряда конденсатора
2,5 нКл. В момент времени t сила тока в катушке равна
3 мА. Найдите заряд конденсатора в этот момент.
Образец возможного решения
19. В электрической цепи, показанной на
рисунке, ЭДС источника тока равна 12 В, емкость конденсатора
2 мФ, индуктивность катушки 5 мГн, сопротивление лампы 5 Ом
и сопротивление резистора 3 Ом. В начальный момент времени
ключ К замкнут. Какая энергия выделится в лампе после размыкания
ключа? Внутренним сопротивлением источника тока, а также сопротивлением
катушки и проводов пренебречь.
Образец возможного решения
Избранные задачи
прошлых лет (с ответами)
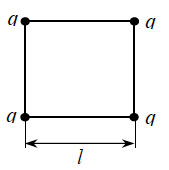
20. Четыре одинаковых
заряда q расположены на плоскости в вершинах квадрата
со стороной L и удерживаются в равновесии связывающими
их попарно нитями (см. рис.). Сила отталкивания соседних зарядов
равна F0 = 20•10-3 Н. Чему
равно натяжение каждой из нитей?
21. В двух
вершинах (точках 1 и 2) равностороннего треугольника со стороной
L помещены заряды q и -2q. Каковы
направление и модуль вектора напряженности электрического поля
в точке 3, являющейся третьей вершиной этого треугольника? Известно,
что точечный заряд q создает на расстоянии L
электрическое поле напряженностью Е = 10 мВ/м.
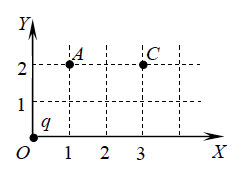
22. Точечный заряд q,
помещенный в начало координат, создает в точке А (см.
рисунок) электростатическое поле напряженностью Е1
= 65 В/м. Какова напряженность поля Е2 в
точке С?
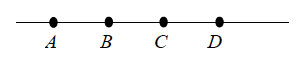
23. Точки А,
В, С и D расположены на прямой и
разделены равными промежутками L (см. рисунок). В точке
А помещен заряд q1 = 8•10-12
Кл, в точке В — заряд q2
= -5•10-12 Кл. Какой заряд q3
надо поместить в точку D, чтобы напряженность поля
в точке С была равна нулю?
24. Горизонтально
расположенная, неподвижная, положительно заряженная пластина
из диэлектрика создает электрическое поле напряженностью Е
= 104 В/м. На нее с высоты h = 10 см падает
шарик массой m = 20 г, имеющий заряд q = +10-5
Кл и начальную скорость υ0 = 1 м/с, направленную вертикально вниз.
Какая энергия выделяется при абсолютно неупругом ударе шарика
о пластину?
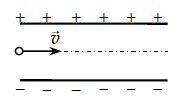
25. Электрон влетает в
электрическое поле, созданное двум разноименно заряженными пластинами
плоского конденсатора, со скоростью υ (υ <<
c) на равном расстоянии от них (см. рисунок). Расстояние
между пластинами d, длина пластин L (L
>> d). При какой минимальной разности потенциалов
между пластинами конденсатора электрон не вылетит из него?
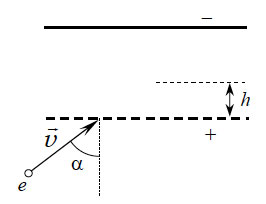
26. Электрон со скоростью
υ = 5•106 м/с влетает в пространство между
пластинами плоского конденсатор, между которыми поддерживается
разность потенциалов U = 500 В (см. рисунок). Каково
максимальное удаление электрона h от нижней пластины
конденсатора? Отношение заряда электрона к его массе γ
= -1,76•1011 Кл/кг, угол падения электрона
α = 600. Расстояние между пластинами конденсатора
равно d = 5 см.
27. Шарик
массой m = 20 г подвешен на шелковой нити и помещен
над положительно заряженной плоскостью, создающей однородное
вертикальное электрическое поле напряженностью Е =
104 В/м. Шарик имеет положительный заряд q
= 10-5 Кл. Период малых колебаний шарика Т
= 1 с. Какова длина нити?
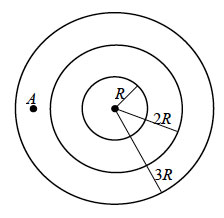
28. Точечный заряд q
= 10 пКл создает на расстоянии R электрическое поле с потенциалом
φ1 = 1 В. Три концентрические сферы с радиусами
R, 2R и 3R несут равномерно распределенные
по их поверхностям заряды q1 = +2q,
q2 и q3 = -2q
соответственно (см. рисунок). Значение потенциала поля в точке
А, отстоящей на расстояние RA =
2,5R от центра сфер, равно φ2 = 2,6
В. Чему равна величина заряда q2?
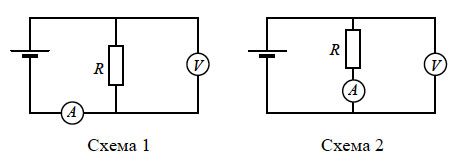
29. Одни и те же элементы
соединены в электрическую цепь сначала по схеме 1, а затем по
схеме 2 (см. рисунок). Сопротивление резистора равно R,
сопротивление амперметра 0,01R, сопротивление вольтметра
9R. Найдите отношение I2/I1
показаний амперметра в схемах. Внутренним сопротивлением источника
и сопротивлением проводов пренебречь.
30. Чему равна напряженность
электрического поля внутри плоского конденсатора (см. рисунок),
если внутреннее сопротивление источника тока r = 10
Ом, ЭДС его равна ε = 30 В, сопротивление резисторов R1
= 20 Ом, R2 = 40 Ом? Расстояние между обкладками
конденсатора d = 1 мм.
31. Лампочки
поочередно подключают к источнику постоянного тока. Сопротивления
лампочек равны 3 Ом и 12 Ом. Мощность тока в лампочках одинакова.
Чему равно внутреннее сопротивление источника тока?
32. Источник постоянного
напряжения с ЭДС 100 В подключен через резистор к конденсатору
переменной ёмкости, расстояние между пластинами которого можно
изменять (см. рисунок). Пластины медленно сблизили, при этом
силы притяжения пластин совершили работу 10 мкДж. Какое количество
теплоты выделилось в электрической цепи с момента начала движения
пластин до полного затухания возникших при этом переходных процессов,
если заряд конденсатора в итоге изменился на 1 мкКл?
33. Заряженная
частица ускоряется постоянным электрическим полем конденсатора,
напряжение на обкладках которого 1280 В. Затем она влетает в
однородное магнитное поле, модуль вектора магнитной индукции
которого равен 200 мкТл, и движется по дуге окружности радиусом
60 см в плоскости, перпендикулярной линиям магнитной индукции.
Определите отношение заряда частицы к ее массе.
34. В циклотроне поддерживается
разность потенциалов между дуантами U = 500 В. Чему
равен радиус конечной орбиты иона Ве++,
если ион, двигаясь в магнитном поле с индукцией В =
1,53 Тл, успел совершить N = 50000 оборотов? Масса
иона бериллия m = 1,5•10-26 кг.
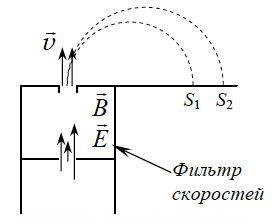
35. В масс-спектрограф
влетают однократно ионизированные ионы неона с одинаковыми зарядами,
но разными массами m1 = 20 а.е.м. и m2
= 22 а.е.м., предварительно пройдя «фильтр скоростей»,
выделяющий ионы с одинаковой скоростью υ. Фильтр создан
электрическим полем напряженностью Е
и магнитным полем индукцией В, причем
векторы и взаимно перпендикулярны. Отклоняющее магнитное поле,
перпендикулярное пучку ионов, имеет индукцию В0.
Ионы совершают половину оборота в отклоняющем магнитном поле.
Чему равно расстояние между точками S1 и
S2 (см. рисунок)?
36. Электрон
влетает в однородное магнитное поле со скоростью υ под
острым углом α к параллельно направленным векторам E
и B. Определите, сколько оборотов
успеет сделать электрон до того, как начнет движение в направлении,
обратном направлению векторов E и
B. Величины Е и В
считать известными.
37. Медный
куб с длиной ребра a = 0,1 м скользит по столу с постоянной
скоростью υ = 10 м/с, касаясь стола одной из плоских поверхностей.
Вектор индукции магнитного поля В = 0,2 Тл направлен
вдоль поверхности стола и перпендикулярно вектору скорости куба.
Найдите модуль вектора напряженности электрического поля, возникающего
внутри металла, и разность потенциалов между центром куба и
одной из его вершин.
38. По прямому горизонтальному
проводнику длины 1 м с площадью поперечного сечения 12,5 мм2,
подвешенному с помощью двух одинаковых невесомых пружинок с
коэффициентами упругости 100 Н/м течет электрический ток I.
При включении вертикального магнитного поля с индукцией В
= 0,1 Тл проводник отклонился от исходного положения к составляют
с вертикалью угол α (см. рисунок). Абсолютное удлинение
каждой из пружинок при этом составляет 7 мм. Найдите силу тока
I в проводе. Плотность материала проводника ρ
= 8•103 кг/м3.
39. Медное
кольцо, диаметр которого 20 см, а диаметр провода кольца 2 мм,
расположено в магнитном поле, магнитная индукция которого меняется
по модулю со скоростью 1,09 Тл/с. Плоскость кольца перпендикулярна
вектору магнитной индукции. Чему равен возникающий в кольце
индукционный ток? Удельное сопротивление меди 1,72•10-8
Ом•м.
40. Плоская
катушка диаметром 6 см находится в однородном магнитном поле,
индукция которого 6•10-2 Тл. Катушка поворачивается
вокруг оси, перпендикулярной линиям магнитной индукции, на угол
180o за 0,2 с. Плоскость катушки до и после поворота
перпендикулярна линиям магнитной индукции. Среднее значение
ЭДС индукции, возникающей в катушке, равно 0,2 В. Чему равно
число витков катушки?
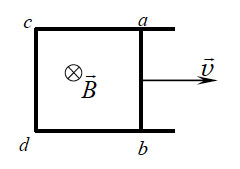
41. По П-образному
проводнику acdb постоянного сечения со скоростью скользит
проводящая перемычка ab такого же сечения, длиной l.
Проводники помещены в постоянное однородное магнитное поле,
вектор индукции которого направлен перпендикулярно плоскости
проводников (см. рисунок). Определите разность потенциалов U
= φa – φb
между точками a и b в тот момент, когда ab
= aс. Сопротивление между проводниками в точках контакта
пренебрежимо мало.
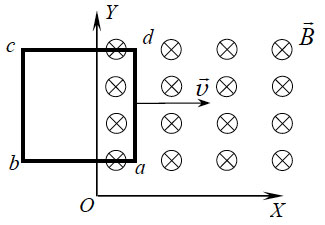
42. Квадратная проволочная
рамка abcd со стороной ab = l движется равномерно со
скоростью υ вдоль оси ОХ системы отсчета, связанной с
магнитами, и попадает в область магнитного поля с индукцией
B, отмеченную на рисунке. Сопротивление
проводников рамки равно R. Определить работу силы Ампера,
действующей на рамку, за то время, когда она войдет в область,
занятую полем, если в начальный момент рамка находилась полностью
вне поля.
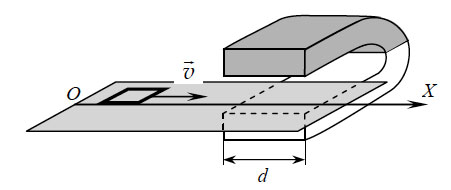
43. Квадратную рамку из
медной проволоки со стороной b = 5 см и сопротивлением
R = 0,1 Ом перемещают вдоль оси ОХ по гладкой
горизонтальной поверхности с постоянной скоростью υ. Начальное
положение рамки изображено на рисунке. За время движения рамка
успевает пройти между полюсами магнита и оказаться в области,
где магнитное поле отсутствует. Ширина полюсов магнита d
= 20 см, магнитное поле имеет резкую границу и однородно между
полюсами, а его индукция В = 1 Тл. Возникающие в рамке
индукционные токи нагревают проволоку. Чему равна скорость движения
рамки, если за время движения в ней выделяется количество теплоты
Q = 2,5•10-3 Дж?
44. Плоский контур с источником
постоянного тока находится во внешнем однородном магнитном поле,
вектор магнитной индукции которого перпендикулярен плоскости
контура (см. рисунок). На сколько процентов изменится мощность
тока в контуре после того, как поле начнет уменьшаться со скоростью
0,01 Тл/с? Площадь контура 0,1 м2, ЭДС источника
10 мВ.
45. В колебательном контуре,
состоящем из катушки с индуктивностью L и воздушного
конденсатора емкостью С, происходят гармонические колебания
силы тока с амплитудой I0. В тот момент,
когда сила тока в катушке равна нулю, пространство между пластинами
быстро заполняют диэлектриком с диэлектрической проницаемостью
ε = 1,5. На сколько изменится полная энергия контура?
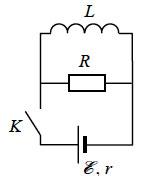
46. Ключ в схеме, показанной
на рисунке, в начальный момент был замкнут. Определить количество
теплоты, выделившееся на резисторе R после размыкания
ключа. Индуктивность катушки L = 0,2 Гн, сопротивление
резистора R = 100 Ом, величина ЭДС источника ε
= 9 В, его внутреннее сопротивление r = 3 Ом.
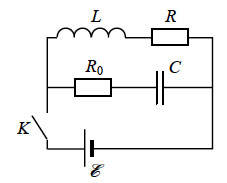
47. Ключ К в
схеме, показанной на рисунке, в начальный момент был замкнут.
Определить количество теплоты, выделившееся на резисторе R
после размыкания ключа. Индуктивность катушки L = 4•10-6
Гн, емкость конденсатора C = 7•10-5
Ф, сопротивление резисторов R0 = 10 Ом,
R = 15 Ом, величина ЭДС источника ε = 450 В.
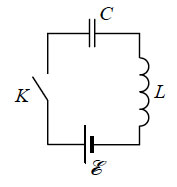
48. В цепи, состоящей
из источника тока с ЭДС ε, конденсатора емкости С,
катушки индуктивности L и идеального диода D,
ключ K первоначально разомкнут. Определите напряжение,
до которого зарядится конденсатор после замыкания ключа. Диод
считается идеальным, если его сопротивление в прямом направлении
бесконечно мало, а в обратном направлении — бесконечно велико.
Внутреннее сопротивление источника тока равно нулю.
49. Ключ в схеме, показанной
на рисунке, в начальный момент был замкнут. Определить количество
теплоты, выделившееся на резисторе R после размыкания
ключа. Индуктивность катушки L = 7•10-4
Гн, сопротивление резисторов R0 = 1,8 Ом,
R = 1,2 Ом, величина ЭДС источника ε = 50 В.
прошлых лет
Здесь собраны задачи с конденсаторами и ключами.
Задача 1.
В схеме, показанной на рисунке, при замкнутом ключе обе лампы светились, потребляя одинаковую мощность. После размыкания ключа лампа Л1 вспыхнула и перегорела, причем заряд конденсатора успел вырасти ровно в два раза по сравнению с его величиной при замкнутом ключе. Найдите заряд конденсатора, накопленный до размыкания ключа. Какая энергия выделилась в Л1 после размыкания ключа? Величину сопротивления ламп можно считать примерно постоянной. Сопротивление Л1 равно внутреннему сопротивлению источника, ЭДС батареи равна В, емкость конденсатора
мкФ.
К задаче 1
Решение. Так как обе лампы светились одинаково, при условии протекания через них одного и того же тока, то можно сделать вывод, что их сопротивления равны.
Тогда напряжение на источнике равно
И, так как конденсатор подключен параллельно, то на нем такое же напряжение. А, значит, заряд на нем равен
Так как заряд конденсатора вырос вдвое, то для нового состояния
Откуда понятно, что напряжение на конденсаторе выросло вдвое и равно
Заряд изменился на , энергия изменилась на
Работа источника
Закон сохранения энергии
Лампы одинаковы, соединены последовательно, следовательно, на них выделяется одинаковое количество тепла – по .
Ответ: ,
.
Задача 2.
В схеме, изображенной на рисунке, ключ долгое время находился в положении 1. Какое количество теплоты выделится в резисторе после перевода его в положение 2? В,
мкФ, внутренние сопротивления аккумуляторов одинаковы и в
раза меньше сопротивления резистора. Сопротивление проводов, а также индуктивность контура с конденсаторами пренебрежимо малы.
К задаче 2
Решение. За то время, что ключ находился в положении 1, левый конденсатор зарядился до напряжения , а правый до напряжения
. После переброса ключа во второе положение произойдет перезаряд конденсаторов. Напряжение на них одинаковое – они соединены параллельно – и емкости одинаковые, значит, и заряд один и тот же:
то есть
Но конденсаторы подключены к источнику , значит, после наступления установившегося режима на них будет напряжение
, и заряд
на каждом. Следовательно, общий заряд уменьшится на
. Это тот заряд, который протечет через источник, значит, работа источника равна
.
Закон сохранения энергии:
В цепь последовательно включены и
— внутреннее сопротивление источника. Так как через них течет один и тот же ток, то тепло, выделяемое на каждом, пропорционально его сопротивлению. То есть три части тепла выделится на
, а одна – на
. Одна часть – это
, три части —
.
Ответ: 2,7 мкДж
Задача 3.
В цепи, схема которой изображена на рисунке, в начальный момент времени конденсатор ёмкостью мкФ заряжен до напряжения
В, конденсаторы ёмкостью
и
не заряжены. Переключатель П в среднем положении. Переключатель П сначала перекидывают в положение 1 на короткое время (много меньшее
), а затем в положение 2 на гораздо большее время. Определите заряды конденсаторов после многократного повторения этих двух операций. Найдите приближённо, какое количество теплоты выделяется в каждом из резисторов.
К задаче 3
Решение. Когда ключ в положении 1, то конденсатор немного заряда передает среднему конденсатору, а затем ключ переводят в положение 2 и тогда средний, будучи подключен параллельно с правым, передает ему большую часть своего заряда. Напряжение одинаково, поэтому
Закон сохранения энергии:
Теперь разберемся, что будет при многократных переключениях. Пусть при каждом из них перетекает заряд . Возьмем состояние системы, когда на левом конденсаторе заряд
, а на центральном и правом —
и
соответственно. Тогда можно записать:
Первое слагаемое – энергия левого конденсатора, а второе – центрального.
После перетекания :
Разность этих энергий равна:
Пренебрегая малым , имеем:
Суммируем и получим выделившееся на первом резисторе:
На втором резисторе выделилось:
Ответ: ,
.