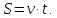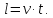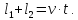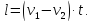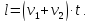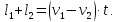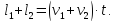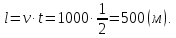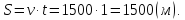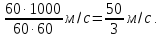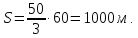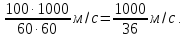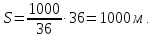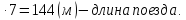Всего: 24 1–20 | 21–24
Добавить в вариант
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Из двух городов, расстояние между которыми 720 км, по параллельным путям отправляются навстречу друг другу два поезда и встречаются на середине пути. Второй поезд вышел на 1 ч позже первого со скоростью, на 4 км/ч большей, чем скорость первого поезда. Найдите скорость второго поезда. Ответ дайте в км/ч.
Источник: Пробный вариант ЕГЭ по математике 03.12.22 Москва.
По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Источник: Пробный экзамен по математике. Санкт-Петербург 2013. Вариант 1.
По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 70 км/ч и 50 км/ч. Длина пассажирского поезда равна 800 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 45 секундам. Ответ дайте в метрах.
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Длина товарного поезда равна 1200 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам. Ответ дайте в метрах.
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 900 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте 3 секундам. Ответ дайте в метрах.
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 50 км/ч и 40 км/ч. Длина товарного поезда равна 800 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 6 минутам. Ответ дайте в метрах.
Поезд Казань-Москва отправляется в 21:35, а прибывает в 10:35 на следующий день (время московское). Сколько часов поезд находится в пути?
Поезд Новосибирск-Красноярск отправляется в 15:20, а прибывает в 4:20 на следующий день (время московское). Сколько часов поезд находится в пути?
Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Товарный поезд каждую минуту проезжает на 300 метров меньше, чем скорый, и на путь в 420 км тратит времени на 3 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метров, за 39 секунд. Найдите длину поезда в метрах.
Товарный поезд каждую минуту проезжает на 450 метров меньше, чем скорый, и на путь в 630 км тратит времени на 3 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 560 км тратит времени на 4 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Поезд Самара-Волгоград отправляется в 7:58, а прибывает в 2:58 на следующий день (время московское). Сколько часов поезд находится в пути?
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 9 секунд. Найдите длину поезда в метрах.
Семья из трех человек едет из Москвы в Чебоксары. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 930 рублей. Автомобиль расходует 11 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 18,5 рублей за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?
Семья из трех человек едет из Санкт-Петербурга в Вологду. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 660 рублей. Автомобиль расходует 8 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 19,5 рублей за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?
Всего: 24 1–20 | 21–24
10 сентября 2021
В закладки
Обсудить
Жалоба
Задачи на движение протяжённых объектов
Текстовая задача ЕГЭ по математике (№8). По материалам открытого банка ФИПИ.
1. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
2. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
3. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
4. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
5. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Ответы
1. 800
2. 600
3. 6
4. 400
5. 300
Задачи на движение протяженных тел
Протяженными будем считать тела, длина которых соизмерима с расстоянием, которое они проезжают.
В задачах на движение протяженных тел обычно требуется определить длину одного из них. Наиболее типичные ситуации, предлагаемые в таких задачах, — определить длину поезда проезжающего мимо:
-
придорожного столба;
-
идущего параллельно путям пешехода;
-
лесополосы определенной длины;
-
другого двигающегося поезда.
Помним, что во всех задачах на движение используется только одна формула: это формула пути
Если поезд движется мимо столба, то он проходит расстояние равное его длине. Обозначим:
l – длина поезда,
v – скорость поезда,
Если поезд движется мимо протяженной лесополосы (платформы), то он проходит расстояние равное сумме длины самого поезда и лесополосы. Обозначим:
l1 – длина поезда,
l2 – длина лесополосы (платформы),
v – скорость поезда,
Если поезд движется мимо движущегося человека, то учитываем направление движения человека. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:
l – длина поезда,
v1 – скорость поезда,
v2 – скорость человека,
В одну сторону:
В разные стороны:
Если поезд движется мимо движущегося поезда, то учитываем направление движения второго поезда. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:
l1 – длина первого поезда,
l2 – длина второго поезда,
v1 – скорость первого поезда,
v2 – скорость второго поезда,
В одну сторону:
В разные стороны:
Рассмотрим несколько задач.
Задача 1. Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.
Решение:
v = 60 км/ч = 1000 м/мин, t = 30 сек. = 1/2 мин. Длину поезда находим как пройденное расстояние:
Ответ: 500 метров.
Задача 2. Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которой равна 800 метрам, за 1 минуту. Найти длину поезда в метрах.
Решение:
v = 90 км/ч = 1500 м/мин, t = 1 мин. Тогда пройденное поездом расстояние:
Это собственная длина поезда плюс длина лесополосы. Длина поезда равна: 1500 – 800 = 700 (м).
Ответ: 700 метров.
Задача 3. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Решение: Так как поезда двигаются в одном направлении, их относительная скорость равна:
v = 90 – 30 = 60 км/ч =
За 60 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:
Это длина пассажирского и товарного поездов. Тогда длина пассажирского поезда равна:
1000 – 600 = 400 (м).
Ответ: 400 метров.
Задача 4. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Решение: Так как поезда двигаются в противоположных направлениях, их относительная скорость равна:
v = 65 + 35 = 100 км/ч =
За 36 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:
Это расстояние, равное сумме длин обоих поездов. Значит, длина скорого поезда равна:
1000 – 700 = 300 (м).
Ответ: 300 метров.
Задача 5. Поезд проходит мимо неподвижного наблюдателя за 7 секунд, а мимо платформы длиной 378 метров – за 25 секунд. Найдите длину поезда.
Решение: Из первого условия следует, что за 7 секунд поезд проедет расстояние, равное собственной длине поезда. За 25 же секунд ему надо проехать собственно саму длину платформы, т.е. 378 метров и ещё надо «вытащить» головной вагон вперед на расстояние, равное длине поезда.
1) 25 – 7 = 18 (с) – время, за которое поезд проехал 378 м
2) 378 : 18 = 21 (м/с) – скорость поезда
3) 21
Ответ: 144 м.
Задача 6. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и скорый поезда. Скорый поезд, двигаясь со скоростью 120 км/ч, догнал пассажирский поезд и прошёл мимо него за 100 секунд. Найдите скорость пассажирского поезда, если его длина составляет 800 метров, а длина скорого поезда – 700 метров. Ответ дайте в км/ч.
Решение: Считаем, что пассажирский поезд неподвижен, а скорый приближается к нему со скоростью, равной разности скоростей поездов.
1) 700 + 800 = 1500 (м) – прошёл скорый поезд за 100 секунд
2) 1500 : 100 = 15 (м/с) – разность скоростей (скорость вдогонку)
15 м/с =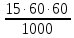
3) 120 – 54 = 66 (км/ч) – скорость пассажирского поезда.
Ответ: 66 км/ч.
Задача 7. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 110 метров, второй — длиной 90 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 1000 метров. Через 16 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 400 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение: Пока сухогрузы перейдут из первого положения во второе, второй сухогруз переместился относительно первого на
1000 + 110 + 90 + 400 = 1600 (м).
Пусть v — разность скоростей сухогрузов, тогда
v = 1600 : 16 = 100 м/мин = 6 км/ч.
Ответ: на 6 км/ч.
ЕГЭ Профиль №9. Задачи на движение по прямой
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Задачи на движение по прямой
|
Задача 1. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. Пусть x км/ч – скорость первого автомобиля, тогда скорость второго на второй половине пути равна x + 16 км/ч. Возьмём расстояние между пунктами за 2 S км.
Автомобили были в пути одно и то же время. Следовательно: (frac{S}{{24}} + frac{S}{{x + 16}} = frac{{2S}}{x},,left| {,:,S ne 0,,,,, Leftrightarrow ,,,,,} right.frac{1}{{24}} + frac{1}{{x + 16}} = frac{2}{x},,,, Leftrightarrow ,,,,,frac{{x + 16 + 24}}{{24left( {x + 16} right)}} = frac{2}{x},,,,, Leftrightarrow ) ( Leftrightarrow ,,,,xleft( {x + 40} right) = 48left( {x + 16} right),,,, Leftrightarrow ,,,,{x^2} — 8x — 768 = 0) (D = 64 + 3072 = 3136;,,,,,{x_1} = frac{{8 + 56}}{2} = 32;,,,,{x_2} = frac{{8 — 56}}{2} = — 24.) Так как (x > 0), то скорость первого автомобиля равна 32 км/ч. Ответ: 32. |
||||||||||||||||||||||||
| Задача 2. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Пусть x км/ч – скорость первого автомобиля, тогда скорость второго на первой половине пути равна x – 13 км/ч. Возьмём расстояние между пунктами за 2 S км.
Автомобили были в пути одно и то же время. Следовательно: (frac{S}{{x — 13}} + frac{S}{{78}} = frac{{2S}}{x},,left| {,:,S ne 0,,,,, Leftrightarrow ,,,,,} right.frac{1}{{x — 13}} + frac{1}{{78}} = frac{2}{x},,,, Leftrightarrow ,,,,,frac{{78 + x — 13}}{{78left( {x — 13} right)}} = frac{2}{x},,,,, Leftrightarrow ) ( Leftrightarrow ,,,,xleft( {x + 65} right) = 156left( {x — 13} right),,,, Leftrightarrow ,,,,{x^2} — 91x + 13 cdot 156 = 0) (D = {91^2} — 4 cdot 13 cdot 156 = {13^2} cdot {7^2} — 4 cdot {13^2} cdot 12 = {13^2}left( {49 — 48} right) = {13^2};,,,,,{x_1} = frac{{91 + 13}}{2} = 52;,,,,{x_2} = frac{{91 — 13}}{2} = 39.) Так как по условию задачи (x > 48), то скорость первого автомобиля равна 52 км/ч. Ответ: 52. |
||||||||||||||||||||||||
| Задача 3. Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Пусть x км/ч – скорость велосипедиста, тогда скорость автомобиля равна x + 40 км/ч.
Так как, велосипедист прибыл в пункт В на 6 часов позже автомобилиста, то его время на 6 часов больше. Следовательно: (frac{{75}}{x} — frac{{75}}{{x + 40}} = 6,,,,,, Leftrightarrow ,,,,,frac{{75left( {x + 40} right) — 75x}}{{xleft( {x + 40} right)}} = 6,,, Leftrightarrow ,,,,,frac{{75 cdot 40}}{{xleft( {x + 40} right)}} = 6,,,, Leftrightarrow ,,,,6xleft( {x + 40} right) = 75 cdot 40,,left| {,:6,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,{x^2} + 40x — 500 = 0;,,,,D = 1600 + 2000 = 3600;,,,,{x_1} = frac{{ — 40 + 60}}{2} = 10;,,,,{x_2} = frac{{ — 40 — 60}}{2} = — 50) Так как (x > 0), то скорость велосипедиста равна 10 км/ч. Ответ: 10. |
||||||||||||||||||||||||
| Задача 4. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 70 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Пусть x км/ч – скорость велосипедиста из В в А, тогда его скорость из А в В равна x – 3 км/ч.
Так как, на обратном пути велосипедист сделал остановку на 3 часа и в результате затратил столько же времени, то: (frac{{70}}{{x — 3}} — frac{{70}}{x} = 3,,,,,, Leftrightarrow ,,,,,frac{{70x — 70left( {x — 3} right)}}{{xleft( {x — 3} right)}} = 3,, Leftrightarrow ,,,,,frac{{70 cdot 3}}{{xleft( {x — 3} right)}} = 3,,,, Leftrightarrow ,,,,3xleft( {x — 3} right) = 70 cdot 3,,,, Leftrightarrow ) ( Leftrightarrow ,,,{x^2} — 3x — 70 = 0;,,,,D = 9 + 280 = 289;,,,,{x_1} = frac{{3 + 17}}{2} = 10;,,,,{x_2} = frac{{3 — 17}}{2} = — 7) Так как (x > 0), то скорость велосипедиста из В в А равна 10 км/ч. Ответ: 10. |
||||||||||||||||||||||||
| Задача 5. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Пусть x км/ч – скорость велосипедиста из А в В, тогда его скорость из В в А равна x + 7 км/ч.
Так как, на обратном пути велосипедист делал остановку на 7 часов и в результате затратил столько же времени, то: (frac{{98}}{x} — frac{{98}}{{x + 7}} = 7,,,,,, Leftrightarrow ,,,,,frac{{98left( {x + 7} right) — 98x}}{{xleft( {x + 7} right)}} = 7,, Leftrightarrow ,,,,,frac{{98 cdot 7}}{{xleft( {x + 7} right)}} = 7,,,, Leftrightarrow ,,,,7xleft( {x + 7} right) = 98 cdot 7,,, Leftrightarrow ) ( Leftrightarrow ,,,{x^2} + 7x — 98 = 0;,,,,D = 49 + 392 = 441;,,,,{x_1} = frac{{ — 7 + 21}}{2} = 7;,,,,{x_2} = frac{{ — 7 — 21}}{2} = — 14) Так как (x > 0), то скорость велосипедиста из А в В равна 7 км/ч. Ответ: 7. |
||||||||||||||||||||||||
|
Задача 6. Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч. Пусть x км/ч – скорость велосипедиста, пришедшего к финишу первым, тогда скорость второго велосипедиста x – 1 км/ч.
Так как первый велосипедист приехал на 1 час раньше второго, то его время на 1 час меньше. Следовательно: (frac{{240}}{{x — 1}} — frac{{240}}{x} = 1,,,,,, Leftrightarrow ,,,,,frac{{240x — 240left( {x — 1} right)}}{{xleft( {x — 1} right)}} = 1,,,,, Leftrightarrow ,,,,,frac{{240}}{{xleft( {x — 1} right)}} = 1,,,, Leftrightarrow ,,,,xleft( {x — 1} right) = 240,,, Leftrightarrow )( Leftrightarrow ,,,,,{x^2} — x — 240 = 0;,,,,,D = 1 + 4 cdot 240 = 961;,,,,,{x_1} = frac{{1 + 31}}{2} = 16;,,,,,{x_2} = frac{{1 — 31}}{2} = — 15.) Так как (x > 0), то скорость велосипедиста, пришедшего к финишу первым, равна 16 км/ч. Ответ: 16. |
||||||||||||||||||||||||
| Задача 7. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
Пусть t ч – время движения автомобилей до встречи. Тогда первый автомобиль пройдет расстояние – 65t км, а второй – 75t км. Следовательно: (65t + 75t = 560,,,, Leftrightarrow ,,,,140t = 560,,,, Leftrightarrow ,,,,t = 4). Таким образом, автомобили встретятся через 4 часа. Ответ: 4. |
||||||||||||||||||||||||
| Задача 8. Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
Так как автомобили встретились на расстоянии 180 км от города В, то автомобиль, выехавший из города А, проехал расстояние (330 — 180 = 150) км за 3 часа. Следовательно, его скорость равна: (V = frac{{150}}{3} = 50) км/ч. Ответ: 50. |
||||||||||||||||||||||||
| Задача 9. Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.
Пусть t ч – время движения до встречи автомобиля, выехавшего из города А, тогда время второго автомобиля t – 1 ч. За t часов первый автомобиль проехал расстояние 60t км, а второй за t – 1 ч проехал 65(t – 1), а вместе до встречи они проехали 435 км. Следовательно: (60t + 65left( {t — 1} right) = 435,,,,, Leftrightarrow ,,,,,60t + 65t — 65 = 435,,,,, Leftrightarrow ,,,,125,t = 500,,,,, Leftrightarrow ,,,,,t = 4.) Следовательно, первый проехал расстояние (60 cdot 4 = 240) км, и оно равно расстоянию от города А до встречи автомобилей. |
||||||||||||||||||||||||
| Задача 10. Расстояние между городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города A. Ответ дайте в км/ч.
Автомобиль, выехавший из города В со скоростью 60 км/ч, проехал расстояние (470 — 350 = 120) км. Следовательно, он затратил на этот путь время равное: (frac{{120}}{{60}} = 2) часа. Тогда автомобиль, выехавший из города А, затратил на расстояние равное 350 км время равное: (2 + 3 = 5) часов. Поэтому его скорость равна: (frac{{350}}{5} = 70) км/ч. Ответ: 70. |
||||||||||||||||||||||||
| Задача 11. Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Пусть время движения велосипедиста из В в А равно x ч, тогда время движения мотоциклиста из А в В равно x – 3 ч, при этом (x — 3 > 0), то есть (x > 3). Обозначим расстояние между городами за S км. Тогда скорость велосипедиста равна: (frac{S}{x}), а скорость мотоциклиста (frac{S}{{x — 3}}). За время 48 минут ((frac{{48}}{{60}} = frac{4}{5}) ч) велосипедист проехал расстояние: (frac{4}{5} cdot frac{S}{x}) км, а мотоциклист: (frac{4}{5} cdot frac{S}{{x — 3}}) км, а вместе они преодолели расстояние равное S км. Следовательно: (frac{4}{5} cdot frac{S}{x} + frac{4}{5} cdot frac{S}{{x — 3}} = S,,left| : right.,,S ne 0,,,,, Leftrightarrow ,,,,,frac{4}{{5x}} + frac{4}{{5left( {x — 3} right)}} = 1,,,,, Leftrightarrow ,,,,,frac{{4left( {x — 3} right) + 4x}}{{5xleft( {x — 3} right)}} = 1,,,, Leftrightarrow ) ( Leftrightarrow ,,,,5{x^2} — 15x = 8x — 12,,,, Leftrightarrow ,,,,5{x^2} — 23x + 12 = 0;) (D = 529 — 240 = 289;,,,,{x_1} = frac{{23 + 17}}{{10}} = 4;,,,,{x_2} = frac{{23 — 17}}{{10}} = frac{3}{5}.) Так как (x > 3), то время велосипедиста их В в А равно 4 часа. Ответ: 4. |
||||||||||||||||||||||||
| Задача 12. Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Пусть x км/ч – скорость товарного поезда, тогда скорость скорого x км/ч +750 м/мин = (x + frac{{750}}{{1000}} cdot 60 = x + 45) км/ч.
По условию задачи время товарного поезда на 2 часа больше. Следовательно: (frac{{180}}{x} — frac{{180}}{{x + 45}} = 2,,,,,, Leftrightarrow ,,,,,frac{{180left( {x + 45} right) — 180x}}{{xleft( {x + 45} right)}} = 2,, Leftrightarrow ,,,,,frac{{180 cdot 45}}{{xleft( {x + 45} right)}} = 2,,,, Leftrightarrow ) ( Leftrightarrow ,,,,2xleft( {x + 45} right) = 180 cdot 45,left| {,:} right.2,,,, Leftrightarrow ,,,,{x^2} + 45 — 90 cdot 45 = 0) (D = {45^2} + 4 cdot 90 cdot 45 = {45^2}left( {1 + 4 cdot 2} right) = {45^2} cdot 9;,,,,,,sqrt D = ,,45 cdot 3 = 135;) (,,,{x_1} = frac{{ — 45 + 135}}{2} = 45;,,,,{x_2} = frac{{ — 45 — 135}}{2} = — 90.) Так как (x > 0), то скорость товарного поезда равна 45 км/ч. Ответ: 45. |
||||||||||||||||||||||||
| Задача 13. Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Пусть x км – расстояние от А до С, а y км/ч – скорость автомобиля. Рассмотрим сначала движение автомобиля и мотоцикла от А до С.
Так как автомобиль выехал на 30 мин раньше, то его время на (frac{1}{2}) часа больше. Тогда первое уравнение будет иметь вид: (frac{x}{y} — frac{x}{{90}} = frac{1}{2}.) Теперь рассмотрим случай движения автомобиля из С в В, а мотоциклиста из С в А.
Так как мотоциклист вернулся в А одновременно с автомобилистом, приехавшим в В, то второе уравнение будет иметь вид: (frac{{150 — x}}{y} = frac{x}{{90}}.) Таким образом, получаем систему уравнений: (left{ {begin{array}{*{20}{c}} {frac{x}{y} — frac{x}{{90}} = frac{1}{2};} \ {frac{{150 — x}}{y} = frac{x}{{90}}.} end{array}} right.) Из второго уравнения: (y = frac{{90left( {150 — x} right)}}{x}) подставляя в первое уравнение, получим: (frac{{{x^2}}}{{90left( {150 — x} right)}} — frac{x}{{90}} = frac{1}{2},,,,,, Leftrightarrow ,,,,,,frac{{{x^2} — xleft( {150 — x} right)}}{{90left( {150 — x} right)}} = frac{1}{2},,,,,, Leftrightarrow ,,,,,,frac{{2{x^2} — 150x}}{{90left( {150 — x} right)}} = frac{1}{2},,,,,, Leftrightarrow ) ( Leftrightarrow ,,,,4{x^2} — 300x = 90 cdot 150 — 90x,,left| {,:,2,,,,, Leftrightarrow ,,,,2{x^2} — 105x — 6750 = 0} right.;) (D = {105^2} + 4 cdot 2 cdot 6750 = {15^2} cdot {7^2} + 4 cdot 2 cdot {15^2} cdot 30 = {15^2}left( {49 + 240} right) = {15^2} cdot 289;,,,) (sqrt D = 15 cdot 17 = 255;,,,,,{x_1} = frac{{105 + 255}}{4} = 90;,,,,,{x_2} = frac{{105 — 255}}{4} = — 37,5.) Так как (x > 0), то расстояние от А до С равно 90 км. Ответ: 90. |
| Задача 14. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Пусть x км/ч – скорость второго пешехода, тогда x + 1,5 км/ч – скорость первого, а в пути они были t ч.
Так как расстояние между пешеходами должно стать равно 300 м = 0,3 км, то первый должен пройти на 0,3 км больше. Следовательно: (left( {x + 1,5} right)t — x,t = 0,3,,,,,, Leftrightarrow ,,,,,x,t + 1,5,t — x,t = 0,3,, Leftrightarrow ,,,,,1,5t = 0,3,,,, Leftrightarrow ,,,,t = frac{1}{5},.,,) Следовательно, через (frac{1}{5}) часа или (frac{1}{5} cdot 60 = 12) минут расстояние между пешеходами будет ровно 300 м. Ответ: 12. Второй вариант решения: Так как скорость первого пешехода на 1,5 км/ч больше скорости второго, то через 1 час (60 минут) расстояние между пешеходами будет равно 1,5 км (1500 м). Следовательно, чтобы расстояние между пешеходами стало равно 300 м (это в 5 раз меньше чем 1500 м) понадобиться 12 минут (это в 5 раз меньше чем 60 минут). Ответ: 12. |
||||||||||||
| Задача 15. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, которое ему понадобилось, чтобы догнать второго велосипедиста. Тогда за время t ч третий проехал расстояние равное (x cdot t) км, а второй выехал на 1 час раньше третьего, поэтому он проехал расстояние (10left( {t + 1} right)) км. Следовательно, первое уравнение будет иметь вид: (x cdot t = 10left( {t + 1} right)). Теперь рассмотрим, как третий велосипедист догоняет первого. Третьему велосипедисту понадобилось t ч, чтобы догнать второго, а затем еще 2 часа 20 минут, чтобы догнать первого, то есть третий догонял первого (t + frac{7}{3}) часа и проехал расстояние: (x cdot left( {t + frac{7}{3}} right)). Первый выехал на 2 часа раньше третьего, поэтому он проехал расстояние равное: (15 cdot left( {t + frac{7}{3} + 2} right)). Следовательно, второе уравнение будет иметь вид: (xleft( {t + frac{7}{3}} right) = 15left( {t + frac{{13}}{3}} right)). Таким образом, получаем систему уравнений: (left{ {begin{array}{*{20}{c}} {x cdot t = 10left( {t + 1} right);,,,,,,,,,,,,,,,,,,,,} \ {x cdot left( {t + frac{7}{3}} right) = 15left( {t + frac{{13}}{3}} right).} end{array}} right.) Из первого уравнения: (x = frac{{10left( {t + 1} right)}}{t}). Подставляя во второе первое, получим: (frac{{10t + 10}}{t} cdot frac{{3t + 7}}{3} = 15t + 65,,,, Leftrightarrow ,,,,30{t^2} + 70t + 30t + 70 = 45{t^2} + 195t,,,, Leftrightarrow ) ( Leftrightarrow ,,,,15{t^2} + 95t — 70 = 0,,left| {,:} right.5,,,, Leftrightarrow ,,,,3{t^2} + 19t — 14 = 0;) (D = 361 + 168 = 529;,,,,{t_1}, = frac{{ — 19 + 23}}{6} = frac{2}{3};,,,,{t_2} = frac{{ — 19 — 23}}{6} = — 7) Так как, (t > 0), то (t = frac{2}{3}) часа. Следовательно, скорость третьего велосипедиста: (x = frac{{10 cdot left( {frac{2}{3} + 1} right)}}{{frac{2}{3}}} = 25) км/ч. ()Ответ: 25. |
||||||||||||
| Задача 16. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Пусть автомобиль находился в пути 2t часов. Тогда за первую половину времени (то есть за t часов) он проехал расстояние равное 74t км, а за вторую половину 66t км. Тогда средняя скорость автомобиля будет равна: (V = frac{{74t + 66t}}{{2t}} = frac{{140t}}{{2t}} = 70) км/ч. Ответ: 70. |
||||||||||||
| Задача 17. Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Пусть путешественник проплыл расстояние на яхте равное S км, тогда его время на яхте составило ({t_1} = frac{S}{{20}}) ч, а на самолете ({t_2} = frac{S}{{480}}) ч. Тогда средняя скорость будет равна: (v = frac{{S + S}}{{{t_1} + {t_2}}} = frac{{2S}}{{frac{S}{{20}} + frac{S}{{480}}}} = frac{{2S}}{{frac{{24S + S}}{{480}}}} = frac{{2S cdot 480}}{{25,S}} = 38,4) км/ч. Ответ: 38,4. |
||||||||||||
| Задача 18. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Пусть 3S км – весь путь автомобиля, тогда его время на первом участке ({t_1} = frac{S}{{60}}), на втором ({t_2} = frac{S}{{120}}), а на третьем ({t_3} = frac{S}{{110}}). Тогда средняя скорость будет равна: (V = frac{{S + S + S}}{{{t_1} + {t_2} + {t_3}}} = frac{{3S}}{{frac{S}{{60}} + frac{S}{{120}} + frac{S}{{110}}}} = frac{{3S}}{{frac{{2S + S}}{{120}} + frac{S}{{110}}}} = frac{{3S}}{{frac{S}{{40}} + frac{S}{{110}}}} = frac{{3S}}{{frac{{11S + 4S}}{{440}}}} = frac{{3S cdot 440}}{{15S}} = 88) км/ч. Ответ: 88. |
||||||||||||
| Задача 19. Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Автомобиль был в пути время равное (2 + 1 + 2 = 5) часов и проехал за это время расстояние равное (2 cdot 50 + 1 cdot 100 + 2 cdot 75 = 350) км. Тогда его средняя скорость: (V = frac{{350}}{5} = 70) км/ч. Ответ: 70. |
||||||||||||
| Задача 20. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Чтобы найти среднюю скорость на протяжении пути, нужно весь пройденный путь разделить на все время движения. Первые 190 км автомобиль проехал за время ({t_1} = frac{{190}}{{50}} = frac{{19}}{5}) часа, следующие 180 км за ({t_2} = frac{{180}}{{90}} = 2) часа, а последние 170 км за ({t_3} = frac{{170}}{{100}} = frac{{17}}{{10}}) часа. Таким образом, он проехал расстояние равное (190 + 180 + 170 = 540) км за время ({t_{}} = frac{{19}}{5} + 2 + frac{{17}}{{10}} = frac{{15}}{2}) часа. Следовательно, его средняя скорость равна: (V = frac{{540}}{{frac{{15}}{2}}} = 72) км/ч. Ответ: 72. |
||||||||||||
| Задача 21. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Проезжая мимо столба, поезд проезжает расстояние равное своей длине, то есть длина поезда равна расстоянию, которое проехал поезд. (t = 36) с ( = frac{{36}}{{3600}}) ч ( = frac{1}{{100}}) ч. (S = V cdot t = 80 cdot frac{1}{{100}} = 0,8) км. Следовательно, длина поезда равна 0,8 км = 800 м. Ответ: 800. |
||||||||||||
| Задача 22. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
Проезжая мимо лесополосы, поезд проезжает расстояние равное сумме длин лесополосы и самого поезда, то есть длина поезда равна расстоянию, которое проехал поезд минус длина лесополосы. (t = 1) мин ( = frac{1}{{60}}) ч. (S = V cdot t = 60 cdot frac{1}{{60}} = 1) км. Следовательно, поезд проехал расстояние равное 1000 м, тогда длина поезда (1000 — 400 = 600) м. Ответ: 600. |
||||||||||||
| Задача 23. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Так как поезда едут в одном направлении, то их скорость сближения равна (V = 90 — 30 = 60) км/ч. Следовательно, за 1 минуту пассажирский поезд сместится относительно товарного на 1 км. При этом он преодолеет расстояние равное сумме длин поездов. Поэтому длина пассажирского поезда равна (1000 — 600 = 400) м. Ответ: 400. |
||||||||||||
| Задача 24. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Так как поезда едут навстречу друг другу, то их скорость сближения равна (V = 65 + 35 = 100) км/ч. За 36 секунд скорый поезд сместится относительно пассажирского на расстояние: (S = 100 cdot frac{{36}}{{3600}} = 1) км. При этом он преодолел расстояние равное сумме длин поездов. Поэтому длина скорого поезда равна (1000 — 700 = 300)м. Ответ: 300. |
||||||||||||
| Задача 25. Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 4,4 км от места отправления. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
Пусть x км – расстояние, которое не дошел до опушки первый человек, оно равно расстоянию, которое прошел от опушки до места встречи второй человек. Следовательно, первый прошел расстояние равное (4,4 — x) км, а второй (4,4 + x).
Путники затратили одно и тоже время: (frac{{4,4 — x}}{{2,5}} = frac{{4,4 + x}}{3},,,,,, Leftrightarrow ,,,,,4,4 cdot 3 — 3x = 2,5 cdot 4,4 + 2,5x,, Leftrightarrow ,,,,,5,5x = 4,4 cdot 3 — 2,5 cdot 4,4,,,, Leftrightarrow ,,,)( Leftrightarrow ,,,,5,5x = 4,4left( {3 — 2,5} right),,,, Leftrightarrow ,,,,5,5 = 4,4 cdot 0,5,,,, Leftrightarrow ,,,,x = frac{{4,4 cdot 0,5}}{{5,5}} = 0,4). Следовательно, встреча произойдет от точки отправления на расстоянии (4,4 — 0,4 = 4) км. Ответ: 4. |
||||||||||||
| Задача 26. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Турист прошёл путь из А в В за 5 часов. Время его движения на спуске составило 1 час. С какой скоростью турист шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 3 км/ч?
Пусть x км/ч – скорость туриста на спуске, тогда скорость на подъёме (x — 3) км/ч. Время на подъёме: (5 — 1 = 4) часа.
Так как весь путь равен 8 км, то: (4left( {x — 3} right), + x = 8,,,,, Leftrightarrow ,,,,,5x = 20,,,,, Leftrightarrow ,,,,,x = 4) км/ч. Ответ: 4. |
||||||||||||
| Задача 27. Иван и Алексей договорились встретиться в N-ске. Иван звонит Алексею и узнаёт, что тот находится в 275 км от N-ска и едет с постоянной скоростью 75 км/ч. Иван в момент разговора находится в 255 км от N-ска и ещё должен по дороге сделать 50-минутную остановку. С какой скоростью должен ехать Иван, чтобы прибыть в N-ск одновременно с Алексеем?
Пусть x км/ч – скорость Ивана.
Поскольку Иван должен сделать 50 – минутную остановку, то его время движения будет на (frac{5}{6}) часа меньше. (frac{{275}}{{75}} — frac{{255}}{x} = frac{5}{6},,,,,,, Leftrightarrow ,,,,,,frac{{255}}{x} = frac{{11}}{3} — frac{5}{6},,,,,, Leftrightarrow ,,,,,,,frac{{255}}{x},, = frac{{17}}{6},,,,,,, Leftrightarrow ,,,,,,,x = frac{{255 cdot 6}}{{17}} = 90,) км/ч. Ответ: 90. |
Предлагаю вашему вниманию задания на прямолинейное движение. Это задачки, в которых в качестве движущихся объектов рассматриваются поезда. Всё просто! Решаются путём простых логических рассуждений, без таблиц и составления уравнений. Нюансы, конечно же, имеются.
На блоге уже опубликованы материалы с задачами на прямолинейное движение, обязательно посмотрите их. Это «Задачи на прямолинейное движение. Часть 1» и «Задачи на прямолинейное движение. Часть 2» Напомню закон прямолинейного равномерного движения, формула известная, но всё таки:
Что хочу отметить особо!
1. Не забывайте переводить единицы измерения. Если речь в условии идёт о километрах и часах, то метры переводите в километры, секунды переводите в часы и только после этого производите действия.
2. Обратите внимание в каких единицах измерения требуется записать ответ. Если вы в ответе запишите результат в километрах, а в условии требуется записать в метрах, то ответ будет неверным.
3. Обязательно делайте эскиз, попробуйте (если возможно) мысленно представить процесс движения, это очень помогает при решении.
Рассмотри задачи:
99608. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Из условия понятно, что за 36 секунд поезд проезжает расстояние равное своей длине. Наглядно перемещение поезда изобразим на эскизе:
Нам известны время и скорость. По закону равномерного прямолинейного движения расстояние равно их произведению.
*Не забываем перевести секунды в часы.
Тридцать шесть секунд это одна сотая часа (в часе 3600 секунд). В данном случае это определяется легко, так как числа «красивые». Если в аналогичной задаче будет дано другое время, то переводите с помощью пропорции, подробно это описано здесь.
Таким образом, за 36 секунд поезд со скоростью 80 км/ч пройдёт
0,01∙80 = 0,8 км.
То есть 800 метров.
Ответ: 800
99609. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
Давайте представим мысленно процесс проезда поезда мимо лесополосы: вы находитесь в кабине локомотива, подъезжаете к лесу, проезжаете его (это 400 метров) и далее, чтобы поезд совсем проехал лес, его последний вагон должен сравняться с концом лесополосы, то есть поезд ещё проезжает расстояние равное своей длине. Для наглядности построим эскиз:
Сказано, что поезд проезжает мимо леса за 1 минуту. В данном случае без вычислений можно определить, что за 1 минуту со скоростью 60 км/ч поезд преодолеет 1 километр (по одному км в минуту), то есть 1000 метров.
Таким образом, можем вычислить длину поезда 1000 – 400 = 600 метров.
Ответ: 600
Теперь интереснее!
99612. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Данная задача немного сложнее, но с другой стороны абсолютна схожа с предыдущей. Два движущихся поезда могут ввести в замешательство. Как решать? Какое уравнение составлять? С чего начинать? Относительно чего они движутся? А задача на самом деле в два действия, или даже в одно.
С чего начнём? Небольшое отступление. Представьте что вы едите на автомобиле со определённой скоростью и рядом с вами едет ещё один автомобиль с точно такой же скоростью. Вопрос – какова скорость автомобилей относительно друг друга? Конечно, ноль километров в час (автомобили едут рядом не обгоняя друг друга).
Теперь представьте, что один едет со скоростью 80 км/ч, а другой 100 км/ч в том же направлении. Какова относительная скорость автомобилей? Правильно! Второй обгонит первый со скоростью 20 км/ч (то есть второй относительно первого едет со скоростью 20 км/ч). Если автомобили едут на встречу друг другу, то ситуации аналогичная, только относительная скорость будет равна сумме их скоростей.
Вернёмся к задаче. Данное условие представим следующим образом.
Пассажирский поезд стоит на месте, а на встречу ему следует скорый со скоростью 100 км в час.
*Это относительная скорость, с которой поезда проезжают друг мимо друга
65 + 35 = 100 км/ч
Теперь задача стала похожей на предыдущую. Построим эскиз:
Скорый проезжает расстояние равное длине пассажирского (700 м) плюс расстояние равное своей длине.
Определим какое расстояние за 36 секунд проходит скорый со скоростью 100 км в час. 36 секунд это одна сотая часа. Таким образом, за 36 секунд поезд со скоростью 100 км/ч пройдёт 0,01∙100 = 1 км.
Можно вычислять через пропорцию:
100 км – 3600 сек
х км – 36 сек
Таким образом, длина скорого поезда будет равна 1000 – 700 = 300 метров.
Ответ: 300
99611. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 50 км/ч и 30 км/ч. Длина товарного поезда равна 1000 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 4 минутам 3 секундам. Ответ дайте в метрах.
Пассажирский (скорость 50 км/ч) следует в одном направлении с товарным (скорость 30 км/ч) и обгоняет его. Так как они следуют в одном направлении, получается, что пассажирский относительно товарного проезжает мимо него со скоростью 20 км/ч. То есть это тоже самое, как если бы товарный стоял на месте, а пассажирский проехал мимо него со скоростью 20 км/ч.
При решении подобных задач лучше условие интерпретировать именно так, суть задачи не изменится. Итак, имеем: скорость товарного 0 км/ч, пассажирского 20 км/ч (это относительная скорость).
Переведём минуты в часы: 4 минуты 3 секунды это 243 секунды. В часе 3600 секунд. Поэтому 4 минуты 3 секунды равно
За 243/3600 часа пассажирский поезд со скоростью 20 км/ч пройдёт
Сделаем эскиз:
Таким образом длина пассажирского поезда будет равна:
1,35 – 1 = 0,35 километра, это 350 метров
Ответ: 350
*Повторюсь: если в задаче будет сказано, что транспортные средства двигаются навстречу друг другу, то тогда приняв за ноль скорость одного из них, скорость другого (относительная скорость) будет равна сумме скоростей.
Например, составы движутся навстречу друг другу со скоростями 120 и 150 км/ч, понятно, что один относительно другого будет передвигаться со скоростью 270 км/ч.
Решите самостоятельно:
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Посмотреть решение
Такие вот дела! На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Поезд, двигаясь равномерно со скоростью 26 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4 км/ч навстречу поезду, за 90 секунд. Найдите длину поезда в метрах.
Решение:
1. 26+4=30(км/ч) — скорость сближения поезда и пешехода, так как они движутся в разных направлениях.
2. 90/3600=1/40(ч) — время, за которое поезд проезжает мимо пешехода.
3. 30/40=0,75(км) — длина поезда в километрах.
4. 0,75·1000=750(м) — длина поезда в метрах.
Ответ: длина поезда 750 метров.
Поезд, двигаясь равномерно со скоростью 62 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 2 км/ч, за 33 секунды. Найдите длину поезда в метрах.
Решение:
1. 62-2=60(км/ч) — скорость сближения, так как пешеход и поезд движутся в одном направлении.
2. 33/3600=11/1200(ч) — время, за которое поезд проезжает мимо пешехода.
3. 60·11/1200=11/20(км) — длина поезда в километрах.
4. 11/20·1000=50·11=550(м) — длина поезда в метрах
Ответ: длина поезда 550 метров.
Задачи для самостоятельного решения:
1. Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 8 секунд. Найдите длину поезда в метрах.
2. Поезд, двигаясь равномерно со скоростью 36 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 4км/ч навстречу поезду, за 54 секунды. Найдите длину поезда в метрах.