Задачи на движение егэ профильный уровень презентация

Слайд 1

Решение текстовых задач на движение (подготовка к ОГЭ и ЕГЭ) Подготовили Никитина Ирина Александровна Алышова Наталья Сергеевна

Слайд 2

Текстовые задачи являются традиционным разделом на вступительных экзаменах. Как правило, основная трудность при решении текстовой задачи состоит в переводе её условий на математический язык уравнений. Общего способа такого перевода не существует. Однако многие задачи на вступительных экзаменах, достаточно типичны.

Слайд 3

Цель урока: Закрепление умений решения задач различными способами (с помощью уравнений и по действиям) ; знакомство с другими способами решения текстовых задач (подбор, полный перебор, метод предположения) ; привитие аккуратности, математической грамотности.

Слайд 4

Основные цели решения текстовых задач в школьном курсе математики: научить переводить реальные предметные ситуации в различные математические модели, обеспечить действенное усвоение учащимися основных методов и приемов решения учебных математических задач.

Слайд 5

Этапы решения текстовых задач: Анализ содержания задачи. Поиск пути решения задачи и составление плана ее решения. Осуществление плана решения задачи. Проверка решения задачи.

Слайд 6

Стандартная схема решения таких задач включает в себя: 1.Выбор и обозначение неизвестных. 2.Составление уравнений (возможно неравенств) с использованием неизвестных и всех условий задачи. 3.Решение полученных уравнений (неравенств). 4.Отбор решений по смыслу задачи.

Слайд 7

Основными типами задач на движение являются : задачи на движение по прямой (навстречу и вдогонку); задачи на движение по замкнутой трассе; задачи на движение по воде; задачи на среднюю скорость; задачи на движение протяжённых тел.

Слайд 8

Задачи на движение. При решении этих задач принимают следующие допущения: Если нет специальных оговорок, то движение считают равномерным. Скорость считается величиной положительной. Всякие переходы на новый режим движения, на новое направление движения считают происходящим мгновенно. Если тело с собственной скоростью х движется по реке, скорость течения которой равна у , то скорость движения тела по течению считается равной ( х + у ), а против течения – равной ( х – у ).

Слайд 9

Задачи на движение: В задачах на движение используются обычно формулы, выражающие законы равномерного движения: S=V·t , где S- пройденное растояние, V- cкорость равномерного движения, t — время движения. При составлении уравнений в таких задачах часто бывает удобно прибегнуть к геометрической иллюстрации процесса движения: путь изображается в виде отрезка прямой, место встречи движущихся с разных сторон обьектов точкой на отрезке и т.д. Часто для усложнения задачи её условие формулируется в различных единицах измерения(метры, километры, часы, минуты и т.д.). В этом случае при выписывании уравнений необходимо пересчитывать все данные задачи в одинаковых единицах измерения:

Слайд 10

Задачи на движение: Движение на встречу: Движение вдогонку: Движение по окружности (замкнутой трассе): Средняя скорость:

Слайд 11

Задачи на движение Встречное движение v 1 v 2 t 1 t 2 s 1 t встр s 2 s t 1 =t 2 =t встр. V сбл = v 1 +v 2 s=v сбл * t сближ Обьекты, начавшие двигаться навстречу друг другу одновременно, движутся до момента встречи одинаковое время .

Слайд 12

1. Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист? 1 1 у х S, часть Велосипедист Мотоциклист v , часть/ч t, ч 1 у 1 х на весь путь Если в задаче не дано расстояние, очень удобно считать весь путь, как 1 целая часть.  На 3 часа > x – у = 3 1 у 1 х + навстречу v 48 60 встречи t S 1 1 у 1 х + = 1 4 5 1 часть часть/ч 1 у 1 х часть/ч 4 5 ч Ответ: 4 ч

Слайд 13

Движение в одном направлении v 1 v 2 t 1 t 2 s s 2 s 1 v сближ = v 1 -v 2 ,. s=s 1 -s 2 , s=v сбл * t встр

Слайд 14

10 км/ч 2. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч. 2 x 3 15 км/ч Удобно показать на схеме тот момент, когда 1-й вел. был в пути уже 2 ч, а 2-й вел. один час.  t 3 0 км 1 0 км 3 1 2  t х – 10 3 й и 2 й v, вдогонку S , км t, ч 3 й и 1 й х – 15 t 3 1 2  t 3 1 2  ( t ) ( х – 15 ) (х – 10) t = 10 = 30 С системой придется потрудиться. При выборе ответа учтем, что скорость 3-го велосипедиста должна быть больше 15. Ответ: 25. 1 2 1 3 Отметим на схеме примерное место встречи 2 го и 3 го И примерное место встречи 1 го и 3 го  t 3 1 2  t

Слайд 15

Движение в противоположных направлениях В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки: а) одновременно; б) в разное время. А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время. Общим теоретическим положением для них будет следующее: v удал. = v 1+ v 2 , где v 1 и v 2 соответственно скорости первого и второго тел. (Схематический чертеж строится аналогично предыдущим).

Слайд 16

3 . Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 72 км. На следующий день он отправился обратно со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч. Путь В-А х Путь А-В v, км/ч t , ч S, км 72 х 72 х+6 72 = х+6 Решите уравнение самостоятельно и найдите ответ на вопрос задачи. Чтобы найти время надо расстояние разделить на скорость t =  S v 72 Остановка 6 72 х+6 + 6 = 72 х А В 72 км 6ч Это условие поможет ввести х … 6 км/ч

Слайд 17

Движение по воде При движении по течению реки скорость объекта складывается из его скорости в стоячей воде и скорости течения реки. При движении против течения реки, скорость объекта равна разности скорости объекта в стоячей воде и скорости течения реки. Движущийся плот всегда имеет скорость течения реки.

Слайд 18

4. Теплоход проходит по течению реки до пункта назначения 560 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 56 часов после отплытия из него. Ответ дайте в км/ч. х – 4 По. теч. Пр. теч. 560 Пусть v соб. = x х+4 v, км/ч 560 S , км справка Это условие поможет ввести х … Чтобы найти время надо расстояние разделить на скорость  t = S v 560 х+4 t, ч справка 560 х–4 56ч Реши уравнение самостоятельно Стоянка 8 + + = 560 х+4 560 х–4 8 56 Чтобы найти скорость по течению надо к собственной скорости прибавить скорость течения  Стоянка длилась 8 ч – это время также надо учесть  Чтобы найти скорость против течения надо из собственной скорости отнять скорость течения  Ответ: 24

Слайд 19

движение по замкнутой трассе Е сли два велосипедиста одновременно начинают движение по окружности в одну сторону со скоростями v 1 и v 2 соответственно (v 1 > v 2 соответственно), то 1-й велосипедист приближается ко 2 со скоростью v 1 – v 2 . В момент, когда 1-й велосипедист в первый раз догоняет 2-го , он проходит расстояние на один круг больше. Продолжить Показать В момент, когда 1-й велосипедист в о второй раз догоняет 2-го , он проходит расстояние на два круг а больше и т.д .

Слайд 20

1 2 5. Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг? 1 красный 2 зеленый 60 80 v, км/ч на 15 км меньше (1 кру г) Уравнение: Ответ: 45 х получим в часах. Не забудь перевести в минуты. t , ч х х S, км 60х 80х Показать

Слайд 21

Движение протяжённых тел. В задачах на движение протяженных тел требуется, как правило, определить длину одного из них. Наиболее типичная ситуация: определение длины поезда, проезжающего мимо столба или протяженной платформы. В первом случае поезд проходит мимо столба расстояние, равное длине поезда, во втором случае — расстояние, равное сумме длин поезда и платформы. При решении задач на движение двух тел часто очень удобно считать одно тело неподвижным, а другое — приближающимся к нему со скоростью, равной сумме скоростей этих тел (при движении навстречу) или разности скоростей (при движении вдогонку). Такая модель помогает разобраться с условием задачи.

Слайд 22

2 6. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго? Р ешение. Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью v (м/мин) , равной разности скоростей второго и первого сухогрузов. Тогда за 12 минут второй сухогруз проходит расстояние 120 м 400 м 600 м 80 м 1200 м t S v  * 60 : 100 0 + + + 1

Слайд 23

Чтобы определить среднюю скорость при неравномерном движении, надо весь пройденный путь разделить на все время движения:

Слайд 25

7. Автомобиль двигался 3,2ч по шоссе со скоростью 90км/ч, затем 1,5ч по грунтовой дороге со скоростью 45км/ч, наконец, 0,3ч по проселочной дороге со скоростью 30км/ч. Какова средняя скорость движения автомобиля на всем пути? Средняя скорость движения определяется по формуле:

Слайд 26

3. Определим все время движения : 2. Определим весь путь: . 90 3,2 = 288 (км) (км) 67,5 45 1,5 = . 288 + 67,5 + 9 = (км) 9 30 = 0,3 . 3,2 + 1,5 + 0,3 = 1. Определим длину каждого участка пути: 364,5 (км) 5 (ч) 4. Найдем среднюю скорость движения: 364,5 : 5 = 72,9 (км/ч)

Слайд 27

Примеры задач на движение из открытого банка заданий ЕГЭ: 1 . Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. 2. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 70 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. 3. Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым.

Слайд 28

4. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. 5. Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 30 минут, лодка отправилась назад и вернулась в пункт А в 18:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч. 6. Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. 7. От пристани А к пристани В, расстояние между которыми равно 110 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью на 1 км/ч большей, отправился второй. Найдите скорость второго теплохода, если в пункт В он прибыл одновременно с первым.

Слайд 29

8. Пристани А и В расположены на озере, расстояние между ними равно 390 км. Баржа отправилась с постоянной скоростью из А в В . На следующий день она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из А в В . Найдите скорость баржи на пути из А в В. 9. Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч? 10. Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. 11. Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся?

Слайд 30

12. Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. 13. Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. 14. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого? 15. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.

Слайд 31

16. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. 17. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой? 18. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. 19. Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч. 20. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Слайд 32

21. Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час — со скоростью 100 км/ч, а затем два часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. 22. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. 23. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах. 24. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.

Слайд 33

Литература 1.Ф. Ф. Лысенко, С. Ю. Кулабухова Математика Повторение курса в формате ЕГЭ Рабочая программа 11 класс Ростов-на-Дону: Легион 2. Д. А. Мальцев, А.А. Мальцев, Л.И. Мальцева Математика. Всё для ЕГЭ 2011. Часть I , Ростов-на-Дону: Мальцев Д.А., М.:НИИ школьных технологий, 2010 3.ЕГЭ 2010. Математика. Типовые тестовые задания. Под ред. СеменоваА.Л., Ященко И.В. М.: Экзамен, 2010 — 96 с. 4.ЕГЭ. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ. Лаппо Л.Д., Попов М.А. М.: Экзамен, 2010 — 62 с 5.Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010. Математика. Высоцкий И.Р, Гущин Д.Д, Захаров П.И. и др. М.: АСТ, Астрель, 2010 — 96 с. 6.ЕГЭ 2011 .Математика. Типовые экзаменационные варианты (30 вариантов) под редакцией А.Л.Семенова и И.В.Ященко ,нац.образование ,2011, 240 стр. 7. С.А. Шестаков, Д.Д. Гущин ЕГЭ 2010 математика задача В12 Рабочая тетрадь, под редакцией А.Л.Семенова и И.В.Ященко , разработано МИОО 8. Анимация http://animashky.ru/index/0-6 http://svetlanal.narod.ru/anim.html http://www.uzdaily.com/ru/sections.php?page=7&mid=5 ; http://www.lenagold.ru/fon/clipart/alf.html 9. Картины http://www.ogoniok.ru/archive/1996/4475/44-32-33/ http://qrok.net/2126-raboty-xudozhnikov-eleny-i-mixail-ivanenko.html 10. Диагностические и тренировочные работы ГИА и ЕГЭ. Сайт А. А. Ларина http://alexlarin.net/ege.html 11.сайт Савченко Елены Михайловны .

1. Задачи на движение Подготовка к ЕГЭ

2.

S = vt
S — это пройденный путь, или расстояние,
V – скорость движения,
t – время движения.
v=S/t
t=S/v

3. Основными типами задач на движение являются следующие:

• задачи на движение по прямой (навстречу и вдогонку, с задержкой в
пути),
• задачи на движение по замкнутой трассе,
• задачи на движение по воде,
• задачи на среднюю скорость,
• задачи на движение протяжных тел

4.

Задача № 1
Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали
автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км
больше, чем велосипедист. Определите скорость велосипедиста, если известно, что
он прибыл в пункт В на 4 часа позже автомобилиста. Ответ дайте в км/ч.
А
В
50 км
Составим таблицу

5.

50
50
х+40
х
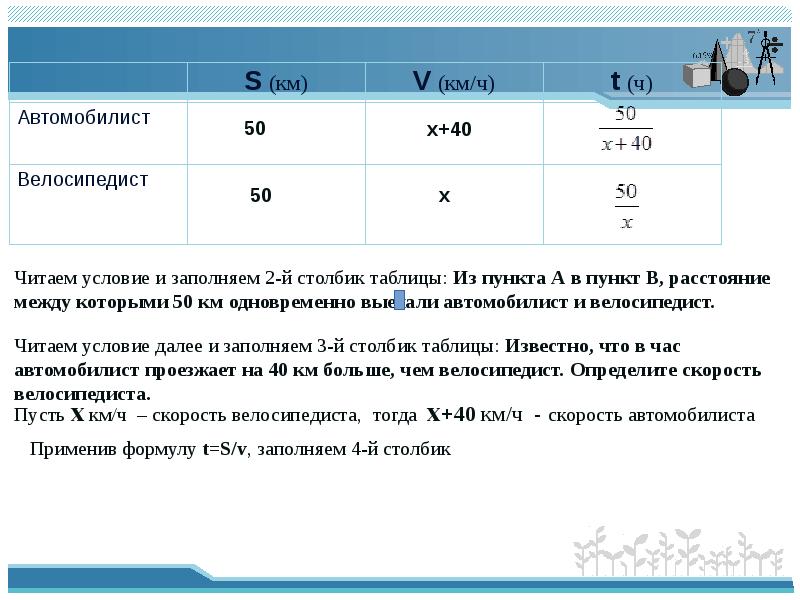
Читаем условие и заполняем 2-й столбик таблицы: Из пункта А в пункт В, расстояние
между которыми 50 км одновременно выехали автомобилист и велосипедист.
Читаем условие далее и заполняем 3-й столбик таблицы: Известно, что в час
автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость
велосипедиста.
Пусть х км/ч – скорость велосипедиста, тогда х+40 км/ч — скорость автомобилиста
Применив формулу t=S/v, заполняем 4-й столбик

6.

х
50
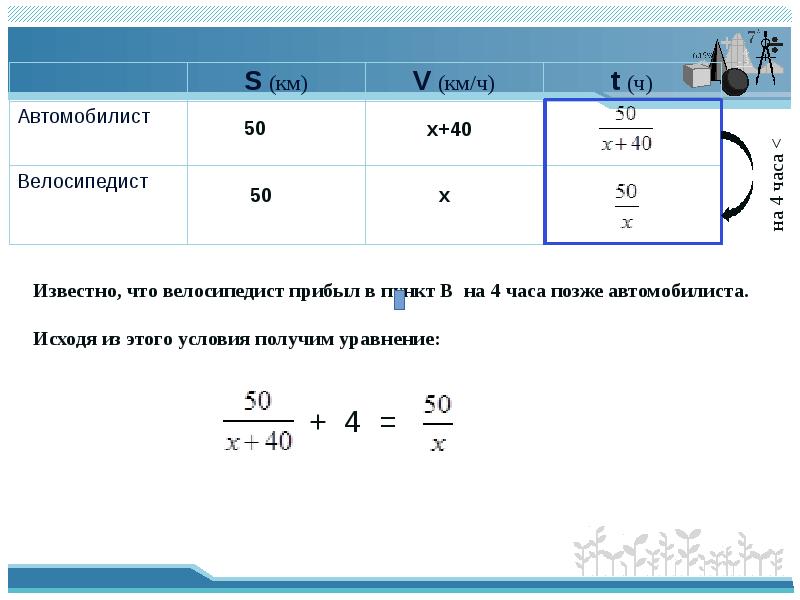
Известно, что велосипедист прибыл в пункт В на 4 часа позже автомобилиста.
Исходя из этого условия получим уравнение:
+ 4 =
на 4 часа <
х+40
50

7.

Решим уравнение:
+ 4 =
50х + 4х(х+40) = 50(х+40)
50х+4х2 +160х = 50х+2000
4х2 +160х – 2000 = 0
х2 +40х – 500 = 0
D = 3600
х1 =10, х2 = — 50
Скорость не может быть отрицательной, следовательно скорость
велосипедиста равна 10 км/ч.
Ответ: 10

8.

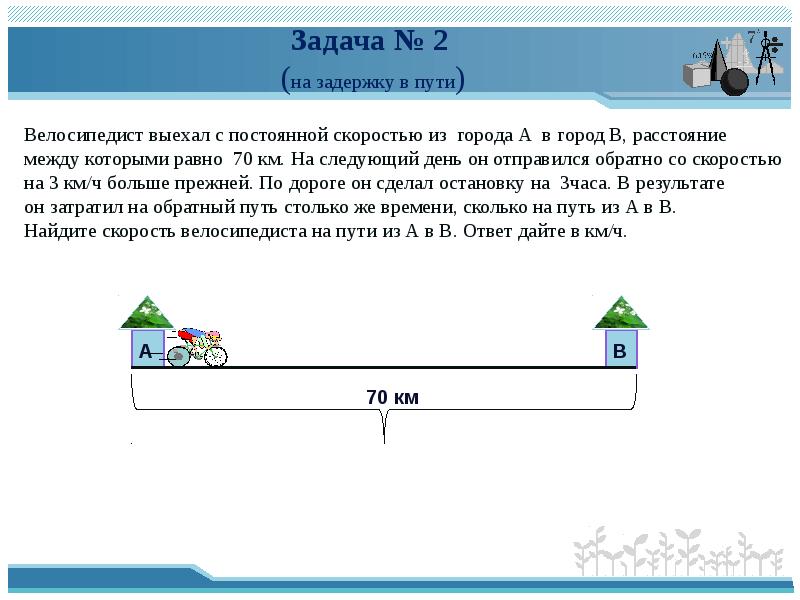
Задача № 2
(на задержку в пути)
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние
между которыми равно 70 км. На следующий день он отправился обратно со скоростью
на 3 км/ч больше прежней. По дороге он сделал остановку на 3часа. В результате
он затратил на обратный путь столько же времени, сколько на путь из А в В.
Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
А
В
70 км

9.

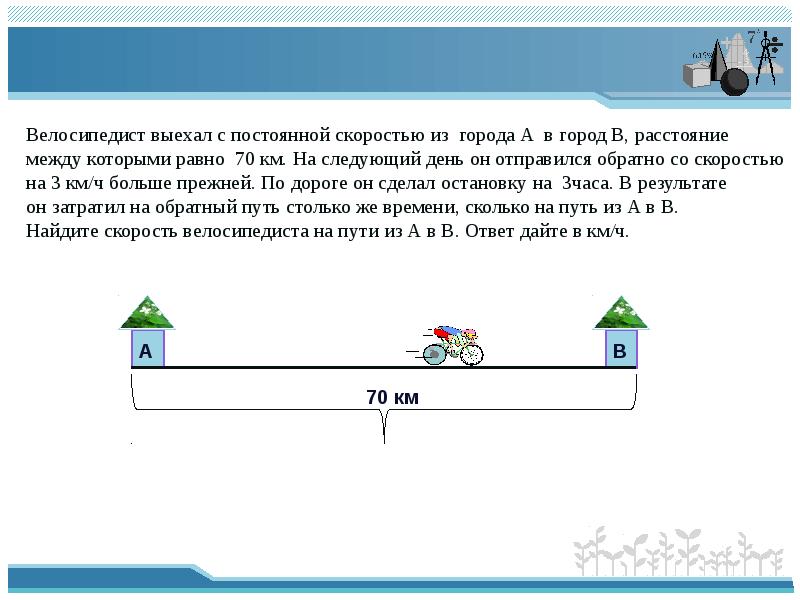
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние
между которыми равно 70 км. На следующий день он отправился обратно со скоростью
на 3 км/ч больше прежней. По дороге он сделал остановку на 3часа. В результате
он затратил на обратный путь столько же времени, сколько на путь из А в В.
Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
А
В
70 км

10.

Велосипедист выехал с постоянной скоростью из города А в город В, расстояние
между которыми равно 70 км. На следующий день он отправился обратно со скоростью
на 3 км/ч больше прежней. По дороге он сделал остановку на 3часа. В результате
он затратил на обратный путь столько же времени, сколько на путь из А в В.
Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
А
В
70 км

11.

Заполним таблицу
s
v
из А в В
70
х
из В в А
70
х+3
t
+3
Читаем условие задачи и заполняем 2-й столбик таблицы:
Велосипедист выехал с постоянной скоростью из города А в город В,
расстояние между которыми равно 70 км
На следующий день он отправился обратно со скоростью на 3 км/ч больше прежней.
Из этого условия определим, что скорость из А в B — х км/ч, из B в A – (х+3) км/ч
По дороге он сделал остановку на 3часа.
В результате он затратил на обратный путь столько же времени, сколько
на путь из А в В.
+3
=

12.

Решим уравнение:
=
+3
70(х + 3) = 70х + 3х(х+3)
х2 +3х – 70 = 0
D = 289
х1 = — 10, х2 = 7
Скорость велосипедиста число положительное,
следовательно скорость равна 7 км/ч.
Ответ: 7

13. Задача № 3 (на встречное движение)

Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью
60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B
выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A
автомобили встретятся? Ответ дайте в километрах.
?
В
А
435 км

14.

Заполним таблицу
60
60
1
60х
60
х
65х
65
х
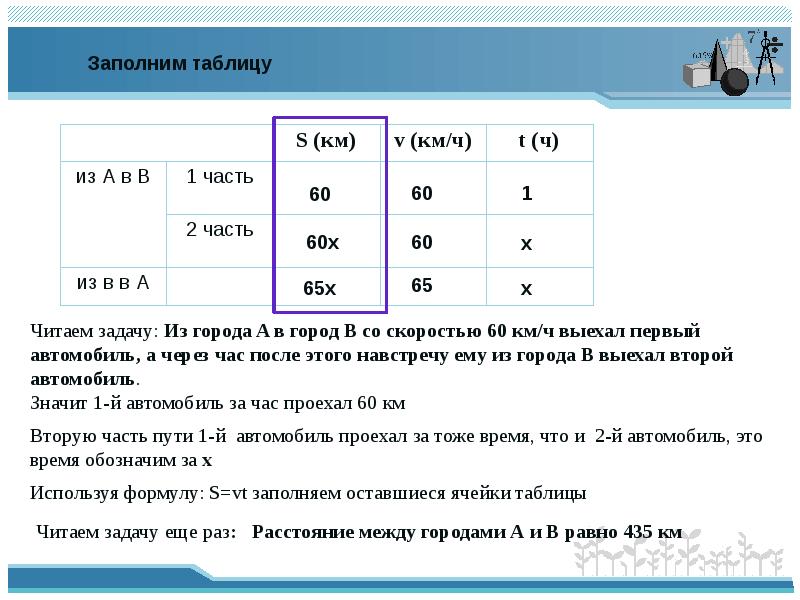
Читаем задачу: Из города A в город B со скоростью 60 км/ч выехал первый
автомобиль, а через час после этого навстречу ему из города B выехал второй
автомобиль.
Значит 1-й автомобиль за час проехал 60 км
Вторую часть пути 1-й автомобиль проехал за тоже время, что и 2-й автомобиль, это
время обозначим за х
Используя формулу: S=vt заполняем оставшиеся ячейки таблицы
Читаем задачу еще раз: Расстояние между городами А и В равно 435 км

15.

60
60
1
60х
60
х
65х
65
х
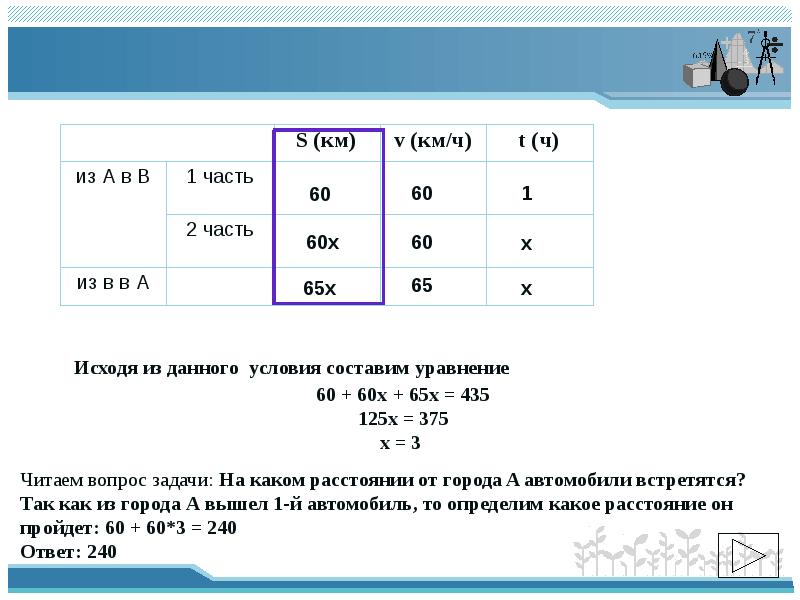
Исходя из данного условия составим уравнение
60 + 60х + 65х = 435
125х = 375
х=3
Читаем вопрос задачи: На каком расстоянии от города A автомобили встретятся?
Так как из города А вышел 1-й автомобиль, то определим какое расстояние он
пройдет: 60 + 60*3 = 240
Ответ: 240

16.

Задача №5
(по прямой вдогонку)
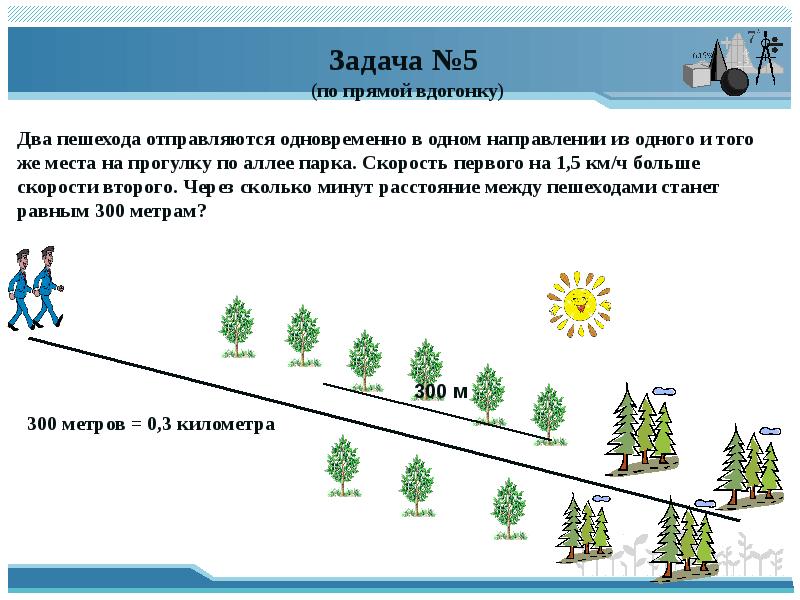
Два пешехода отправляются одновременно в одном направлении из одного и того
же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше
скорости второго. Через сколько минут расстояние между пешеходами станет
равным 300 метрам?
300 м
300 метров = 0,3 километра

17. Составим таблицу

S (км)
v(км/ч)
t(ч)
I пешеход
(х+1,5)t
х+1,5
t
II пешеход
xt
х
t
Читаем задачу и заполняем таблицу: Скорость первого на 1,5 км/ч больше
скорости второго. скорость 2-го пешехода обозначим за х
Читаем задачу далее: Через сколько минут расстояние между пешеходами
станет равным 300 метрам?
Нам неизвестно время, возьмем его за t
Применив формулу: S = vt, заполним пустые ячейки таблицы
Составим уравнение учитывая вопрос: Через сколько минут расстояние между
пешеходами станет равным 300 метрам?
(х+1,5)t – xt = 0,3

18.

(х+1,5)t —
xt
= 0,3
решим данное уравнение
(х + 1,5)t- хt = 0,3
xt + 1,5t – xt = 0,3
1,5t = 0,3
t = 0,2
Ответ: 0,2

19.

Следующий тип задач — когда что-нибудь плавает по реке, в которой есть течение.
Например, теплоход, катер или моторная лодка.
Обычно в условии говорится о собственной скорости плавучей посудины
и скорости течения.
Собственной скоростью называется скорость в неподвижной воде.
При движении по течению эти скорости складываются.
Скорость при движении по течению равна сумме собственной скорости судна
и скорости течения.
А если двигаться против течения, то течение будет мешать, относить назад. Теперь
скорость течения будет вычитаться из собственной скорости судна.

20.

Задача №6
(на движение по воде)
Моторная лодка прошла против течения реки 255 км и вернулась в пункт
отправления, затратив на обратный путь на 2часа меньше. Найдите скорость лодки
в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.

21.

Моторная лодка прошла против течения реки 255 км и вернулась в пункт
отправления, затратив на обратный путь на 2часа меньше. Найдите скорость лодки
в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.

22.

Моторная лодка прошла против течения реки 255 км и вернулась в пункт
отправления, затратив на обратный путь на 2часа меньше. Найдите скорость лодки
в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Пусть Х км/ч — скорость лодки в неподвижной воде,
Против течения скорость уменьшается на 1 км/ч, т.е.
(Х -1) км/ч — скорость против течения
По течению скорость увеличивается на 1 км/ч, т.е.
(Х + 1) км/ч — скорость по течению

23.

Составим таблицу:
По течению
S(км)
V (км/ч)
255
х +1
t (ч)
Против
255
х -1
течения
Т.к. на обратный путь лодка затратила времени меньше на 2 часа,
то получим уравнение:
= 2
Решим данное уравнение:
255(х+1) – 255(х-1) = 2
255х+255-255х+255=2(х-1)(х+1)
2х2 – 512 = 0
х1 =16, х2 = — 16
Скорость должна быть положительным числом, следовательно скорость лодки
в неподвижной воде равна 16 км/ч.
Ответ: 16

24. Задача №7 (по замкнутой трассе)

Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном
направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч,
скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем
первый автомобиль будет опережать второй ровно на 1 круг?
V (км/ч)
t (ч)
S (км)
I автомобиль
60
х
60х
II автомобиль
80
х
80х
Из условия задачи известно, что: Скорость первого автомобиля равна 60 км/ч, скорость
второго равна 80 км/ч.
Читаем вопрос задачи: Сколько минут с момента старта пройдет, прежде чем
первый автомобиль будет опережать второй ровно на 1 круг?
Пусть это время — х
Тогда по формуле: S=vt заполняем последний столбик
1 круг равен 15 км, следовательно: 80х-60х=15
х=3/4 (ч)
Переведем ¾ часа в минуты, получим 45 минут

25. Задача №8 (нахождение средней скорости)

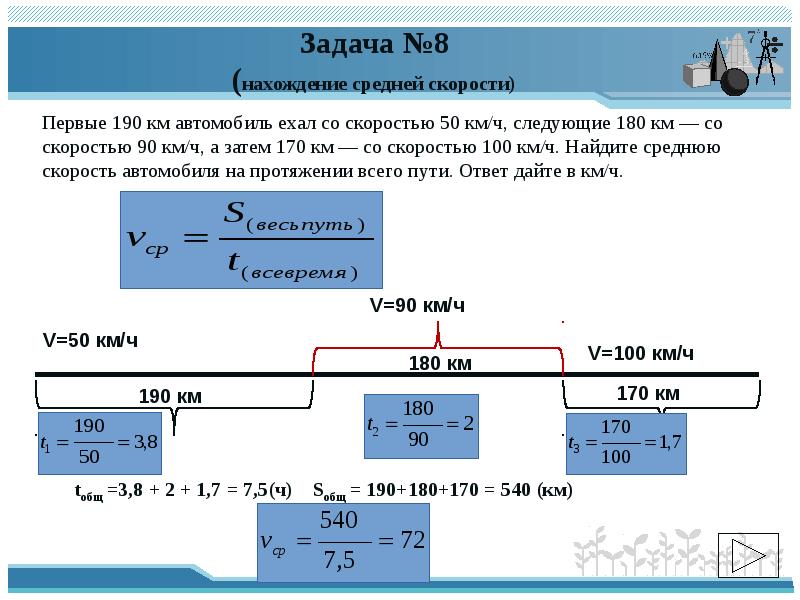
Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со
скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю
скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
vср
S ( весьпуть )
t ( всевремя )
V=90 км/ч
V=50 км/ч
V=100 км/ч
180 км
190 км
t1
190
50
t2
3,8
tобщ =3,8 + 2 + 1,7 = 7,5(ч)
v ср
180
90
170 км
2
t3
Sобщ = 190+180+170 = 540 (км)
540
7,5
72
170
100
1,7

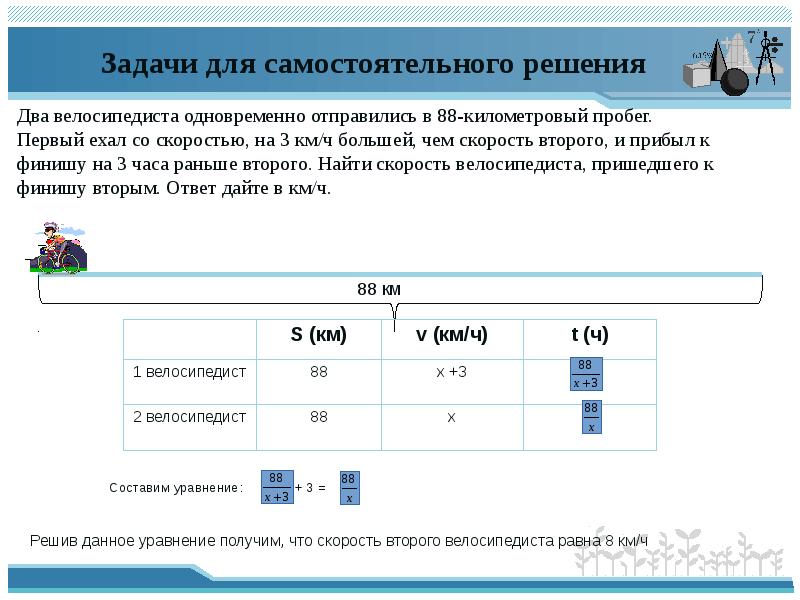
26. Задачи для самостоятельного решения

Два велосипедиста одновременно отправились в 88-километровый пробег.
Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к
финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к
финишу вторым. Ответ дайте в км/ч.
88 км
S (км)
v (км/ч)
t (ч)
1 велосипедист
88
х +3
88
х 3
2 велосипедист
88
х
Составим уравнение:
88
+3=
х 3
88
х
88
х
Решив данное уравнение получим, что скорость второго велосипедиста равна 8 км/ч

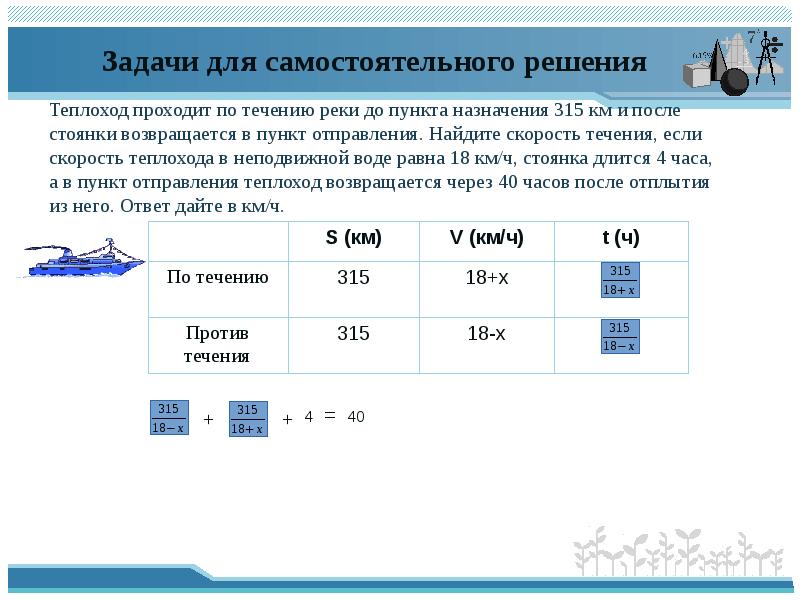
27. Задачи для самостоятельного решения

Теплоход проходит по течению реки до пункта назначения 315 км и после
стоянки возвращается в пункт отправления. Найдите скорость течения, если
скорость теплохода в неподвижной воде равна 18 км/ч, стоянка длится 4 часа,
а в пункт отправления теплоход возвращается через 40 часов после отплытия
из него. Ответ дайте в км/ч.
S (км)
V (км/ч)
По течению
315
18+х
Против
течения
315
18-х
315
18 х
+
315
18 х
+
4
=
40
t (ч)
315
18 х
315
18 х

28.

Задачи для самостоятельного решения
1. Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15км
от А. Пробыв в пункте В — 1 час20 минут, баржа отправилась назад
и вернулась в пункт А в16 :00. Определите (в км/час) скорость течения
реки, если известно, что собственная скорость баржи равна 7 км/ч.
2. Два велосипедиста одновременно отправились в 130-километровый пробег.
Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл
к финишу на 3 часа раньше второго. Найти скорость велосипедиста,
пришедшего к финишу первым. Ответ дайте в км/ч
3. Из пункта А в пункт В, расстояние между которыми 60 км, одновременно
выехали автомобилист и велосипедист. Известно, что в час автомобилист
проезжает на 110 км больше, чем велосипедист. Определите скорость
велосипедиста, если известно, что он прибыл в пункт В на 5,5 часов позже
автомобилиста. Ответ дайте в км/ч.

Слайды и текст этой онлайн презентации

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---