Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
2
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
3
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
4
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
5
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.
Пройти тестирование по этим заданиям
На чтение 9 мин Просмотров 18.1к. Опубликовано 16 ноября, 2020
Задачи на движение начинают проходить в 5 классе и решают все оставшиеся учебные годы вплоть до 11 класса. В ЕГЭ по математике вы найдете задачи на движение в задании 11, в котором собраны все текстовые задачи. Рассмотрим как надо решать задачи на движение из ЕГЭ. Но сначала немного теории.
Содержание
- Как решать задачи на движение
- Примеры решения
- Виды задач на движение
- Движение навстречу друг другу, движение в противоположных направлениях
- Движение друг за другом (вдогонку)
- Задачи на движение по кругу
- Задачи на движение мимо объекта
- Задачи на движение по течению и против течения
- Задачи на движение из ЕГЭ по математике (профильный уровень)
- Задача 1.
- Задача 2.
- Задача 3
- Задача 4
- Задача 5
Как решать задачи на движение
Решение задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
S = v · t.
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Примеры решения
Пример:
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Решение:
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
| Первый велосипедист | x + 10 | 60 | |
| Второй велосипедист | x | 60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
3x2 + 90x = 600 + 60x;
x2 + 10x – 200 = 0.
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Ответ: 10 км/ч.
Виды задач на движение
Движение навстречу друг другу, движение в противоположных направлениях
Если два объекта движутся навстречу друг другу, то они сближаются:
При движении в противоположном направлении объекты удаляются:
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
v = v1 + v2.
Движение друг за другом (вдогонку)
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Таким образом:
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.
Задачи на движение по кругу
При движении по кругу объекты могут:
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0 км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S: S1 – S2 = m · S.
Задачи на движение мимо объекта
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
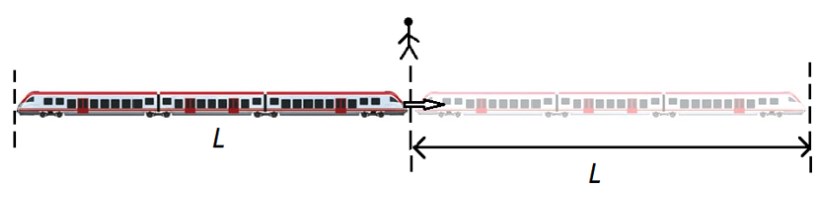
Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
S = L = v0 · t.
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
Задачи на движение по течению и против течения
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.
Задачи на движение из ЕГЭ по математике (профильный уровень)
Задача 1.
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: Пусть скорость второго автомобиля равна v км/ч. За 4/5 часа первый автомобиль прошел на 44 км больше, чем второй, отсюда имеем:
112 ∙ = v ∙
= v ∙
+ 44 ⇔ 4 ∙ v = 112 ∙ 4 – 44 ∙ 5 ⇔ v = 57.
Следовательно, скорость второго автомобиля была равна 57 км/ч.
Ответ: 57 км/ч.
Задача 2.
Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.
Решение:
До первой встречи велосипедист провел на трассе 1/5 часа, а мотоциклист 1/30 часа. Пусть скорость мотоциклиста равна v км/ч, тогда скорость велосипедиста равна
Тогда если скорость велосипедиста – это 1 единица отношения, то скорость мотоциклиста – это 6 единиц отношения.
Так как они едут в одном направлении, их общая скорость 5 единиц отношения.
∙5 ед.отн. = 5
1 ед.отн. = 20
6 ед.отн. = 120
Таким образом, скорость мотоциклиста была равна 120 км/ч.
Ответ: 120 км/ч.
Задача 3
Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?
Решение: Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой ― 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет L делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
, отсюда
, отсюда
и
.
Ответ: через 9 минут.
Задача 4
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Данную задачу можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т. к. сказано, что на один круг). Найти скорость второго. Очень важно в заданиях на движение представить сам процесс этого движения.
Сравнение так же производим по расстоянию.
За x принимаем искомую величину ― скорость второго. Время движения 40 минут (2/3 часа) для обоих. Заполним графу «расстояние»:
| v | t | S | |
| 1 | 80 | 2/3 | |
| 2 | x | 2/3 |
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.
80 ∙ больше, чем x ∙
больше, чем x ∙
на 14.
80 ∙ = x ∙
= x ∙
+ 14;
–
–
= x ∙
;
160 – 42 = х ∙ 2;
х = 59.
Скорость второго автомобиля 59 (км/ч).
Ответ: 59 км/ч.
Задача 5
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение:
Пусть v км/ч – скорость велосипедиста, тогда скорость автомобилиста равна v + 40 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:
Таким образом, скорость велосипедиста была равна 10 км/ч.
Ответ: 10 км/ч.
Разберем подробнее некоторые особенности, возникающие при решении задач на движение.
Прочитай задачу несколько раз
Осознай ее настолько, чтобы тебе было понятно абсолютно все.
Например, часто возникают трудности с понятием “собственная скорость лодки/катера” и т.д.
Подумай, что это может значить? Правильно, скорость лодки в стоячей воде, например, в пруду, когда на нее НЕ влияет скорость течения.
Кстати, в задачах иногда пишут «найти скорость лодки в стоячей воде».
Теперь ты знаешь, что собственная скорость лодки и скорость лодки в стоячей воде – одно и тоже, так что не теряйся, если встретишь оба этих определения.
Сделай рисунок
Пойми точно кто куда едет, кто к кому приехал, и где они все встретились.
Сделай рисунок, попутно записывая на нем все известные величины (ну либо под ним, если не знаешь, как их отобразить схематически).
Рисунок должен четко отражать весь смысл задачи.
Его следует сделать таким образом, чтобы на нем была видна динамика движения – направления движения, встречи, развороты, повороты.
Качественный рисунок позволяет понять задачу, не заглядывая в ее текст. Он – твоя основная подсказка для дальнейшего составления уравнения.
Рассмотрим возможные виды движения двух тел.
Относительное движение
Если какие-то тела движутся друг относительно друга, часто бывает полезно посчитать их относительную скорость. Она равна:
- сумме скоростей, если тела движутся навстречу друг другу;
- разности скоростей, если тела движутся в одном направлении.
Пример №1
Допустим, из точки ( displaystyle A) и из точки ( displaystyle B) навстречу друг другу выехали две машины. Скорость одной машины – ( displaystyle 60) км/ч, а скорость ( displaystyle 2) машины – ( displaystyle 40) км/ч. Они встретились через ( displaystyle 1,2) часа.
Какое расстояние между пунктами ( displaystyle A) и ( displaystyle B)?
1 вариант решения
Можно рассуждать так: машины встретились, значит расстояние между городами – это сумма расстояния, которая прошла первая машина, и расстояния, которое прошла вторая.
( displaystyle 60cdot 1,2text{ }=text{ }72) (км) – путь, который проехала первая машина
( displaystyle 40cdot 1,2text{ }=text{ }48) (км) – путь, который проехала вторая машина
( displaystyle 72 + 48 = 120) (км) – расстояние, которое проехали обе машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).
2 вариант решения (более рациональный)
А можно просто воспользоваться очень логичной формулой о сложении скоростей.
Проверим, работает ли она:
( displaystyle 60 + 40 = 100) (км/ч) – скорость сближения машин
( displaystyle 100cdot 1,2text{ }=text{ }120) (км) – расстояние, которые проехали машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).
Оба решения являются верными. Второе просто более рациональное.
Пример №3
Итак, задача:
Из пункта ( displaystyle A) и пункта ( displaystyle B) машины движутся навстречу друг другу со скоростями ( displaystyle 50) км/ч и ( displaystyle 80) км/ч. Расстояние между пунктами – ( displaystyle 195) км.
Через сколько времени машины встретятся?
1 вариант решения
Пусть ( displaystyle x) – время, которое едут машины, тогда путь первой машины – ( displaystyle 50x), а путь второй машины – ( displaystyle 80x).
Их сумма и будет равна расстоянию между пунктами ( A) и ( B) – ( displaystyle 50x+80x=195).
Решим уравнение:
( displaystyle 50x+80x=195)
( displaystyle 130x=195)
( displaystyle x=1,5) (ч) – время, через которое встретились машины.
2 вариант решения (более рациональный)
( displaystyle 50 + 80 = 130) (км/ч) – скорость сближения машин;
( displaystyle 195:130 = 1,5) (ч) – время, которое машины были в пути.
Задача решена.
Пример №4
Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями ( displaystyle 60) км/ч и ( displaystyle 40) км/ч. Через сколько минут они встретятся. Если расстояние между пунктами ( displaystyle 100) км?
2 способа решения:
I способ
Относительная скорость автомобилей ( displaystyle 60+40=100) км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью ( displaystyle 100) км/ч. Так как между автомобилями изначально расстояние ( displaystyle 100) км, время, через которое второй автомобиль проедет мимо первого:
( displaystyle t=frac{100}{100}=1 час=60 минут).
II способ
Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его ( displaystyle t). Тогда первый автомобиль проехал путь ( displaystyle 60t), а второй – ( displaystyle 40t).
В сумме они проехали все ( displaystyle 100) км. Значит,
( displaystyle 60t+40t=100Rightarrow t=1 час=60 минут).
Пример №5
А вот и задача: из Москвы в противоположные стороны выехало ( displaystyle 2) машины. Скорость одной машины – ( displaystyle 85) км/ч, скорость другой – ( displaystyle 60) км/ч.
На каком расстоянии друг от друга будут находиться машины через ( displaystyle 2) часа?
Решил?
Решая первым способом, у меня получилось, что путь, проделанный первой машиной, равен ( displaystyle 170) км, а второй – ( displaystyle 120) км.
Соответственно, расстояние между машинами – ( displaystyle 290) км.
Решая вторым способом, выходит, что скорость удаления равна (displaystyle 145 км/ч), а путь равен (displaystyle 145 км/ч)( displaystyle cdot 2 ч) = (displaystyle 290 км).
Теперь разберемся, как вычисляется время при подобном случае.
Время, проведенное телами в пути, при удалении друг от друга равно пройденному расстоянию (то есть, если между телами изначально было некое расстояние ( {{S}_{0}}), то его следует вычесть из общего расстояния), деленному на сумму скоростей тел:
( displaystyle {{text{t}}_{пути}}=frac{S}{{{nu }_{1}}+{{nu }_{2}}})
Как ты видишь, формула аналогична выведенной нами при движении тел навстречу друг другу.
Считаешь, что такого не может быть?
Проверь ее на практике!
Из пункта ( displaystyle A) в пункт ( displaystyle B), расстояние между которыми ( displaystyle 30) км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на ( displaystyle 65) км больше, чем велосипедист.
Определите скорость велосипедиста, если известно, что он прибыл в пункт ( displaystyle B) на ( displaystyle 156) минут позже, чем мотоциклист.
Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать – прямая, пункт ( displaystyle A), пункт ( displaystyle B), две стрелочки…
В общем рисуй, и сейчас сравним, что у тебя получилось.
Пустовато как-то, правда? Рисуем таблицу.
Как ты помнишь, все задачи на движения состоят из ( displaystyle 3) компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах.
Правда, мы добавим еще один столбец – имя, про кого мы пишем информацию – мотоциклист и велосипедист.
Так же в шапке укажи размерность, в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?
У тебя получилась вот такая таблица?
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | |||
| мотоциклист |
Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.
Первое, что мы имеем – это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен ( displaystyle 30) км. Вносим!
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | ( displaystyle 30) | ||
| мотоциклист | ( displaystyle 30) |
Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на ( displaystyle 65) км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста…
Возьмем скорость велосипедиста за ( displaystyle x), тогда скорость мотоциклиста будет ( displaystyle x+65)…
Если с такой переменной решение задачи не пойдет – ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | ( displaystyle x) | ( displaystyle 30) | |
| мотоциклист | ( displaystyle x+65) | ( displaystyle 30) |
Таблица преобразилась. У нас осталась не заполнена только одна графа – время. Как найти время, когда есть путь и скорость?
Правильно, разделить путь на скорость. Вноси это в таблицу.
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | ( displaystyle x) | ( displaystyle frac{30}{x}) | ( displaystyle 30) |
| мотоциклист | ( displaystyle x+65) | ( displaystyle frac{30}{65+x}) | ( displaystyle 30) |
Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.
Что мы можем на нем отразить?
Молодец. Скорость передвижения мотоциклиста и велосипедиста.
Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.
Какие данные не отражены ни в таблице, ни на рисунке?
Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени – ( displaystyle 156) минут.
Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.
( displaystyle 156) минут / ( displaystyle 60) минут = ( displaystyle 2,6) часа.
И что дальше, спросишь ты? А дальше числовая магия!
Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?
Правильно. Мы можем составить уравнение, основываясь на разнице во времени!
( displaystyle frac{30}{x}-frac{30}{65+x}=2,6)
Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.
Это уравнение – рациональное. Если не знаешь, что это такое, прочти тему «Рациональные уравнения».
Приводим слагаемые к общему знаменателю:
( displaystyle frac{30cdot left( 65+x right)}{xcdot left( 65+x right)}-frac{30x}{xcdot left( 65+x right)}=2,6)
Раскроем скобки и приведем подобные слагаемые: Уф! Усвоил? Попробуй свои силы на следующей задаче.
( displaystyle frac{1950}{xcdot left( 65+x right)}=2,6)
Из этого уравнения мы получаем следующее:
( displaystyle 2,6cdot xcdot left( 65+x right)=1950)
( displaystyle xcdot left( 65+x right)=frac{1950}{2,6})
( displaystyle xcdot left( 65+x right)=750)
Раскроем скобки и перенесем все в левую часть уравнения:
( displaystyle {{x}^{2}}+65{x}-750=0)
Вуаля! У нас простое квадратное уравнение. Решаем!
( displaystyle {{x}^{2}}+65{x}-750=0)
( displaystyle D={{b}^{2}}-4ac)
( displaystyle D={{65}^{2}}-4cdot 1cdot left( -750 right)=4225+3000=7225)
( displaystyle sqrt{D}=sqrt{7225}=85)
( displaystyle {{x}_{1,2}}=frac{-bpm sqrt{D}}{2a})
( displaystyle {{x}_{1}}=frac{-65+85}{2}=10)
( displaystyle {{x}_{2}}=frac{-65-85}{2}=-75)
Мы получили два варианта ответа. Смотрим, что мы взяли за ( displaystyle x)? Правильно, скорость велосипедиста.
Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь, о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ – ( displaystyle 10) км/ч.
Пример №9
Два велосипедиста одновременно отправились в ( displaystyle 165)-километровый пробег. Первый ехал со скоростью, на ( displaystyle 5) км/ч большей, чем скорость второго, и прибыл к финишу на ( displaystyle 5,5) часов раньше второго.
Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Напоминаю:
- Прочитай задачу пару раз – усвой все-все детали. Усвоил?
- Начинай рисовать рисунок – в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
- Проверь, все ли величины у тебя одинаковой размерности, и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь, какие там графы?).
- Пока все это пишешь, думай, что взять за ( displaystyle x)? Выбрал? Записывай в таблицу!
- Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок – помни о «3Р»!
Все сделал? Молодец! У меня получилось, что скорость велосипедиста – ( displaystyle 10) км/ч.
Отвечайте точно на поставленный вопрос
– Какого цвета твоя машина?
– Она красивая!
Продолжим наш разговор. Так какая там скорость у первого велосипедиста? ( displaystyle 10) км/ч? Очень надеюсь, что ты сейчас не киваешь утвердительно!
Внимательно прочти вопрос: «Какая скорость у первого велосипедиста?»
Понял, о чем я?
Именно! Полученный ( displaystyle x) – это не всегда ответ на поставленный вопрос!
Вдумчиво читай вопросы – возможно, после нахождения ( displaystyle x) тебе нужно будет произвести еще некоторые манипуляции, например, прибавить ( displaystyle 5) км/ч, как в нашей задаче.
Еще один момент: часто в задачах все указывается в часах, а ответ просят выразить в минутах, или же все данные даны в км, а ответ просят записать в метрах.
Смотри за размерностью не только в ходе самого решения, но и когда записываешь ответы.
Пример №10
Из пункта ( displaystyle A) круговой трассы выехал велосипедист. Через ( displaystyle 40) минут он еще не вернулся в пункт ( displaystyle A) и из пункта ( displaystyle A) следом за ним отправился мотоциклист.
Через ( displaystyle 20) минут после отправления он догнал велосипедиста в первый раз, а еще через ( displaystyle 40) минут после этого догнал его во второй раз.
Найдите скорость велосипедиста, если длина трассы равна ( displaystyle 50) км. Ответ дайте в км/ч.
Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:
Пусть скорость велосипедиста будет ( displaystyle x), а мотоциклиста – ( displaystyle y). До момента первой встречи велосипедист был в пути ( displaystyle 60) минут, а мотоциклист – ( displaystyle 20).
При этом они проехали равные расстояния:
( displaystyle 60x=20y (1))
Между встречами велосипедист проехал расстояние ( displaystyle 40x), а мотоциклист – ( displaystyle 40y).
Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:
(Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили – спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.)
Значит,
( displaystyle 40x+50=40y (2))
Полученные уравнения решаем в системе:
( displaystyle left{ begin{array}{l}60x=20y\40x+50=40yend{array} right.Leftrightarrow left{ begin{array}{l}y=3x\4x+5=4yend{array} right.Rightarrow text{4}x+5=12xRightarrow )
( displaystyle Rightarrow x=frac{5}{8}=0,625frac{text{км}}{мин}=0,625cdot 60frac{text{км}}{text{ч}}=37,5frac{text{км}}{text{ч}})
Ответ: ( displaystyle 37,5).
Разобрался? Попробуй решить самостоятельно следующие задачи:
Пример №13
Из пункта A круговой трассы выехал велосипедист. Через ( displaystyle 40) минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через ( displaystyle 20) минут после отправления он догнал велосипедиста в первый раз, а еще через ( displaystyle 40) минут после этого догнал его во второй раз.
Найдите скорость велосипедиста, если длина трассы равна ( displaystyle 50) км. Ответ дайте в км/ч.
Решение:
Здесь будем приравнивать расстояние.
Пусть скорость велосипедиста будет ( displaystyle x), а мотоциклиста – ( displaystyle y). До момента первой встречи велосипедист был в пути ( displaystyle 60) минут, а мотоциклист – ( displaystyle 20).
При этом они проехали равные расстояния:
( displaystyle 60x=20ytext{ }left( 1 right))
Между встречами велосипедист проехал расстояние ( displaystyle 40x), а мотоциклист – ( displaystyle 40y). Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:
Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили– спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.
Значит:
Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, – это стоячая вода.
Скорость течения в озере равна ( displaystyle 0).
Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь – налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести.
Это понятно? Логично же.
А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…
Это происходит потому что у реки есть скорость течения, которая относит твой плот по направлению течения.
Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) – он движется со скоростью течения.
Разобрался? Тогда ответь вот на какой вопрос – «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?
Здесь возможно два случая:
1 случай – ты плывешь по течению, и тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.
2 случай – ты плывешь против течения. Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы ( displaystyle 100) метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость – скорость течения.
Пример №15
Байдарка в ( displaystyle 8:00) вышла из пункта ( displaystyle A) в пункт ( displaystyle B), расположенный в ( displaystyle 26) км от ( displaystyle A).
Пробыв в пункте ( displaystyle B) ( displaystyle 1) час ( displaystyle 20) минут, байдарка отправилась назад и вернулась в пункт ( displaystyle A) в ( displaystyle 20:00).
Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки ( displaystyle 5) км/ч.
Итак, приступим. Прочитай задачу несколько раз и сделай рисунок. Думаю, ты без труда сможешь решить это самостоятельно.
Все величины у нас выражены в одном виде? Нет. Время отдыха у нас указано и в часах, и в минутах.
Переведем это в часы:
( displaystyle 1) час ( displaystyle 20) минут = ( displaystyle 1frac{20}{60}=1frac{1}{3}) ч.
Теперь все величины у нас выражены в одном виде. Приступим к заполнению таблицы и поиску того, что мы возьмем за ( displaystyle x).
Пусть ( displaystyle x) – собственная скорость байдарки. Тогда, скорость байдарки по течению равна ( displaystyle x+5), а против течения равна ( displaystyle x-5).
Запишем эти данные, а так же путь (он, как ты понимаешь, одинаков) и время, выраженное через путь и скорость, в таблицу:
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Задачи на движение»
Открытый банк заданий по теме задачи на движение. Задания B11 из ЕГЭ по математике (профильный уровень)
Задание №1105
Тип задания: 11
Тема:
Задачи на движение
Условие
Два велосипедиста одновременно отправились из деревни A в деревню B, расстояние между которыми 21 км. Скорость первого велосипедиста была на 3 км/ч больше скорости второго велосипедиста. Найдите скорость второго велосипедиста, если он приехал в деревню B на 10 мин позже первого. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость второго велосипедиста через x км/ч. Тогда скорость первого (x+3) км/ч, а время первого велосипедиста на прохождение всего пути frac{21}{x+3}ч, время второго велосипедиста, затраченное на прохождение всего пути frac{21}{x}ч. Разница во времени равна 10 мин = frac16часа.
Составим и решим уравнение: frac{21}{x}-frac{21}{x+3}=frac16,
6(21(x+3)-21x)=x(x+3),
x^2+3x-378=0,
x_1=18, x_2=-21.
Отрицательная скорость не удовлетворяет условию задачи. Скорость второго велосипедиста равна 18 км/ч.
Ответ
18
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1101
Тип задания: 11
Тема:
Задачи на движение
Условие
Моторная лодка прошла против течения реки 160 км и вернулась в пункт отправления, затратив на обратный путь на 8 часов меньше времени. Известно, что в неподвижной воде лодка движется со скоростью 15 км/ч. Найдите скорость течения реки. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость течения реки через x км/ч. Тогда скорость лодки по течению реки (15 + x) км/ч, скорость лодки против течения реки (15 — x) км/ч. Время, затраченное лодкой на путь по течению реки frac{160}{15+x} ч, время, затраченное на путь против течения реки — frac{160}{15-x} ч.
Составим и решим уравнение:
frac{160}{15-x}-frac{160}{15+x}=8,
frac{20}{15-x}-frac{20}{15+x}=1,
20(15+x-15+x)= (15-x)(15+x),
20cdot2x=225-x^2,
40x=225-x^2,
x^2+40x-225=0,
x_1=5, x_2=-45.
Скорость течения положительна, она равна 5 км/ч.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1100
Тип задания: 11
Тема:
Задачи на движение
Условие
Два мотоциклиста выехали одновременно из города A в город B, расстояние между которыми 171 км. За один час первый мотоциклист проезжает расстояние на 40 км больше второго мотоциклиста. Найдите скорость второго мотоциклиста, если он приехал в пункт В на 2,5 часа позже первого. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость второго мотоциклиста через x км/ч, тогда по условию скорость первого мотоциклиста (x + 40) км/ч. Время, затраченное на прохождение всего пути первым мотоциклистом, равно frac{171}{x+40} ч. Время, затраченное на прохождение всего пути вторым мотоциклистом, равно frac{171}{x} ч.
Составим и решим уравнение:
frac{171}{x}-frac{171}{x+40}=2,5,
171(x + 40) — 171x = 2,5x(x + 40),
171x+171cdot40-171x = 2,5x^2 + 100x,
2,5x^2+100x-171cdot40 =0,
x^2+40x-171cdot16=0,
x_1 = 36, x_2 = -76.
Отрицательная скорость не удовлетворяет условию. Скорость второго мотоциклиста
36 км/ч.
Ответ
36
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1096
Тип задания: 11
Тема:
Задачи на движение
Условие
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 80 км/ч и 50 км/ч. Товарный поезд имеет длину 1100 метров. Какова длина пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минуты 6 секунд. Ответ дайте в метрах.
Показать решение
Решение
Скорость пассажирского поезда относительно товарного равна 80-50=30 (км/ч) = frac{30000}{60} (м/мин) =500 (м/мин). Обозначим длину пассажирского поезда через x метров, тогда пассажирский поезд пройдёт мимо товарного поезда расстояние, равное (1100 + x) метров, за 3 мин 6 сек (3 мин 6 сек = 3,1 мин).
Составим и решим уравнение:
frac{1100+x}{3,1}=500,
1100+x=500cdot3,1,
x=1550-1100,
x=450.
Длина пассажирского поезда 450 м.
Ответ
450
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1095
Тип задания: 11
Тема:
Задачи на движение
Условие
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо семафора за 45 секунд. Найдите длину поезда в метрах.
Показать решение
Решение
Обозначим длину поезда x км. Тогда время, за которое поезд проезжает мимо семафора, равно frac{x}{60}ч. По условию это 45 секунд, то есть frac{45}{3600}ч.
frac{x}{60}=frac{45}{3600},
x=frac{60cdot45}{3600},
x=0,75 (км).
Длина поезда равна 750 м.
Ответ
750
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1094
Тип задания: 11
Тема:
Задачи на движение
Условие
Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо здания вокзала, длина которого равна 150 метров, за 1 минуту. Найдите длину поезда в метрах.
Показать решение
Решение
Обозначим длину поезда x км. Длина здания равна 150 метров, то есть 0,15 км. Путь, который поезд проехал мимо здания вокзала, равен (x+0,15) км. Время, за которое поезд проезжает мимо здания вокзала, равно frac{x+0,15}{63}ч. По условию это 1 минута (1 мин = frac{1}{60} часа).
оставим и решим уравнение: frac{x+0,15}{63}=frac{1}{60},
x=0,9 (км).
Длина поезда равна 900 м.
Ответ
900
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1093
Тип задания: 11
Тема:
Задачи на движение
Условие
Из двух посёлков, расстояние между которыми 88 км, навстречу друг другу одновременно выехали два велосипедиста. Через сколько часов велосипедисты встретятся, если их скорости равны 18 км/ч и 22 км/ч?
Показать решение
Решение
Обозначим время велосипедистов до встречи через x ч. Тогда первый велосипедист до встречи проедет 18x км, а второй велосипедист проедет до встречи 22x км.
Составим и решим уравнение:
8x + 22x = 88, 40x = 88, x = 2,2.
Велосипедисты встретятся через 2,2 часа.
Ответ
2,2
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №945
Тип задания: 11
Тема:
Задачи на движение
Условие
Теплоход проходит по течению реки до пункта назначения 221 км и после стоянки возвращается в пункт отправления. Скорость движения теплохода в воде без течения равна 15 км/ч. Стоянка длилась 7 часов. Найдите скорость течения реки, если в пункт отправления теплоход вернулся через 37 часов после отплытия из него. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость течения через x км/ч, тогда скорость теплохода по течению реки равна (15+x) км/ч, скорость теплохода против течения (15-x) км/ч. Время движения теплохода равно 37-7=30 ч.
Составим и решим уравнение:
frac{221}{15+x}+frac{221}{15-x}=30,
221(15-x+15+x)=30(15-x)(15+x),
221=225-x^2,
x^2=4,
x_1=2,,x_2=-2.
Скорость течения положительна, она равна 2 км/ч.
Ответ
2
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №944
Тип задания: 11
Тема:
Задачи на движение
Условие
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми 288 км. На следующий день он поехал обратно со скоростью на 6 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 4 часа. В итоге на возвращение в город A у него ушло сколько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость велосипедиста на пути от A до B через x км/ч, x>0. Тогда его скорость на обратном пути будет (x+6) км/ч. Время, затраченное велосипедистом на путь от A до B, равно frac{288}{x}ч, время движения на обратном пути frac{288}{x+6}ч.
Составим и решим уравнение:
frac{288}{x}-frac{288}{x+6}=4,
288(x+6-x)=4x(x+6),
72cdot6=x^2+6x,
x^2+6x-432=0,
x_1=18,,x_2=-24.
Отрицательная скорость не удовлетворяет условию задачи. Скорость велосипедиста равна 18 км/ч.
Ответ
18
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №943
Тип задания: 11
Тема:
Задачи на движение
Условие
Из пункта A в пункт B одновременно выехали две дорожные машины. Первая машина проехала с постоянной скоростью весь путь. Вторая проехала первую половину пути со скоростью 39 км/ч, а вторую половину пути — со скоростью на 26 км/ч большей скорости первой машины, в результате чего в пункт B обе машины прибыли одновременно. Найдите скорость первой машины. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость первой машины через x км/ч, путь от A до B s км, тогда путь от пункта A в пункт B она пройдёт за frac sxч. Половина пути пройдена второй машиной со скоростью 39 км/ч за frac{0,5s}{39}=frac{s}{78}ч. Скорость второй машины на второй половине пути равна (x+26) км/ч, таким образом, время, затраченное на вторую половину пути второй машиной, равно frac{0,5s}{x+26}ч.
Составим и решим уравнение:
frac sx=frac{s}{78}+frac{0,5s}{x+26},
frac 2x=frac{2}{78}+frac{1}{x+26},
frac 2x-frac{1}{39}-frac{1}{x+26}=0,
frac{2cdot39(x+26)-x(x+26)-39x}{39x(x+26)}=0,
78x+39cdot52-x^2-26x-39x=0,
x^2-13x-39cdot52=0,
x_1=52,,x_2=-39.
Отрицательная скорость не удовлетворяет условию. Скорость первой машины 52 км/ч.
Ответ
52
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
В задачах на движение по прямой часто надо отыскать среднюю скорость транспортного средства.
Средняя скорость – это величина, равная отношению пути, пройденного телом, ко времени, за которое пройден этот путь.
$v_{ср}={S_{общий}}/{t_{общее}}$
Пример:
Первые $140$ км автомобиль ехал со скоростью $70$ км/ч, следующие $220$ км — со скоростью $80$ км/ч, а затем $30$ км — со скоростью $120$ км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
Для простоты решения задачи сделаем таблицу.
| $S_1=140км$ | $S_2=220км$ | $S_3=30км$ |
| $v_1=70$км/ч | $v_2=80$км/ч | $v_3=120$км/ч |
| $t_1-?$ | $t_2-?$ | $t_3-?$ |
Получилось три участка пути, про каждый участок мы знаем его путь и скорость, но для расчета средней скорости необходимо знать путь и время каждого участка. Найдем время каждого участка пути, для этого разделим путь на скорость.
$t_1={S_1}/{v_1}={140}/{70}=2$ часа
$t_2={S_2}/{v_2}={220}/{80}=2.75$ часа
$t_3={S_3}/{v_3}={30}/{120}=0.25$ часа
$v_{ср}={S_1+S_2+S_3}/{t_1+t_2+t_3}={140+220+30}/{2+2.75+0.25}={390}/{5}=78$ км/ч
Ответ: $78$ км/ч
Иногда встречаются такие задачи на движение, в которых учитываются размеры транспортного средства. Чаще всего в таких задачах необходимо рассчитать длину поезда, например.
Поезд, двигаясь равномерно со скоростью $60$ км/ч, проезжает мимо платформы, длина которой равна $200$ метрам, за $3$ минуты. Найдите длину поезда в метрах.
Решение:
Считается, что поезд проедет полностью мимо платформы, если он проедет длину платформы и еще свою длину.
Найдем расстояние, которое поезд проедет за три минуты. Время переведем в секунды и умножим на скорость поезда, которую переведем из км/ч в м/с.
$3$ минуты $=3·60=180$ секунд
$60$ км/ч$={60}/{3.6}={600}/{36}={50}/{3}$ м/с
$S=v·t={50·180}/{3}=3000$ метров
Чтобы найти длину поезда из всего пройденного пути за $3$ минуты вычтем длину платформы:
$l=3000-200=2800$ метров.
Ответ: $2800$
Пример:
Два велосипедиста одновременно отправились в пробег протяжённостью $84$ километра. Первый ехал со скоростью, на $5$ км/ч большей скорости второго, и прибыл к финишу на $5$ часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Решение:
Пусть $х$ км/ч –скорость второго велосипедиста, тогда $(х+5)$ км/ч – скорость первого велосипедиста.
Создаем стандартную таблицу и столбец $«v»$ заполняем данными с неизвестными.
| $S$(км) | $v$(км) | $t$(ч) | |
| Первый велосипедист | $(x+5)$ | ||
| Второй велосипедист | $x$ |
Так как расстояние, которое проехали велосипедисты одинаково и равно $84$ км, заполняем столбец $«S»$.
| $S$(км) | $v$(км) | $t$(ч) | |
| Первый велосипедист | $84$ | $(x+5)$ | |
| Второй велосипедист | $84$ | $x$ |
Третий столбец заполняем по формуле $t={S}/{v}$.
| $S$(км) | $v$(км) | $t$(ч) | |
| Первый велосипедист | $84$ | $(x+5)$ | ${84}/{(x+5)}$ |
| Второй велосипедист | $84$ | $x$ | ${84}/{x}$ |
Именно содержимое третьего столбца будем использовать для составления уравнения к задаче. По условию задачи разница между временами движения велосипедистов равна $5$ часов. Дольше в пути находился второй велосипедист, следовательно, из большего времени отнимаем меньшее время и все это равно разнице времен.
${84}/{х}-{84}/{(х+5)}=5$
Перенесем все слагаемые в левую сторону уравнения
${84}/{х}-{84}/{(х+5)}-5=0$
Приведем все слагаемые к общему знаменателю $х(х+5)$, тогда к первой дроби дополнительный множитель равен $(х+5)$, ко второй $х$, а к третьему слагаемому $(х^2+5х)$.Получаем:
${84х+420-84х-5х^2-25х}/{х(х+5)}=0$
Далее проговариваем: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
$84х+420-84х-5х^2-25х=0; х(х+5)≠0$
Найдем сначала корни знаменателя (ОДЗ дроби)
$х(х+5)≠0$
$х≠0$ или $х+5≠0$
$х≠0$ или $х≠-5$
Найдем корни числителя.
$84х+420-84х-5х^2-25х=0;$
Приведем подобные слагаемые и расставим поставим их в порядке убывания степеней
$-5х^2-25х+420=0$
Разделим уравнение на $(-5)$
$х^2+5х-84=0$
По теореме Виета
$х_1=-12, х_2=7$
$х_1=-12$ нам не подходит, так как отрицательная величина.
$х_2=7$ км/ч – скорость велосипедиста.
Ответ: $7$
Некоторые нюансы в задачах с круговым движением:
- В задачах на движение по окружности желательно делать рисунок, чтобы расставить величины и увидеть взаимосвязь между транспортными средствами.
- Если транспортные средства начали двигаться из одной точки в диаметрально противоположных направлениях, то между ними расстояние равное половине длины окружности.
- Если в задаче сказано, что транспортные средства двигаются в одном направлении, то необходимо узнать их скорость опережения: для этого из большей скорости вычитается меньшая.
- Любую задачу на круговое движение можно представить как задачу на прямолинейном отрезке, мысленно развернув круговую трассу в прямую.
Пример:
Из одной точки круговой трассы, длина которой равна $18$ км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна $92$ км/ч, и через $45$ минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Сделаем рисунок к задаче, для этого мысленно развернем круговую трассу в прямую.
$S=18$ км
$t=45$мин$={3}/{4}$часа
Пусть $х$ км/ч — скорость второго автомобиля.
Скорость опережения равна разности скоростей.
Тогда скорость опережения равна $v_{опережения}=(92-х)$. Так как первый автомобиль обгонит второй на один круг за $45$ минут, то скорость опережения можно выразить еще одним способом: для этого длину круга надо разделить на время опережения.
Не забываем перевести время из минут в часы $45$минут$={45}/{60}={3}/{4}$часа
$v_{опережения}={S}/{t}={18}/{{3}/{4}}={18·4}/{3}=24$
Так как мы разными записями выразили скорость опережения, то для составления уравнения приравняем обе записи друг к другу.
$92-х=24$
$-х=24-92$
$х=68$ км/ч – скорость второго автомобиля.
Ответ: $68$
Скорость по течению реки равна сумме собственной скорости транспортного средства и скорости течения реки
$v=v_{собственная}+v_{течения реки}$
Чтобы найти скорость против течения, нужно отнять от собственной скорости транспортного средства скорость течения реки
$v=v_{собственная}-v_{течения реки}$
Пример:
Катер прошел против течения реки $120$ км и вернулся обратно, затратив на обратный путь на $4$ часа меньше времени. Найдите скорость катера в стоячей воде, если скорость течения реки $4$ км/ч. Ответ дайте в км/ч.
Решение:
Для начала необходимо за «х» взять неизвестную. В нашем случае(и чаще всего) за «х» берется скорость.
Пусть $х$ км/ч – собственная скорость катера, тогда $(х+4)$ км/ч – скорость катера по течению; $(х-4)$ км/ч – скорость катера против течения.
Создаем стандартную таблицу и столбец $«v»$ заполняем данными с неизвестными.
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $(x+4)$ | ||
| Против течения | $(x-4)$ |
Так как расстояние, которое катер проплыл по течению и против течения одинаково и равно $120$ км, заполняем столбец $«S»$
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $120$ | $(x+4)$ | |
| Против течения | $120$ | $(x-4)$ |
Третий столбец заполняем по формуле $t={S}/{v}$
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $120$ | $(x+4)$ | ${120}/{(х+4)}$ |
| Против течения | $120$ | $(x-4)$ | ${120}/{(х-4)}$ |
Именно содержимое третьего столбца будем использовать для составления уравнения к задаче. По условию задачи разница между временами движения против течения и по течению равна $4$ часа, следовательно, из большего времени отнимаем меньшее время и все это равно разнице времен.
${120}/{(х-4)}-{120}/{(х+4)}=4$
Решим полученное дробно рациональное уравнение, для этого перенесем все слагаемые в левую часть.
${120}/{(х-4)}-{120}/{(х+4)}-4=0$
Приведем дроби к общему знаменателю $(х-4)(х+4)$, тогда к первой дроби дополнительный множитель равен $(х+4)$, ко второй $(х-4)$, а к третьему слагаемому $(х+4)(х-4)$. Получаем:
${120(х+4)-120(х-4)-4(х-4)(х+4)}/{(х-4)(х+4)}=0$
Далее проговариваем: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
$120(х+4)-120(х-4)-4(х-4)(х+4)=0; (х-4)(х+4)≠0$
Найдем сначала корни знаменателя (ОДЗ дроби)
$(х-4)(х+4)≠0$
$х-4≠0$ или $х+4≠0$
$х≠4$ или $х≠-4$
Найдем корни числителя.
$120(х+4)-120(х-4)-4(х-4)(х+4)=0$
Для этого раскроем скобки и приведем подобные слагаемые.
$120х+480-120х+480-4х^2+64=0$
$-4х^2+1024=0$
$-4х^2=-1024$
Разделим обе части уравнения на $(-4)$
$х^2=256$
$х_{1,2}=±16$
Так как за «х» мы брали собственную скорость катера, а она отрицательной быть не может, следовательно, нам подходит только корень $х=16$ км/ч
Ответ: $16$
Пример:
От пристани $А$ к пристани $В$, расстояние между которыми равно $70$ км, отправился с постоянной скоростью первый теплоход, а через $1$ час после этого следом за ним, со скоростью, на $8$ км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт $В$ оба теплохода прибыли одновременно.
Решение:
Пусть $х$ км/ч- это скорость первого теплохода, тогда $(х+8)$ км/ч –это скорость второго теплохода.
Составим таблицу, в которой заполним столбцы путь $«S»$ и скорость $«v»$ по условию задачи, а третий столбец время $«t»$ заполним по формуле $t={S}/{v}$
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| Первый теплоход | $70$ | $x$ | ${70}/{х}$ |
| Второй теплоход | $70$ | $(x+8)$ | ${70}/{(х+8)}$ |
Так как второй теплоход выехал на час позже, то время его в пути на час меньше относительно времени первого теплохода. Составим и решим уравнение: из большего времени отнимаем меньшее время и все это равно разнице времен
${70}/{х}-{70}/{(х+8)}=1$
${70}/{х}-{70}/{(х+8)}-1=0$
Приводим дроби к общему знаменателю
${70(х+8)-70х-х(х+8)}/{х(х+8)}=0$
${70х+560-70х-х^2-8х}/{х(х+8)}=0$
Найдем сначала корни знаменателя(ОДЗ дроби)
$х(х+8)≠0$
$х≠0$ или $х+8≠0; х≠-8$
Найдем корни числителя
$70х+560-70х-х^2-8х=0$
$-х^2-8х+560=0$
$х^2+8х-560=0$
По т.Виета $х_1+х_2=-8$
$х_1∙х_2=-560$
$х_1=-28; х_2=20$, первый корень нам не подходит, так как он отрицательный, следовательно скорость первого теплохода равна $20$ км/ч.
Ответ: $20$
Задача 1. Два велосипедиста одновременно отправились в -километровый пробег. Первый ехал со скоростью, на
км/ч большей, чем скорость второго, и прибыл к финишу на
часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Решение: + показать
Задача 2. Из пункта А в пункт В, расстояние между которыми км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на
км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на
часов позже автомобилиста. Ответ дайте в км/ч.
Решение: + показать
Задача 3. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно км. На следующий день он отправился обратно со скоростью на
км/ч больше прежней. По дороге он сделал остановку на
часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Решение: + показать
Задача 4. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 10 км/ч, а вторую половину пути – со скоростью 60 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 39 км/ч. Ответ дайте в км/ч.
Решение: + показать
Задача 5. Из двух городов, расстояние между которыми равно км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны
км/ч и
км/ч?
Решение: + показать
Задача 6. Из городов A и B, расстояние между которыми равно км, навстречу друг другу одновременно выехали два автомобиля и встретились через
часа на расстоянии
км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
Решение: + показать
Задача 7. Расстояние между городами A и B равно км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью
км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии
км от города A. Ответ дайте в км/ч.
Решение: + показать
Задача 8. Товарный поезд каждую минуту проезжает на метров меньше, чем скорый, и на путь в
км тратит времени на
часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.
Решение: + показать
Задача 9. Расстояние между городами A и B равно км. Из города A в город B выехал автомобиль, а через
часа следом за ним со скоростью
км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Решение: + показать
Задача 10. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным
метрам?
Решение: + показать
Задача 11. Первый велосипедист выехал из поселка по шоссе со скоростью км/ч. Через час после него со скоростью
км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через
часа
минут после этого догнал первого. Ответ дайте в км/ч.
Решение: + показать
Задача 12. Поезд, двигаясь равномерно со скоростью км/ч, проезжает мимо придорожного столба за
секунд. Найдите длину поезда в метрах.
Решение: + показать
Задача 13. Поезд, двигаясь равномерно со скоростью км/ч, проезжает мимо лесополосы, длина которой равна
метров, за
секунд. Найдите длину поезда в метрах. Видео*
Решение: + показать
Задача 14. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно км/ч и
км/ч. Длина товарного поезда равна
метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно
минутам. Ответ дайте в метрах.
Решение: + показать
Задача 15. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно км/ч и
км/ч. Длина пассажирского поезда равна
метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно
секундам. Ответ дайте в метрах.
Решение: + показать
Вы можете пройти тест по задачам на движение по прямой.
Классическим примером текстовой задачи, которая может встретиться вам на ЕГЭ, является задача на движение. Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.
Научиться решать такие задачи довольно легко, для этого нужно знать алгоритм, состоящий всего из 3 шагов.
- Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
- Как решать задачи на движение: 3 простых шага
- Задачи на движение вдогонку: примеры с решением
- Задачи на движение навстречу: примеры с решением
- Задачи на движение по течению и против течения: примеры с решением
Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
Для решения любой задачи на движение вам обязательно нужно знать всего одну формулу, которая вам уже давно известна:


Чтобы правильно решить задачу на движение нужно:
- Определить неизвестное и составить таблицу на основании условия задачи.
- Составить уравнение на основании таблицы.
- Вернуться к условиям задачи и записать правильный ответ.
Давайте подробнее разберем каждый шаг:
- Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
- На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
- После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти. Находим неизвестное и записываем ответ.
Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.
Задачи на движение вдогонку: примеры с решением
При решении задачи, по условия которой оба участника движения двигаются в одном направлении, как правило, сравнивается время их движения. Необходимо запомнить правила:
- Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
- Если условия задачи содержат общее время, то дроби, выражающее время, складываются.
Давайте разберем, как работают эти правила при решении задач.
Задача 1
Велосипедист и автомобилист одновременно выехали из пункта А в пункт Б, расстояние между которыми равно 50 км. Известно, что скорость автомобилиста на 40 км/ч больше, чем у велосипедиста, в результате чего автомобилист приехал в пункт Б на 4 часа раньше. Найдите скорость велосипедиста.
Решение:
1. Необходимо определить, что взять за переменную Х и составить таблицу. Вспоминаем, что удобнее всего за Х обозначить скорость в том случае, если она прямо не указано в условиях задачи.
В нашем случае скорость в условиях задачи не указана, поэтому скорость велосипедиста обозначаем за Х.
Составляем таблицу, данные для которой берем из условий задачи.
Итак, расстояние (S) нам известно – 50 км, скорость велосипедиста – х, скорость автомобилиста на 40 км/ч больше, значит она равна х + 40. Чтобы определить время вспоминаем формулу t = S / V и подставляем в нее наши значения. Время, затраченное велосипедистом, получится 50 / х, а время, затраченное автомобилистом — 50 / (х + 40).
Из условий задачи нам известно, что автомобилист приехал раньше велосипедиста на 4 часа (смотрим наше первое правило). Это значит, что велосипедист затратил на 4 часа больше времени, чем автомобилист. Следовательно,
50 / (х + 40) + 4 = 50 / х
Решаем полученное уравнение, для этого приводим наши дроби к одному знаменателю:
50х + 4х (х + 40) – 50 (х+40) / х (х + 40) = 0
(50х + 4х2 + 160х – 50х – 2000) / х (х+40) = 0
(4х2 + 160х – 2000) / (х2 + 40х) = 0
Умножим обе части уравнение на х2 + 40х:
4х2 + 160х – 2000 = 0
Разделим обе части уравнения на 4:
х2 + 40х – 500 = 0
Находим дискриминант:
D = 402 – 4 * 1 * (-500) = 3600
Далее находим корни уравнения:
х1 = 10
х2 = — 50
3. Возвращаемся к условиям задачи и вспоминаем, что же требовалось найти.
Нам нужно было определить скорость велосипедиста, которую мы обозначили за Х.
Скорость велосипедиста должна быть положительна, поэтому х2 не подходит по смыслу задачи. Следовательно, нас интересует только х1 и скорость велосипедиста равна 10 км/ч.
Ответ: 10 км/ч.
Задача 2
Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 80 км. На следующий день он поехал обратно, при этом его скорость была на 2 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 2 часа. В итоге на возвращение из города Б в город А у него ушло времени столько же, сколько на путь из города А в город Б. Найдите скорость велосипедиста на пути из города А в город Б.
Решение:
1. Обозначим скорость велосипедиста на пути из города А в город Б как переменную Х.
Составим таблицу.
Из условий задачи: расстояние — 80 км, скорость велосипедиста во второй день – х. Его скорость во второй день была на 2 км/ч больше, чем в первый день, т.е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).
Из условий задачи нам известно, что во второй день велосипедист останавливался и отдыхал 2 часа, следовательно, в пути он провел на 2 часа меньше (смотрим наше первое правило). Также нам известно, что общее затраченное велосипедистом время в первый и во второй дни равно. Следовательно:
80 / (х + 2) + 2 = (80 / х)
Решаем полученное уравнение, для чего приводим дроби к общему знаменателю:
(80х + 160 – 80х – 2х (х+2)) / х (х + 2) = 0
Умножаем обе части уравнения на х (х + 2):
160 – 2х2 + 4х = 0
— 2х2 — 4х + 160 = 0
Делим обе части уравнения на -2:
х2 + 2х – 80 = 0
Находим дискриминант:
D = 22 – 4 * 1 * (-80) = 4 + 320 = 324
Тогда корни уравнения равны:
х1 = 8
х2 = — 10
3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.
Скорость должна быть положительна, поэтому х2 = — 10 не подходит по смыслу задачи. Следовательно, скорость велосипедиста равна 8.
Ответ: 8 км/ч.
Задачи на движение навстречу: примеры с решением
Главное, что нужно помнить о движении навстречу: скорости участников движения складываются.
В тех случаях, когда нам неизвестно общее расстояние, то есть мы не можем его определить из условий задачи и из составленных уравнений, данное расстояние следует принимать за единицу.
Примеры решения задач на движение навстречу:
Задача 1
Из города А в город Б выехал автомобилист, через 3 часа навстречу ему выехал мотоциклист со скоростью 60 км/ч. Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Расстояние между городами А и Б равно 470 км. Найдите скорость автомобилиста.
Решение:
1. Обозначим скорость автомобилиста как Х.
Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Следовательно, автомобилист проехал 350 км, а мотоциклист 470 – 350 = 120 км.
Составим таблицу:
Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно:
350/х = 120/60 + 3
350/х = 5
Решаем полученное уравнение:
5х = 350
х = 70
3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость автомобилиста, которую мы обозначали за Х. Следовательно, скорость автомобилиста равна 70 км/ч.
Ответ: 70 км/ч.
Задача 2
Из городов А и Б одновременно навстречу друг другу выехали автомобилист и велосипедист. Автомобилист приехал в город А на 6 часов раньше, чем велосипедист приехал в город Б. Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?
Решение:
1. Время автомобилиста обозначим как Х.
Примем расстояние между городами А и Б за единицу. Остальные данные берем из условий задачи.
Составим таблицу:
Известно, что велосипедист и автомобилист встретились через 4 часа после начала движения и в сумме преодолели все расстояние от города А до города Б. То есть все расстояние от города А до города Б было преодолено за 4 часа.
Вспоминаем, что при движении навстречу скорости движения участников складываются. Подставим в формулу пути известные нам данные:
((1 / х) + (1 / (х — 6))) * 4 = 1
Решаем полученное уравнение:
(4 / х) + (4 / (х — 6)) = 1
Приводим дроби к одному знаменателю:
(4х — 24 + 4х — х2 + 6х) / (х (х — 6)) = 0
Делим обе части уравнения на х (х — 6), при условии, что х > 6:
-х2 + 14х — 24 = 0
Умножим обе части уравнение на -1:
х2 — 14х + 24 = 0
Находим дискриминант нашего квадратного уравнения:
D = 142 – 4 * 1 * 24 = 100
Находим корни уравнения:
х1 = 12
х2 = 2
х2 < 6, следовательно, корнем уравнения не является.
3. Возвращаемся к условиям задачи. Нам необходимо было определить, сколько времени затратил автомобилист на путь из города Б в город А. Это время мы обозначали за Х. Следовательно, автомобилист затратил на путь из города Б в город А 12 часов.
Ответ: 12 часов.
Задачи на движение по течению и против течения: примеры с решением
В условиях задач на движение по реке всегда дано две скорости: собственная скорость судна (скорость, с которой он может двигаться в неподвижной воде) и скорость течения.
При этом возможны две ситуации: когда судно движется по течению и когда судно движется против течения.
Когда судно движется по течению, то течение помогает судну двигаться, оно начинает двигаться быстрее, следовательно, собственная скорость судна и скорость течения складываются.
Когда же судно двигается против течения, то оно ощущает сопротивление, плыть ему становится тяжелее. В этом случае скорость течения будет вычитаться из собственной скорости судна.
Давайте рассмотрим примеры решения задач на движение по реке.
Задача 1
Катер прошел против течения реки 160 км/ч и вернулся в пункт отправления, затратив времени на обратный путь на 8 часов меньше. Найдите скорость катера в неподвижной воде, если известно, что скорость течения реки равна 5 км/ч.
Решение:
1. Обозначим собственную скорость катера – х.
Составим таблицу:
По условиям задачи известно, что время, затраченное на путь по течению реки, на 8 часов меньше, чем время, затраченное на путь против течения реки (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Соответственно:
160 / (х + 5) + 8 = 160 / (х — 5)
Решаем данное уравнение. Для этого приводим дроби к общему знаменателю:
(160 (х – 5) + 8 (х – 5) (х + 5) – 160 (х + 5)) / (х – 5) (х + 5) = 0
(160х – 800 + (8х – 40) (х + 5) – 160х — 800) / (х – 5) (х + 5) = 0
Умножаем обе части уравнения на (х – 5) (х + 5):
-1600 + 8х2 + 40х – 40х – 200 = 0
8х2 – 1800 = 0
8х2 = 1800
х2 = 225
х1,2 = ±15
3. Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х1 = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.
Ответ: 15 км/ч.
Задача 2
Моторная лодка вышла в 9:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв в пункте Б 3 часа, моторная лодка повернула назад и вернулась в пункт А в 20:00. Найдите скорость течения реки, если известно, что собственная скорость моторной лодки 8 км/ч.
Решение:
1. Обозначим скорость течения реки за х. Остальные данные берем из условия задачи.
Составим таблицу:
Нам известно, что моторная лодка начала свое движение в 9:00, а закончила в 20:00, а также в течение этого времени пробыла без движения во время стоянки – 3 часа. Таким образом, общее время движения будет 20 – 9 – 3 = 8 часов. Когда речь идет об общем времени движения, то нам нужно сложить время движения по течению и время движения против течения (пользуемся вторым правилом, которое разбирали при решении задач на движение вдогонку). Получаем:
30 / (8+х) + 30 / (8-х) = 8
Решаем полученное уравнение. Для этого приводим дроби к общему знаменателю:
(30 (8+х) + 30 (8-х) – 8 (8-х) (8+х)) / (8-х) (8+х) = 0
Умножаем обе части уравнения на (8-х) (8+х):
240 + 30х + 240 – 30х – (64 – 8х) (8+х) = 0
480 – 512 – 64х + 64х – 8х2 = 0
8х2 = 32
х2 = 4
х1,2 = ±2
3. Возвращаемся к условию задачи. Нам необходимо было найти скорость течения, которую мы обозначили за х. Так как скорость не может быть отрицательной, то х1 = -2 противоречит условию задачи. Следовательно, скорость течения равна 2 км/ч.
Ответ: 2 км/ч.
Итак, мы разобрались, как решать задачи на движения. В ЕГЭ 2023 помимо задач на движение могут содержаться и другие текстовые задачи: на смеси и сплавы, на работу, на проценты. О том, как их решать, вы можете узнать на нашем сайте, а также .