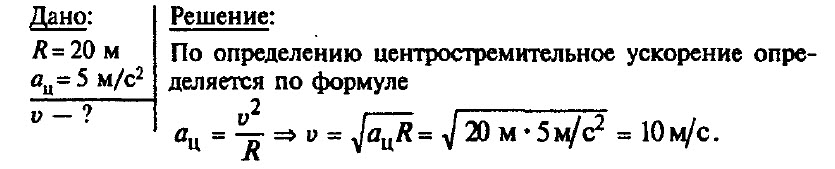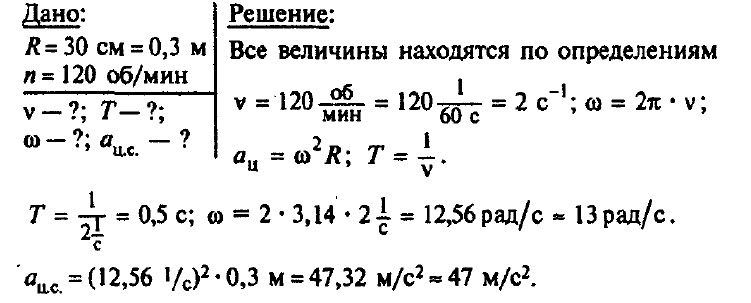Задачи на Движение тела по окружности с решениями
Формулы, используемые на уроках «Задачи на Движение тела по окружности».
Название величины |
Обозначение |
Единица измерения |
Формула |
Радиус окружности |
r |
м |
|
Линейная скорость (модуль) |
v |
м/с |
|
Центростремительное ускорение (модуль) |
a |
м/с2 |
|
Центростремительная сила (модуль) |
F |
Н |
|
Масса тела |
m |
кг |
|
Угловая скорость при равномерном вращении |
ω |
рад/с |
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Какова линейная скорость тела, движущегося по окружности радиусом 40 м с ускорением 2,5 м/с2 ?
Задача № 2.
С какой наибольшей скоростью может двигаться автомобиль массой 1 т на повороте радиусом 100 м, чтобы его не «занесло», если максимальная сила трения 4 кН?
Задача № 3.
Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.
Задача № 4.
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Задача № 5.
Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?
Задача № 6.
Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.
Задача № 7.
Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с2.
Задача № 8.
Шкив радиусом 30 см имеет частоту вращения 120 об/мин. Определите частоту, период обращения, угловую скорость шкива и центростремительное ускорение точек шкива, наиболее удаленных от оси вращения.
Задача № 9.
Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли. Радиус Земли считайте равным 6370 км.
Задача № 10.
ОГЭ
Точка движется равномерно по окружности. Как изменится её центростремительное ускорение, если скорость возрастёт вдвое, а радиус окружности вдвое уменьшится?
Задача № 11.
ЕГЭ
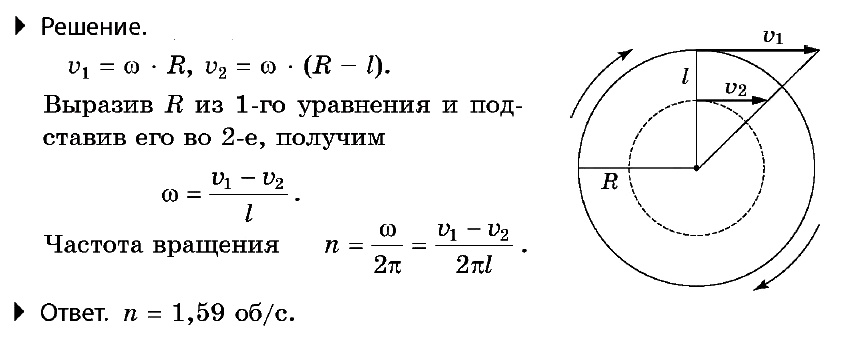
Линейная скорость точек обода вращающегося диска v1 = 3 м/с, а точек, находящихся на l = 10 см ближе к оси вращения, v2 = 2 м/с. Найти частоту вращения диска.
Задача № 12.
Груз, привязанный к шнуру длиной l = 50 см, описывает окружность в горизонтальной плоскости. Какой угол φ образует шнур с вертикалью, если частота вращения n = 1 с-1 ?
Рассуждение: На схеме покажем груз, подвешенный на нити и движущийся по окружности некого радиуса R в горизонтальной плоскости так, что нить составляет с вертикалью угол φ. На груз действуют две силы: 1) сила тяжести mg; 2) сила натяжения нити T. Так как груз не движется вдоль оси y, то запишем первый закон Ньютона в проекции на эту ось: T⋅• cos φ = mg. Поскольку груз описывается окружность, то второй закон Ньютона запишется так: T⋅• sin φ = ma.
Ответ: 60º.
Краткая теория для решения Задачи на Движение тела по окружности.
Это конспект по теме «ЗАДАЧИ на Движение тела по окружности». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Искусственные спутники планет.
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
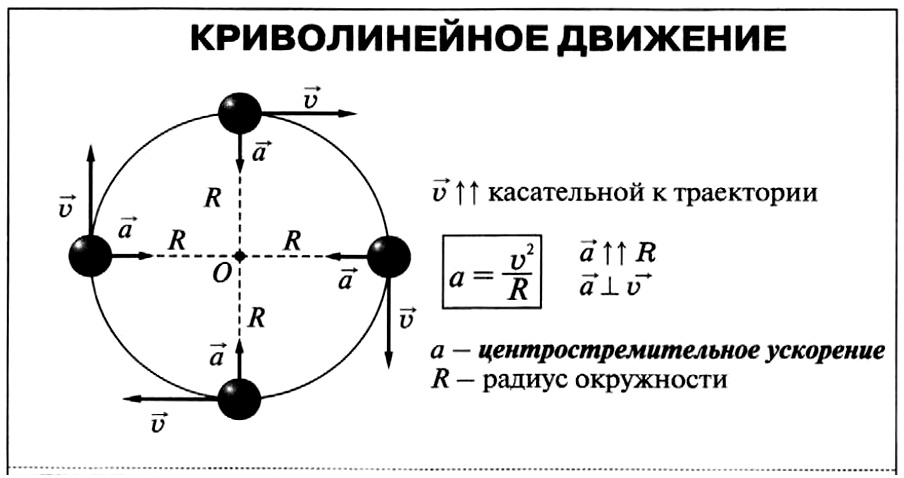
Движение по окружности
Криволинейное движение — механическое движение, траектория которого — кривые линии с произвольным ускорением и произвольной скоростью.
Угловая скорость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. [omega=dfracvarphi t=dfrac{2pi}{t}]
Период обращения — это время одного полного оборота.
Частота обращения — величина, обратная периоду. Частота показывает, сколько полных оборотов совершает материальная точка за секунду. [nu=dfrac1T]
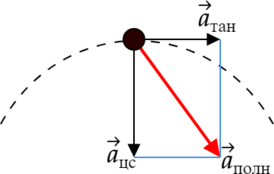
Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения.
Нормальное (центростремительное) ускорение — компонента ускорения, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной, направленное к центру кривизны траектории. [a_text{цс}=dfrac{v^2}{r}]
Полное ускорение тела, движущегося по окружности равно векторной сумме тангенциального и нормального ускорений. [overrightarrow a_text{полн}=overrightarrow a_text{тан}+overrightarrow a_text{цс}]
Шарик движется по окружности радиусом (R_1 = 2) м со скоростью ( upsilon_1 = 3) м/с. Во сколько раз изменится его центростремительное ускорение, если радиус его окружности уменьшить в (n = 3) раза, а скорость увеличить в (k = 5) раз?
По определению центростремительное ускорение равно: [a_{text{ц1}} = frac{upsilon_1^2}{R_1} qquad (1)] [a_{text{ц2}} = frac{upsilon_2^2}{R_2} qquad (2)]
По условию задачи: [upsilon_2=kupsilon_1 qquad (3)] [R_2 = frac{R_1}{n} qquad (4)]
Подставляя (3), (4) и (1) в (2) получаем: [a_{text{ц2}} = dfrac{(kupsilon_1)^2}{dfrac{R_1}{n}} = nk^2frac{upsilon_1^2}{R_1} = nk^2a_{text{ц1}}] [frac{a_{text{ц2}}}{a_{text{ц1}}} = nk^2 = 3cdot5^2 = 75]
Ответ: 75
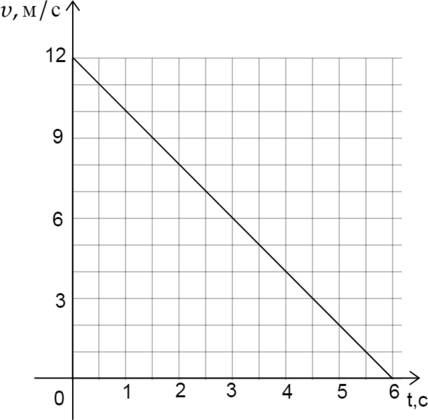
Тело движется по окружности радиусом (R=4) м. В какой момент времени центростремительное ускорение (a_text{цс} = 1 text{ м/с$^2$})?
При движении по окужности центростремительное ускорение можно найти по следующей формуле: [a_text{цс} = frac{upsilon^2}{R}] где (v) – скорость тела
Отсюда: [upsilon = sqrt{a_text{цс} cdot R} = sqrt{1 cdot 4} = 2text{ м/с }] По графику видно, что (upsilon = 2) м/с в момент времени (t=5) с.
Ответ: 5
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Чему равно центростремительное ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)
Центростремительное ускорение (нормальное): (displaystyle a_{text{цс}}=frac{upsilon^2}R=frac{(20 text{ м/с})^2}{100 text{ м}}=4) м/с(^2)
Ответ: 4
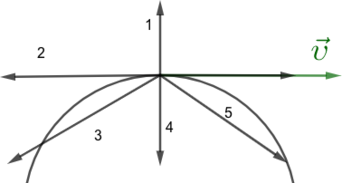
Велосипедист едет по круговому треку и замедляется. На рисунке указано направление скорости велосипедиста. Под каким номером верно указано направление центростремительного ускорения? Тангенциального ускорения? Куда направлено полное ускорение? (В ответе укажите последовательность цифр, например: 153)
Нормальная составляющая ускорения (центростремительное ускорение) характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело.
Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости:
1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное
2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным
Полное ускорение – это сумма нормального и тангенциального: [vec{a}_{text{полн}}=vec{a}_{text{норм}}+vec{a}_{text{танг}}]
Центростремительное ускорение направлено к центру (4). Так как велосепидист замедляется, то тангенциальное направлено против скорости (2). Полное ускорение является суммой 2 и 4, следовательно полное ускорение под номером 3.
Ответ: 423
Тело равномерно движется по окружности. Угловая скорость тела равна (w=6,5) рад/с. За какое время (t) тело совершит 5,5 оборотов? Принять (pi=3,14). Ответ округлить до десятых.
Cпособ 1:
Найдем длину дуги окружности: [l=2pi r,] где (r) — радиус окружности.
Т.к. тело прошло эту длину 5,5 раз, оно прошло путь: [S=5,5l=11pi rquad(1)] Выразим формульно линейную скорость (v) и угловую скорость тела:
[begin{cases}
v=2pi rnu\
w=2pinu
end{cases}
Rightarrow
v=wrquad(2)]
Т.к. тело движется равномерно, (v=const). По закону равномерного движения: [S=vt] Подставим ((1)) и ((2)): [11pi r=wrt] Осталось выразить (t): [t=dfrac{11pi}{w}=dfrac{11cdot3,14}{6,5text{ рад/с}}approx5,3text{ c}]
Cпособ 2 :
Выразим формульно (w): [w=dfrac{Deltavarphi}{t},quad(1)] где (Deltavarphi) — угол поворота тела. [Deltavarphi=dfrac{S}{r},] где (S=5,5l=5,5cdot2pi r=11pi r) — путь, пройденный телом. [Deltavarphi=dfrac{11pi r}{r}=11piquad(2)] Подставим (2) в (1): [w=dfrac{11pi}{t}] Осталось выразить (t): [t=dfrac{11pi}{w}=dfrac{11cdot3,14}{6,5text{ рад/с}}approx5,3text{ c}]
Ответ: 5,3
Две материальные точки движутся по окружностям радиусами (R_1) и (R_2), причем (R_2 = 3R_1). Скорости тел равны. Чему равно отношение их центростремительных ускорений?
По определению центростремительное ускорение равно: [a_{text{ц1}} = frac{upsilon^2}{R_1}] [a_{text{ц2}} = frac{upsilon^2}{R_2}]
Тогда искомое отношение равно: [frac{a_{text{ц1}}}{a_{text{ц2}}} = frac{dfrac{upsilon^2}{R_1}}{dfrac{upsilon^2}{R_2}} = frac{R_2}{R_1} = frac{3R_1}{R_1} = 3]
Ответ: 3
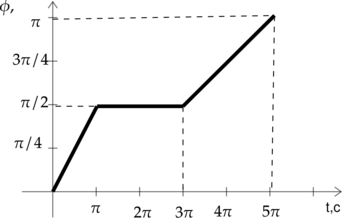
Точечное тело равномерно движется по окужности радиусом (R=2) м. На рисунке изображён график зависимости угла поворота (varphi) от времени (t). Найдите значение линейной скорости тела в интервале времени (3pi<t<5pi).
Линейная скорость тела, движущегося по окружности: [upsilon = omega cdot R qquad (1)] где (omega) – угловая скорость.
Угловая скорость: [omega = frac{Deltavarphi}{Delta t} qquad (2)] Подставив (2) в (1), получим: [upsilon = frac{Deltavarphi}{Delta t} cdot R] [upsilon = frac{dfrac{pi}{2}}{2pi} cdot 2 =0,5 text{ м/с}]
Ответ: 0,5

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Решение сложных задач. Движение по кругу
В статье собраны задачи из книги «Отличник ЕГЭ. Решение сложных задач» на тему «Движение по окружности». Правда, понадобятся знание формул равноускоренного движения и закон сложения классических скоростей, потому что такие задачи, как правило, сочетают в себе несколько областей знаний.
Задача 1.
У мальчика, сидящего на расстоянии м от оси на вращающейся с угловой скоростью
рад/с карусели, выпали из кармана с интервалом
с два камушка. На каком расстоянии друг от друга ударятся о землю эти камушки, если высота, с которой они упали, равна
м?
К задаче 1.
Обозначим искомое расстояние . Тогда по теореме косинусов запишем:
Здесь (обозначено жирной рыжей линией) — расстояние, которое пролетят камушки по горизонтали после отрыва от карусели,
— неизвестный нам отрезок касательной,
— угол, на который повернется карусель за 1 с. Все эти величины нам предстоит определить.
Сначала займемся отрезком . Запишем теорему косинусов для треугольника
:
Теперь запишем теорему косинусов для треугольника :
Отсюда, приравняв оба выражения, найдем:
Теперь определим . Движение камушков по вертикали – свободное падение. С высоты
камушки будут падать время
. При этом камушки будут обладать линейной скоростью
, поэтому улетят на расстояние
Наконец, угол поворота карусели:
Теперь упростим выражение для :
Подставим выражение для :
Заменим выражение на
:
Подставим найденный угол:
Подставляем :
Наконец, извлекаем корень:
Подставим числа:
Ответ: 6 м.
Задача решена в общем виде. Но ведь можно заметить, что 1,57 радиана — это прямой угол. Тогда задача сразу решается по теореме Пифагора без привлечения теоремы косинусов, и заметно упрощается.
Задача 2.
Колесо катится без проскальзывания по ленте транспортера, движущейся горизонтально со скоростью м/с, в направлении движения ленты. Известно, что относительно неподвижного наблюдателя скорость точки
, находящейся на ободе колеса на его горизонтальном диаметре, составляет с горизонтом угол
. Найти скорость
центра колеса относительно неподвижного наблюдателя.
К задаче 2
Тангенс угла равен отношению вертикальной и горизонтальной составляющей скорости:
Вертикальная составляющая скорости точки — скорость точки
относительно центра колеса — равна скорости центра колеса относительно мгновенного центра вращения – точки соприкосновения с лентой.
Относительно неподвижного наблюдателя скорость центра колеса равна сумме скоростей колеса (объект относительно системы отсчета) и системы отсчета (лента транспортера). Поэтому чтобы найти скорость объекта относительно системы отсчета, нужно вычесть из скорости точки
, а именно, ее горизонтальной составляющей, скорость ленты транспортера:
Горизонтальная составляющая скорости как раз равна скорости колеса относительно неподвижного наблюдателя. Тогда:
Подставим числа:
Ответ: 2,36 м/с
Задача 3.
Ведущая шестерня радиусом см вращается с постоянной угловой скоростью
рад/с и приводит во вращение шестерню радиусом
см. В некоторый момент времени метки
и
совпадают. Через какой минимальный промежуток времени относительная скорость меток станет равной нулю?
К задаче 3
Вектора линейных скоростей всегда равны по модулю. Относительная скорость будет равна нулю тогда, когда вектора линейных скоростей будут параллельны. То есть это случится тогда, когда оба вектора вместе, суммарно развернутся на — это минимальное время, до этого момента между векторами всегда есть некоторый угол. Вследствие разных радиусов угловые скорости вращения тоже разные:
Отсюда:
С другой стороны:
Угол, на который повернется ведущая шестерня, равен , а угол, на который повернется ведомая шестерня,
.
Перепишем последнюю пропорцию:
Определим угол :
Найдем теперь время:
Ответ: 2,1 с
1 комментарий
Евгения
✉️
19.04.2021 18:18:21
Задачу 2 хорошо через мгновенную ось вращения решить.
Задание 1 ЕГЭ по физике
Кинематика. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности.
Первое задание ЕГЭ по физике проверяет ваши знания по разделу «Кинематика». Оно относится к базовому уровню, и в нем нет возможности выбора ответа. Для его решения необходимо проанализировать условие задачи, внимательно рассмотреть график зависимости кинематической величины от времени (при наличии такого графика), правильно подобрать формулу, провести расчет и записать ответ в предлагаемых единицах измерения.
Определение кинематических величин по графику
1. На рисунке приведён график зависимости проекции скорости тела от времени t.
Определите проекцию ускорения тела в промежутке времени от 15 до 20 с.
Ответ: _________________________ м/с 2 .Решение:
На графике представлена зависимость проекции скорости от времени. На участке от 15 до 20 с скорость тела изменяется от 10 м/с до -10 м/с. Это говорит о равноускоренном движении, причем проекция ускорения тела должна быть отрицательной. Для решения задачи необходимо воспользоваться формулой для определения проекции ускорения:
Проведем расчет: (м/с 2 ).Полученный результат подтверждает, что движение равноускоренное, причем проекция ускорения отрицательная.
Секрет решения: Долгое время в учебниках физики движение с переменной скоростью делилось на равноускоренное и равнозамедленное Но в последнее время в основном применяют термин «равноускоренное движение», подразумевая постоянство ускорения. Только знак проекции ускорения определяет возрастание или убывание скорости движения тела.
2. На рисунке приведён график зависимости координаты тела x от времени t при его прямолинейном движении по оси x.
Определите проекцию скорости тела в промежутке времени от 25 до 30 с.
Ответ: ___________________________ м/с.
Согласно представленному графику, зависимость координаты тела от времени является линейной. Это указывает на равномерный характер движения тела. Чтобы решить задачу, необходимо воспользоваться формулой для определения скорости при равномерном движении:
Проведем расчет: (м/с)
Проекция скорости получилась отрицательной, и это означает, что в указанный временной интервал тело двигалось в направлении, противоположном выбранной оси Ох.
3. Автомобиль движется по прямой улице вдоль оси Ox. На графике представлена зависимость проекции его скорости от времени.
Определите путь, пройденный автомобилем за 30 с от момента начала наблюдения.
Ответ: _________________________ м.
Так как по условию задачи нам дается график зависимости проекции скорости от времени, то пройденный путь будет определяться площадью геометрической фигуры под графиком. Для вычисления площади получившегося пятиугольника его можно разбить на несколько фигур, например, на две трапеции (см. рис.).
Используя известные формулы для нахождения площади трапеции, можно рассчитать путь за первые 10 с и последующие 20 с (от 10 с до 30 с).
Полученный пятиугольник можно разбить не только на две трапеции. Здесь можно выделить трапецию, прямоугольник и треугольник. Тогда необходимо рассчитывать площади трех фигур и так же их суммировать.
4. На рисунке приведен график зависимости проекции скорости тела, движущегося вдоль оси Ох, от времени.
Определите проекцию перемещения тела за 10 с от начала наблюдения.
Ответ: ________________________ м.
Так же, как в задаче №3, модуль перемещения будет определяться площадью геометрической фигуры под графиком. Но проекция перемещения за время от 0 до 6 с будет положительной, а от 6 до 10 с отрицательной. Общая проекция перемещения будет определяться их суммой.
При расчете можно получить положительное число, но надо помнить, что в интервале от 6 до 10 с тело движется в направлении, противоположном оси Ох. Это означает, что проекция перемещения будет отрицательной. Пройденный путь за указанное время от 0 до 10 с определяется суммой модулей проекций перемещений и будет равным 60 м.
Относительность движения
5. Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость второго автомобиля 25 м/с. С какой скоростью движется первый автомобиль?
Ответ: ________________________ м/с.
Формула для нахождения относительной скорости в векторной форме имеет вид:
Если два тела движутся навстречу друг другу, то в проекциях на ось оХ это уравнение выглядит следующим образом:
С учетом данных графика можно рассчитать относительную скорость этих автомобилей при движении навстречу друг другу. Это происходит на интервале от 0 до 60 мин.

В курсе математики при изучении движения двух тел вводятся понятия «скорость сближения» и «скорость удаления». В первом случае скорости тел суммируются, во втором вычитаются. Эти действия основаны на знаках проекций скоростей движущихся тел. Действия с векторами и их проекциями на оси координат используются как в физике, так и в математике.
6. Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей Vx на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?
Ответ: ___________________________ м.
Эта задача является комбинированной. Для её решения необходимо воспользоваться материалом двух тем: «Определение кинематических величин по графику» и «Относительность движения». Для определения проекций перемещений тел за 8 с необходимо рассчитать площади фигур под графиком.
Знак «минус» для показывает, что тела движутся в противоположных направлениях. Поэтому расстояние между ними через 8 с равно сумме модулей перемещений.
Секрет решения:. Самое главное в этой задаче – выяснить, в каких направлениях двигаются тела. Для этого надо уметь извлекать информацию из графических зависимостей, другими словами, надо уметь «читать» графики. Это умения необходимы почти во всех разделах физики.
7. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды?
Ответ: ___________________________ км/ч
Решение задачи удобно сопроводить чертежом или рисунком. Выберем направление скорости реки вправо. Тогда катеру необходимо держать курс немного левее, чтобы двигаться перпендикулярно береговой линии.
Векторы собственной скорости катера, скорости течения реки и скорости катера относительно береговой линии образуют прямоугольный треугольник. Запишем для него теорему Пифагора:
Равномерное движение тел по окружности
8. Установленная на станке фреза равномерно вращается с частотой 600 оборотов в минуту. Чему равен модуль ускорения точек, находящихся на расстоянии 3 см от оси фрезы? Ответ округлите до целого числа.
Ответ: ___________________________ м/с 2 .
Так как тело движется равномерно по окружности, то найти требуется центростремительное ускорение. Его можно рассчитать по формуле: 

Проведем расчет:
В теме «Равномерное движение тел по окружности» достаточно много формул, которые трудно запоминаются. Из них надо знать базовые, которые относятся к периоду, частоте, линейной скорости, угловой скорости и центростремительному ускорению. Все остальные можно получить через достаточно простые рассуждения и выводы.
9. Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 секунд. Сколько оборотов в секунду делает меньшая шестерня радиусом 10 см?
Ответ: ___________________________ Гц.
Так как шестерни касаются друг друга, это условие говорит о равенстве линейных скоростей этих тел. Выразим скорости вращения через радиусы и периоды обращения.
Приравняем скорости и проведем сокращения.
с учетом того, что период и частота величины обратные, запишем следующее равенство:
Проведем расчет: (Гц).
В задачах подобного типа всегда надо искать физическую величину, которая является общей для нескольких тел. В данной задаче – это скорость вращения обеих шестерней. Но надо иметь ввиду, что частоты их вращения и угловые скорости различны.
10. Волчок, вращаясь с частотой 20 с -1 , свободно падает с высоты 5 м. Сколько оборотов сделает волчок за время падения?
Ответ: ___________________________ оборотов.
Вначале определим время падения волчка с высоты 5 м. Так как он падает свободно, то начальную скорость будет равна 0. Тогда высота и время падения будут связаны формулой отсюда Проведем расчет времени падения: (с). Так как волчок вращается с частотой 20 то это означает, что за 1 секунду он делает 20 оборотов. Так как время падения составляет 1 с, то количество оборотов также равно 20.
Секрет решения: Эта задача — комбинированная. В ней связаны два раздела кинематики: «Равноускоренное движение» и «Равномерное движение тел по окружности». Надо знать, что суть формул при движении тел с ускорением по горизонтали или по вертикали под действием силы тяжести не меняется. Главное — не ошибиться со знаками проекций для скорости и ускорения.
Решение задач по теме: «Движение по окружности» Подготовка к ЕГЭ задание «В»
материал для подготовки к егэ (гиа) по физике по теме
Решение задач по теме «Движение по окружности».
Скачать:
| Вложение | Размер |
|---|---|
| zadachi_v.doc | 166 КБ |
Предварительный просмотр:
Решение задач по теме: «Движение по окружности»
Подготовка к ЕГЭ задание «В»
В задачах по элементарному курсу электромагнетизма можно выделить основные группы:
а) задачи о силовом действии ЭМ-поля на проводники с током и
б) задачи о силовом действии ЭМ-поля на движущиеся в нем заряженные частицы.
Плоское движенце заряженной частицы в однородном магнитном поле.
При движении заряженной частицы в магнитном поле на нее действует сила Лоренца, которая, как известно, направлена перпендикулярно вектору скорости частицы, поэтому эта сила работы не совершает. Следовательно, при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются — изменяется только направление вектора скорости частицы.
Рассмотрим движение заряженной частицы в однородном магнитном поле, когда вектор скорости частицы направлен перпендикулярно вектору индукции магнитного поля. Так как модуль скорости частицы сохраняется, сила Лоренца перпендикулярна вектору индукции поля, то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным Fл = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона.
из которого находим:
Найдем период обращения частицы в магнитном поле: .
Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы при увеличении скорости движения?
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Курс подготовки к ЕГЭ. Движение материальной точки по окружности
Светлана Юрьевна Трофимова и Валерий Евгеньевич Фрадкин
Техническая поддержка Александра Мыльникова
| Краткий конспект | Задания | Ссылки |

Применение знаний о движении по окружности в других темах: Задания для самостоятельного решения Задачи для решения по темам источники: http://nsportal.ru/shkola/fizika/library/2013/11/30/reshenie-zadach-po-teme-dvizhenie-po-okruzhnosti-podgotovka-k-ege http://www.eduspb.com/node/2369 |
ЕГЭ Профиль №9. Задачи на движение по окружности
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Задачи на движение по окружности
| Задача 1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Пусть x км/ч – скорость первого мотоциклиста, тогда скорость второго равна x + 21 км/ч. Пусть первый раз мотоциклисты поравняются через t часов.
Чтобы мотоциклисты поравнялись, второй мотоциклист (скорость которого больше) должен проехать на изначально разделяющее их расстояние, которое равно половине длины трассы, то есть 7 км. Следовательно: (left( {x + 21} right),t — x,t = 7,,,, Leftrightarrow ,,,,x,t + 21,t — x,t = 7,,,, Leftrightarrow ,,,,21,t = 7,,,, Leftrightarrow ,,,,frac{1}{3}.) Таким образом, мотоциклисты поравняются через (t = frac{1}{3}) часа, что составляет 20 минут. Ответ: 20. |
||||||||||||||||||||||||
| Задача 2. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Пусть x км/ч – скорость второго автомобиля.
Для того чтобы первый автомобиль опережал второго ровно на один круг, необходимо, чтобы он проехал на один круг больше, длина которого равна 14 км. (80 cdot frac{2}{3} — frac{2}{3}x = 14,,left| {, cdot 3} right.,,,, Leftrightarrow ,,,,160 — 2x = 42,,,, Leftrightarrow ,,,,2x = 118,,,, Leftrightarrow ,,,,x = 59) км/ч. Ответ: 59. |
||||||||||||||||||||||||
| Задача 3. Из пункта A круговой трассы выехал велосипедист. Через 30 минут он ещё не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
За (frac{1}{2}) часа мотоциклист проехал на 30 км больше. (frac{1}{2} cdot x — frac{1}{2} cdot frac{x}{4} = 30,,left| {, cdot 8,,,,} right. Leftrightarrow ,,,,4x — x = 240,,,, Leftrightarrow ,,,,3x = 240,,,, Leftrightarrow ,,,,x = 80) км/ч. Ответ: 80. |
||||||||||||||||||||||||
| Задача 4. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
Первый раз стрелки встретятся между 8 и 9 часами, второй – между 9 и 10 часами, третий – между 10 и 11 часами, четвертый ровно в 12 часов, то есть через 4 часа после начала движения, что составляет 240 минут. Ответ: 240. |
||||||||||||||||||||||||
| Задача 5. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
Пусть x км/ч – скорость второго гонщика, а y км/ч – скорость первого. Составим уравнение на случай, когда гонщики проехали 60 кругов по 3 км, то есть 180 км.
Так как, на финиш первый приехал раньше второго на 10 минут, то есть на (frac{1}{6}) часа, то: (frac{{180}}{x} — frac{{180}}{y} = frac{1}{6}.) Составим уравнение на случай, когда гонщики едут 15 минут, то есть (frac{1}{4}) часа.
Так как, за 15 минут первый гонщик обогнал второго на круг, то он проехал на 3 км больше, то есть: (frac{1}{4}y — frac{1}{4}x = 3,left| {, cdot 4,,,, Leftrightarrow ,,,,y — x = 12} right..) Таким образом, получаем систему уравнений: (left{ {begin{array}{*{20}{c}} {frac{{180}}{x} — frac{{180}}{y} = frac{1}{6};} \ {y — x = 12.,,,,,,,,,,} end{array}} right.) Из второго уравнения: (y = x + 12). Подставляя в первое уравнение, получим:
(D = {12^2} + 4 cdot 6 cdot 180 cdot 12 = {12^2} + {12^2} cdot 2 cdot 180 = {12^2}left( {1 + 360} right) = {12^2} cdot 361;,,,,sqrt D = 12 cdot 19;) ({x_1} = frac{{ — 12 + 12 cdot 19}}{2} = frac{{12left( {19 — 1} right)}}{2} = 12 cdot 9 = 108;) ({x_2} = frac{{ — 12 — 12 cdot 19}}{2} = frac{{12left( { — 1 — 19} right)}}{2} = 12 cdot left( { — 10} right) = — 120.) Так как (x > 0), то скорость второго гонщика равна 108 км/ч. Ответ: 108. |