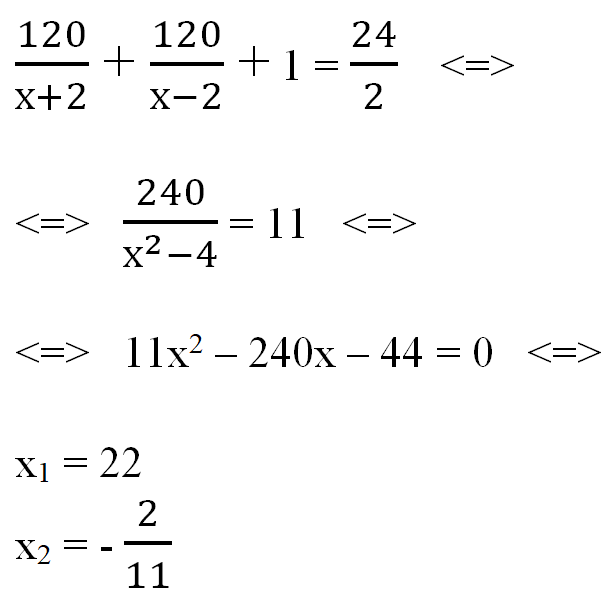11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на движение по воде
Верны те же формулы: [{large{S=vcdot t quad quad quad v=dfrac
St quad quad quad
t=dfrac Sv}}]
(blacktriangleright) Если тело движется по реке по течению:
(v_c) — собственная скорость тела (скорость в неподвижной воде);
(v_t) — скорость течения;
тогда скорость движения тела (v=v_c+v_t).
Значит, [{large{S=(v_c+v_t)cdot t}}]
(blacktriangleright) Если тело движется по реке против течения:
(v_c) — собственная скорость тела (скорость в неподвижной воде);
(v_t) — скорость течения;
тогда скорость движения тела (v=v_c-v_t).
Значит, [{large{S=(v_c-v_t)cdot t}}]
(blacktriangleright) Заметим, что плот — это тело, у которого собственная скорость (v_c=0). Значит, плот может плыть только по течению и со скоростью течения.
Задание
1
#2120
Уровень задания: Легче ЕГЭ
Антон знает, что собственная скорость его лодки равна (10, км/ч). При этом ему надо успеть проплыть (25, км) за (2) часа. Плыть он будет по течению. Какой должна быть скорость течения реки, чтобы Антон успел? Ответ дайте в км/ч. Если в задаче может быть более одного ответа – выберите наименьший.
Чтобы Антон успел, необходимо и достаточно, чтобы его лодка перемещалась со скоростью не меньше, чем (25 : 2 = 12,5, км/ч). То есть для того, чтобы Антон успел, необходимо и достаточно, чтобы скорость течения была не меньше, чем (2,5, км/ч).
Ответ: 2,5
Задание
2
#2124
Уровень задания: Легче ЕГЭ
Лодка прошла (10, км) по течению, а затем (5, км) против течения. На весь путь лодка затратила (3, часа). Найдите среднюю скорость лодки на описанном участке пути, если скорость течения равна (2, км/ч). Ответ дайте в км/ч.
Средняя скорость есть отношение всего пути ко времени, затраченному на этот путь. Независимо от скорости течения, средняя скорость лодки:[v_{ср} = dfrac{10 + 5}{3} = 5, км/ч,.]
Ответ: 5
Задание
3
#826
Уровень задания: Равен ЕГЭ
Катер береговой охраны прошёл по течению реки Конго 120 км и вернулся обратно. Известно, что обратный путь занял на 1 час больше времени, а скорость катера в неподвижной воде равна 27 км/ч. Найдите скорость течения. Ответ дайте в км/ч.
Пусть (v) км/ч – скорость течения, (v > 0), тогда
(27 + v) – скорость перемещения катера по течению,
(27 — v) – скорость перемещения катера против течения,
(dfrac{120}{27 + v}) – время, затраченное катером на перемещение по течению,
(dfrac{120}{27 — v}) – время, затраченное катером на перемещение против течения.
Так как время перемещения против течения на час больше, чем время по течению, то: [dfrac{120}{27 + v} + 1 = dfrac{120}{27 — v}qquadLeftrightarrowqquad v^2 + 240 v — 729 = 0] – при (v neq pm 27), что равносильно (v_1 = 3, v_2 = -243), откуда получаем, что (v = 3) км/ч, так как (v > 0).
Ответ: 3
Задание
4
#3075
Уровень задания: Равен ЕГЭ
Катер прошел 40 км по течению реки и 6 км против течения реки, затратив на весь путь 3 ч. Найдите скорость катера в стоячей воде, если известно, что скорость течения реки равна 2 км/ч.
Пусть (x) км/ч – скорость катера в стоячей воде. Тогда можно составить следующее уравнение: [dfrac{40}{x+2}+dfrac 6{x-2}=3 quadRightarrowquad
dfrac{46x-68}{x^2-4}=3 quadRightarrowquad 3x^2-46x+56=0] Дискриминант равен (D=4cdot 361=(38)^2), следовательно, корнями будут (x_1=dfrac43) и (x_2=14). Так как скорость катера не может быть меньше скорости течения, то (x_1) не подходит. Следовательно, (x=14).
Ответ: 14
Задание
5
#3864
Уровень задания: Равен ЕГЭ
Теплоход, скорость которого в неподвижной воде равна (24) км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна (3) км/ч, стоянка длится (2) часа, а в исходный пункт теплоход возвращается через (34) часа после отправления из него. Сколько километров прошёл теплоход за весь рейс?
Пусть (S) – расстояние в километрах, которое проходит теплоход, двигаясь в одну сторону. Тогда: [dfrac S{24+3}+dfrac S{24-3}+2=34quadLeftrightarrowquad S=378] Тогда за весь рейс теплоход прошел (2S=2cdot 378=756) километров.
Ответ: 756
Задание
6
#827
Уровень задания: Равен ЕГЭ
От пристани A в направлении пристани В с постоянной скоростью отправился первый теплоход. Через час после этого от пристани В в направлении пристани А отправился второй теплоход, причём скорость второго теплохода на 1 км/ч меньше, чем скорость первого. При этом скорость течения составляет 2 км/ч. Найдите скорость первого теплохода в неподвижной воде, если расстояние от А до В равно 120 км, а встретились теплоходы посередине между пристанями А и В. Ответ дайте в км/ч.
Так как теплоходы встретились посередине, а время, затраченное на это теплоходом с меньшей скоростью в неподвижной воде, меньше, чем время теплохода с большей скоростью в неподвижной воде, то теплоход с большей скоростью в неподвижной воде плыл против течения, то есть течение направлено от В к А.
Пусть (v) км/ч – скорость первого теплохода в неподвижной воде, (v > 0), тогда
(v — 2) км/ч – скорость перемещения первого теплохода,
((v — 1) + 2) км/ч – скорость перемещения второго теплохода,
(dfrac{60}{v — 2}) ч – время, затраченное первым теплоходом,
(dfrac{60}{v + 1}) ч – время, затраченное вторым теплоходом.
Так как время, затраченное первым теплоходом, на час больше, то: [dfrac{60}{v — 2} — dfrac{60}{v + 1} = 1qquadLeftrightarrowqquad v^2 — v — 182 = 0] – при (v neq 2, v neq -1), откуда находим (v_1 = 14, v_2 = -13), значит, (v = 14) км/ч (т.к. (v > 0)).
Ответ: 14
Задание
7
#828
Уровень задания: Равен ЕГЭ
На озере расположены пристани А и В. Расстояние между пристанями равно 90 км. Моторная лодка проплыла от А до В с постоянной скоростью, после чего сразу отправилась обратно со скоростью на 5 км/ч больше прежней. На середине пути из В в А лодка замедлилась и поплыла со скоростью на 2,5 км/ч меньшей, чем по дороге из А в В. В результате лодка затратила на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость лодки на пути из А в В. Ответ дайте в км/ч.
Пусть (v) км/ч – скорость лодки по пути от А до В, тогда
(dfrac{90}{v}) ч – время, затраченное лодкой на путь из А в В,
(dfrac{45}{v + 5}) ч – время, затраченное лодкой на первую половину пути из В в А,
(dfrac{45}{v — 2,5}) – время, затраченное лодкой на вторую половину пути из В в А.
Так как в итоге лодка проплыла из В в А за такое же время, как и из А в В, то: [dfrac{90}{v} = dfrac{45}{v + 5} + dfrac{45}{v — 2,5},] откуда (v = 10) км/ч.
Ответ: 10

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Тема 9.
Сюжетные текстовые задачи
9
.
02
Задачи на движение по воде
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
сюжетные текстовые задачи
9.01Задачи на прямолинейное движение
9.02Задачи на движение по воде
9.03Задачи на круговое движение
9.04Задачи на работу и производительность
9.05Задачи на проценты
9.06Задачи на растворы, смеси и сплавы
9.07Задачи на прогрессии
9.08Задачи повышенного уровня сложности
Решаем задачу:
Показать ответ и решение
Плот проплыл 13 км за часа. Тогда дорога из M в N и обратно заняла у катера
часов.
Пусть км/ч — скорость катера в стоячей воде,
Тогда имеем:
часов — время, затраченное катером на дорогу из M в N, так как плот плывёт по течению из M в N;
часов — время, затраченное катером на дорогу из N в M.
Так как суммарное время катера на дорогу из M в N и обратно равно 5,5 часа, то
Отсюда находим
Так как , то ответ 22 км/ч.
Разбираем задание №11 из ЕГЭ прошлых лет, рекомендованные как тренировочные.
Задача №1
Расстояние между пристанями А и В равно 120 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
Решение
Скорость плота равна скорости течения реки 2 км/ч. Пусть «х» км/ч – скорость яхты, тогда скорость яхты по течению равна:
х + 2 км/ч
а скорость яхты против течения равна:
х — 2 км/ч
Яхта, прибыв в пункт В, тотчас повернула обратно и возвратилась в А, а плоту понадобилось на час больше времени, чтобы пройти 24 км.
Получим уравнение:
Второй корень отрицательный, не подходит по условию задачи.
Скорость яхты в неподвижной воде равна 22 км/ч.
Ответ: 22.
Задача №2
Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Решение
Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Пусть «2S» км — весь путь путешественника, тогда средняя скорость равна:
Подставим числовые значения, получим:
Поэтому средняя скорость путешественника 38,4 км/ч.
Ответ: 38,4.
© devblog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.
2
Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
3
Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 30 минут, лодка отправилась назад и вернулась в пункт А в 18:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч.
4
Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.
5
Теплоход проходит по течению реки до пункта назначения 255 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 1 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается через 34 часа после отплытия из него. Ответ дайте в км/ч.
Источник: Досрочный ЕГЭ по математике (Центр) 30.03.2018
Пройти тестирование по этим заданиям
28 января 2014
Задачи на движение по воде традиционно вызывают трудности у многих учеников. Сегодня мы научимся решать такие задачи с помощью таблиц. Ключевой момент, который надо усвоить для успешного решения задач на движение поводе: в условии всегда фигурируют две ситуации — движение по течению и движение против течения. При этом при движении по течению скорости катера и течения складываются, а при движении против течения — вычитаются.
Задача B14. Катер вышел в 10:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв 3 часа в пункте Б, катер отправился назад и вернулся в пункт А в 21:00. Определите собственную скорость катера, если известно, что скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
Как видим, с помощью таблиц данная задача B14 решается элементарно (правда, уравнение получается довольно трудоемким). Единственный нюанс — время движения по течению и против течения складывается, потому что в задаче нам дано общее время, потраченное на путь. Но далеко не всегда речь будет идти именно о сложении времен: иногда время по течению сравнивается с временем против течения — и тогда полученные дроби надо не складывать, а вычитать. Но это уже совсем другая история и, соответственно, другой видеоурок.:)
Смотрите также:
- Тест по задачам B14: средний уровень, 1 вариант
- Тест по задачам B14: средний уровень, 2 вариант
- Тест к уроку «Сложение и вычитание дробей» (легкий)
- Сводный тест по задачам B15 (2 вариант)
- Изюм и виноград (смеси и сплавы)
- Задача B4: резка стекол
16
Окт 2013
Категория: 09 Текстовые задачиТекстовые задачи
09. Задачи на движение по воде
2013-10-16
2022-09-11
Задача 1. Моторная лодка прошла против течения реки км и вернулась в пункт отправления, затратив на обратный путь на
часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна
км/ч. Ответ дайте в км/ч.
Решение: + показать
Задача 2. Байдарка в 10:00 вышла из пункта А в пункт В, расположенный в км от А. Пробыв в пункте В
час
минут, байдарка отправилась назад и вернулась в пункт А в 16:00. Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки
км/ч.
Решение: + показать
Задача 3. От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через часа после этого следом за ним со скоростью на
км/ч большей отправился второй. Расстояние между пристанями равно
км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Решение: + показать
Задача 4. Пристани A и B расположены на озере, расстояние между ними км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на
часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Решение: + показать
Задача 5. Расстояние между пристанями A и B равно км. Из A в B по течению реки отправился плот, а через
часа вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел
км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна
км/ч. Ответ дайте в км/ч.
Решение: + показать
Задача 6. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной метров, второй — длиной
метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет
метров. Через
минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно
метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго? Видео*
Решение: + показать
Задача 7. Весной катер идёт против течения реки в раза медленнее, чем по течению. Летом течение становится на
км/ч медленнее. Поэтому летом катер идёт против течения в
раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Решение: + показать
Вы можете пройти тест “Движение по воде”
Автор: egeMax |
комментария 3
Печать страницы
Текстовые задачи на движение по воде
Текстовые задачи на движение по воде отличаются от задач на движение по прямой только наличием течения воды, которое нужно учитывать.
-
Если объект плывет по течению, то их общая скорость является результатом сложения их скоростей.
-
Если объект плывет против течения, то их общая скорость является результатом разности их скоростей.
-
При этом, если у объекта нет собственной скорости (это плот или транспорт, не имеющий двигателя), его скорость равна скорости течения воды.
Общая формула, связывающая скорость время и расстояние, остается неизменной:
(S = vartheta t)
где (S) – расстояние, (vartheta) – скорость, (t) – время.
Пример:
Моторная лодка прошла против течения 91 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
-
Составим таблицу. В строчки назовем соответственно особенностям её движения в воде: против течения и по течению. За (x) обозначим искомое – скорость течения. Тогда скорость лодки по течению и против течения будут следующей:
-
При этом и в одну, и в другую лодка проплыла одинаковое расстояние – 91 км:
-
Выразим время, соответствующее каждому виду движения:
-
Составим уравнение, используя тот факт, что при движении по течению лодка потратила на 6 часов меньше, чем при движении против течения:
(frac{91}{10 + x} + 6 = frac{91}{10 –x})
-
Приведем каждое слагаемое к общему знаменателю. В данном случае это знаменатель ((10 + + x)(10 –x)). Перенесем все слагаемые в одну сторону и раскроем скобки:
(frac{91left( 10 –x right)}{left( 10 + x right)left( 10 –x right)} + frac{6left( 10 + x right)left( 10 –x right)}{left( 10 + x right)left( 10 –x right)} = frac{91left( 10 + x right)}{left( 10–x right)left( 10 + x right)})
(frac{910 –91x + 600 –6x^{2} –910 –91x}{100 –x^{2}} = 0)
-
Дробь равна нулю, если числитель дроби равен нулю, а знаменатель – нет, т. е. (x neq pm 10), тогда:
(910 –91x + 600 –6x^{2} –910 –91x)
(–6x^{2} –182 + 600 = 0)
(6x^{2} + 182 –600 = 0)
(3x^{2} + 91 –300 = 0)
(D = 91^{2} + 4 bullet 3 bullet 300 = 11881 = 109^{2})
(frac{x_{1} = frac{–91 + 109}{6} = 3}{x_{2} = frac{–91 –109}{6} = –103})
-
Проверим корни уравнения на адекватность. Искомая скорость течения не может быть отрицательной, значит ответом будет являться корень уравнения (x_{1} = 3). Запишем ответ.
Ответ: 3.