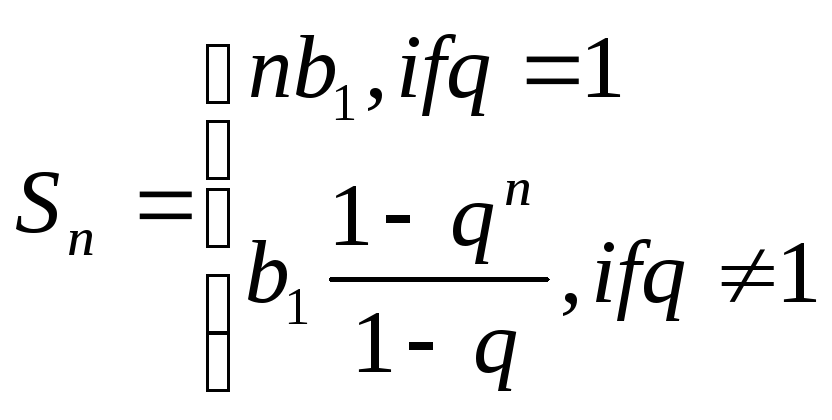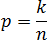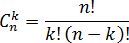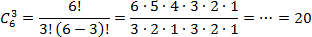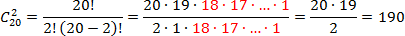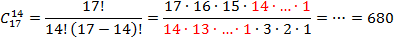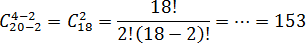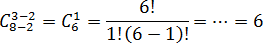Задачи на факториал егэ - Помощь в подготовке к экзаменам и поступлению

Алгоритм решения задач с факториалами

Факториалом называется произведение последовательных натуральных чисел, начиная с единицы.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Примеры решений задач с факториалами

Задача

Найти $frac{3! - 2!}{4}$

Решение

$[frac{2!(3 - 1)}{4} = frac{2!cdot2}{4} = frac{4}{4} = 1]$

Ответ

Задача

Найти $frac{8! - 6!}{55}$

Решение

$[frac{6!(7cdot8 - 1)}{55} = frac{6!(56 - 1)}{55} = frac{6!55}{55} = 6! = 720]$

Ответ

Задача

Найти $frac{8! - 4!}{2}$

Решение

$[frac{4!(5cdot6cdot7cdot8 - 1)}{2} = 12(5cdot6cdot7cdot8 - 1) = 12cdot1679 = 20148]$

Ответ

Задача

Найти $frac{4! - 2!}{2}$

Решение

$[frac{2!(3cdot4 - 1)}{2} = 11]$

Ответ

Задача

Найти $frac{5! - 3!}{3!}$

Решение

$[frac{3!(4cdot5 - 1)}{3!} = 19]$

Ответ

Задача

Найти $frac{121! - 120!}{120!}$

Решение

$[frac{120!(121 - 1)}{120!} = 120]$

Ответ

Задача

Найти $C^{2}_{4}$

Решение

$[C^{m}_{n} = frac{n!}{m!(n - m)!}]$

$[C^{2}_{4} = frac{4!}{2!(4 - 2)!} = frac{4!}{2!cdot2!} = frac{2!cdot3cdot4}{2!cdot2!} = frac{12}{2} = 6]$

Ответ

Задача

Найти $C^{3}_{5}$

Решение

$[C^{m}_{n} = frac{n!}{m!(n - m)!}]$

$[C^{3}_{5} = frac{5!}{3!(5 - 3)!} = frac{3!cdot4cdot5}{3!cdot2!} = frac{20}{2} = 10]$

Ответ

Задача

Найти $C^{20}_{22}$

Решение

$[C^{m}_{n} = frac{n!}{m!(n - m)!}]$

$[C^{20}_{22} = frac{22!}{20!(22 - 20)!} = frac{20!cdot21cdot22}{20!cdot2!} = 21cdot11 = 231]$

Ответ

Задача

Найти $C^{11}_{11}$

Решение

$[C^{m}_{n} = frac{n!}{m!(n - m)!}]$

$[C^{11}_{12} = frac{12!}{11!(12 - 11)!} = frac{11!cdot12}{11!cdot1!} = 12]$

Ответ

Примеры решения задач с факториалами с ответами обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру

Источник

29 декабря 2011

Решая задачи по теории вероятностей, мы постоянно используем одну и ту же формулу, которая одновременно является классическим определением вероятности:

где k — число благоприятных исходов, n — общее число исходов (см. «Тест по теории вероятностей»).

И эта формула прекрасно работает до тех пор, пока задачи были легкими, а числа, стоящие в числителе и знаменателе — очевидными.

Однако последние пробные экзамены показали, что в настоящем ЕГЭ по математике могут встречаться значительно более сложные конструкции. Отыскание значений n и k становится проблематичным. В таком случае на помощь приходит комбинаторика. Ее законы работают там, где искомые значения не выводятся непосредственно из текста задачи.

В сегодняшнем уроке не будет строгих формулировок и длинных теорем — они слишком сложны и, к тому же, совершенно бесполезны для решения настоящих задач B6. Вместо этого мы рассмотрим простые правила и разберем конкретные задачи, которые действительно встречаются на ЕГЭ. Итак, поехали!

Число сочетаний и факториалы

Пусть имеется n объектов (карандашей, конфет, бутылок водки — чего угодно), из которых требуется выбрать ровно k различных объектов. Тогда количество вариантов такого выбора называется числом сочетаний из n элементов по k. Это число обозначается C_n^k и считается по специальной формуле.

Обозначение:

Выражение n! читается как «эн-факториал» и обозначает произведение всех натуральных чисел от 1 до n включительно: n! = 1 · 2 · 3 · … · n.

Кроме того, в математике по определению считают, что 0! = 1 — подобный бред редко, но все же встречается в задачах по теории вероятностей.

Что дает нам эта формула? На самом деле, без нее не решается практически ни одна серьезная задача.

К сожалению, в школе совершенно не умеют работать с факториалами. Кроме того, в формуле числа сочетаний очень легко запутаться: где стоит и что обозначает число n, а где — k. Поэтому для начала просто запомните: меньшее число всегда стоит сверху — точно так же, как и в формуле определения вероятности (вероятность никогда не бывает больше единицы).

Для лучшего понимания разберем несколько простейших комбинаторных задач:

Задача. У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ?

Тут все просто: есть n = 6 сортов, из которых надо выбрать k = 3 сорта. Число сочетаний можно найти по формуле:

Задача. В группе из 20 студентов надо выбрать 2 представителей для выступления на конференции. Сколькими способами можно это сделать?

Опять же, всего у нас есть n = 20 студентов, а выбрать надо k = 2 студента. Находим число сочетаний:

Обратите внимание: красным цветом отмечены множители, входящие в разные факториалы. Эти множители можно безболезненно сократить и тем самым значительно уменьшить общий объем вычислений.

Задача. На склад завезли 17 серверов с различными дефектами, которые стоят в 2 раза дешевле нормальных серверов. Директор купил в школу 14 таких серверов, а сэкономленные деньги своровал и купил дочке шубу из меха соболя за 200 000 рублей. Сколькими способами директор может выбрать бракованные серверы?

В задаче довольно много лишних данных, которые могут сбить с толку. Наиболее важные факты: всего есть n = 17 серверов, а директору надо k = 14 серверов. Считаем число сочетаний:

Красным цветом снова обозначены множители, которые сокращаются. Итого, получилось 680 комбинаций. В общем, директору есть из чего выбрать.

Как видите, число сочетаний из n по k считается достаточно просто. Проблема в том, что многие школьники никогда не работали с факториалами. Для них это новый и незнакомый математический объект, и для его освоения требуется некоторая тренировка.

Хорошая новость состоит в том, что во многих задачах формулы C_n^k оказывается вполне достаточно для нахождения ответа. Но есть и плохая новость: в тех редких случаях, когда нужны дополнительные правила, решение задачи резко усложняется. Эти правила мы сейчас и рассмотрим.

Закон умножения

Закон умножения в комбинаторике: число сочетаний (способов, комбинаций) в независимых наборах умножается.

Другими словами, пусть имеется A способов выполнить одно действие и B способов выполнить другое действие. Путь также эти действия независимы, т.е. никак не связаны между собой. Тогда можно найти число способов выполнить первое и второе действие по формуле: C = A · B.

Задача. У Пети есть 4 монеты по 1 рублю и 2 монеты по 10 рублей. Петя, не глядя, достал из кармана 1 монету номиналом 1 рубль и еще 1 монету номиналом 10 рублей, чтобы купить сигарету за 11 рублей у бабули в подземном переходе. Сколькими способами он может выбрать эти монеты?

Итак, сначала Петя достает k = 1 монету из n = 4 имеющихся монет номиналом 1 рубль. Число способов сделать это равно C₄¹ = … = 4.

Затем Петя снова лезет в карман и достает k = 1 монету из n = 2 имеющихся монет номиналом 10 рублей. Здесь число сочетаний равно C₂¹ = … = 2.

Поскольку эти действия независимы, общее число вариантов равно C = 4 · 2 = 8.

Задача. В корзине лежат 8 белых шаров и 12 черных. Сколькими способами можно достать из этой корзины 2 белых шара и 2 черных?

Всего в корзине n = 8 белых шаров, из которых надо выбрать k = 2 шара. Это можно сделать C₈² = … = 28 различными способами.

Кроме того, в корзине имеется n = 12 черных шаров, из которых надо выбрать опять же k = 2 шара. Число способов сделать это равно C₁₂² = … = 66.

Поскольку выбор белого шара и выбор черного — события независимые, общее число комбинаций считается по закону умножения: C = 28 · 66 = 1848. Как видим, вариантов может быть довольно много.

Закон умножения показывает, сколькими способами можно выполнить сложное действие, которое состоит из двух и более простых — при условии, что все они независимы.

Именно этой формулы многим не хватило для решения задачи B6 на пробном ЕГЭ по математике. Разумеется, существуют и другие методы решения, в которых комбинаторика не используется — и мы обязательно рассмотрим их ближе к настоящему экзамену. Однако ни один из них не сравнится по надежности и лаконичности с теми приемами, которые мы сейчас изучаем.

Закон сложения

Если закон умножения оперирует «изолированными» событиями, которые не зависят друг от друга, то в законе сложения все наоборот. Здесь рассматриваются взаимоисключающие события, которые никогда не случаются одновременно.

Например, «Петя вынул из кармана 1 монету» и «Петя не вынул из кармана ни одной монеты» — это взаимоисключающие события, поскольку вынуть одну монету и при этом не вынуть ни одной невозможно.

Аналогично, события «Выбранный наугад шар — белый» и «Выбранный наугад шар — черный» также являются взаимоисключающими.

Закон сложения в комбинаторике: если два взаимоисключающих действия можно выполнить A и B способами соответственно, то эти события можно объединить. При этом возникнет новое событие, которое можно выполнить X = A + B способами.

Другими словами, при объединении взаимоисключающих действий (событий, вариантов) число их комбинаций складывается.

Можно сказать, что закон сложения — это логическое «ИЛИ» в комбинаторике, когда нас устраивает любой из взаимоисключающих вариантов. И наоборот, закон умножения — это логическое «И», при котором нас интересует одновременное выполнение и первого, и второго действия.

Задача. В корзине лежат 9 черных шаров и 7 красных. Мальчик достает 2 шара одинакового цвета. Сколькими способами он может это сделать?

Если шары одинакового цвета, то вариантов немного: оба они либо черные, либо красные. Очевидно, что эти варианты — взаимоисключающие.

В первом случае мальчику предстоит выбирать k = 2 черных шара из n = 9 имеющихся. Число способов сделать это равно C₉² = … = 36.

Аналогично, во втором случае выбираем k = 2 красных шара из n = 7 возможных. Число способов равно C₇² = … = 21.

Осталось найти общее количество способов. Поскольку варианты с черными и красными шарами — взаимоисключающие, по закону сложения имеем: X = 36 + 21 = 57.

Задача. В ларьке продаются 15 роз и 18 тюльпанов. Ученик 9-го класса хочет купить 3 цветка для своей одноклассницы, причем все цветы должны быть одинаковыми. Сколькими способами он может составить такой букет?

По условию, все цветы должны быть одинаковыми. Значит, будем покупать либо 3 розы, либо 3 тюльпана. В любом случае, k = 3.

В случае с розами придется выбирать из n = 15 вариантов, поэтому число сочетаний равно C₁₅³ = … = 455. Для тюльпанов же n = 18, а число сочетаний — C₁₈³ = … = 816.

Поскольку розы и тюльпаны — это взаимоисключающие варианты, работаем по закону сложения. Получаем общее число вариантов X = 455 + 816 = 1271. Это и есть ответ.

Дополнительные условия и ограничения

Очень часто в тексте задачи присутствуют дополнительные условия, накладывающие существенные ограничения на интересующие нас сочетания. Сравните два предложения:

Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа?
Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа, если среди них обязательно должен быть красный цвет?

Чувствуете разницу? В первом случае мы вправе брать любые цвета, какие нам нравятся — дополнительных ограничений нет. Во втором случае все сложнее, поскольку мы обязаны выбрать ручку красного цвета (предполагается, что она есть в исходном наборе).

Очевидно, что любые ограничения резко сокращают итоговое количество вариантов. Ну и как в этом случае найти число сочетаний? Просто запомните следующее правило:

Пусть имеется набор из n элементов, среди которых надо выбрать k элементов. При введении дополнительных ограничений числа n и k уменьшаются на одинаковую величину.

Другими словами, если из 5 ручек надо выбрать 3, при этом одна из них должна быть красной, то выбирать придется из n = 5 − 1 = 4 элементов по k = 3 − 1 = 2 элемента. Таким образом, вместо C₅³ надо считать C₄².

Теперь посмотрим, как это правило работает на конкретных примерах:

Задача. В группе из 20 студентов, среди которых 2 отличника, надо выбрать 4 человека для участия в конференции. Сколькими способами можно выбрать этих четверых, если отличники обязательно должны попасть на конференцию?

Итак, есть группа из n = 20 студентов. Но выбрать надо лишь k = 4 из них. Если бы не было дополнительных ограничений, то количество вариантов равнялось числу сочетаний C₂₀⁴.

Однако нам поставили дополнительное условие: 2 отличника должны быть среди этих четырех. Таким образом, согласно приведенному выше правилу, мы уменьшаем числа n и k на 2. Имеем:

Задача. У Пети в кармане есть 8 монет, из которых 6 монет по рублю и 2 монеты по 10 рублей. Петя перекладывает какие-то три монеты в другой карман. Сколькими способами Петя может это сделать, если известно, что обе монеты по 10 рублей оказались в другом кармане?

Итак, есть n = 8 монет. Петя перекладывает k = 3 монеты, из которых 2 — десятирублевые. Получается, что из 3 монет, которые будут переложены, 2 уже зафиксированы, поэтому числа n и k надо уменьшить на 2. Имеем:

В обоих примерах я намеренно пропустил детали работы с факториалами — попробуйте выполнить все расчеты самостоятельно. Разумеется, для этих задач существуют и другие способы решения. Например, с помощью закона умножения. В любом случае, ответ будет один и тот же.

В заключение отмечу, что в первой задаче мы получили 153 варианта — это намного меньше, чем исходные C₂₀⁴ = … = 4845 вариантов. Аналогично, 3 монеты из 8 можно переложить C₈³ = … = 56 способами, что значительно больше 6 способов, которые мы получили в последней задаче.

Эти примеры наглядно демонстрируют, что введение любых ограничений значительно сокращает нашу «свободу выбора».

Смотрите также:

Комбинаторика в задаче B6: легкий тест
Задачи B6 с монетами
Что такое логарифм
Четырехугольная пирамида: как найти координаты вершин
Задача B15: работаем с показательной функцией без производной
Сложные задачи B15: комбинация тригонометрии и многочленов

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = F(n–1) * n, при n >1

Чему равно значение функции F(5)? В ответе запишите только натуральное число.

Источник: Демонстрационная версия ЕГЭ—2013 по информатике.

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 3

F(n) = F(n–1) * (n–1), при n >1

Чему равно значение функции F(6)?

В ответе запишите только натуральное число.

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = 5*F(n–1) + 3*n, при n >1

Чему равно значение функции F(4)?

В ответе запишите только натуральное число.

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = F(n–1) * F(n–1) − F(n–1) * n + 2 * n, при n >1

Чему равно значение функции F(4)?

В ответе запишите только натуральное число.

Алгоритм вычисления значения функции F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 0

F(n) = F(n–1) + n, при n >1

G(1) = 1

G(n) = G(n–1) * n, при n >1

Чему равно значение функции F(5) + G(5)?

В ответе запишите только натуральное число.

Пройти тестирование по этим заданиям

Источник

Тема не так уж часто встречающаяся в
ЕГЭ, но тоже заслуживает рассмотрения.

Необходимая теория.

Факториал числа n — произведение всех
натуральных чисел до n включительно:

По определению полагают 0! = 1. Факториал
определён только для целых неотрицательных
чисел.

Примеры.

№1

Найдите все тройки натуральных чисел

и
,
удовлетворяющие уравнению

Решение: Очевидно, что

и

Предположим, что

Разделим все на

Отсюда очевидно, что
,
то же самое справедливо для
.

Далее перебором получаем все возможные
результаты.

Ответ:

№2

Найдите все натуральные значения
,
для которых выполняется равенство

Решение: Представим уравнение в
виде

Разделим обе части на

и получим

Понятно, что

очень мало. Переберем значения начиная
с
.

Отсюда видно, что верное решение только
при
.

Ответ:

Номера для самостоятельного решения.

№1

Решите в натуральных числах уравнение

№2

Уравнение

решите в целых числах

№3

Найти наибольшее натуральное число
,
для которого число

делится на
=1,2,…,

Ответы и решения.

№1

Ответ:

№2

Ответ:

№3

Указание: Рассмотреть случаи при

и при

Ответ: 46

Тема 5. “Прогрессии ”

Тоже небольшая и редкая тема, но нужно
уметь ее решать.

Необходимая теория.

Арифметическая прогрессия — числовая
последовательность вида

то есть последовательность чисел (членов
прогрессии), каждое из которых, начиная
со второго, получается из предыдущего
добавлением к нему постоянного числа
d (шага или разности прогрессии):

Любой член прогрессии может быть вычислен
по формуле общего члена:

Шаг прогрессии может быть вычислен по
формуле:
,
если

Если шаг d > 0, прогрессия является
возрастающей; если d < 0, — убывающей.

Сумма n последовательных членов
арифметической прогрессии начиная с
члена k:

Любой член арифметической прогрессии,
начиная со второго, является средним
арифметическим предыдущего и следующего
члена прогрессии:

Геометрическая прогрессия —
последовательность чисел

(членов прогрессии), в которой каждое
последующее число, начиная со второго,
получается из предыдущего умножением
его на определённое число (знаменатель
прогрессии), где
:

Любой член геометрической прогрессии
может быть вычислен по формуле:

Если b1 > 0 и q > 1, прогрессия является
возрастающей последовательностью, если
0 < q < 1, — убывающей последовательностью,
а при q < 0 — знакопеременной

Своё название прогрессия получила по
своему характеристическому свойству:

то есть каждый член равен среднему
геометрическому его соседей.

Сумма n первых членов геометрической
прогрессии:

Примеры.

№1

В арифметической прогрессии четвертый
член равен 1. При каком значение

произведение второго и седьмого члена
будет наибольшим?

Решение:

Посчитаем производную и найдем максимум

Ответ:

№2

Могут ли числа 2,3 и 17 быть членами (не
обязательно последовательными) одной
геометрической прогрессии?

Решение: Все 3 числа простые,
следовательно, такой геометрической
прогрессии не существует.

Ответ: нет

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Комбинаторная теория является одной из важнейших областей математики, без знания которой не обойтись ни менеджеру, ни программисту, ни другим специалистам. Знать, как проводится решение задач по комбинаторике, значит быть востребованным работником, умеющим решать широкий круг практических задач.

Возникновение комбинаторной теории

Комбинаторика – это область математики, изучающая вопрос, сколько разных комбинаций (наборов) можно составить из элементов заданного множества. При этом нужные комбинации подчиняются определенным требованиям, что приводит к различным методам решения задач по комбинаторике.

Истоки этой науки были положены знаменитым математиком и философом Готфридом Лейбницем.

Два основных правила комбинаторной теории

Теория комбинаторики зиждется на двух основных принципах – это правило сложения и правило умножения. Рассмотрим их подробнее.

Правило сложения: Пусть объект А мы можем выбрать из множества $m$ способами, а объект В можно выбрать $n$ способами, то объект «А+В» можно выбрать $m+n$ способами.

Возможно, это правило покажется непосвященному человеку абракадаброй, но ничего сложного нет. Рассмотрим пример – пусть в одном ящике есть $m$ шариков, а во втором ящике – $n$ шариков. Сколькими способами можно вытащить шарик из одного этих ящиков. Очевидно, что ОДИН шарик можно достать $m+n$ способами.

Правило умножения: Пусть объект А выбирается $m$ способами, объект В выбирается $n$ способами, то оба объекта можно выбрать $mn$ способами.
Все очень просто – каждый из $m$ способов выбора объекта А комбинируется с каждым из $n$ способов выбора объекта В, то есть количество способов просто умножается друг на друга.

Рассмотрим простой пример: сколько чисел можно составить из цифр 0,1,2,3,4,5,6,7,8,9, если число должно быть двузначным?
Можно составить 90 чисел – первую цифру числа (объект А) можем выбрать 9 способами, так как число не может начинаться с нуля. Вторую цифру числа (объект В) можем выбрать 10 способами, так как у нас есть 10 цифр. Итого получается $9*10=90$ чисел.

Это были главные правила, на которые опираются все методы решения задач по комбинаторике. Еще больше теории о началах комбинаторики вы найдете в онлайн учебнике: Элементы комбинаторики онлайн.

Готовые решения задач по теории вероятностей, в том числе по комбинаторике – более 400 решений. Найди свою задачу:

Примеры решения задач по комбинаторике

Перейдем к более продвинутым случаям и рассмотрим другие понятия комбинаторики.

Есть 5 книг. Сколькими способами их можно расположить на книжной полке?
Ответ – 120 способов. Первую книгу можем выбрать 5 способами, вторую книгу 4 способами и т.д. Перемножая числа с 5 до 1, получим 120.

С этой задачи начинается понятие факториала. N-факториал или N! – это количество перестановок из N объектов, вычисляемое по формуле $P_N =N!= 1*2*3*…*(N-1)*N$.

Следующий пример – в чемпионате мира участвуют 18 команд по футболу. Сколькими способами можно распределить золотые, серебряные и бронзовые комплекты?
Ясно, что золотые медали может получить любая из команд, значит золотого призера (объект А) можно выбрать 18 способами. Остается два комплекта и 17 команд. Серебряным медалистом может стать одна из 17 команд, а бронзовым – одна из 16 команд. Значит, серебряного и бронзового медалиста можно выбрать 17 и 16 способами.
Итого, три комплекта медалей могут распределиться 18*17*16 = 4896 способами.

Факториал числа $n!$ равен произведению чисел от 1 до $n$. Например, $5! = 1cdot 2cdot 3cdot 4cdot 5$. Для решения примеров на пределы с факториалами понадобится знать и понимать формулу разложения на множители. $$ (n+1)! = n!(n+1) qquad (1) $$

Например, $5! = 4! cdot 5 $, или $5! = 3! cdot 4 cdot 5$, а можно еще так $5! = 2! cdot 3 cdot 4 cdot 5 $.

Основная суть идеи:

Выносим наименьший факториал числа за скобки в числителе и знаменателе
Сокращаем факториалы, избавляя тем самым предел от них
Вычисляем предел подходящим способом

Пример 1

Вычислить предел с факториалами $lim_limits frac<(n+1)!>$

Решение

Подставляя $x=infty$ в предел получаем неопределенность бесконечность делить на бесконечность. Избавимся от факториалов. Для этого используем формулу (1) для их разложения на множители.

Подставляем в предел полученное выражение и сокращаем на $n!$ числитель со знаменателем.

Теперь подставляя бесконечность в предел вычисляем ответ.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$lim_limits frac <(n+1)!>= 0 $$

Определяем наименьший факториал $(2n+1)!$. Его нужно вынести за скобки. Но перед этим нужно разложить остальные факториалы на множители, одним из которых будет $(2n+1)!$. Для этого воспользуемся формулой (1).

$$(2n+2)! = (2n+1)! cdot (2n+2) $$ $$ (2n+3)! = (2n+1)! cdot (2n+2)cdot(2n+3) $$

Выполняем замену в пределе на полученные выражения.

Выносим общий множитель с факториалом в числителе за скобки и выполняем сокращение со знаменателем.

Раскрываем полученные скобки и сокращаем на $2n+3$.

Пример 2

Решить предел с факториалом $ lim_limits frac<(2n+1)! + (2n+2)!> <(2n+3)!>$

Решение

Ответ

$$ lim_limits frac<(2n+1)! + (2n+2)!> <(2n+3)!>= 0 $$

Понятно, что предел имеет неопределенность $frac<infty><infty>$. Попробуем её устранить избавившись от факториалов. Сразу находим среди них наименьший $n!$. Его нужно будет вынести за скобки. Но перед этим остальные факториалы нужно разложить по формуле (1) и затем подставить в предел.

Далее раскрываем скобки, попутно упрощая выражения, и затем выносим $n$.

Осталось выполнить сокращение на $n$ и получить ответ.

29 декабря 2011

где k — число благоприятных исходов, n — общее число исходов (см. «Тест по теории вероятностей»).

Однако последние пробные экзамены показали, что в настоящем ЕГЭ по математике могут встречаться значительно более сложные конструкции. Отыскание значений становится проблематичным. В таком случае на помощь приходит комбинаторика. Ее законы работают там, где искомые значения не выводятся непосредственно из текста задачи.

Число сочетаний и факториалы

Пусть имеется n объектов (карандашей, конфет, бутылок водки — чего угодно), из которых требуется выбрать различных объектов. Тогда количество вариантов такого выбора называется элементов Это число обозначается и считается по специальной формуле.

Выражение n ! читается как «эн-факториал» и обозначает произведение всех натуральных чисел включительно:

Кроме того, в математике по определению считают, подобный бред редко, но все же встречается в задачах по теории вероятностей.

Что дает нам эта формула? На самом деле, без нее не решается практически ни одна серьезная задача.

К сожалению, в школе совершенно не умеют работать с факториалами. Кроме того, в формуле числа сочетаний очень легко запутаться: где стоит и что обозначает Поэтому для начала просто запомните: меньшее число всегда стоит сверху — точно так же, как и в формуле определения вероятности (вероятность никогда не бывает больше единицы).

Для лучшего понимания разберем несколько простейших комбинаторных задач:

Задача. У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ?

Тут все просто: есть n = 6 сортов, из которых надо выбрать сорта. Число сочетаний можно найти по формуле:

Задача. В группе из 20 студентов надо выбрать 2 представителей для выступления на конференции. Сколькими способами можно это сделать?

Опять же, всего у нас есть n = 20 студентов, а выбрать надо студента. Находим число сочетаний:

Задача. На склад завезли 17 серверов с различными дефектами, которые стоят в 2 раза дешевле нормальных серверов. Директор купил в школу 14 таких серверов, а сэкономленные деньги своровал и купил дочке шубу из меха соболя за 200 000 рублей. Сколькими способами директор может выбрать бракованные серверы?

В задаче довольно много лишних данных, которые могут сбить с толку. Наиболее важные факты: всего есть серверов, а директору надо серверов. Считаем число сочетаний:

Хорошая новость состоит в том, что во многих задачах формулы оказывается вполне достаточно для нахождения ответа. Но есть и плохая новость: в тех редких случаях, когда нужны дополнительные правила, решение задачи резко усложняется. Эти правила мы сейчас и рассмотрим.

Закон умножения

в комбинаторике: число сочетаний (способов, комбинаций) в независимых наборах умножается.

Другими словами, пусть имеется A способов выполнить одно действие выполнить другое действие. Путь также эти действия независимы, т.е. никак не связаны между собой. Тогда можно найти число способов выполнить первое и второе действие по формуле:

Задача. У Пети есть 4 монеты по 1 рублю и 2 монеты по 10 рублей. Петя, не глядя, достал из кармана 1 монету номиналом 1 рубль и еще 1 монету номиналом 10 рублей, чтобы купить сигарету за 11 рублей у бабули в подземном переходе. Сколькими способами он может выбрать эти монеты?

Итак, сначала Петя достает монету имеющихся монет номиналом 1 рубль. Число способов сделать это равно

Затем Петя снова лезет в карман и достает монету имеющихся монет номиналом 10 рублей. Здесь число сочетаний равно

Поскольку эти действия независимы, общее число вариантов равно

Задача. В корзине лежат 8 белых шаров и 12 черных. Сколькими способами можно достать из этой корзины 2 белых шара и 2 черных?

Всего в корзине белых шаров, из которых надо выбрать шара. Это можно сделать различными способами.

Кроме того, в корзине имеется черных шаров, из которых надо выбрать опять же шара. Число способов сделать это равно

Поскольку выбор белого шара и выбор черного — события независимые, общее число комбинаций считается по закону умножения: Как видим, вариантов может быть довольно много.

Закон сложения

в комбинаторике: если два взаимоисключающих действия можно выполнить способами соответственно, то эти события можно объединить. При этом возникнет новое событие, которое можно выполнить способами.

Задача. В корзине лежат 9 черных шаров и 7 красных. Мальчик достает 2 шара одинакового цвета. Сколькими способами он может это сделать?

В первом случае мальчику предстоит выбирать черных шара имеющихся. Число способов сделать это равно

Аналогично, во втором случае выбираем красных шара возможных. Число способов равно

Осталось найти общее количество способов. Поскольку варианты с черными и красными шарами — взаимоисключающие, по закону сложения имеем:

Задача. В ларьке продаются 15 роз и 18 тюльпанов. Ученик хочет купить 3 цветка для своей одноклассницы, причем все цветы должны быть одинаковыми. Сколькими способами он может составить такой букет?

По условию, все цветы должны быть одинаковыми. Значит, будем покупать либо 3 розы, либо 3 тюльпана. В любом случае,

В случае с розами придется выбирать вариантов, поэтому число сочетаний равно Для тюльпанов же а число сочетаний —

Поскольку розы и тюльпаны — это взаимоисключающие варианты, работаем по закону сложения. Получаем общее число вариантов Это и есть ответ.

Дополнительные условия и ограничения

Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа?
Имеется набор из 5 ручек разных цветов. Сколькими способами можно выбрать 3 ручки для обводки чертежа, если среди них обязательно должен быть красный цвет?

Пусть имеется набор элементов, среди которых надо выбрать При введении дополнительных ограничений числа уменьшаются на одинаковую величину.

Другими словами, если из 5 ручек надо выбрать 3, при этом одна из них должна быть красной, то выбирать придется элементов элемента. Таким образом, вместо надо считать

Теперь посмотрим, как это правило работает на конкретных примерах:

Задача. В группе из 20 студентов, среди которых 2 отличника, надо выбрать 4 человека для участия в конференции. Сколькими способами можно выбрать этих четверых, если отличники обязательно должны попасть на конференцию?

Итак, есть группа студентов. Но выбрать надо из них. Если бы не было дополнительных ограничений, то количество вариантов равнялось числу сочетаний

Однако нам поставили дополнительное условие: 2 отличника должны быть среди этих четырех. Таким образом, согласно приведенному выше правилу, мы уменьшаем числа на 2. Имеем:

Задача. У Пети в кармане есть 8 монет, из которых 6 монет по рублю и 2 монеты по 10 рублей. Петя перекладывает какие-то три монеты в другой карман. Сколькими способами Петя может это сделать, если известно, что обе монеты по 10 рублей оказались в другом кармане?

Итак, есть монет. Петя перекладывает монеты, из которых 2 — десятирублевые. Получается, что из 3 монет, которые будут переложены, 2 уже зафиксированы, поэтому числа надо уменьшить на 2. Имеем:

В заключение отмечу, что в первой задаче мы получили 153 варианта — это намного меньше, чем исходные вариантов. Аналогично, 3 монеты из 8 можно переложить способами, что значительно больше 6 способов, которые мы получили в последней задаче.

Пример 3

Найти предел $lim_limits frac<3(n+1)!> <2(n+1)!-n!>$

Решение

Источник