Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Если при сжатии объём идеального газа уменьшился в 2 раза, а давление газа увеличилось в 2 раза, то во сколько раз изменилась при этом абсолютная температура газа?
2
Во сколько раз изменяется давление идеального газа при уменьшении объёма идеального газа в 2 раза и увеличении его абсолютной температуры в 4 раза?
4
Идеальный газ в цилиндре переводится из состояния А в состоянии В так, что его масса при этом не изменяется. Параметры, определяющие состояния газа, приведены в таблице. Какое число должно быть в свободной клетке таблицы?
|
|
|
|
|
| Состояние A |
1,0 |
4 |
|
| Состояние B |
1,5 |
8 |
900 |
5
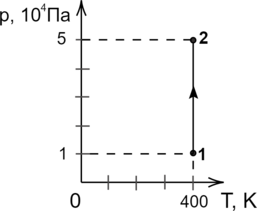
В сосуде находится некоторое количество идеального газа. Во сколько раз изменится температура газа, если он перейдёт из состояния 1 в состояние 2 (см. рис.)?
Пройти тестирование по этим заданиям
8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Газовые законы
1 моль гелия изохорно нагревают на 154 К, при этом давление газа увеличивается в 2,1 раза. До какой температуры нагрели газ? Ответ дайте в кельвинах.
Процесс изохорный, т.е. объём не меняется. Запишем закон Шарля: [hspace{ 5 mm} dfrac{p_1}{T_1}=dfrac{p_2}{T_2} hspace{ 5 mm} (1)] Изменение температуры есть разница конечной и начальной температуры газа: [hspace{ 5 mm} Delta T = T_2 — T_1 hspace{3 mm} Rightarrow hspace{3 mm} T_1 = T_2 — Delta T hspace{ 5 mm} (2)] По условию давление газа увеличивается в 2,1 раза: [hspace{ 5 mm}p_2 = 2,1 p_1hspace{ 5 mm} (3)] Подставим (2), (3) в (1) и выразим температуру, до которой нагрели газ: [dfrac{p_1}{T_2 — Delta T}=dfrac{2,1 p_1}{T_2}] [T_2 = dfrac{2,1 p_1 Delta T}{2,1p_1 — p_1} = dfrac{2,1 Delta T}{1,1} = dfrac{2,1 cdot 154text{ K}}{1,1} = 294 text{ K}]
Ответ: 294
Воздух при температуре 27(^{circ})C и давлении 202,65 кПа занимает объём 0,3 м(^3). Газ изобарно нагрели, причём объём газа увеличился до 0,5 м(^3). Найдите конечную температуру воздуха. Ответ дайте в кельвинах.
Т.к. процесс изобарный ((p=const)), используем закон Гей – Люссака: [dfrac{V_1}{T_1}=dfrac{V_2}{T_2}hspace{3 mm}Rightarrow hspace{3 mm} T_2=dfrac{T_1 cdot V_2}{V_1}] Переведём (T_1) в кельвины: 27(^{circ})С + 273 = 300 К. [T_2=dfrac{300 text{ К} cdot 0,5 text{ м$^3$}}{0,3text{ м$^3$}}=500 text{ К}]
Ответ: 500
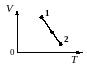
На графике изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 1 равна 56(^{circ})C. Какова температура аргона в состоянии 2? Ответ дайте в кельвинах.
Из графика видно, что процесс 1–2 — изобарный ((p=const)). Воспользуемся законом Гей – Люссака: [dfrac{V_1}{T_1}=dfrac{V_2}{T_2}hspace{3 mm}Rightarrow hspace{3 mm} T_2=dfrac{T_1 cdot V_2}{V_1}] Переведём (T_1) в кельвины: 56(^{circ})С + 273 = 329 К. [T_2=dfrac{329text{ К} cdot 14text{ м$^3$}}{7text{ м$^3$}} = 658 text{ К}]
Ответ: 658
На графике изображено изменение состояния постоянной массы разреженного аргона. Температура газа в состоянии 2 равна 212(^{circ})C. Какова температура аргона в состоянии 1? Ответ дайте в кельвинах.
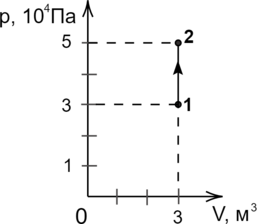
Из графика видно, что процесс 1–2 — изохорный ((V=const)). Воспользуемся законом Шарля: [dfrac{p_1}{T_1}=dfrac{p_2}{T_2}hspace{3 mm}Rightarrow hspace{3 mm} T_1=dfrac{p_1 cdot T_2}{p_2}] Переведём (T_2) в кельвины: 212(^{circ})С + 273 = 485 К. [T_1=dfrac{3cdot 10^4 text{ Па} cdot 485text{ К}}{5 cdot 10^4text{ Па}} = 291 text{ К}]
Ответ: 291
Давление газа при температуре 306 К равно 159 кПа. Газ нагрели до температуры (T_2), при этом объём газа не изменился. После нагревания давление газа стало равно 212 кПа. Найдите, до какой температуры (T_2) нагрели газ. Ответ дайте в кельвинах.
По условию процесс изохорный ((V=const)).
Согласно закону Шарля: [dfrac{p_1}{T_1} = dfrac{p_2}{T_2}hspace{3 mm}Rightarrowhspace{3 mm} T_2 = dfrac{T_1 p_2}{p_1}] [T_2 = dfrac{306 text{ K} cdot 212 cdot 10^3 text{ Па}}{159 cdot 10^3 text{ Па}} = 408 text{ K}]
Ответ: 408
Газ занимает объём 0,03 м(^3) при температуре 418 К. Какой объём займёт этот же газ, если его температура понизится до 209 К? Давление и масса газа не меняются. Ответ дайте в м(^3).
По условию процесс изобарный ((p=const)). По закону Гей – Люссака: [dfrac{V_1}{T_1} = dfrac{V_2}{T_2}hspace{3 mm}Rightarrowhspace{3 mm} V_2 = dfrac{V_1T_2}{T_1}] [V_2 = dfrac{0,03 text{ м$^3$} cdot 209 text{ К}}{418 text{ К}} = 0,015 text{ м$^3$}]
Ответ: 0,015
На рисунке представлен график зависимости давления от температуры газа. Объём газа в состоянии 2 равен 6 л. Какой объём занимает газ в состоянии 1? Масса газа не меняется. Ответ дайте в м(^3).
По графику видно, что процесс 1–2 — изотермический ((T=const)). По закону Бойля – Мариотта: [p_1V_1 = p_2V_2hspace{3 mm}Rightarrowhspace{3 mm} V_1 = dfrac{p_2V_2}{p_1}] Переведём объём газа в м(^3): (; 
Ответ: 0,03

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Уравнение Менделеева-Клапейрона и газовые законы: простые задачи
Задачи из пособия Г.А. Никуловой и А.Н. Москалева (2017 г). По теме «Тепловое равновесие, уравнение состояния идеального газа»
Задача 1.
Во сколько раз средняя квадратичная скорость молекул кислорода меньше средней квадратичной скорости молекул водорода, если температуры этих газов одинаковы?
Ответ: в 4 раза
Задача 2.
Три одинаковых сосуда соединены трубками с краном. Первый сосуд содержит 2 моль водорода, второй – 1 моль гелия, третий – 1,5 моль аргона. Как изменится давление в каждом сосуде после того, как краны откроют? Температура неизменна.
Согласно основному уравнению МКТ
Поэтому давление будет определяться концентрацией, а именно количеством вещества, приходящимся на объем. Когда краны откроют, все 4,5 моля газов распределятся по всему объему сосуда – по всем . Поэтому на один объем
станет приходиться по 1,5 моля газов. То есть в первом сосуде давление уменьшится (в нем изначально было 2 моль газа), во втором – увеличится, а в третьем – не изменится.
Задача 3.
В закрытом сосуде вместимостью 2 м находится 280 г азота и 320 г кислорода. Чему равно давление в такой газовой смеси при температуре
?
Согласно уравнению Менделеева-Клапейрона
Ответ: 24 кПа.
Задача 4.
Два баллона объемами 4 и 6 л соединены трубкой с краном. В первом баллоне находится 1,5 моль кислорода под давлением 200 кПа. Второй пуст. Определите давление в сосудах после того, как открыли кран. Температура постоянна.
Если температура постоянна, то можно воспользоваться законом Бойля -Мариотта:
Ответ: 80 кПа
Задача 5.
Воздушный шар радиусом 5 м удерживается веревкой, массой которой можно пренебречь. На сколько изменится натяжение веревки при повышении температуры воздуха с С до
С? Атмосферное давление нормальное.
При повышении температуры увеличится объем шара согласно закону Гей-Люссака, и в связи с этим вырастет сила Архимеда.
Ответ: 482 Н
Задача 6.
По рисунку определите отношение максимального и минимального объемов газа.
К задаче 6
Согласно уравнению Менделеева-Клапейрона
Тогда для точки 2
Откуда
И для точки 3
Откуда
Отношение объемов будет равно 6.
Ответ: 6.
Инфоурок
›
Физика
›Презентации›Подготовка к ЕГЭ по физике. Решение задач на тему «МКТ и газовые законы»
Подготовка к ЕГЭ по физике. Решение задач на тему «МКТ и газовые законы»
Скачать материал

Скачать материал


- Сейчас обучается 461 человек из 73 регионов


- Сейчас обучается 140 человек из 50 регионов


- Сейчас обучается 46 человек из 28 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «Молекулярно-кинетическая теория»
(подготовка к ЕГЭ по физике, 11 класс)
Учитель физики МБОУ «Обоянская СОШ №2»
Мазуркевич Наталья Вячеславовна -
2 слайд
ОТВЕТЬТЕ НА ВОПРОСЫ
Перечислите три утверждения. Которые лежат в основе молекулярно-кинетической теории строения вещества
Что нам известно о строении газообразных, жидких и твёрдых тел? -
3 слайд
ОТВЕТЬТЕ НА ВОПРОСЫ
Что характеризует температура?
Какой газ называется идеальным?
Что называют тепловым равновесием?
Какие макроскопические параметры вам известны? -
4 слайд
ОТВЕТЬТЕ НА ВОПРОСЫ
Перечислите газовые законы, известные вам.
Какой пар называется насыщенным?
Какие формулы МКТ вам известны? -
-
-
7 слайд
Выбери правильный ответ
Одним из подтверждений положения молекулярно-кинетической теории строения вещества о том, что частицы вещества хаотично движутся, может служить:A. Возможность испарения жидкости при любой температуре.
Б. Зависимость давления столба жидкости от глубины.
B. Выталкивание из жидкости погруженных в нее тел. -
8 слайд
Выбери правильный ответ
Идеальный газ, находящийся в закрытом сосуде, оказывает давление на его стенки. Это объясняется тем что1) молекулы прилипают к стенкам сосуда;
2) идеальный газ имеет большую плотность;
3) молекулы газа передают стенкам энергию;
4) молекулы газа передают стенкам импульс. -
9 слайд
Выбери правильный ответ
Выберите неверное утверждение:1) все вещества состоят из частиц;
2) между всеми частицами действуют гравитационные силы;
3) в любом агрегатном состоянии вещество не является сплошным;
4) силы притяжения между частицами вещества всегда меньше сил отталкивания. -
10 слайд
Выбери правильный ответ
Аморфными называют тела,1) атомная структура которых имеет ближний порядок и не имеет дальнего порядка;
2) которые находятся в твёрдом состоянии и представляют собой один большой кристалл;
3) которые находятся в твёрдом состоянии и состоят из большого числа хаотически расположенных мелких кристаллов;
4) которые находятся в жидком состоянии; -
11 слайд
Выбери правильный ответ
Дима и Лена схематически изобразили на доске сосуд, в котором находится идеальный газ.Отвечающим модели броуновского движения можно признать рисунок, сделанный А) Димой Б) Леной
1) только А;
2) только Б;
3) и А, и Б;
4) ни А, ни Б. -
12 слайд
Задача №1
В 4 м. куб. воздуха при температуре 289К находится 40г водяного пара. Найти относительную влажность воздуха, если Ро=1, 81 кПа. -
13 слайд
Задача №2
Какова средняя квадратичная скорость движения молекул газа, если имея массу 6 кг, он занимает объём 5метров куб. при давлении 200кПа? -
14 слайд
Задача №3
Определите среднюю кинетическую энергию молекулы одноатмного газа и концентрацию молекул при давлении 0,8 МПа и температуре 17 градусов по Цельсию? -
15 слайд
Задача №4
Каково давление сжатого воздуха, находящегося в баллоне вместимостью 20л при 12 градусах по Цельсию, если масса этого воздуха 2 кг? -
16 слайд
Задача №5
Сколько молекул содержится в 2г водорода?
-
17 слайд
Задача №6
1. Назовите каждый цикл процесса
2. Изобразите этот процесс в координатах РТ -
18 слайд
Задача №7
В баллоне вместимостью 25л находится смесь газов, состоящая из аргона массой 20г и гелия массой 2г при температуре 301К. Найти давление смеси газов на стенки сосудов. -
19 слайд
ДОМАШНЕЕ ЗАДАНИЕ
1. Портал РЕШУ ЕГЭ. Каталог заданий.
Качественные задачи и основные положения МКТ
2. Смесь одинаковых масс гелия, водорода и азота помещена в сосуд и нагрета до температуры 350К. Плотность смеси оказалась равной 50г/м.куб. Чему равно давление в сосуде? -
20 слайд
СПАСИБО ЗА РАБОТУ
Краткое описание документа:
В данной презентации рассмотрены задачи по физике 10 класса на знание законов МКТ и газовых законов. Слайды сопровождаются рисунками, тестами, вопросами с выбором правильного ответа. Даётся материал на повторение законов и формул.Материал презентации соответствует ФГОС. В конце даётся домашнее задание: задачи на закрепление темы «МКТ и газовые законы»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 784 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 25.03.2019
- 410
- 0

- 25.03.2019
- 1732
- 57
- 25.03.2019
- 358
- 0




- 24.03.2019
- 2199
- 50

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
-
Курс повышения квалификации «Экономика и право: налоги и налогообложение»
-
Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
-
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
-
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
-
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»
-
Курс профессиональной переподготовки «Гостиничный менеджмент: организация управления текущей деятельностью»
-
Курс профессиональной переподготовки «Стандартизация и метрология»
-
Настоящий материал опубликован пользователем Мазуркевич Наталья Вячеславовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 5 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 159111
-
Всего материалов:
63
В данной работе предлагается определенный подход к классификации и способам решения задач на газовые законы. Такой подход позволит быстро сориентироваться в большом количестве задач на свойства газов и применить к ним те или иные приемы решения.
Основные теоретические сведения
Состояние газа характеризуется совокупностью трех физических величин или термодинамических параметров: объемом газа V, давлением Р и температурой Т. Состояние газа, при котором эти параметры остаются постоянными считают равновесным состоянием. В этом состоянии параметры газа связаны между собой уравнением состояния. Самый простой вид уравнение состояния имеет для идеального газа. Идеальным газом называют газ, молекулы которого не имеют размеров (материальные точки) и взаимодействуют друг с другом лишь при абсолютно упругих соударениях (отсутствует межмолекулярное притяжение и отталкивание). Реальные газы тем точнее подчиняются законам идеальных газов, чем меньше размеры их молекул (т.е. газ одноатомный), и чем больше он разряжен.
Уравнение состояния идеального газа или уравнение Менделеева-Клапейрона имеет вид:
— универсальная газовая постоянная
Из этого закона вытекает, что для двух произвольных состояний газа справедливо равенство, называемое уравнением Клапейрона:
Так же для идеальных газов имеют место следующие экспериментальные законы:
Закон Бойля — Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, то результирующее давление определяется по закону Дальтона: давление смеси равно сумме давлений, производимых каждым газом в отдельности, как если бы он один занимал весь сосуд.
Р = Р1 + Р2 +… + РN
Задачи, решение которых основывается на данных уравнениях, можно разделить на две группы:
- задачи на применение уравнения Менделеева-Клапейрона.
- задачи на газовые законы.
ЗАДАЧИ НА ПРИМЕНЕНИЕ УРАВНЕНИЯ МЕНДЕЛЕЕВА-КЛАПЕЙРОНА.
Уравнение Менделеева-Клапейрона применяют тогда, когда
- дано только одно состояние газа и задана масса газа (или вместо массы используют количество вещества или плотность газа).
- масса газа не задана, но она меняется, то есть утечка газа или накачка.
При решении задач на применение равнения состояния идеального газа надо помнить:
- если дана смесь газов, то уравнение Менделеева-Клапейрона записывают для каждого компонента в отдельности. Связь между парциальными давлениями газов, входящих в смесь и результирующим давлением смеси, устанавливается законом Дальтона.
- если газ меняет свои термодинамические параметры или массу, уравнение Менделеева-Клапейрона записывают для каждого состояния газа в отдельности и полученную систему уравнений решают относительно искомой величины.
P.S.
- Необходимо пользоваться только абсолютной температурой и сразу же переводить значения температуры по шкале Цельсия в значения по шкале Кельвина.
- В задачах, где рассматривается движение сосуда с газом (пузырька воздуха, воздушного шара) к уравнению газового состояния добавляют уравнения механики.
- если между газами происходит реакция, то надо составить уравнение реакции и определить продукты реакции
ПЕРВЫЙ ТИП ЗАДАЧ: НЕТ ИЗМЕНЕНИЯ МАССЫ
- Определить давление кислорода в баллоне объемом V = 1 м3 при температуре t=27 °С. Масса кислорода m = 0,2 кг.
|
V = 1 м3 μ = 0,032кг/моль m = 0,2 кг t=27 °С |
Т=300К |
Записываем уравнение Менделеева-Клапейрона и находим из него давление, производимое газом: |
|
Р-? |
- Баллон емкостью V= 12 л содержит углекислый газ. Давление газа Р = 1 МПа, температура Т = 300 К. Определить массу газа.
|
V = 12 л μ =0,044кг/моль Т=300К Р =1 МПа |
0,012м3 1∙106Па |
Записываем уравнение Менделеева-Клапейрона и находим массу газа |
|
m -? |
- При температуре Т = 309 К и давлении Р = 0,7 МПа плотность газа ρ = 12 кг/м3. Определить молярную массу газа.
|
V = 12 л Т=309К Р =0,7 МПа ρ = 12 кг/м3 |
0,012м3 0,7∙106Па |
Записываем уравнение Менделеева-Клапейрона Так как масса газа может быть определена через плотность газа и его объем имеем: |
|
μ -? |
||
|
Отсюда находим молярную массу газа: |
- Какова плотность водорода при нормальном атмосферном давлении и температуре 20°С.
|
V = 12 л t=20°C Р =105 Па μ =0,002кг/моль |
0,012м3 T=293К |
Нормальное атмосферное давление – это давление, равное 105 Па. И эту информацию запишем как данные задачи. Записываем уравнение Менделеева-Клапейрона |
|
ρ -? |
||
|
Так как масса газа может быть определена через плотность газа и его объем имеем: Отсюда находим плотность газа: |
- До какой температуры Т1 надо нагреть кислород, чтобы его плотность стала равна плотности водорода при том же давлении ,но при температуре Т2 = 200 К?
|
Т2=200К ρ1 = ρ2 μ1 =0,032кг/моль μ2 =0,002кг/моль |
Записываем уравнение Менделеева-Клапейрона для кислорода и для водорода через плотности газов: Так как по условию давление у двух газов одинаковое, то можно приравнять правые части данных уравнений: Сократим на R и на плотность ρ (по условию плотности газов равны) и найдем Т1 |
|
Т1 -? |
|
|
|
- В сосуде объемом 4·10-3 м3 находится 0,012 кг газа при температуре 177°С. При какой температуре плотность этого газа будет равна 6·10-6 кг /см3, если давление газа остается неизменным.
|
V=4·10-3 м3 m=0,012 кг t1=177°C ρ2=6·10-6 кг /см3 |
Т1=450К 6 кг/м3 |
|
|
Т2 -? |
|
Смесь газов
- В баллоне объемом 25 литров находится 20 г азота и 2 г гелия при 301К. Найдите давление в баллоне.
|
V = 25 л μ1 = 0,028кг/моль m1 = 20 г μ2 = 0,004кг/моль m2 = 2 г Т=301К |
0,025м3 0,02кг 0,002кг |
Записываем уравнение Менделеева для каждого газа и находим из него давление газов По закону Дальтона результирующее давление в сосуде равно сумме парциальных давлений газов: |
|
Р-? |
|
- Определить плотность смеси, состоящей из 4 граммов водорода и 32 граммов кислорода при давлении 7°С и давлении 93кПа?
|
μ1 = 0,002кг/моль m1 = 4 г μ2 = 0,032кг/моль m2 = 32 г t=7°С Р =93кПа |
0,004кг 0,032кг T=280K 93000Па |
По закону Дальтона: |
|
ρ-? |
|
|
|
|
- Сосуд емкостью 2V разделен пополам полупроницаемой перегородкой. В одной половине находится водород массой mВ и азот массой mА. В другой половине вакуум. Во время процесса поддерживается постоянная температура Т. Через перегородку может диффундировать только водород. Какое давление установиться в обеих частях сосуда?
|
μа m1 = m2 = m3 = m μв μк Т |
Диффундирует только водород. |
|
РI-? РII-? |
|
|
половину меньшей, чем была, и весь азот. А во втором отсеке только половина массы водорода. Тогда для первого отсека установившееся давление равно: Для отсека II можно так же определить установившееся давление: |
- Вакуумированный сосуд разделен перегородками на три равных отсека, каждый объемом V. В средний отсек ввели одинаковые массы кислорода, азота и водорода. В результате чего давление в этом отсеке стало равно Р. Перегородка I проницаема только для молекул водорода, перегородка II проницаема для молекул всех газов. Найти давления Р1 Р2 и Р3, установившиеся в каждом отсеке, если температура газа поддерживается постоянной и равной Т.
|
μа m1 = m2 = m3 = m μв μк Р |
После диффундирования газов через перегородки в первом отсеке окажется треть массы водорода. Во втором и в третьем отсеках будет треть водорода, половина массы кислорода и половина всей массы азота. Тогда для первого отсека установившееся давление равно: |
|
Р1-? Р2-? Р3-? |
|
|
|
|
|
Если до диффундирования первоначальное давление во втором отсеке было Р, то можно записать: Отсюда можно найти Находим выражение для давления во втором и в третьем отсеках |
|
|
И тогда давление в первом отсеке равно: |
С химическими реакциями
- В сосуде находится смесь азота и водорода. При температуре Т, когда азот полностью диссоциирован на атомы, давление равно Р (диссоциацией водорода можно пренебречь). При температуре 2Т, когда оба газа полностью диссоциированы, давление в сосуде 3Р. Каково отношение масс азота и водорода в смеси?
|
μа μв Т1 =Т Т2 =2Т Р1=Р Р2=3Р |
При температуре Т параметры газов в сосуде следующие: И результирующее давление в сосуде по закону Дальтона равно: |
|
|
|
|
При температуре 2Т параметры газов в сосуде следующие: И результирующее давление в сосуде по закону Дальтона равно: |
- В герметично закрытом сосуде находится 1 моль неона и 2 моля водорода. При температуре Т1=300К, когда весь водород молекулярный, атмосферное давление в сосуде Р1=105 Па. При температуре Т2=3000К давление возросло до Р2=1,5∙105 Па. Какая часть молекул водорода диссоциировала на атомы?
|
ν1=1 моль ν2=2 моль Т1 =300К Т2 =3000К Р1=105 Па Р2=1,5∙105 Па |
При температуре Т1 давление газа в сосуде складывается из парциальных давлений двух газов и равно: При температуре Т2 давление газа равно: |
|
|
|
|
Из уравнения (1): Из первого находим объем V: |
|
|
|
- В закрытом баллоне находится смесь из m1= 0,50 г водорода и m2 = 8,0 г кислорода при давлении Р1= 2,35∙105 Па. Между газами происходит реакция с образованием водяного пара. Какое давление Р установится в баллоне после охлаждения до первоначальной температуры? Конденсации пара не происходит.
|
V = 25 л μ1 = 2г/моль m1 = 0,5 г μ2 = 32г/моль m2 = 8 г |
В сосуде будет происходить реакция водорода с кислородом с образованием воды:
|
|
Р-? |
Из уравнения реакции видно, что если в реакцию вступит весь водород, то кислорода только половина |
|
В результате образуется ν3=0,25 молей водяного пара и останется ν4= 0,125молей кислорода. По закону Дальтона результирующее давление в сосуде равно сумме парциальных давлений Так как известно, что до реакции давление в сосуде было Р1, то для этого момента можно так же применить закон Дальтона: Решаем полученные уравнение в системе относительно неизвестного: |
С добавлением законов механики.
- На дне сосуда, заполненного воздухом, лежит шарик радиусом r и массой m. До какого давления надо сжать воздух в сосуде, чтобы шарик поднялся вверх. Температура воздуха Т известна.
|
m r Т Т |
Запишем уравнение динамики и уравнение Менделеева-Клапейрона. Решаем полученную систему уравнений относительно неизвестного: |
|
Р-?Р Р-? |
- Тонкостенный резиновый шар массой 50г наполнен азотом и погружен в озеро на глубину 100 м. Найти массу азота, если шар находится в положении равновесия. Атмосферное давление 760мм. рт. ст. Температура воды в озере на глубине 100м равна 4°С.
|
mоб=50г h=100м Р=760мм.рт.ст. t=4°С μ=0,028кг/моль |
0,05кг 105Па Т=277К |
|
Запишем второй закон Ньютона в проекции на вертикальную ось. Объем шара равен объему азота в нем. Запишем уравнение Менделеева-Клапейрона для азота и выразим из него объем азота |
|
ma-? |
|||
|
Р-? Давление азота на этой глубине равно давлению внешнему на шар, так как по условию оболочка шара не пульсирует. Следовательно: |
- Надувной шарик, заполненный гелием, удерживают на нити. Найдите натяжение нити, если масса оболочки шарика 2г, объем 3литра, давление гелия 105 Па, температура 27°С. Плотность воздуха 1,3 кг/м3
|
mоб=2г Р=105Па t=27°С μгел=0,004кг/моль Vшара=3л μвоз=0,029 кг/моль |
0,002кг Т=300К 0,003м3 |
Запишем второй закон Ньютона в проекции на вертикальную ось х. |
|
|
Т-? |
|||
|
Объем шара равен объему гелия в нем, а значит 3литра; Запишем уравнение Менделеева-Клапейрона для воздуха (среда, в которой находится шар), и введем в него плотность воздуха: Тогда уравнение (1) принимает вид: Теперь надо записать уравнение Менделеева-Клапейрона для гелия и выразить из него массу гелия. Надо учесть, что объем азота равен объему шара. А так же температура окружающего воздуха и температура гелия равны, как равны и давления воздуха и гелия. С учетом определенной массы гелия, сила натяжения равна: |
- В вертикально расположенном цилиндре находится кислород массой m = 64 г, отделенный от атмосферы поршнем, который соединен с дном цилиндра пружиной жесткостью k = 830 H/м. При температуре T1= 300 К поршень располагается на расстоянии h = 1 м от дна цилиндра. До какой температуры T2 надо нагреть кислород, чтобы поршень расположился на высоте H = 1,5м от дна цилиндра? Универсальная газовая постоянная R= 8,31 Дж/(моль∙ К), молярная масса кислорода μ = 32 г/моль.
|
m=0,064кг Т1=300К h=1м H=1,5м k=830 Н/м μ = 0,032 кг/моль |
|
|
Т2-? |
|
|
Здесь через Р1 и через Р2 обозначено давление газа в первом и во втором состояниях. Через х1 и х2 обозначена деформация пружины в двух состояниях. Вычтем из второго уравнения первое уравнение: Запишем уравнение Менделеева-Клапейрона для двух состояний газа: Приравняем разности давлений газа, найденные двумя способами: Из полученного уравнения находим Т2: |
ВТОРОЙ ТИП ЗАДАЧ: ЕСТЬ ИЗМЕНЕНИЯ МАССЫ
- Температуру воздуха в комнате подняли с t1 = 7 °С до t2 = 27 °С. Какая масса воздуха должна выйти из комнаты, чтобы давление осталось неизменным, Р = 105 Па? Объем воздуха в комнате V = 50 м3.
|
μ = 0,029кг/моль t1 = 7°C t2 = 27°C Р =105 Па V=50м3 |
Т1=280К Т2=300К |
Так как при нагревании все тела расширяются, а комната не герметична, следовательно, масса воздуха в комнате при нагревании уменьшается (есть утечка газа), но при этом, понятно, что объем газа не меняется и остается равным объему комнаты. Для каждого состояния газа запишем уравнение Менделеева-Клапейрона, и определим из них массу воздуха в комнате при разной температуре. |
|
ρ-? |
|
|
|
|
- Стеклянная колба закрыта пробкой и взвешена при температуре t1 = 15 °С. Открыв пробку, колбу нагрели до температуры t2 = 80 °С. При следующем взвешивании масса колбы оказалась на m = 0,25 г меньше. Чему равен объем колбы?
|
μ = 0,029кг/моль t1 = 15°C t2 = 80°C Р =105 Па ∆m=0,25 г |
Т1=288К Т2=353К 0,25∙10-3кг |
Масса стеклянной колбы не меняется, меняется масса газа в ней, так как есть утечка: при нагревании все тела расширяются, а колба не герметична, следовательно, масса воздуха в ней при нагревании уменьшается, но при этом, понятно, что объем газа не меняется и остается равным объему колбы. Будем считать, что атмосферное давление нормальное. Для каждого состояния газа запишем уравнение Менделеева-Клапейрона, и определим из них массу воздуха в колбе при разной температуре. |
|
V -? |
|
|
|
Выразим отсюда объем колбы: |
- В баллоне емкостью V = 12 л находится азот массой m1 = 1,5 кг при температуре t1 = 37°С. Каким станет давление в баллоне при температуре t2 =50 °С, если выпустить 35% азота? Первоначальное давление считать нормальным.
|
μ = 0,028кг/моль t1 = 37°C t2 = 50°C Р1 =105 Па m2=0,65m1 |
Т1=310К Т2=323К |
Для каждого состояния газа запишем уравнение Менделеева-Клапейрона. |
|
Р2 −? |
|
- В сосуде объемом V = 1 л находится идеальный газ. В сосуде объемом V = 1 л находится идеальный газ. Сколько молекул газа нужно выпустить из сосуда, чтобы при понижении температуры в k=2 раза его давление уменьшилось в z =4 раза?
|
μ = 0,028кг/моль t1 = 37°C t2 = 50°C Р1 =105 Па m2=0,65m1 |
Т1=310К Т2=323К |
Для каждого состояния газа запишем уравнение Менделеева-Клапейрона. |
|
Р2 −? |
|
- Когда из сосуда выпустили некоторое количество газа, давление в нем упало на 40%, а абсолютная температура на 20%. Какую часть газа выпустили?
|
T2 = 0,8T1 Р2 =0,6Р1 m2=0,65m1 |
Для каждого состояния газа запишем уравнение Менделеева-Клапейрона. |
|
|
|
|
|
- В сосуде объемом V = 0,5 л находится идеальный газ при давлении Р1=1 атм. и температуре t = 27 °С. Сколько молекул газа нужно выпустить из сосуда, чтобы давление в нем уменьшилось в 2 раза? Температура газа не изменяется.
|
T = 300К Р=1 атм. =105Па Р1=2Р2 V=0,5л=0,5∙10-3м3 |
Для каждого состояния газа запишем уравнение Менделеева-Клапейрона. |
|
∆N−? |
|
|
|
- В пустой сосуд объемом V нагнетают воздух при помощи поршневого насоса, объем цилиндра которого V0. Каким будет давление воздуха в сосуде после N качаний?
|
V N V0 |
Задачи про насосы решаются так же на основе уравнения Менделеева-Клапейрона. Надо записать уравнение для накаченной массы, то есть той, что поступила в сосуд. И так же записать уравнение Менделеева-Клапейрона для газа, поступающего в рабочий резервуар насоса. И учесть, что вся масса газа, попавшая в сосуд – это масса газа, попадавшая в резервуар насоса N раз. Будем считать, что в насос газ поступает при атмосферном давлении |
|
Р−? |
|
|
Запишем уравнение Менделеева-Клапейрона для газа, поступившего в цилиндр насоса: Запишем уравнение Менделеева-Клапейрона для газа, поступившего в сосуд: Поделим второе уравнение на первое: |
- Компрессор засасывает из атмосферы каждую секунду 3 литра воздуха, которые подаются в баллон емкостью 45 литров. Через сколько времени давление в баллоне будет превышать атмосферное в 9 раз? Начальное давление в баллоне равно атмосферному.
|
V=45л V0=3л Ррез=9Ратм |
Данная задача решается так же, как предыдущая, но с одним отличием: в баллоне уже был воздух при атмосферном давлении. Поэтому, записывая уравнение Менделеева-Клапейрона для накаченного воздуха, надо учесть, что создаваемое им давление превышает атмосферное в 8 раз. Р=8Ратм Так как по условию задачи компрессор работает так, что ежесекундно засасывает воздух, то число секунд равно числу «засасываний» |
|
t−? |
|
|
Запишем уравнение Менделеева-Клапейрона для газа, поступившего в цилиндр компрессора: Запишем уравнение Менделеева-Клапейрона для газа, поступившего в баллон: Поделим второе уравнение на первое: Время, потребовавшееся для такого накачивания, так же составляет 120с |
Задачи на применение газовых законов.
Газовые законы применяют тогда, когда даны два состояния газа и при переходе газа из одного состояния в другое масса газа не меняется.
ГРАФИЧЕСКИЕ ЗАДАЧИ НА ГАЗОВЫЕ ЗАКОНЫ
- На диаграмме РT изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме Р,V.
|
|
Проведем поэтапный анализ представленного цикла: 1–2: изохорический процесс; V – const; Р↑ T↑ 2–3: изотермический процесс; V↑ Р↓ Т – const 3–1: изобарический процесс; V↓; Р– const; T↓ Теперь результаты поэтапного анализа перенесем на диаграмму РV ⇒ |
|
- Для постоянной массы идеального газа представлен цикл на диаграмме РV. Изобразить этот цикл на диаграмме VT.
|
|
Решение: ⇒ |
|
- Изобразите на диаграмме РТ цикл постоянной массы идеального газа, представленный на диаграмме РV.
|
|
Решение: ⇒ |
|
- Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: Р1V1 = Р2V2, то Р1 > Р2.
- При нагревании идеального газа постоянной массы получена зависимость Р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»). Проведем через начальную и конечную точки линии графика две изохоры. Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1.
При изобарическом процессе, по закону Гей-Люссака, V ~ T, следовательно, V2 > V1. А так как плотность и объем связаны обратной зависимостью (при данной массе), то ρ1 > ρ2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
- Как менялась температура постоянной идеального массы газа на протяжении цикла?
|
|
Точки 1 и 2 лежат на одной изотерме. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах ⇒ |
|
- Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
|
|
Запишем уравнение Клапейрона–Менделеева: По условию, T, M и R – постоянные, следовательно, m ~ рV. Рассмотрим процессы цикла поэтапно: 1–2: T = const, V = const; m ~ р; 2–3: T = const, р = const; m ~ V; 3–4: T = const, V = const; m ~ р; 4–1: T = const, р = const; m ~ V; ⇒ |
|
Аналитические задачи на газовые законы
При решении аналитических задач на газовые законы надо:
- Убедиться, что при изменении состояния масса газа остается постоянной.
- Сделать схематический чертеж, на котором условно отметить состояния газа параметрами Р, V, Т. Записать закон Клапейрона для данных двух состояний.
- Если какой-либо параметр при переходе газа из одного состояния в другое остается неизменным (могут меняться все три параметра), то уравнение Клапейрона перевести в закон Бойля — Мариотта, Гей-Люссака или Шарля.
В случае, когда газ заключен в цилиндрический сосуд и объем газа меняется только за счет изменения высоты его столба h, уравнение Клапейрона можно сразу записывать в виде:
- Используя условия задачи, определить термодинамические параметры, выразив их через заданные величины. И если газ граничит с жидкостью, то особое внимание следует обратить на определение давления. Для его определения тех случаях, когда газ производит давление на жидкость, следует использовать закон Паскаля: провести нулевой уровень через границу, отделяющую газ от жидкости, и записать уравнение равновесия жидкости.
- Полученную систему уравнений решить относительно неизвестной величины.
P.S.
- Если в задаче рассматривают состояния нескольких газов, отделенных друг от друга поршнями или входящих в состав смеси, то все указанные действия нужно проделать для каждого газа отдельно.
- В задачах на газовые законы используется только абсолютная температура.
- При увеличении абсолютной температуры газа в 2 раза давление увеличилось на 25%. во сколько раз изменился объем газа?
|
Т2=2Т1 Р2=1,25Р1 |
Запишем уравнение Клапейрона, так как меняются все три параметра идеального газа: |
|
|
С учетом данных, уравнение принимает вид: |
- Газ изотермически сжат от объема V1 = 8 л до объема V2 = 6 л. Давление при этом возросло на ΔР = 4∙103 Па. Определить первоначальное давление.
Запишем уравнение Клапейрона и, так как процесс изотермический, переведем его в закон Бойля-Мариотта
Поэтому можно записать:
Отсюда находим первоначальное давление:
И объемы газов можно оставить в литрах, не переводить в систему СИ.
- При нагревании газа при постоянном давлении на 1К его объем увеличился на 5% от первоначального. При какой температуре находился газ?
- Сколько ртути войдет в стеклянный баллончик объемом V0, нагретый до Т0, если плотность ртути при температуре Т равна ρ.
- Закрытый с обоих концов цилиндрический сосуд разделен на две равные части теплонепроницаемым поршнем. Длина каждой части 42см. В обеих половинках находится одинаковое количество азота при температуре 27°С и давлении 1 атмосфера. На сколько надо нагреть газ в одной части сосуда, чтобы поршень переместился на 2 см?
Для газа в отделе I:
Для газа в отделе II:
Отсюда следует:
- Объем баллона, содержащего газ под давлением 1,2·105 Па составляет 6 литров. Каким станет давление газа, если этот баллон соединить с другим баллоном объем которого 10 литров и он практически не содержит газа.
- Два одинаковых стеклянных шара соединены трубкой. При 0° С капелька ртути находится посередине трубки. Объем воздуха в каждом шаре и части трубки У= 200 см3 . На какое расстояние х сместится капелька, если один шар нагреть на 2° С, а другой на столько же охладить? Поперечное сечение трубки S=20 мм2
Для газа в отделе I:
- Температура воздуха в цилиндре 7°С. На сколько переместиться поршень при нагревании воздуха на 20К, если ℓ1=14см?
Газ граничит с жидкостью
- Электрическая лампа наполнена азотом при давлении Р= 600 мм рт. ст. Объем лампы V = 500 см3. Какая масса воды войдет в лампу, если у нее отломить кончик под водой? Атмосферное давление 760 мм рт. ст.?
Объем воды, поступившей в сосуд равен изменению объема газа при изотермическом процессе. Вода будет заходить в колбу до тех пор, пока давление внутри колбы не станет равным давлению наружному, то есть атмосферному.
Запишем закон Бойля-Мариотта для газа в колбе:%
Отсюда определим изменение объема:
Масса поступившей воды равна:
- Объем пузырька воздуха по мере всплывания со дна озера на поверхность увеличивается в 3 раза. Какова глубина озера?
- Открытую стеклянную трубку длиной ℓ=1м наполовину погружают в ртуть.Затем трубку закрывают пальцем и вынимают из ртути. Какой длины столбик ртути останется в трубке? атмосферное давление нлормальное.
- Узкая вертикальная цилиндрическая трубка длиной L,закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути длиной h. Плотность ртути ρ. Трубка расположена открытым концом вверх. Какова была длина ℓ столбика воздуха в трубке, если при перевертывании трубки открытым концом вниз, из трубки вылилось половина ртути. атмосферное давление Р0
- В стеклянной трубке, запаянной с одного конца и расположенной горизонтально, находится столбик воздуха длиной 300мм, закрытый столбиком ртути длиной 200мм. На сколько изменится длина воздушного столбика, если трубку расположить открытым концом вверх? Атмосферное давление нормальное.
- Длинная пробирка открытым концом погружена в сосуд с ртутью. При температуре t1 = 47 °С уровни ртути в пробирке и в сосуде совпадают. Над уровнем ртути остается часть пробирки длины L = 76см. На какую высоту ℓ поднимется ртуть в пробирке, если ее охладить до температуры t2 = -33 °С? Атмосферное давление Р0 = 0,1 МПа.
- Посередине откачанной и запаянной с обоих концов горизонтально расположенной трубки длины L = 1 м находится столбик ртути длины h = 20 см. Если трубку поставить вертикально, столбик ртути сместится на расстояние ℓ = 10 см. До какого давления Р была откачана трубка? Плотность ртути ρ= 13,6∙103 кг/м3.
В обоих концах трубки воздух первоначально занимал объем
V = S(L — h)/2,
где S — площадь поперечного сечения трубки, и имел давление Р.
Когда трубку поставили вертикально, объем воздуха в верхней части трубки стал
V1 = S[(L — h)/2 + ℓ],
а давление стало Р1;
В нижней части трубки объем стал V2 = S[(L — h)/2 — ℓ], а давление стало равным Р2
Согласно закону Бойля-Мариотта для верхней части трубки PV = P1V2
Откуда (L — h) P =(L-h + 2ℓ)P1;
Для нижней части трубки
PV = P2V2, откуда (L-h)P = (L-h-2ℓ)Р2.
С другой стороны, столбик ртути находится в равновесии, когда давление воздуха в нижней части трубки равно сумме давлений воздуха в верхней части трубки и столбика ртути, т.е.
P2=P1+ρgh
Исключив Р1 иР2 из уравнений, найдем = 50 кПа.
Эксперт ЕГЭ Н. Л. Точильникова
Задача 29 на ЕГЭ по физике – это расчетная задача на механику. До 2014 года включительно она фигурировала под номером «С2».
Это может быть кинематика, динамика, динамика движения по окружности, задача на законы сохранения в механике, статику или гидростатику.
Например, задача на движение тела, брошенного под углом к горизонту:
1. Маленький шарик падает сверху на наклонную плоскость и упруго отражается от нее. Угол наклона плоскости к горизонту равен . На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в момент первого удара направлена вертикально вниз и равна
м/с.
Запишем «дано»:
м/с
Найти: .
Решение:
В задачах части «С» необходимо описывать все параметры, которых нет в дано, иначе оценку снижают на один балл.
Поэтому пишем:
– расстояние по горизонтали между первым и вторым ударами о плоскость.
Нарисуем наклонную плоскость и начальную скорость шарика . Как известно из геометрии, углы с перпендикулярными сторонами равны. Начальная скорость шарика перпендикулярна основанию наклонной плоскости. Восстановим перпендикуляр к наклонной плоскости в точке падения на нее шарика. Тогда угол между этим перпендикуляром и вектором начальной скорости равен углу наклона плоскости к горизонту (углы с перпендикулярными сторонами, зеленые пунктирные линии на рисунке). Угол падения шарика (с перпендикуляром) равен углу отражения
. Тогда угол между начальной скоростью отскочившего шарика и наклонной плоскостью равен
. Модуль скорости не меняется, так как удар упругий.
Итак, убираем построения, которые нам больше не нужны:
Тело будет двигаться по параболе и упадет на расстоянии от точки бросания вдоль наклонной плоскости. Это не то расстояние, которое нам надо найти, мы ищем
— расстояние по горизонтали. Но, если мы знаем
, найти
очень легко:
.
Теперь нужно выбрать систему отсчета. С началом отсчета все ясно, очевидно, мы берем его в точке падения шарика. А вот с направлениями осей все не так просто.
Можно выбрать оси традиционным способом: «» горизонтально и «
» вертикально:
Но при таком выборе осей трудно определить точку падения. Поэтому в подобных задачах оси обычно выбирают иначе: «» вдоль наклонной плоскости, а «
» перпендикулярно наклонной плоскости:
При таком выборе осей точка падения определяется элементарно: там координата «» обращается в ноль. Зато движение становится равноускоренным по двум осям, поскольку ускорение
проектируется на обе оси:
— противолежащий катет;
— прилежащий катет.
Начальная скорость также проектируется на обе оси:
– прилежащий катет;
– противолежащий катет
Зависимости координат от времени при равноускоренном движении выражаются формулами:
Подставляя значения проекций скорости и ускорения, получаем:
Начальные координаты: ;
Конечная координата y также равна нулю, так как тело падает на наклонную плоскость.
Из второго уравнения получаем:
Это уравнение равносильно совокупности:
Из второго уравнения находим :
Подставляем в уравнение для
:
Откуда:
Тогда:
Но и
То есть:
м
Задача 30 на ЕГЭ по физике
Задача 30 на ЕГЭ по физике (раньше называлась С3) – это задача на газовые законы или термодинамику.
Например:
2. Вертикально расположенный замкнутый цилиндрический сосуд высотой см разделен подвижным поршнем весом
на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре
. Сколько молей газа находится в каждой части цилиндра, если поршень расположен на высоте
см от дна сосуда? Толщиной поршня пренебречь.
Дано:
см
м
см
м
Найти: (число молей в каждой части цилиндра.)
– давление в верхней части цилиндра;
– давление в нижней части цилиндра;
– площадь сечения поршня.
– сила давления на поршень газа в верхней части цилиндра;
— сила давления на поршень газа нижней части цилиндра.
Так как поршень неподвижен, сумма всех действующих на него сил равна нулю.
То есть:
Запишем уравнение Менделеева-Клапейрона для верхней и нижней частей цилиндра:
Где – объем верхней части цилиндра;
— объем нижней части цилиндра.
Выражаем и
:
И подставляем в уравнение для сил:
Подставляем выражения для объемов:
Сокращаем :
Откуда:
моль
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи 29 и 30 на ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Конспект урока в 10-м классе
Подготовка к ЕГЭ на уроках физики.
Тема урока: Решение задач по теме «Газовые законы»
Цели урока:
• развивать навыки логического мышления, самостоятельной исследовательской работы, внимательность, умение сравнивать и анализировать, находить закономерности, рассуждать, делать вывод;
• формировать навыки работы с графиками;
• воспитывать целеустремленность, настойчивость в достижении поставленной цели, ответственное отношение к труду.
Эпиграф урока:
“Всякая физическая теория должна быть математически красивой” — М.Дирак.
Задачи:
1. Образовательные: изучить газовые законы; изображать графики изопроцессов; сформировать умения выделять и описывать изопроцессы; начать обучение учащихся решать графические и аналитические задачи, используя уравнение состояния и газовые законы.
2. Воспитательные: продолжить формирование познавательного интереса учащихся; стремления глубокого усвоения теоретических знаний через решение задач; умения слушать товарищей, аргументировать свою точку зрения.
3. Развивающие: активизация мыслительной деятельности, формирование логического и алгоритмического мышления; совершенствование навыков исследовательской деятельности; формирование качеств личности: самостоятельность, внимательность, критичность, объективность.
Оснащение урока: компьютер, проектор, экран, презентация по теме урока, задания к ЕГЭ, карточки с тестом
Ожидаемый результат:
1. Успешная самореализация учащихся в учебной деятельности.
2. Умения ставить перед собой задачи, решать их, представлять полученные результаты.
Ход урока
1. Организационный момент.
2. Повторение теоретического материала по изученной теме.
а) мозговой штурм
б) физический диктант
3. Разбор и решение задач из материалов ЕГЭ
4. Самостоятельная работа (тест) и самопроверка.
5. Обобщение (таблица)
6. Постановка домашнего задания.
7. Итоги урока. Рефлексия
1. Вступительное слово учителя (слайд 1-3)
На этом уроке мы повторим темы «Уравнение Менделеева- Клапейрона. Газовые законы», решим тест, качественные и расчетные задачи. Многие задания которые мы будем выполнять были предложены выпускникам при проведении ЕГЭ по физике.
2. Повторение теоретического материала по изученной теме.
а) мозговой штурм (слайд 4-8)
1.Найти во всех трех системах координат:
а) изотермы; б) изобары; в) изохоры
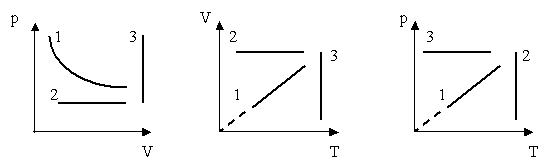
2.Сравнить давление газа в этих состояниях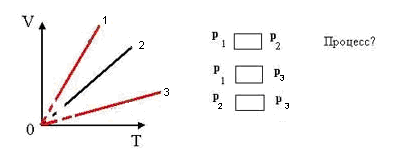
3.Сравнить объёмы газа в этих состояниях.
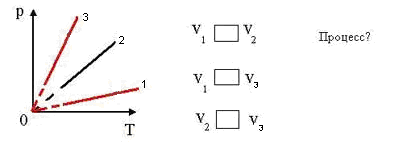
4.Сравнить температуры газа в этих состояниях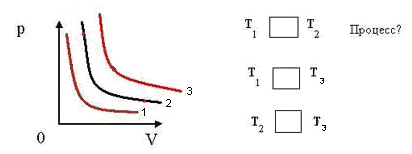
б) физический диктант (верно или неверно) (слайд 9-11)
-
Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами.
-
Давление, объём и температура – это макроскоспические параметры характеризующие состояние данной массы газа.
-
Это уравнение состояния идеального газа : рV= м/М *RT
-
Если температура газа остаётся постоянной, то выполняется закон Шарля: pV=const
-
Идеальный газ – это газ в котором взаимодействие между молекулами можно не учитывать.
-
Процесс изменения состояния термодинамической системы макроскопических тел при постоянном давлении называется изобарным.
-
Универсальная газовая постоянная равна 8,31 Дж/мольК.
-
Если объём газа остаётся постоянным, то выполняется закон Бойля-Мариотта: V/T=const
Самопроверка (слайд12)
1 2 3 4 5 6 7 8
+ + + — + + + —
Каждый правильный ответ оцените
0,5 баллов
3. Разбор и решение задач из материалов ЕГЭ (слайд 15-19)
1. На рисунке показаны графики четырех процессов изменения состояния постоянной массы идеального газа. Изохорным нагреванием является процесс
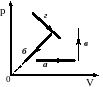
1) а
2) б
3) в
4) г
2. На диаграмме V-T представлен график изменения объема идеального газа постоянной массы при изменении его температуры. Как изменяется давление газа в этом процессе?
1) все время увеличивается
2) все время уменьшается
3) сначала уменьшается, а затем увеличивается
4) сначала увеличивается, затем уменьшается
3. В цилиндрическом сосуде под поршнем находится идеальный газ, давление которого 4·105 Па и температура 300 К. Как надо изменить объем газа, не меняя его температуры, чтобы давление увеличилось до 0,8·106 Па?
1) увеличить в 2 раза
2) увеличить в 4 раза
3) уменьшить в 2 раза
4) уменьшить в 4 раза
4. В цилиндре закрытом подвижном поршнем,находиться газ.который может просачиваться сквозь зазор вокруг пошрня.В опыте по изобарному сжатию газа его обьём уменьшился в 8 раз,а абсолютная температура газа уменьшилась в 2 раза.Во сколько раз изменилась внутренняя энергия газа в цилиндре?(газ считать идеальным)
4. Самостоятельная работа (тест) и самопроверка. (Приложение)
( слайд 22 )
|
Каждый правильный ответ оцените в 1 балл. Ответ В в 2 балла. |
В |
|||||
|
5. Обобщение((таблица) (слайд 23) 6. Постановка домашнего задания. (слайд 24) Повторить §70,71 Решить: А: Р-508,527,536 В: Р-521,529,539 С: Р-540,544,531 7. Итоги урока. Рефлексия (слайд 25) Оценить работу в классе согласно критериям |
4*103Па |
|||||
|
1,38*10-2кг |
Используемые ресурсы:
1. «Физика 10 класс» учебник для общеобразовательных учреждений. Г.А. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Москва «Просвещение» 2010
2. Анофрикова С.В. Методика преподавания физики в средней школе. М.: Просвещение 1987 г.
3. http://files.school-collection.edu.ru/
4. http://kotovskobraz.68edu.ru/MEROPRIAT/Seminar/Anisimova.htm
5. http://nsportal.ru/shkola/fizika/library/urok-po-teme-gazovye-zakony