Задачи на гидростатику егэ физика

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Тело, находящееся в воде или на поверхности, медленно, не останавливаясь, двигают по вертикали.

Установите соответствие между графиками и процессами, которые их описывают.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

ГРАФИКИ

ПРОЦЕССЫ

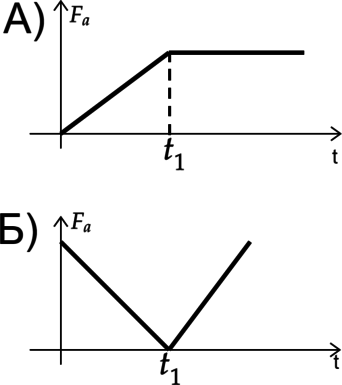
1) Тело до (t_1) опускали вниз, а после (t_1) оно полностью погрузилось в воду.

2) Тело до (t_1) поднимали, а после оно находилось на поверхности.

3) Тело до (t_1) поднимали, а после опускали вниз.

4) Тело всё время находилось на одной глубине погружения.

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Сила Архимеда находится по формуле [F_a=rho g V] Где (rho) — плотность жидкости, а (V) — объем погруженной части тела. Так как сила Архимеда сначала увеличивалась, а затем была постояна, то объем погруженной части тоже увеличивался, а затем был постоянный, а значит тело погружали, пока оно не погрузилось полностью. Ответ — 1
Б) Сила Архимеда сначала уменьшалась, а затем увеличивалась, значит тоже самое происходило и с объемом тела. Ответ — 3

Ответ: 13

Тело массой (m) и объемом (V) плавает на поверхности жидкости плотностью (rho) и погружено на (dfrac{1}{4}V).

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

[begin{array}{ll}

text{Физические величины}&text{Формулы}\

text{А) Сила тяжести} & text{1)} dfrac{1}{4}rho g V \
text{Б) Плотность тела} &text{2)} rho g V \
&text{3)} dfrac{1}{4} rho \
&text{4)} rho \

end{array}]

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Так как тело плавает, то силу тяжести уравновешивает сила Архимеда [F_text{т}=dfrac{1}{4}rho g V]

Ответ – 1

Б) Из пункта А) [mg= F_text{т}=dfrac{1}{4}rho V]

Заменим (m) на (rho_o cdot V), где (rho_0) – плотность тела. Получим [rho_0 cdot V= dfrac{1}{4}rho V]

Или [rho_o=dfrac{1}{4}rho]

Ответ – 3

Ответ: 13

Тело сделанное из железа плотностью (rho_0)=7800 кг/м(^3) и объемом (V)=0,001 м(^3) в первом случае погружают в воду, а во втором в ртуть.

Установите соответствие между физическими величинами и их значениями.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

[begin{array}{ll}

text{Физические величины}&text{Значения}\

text{А) Сила Архимеда в воде} &1) 78text{ Н} \
text{Б) Сила Архимеда в ртути} &2) 10 text{ Н} \
&3) 136 text{ Н} \
&4) 100 text{ Н} \

end{array}]

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Так как плотность железа больше плотности воды, то тело тонет. Значит сила Архимеда находится по формуле [F_a=rho_1 g V_text{т}]

Где (rho_1) — плотность воды, а (V_text{т}) — объем погруженной части (т.к. тело тонет, то он равен (V)).

Найдем силу Архимеда (F_a=1000text{ кг/м$^3$} cdot 10 text{ м/с$^2$} cdot 0,001 text{ м$^3$}= 10text{ Н} ). Ответ – 2

Б) Так как плотность железа меньше плотности ртути, то тело будет плавать на поверхности и сила Архимеда будет уравновешивать силу тяжести [F_a=F_text{т}=mg=rho_0cdot Vcdot g]

Найдем силу Архимеда (F_a= 7800text{ кг/м$^3$} cdot 0,001 text{ м$^3$} cdot 10 text{ м/с}^2= 78 text{ Н}). Ответ – 1

Ответ: 21

Тело объемом (V)=0,002 м(^3), находящееся в сосуде с водой плотностью (rho)=1000 кг/м(^3), двигают по вертикали.

Установите соответствие между графиками и процессами, которые их описывают.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

ГРАФИКИ

ПРОЦЕССЫ

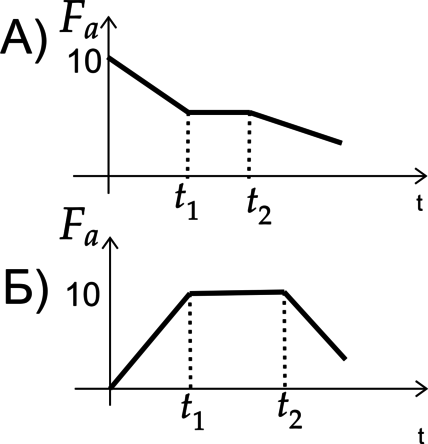
1) Тело до (t_1) погружали в жидкость, от (t_1) до (t_2) находилось полностью под водой, а от (t_2) поднимали вверх.

2) Тело до (t_1) поднимали, от (t_1) до (t_2) было на одной глубине погружений, от (t_2) поднимали вверх.

3) Тело до (t_1) погружали в жидкость, от (t_1) до (t_2) было на одной глубине погружений, от (t_2) поднимали вверх.

4) Тело всё время находилось на одной глубине погружения.

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

Найдем максимальную силу Архимеда по формуле (F_a=rho cdot g cdot V). [F_a=1000text{ кг/м$^3$} cdot 10 text{ Н/м} cdot 0,002 text{ м$^3$}= 20text{ Н}]

А) Заметим, что до (t_1) (F_a) уменьшалась, от (t_1) до (t_2) оставалась неизменной, после опять уменьшалась, значит и объем ведет себя также. Ответ – 2

Б) Проанализируем график до (t_1) (F_a) увеличивалась, от (t_1) до (t_2) оставалась неизменной, но не доходила до своего максимума, после уменьшалась, найдем подходящий. Ответ 1) не подходит, так как от (t_1) до (t_2) (F_a) не достигла максимума. Ответ – 3

Ответ: 23

Тело поочередно погружали на полный объем в одну из трех жидкостей с плотностями (rho_1)=(rho), (rho_2)=(2rho) и (rho_3)=(4rho). Представлены два графика. Определите последовательность жидкостей в каждом опыте.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

ГРАФИКИ

ПОЛЕДОВАТЕЛЬНОСТЬ

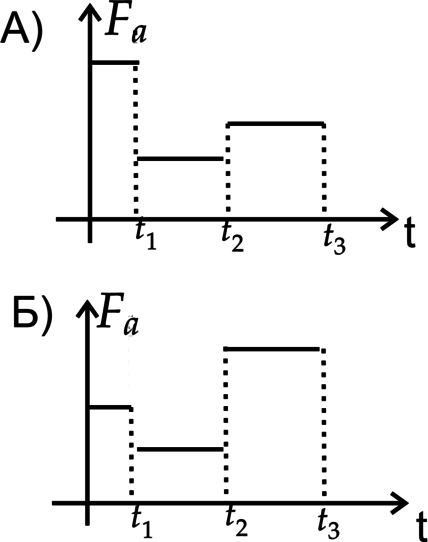
1) (rho_1), (rho_2), (rho_3)

2) (rho_2), (rho_3), (rho_1)

3) (rho_2), (rho_1), (rho_3)

4) (rho_3), (rho_1), (rho_2)

Сила Архимеда рассчитывается по формуле (F_a=rho g V), где (rho) — плотность жидкости. (V) — объем погруженной части тела. Так как (V) везде одинаковый, то (F_a) зависит только от (rho).

А) До (t_1) (F_a) максимальна, а значит первым идет жидкость с плотностью (rho_3). На втором этапе сила Архимеда минимальна, следовательно, плотность жидкости (rho_1). Последняя жидкость (rho_2). Ответ – 4

Б) Первый этап — (F_a) принимает среднее значение, значит жидкость с плотностью (rho_2), второй — минимальное, значит — (rho_1). Третья жидкость с максимальной плотностью — (rho_3). Ответ– 3

Ответ: 43

Тело массой (m) и объёмом (V) плавает на поверхности жидкости плотностью (rho). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

[begin{array}{ll}

text{Физические величины}&text{Формула}\

text{А) Сила Архимеда } &1) rho g V \
text{Б) Объём погружённой части тела } &2) V \
&3) mg \
&4) dfrac{m}{rho} \
end{array}]

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Так как тело плавает на поверхности воды, то сила Архимеда уравновешивает силу тяжести, значит (F_a=mg). Ответ – 3

Б) Выразим объем погруженной части (V_text{п} ) из (F_a=rho g V_text{п}= mg), значит (V_text{п}=dfrac{m}{rho}). Ответ – 4

Ответ: 34

Тело массой (m) и объёмом (V) лежит на дне сосуда с жидкостью плотностью (rho). Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

[begin{array}{ll}

text{Физические величины}&text{Формула}\

text{А) Сила Архимеда } &1) rho g V \
text{Б) Разность силы тяжести и силы Архимеда } &2) g(rho cdot V — m) \
&3) 0 \
&4) g(m — rho cdot V ) \
end{array}]

[begin{array}{|c|c|}
hline
text{А}&text{Б}\
hline
&\
hline
end{array}]

А) Так как тело лежит на дне сосда, то оно погружено на весь свой объем в жидкость и сила Архимеда находится по формуле: (F_a=rho g V). Ответ – 1

Б) Разность силы тяжести и силы Архимеда в этом случае (g(m — rho cdot V) ). Так как тело погружено на весь свой объем. Ответ – 4

Ответ: 14