Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
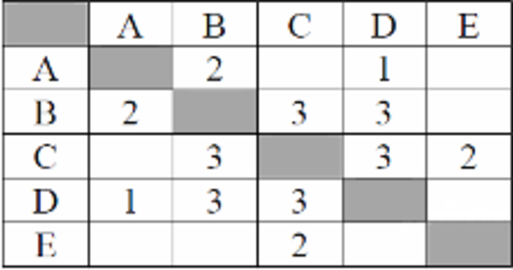
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 45 | 10 | |||||
| П2 | 45 | 40 | 55 | ||||
| П3 | 15 | 60 | |||||
| П4 | 10 | 40 | 20 | 35 | |||
| П5 | 15 | 55 | |||||
| П6 | 55 | 60 | 20 | 55 | 45 | ||
| П7 | 35 | 45 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
Источник: Демонстрационная версия ЕГЭ—2016 по информатике.
2
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 45 | 10 | |||||
| П2 | 45 | 40 | 55 | ||||
| П3 | 15 | 60 | |||||
| П4 | 10 | 40 | 20 | 35 | |||
| П5 | 15 | 55 | |||||
| П6 | 55 | 60 | 20 | 55 | 45 | ||
| П7 | 35 | 45 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта Г в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
3
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 45 | 10 | |||||
| П2 | 45 | 40 | 55 | ||||
| П3 | 15 | 60 | |||||
| П4 | 10 | 40 | 20 | 35 | |||
| П5 | 15 | 55 | |||||
| П6 | 55 | 60 | 20 | 55 | 45 | ||
| П7 | 35 | 45 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Г. В ответе запишите целое число – так, как оно указано в таблице.
4
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 40 | 15 | |||||
| П2 | 40 | 35 | 50 | ||||
| П3 | 10 | 65 | 8 | ||||
| П4 | 15 | 35 | 22 | 33 | |||
| П5 | 10 | 50 | |||||
| П6 | 50 | 65 | 22 | 50 | 40 | ||
| П7 | 8 | 33 | 40 |
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Д. В ответе запишите целое число.
5
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 40 | 15 | |||||
| П2 | 40 | 35 | 48 | ||||
| П3 | 10 | 65 | 11 | ||||
| П4 | 15 | 35 | 22 | 33 | |||
| П5 | 10 | 50 | |||||
| П6 | 48 | 65 | 22 | 50 | 40 | ||
| П7 | 11 | 33 | 40 |
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Д. В ответе запишите целое число.
Пройти тестирование по этим заданиям
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Простейшие задачи на графы
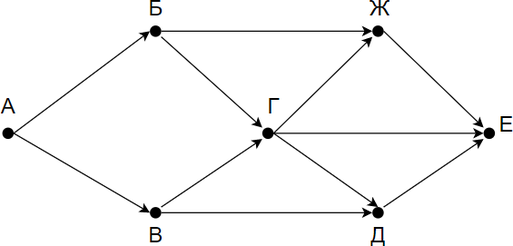
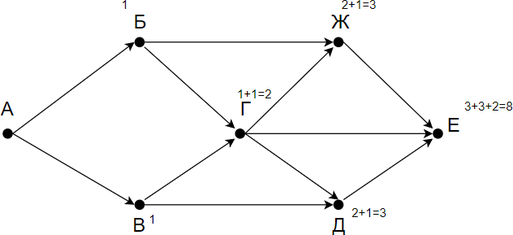
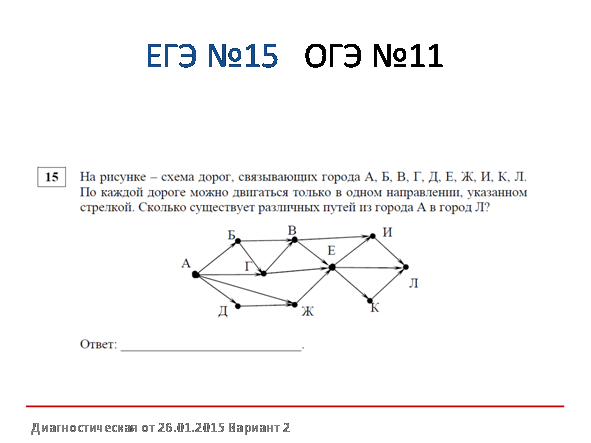
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е?
Заметим, что количество путей в город Е является суммой путей в города Ж, Г и Д. Количество путей в город Ж — сумма путей в города Г и Б. Таким образом получаем:
Г = Б + В
Д = Г + В
Ж = Б + Г
Е = Ж + Г + Д
Заметим, что в пункты Б и В можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
Ответ: 8
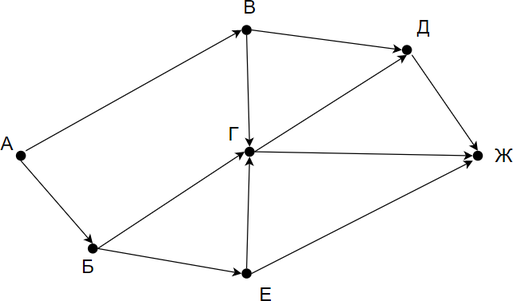
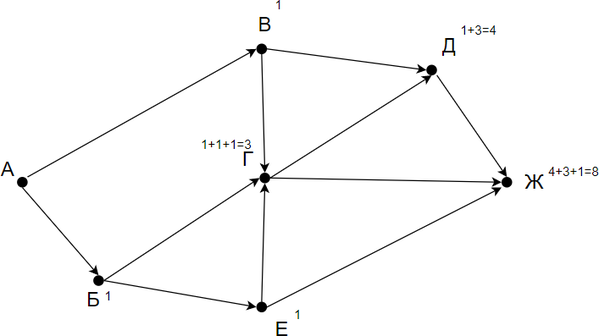
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Заметим, что количество путей в город Ж является суммой путей в города Д, Г и Е. Количество путей в город Г — сумма путей в город В, Б и Е. Таким образом получаем:
Г = Б + В + Е
Д = В + Г
Ж = Д + Г + Е
Заметим, что в пункты Б, В и Е можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
Ответ: 8
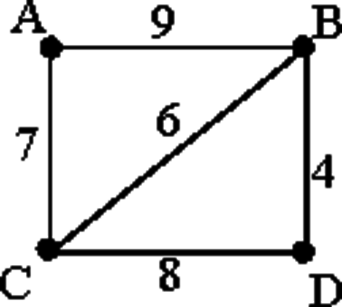
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, D.
Из пункта B можно попасть в пункты C, D.
Из пункта C можно попасть в пункты D, E.
A—B—C—E: длина маршрута 7 км.
A—D—B—C—E: длина маршрута 9 км.
A—D—C—E: длина маршрута 6 км.
Самый короткий путь: A—D—C—E. Длина маршрута 6 км.
Ответ: 6
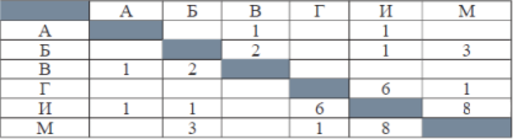
Геральт спешит выручить Цири из плена Кагыра. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого короткого участка кратчайшего пути от Геральта до Цири (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице:
Найдём все варианты маршрутов из И в М и выберем самый короткий.
Из пункта И можно попасть в пункты А, Б, Г, М.
Из пункта Г можно попасть в пункты И, М.
Из пункта В можно попасть в пункты А, Б.
Из пункта Б можно попасть в пункты В, И, М.
И—А—В—Б—М: длина маршрута 7 км.
И—Б—М: длина маршрута 4 км.
И—Г—М: длина маршрута 7 км.
И—М: длина маршрута 8 км.
Самый короткий путь: И—Б—М. Длина маршрута 4 км. Самый короткий участок этого пути равен 1 км.
Ответ: 1
На схеме нарисованы дороги между четырьмя населёнными пунктами A, B, C, D и указаны протяжённости данных дорог.
Определите, какие два пункта наиболее удалены друг от друга (при условии, что передвигаться можно только по указанным на схеме дорогам). В ответе укажите кратчайшее расстояние между этими пунктами.
Заметим, что наиболее удалены друг от друга пункты A и D. Найдём все варианты маршрутов из A в D и выберем самый короткий.
A—B—D: длина маршрута 13 км.
A—C—D: длина маршрута 15 км.
A—B—C—D: длина маршрута 23 км.
A—C—B—D: длина маршрута 17 км.
Заметим, что кратчайшее расстояние между пунктами A и D равняется 13.
Ответ: 13
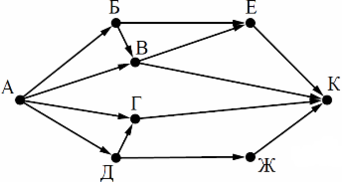
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, В, Г или Ж, поэтому N = NК = NЕ + NВ + N Г + NЖ (*).
Аналогично:
NЕ = NБ + NВ = 1 + 2 = 3;
NЖ = NД = 1;
NВ = NА + NБ = 1 + 1 = 2;
NГ = NА + NД = 1 + 1 = 2;
NД = NА = 1;
NБ = NА = 1.
Подставим в формулу (*): N = 3 + 2 + 2 + 1 = 8.
Ответ: 8
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами B и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Проанализируем некоторые возможные маршруты.
Маршрут B—D—E, длина 11 км.
Маршрут B—C—D—E, длина 10 км.
Маршрут B—С—D—A—E, длина 9 км.
Любые другие маршруты будут длиннее маршрута B—С—D—A—E. Самый короткий путь: B—С—D—A—E. Длина маршрута 9 км.
Ответ: 9

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
На уроке рассматривается решение 13 задания ЕГЭ по информатике
Содержание:
- Объяснение заданий 13 ЕГЭ по информатике
- Графы. Поиск количества путей
- Решение заданий 13 ЕГЭ по информатике
13-е задание: «Информационные модели»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)
До ЕГЭ 2021 года — это было задание № 15 и № _ ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование указаний в условии задания, что путь должен включать (или не включать) заданные промежуточные вершины»
ФГБНУ «Федеральный институт педагогических измерений»
Графы. Поиск количества путей
- Если в город
Rиз городаAможно добраться только из городовX,YиZ, то количество различных путей из городаAв городRравно сумме числа различных путей проезда изAвX, изAвYи изAвZ, то есть: - где NR — это количество путей из вершины
Aв вершинуR - Число путей не бесконечно, исключением является только граф, в котором есть циклы – замкнутые пути.
- Часто задачи с графами целесообразней решать с конца.
NR = NX + NY + NZ
Решение заданий 13 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
13_1:
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей, ведущих из города А в город М и проходящих через город Г?

✍ Решение:
- Удалим ребра, которые проходят «мимо» вершины Г или до которых от пункта А можно дойти, минуя вершину Г:
- Вершина В удалена, т.к. возможны только следующие траектории движения через этот пункт (которые НЕ проходят через пункт Г):
- 1. А — Б — В — И — М
- 2. А — Б — В — Е — И — М
- 3. А — Б — В — Е — М
- 4. А — Б — В — Е — К — М
- Теперь посчитаем результаты по оставшимся вершинам:
М = И + Е + К
-----
И = Е
Е = Г + Ж
Г = Б + А + Д = 1 + 1 + 1 = 3
Ж = Г = 3
К = Е + Ж
Теперь возвращаемся, подставляя найденные значения: ↑
Е = Г + Ж = 3 + 3 = 6
Ж = Г = 3
И = Е = 6 (получили из последующих шагов)
К = Е + Ж = 6 + 3 = 9
М = И + Е + К = 6 + 6 + 9 = 21
Результат: 21
Видео ЕГЭ по информатике (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
13_2:
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей, ведущих из города А в город М и не проходящих через город Г?

✍ Решение:
- Удалим ребра, которые проходят через вершину Г:
- Теперь посчитаем результаты по оставшимся вершинам:
М = И + Е + К
-----
И = В + Е
В = 1
Е = В + Ж
Ж = 1
Теперь возвращаемся, подставляя найденные значения: ↑
Е = В + Ж = 1 + 1 = 2
И = В + Е = 1 + 2 = 3
К = Е = 2
М = И + Е + К = 3 + 2 + 2 = 7
Результат: 7
Подробное решение данного 13 задания в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
13 задание. Демоверсия ЕГЭ 2018 информатика:
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, проходящих через город Ж?

✍ Решение:
Результат: 20
Подробное решение 13 задания демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
13_4:
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Какова длина самого длинного пути из города А в город М?
Длиной пути считать количество дорог, составляющих этот путь.

✍ Решение:
Использование теории графов для решения заданий ЕГЭ
|
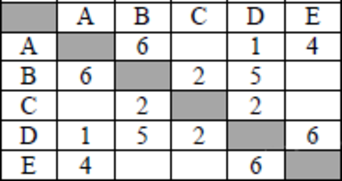
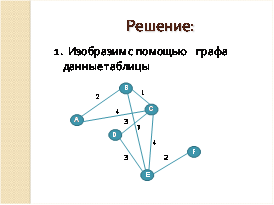
1. Между населенными пунктами A,B,C,D,E,Fпостроены дороги, протяженность которых приведена в таблице(отсутствие числа означает, что прямой дороги нет). Определить длину кратчайшего пути между пунктами E и F. (Передвигаться можно только по построенным дорогам).
Решение: |
Сначала изобразим конечный пункт F. В этот пункт можно попасть только из пункта Е. Соединяем пункты Е и F дугой и указываем вес этой дуги. Он равен двум, то есть расстоянию между пунктами Е и F. Соответственно по графу можно увидеть, что в пункт Е можно попасть из пунктов B, C и D. В пункт В можно попасть из А. В пункт С – из В и А. В пункт D – из С. В пункт В попадаем из А. В пункт С – из В и А. И в пункт В из А.
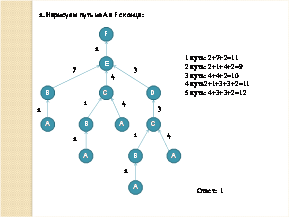
Данную схему можно рассматривать как ориентированный взвешенный граф, который наглядно показывает, что есть 5 путей из пункта А в пункт F. Подсчитываем длину каждого пути
1 путь: 2+7+2=11;
2 путь: 2+1+4+2=9;
3 путь: 4+4+2=10;
4 путь2+1+3+3+2=11;
5 путь: 4+3+3+2=12.
Так как нам надо определить длину кратчайшего пути, то выбираем второй путь, длина которого равна 9. Данный ответ находится под цифрой 1. Поэтому в ответе надо поставить крестик в клеточке, соответствующей первому ответу.
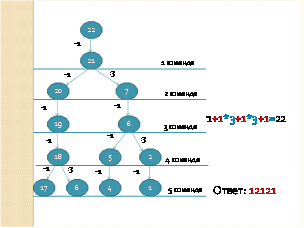
2. У исполнителя Утроитель две команды, которым присвоены номера
1. Прибавь 1;
2. Умножь на 3.
Запишите порядок команд в программе преобразования числа 1 в число 22, содержащей не более 5 команд.
Решение:
Для решения данного задания используем метод от обратного, то есть будем преобразовывать число 22 в 1. Соответственно команды исполнителя заменим командами антагонистами, то есть команду «Прибавь 1» заменим командой «Вычти 1», а «Умножь на 3» заменим командой «Раздели на 3». Ход выполнения команд можно изобразить в виде дерева, каждая вершина которого имеет две ветки, соответствующие командам 1 и 2. Корнем этого дерева является число 22. Это дерево будет иметь 5 ярусов, так как программа должна содержать не более 5 команд. Но здесь нужно учесть один момент. Если число делится на 3, то вершина будет иметь 2 потомка, а если нет, то одного (то есть делить на 3 мы не можем, а можем только вычитать 1). Получаем следующее дерево.
Инвертируем теперь команды и преобразуем число 1 в 22.
1+1*3+1*3+1=22.
Учитывая номера команд, записываем программу решения данной задачи в виде последовательности соответствующих команд. Ответ: 12121
Решение: (1 способ)
Условие данного задания представлено в виде ориентированного графа, вершинами которого являются названия городов, а дороги, соединяющие эти города, являются дугами графа. Для того, чтобы решить данную задачу, построим еще один ориентированный граф, но с учетом того, по каким дорогам можно будет попасть в пункт Л.
По графу легко подсчитать количество дорог, ведущих из города А в город Л.
3.У Исполнителя Кузнечик 2 команды:
1. Прибавь 3;
2. Вычти 2.
Сколько различных чисел можно получить из числа 1 с помощью программы, которая содержит ровно 5 команд.
Решение:
Оформим решение данной задачи в виде дерева, вершинами которого будут являться числа, соответствующие промежуточным значениям. Данное дерево будет иметь корень, равный 1 и 5 ярусов, так как у нас должно быть ровно 5 команд.

4. У исполнителя Устроитель две команды, которым присвоены номера:
1. Прибавь 1;
2. Умножь на 3.
Программа для Устроителя – это последовательность команд.
Сколько есть программ, которые преобразуют 1 в число 29?
При решении данной задачи следует учитывать, что если число больше 9, то умножать на 3 мы не можем, так как получится число, большее 29, следовательно, вершины с числами большими 9 будут иметь только одну ветвь, соответствующую команде +1.

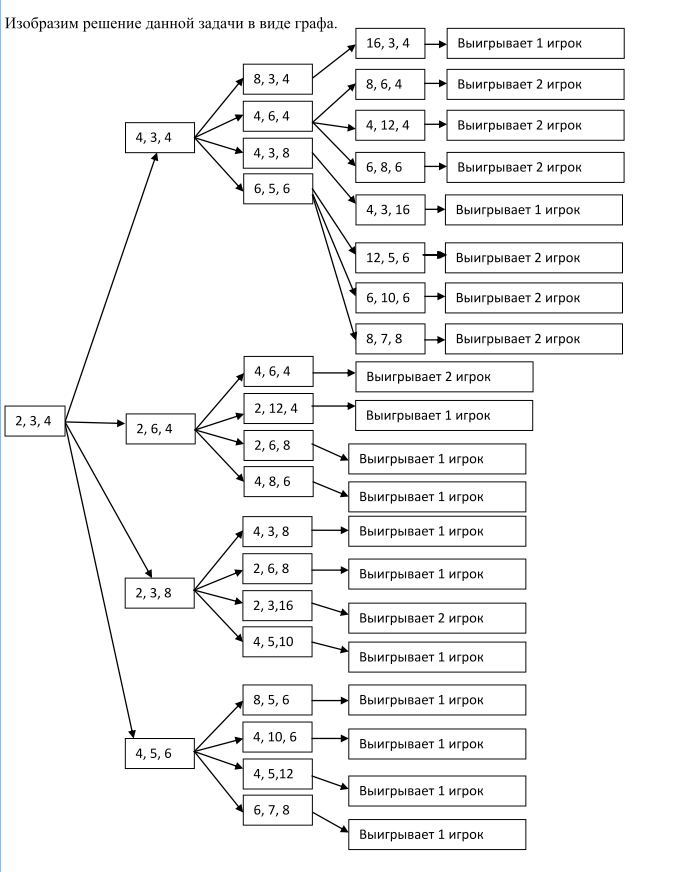
5.Даны три кучи камней, содержащих соответственно 2, 3, 4 камня. За один ход разрешается или удвоить количество камней в какой-нибудь куче, или добавить по 2 камня в каждую из всех трех куч. Выигрывает тот, после чьего хода в какой-нибудь куче становится больше или равно 15 камней или во всех трех кучах суммарно становится больше либо равно 25 камней. Игроки ходят по очереди. Выяснить, кто выигрывает при правильной игре – первый или второй игрок?
Решение: В разумной партии каждый игрок должен стараться следовать общему правилу – всегда оставлять противнику проигрышную позицию. В ходе решения задач можно заметить, что в одной партии в Камешки только один из игроков может следовать этому правилу – тот, кто первым может занять выигрышную позицию (имеет выигрышную стратегию). Если он будет ей следовать, а, значит, делать только разумные ходы и оставлять противнику только проигрышные позиции, то выиграет при любой игре противника. Если начальная позиция выигрышная, то выигрышную стратегию имеет Первый, если проигрышная – Второй.
Изобразим решение данной задачи в виде графа.
Ответ: при правильной стратегии игры выигрывает первый игрок. При этом первый его ход должен быть 2, 3, 4 4, 5, 6.
Литература:
ФИПИ (открытый банк данных)
Материалы демонстрационных вариантов ЕГЭ по информатике 2016, 2015 года
Материалы диагностической работы 2015 года.
Автор — Лада Борисовна Есакова.
Подсчет путей в ориентированном графе. ЗАДАЧА № 15.
В этой задаче требуется подсчитать количество путей, ведущих из одной вершины графа в другую. Обычно задачу решают преобразованием графа в дерево. Однако, при сложной структуре графа такое решение становится очень трудоемким. Велика вероятность ошибки.
Рассмотрим простой и эффективный способ решения.
В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.
Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.
Пример:
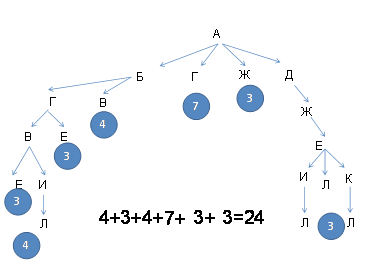
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Решение:
Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один – вершина A).
У вершины Д предками являются А и Б, значит индекс вершины Д равен 1+1=2.
Очевидно, что мы можем посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В. Двигаясь последовательно, мы рассчитаем индексы всех вершин.
Индекс вершины Ж и будет ответом задачи.
Ответ: 11
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задача №15. Графы. Поиск количества путей.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Задачи на графы для подготовки к ЕГЭ. Использовался сайт Константина Полякова (kpolyakov.narod.ru).
Пример задания 1:
Между четырьмя местными аэропортами: ОКТЯБРЬ, БЕРЕГ, КРАСНЫЙ и СОСНОВО, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними:
Аэропорт вылета Аэропорт прилета Время вылета Время прилета
СОСНОВО КРАСНЫЙ 06:20 08:35
КРАСНЫЙ ОКТЯБРЬ 10:25 12:35
ОКТЯБРЬ КРАСНЫЙ 11:45 13:30
БЕРЕГ СОСНОВО 12:15 14:25
СОСНОВО ОКТЯБРЬ 12:45 16:35
КРАСНЫЙ СОСНОВО 13:15 15:40
ОКТЯБРЬ СОСНОВО 13:40 17:25
ОКТЯБРЬ БЕРЕГ 15:30 17:15
СОСНОВО БЕРЕГ 17:35 19:30
БЕРЕГ ОКТЯБРЬ 19:40 21:55
Путешественник оказался в аэропорту ОКТЯБРЬ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт СОСНОВО.
1) 15:40 2) 16:35 3)17:15 4) 17:25
Решение:
- сначала заметим, что есть прямой рейс из аэропорта ОКТЯБРЬ в СОСНОВО с прибытием в 17:25:
ОКТЯБРЬ СОСНОВО 13:40 17:25
- посмотрим, сможет ли путешественник оказаться в СОСНОВО раньше этого времени, если полетит через другой аэропорт, с пересадкой
- можно лететь, через КРАСНЫЙ, но, как следует из расписания,
ОКТЯБРЬ КРАСНЫЙ 11:45 13:30
…
КРАСНЫЙ СОСНОВО 13:15 15:40
путешественник не успеет на рейс КРАСНЫЙ – СОСНОВО, который улетает в 13:15, то есть на 15 минут раньше, чем в КРАСНЫЙ прилетает самолет ОКТЯБРЬ – КРАСНЫЙ
- можно лететь через БЕРЕГ,
БЕРЕГ СОСНОВО 12:15 14:25
…
ОКТЯБРЬ БЕРЕГ 15:30 17:15
но рейс БЕРЕГ – СОСНОВО вылетает даже раньше, чем рейс ОКТЯБРЬ – БЕРЕГ, то есть, пересадка не получится
- поскольку даже перелеты с одной пересадкой не стыкуются по времени, проверять варианты с двумя пересадками в данной задаче бессмысленно (хотя в других задачах они теоретически могут дать правильное решение)
- таким образом, правильный ответ – 4 (прямой рейс).
Возможные ловушки и проблемы:
- можно не заметить, что путешественник не успеет на пересадку в КРАСНОМ (неверный ответ 15:40)
- можно перепутать аэропорты вылета и прилета (неверный ответ 16:35)
Решение (вариант 2, граф):
- для решения можно построить граф, показывающий, куда может попасть путешественник из аэропорта ОКТЯБРЬ
- из аэропорта ОКТЯБРЬ есть три рейса:
ОКТЯБРЬ СОСНОВО 13:40 17:25
ОКТЯБРЬ КРАСНЫЙ 11:45 13:30
ОКТЯБРЬ БЕРЕГ 15:30 17:15
- построим граф, около каждого пункта запишем время прибытия
- проверим, не будет ли быстрее лететь с пересадкой: рейс «КРАСНЫЙ-СОСНОВО» вылетает в 13:15, то есть, путешественник на него не успевает; он не успеет также и на рейс «БЕРЕГ-СОСНОВО», вылетающий в 12:15
- таким образом, правильный ответ – 4 (прямой рейс).
Еще пример задания 2:
Грунтовая дорога проходит последовательно через населенные пункты А, B, С и D. При этом длина дороги между А и В равна 80 км, между В и С – 50 км, и между С и D – 10 км. Между А и С построили новое асфальтовое шоссе длиной 40 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге – 20 км/час, по шоссе – 40 км/час.
1) 1 час 2) 1,5 часа 3)3,5 часа 4) 4 часа
Решение:
- нарисуем схему дорог, обозначив данные в виде дроби (расстояние в числителе, скорость движения по дороге – в знаменателе):
- разделив числитель на знаменатель, получим время движения по каждой дороге
- ехать из А в B можно
- напрямую, это займет 4 часа, или …
- через пункт C, это займет 1 час по шоссе (из А в С) и 2,5 часа по грунтовой дороге
(из В в С), всего 1 + 2,5 = 3,5 часа
- таким образом, правильный ответ – 3.
Возможные ловушки и проблемы:
- можно не заметить, что требуется найти минимальное время поездки именно в В, а не в С (неверный ответ 1 час)
- можно ограничиться рассмотрением только прямого пути из А в В и таким образом получить неверный ответ 4 часа
- можно неправильно нарисовать схему
Еще пример задания:
Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6». Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.
|
1) |
2) |
3) |
4) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение (вариант 2, с рисованием схемы):
- для каждой таблицы нарисуем соответствующую ей схему дорог, обозначив стоимость перевозки рядом с линиями, соединяющими соседние станции:
|
1) |
2) |
3) |
4) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
- теперь по схемам определяем кратчайшие маршруты для каждой таблицы:
1: или
, стоимость 7
2: или
, стоимость 7
3: , стоимость 6
4: , стоимость 8
- условие «не больше 6» выполняется только для таблицы 3
- таким образом, правильный ответ – 3.
Возможные ловушки и проблемы:
- нужно внимательно строить схемы по таблицам, этот дополнительный переход (от табличных моделей к графическим) повышает наглядность, но добавляет еще одну возможность для ошибки
- наглядность схемы зависит от того, как удачно вы выберете расположение ее узлов; один из подходов – сначала расставить все узлы равномерно на окружности, нарисовать все связи и посмотреть, как можно расположить узлы более удобно
- по невнимательности можно пропустить решение с минимальной стоимостью
Еще пример задания:
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
|
A |
B |
C |
D |
E |
F |
|
|
A |
2 |
4 |
||||
|
B |
2 |
1 |
7 |
|||
|
C |
4 |
1 |
3 |
4 |
||
|
D |
3 |
3 |
||||
|
E |
7 |
4 |
3 |
2 |
||
|
F |
2 |
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
1) 9 2) 10 3) 11 4) 12
Решение (вариант 1, использование схемы):
- построим граф – схему, соответствующую этой весовой матрице; из вершины А можно проехать в вершины B и C (длины путей соответственно 2 и 4):
- для остальных вершин можно рассматривать только часть таблицы над главной диагональю, которая выделена серым цветом; все остальные рёбра уже были рассмотрены ранее
- например, из вершины В можно проехать в вершины C и E (длины путей соответственно 1 и 7):
- новые маршруты из С – в D и E (длины путей соответственно 3 и 4):
- новый маршрут из D – в E (длина пути 3):
- новый маршрут из E – в F (длина пути 2):
- нужно проехать из А в F, по схеме видим, что в любой из таких маршрутов входит ребро EF длиной 2; таким образом, остается найти оптимальный маршрут из A в E
- попробуем перечислить возможные маршруты из А в Е:
А – В – Е длина 9
А – В – С – Е длина 7
А – В – C – D – Е длина 9
А –C – Е длина 8
А –C – B – Е длина 12
А –C – D – Е длина 10
- из перечисленных маршрутов кратчайший – A-B-C-E – имеет длину 7, таким образов общая длина кратчайшего маршрута A-B-C-E-F равна 7 + 2 = 9
- таким образом, правильный ответ – 1.
Еще пример задания[1]:
Между четырьмя местными аэропортами: ВОСТОРГ, ЗАРЯ, ОЗЕРНЫЙ и ГОРКА, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними:
Аэропорт вылета Аэропорт прилета Время вылета Время прилета
ВОСТОРГ ГОРКА 16:15 18:30
ОЗЕРНЫЙ ЗАРЯ 13:40 15:50
ОЗЕРНЫЙ ВОСТОРГ 14:10 16:20
ГОРКА ОЗЕРНЫЙ 17:05 19:20
ВОСТОРГ ОЗЕРНЫЙ 11:15 13:20
ЗАРЯ ОЗЕРНЫЙ 16:20 18:25
ВОСТОРГ ЗАРЯ 14:00 16:15
ЗАРЯ ГОРКА 16:05 18:15
ГОРКА ЗАРЯ 14:10 16:25
ОЗЕРНЫЙ ГОРКА 18:35 19:50
Путешественник оказался в аэропорту ВОСТОРГ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт ГОРКА.
1) 16:15 2) 18:15 3)18:30 4) 19:50
Решение («обратный ход»):
- сначала заметим, что есть прямой рейс из аэропорта ВОСТОРГ в ГОРКУ с прибытием в 18:30:
ВОСТОРГ ГОРКА 16:15 18:30
- посмотрим, сможет ли путешественник оказаться в ГОРКЕ раньше этого времени, если полетит через другой аэропорт, с пересадкой; рассмотрим все остальные рейсы, который прибывают в аэропорт ГОРКА:
ЗАРЯ ГОРКА 16:05 18:15
ОЗЕРНЫЙ ГОРКА 18:35 19:50
- это значит, что имеет смысл проверить только возможность перелета через аэропорт ЗАРЯ (через ОЗЕРНЫЙ явно не получится раньше, чем прямым рейсом); для этого нужно быть в ЗАРЕ не позже, чем в 16:05
- смотрим, какие рейсы прибывают в аэропорт ЗАРЯ раньше, чем в 16:05:
ОЗЕРНЫЙ ЗАРЯ 13:40 15:50
- дальше проверяем рейсы, который приходят в ОЗЕРНЫЙ раньше, чем в 13:40
ВОСТОРГ ОЗЕРНЫЙ 11:15 13:20
- таким образом, мы «пришли» от конечного пункта к начальному, в обратном направлении
- поэтому оптимальный маршрут
- и правильный ответ – 2.
Возможные ловушки и проблемы:
- «напрашивается» ошибочный ответ 18:30 (прямой рейс)
- при решении задачи «прямым ходом», с начального пункта, легко пропустить вариант с двумя пересадками
|
A |
B |
C |
D |
|
|
A |
1 |
2 |
||
|
B |
2 |
3 |
||
|
C |
1 |
2 |
5 |
|
|
D |
2 |
3 |
5 |
- В таблице приведена стоимость перевозки пассажиров между соседними населенными пунктами. Укажите схему, соответствующую таблице.
- В таблицах приведена стоимость перевозки грузов между соседними станциями. Если пересечение строки и столбца пусто, то соответствующие станции не являются соседними. Укажите номер таблицы, для которой выполняется условие «Максимальная стоимость перевозки грузов от пункта В до пункта D не больше 6».
|
1) |
2) |
3) |
4) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
- Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
|
A |
B |
C |
D |
E |
F |
|
|
A |
2 |
4 |
3 |
7 |
||
|
B |
5 |
3 |
||||
|
C |
2 |
2 |
||||
|
D |
4 |
|||||
|
E |
3 |
5 |
||||
|
F |
7 |
3 |
2 |
Определите длину кратчайшего пути между пунктами B и D (при условии, что передвигаться можно только по построенным дорогам).
1) 8 2) 9 3) 10 4) 11
[1] Крылов С.С., Ушаков Д.М. ЕГЭ 2010. Информатика. Тематическая рабочая тетрадь. — М.: Экзамен, 2010.