Всего: 77 1–20 | 21–40 | 41–60 | 61–77
Добавить в вариант
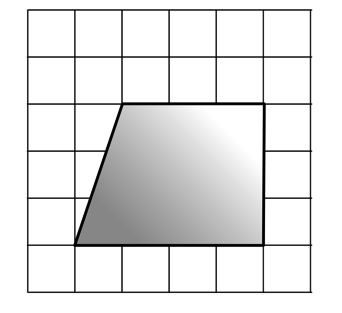
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
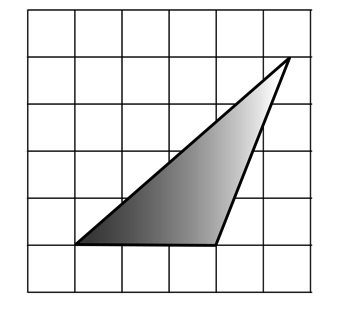
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см 1 см (см. рис.). В ответе запишите
На клетчатой бумаге с размером клетки изображён угол. Найдите его градусную величину.
На клетчатой бумаге с размером клетки 1×1 отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC.
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). В ответе запишите
Всего: 77 1–20 | 21–40 | 41–60 | 61–77
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на клетчатой бумаге
(blacktriangleright) Помним, что каждая клетка представляет собой квадрат.
(blacktriangleright) В равных прямоугольниках равны диагонали.
(blacktriangleright) Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
(blacktriangleright) В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.
И наоборот: катет, равный половине гипотенузы, лежит против угла (30^circ) (рис. 1).
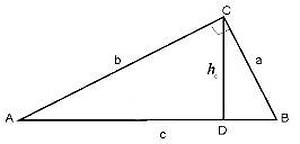
(blacktriangleright) Медиана, проведенная к основанию в равнобедренном треугольнике, является высотой и биссектрисой (рис. 2).
Задание
1
#3089
Уровень задания: Равен ЕГЭ
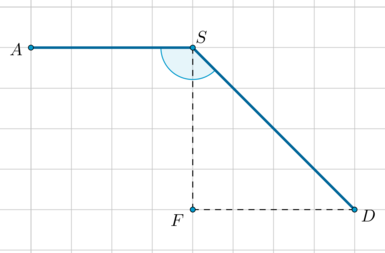
На клетчатой бумаге изображен угол. Найдите его градусную величину.
Обозначим этот угол (ASD). Отметим точку (F) так, чтобы получился прямоугольный (triangle SDF):
Тогда (angle ASD=angle ASF+angle FSD). Заметим, что (angle
ASF=90^circ). Заметим также, что (FS=FD), следовательно, (triangle
SDF) прямоугольный и равнобедренный, значит, его острые углы равны по (45^circ).
Следовательно, [angle ASD=90^circ+45^circ=135^circ.]
Ответ: 135
Задание
2
#3088
Уровень задания: Равен ЕГЭ
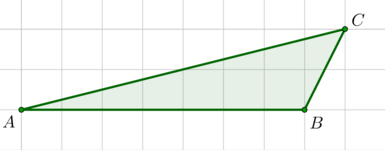
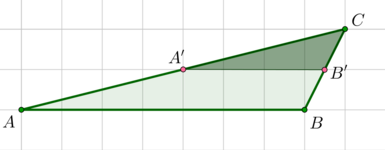
На клетчатой бумаге с размером клетки (1times 1) изображен треугольник (ABC). Найдите площадь треугольника (A’B’C), где (A’B’) – средняя линия, параллельная стороне (AB).
Пусть (A’in AC, B’in BC).
По свойству средней линии (triangle ABCsim triangle A’B’C) с коэффициентом подобия, равным (2). Следовательно, их площади относятся как коэффициент подобия в квадрате, то есть [dfrac{S_{ABC}}{S_{A’B’C}}=4] Высота (triangle ABC), опущенная из (C), равна (2), (AB=7). Следовательно, (S_{ABC}=frac12cdot 2cdot 7=7). Тогда [S_{A’B’C}=dfrac74=1,75.]
Ответ: 1,75
Задание
3
#3087
Уровень задания: Равен ЕГЭ
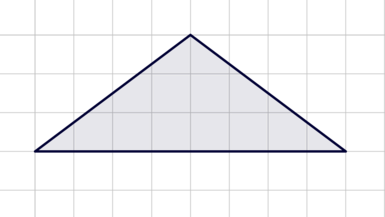
На клетчатой бумаге с размером клетки (1times 1) изображен треугольник (ABC). Найдите длину средней линии, параллельной стороне (AB).
Длина средней линии треугольника, параллельной стороне (AB), равна (frac12AB). Так как (AB=7), то средняя линия равна (3,5).
Ответ: 3,5
Задание
4
#3086
Уровень задания: Равен ЕГЭ
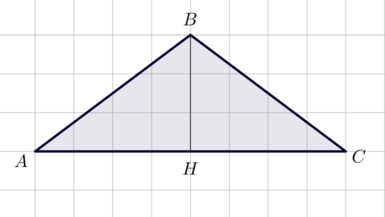
На клетчатой бумаге изображен треугольник. Найдите радиус вписанной в него окружности, если сторона одной клетки равна (3).
Будем искать радиус вписанной окружности по формуле (S=pcdot r), где (S) – площадь, (p) – полупериметр.
Заметим, что треугольник равнобедренный: (AB=BC.)
Так как длина стороны клетки равна (3), то (AH=12, BH=9), следовательно, (AB=sqrt{AH^2+BH^2}=15.) Тогда [dfrac12cdot BHcdot AC=dfrac{AB+BC+AC}2cdot r quadRightarrowquad
r=4.]
Заметим, что в задачах подобного типа можно вычислять все длины, как будто длина стороны клетки равна (1), а затем умножать полученный ответ на (3). Если бы длина одной клетки была равна (1), то (AH=4, BH=3), (AB=5) и (r=frac43). Тогда после умножения на (3) также получили бы (r=4). При решении задачи таким способом вычисления будут легче.
Ответ: 4
Задание
5
#297
Уровень задания: Равен ЕГЭ
На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисована трапеция. Найдите её площадь. Ответ дайте в квадратных миллиметрах.
Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции есть (0,5cdot (3 text{мм} + 4 text{мм})cdot 3 text{мм} = 10,5)мм(^2).
Ответ: 10,5
Задание
6
#298
Уровень задания: Равен ЕГЭ
На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисован треугольник. Найдите его площадь. Ответ дайте в квадратных миллиметрах.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию, тогда площадь нарисованного треугольника есть (0,5cdot 3)мм (cdot 4)мм (= 6)мм(^2).
Ответ: 6
Задание
7
#299
Уровень задания: Равен ЕГЭ
На клетчатой бумаге с клетками размером (1)мм (times 1)мм нарисован четырёхугольник. Найдите его площадь. Ответ дайте в квадратных миллиметрах.
У данного четырёхугольника две стороны параллельны, а две другие не параллельны, следовательно, это трапеция. Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции равна (0,5(2 text{мм} + 3 text{мм})cdot 4 text{мм} = 10) мм(^2).
Ответ: 10
Если выпускник готовится к сдаче ЕГЭ по математике и при этом рассчитывает на получение конкурентных баллов, ему непременно стоит освоить принцип решения задач на клетчатой бумаге. Подобные планиметрические задания каждый год включаются в программу аттестационного испытания. Таким образом, справляться с задачами ЕГЭ на клетчатой бумаге должны все учащиеся, независимо от уровня их подготовки.
Полезная информация
Задания ЕГЭ на клетчатой бумаге часто решаются гораздо проще, чем задачи, для выполнения которых требуется применение аналитических методов. Чаще всего в подобных упражнениях необходимо найти площадь фигуры. Решить такие задачи можно, вспомнив основные теоремы и свойства трапеции, треугольника, шестиугольника и т. д.
Как подготовиться к экзамену?
Если задания ЕГЭ на клетчатой бумаге вызывают у вас трудности, обратитесь к образовательному порталу «Школково». С нами вы сможете повторить материал по темам, которые являются для вас сложными, например, векторы на координатной плоскости и таким образом восполнить пробелы в знаниях. В разделе «Теоретическая справка» представлена вся базовая информация. Ее наши специалисты подготовили и изложили в максимально доступной форме на основе богатого практического опыта.
Освоить принцип решения задач на клетчатой бумаге помогут упражнения, представленные в разделе «Каталог». Мы подготовили простые и более сложные задания. Тренироваться в их выполнении учащиеся из Москвы и других российских городов могут в онлайн-режиме.
Справившись с заданием, выпускники имеют возможность сохранить его в разделе «Избранное». Это позволит в дальнейшем вернуться к нему и, к примеру, обсудить алгоритм его решения со школьным преподавателем. База заданий на сайте «Школково» регулярно обновляется.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задачи на клетчатой бумаге. Формула Пика.
Задачи на бумаге в клетку помогают как можно раньше формировать геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе.
При решении задач на клетчатой бумаге ученикам не понадобится знание основ планиметрии, а будет нужна именно смекалка, геометрическое воображение и достаточно простые геометрические сведения, которые известны всем.
Формула Пика
Наш сюжет будет разворачиваться на обычном листке клетчатой бумаги.[1]
Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах (рис. 1) и найдем его площадь. Искать её можно по-разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площадь и сложить.
Но тут нас ждёт много хлопот (попробуйте!). Давайте «схитрим»:
вычислим площадь заштрихованной фигуры, которая «дополняет» наш
Рис. 1
многоугольник до прямоугольника АВСD, и вычтем её из площади прямоугольника. Заштрихованная фигура легко разбивается на прямоугольники и прямоугольные треугольники, и её площадь вычисляется без усилий.
Итак, хотя многоугольник и выглядел достаточно просто, для вычисления его площади нам пришлось потрудиться. А если бы многоугольник выглядел более причудливо?
Оказывается площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.
Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рис. 2).
Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую
Рис. 2
клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна
S = В + 


Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу S = В + 
Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки!
Это и есть формула Пика.
Задача 1. Проверить формулу Пика для многоугольника на рисунке 1.
Решение.
В = 14, Г = 8. По формуле Пика: S = В + 
S = 14 + 8/2 – 1 = 17
Ответ: 17 кв. ед.
Можно убедиться в том, что формула Пика верна для всех рассмотренных примеров.
Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.
Попробуйте вычислить площади многоугольников с рисунка 3, используя формулу Пика. Правда ведь, легко получается!
Рис. 3
Рассмотрим ещё некоторые задачи на клетчатой бумаге с клетками размером 1 см 
Задача 2.[3]
Найдите площадь прямоугольника АВСD (рис.4).
Решение. По формуле Пика: S = В + 
В = 8, Г = 6
S = 8 + 6/2 – 1 = 10 (см²)
Рис. 4 Ответ: 10 см².
Задача 3. Найдите площадь параллелограмма АВСD (рис.5)
Решение. По формуле Пика: S = В + 
В = 6, Г = 6
S = 6 + 6/2 – 1 = 8 (см²)
Ответ: 8 см².
Рис. 5
Задача 4. Найдите площадь треугольника АВС (рис.6)
Решение. По формуле Пика: S = В + 
В = 6, Г = 5
S = 6 + 5/2 – 1 = 7,5 (см²)
Ответ: 7,5 см².
Рис. 6
Задача 5. Найдите площадь четырёхугольника АВСD (рис. 7)
Решение. По формуле Пика: S = В + 
В = 5, Г = 7
S = 5 + 7/2 – 1 = 7,5 (см²)
Ответ: 7,5 см².
Рис. 7
Согласитесь, рассмотренные задания аналогичны заданию В
Например:
Задача 6.[2] В

Решение. По формуле Пика: S = В + 
В = 12, Г = 6
S = 12 + 6/2 – 1 = 14 (см²)
Ответ: 14
Рис. 8
Задача 7. В

Решение. Воспользуемся формулой Пика:
В = 12, Г = 17
S = 12 + 17/2 – 1 = 19,5 (см²)
Ответ: 19,5
Рис. 9
Поможет нам формула Пика и для решения геометрических задач с практическим содержанием.
Задача 8.[4] Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м (рис. 10)
Решение. Найдём S

В = 8, Г = 7. S
1 см² — 200² м²; S = 40000 · 10,5 = 420 000 (м²)
Ответ: м²
Рис. 10
Задача 9. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1(см) в масштабе 1 см – 200 м. (рис. 11)
Решение. Найдём S

В = 7, Г = 4. S
1 см² — 200² м²; S = 40000 · 8 = 320 000 (м²)
Ответ: м²
Рис. 11
Получить полный текс
Тема 1.
Геометрия на плоскости (планиметрия)
1
.
26
Задачи на клетчатой бумаге
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
геометрия на плоскости (планиметрия)
1.01Треугольник: внутренние и внешние углы
1.02Треугольник: высота, биссектриса, медиана
1.03Треугольник: задачи на подобие
1.04Прямоугольный треугольник и теорема Пифагора
1.05Треугольник: площадь и периметр
1.06Параллелограмм и его свойства
1.07Параллелограмм и свойство его биссектрисы
1.08Прямоугольник и его свойства
1.09Ромб и его свойства
1.10Квадрат и его свойства
1.11Трапеция и ее свойства
1.12Равнобедренная трапеция
1.13Окружность: центральный и вписанный углы
1.14Окружность: углы, образованные хордами, секущими, касательными
1.15Окружность: отрезки хорд, секущих, касательных
1.16Окружность: описанная около многоугольника
1.17Окружность: вписанная в многоугольник или угол
1.18Длина окружности или дуги и площадь круга или сектора
1.19Правильный шестиугольник и его свойства
1.20Площадь многоугольника: различные формулы
1.21Внешние углы многоугольника и тригонометрия
1.22Решение треугольника и других фигур с помощью тригонометрии
1.23Теорема синусов и теорема косинусов
1.24Координатная плоскость
1.25Векторы: сложение, вычитание, координаты
1.26Задачи на клетчатой бумаге
Решаем задачи
На клетчатой бумаге с размером клетки изображен равносторонний треугольник. Найдите радиус описанной около него
окружности.
Показать ответ и решение
Отметим точки
причем
Центр описанной окружности лежит на пересечении серединных перпендикуляров, в равностороннем
треугольнике серединные перпендикуляры — это и высоты, и медианы, и биссектрисы.
То есть центр описанной окружности лежит на высоте которая также является и медианой. Пусть
— центр этой
окружности (а значит, и точка пересечения медиан треугольника). Так как медианы треугольника точкой пересечения делятся в
отношении считая от вершины, то
откуда
Заметим, что по определению радиус описанной около треугольника окружности — это отрезок, соединяющий центр окружности
с вершиной треугольника, то есть Таким образом, радиус равен 6.
На клетчатой бумаге с размером клетки изображен равнобедренный прямоугольный треугольник. Найдите длину его
биссектрисы, выходящей из вершины прямого угла.
Показать ответ и решение
Так как треугольник равнобедренный, то биссектриса, проведенная к гипотенузе-основанию, является также медианой. По
свойству медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. У
данного прямоугольного треугольника гипотенуза равна 5. Следовательно, медиана (она же биссектриса) равна
2,5.
На клетчатой бумаге с размером клетки изображен треугольник
Найдите длину средней линии, параллельной стороне
На клетчатой бумаге с клетками размером нарисована трапеция. Найдите её площадь. Ответ дайте в квадратных
миллиметрах.
Показать ответ и решение
Площадь трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции есть
На клетчатой бумаге с размером клетки изображен угол. Найдите тангенс этого угла.
Показать ответ и решение
Проведем перпендикуляр к стороне
Получим прямоугольный треугольник
Из него
На клетчатой бумаге с размером клетки изображен треугольник
Найдите длину его биссектрисы, проведенной из
вершины
Показать ответ и решение
Из рисунка видно, что треугольник равнобедренный (). Следовательно, биссектриса, опущенная из вершины
будет
также являться медианой и высотой. Тогда биссектриса равна 3:
На клетчатой бумаге с размером клетки изображен ромб. Найдите его площадь.
Показать ответ и решение
Проведем диагонали данного ромба:
Площадь ромба равна полупроизведению диагоналей, следовательно,
Показать ответ и решение
Проведем прямую и перпендикуляр
Из рисунка видно, что
Найдите угол Ответ дайте в градусах.
На клетчатой бумаге изображен треугольник Найдите его высоту, опущенную из вершины
если длина стороны
равна 7.
Вершины треугольника лежат в узлах решетки.
На клетчатой бумаге с размером клетки изображен треугольник
Найдите площадь треугольника
где
—
средняя линия, параллельная стороне
Показать ответ и решение
Пусть
По свойству средней линии с коэффициентом подобия, равным 2. Следовательно, их площади относятся как
коэффициент подобия в квадрате, то есть
Высота треугольника опущенная из
равна 2,
Следовательно,
Тогда
На клетчатой бумаге изображен треугольник. Найдите радиус вписанной в него окружности, если сторона одной клетки равна 3.
Показать ответ и решение
Будем искать радиус вписанной окружности по формуле где
— площадь,
— полупериметр.
Заметим, что треугольник равнобедренный:
Так как длина стороны клетки равна 3, то
следовательно,
Тогда
Заметим, что в задачах подобного типа можно вычислять все длины, как будто длина стороны клетки равна 1, а затем
умножать полученный ответ на 3. Если бы длина одной клетки была равна 1, то
и
Тогда после умножения на 3 также получили бы При решении задачи таким способом вычисления будут
легче.
На клетчатой бумаге нарисован круг площадью Найдите площадь
закрашенного сектора.
Показать ответ и решение
Заметим, что закрашенная фигура состоит из двух непересекающихся частей,
равных и
от
круга:
Таким образом, ее площадь равна
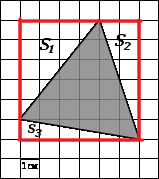
Найдите разность площади фигуры 1 и площади фигуры 2.
Показать ответ и решение
Площадь фигуры 1 можно посчитать следующим образом:
Площадь фигуры 2 — следующим образом:
Тогда
Размер клетки Найдите площадь фигуры с вырезанным кругом, выраженную в квадратных сантиметрах.
Показать ответ и решение
Искомая фигура состоит из квадрата без вырезанного круга с центром
и двух половин круга такого же радиуса,
следовательно, площадь искомой фигуры равна площади квадрата
На рисунке изображен треугольник. Найдите угол
На клетчатой бумаге с клетками размером 1 мм 1 мм нарисован невыпуклый
шестиугольник Найдите его площадь. Ответ дайте в квадратных
миллиметрах.
Показать ответ и решение
Дорисуем несколько отрезков как показано на рисунке ниже:
Площадь треугольника равна половине произведения основания на высоту к этому основанию. Площадь треугольника
равна
Площадь треугольника равна
Площадь трапеции равна
Тогда
На клетчатой бумаге с клетками размером 1 мм 1 мм нарисован четырёхугольник. Найдите его площадь. Ответ дайте в
квадратных миллиметрах.
Показать ответ и решение
У данного четырёхугольника две стороны параллельны, а две другие не параллельны, следовательно, это трапеция. Площадь
трапеции равна произведению полусуммы оснований на высоту. Площадь нарисованной трапеции равна
Найдите радиус окружности, вписанной в треугольник считая стороны квадратных клеток равными 1.
Показать ответ и решение
Так как радиус окружности, вписанной в прямоугольный треугольник, ищется по формуле где
— катеты,
— гипотенуза, то
На клетчатой бумаге с размером клетки изображен угол. Найдите синус
этого угла.
Показать ответ и решение
Продлим одну из сторон тупого угла на отрезок
так, чтобы
Заметим, что все вершины треугольника находятся в узлах решетки,
причем
Тогда
Так как синус острого угла (в прямоугольном треугольнике) — это отношение
противолежащего катета к гипотенузе, то
Угол с тупым углом
— смежные, следовательно, их синусы равны,
значит, синус тупого угла равен также
- ЕГЭ по биологии
Биология 11 класс. Тренировочные задания для подготовки к ЕГЭ по теме «Клетка».
→ Клеточная теория
→ Химический состав клетки
→ Цитология
→ Метаболизм клетки
→ ответы
Пример заданий:
1. Транскрипция представляет собой процесс
1) образования пептидных связей между аминокислотами
2) доставки аминокислот к рибосомам
3) синтеза ДНК в ядре на основе принципа комплементарности
4) синтеза иРНК на одной из полинуклеотидных цепей ДНК
Ответ:
2. В каком из перечисленных процессов участвуют ионы кальция?
1) транспорт газов
2) образование связей между аминокислотами
3) синтез белков
4) процесс свёртывания крови
Ответ:
Связанные страницы:
Методическое пособие для подготовки к ЕГЭ по математике
задания В3
Выполнила
Учитель математики
МБОУ СОШ №7
Тютюнникова Ирина Николаевна
ВЗ.Геометрические задачи с числовым ответом
Немного полезной информации
Мы рассмотрим простые виды задач по геометрии,
а именно задачи, в которых нужно найти площади плоских фигур,
нарисованных на клетчатой бумаге или расположенных на координатной плоскости.
Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому.
Давайте вспомним эти формулы и разберём примеры их приме-
нения.
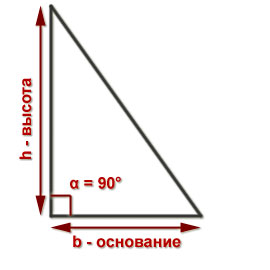
Теорема Пифагора: В прямоугольном треугольнике квад-
рат гипотенузы (с) равен сумме квадратов катетов (а и b).
Площадь прямоугольного треугольника равнаи половине произведения его катетов: .
Напомним, что у прямоугольного треугольника есть прямой угол, равный 90°. Сторона напротив прямого угла (самая длинная
называется гипотенузой, две прилежащие к прямому углу стороны
называют катетами.
Все задачи имеют один вопрос: Найти площадь какой-нибудь фигуры…
Отличие в другом – фигуры заданы по-разному:
либо на клетчатой бумаге:
либо в координатной плоскости:
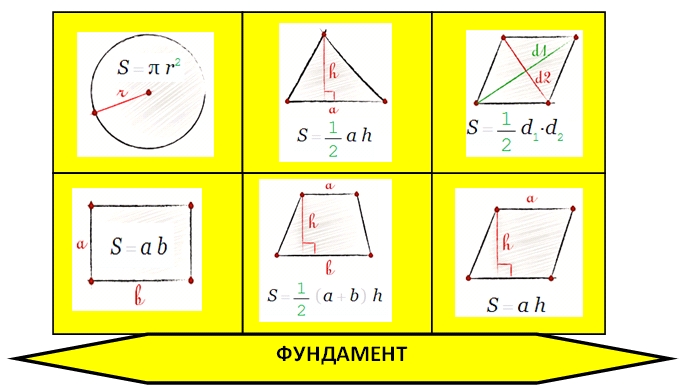
Чтобы решить её, надо знать ФУНДАМЕНТ – площади основных фигур:
На самом деле, для В3 достаточно знать S прямоугольника и S треугольника (чаще прямоугольного). Остальные S очень редко используются. Этот Жёлтый фундамент нужно один раз заложить себе в голову и пользоваться им ещё и в других задачах!
Есть несколько способов найти S. Примерь быстро каждый способ к фигуре и выбери лучший
Способ_1 (самый лучший и часто используемый)
1) достроить фигуру до прямоугольника или прямоугольного треугольника
2) Найти S1 полученной фигуры (прямоугольника или треугольника)
3) Найти S2 добавленных частей
4) Вычесть S1 – S2 = получим S нужной фигуры.
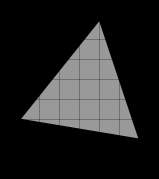
Пример: Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.
Решение:
-
Достроим до квадрата:
2-3-4) Теперь
Ответ: 17.
Способ_1 замечательно подходит для фигур на клетчатой бумаге. Его можно использовать и для фигур на координатной плоскости.
Но тут быстрее вычислить S самой фигуры.
Способ_2
1) ПО формуле – самый простой способ
Способ_2 используется тогда, когда чётко видно, что за фигура и легко найти величины для вычисления S.
Например, для ромба найти длины диагоналей и использовать формулу из Жёлтого фундамента.
Для круга найти радиус.
Для трапеции основания и высоту.
Для треугольника сторону и высоту к этой стороне и т.д.
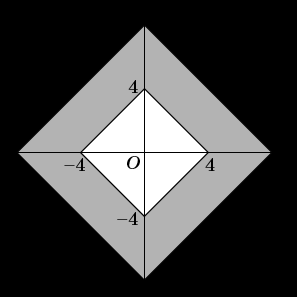
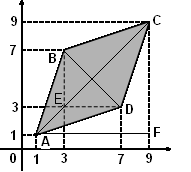
Пример: Найдите площадь ромба, изображенного на рисунке.
Решение:
Площадь ромба равна половине произведения его диагоналей:
Диагонали BD и АС найдем по теореме Пифагора из треугольников BED и AFC соответственно:
BD2 = BE2 + ED2 = 42 + 42 = 16 + 16 = 16·2; BD=
AC2 = AF2 + FC2 = 82 + 82 = 64 + 64 = 64·2; AC =
Ответ: 32
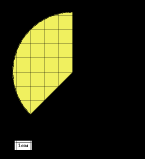
Ещё задача: Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис.).
Решение: 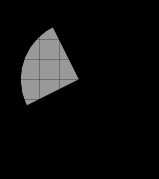
1) Найдем радиус окружности и посчитаем площадь всего круга по формуле
В этой задаче сразу видно, что R = 3 .
2)Теперь определим, какую часть круга составляет выделенный сегмент. Из рисунка видно, что четверть. Значит, его площадь равна
Ответ: 2,25
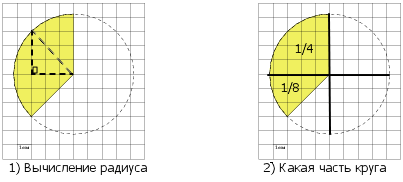
И последний пример: Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис.).
Решение:
1) Радиус вычислим по теореме Пифагора, как показано на рисунке.
(Выбрали точку на окружности, лежащую строго на границе клеток, и мысленно достроили прямоугольный треугольник.)
R2 = 32 + 32 = 9 + 9 = 9·2
2) Выделенный сегмент можно разбить на две части. Одна часть составляет четверть круга, другая — половину четверти, то есть 1/8 круга.
Весь сегмент составит круга.
Ответ: 6,75
Задачи для самостоятельного решения
1.На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах
2.На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
3. Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет.
4.Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8.
5. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
6.Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах
7.Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Фигуры на квадратной решетке»
Открытый банк заданий по теме фигуры на квадратной решетке. Задания B3 из ЕГЭ по математике (профильный уровень)
Задание №1040
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
На клетчатой бумаге с размером клетки sqrt{10}timessqrt{10} изображен четырехугольник ABCD. Найдите его периметр.
Показать решение
Решение
triangle BKC = triangle MDC = triangle AFD = triangle ABE по двум катетам, следовательно BC=CD=AB=AD, откуда следует, что ABCD — ромб.
BK=6sqrt{10}, KC=2sqrt{10}, BC=sqrt{BK^2+KC^2}=sqrt{(6sqrt{10})^2+(2sqrt{10})^2}=20.
Пусть P_{ABCD} — периметр ромба ABCD.
P_{ABCD} = 4cdot BC=4cdot20=80.
Ответ
80
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1039
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
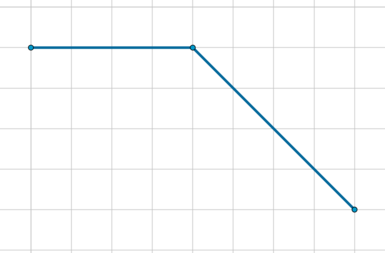
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
Показать решение
Решение
Проведем среднюю линию MN трапеции ABCD. Ее длина равна полусумме оснований трапеции: MN=frac{AD+BC}{2}. По рисунку AD=5, BC=3, а значит MN=frac{5+3}{2}=4.
Ответ
4
Задание №1038
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
На клетчатой бумаге с размером клетки 1×1 изображен треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.
Показать решение
Решение
Построим высоту CH и посчитаем клетки:
CH = 3.
Ответ
3
Задание №867
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его медианы, проведённой из вершины C.
Показать решение
Решение
M — середина стороны AB, следовательно, CM — медиана, CM = 4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №866
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
На клетчатой бумаге с размером клетки 1×1 отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC.
Показать решение
Решение
Посчитаем по клеткам расстояние от точки A до прямой BC. Оно равно 3.
Ответ
3
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №865
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
На клетчатой бумаге изображён круг площадью 36. Найдите площадь заштрихованного сектора.
Показать решение
Решение
Площадь заштрихованного сектора равна половине площади всего круга, т.е. его площадь равна 0,5cdot36=18.
Ответ
18
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №864
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе.
Показать решение
Решение
Длина медианы, проведённой к гипотенузе, равна половине гипотенузы. Гипотенуза AB = 9. Медиана CM = 4,5.
Ответ
4,5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №863
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
На клетчатой бумаге с размером клетки 1×1 отмечены точки A и B. Найдите длину отрезка AB.
Показать решение
Решение
Рассмотрим прямоугольный треугольник ABC, в котором катет BC = 5, катет AC = 12. Гипотенузу AB найдём по теореме Пифагора. AB = sqrt{AC^2+BC^2}=sqrt{12^2+5^2}=13.
Ответ
13
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №862
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB.
Показать решение
Решение
Длина средней линии MN равна половине длины стороны AB, равной 5.
MN=frac12AB=frac12cdot5=2,5
Ответ
2,5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №860
Тип задания: 3
Тема:
Фигуры на квадратной решетке
Условие
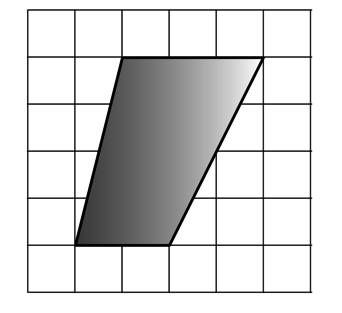
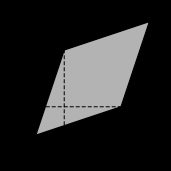
Найдите площадь параллелограмма, изображённого на клетчатой бумаге с размером клетки 1×1 см. Ответ дайте в квадратных сантиметрах.
Показать решение
Решение
Проведём высоту CH параллелограммаABCD.
S_{ABCD}=ADcdot CH.
AD=2, CH=4,
S_{ABCD}=2cdot4=8
Ответ
8
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928















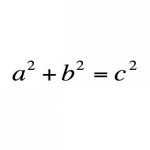





.png)
.png)












