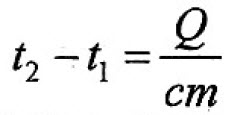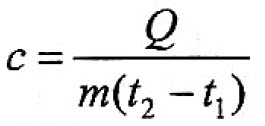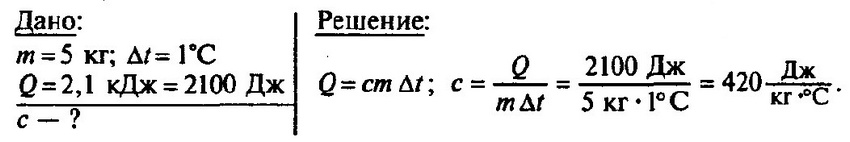Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Зависимость температуры 0,2 кг первоначально газообразного вещества от количества выделенной им теплоты представлена на рисунке. Рассматриваемый процесс идет при постоянном давлении. Какова удельная теплота парообразования этого вещества? Ответ выразите в кДж/кг.
2
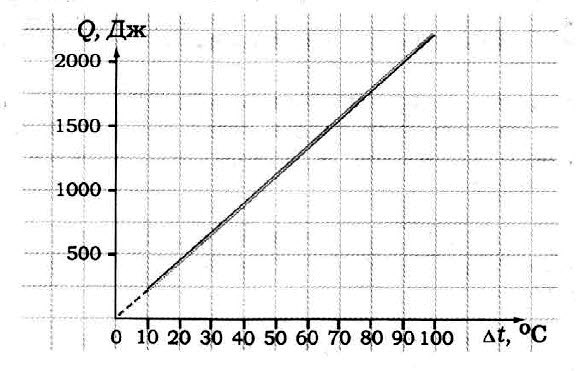
На рисунке приведен график зависимости температуры твердого тела от отданного им количества теплоты. Масса тела 4 кг. Какова удельная теплоемкость вещества этого тела? Ответ дайте в джоулях на килограмм на кельвин.
3
Температура медного образца массой 100 г повысилась с 20 °C до 60 °C. Какое количество теплоты получил образец? (Ответ дать в джоулях. Удельную теплоёмкость меди считать равной
4
На рисунке приведена зависимость температуры твердого тела от полученного им количества теплоты. Масса тела 2 кг. Какова удельная теплоемкость вещества этого тела? Ответ приведите в джоулях на килограмм на Кельвин.
5
На рисунке приведена зависимость температуры твердого тела от полученного им количества теплоты. Масса тела 2 кг. Какова удельная теплоемкость вещества этого тела? Ответ приведите в джоулях на килограмм на Кельвин.
Пройти тестирование по этим заданиям
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
Название величины |
Обозначение |
Единица измерения |
Формула |
Масса |
m |
кг |
|
Температура |
t |
°С |
|
Удельная теплоемкость |
c |
Дж/кг•°С |
|
Количество теплоты |
Q |
Дж |
|
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.
Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.
Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?
Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь
Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?
Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?
Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?
Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?
Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)
Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).
Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.
Ответ: 39 °С.
Задача № 14. (повышенной сложности)
Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?
Краткая теория для решения Задачи на количество теплоты.
Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Тема 25.
Механика. МКТ и Термодинамика (Расчетная задача).
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
механика. мкт и термодинамика (расчетная задача).
25.01Кинематика
25.02Динамика
25.03Законы сохранения в механике
25.04Статика. Равновесие
25.05Гидростатика
25.06Механические колебания
25.07Молекулярно – кинетическая теория
25.08Термодинамика
25.09Влажность. Водяной пар
25.10Тепловые явления
Решаем задачи
С какой скоростью капля воды должна налететь на такую же неподвижную каплю, чтобы в результате
взаимодействия они испарилась? Начальная температура капель .
Показать ответ и решение
Сделаем рисунок и обозначим импульсы
Так как по оси не действуют никакие внешние силы, то можем записать закон сохранения
импульса для двух капель:
Здесь — импульс первой капли до соударения,
— импульс
второй капли до соударения (капля покоилась ),
— импульс
капель после соударения. По условию капли одинаковые, значит , при этом
— искомая скорость (скорость первой капли до соударения),
— скорость капель после
соударения.
Спроецируем закон сохранения импульса на ось :
Откуда скорость после соударения:
Запишем закон сохранения энергии для столкновения. Начальная энергия состояла из кинетической
энергии движущейся первой капли, эта энергия перейдет в кинетическую энергию капель после
соударения, а также пойдет на нагрев и испарение воды. — теплота которая идет на нагрев
капель, Дж/(кг
К) — удельная теплоемкость воды,
— то на сколько
надо нагреть капли, чтобы довести до температуры кипения. — теплота требуемая для
испарения двух капель воды, Дж/кг — удельная теплота парообразования воды.
— кинетическая энергия налетающей капли, — кинетическая энергия капель после
соударения.
Закон сохранения энергии:
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записан закон сохранения
импульса (сначала векторно, после спроецирован на горизонтальную ось). Записан закон сохранения
энергии.)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы) (описаны все вводимые обозначения для масс,
импульсов, скоростей, изменения температуры. Удельная теплоемкость воды и удельная теплота
парообразования должны быть названы и описаны отдельно от формул, в которых они
используются. Теплоты в законе сохранения энергии надо описать (теплоту при нагреве и
парообразовании, кинетическую энергию налетающей капли и кинетическую энергию капель после
соударения))
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
В начале процесса температура куска свинца массой 1 кг равнялась 27 . Ему передали количество
теплоты, равное 47,7 кДж. Температура плавления свинца 327. Какова масса расплавившейся части
свинца? Тепловыми потерями пренебречь.
Показать ответ и решение
Для начала свинец нагрели до температуры плавления , передав ему количество
теплоты
где – удельная теплоемкость свинца,
– масса свинца,
– начальная температура
свинца.
Оставшееся количество теплоты пошло на расплавку свинца массой
где – удельная теплота плавления свинца.
и в сумме они дадут 47,7 кДж
Откуда масса расплавившейся части
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемая для плавления тела, формула количества теплоты, которое требуется для нагрева тела,
уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
На конденсацию пара, массой потребовалось
где – удельная теплота парообразования Так как в некоторый момент масса воды перестала
увеличиваться, значит, ее температура достигла 100 °С. Следовательно, для нагревания воды массой
с 0 до 100
было затрачено
Дж теплоты. Имеем:
, где – удельная теплоемкость воды;
– изменение температуры.
Откуда масса воды
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемая для конденсации пара, формула количества теплоты, которое требуется для нагрева тела,
уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Кусок льда для начала растопился, получив количество теплоты
где – удельная теплота плавления льда,
– масса льда. А затем он нагрелся до температуры
10, получив количество теплоты
Эта теплота будет образована за счет охлаждения воды
где – удельная теплоемкость воды. Откуда масса воды
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемая для плавления тела, формула количества теплоты, которое требуется для нагрева и
охлаждения тела, уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Вода будет охлаждаться до 0 , то есть в этом процессе лед получит количество теплоты,
равное:
где — масса воды,
— удельная теплоемкость воды,
— установившаяся температура,
—
начальная температура.
В то же время 0,5 кг льда расплавится. Значит, количество теплоты можно найти также по
формуле:
где — удельная теплота плавления льда.
Приравняем эти два уравнения и выразим начальную температуру воды:
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемая для плавления тела, формула количества теплоты, которое требуется для охлаждения
тела, уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
Вода будет охлаждаться до 0 , то есть в этом процессе лед получит количество теплоты,
равное:
где — масса воды,
— удельная теплоемкость воды,
— установившаяся температура.
В то же время 0,042 кг льда расплавится. Значит, количество теплоты можно найти также по
формуле:
где — удельная теплота плавления льда.
Приравняем эти два уравнения и выразим начальную массу воды:
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемая для плавления тела, формула количества теплоты, которое требуется для охлаждения
тела, уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Показать ответ и решение
После установления теплового равновесия температура воды в кастрюле составит .
Вода получит количество теплоты, равное:
Кипяток отдаст количество теплоты, равное:
где и
— количество теплоты, отданное кипятком и полученное водой соответственно,
—
удельная теплоемкость воды.
Так как теплообменом с окружающей средой и теплоемкостью кастрюли пренебрегаем, то можно
считать, что отданное количество теплоты равно принятому количеству теплоты.
Приравняем эти два уравнения:
Выразим отсюда температуру воды после установления теплового равновесия:
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
которое требуется для нагрева и охлаждения тела, уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Свинцовому и медному шарикам сообщили количество теплоты , при этом их температуры повысили
на одинаковое значение, найдите отношение массы о шарика к . Ответ округлите до целого
числа.
Показать ответ и решение
Количество теплоты, которое подводили к телу, находится по формуле:
где — изменение температуры.
Выразим отсюда массу тела:
Для свинцового и медного шарика имеем:
Найдем отношение их масс:
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
которое требуется для нагрева тела)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Железному и алюминиевому шарикам сообщили количество теплоты , при этом их температуры
повысили на одинаковое значение. Найдите отношение массы железного шарика к массе алюминиевого:
. (Ответ округлите до десятых.)
Показать ответ и решение
Количество теплоты, которое подводили к телу, находится по формуле:
где – теплоемкость тела,
– масса тела,
— изменение температуры.
Выразим отсюда массу тела:
Для железного и алюминиевого шарика имеем:
Найдем отношение их масс:
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
которое требуется для нагрева тела)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Кусок льда, имеющий температуру 0 помещен в калориметр. Чтобы нагреть лед до температуры 5
требуется 175500 Дж энергии. Какая температура установится в калориметре, если к нему подвести
количество теплоты, равное 70кДж? (Ответ дайте в градусах Цельсия.)
Показать ответ и решение
Чтобы лед нагреть до 5 , его нужно сначала расплавить, а затем нагреть получившуюся воду до
5, тогда количество теплоты, которое потребуется в этом процессе равно:
где — удельная теплота плавления льда,
— масса льда,
— удельная теплоемкость воды,
и — конечная и начальная температура соответственно.
Выразим отсюда массу льда и найдем её:
Теперь рассмотрим процесс, когда лед получит от нагревателя 70 кДж:
Таким образом, количества теплоты, которое система получит от нагревателя не хватит, чтобы
полностью расплавить лед, значит, температура будет равна 0 .
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемая для плавления тела, формула количества теплоты, которое требуется для нагрева тела,
уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Кусок льда, имеющий температуру 0 , помещён в калориметр с электронагревателем. Чтобы
превратить этот лёд в воду температурой 20 , требуется количество теплоты 100 кДж. Какая
температура установится внутри калориметра, если лёд получит от нагревателя количество теплоты 50
кДж? Теплоёмкостью калориметра и теплообменом с внешней средой пренебречь. (Ответ дайте в
градусах Цельсия.)
Показать ответ и решение
Количество теплоты, которое необходимо для плавления льда:
где — масса льда.
Количество теплоты, которое необходимо для нагревания воды от 0 до 20
:
где — удельная теплоемкость воды.
По условию известно, что:
Выразим массу льда:
Теперь рассмотрим процесс, когда лед получит от нагревателя 50 кДж:
Таким образом, количества теплоты, которое система получит от нагревателя не хватит, чтобы
полностью расплавить лед, значит, температура будет равна 0 .
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемая для плавления тела, формула количества теплоты, которое требуется для нагрева
тела)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
В калориметре находится вода, масса которой 230 г при температуре 0 . В него через трубку
впускают пар при температуре 100 . В какой-то момент времени масса воды перестаёт
увеличиваться? Определить на сколько граммов увеличиться масса воды.
Досрочная волна 2019
Показать ответ и решение
Масса воды перестанет увеличиваться, когда температура воды достигнет 100 . Вода нагревается за
счёт тепловой энергии конденсации водяного пара:
где – удельная теплота парообразования воды,
– масса пара.
Составив уравнение теплового баланса
где – масса воды,
– удельная теплоемкость воды,
– изменение температуры.
Откуда масса пара:
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемого для парообразования тела, формула количества теплоты, которое требуется для нагрева
тела, уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
В начале процесса температура куска свинца массой 1 кг была равна 47 . Ему передали количество
теплоты, равное 46,4 кДж. Температура плавления свинца равна 327 . Какова масса расплавившейся
части свинца? Тепловыми потерями пренебречь.
Досрочная волна 2020
Показать ответ и решение
Сначала свинец нагрелся до температуры плавления, в результате чего ему передалось количество
теплоты
где – теплоёмкость свинца,
– масса свинца,
и
– начальная и конечная температура
свинца.
Потом свинец начал плавится, в результате чего он потратил оставшееся количество теплоты,
равное
где – удельная теплота плавления свинца,
– масса расплавившейся части свинца
По условию
Откуда масса расплавившейся части
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемая для плавления тела, формула количества теплоты, которое требуется для нагрева тела,
уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
В калориметре находятся в тепловом равновесии вода и лёд. После опускания в калориметр болта,
имеющего массу 165 г и температуру –40 , 20% воды превратилось в лёд. Удельная теплоёмкость
материала болта равна 500 Дж/(кг К). Какая масса воды первоначально находилась в калориметре?
Теплоёмкостью калориметра пренебречь.
Демоверсия 2021
Критерии оценки
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: формула количества теплоты,
требуемая для плавления тела, формула количества теплоты, которое требуется для нагрева тела,
уравнение теплового баланса)
II) Описаны все вновь вводимые в решении буквенные обозначения физических величин за
исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии
задачи, и стандартных обозначений величин, используемых при написании физических законов.
(введены обозначения для величин не входящих в КИМы)
III) Представлены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями.)
IV) Представлен правильный ответ с указанием единиц измерения искомой величины. (В ответе
обязательно указываются единицы измерений.)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и
проведены преобразования, направленные на решение задачи, но имеется один или несколько из
следующих недостатков.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. (не описаны
вновь вводимые величины, которых нет в условии и КИМ)
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от
решения и не зачёркнуты.
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в
математических преобразованиях/вычислениях пропущены логически важные шаги.
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения
величины)
Во всех остальных случаях за задачу выставляется 0 баллов.
Егэ физика задачи на уравнение теплового баланса
Репетитор
по физике
Репетитор
по физике
Репетитор
по алгебре
Репетитор
по физике
Задачи на определение температуры смеси
(Задачи на уравнение теплового баланса) .
Задача 1. (Температура смеси)
Смешали (m_<хол>=1 кг ) холодной воды при температуре (t_<хол>=10^0C ) и горячую воду при температуре (t_<гор>=90^0C .) Температура смеси при этом оказалась равна ( 50^0 C . )
Какова масса горячей воды?
Показать ответ Показать решение Видеорешение
Составим уравнение теплового баланса:
Разделим на (40) обе части уравнения:
Разделим на (c ) обе части уравнения:
Задача 2. (Температура смеси)
Смешали (m_х=1 кг ) холодной воды при температуре (t_х=10^0C ) и горячую воду при температуре (t_г=90^0C .) Температура смеси при этом оказалась равна (Theta=50^0 C . )
Какова масса горячей воды?
Показать ответ Показать решение Видеорешение
Составим уравнение теплового баланса:
Задача 3. (Температура смеси)
Смешали (m_1=2 кг ) холодной воды при температуре (t_1=5^0C ) и горячую воду при температуре (t_2=95^0C .) Температура смеси при этом оказалась равна (Theta=80^0 C . )
Какова масса горячей воды?
Показать ответ Показать решение Видеорешение
Решение задач на теплообмен с использованием уравнения теплового баланса (методические рекомендации)
Разделы: Физика
Пособие рекомендовано учащимся, желающим получить практические навыки в решении задач на теплообмен, и может быть полезным для учителей и абитуриентов.
При соприкосновении тел, имеющих разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической теории, это объясняется так: молекулы более нагретого тела имеют большую кинетическую энергию, чем молекулы тела, менее нагретого. При “столкновениях” молекул соприкасающихся тел происходит процесс выравнивания их средних кинетических энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии, при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного тела возрастает, поэтому температура этого тела будет увеличиваться. В конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры тел станут одинаковыми. На этом теплообмен прекращается.
Энергию, которую тело получает или отдаёт в процессе теплообмена, называют количеством теплоты (Q).
Количество теплоты, как и все другие виды энергии, измеряется в системе СИ в Джоулях: [Q] = Дж. (Здесь и в дальнейшем единицы измеряются в системе СИ.)
Нагревание или охлаждение
При нагревании или охлаждении тела количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:
(t2 – t1) – разность температур тела,° С (или К);
с – удельная теплоёмкость вещества, из которого состоит тело,
Удельная теплоёмкость вещества – это количество теплоты, которое нужно сообщить одному килограмму данного вещества, чтобы увеличить его температуру на 1° С (или это количество теплоты, которое выделяет один килограмм данного вещества, остывая на 1° С).
Значения удельных теплоемкостей других веществ можно найти в справочниках, а также в школьном учебнике или задачнике.
При нагревании тела его внутренняя энергия увеличивается. Это требует притока энергии к телу от других тел. Значит, оно поглощает некоторое количество теплоты, принимая его от других тел, участвующих в теплообмене.
При охлаждении тела его внутренняя энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое количество теплоты.
Обычно конечную температуру, установившуюся в результате теплообмена, обозначают греческой буквой 
В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью тела и обозначают С:
Размерность теплоемкости: 
Теплообмен между телами, имеющими одинаковые температуры, не происходит, даже если контактируют вещества, находящиеся в разных агрегатных состояниях. Например, при температуре плавления (0° С) лёд и вода могут находиться бесконечно долго, при этом количество льда и количество воды останутся неизменными. Аналогично ведут себя пар и жидкость, находящиеся при температуре кипения. Теплообмен между ними не происходит.
Плавление или кристаллизация
Если при нагревании тела его температура достигнет температуры плавления, то начинает происходить процесс перехода этого вещества из твердого состояния в жидкое. При этом идут изменения в расположении и характере взаимодействия молекул. Температура при плавлении не изменяется. Это означает, что средние кинетические энергии молекул жидкости и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия тела при плавлении возрастает за счет увеличения энергии взаимодействия молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по формуле

где m – масса тела, кг;

При кристаллизации, наоборот, внутренняя энергия тела уменьшается на величину 
Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного вещества, взятого при температуре плавления, чтобы полностью превратить его при этой температуре в жидкость (или сколько энергии выделяет 1 кг жидкости, взятой при температуре кристаллизации, если вся она при этой температуре полностью превратится в твёрдое тело).
Удельную теплоту плавления любого вещества можно найти в справочниках. Для льда же
Температура плавления у каждого вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что температура плавления вещества равна температуре кристаллизации этого же вещества. У льда tпл = 0° С.
Кипение или конденсация
При достижении жидкостью температуры кипения начинает происходить другой фазовый переход – кипение, при котором расстояния между молекулами значительно увеличиваются, а силы взаимодействия молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей между молекулами. При конденсации пара в жидкость, наоборот, расстояния между молекулами значительно сокращаются, а силы взаимодействия молекул увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при конденсации пара энергия выделяется. Количество теплоты, поглощаемое при кипении или выделяемое при конденсации, рассчитывается по формуле:
где m – масса тела, кг; L – удельная теплота парообразования,
Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости, взятой при температуре кипения, чтобы при этой температуре полностью превратить её в пар (для конденсации: сколько энергии выделяет один килограмм пара, взятого при температуре конденсации, полностью превращаясь в жидкость).
При одинаковом давлении температура кипения и температура конденсации одного и того же вещества одинаковы.
Температуры кипения и удельные теплоты парообразования также можно найти в справочниках. Для воды же они соответственно равны: рис. 9 (при нормальном атмосферном давлении).
Уравнение теплового баланса
Тела, участвующие в теплообмене, представляют собой термодинамическую систему. Термодинамическая система называется теплоизолированной, если она не получает энергию извне и не отдаёт её; теплообмен происходит только между телами, входящими в эту систему. Для любой теплоизолированной системы тел справедливо следующее утверждение: количество теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими телами.
Это утверждение описывает частный случай закона сохранения и превращения энергии в применении к процессу теплообмена. А формула (5) является одним из видов уравнения теплового баланса.
При решении задач с помощью данного вида уравнения теплового баланса в формуле (1) в качестве t2 следует брать большую температуру, а в качестве t1 – меньшую. Тогда разность (t2 – t1) будет положительна и всё произведение cm(t2–t1) также будет положительным. Все теплоты, отданные и полученные, будут положительными.
Уравнение теплового баланса можно записать и в таком виде:
где n – количество тел системы.
Алгебраическая сумма всех количеств теплоты (поглощенных и выделенных) в теплоизолированной системе равна нулю.
Q1, Q2, …, Qn – это теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что в этом случае какие-то теплоты должны быть положительны, а какие-то – отрицательны. При записи уравнения теплового баланса в виде (6) всегда t2 – конечная температура, а t1 – начальная.
Если тело нагревается, то разность (t2 – t1) положительна и все произведение cm(t2 – t1) положительно. То есть Q > 0 тогда, когда теплота к данному телу подводится.
А если t2 0; если тело выделяет энергию (кристаллизация, конденсация), то Q
 |
Проведём анализ:
Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t1 = t2 = 20° С. При опускании в воду с температурой 20° С свинцового тела с температурой 90° С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода — нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться. |
 |
Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ).
Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q3. |
| Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают. | |
| Решим задачу с использованием уравнения теплового баланса в виде (5):
|
Решим задачу с использованием уравнения теплового баланса в виде (6):
Ответ: Вода нагреется до 24° С.
Предлагаю читателю самостоятельно сделать проверку размерности.
Егэ физика задачи на уравнение теплового баланса
В эксперименте установлено, что при температуре воздуха в комнате 29 °C на стенке стакана с холодной водой начинается конденсация паров воды из воздуха, если снизить температуру стакана до 27 °C. По результатам этих экспериментов определите абсолютную и относительную влажность воздуха. Для решения задачи воспользуйтесь таблицей. Поясните, почему конденсация паров воды в воздухе может начинаться при различных значениях температуры. Давление и плотность насыщенного водяного пара при различной температуре показано в таблице:
Водяной пар в воздухе становится насыщенным при температуре 27 °C. Следовательно, давление р водяного пара в воздухе равно давлению насыщенного пара при температуре 27 °C, из таблицы 36 гПа.
Абсолютная влажность равна плотности водяных паров. Первое состояние: насыщенный пар при 27 °C. Второе: пар при 29
°C. Пар охлаждается от 29 до 27 °C изобарически, поэтому
Давление насыщенного водяного пара при температуре 29 °C равно 40 гПа. Относительной влажностью воздуха
называется отношение:
Пусть — абсолютная влажность воздуха при температуре 29 °C равно, а
— плотность насыщенных водяных паров при этой температуре. Относительную влажность можно рассчитать как отношение
откуда
Конденсация паров воды происходит при условии равенства давления водяного пара, имеющегося в воздухе, давлению насыщенного водяного пара при данной температуре воздуха. Давление насыщенного водяного пара зависит от температуры. Поэтому при разной плотности водяного пара в воздухе температура начала конденсации пара (точка росы) оказывается различной.
Приведённое решение неверно. В условии нигде не сказано, что можно считать водяной пар идеальным газом, а стало быть уравнение Менделеева-Клайперона даёт неточный результат. Относительная влажность по другому определяется через отношение абсолютной влажности к плотности водяных паров при данной температуре, следовательно мы можем взять значение для абсолютной влажности при 29 градусах непосредственно из таблицы — она равна плотности насыщенных паров при 27 градусах, т.е. 25,8 г/куб. м.
Немного изменили решение. Но при изменении температуры при постоянном давлении меняется (хоть и незначительно) относительная влажность. Поэтому нельзя сказать, что искомая относительная влажность равна плотности насыщенного парам при 27 °С. Составителям следовало бы взять разницу температур побольше.
В аналогичной задаче 2930 принцип нахождения абсолютной влажности описан верно, в данной задаче — нет
Это решение верное и ответ получится такой же. В задаче 2930 более очевидный переход.
В калориметре находился 1 кг льда. Чему равна первоначальная температура льда, если после добавления в калориметр 20 г воды, имеющей температуру 20 °C, в калориметре установилось тепловое равновесие при ? Теплообменом с окружающей средой и теплоемкостью калориметра пренебречь.
Количество теплоты, необходимое для нагрева льда, находящегося в калориметре, до температуры t:
Количество теплоты, отдаваемое водой при охлаждении ее до :
Количество теплоты, выделяющееся при отвердевании воды при :
Количество теплоты, вьделяющееся при охлаждении льда, полученного из воды, до температуры t:
Уравнение теплового баланса:
Объединяя (1)—(5), получаем:
Ответ:
Почему количество теплоты, выделяющееся при отвердевании воды равно Q=Lm (L- лямбда)? Если я не ошибаюсь, то отвердевание это кристаллизация и формула будет Q=-Lm.
Знак не имеет особого значения. Просто нужно писать данное слагаемое в «правильную часть» теплового баланса, то есть правильно указывать, куда переходит данная энергия.
В калориметре находился лед при температуре Какой была масса
льда, если после добавления в калориметр
воды, имеющей температуру
и установления теплового равновесия температура содержимого калориметра оказалась равной
причем в калориметре была только вода?
Количество теплоты, полученное при нагреве льда, находящегося в калориметре, до температуры :
(1).
Количество теплоты, полученное льдом при его таянии при
(2).
Количество теплоты, отданное водой при охлаждении её до
(3).
Уравнение теплового баланса: (4).
Объединяя (1)—(4), получаем:
Ответ:
В калориметре находился 1 кг льда. Какой была температура льда, если после добавления в калориметр 15 г воды, имеющей температуру 20 °С, в калориметре установилось тепловое равновесие при –2 °С? Теплообменом с окружающей средой и теплоемкостью калориметра пренебречь.
Количество теплоты, необходимое для нагревания льда, находящегося в калориметре, до температуры t:
(1)
Количество теплоты, отдаваемое водой при охлаждении её до 0 °С:
(2)
Количество теплоты, выделяющейся при отвердевании воды при 0 °С:
(3)
Количество теплоты, выделяющейся при охлаждении льда, полученного из воды, до температуры t:
(4)
Уравнение теплового баланса:
(5)
Объединяя формулы (1)—(5), получаем
Ответ:
Почему в уравнении (3) удельная теплота плавления взята с плюсом? Т.к. идёт процесс, обратный плавлению, она должна быть с минусом.
Я бы Вам посоветовал забыть про этот знак минус в формуле, лучше все считать положительным, просто понимать, куда перетекает тепло. Писать тепловой баланс в виде: .
Это полностью эквивалентно балансу в виде
А почему в уравнении (2) , при расчете температуры мы вычитаем 0 , не -2 ?
То что происходит с 15 г воды можно представить в виде трёх процессов: а) вода охлаждается до 0 °С, б) замерзает (превращается в лёд) и в) лёд охлаждается до –2 °С.
Уравнение (2) описывает процесс (а).
В 2012 году зима в Подмосковье была очень холодной, и приходилось использовать системы отопления дачных домов на полную мощность. В одном из них установлено газовое отопительное оборудование с тепловой мощностью 17,5 кВт и КПД 85%, работающее на природном газе — метане Сколько пришлось заплатить за газ хозяевам дома после месяца (30 дней) отопления в максимальном режиме? Цена газа составляла на этот период 3 рубля 30 копеек за 1 кубометр газа, удельная теплота сгорания метана 50,4 МДж/кг. Можно считать, что объём потреблённого газа измеряется счётчиком при нормальных условиях. Ответ округлите до десятков рублей.
Метан имеет молярную массу Согласно уравнению Клапейрона — Менделеева, плотность метана
при нормальных условиях (температура
давление
) равна
Удельная теплота сгорания метана в пересчёте на кубометр газа равна КПД газового отопительного оборудования
а тепловая мощность установки
поэтому мощность, выделяющаяся при сгорании газа, равна
Таким образом, за месяц (30 суток по 86400 секунд) потребление энергии составит
Объём потребленного за месяц газа будет равен а его стоимость равна
Ответ: хозяевам пришлось заплатить за месяц отопления дома газом 4960 рублей.
источники:
http://urok.1sept.ru/articles/103594
http://phys-ege.sdamgia.ru/test?theme=307
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 64%
Ответом к заданию 9 по физике может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Определите мощность кипятильника, который за 5 минут нагревает 210 г воды от 14◦C до температуры кипения. Потерю энергии не учитывать. Ответ выразите в (Вт) и округлите до целых.
Решение
Дано:
$t=5=5·60=300$c
$m=0.21$кг
$t_1=14°C$
$t_2=100°C$
$N-?$
Решение:
Мощность по определению равна: $N={A}/{t}={Q}/{t}={cm(t_-t_1)}/{t}$(1), где $m$ — масса воды, $c$ — удельная теплоемкость воды $c=4200$Дж/кг·°C. Подставим числовые значения в (1), имеем: $N={4200·0.21·(100-14)}/{300}=252.84$Bт. После округления до целых: 253 Вт
Ответ: 253
Задача 2
Сколько керосина необходимо сжечь, чтобы 50 л воды нагреть от 20◦C до кипения? КПД нагревателя равен 35%. Удельная теплота сгорания керосина 4,3 · 107 Дж/кг. Ответ выразите в (кг), округлив до десятых.
Решение
Дано:
$V=50·10^{-3}м^3$
$ρ_в=10^3{кг}/{м^3}$
$t_1=20°C; t_2=100°C; η=0.35$
$q=4.3·10^7$Дж/кг
$c=4200$Дж/кг·К
$m-?$
Решение:
$Q_1=q·m$(1) — количество теплоты, которое выделяется при сжимании керосина, $m$ — масса керосина. $Q_2=c·m_в·(t_2-t_1)=c·ρ·V·(t_2-t_1)$(2) — количество теплоты, которое необходимо затратить, чтобы нагреть воду массой $m_в=ρ·V$(3), где $ρ$ — плотность воды, $c$ — удельная теплоемкость воды.
КПД нагревателя определяется выражением: $η={A_{полез}}/{A_{затр}}·100%={c·ρ·V·(t_2-t_1)}/{q_m}·100%$(4), откуда $m={c·ρ·V·(t_2-t_1)·100%}/{q·η}$(5). Подставим в (5): $m={4200·10^3·50·10^{-3}·(100-20)·100%}/{4.3·10^7·35%}={4.2·5·8}/{4.3·35}=1.1$кг.
Ответ: 1.1
Задача 3
В подвальном помещении относительная влажность воздуха 70%, а парциальное давление водяных паров 2100 Па. Чему равно давление насыщенных паров при той же температуре? Ответ выразите в (кПа).
Решение
Дано:
$p=2100$Па
$ϕ=70%$
$p_н-?$
Решение:
Относительная влажность воздуха равна: $ϕ={p}/{p_н}·100%$, откуда давление насыщенных паров $p_н$ равно: $p_н={p·100%}/{ϕ}={2100·100%}/{70%}=3000=3$кПа.
Ответ: 3
Задача 4
Определите КПД нагревателя, расходующего 80 г керосина на нагревание 3 л воды на 90 К. Удельная теплота сгорания керосина 4,3·107 Дж/кг. Ответ выразите в (%) и округлите до целых.
Решение
Дано:
$m_к=0.08$кг
$V_в=3=3·10^{-3}м^3$
$ρ_в=1000{кг}/{м^3}$
$∆T=90K$
$q=4.3·10^7$Дж/кг
$c=4200$Дж/кг·К
$η-?$
Решение:
КПД нагревателя определяется выражением: $η={A_{полез}}/{A_{затр}}·100%$(1), $m_в=ρ_в·V_в$(2) — масса воды, где $A_{полез}=Q_п=cm_в·∆T=c·ρ_в·V_в·∆T$(3) — полезная работа; $A_{затр}=Q_з=q·m_к$(4) — затраченная (полезная) работа. Подставим (3) и (4) в (1) получим: $η={c·ρ_в·V_в·∆T}/{q·m_к}·100%={4200·10^3·3·10^{-3}·90}/{4.3·10^7·8·10^{-2}}·100%={1134000}/{3440000}·100%=32.965%=33%$.
Ответ: 33
Задача 5
Определите относительную влажность воздуха при комнатной температуре, если парциальное давление пара при этой температуре равно 1167 Па, а давление насыщенного пара равно 2333 Па. Ответ выразите в (%).
Решение
Дано:
$p=1167$Па
$p_0=2333$Па
$ϕ-?$
Решение:
Относительная влажность воздуха равна: $ϕ={p}/{p_0}·100%$, где $p$ — парциальное давление пара, $p_0$ — давление насыщенного пара. Подставим числа: $ϕ={1167}/{2333}·100%=0.5·100%=50%$.
Ответ: 50
Задача 6
Относительная влажность воздуха 65%, давление насыщенного пара в нём при некоторой температуре равно 3,4 кПа. Чему равно парциальное давление пара при этой же температуре? Ответ выразите в (кПа), округлив до сотых.
Решение
Дано:
$ϕ=65%$
$p_0=3.4·10^3$Па
$p-?$
Решение:
По определению относительная влажность воздуха равна: $ϕ={p}/{p_0}·100%$(1), где $p$ — парциальное давление пара. Из (1) найдем $p$: $p={ϕ·p_0}/{100%}$(2). Подставим числа: $p={65·3.4·10^3}/{100%}=2210=2.21$кПа.
Ответ: 2.21
Задача 7
Относительная влажность воздуха в закрытом сосуде под поршнем составляет 65%. Какой станет относительная влажность воздуха в сосуде, если объём воздуха в нём изотермически уменьшить в 2 раза за счёт движения поршня? Ответ выразить в (%).
Решение
Дано:
$T=const$
$ϕ_{от.в.}=65%$
$V_2={V_1}/{2}$
Решение:
Из теории известно, что при $T=const$ и уменьшении объема, увеличивается давление по закону Менделеева-Клайперона $PV=υRT$. Тогда как $P∼ϕ_{от.в.}$, но более чем 100% быть не может.
Ответ: 100
Задача 8
Относительная влажность воздуха при температуре 100◦С составляет 60%. Чему равно парциальное давление водяных паров, содержащихся в воздухе? Ответ выразить в (кПа).
Решение
Дано:
$T=100°C$
$ϕ_{от}=60%$
$P_{вп}-?$
Решение:
Известно, что для $T=100°C$ давление насыщенного пара $P_*=100$кПа. Тогда $ϕ={P_{вп}}/{P_*}·100⇒P_{вп}=0.6·100=60$кПа.
Ответ: 60
Задача 9
Давление насыщенного водяного пара при 24◦С равно 22,4 мм рт. ст., а при 13◦С — 11,23 мм рт. ст. Определите относительную влажность воздуха при температуре 24◦С, если точка росы равна 13◦С. Ответ выразите в процентах и округлите до целых. Ответ выразите в (%).
Решение
Дано:
$p_{н.п.24°C}=22.4$мм.рт.ст.
$p_{н.п.13°C}=11.23$мм.рт.ст.
$ϕ_{24°C}-?$
Решение:
Если точка росы 13°C, значит парциальное давление данного водяного пара равно давлению насыщенного водяного пара при температуре 13°C: $p_{24°C}=p_{н.п.13°C}$. Тогда влажность воздуха при температуре 24°C: $ϕ_{24°C}={p_{24°C}}/{p_{н.п.24°C}}·100%={p_{н.п.13°C}}/{p_{н.п.24°C}}·100%={11.23}/{22.4}·100%=50%$
Ответ: 50
Задача 10
Определите массу воды, взятой при температуре 40◦С, которую нагревают до температуры кипения и полностью испаряют. Необходимая для этих процессов энергия составляет 638 кДж. Ответ выразите в (г).
Удельная теплота парообразования воды $2.3·10^6$ Дж/кг, теплоёмкость воды 4200 Дж/(кг·°С)
Решение
Дано:
$m-?$
$T_1=40°$
$Q_{об}=638$кДж
Решение:
$c_вm∆T+r·m=Q_{об}$ — закон теплообмена.
$m={Q_{об}}/{c_в∆T+r}={638·10^3}/{4200·60+2.3·10^6}=250$г.
Ответ: 250
Задача 11
Какое количество теплоты необходимо для нагревания железного бруска массой 200 г от 285 К до 305 К? Ответ выразите в (Дж). Удельная теплоемкость железа 460 Дж/(кг*К)
Решение
Дано:
$m_ж=0.2кг$
$∆T=20K$
$c_ж=460$ Дж/(кг*К)
$Q-?$
Решение:
По закону нагревания тела равно $Q=c_ж·m_x·∆T=460$Дж/(кг*К)·0.2$кг·20$К=1840Дж.
Ответ: 1840
Задача 12
Каково давление насыщенного водяного пара при температуре 100◦С? Атмосферное давление принять равным $10^5$ Па. Ответ выразите в (кПа).
Решение
Дано:
$p_{нв}-?$
$T=100°C$
Решение:
По определению давления насыщенного пара при $T=100°C$. Составляет 100кПа.
Ответ: 100
Задача 13
В сосуде с подвижным поршнем находятся вода и её насыщенный пар. Если одновременно увеличить в 2 раза температуру сосуда и его объём, то как увеличится его давление? В ответ запишите: примерно в _ раз(а).
Решение
Объём сосуда не влияет на давление насыщенного пара. Влияние температуры на давление насыщенного пара можно определить по уравнению Менделеева-Клайперона $pV=υRT$. Если температуру увеличить в 2 раза, то и давление увеличится в 2 раза.
Ответ: 2
Задача 14
Относительная влажность воздуха в цилиндре под поршнем равна 40%. Воздух изотермически сжали, уменьшив его объём в три раза. Какова стала относительная влажность воздуха? Ответ выразите в (%).
Решение
Дано:
$ϕ_{отн}=40%$
$T=const$
$V_2 < V_1$
$V_2={V_1}/{3}$
$ϕ_{отн}-?$
Решение:
Насыщенный пар подчиняется уравнению Менделеева-Клайперона: $ϕ={n}/{n_{нп}}·100%; n_{нп}$ — не изменяется ($T=const$)
$n=0.4n_{нп}$, следовательно, уменьшение в 3 раза приведет к увеличению $n=1.2=n_{нп}$, но $n=n_{нп}$ это максимум (насыщенный пар).
Ответ: 100
Задача 15
Относительная влажность водяного пара в сосуде при температуре 100◦С равна 62%. Какова плотность этого пара? Ответ округлите до сотых. Ответ выразить в (кг/м3).
Решение
Дано:
$ϕ_{отн}=62%$
$T=100°C$
$ρ_{вп}-?$
Решение:
Относительная влажность это отношение парциального давления паров воды в газе к равновесному давлению паров при данной температуре $ϕ={p}/{p_{нп}}$. При 100°C давление насыщенных паров равно атмосферному $p_{нп}=10^5$Па, тогда $ρ={p·M}/{R·T}={ϕ·p_{нп}·M}/{R·T}={0.62·10^5·0.018}/{8.31·373}=0.36{кг}/{м^3}$.
Ответ: 0.36
Задача 16
В кубическом метре воздуха в помещении при температуре 18◦С находится 1,31 · 10−2 кг водяных паров. Пользуясь таблицей плотности насыщенных паров воды, определите относительную влажность воздуха. Ответ выразите в (%). Ответ округлите до целого.
| t, ◦ C | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| ρ, г/м3 | 13,6 | 14,5 | 15,4 | 16,3 | 17,3 | 18,3 | 19,4 | 20,6 | 21,8 |
Решение
Дано:
$V=1м^3$
$T=18°C$
$m_{вп}=1.31·10^{-2}$кг
$ϕ_{отн}-?$
Решение:
1) Определим плотность водяных паров в комнате $ρ_{вп}={m_{вп}}/{V}={1.31·10^{-2}}/{1}{кг}/{м^3}$.
2) Используя таблицу, определим, и по при температуре 18°C плотность насыщенных паров равна $ρ_{нп}=1.54·10^{-2}{кг}/{м^3}$.
3) Тогда относительная влажность воздуха в комнате равна $ϕ_{отн}={ρ_{вп}}/{ρ_{нп}}·100%={1.31·10^{-2}}/{1.54·10^{-2}}≈85%$.
Ответ: 85
Задача 17
Парциальное давление водяного пара в 1,25 раза меньше, чем давление насыщенного пара при той же температуре. Чему равна относительная влажность воздуха? Ответ выразите в (%).
Решение
Дано:
$p_п=p$
$p_н=1.25p$
$ϕ-?$
Решение:
Относительная влажность воздуха определяется как: $ϕ={p_п}/{p_н}·100%$, где $p_п$ — парциальное давление газа; $p_н$ — давление насыщенного газа при той же температуре, тогда имеем: $ϕ={p_п}/{p_н}·100%={p·100%}/{1.25p}=80%$
Ответ: 80
Задача 18
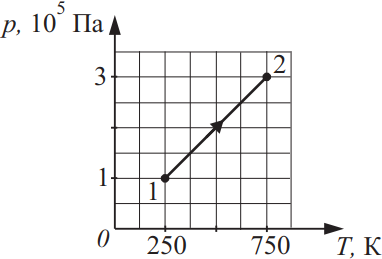
Какое количество теплоты получает 4 моля одноатомного идеального газа в процессе, график которого изображён на рисунке? Ответ выразите в (кДж) и округлите до десятых.
Решение
Дано:
$υ=4$моль
$i=3$
$p_1=10^5$Па
$p_2=3·10^5$Па
$T_1=250K$
$T_2=750K$
$R=8.31{Дж}/{моль·К}$
$Q_{12}-?$
Решение:
Запишем I начало термодинамики: $Q_{12}=A_{12}+∆U_{12}$(1), где $A_{12}=p·∆V$, т.к. $V=const$ (процесс изохорный, то $∆V=0$ и работа газа $A_{12}=0$Дж).
$∆U_{12}={i}/{2}·υ·R∆T={i}/{2}υR(T_2-T_1)$(2) — изменение внутренней энергии газа, где $R$ — универсальная газовая постоянная.
Подставим (2) в (1) и найдем $Q_{12}: Q_{12}={i}/{2}υR(T_2-T_1)$(3)
Подставим числовые значения в (3): $Q_{12}={3}/{2}·4·8.31·(750-250)=24930Дж=24.9кДж$
Ответ: 24.9
Рекомендуемые курсы подготовки
10. Реальные газы. Тепловые явления
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Какое количество теплоты необходимо для нагревания (m=200) г свинца от (T_1=300) К до (T_2=340) К? Удельная теплоёмкость свинца 130 Дж/(кг(cdot)К). (Ответ дайте в джоулях.)
При нагреваниии: [Q=cmDelta T,] где (Delta T) — изменение температуры. [Q=0,2text{ кг}cdot130text{ Дж/(кг$cdot$К) }cdot(340text{ К} -300text{ К})=1040text{ Дж}]
Ответ: 1040
На рисунке показана зависимость температуры (T) от выделенной теплоты (Q) для 0,4 кг вещества, первоначально бывшего жидкостью. Найдите удельную теплоту плавления вещества. Ответ дайте в кДж/кг.
Во время плавления/кристализации температура вещества не изменяется. На графике такой участок один: от (Q_{1} = 5) кДж до (Q_{2} = 15) кДж. Следовательно, всего за процесс кристализации вещества выделилось количество теплоты: [Q = Q_{2} — Q_{1} = 15 text{ кДж} — 5 text{ кДж} = 10 text{ кДж}].
По формуле количества теплоты плавления (кристализации) вещества: [Q = lambda m] [lambda = dfrac{Q}{m} = dfrac{10 text{ кДж}}{0,4 text{ кг}} = 25 text{ кДж/кг}]
Ответ: 25
Через какое время после включения закипит вода в электрическом чайнике мощностью ( P =1200) Вт? Масса воды (m= 4) кг, ее начальная температура (t_0 = 20^{circ})C, КПД чайника (eta=50%). (Ответ дайте в секундах.)
КПД находится по формуле: [eta=frac{A_{text{пол}}}{A_{text{зат}}}]
Полезная работа (A_{text{пол}}) — работа на нагревание воды: [A_{text{пол}}=Q=cmDelta T,] где (c) — удельная теплоемкость воды.
Работа, затрачиваемая (A_{text{зат}}) — работа электрического тока: [A_{text{зат}}=Pt,] где (t) — время работы чайника. [eta=frac{cmDelta T}{Pt}] Выразим время работы чайника: [t=dfrac{cmDelta T}{eta P}] [t =dfrac{4200text{ Дж}/(text{кг}cdottext{К})cdot4text{ кг}cdot(100^circtext{С} -20^circtext{С})}{0,5cdot1200text{ Вт}}=2240 text{ с}]
Ответ: 2240
Какое количество теплоты необходимо сообщить свинцовому кубику объёмом (V=50) см(^3) для его нагревания от начальной температуры (T = 300) К до температуры плавления, равной 601 К? Плотность свинца — 11340 кг/м(^3), удельная теплоемкость — (c=127,5) Дж/(кг(cdot)К). (Ответ дайте в Дж и округлите до целого числа.)
Количество теплоты, необходимое для нагревания свинца: [Q=cmDelta T =crho V (T_2-T_1)] С учетом того, что (m=rho V): [Q =crho V (T_2 — T_1)] [Q =127,5text{ кг/м$^3$}cdot11340text{ кг/м$^3$}cdot5cdot10^{-5}text{ м$^3$} cdot(601text{ К}-300text{ К}) approx 21760 text{ Дж}]
Ответ: 21760
В печь поместили некоторое количество алюминия. Диаграмма изменения температуры алюминия с течением времени показана на рисунке. Печь при постоянном нагреве передает алюминию количество теплоты, равное 1 кДж в минуту. Какое количество теплоты потребуется для плавления алюминия, уже нагретого до температуры его плавления? Ответ выразите в кДж.
Алюминий плавится в течении 15 минут (температура постоянна). Количество теплоты найдем по формуле: [Q=Pcdot t=1000text{ КДж/мин} cdot 15text{ мин}=15000text{ Дж}=15 text{ кДж}]
Ответ: 15
В резервуар налили 100 кг воды при температуре (12^{circ}C). Сколько воды (в кг) при температуре (98^{circ}C) нужно долить в резервуар, чтобы температура смеси была равна (20^{circ}C)? Теплоемкостью резервуара пренебречь. Ответ округлите до сотых.
Пусть (Q_{1}) — количество теплоты, полученное водой массой (m_{1})=100кг, а (Q_{2}) — количество теплоты, отданное водой искомой массы. Составим уравнение теплового баланса:
[Q_{1}= Q_{2}]
[cm_{1}Delta T_{1}=cm_{2}Delta T_{2}]
Пусть температура смеси равна (T_{0}). Тогда:
[m_{1}(T_{1}-T_{0})=m_{2}(T_{0}-T_{2})] [m_{2}=dfrac{m_{1}(T_{0}-T_{1})}{(T_{2}-T_{0})}=dfrac{100text{ кг}cdot (20^{circ}C-12^{circ}C)}{(98^{circ}C-20^{circ}C)}approx 10,26text{ кг}]
Ответ: 10,26
В калориметре смешали 10 кг воды при температуре (54^{circ}C) и 7 кг воды при температуре (17^{circ}C). Найдите температуру смеси (в (^{circ}C)). Теплоемкостью калориметра пренебречь. Ответ округлите до десятых.
Пусть (Q_{1}) — количество теплоты, отданное водой массой (m_{1})=10кг, а (Q_{2}) — количество теплоты, полученное водой массой (m_{2})=7 кг. Составим уравнение теплового баланса:
[Q_{1}= Q_{2}]
[cm_{1}Delta T_{1}=cm_{2}Delta T_{2}]
Пусть температура смеси равна (T_{0}). Тогда:
[m_{1}(T_{1}-T_{0})=m_{2}(T_{0}-T_{2})] [m_{1}T_{1}-m_{1}T_{0}=m_{2}T_{0}-m_{2}T_{2}] [T_{0}=dfrac{m_{1}T_{1}+m_{2}T_{2}}{m_{2}+m_{1}}=dfrac{10text{ кг} cdot 54^{circ}C + 7text{ кг} cdot 17^{circ}C }{10text{ кг} + 7text{ кг}}approx 38,8^{circ}C]
Ответ: 38,8

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Количество теплоты .
Количество теплоты измеряется в Джоулях [Дж]
Количество теплоты обозначается буквой (Q )
(Q=cm(t_2-t_1) )
(c) это удельная теплоемкость вещества.
Удельная теплоемкость это физическая величина численно равная количеству теплоты которое необходимо для изменения температуры тела массой 1 килограмм на 1 градус
Удельная теплоемкость это табличная величина
((t_2-t_1) = Δt )
(Δt) это изменение температуры
( Q=cmΔt )
Репетитор по физике
8 916 478 10 32
1. Найти количество теплоты (Q), необходимое для нагрева воды массой (m=2кг) с температуры (t_1= 15: ^0C) до температуры (t_2= 45: ^0C)
Удельная теплоемкость воды (c=4200frac{Дж}{кгcdot ^0C})
Показать ответ
Показать решение
Видеорешение
2. Какое количество теплоты (Q), потребуется для нагрева воды, массой (m=0,2 кг) от температуры (t_1=0 : ^0C) до температуры кипения (t_2=100 : ^0C) ?
Удельная теплоемкость воды (c=4200frac{Дж}{кгcdot ^0C})
Показать ответ
Показать решение
Видеорешение
3. Найти количество теплоты (Q), необходимое для нагрева стальной детали массой (m = 0,5 кг), от температуры (t_1=100 : ^0C) до температуры (t_2=150 : ^0C) . Удельная теплоемкость стали (c=500frac{Дж}{кгcdot ^0C}) .
Показать ответ
Показать решение
Видеорешение
4. Какое количество теплоты (Q), потребуется для того, чтобы вскипятить ((t_2=100 : ^0C)) воду , взятую при температуре (t_1=10 : ^0C) и массой (m = 50 г)
Удельная теплоемкость воды (c=4200frac{Дж}{кгcdot ^0C})
Показать ответ
Показать решение
Видеорешение
5. Какое количество теплоты (Q), потребуется для того, чтобы вскипятить воду массой (m = 300 г) , взятую при температуре (t_1=5 : ^0C)
Удельная теплоемкость воды (c=4200frac{Дж}{кгcdot ^0C})
Ответ дать в килоджоулях
Показать ответ
Показать решение
Видеорешение
6. Какое количество теплоты (Q), потребуется для того, чтобы вскипятить воду массой (m_в = 300 г) , взятую при температуре (t_1=5 : ^0C) и находящуюся в алюминиевой кастрюле массой (m_к=400г) ?
Удельная теплоемкость воды (c_в=4200frac{Дж}{кгcdot ^0C}), удельная теплоемкость алюминия (c_а=920frac{Дж}{кгcdot ^0C}). Ответ дать в килоджоулях.
Показать ответ
Показать решение
Видеорешение
7. Какое количество теплоты (Q), потребуется для того, чтобы вскипятить воду массой (m_в = 30 г) , взятую при температуре (t_1=0 : ^0C) и находящуюся в стальном чайнике массой (m_ч=200г) ?
Удельная теплоемкость воды (c_в=4200frac{Дж}{кгcdot ^0C}), удельная теплоемкость стали (c_с=500frac{Дж}{кгcdot ^0C})
Ответ дать в килоджоулях.
Показать ответ
Показать решение
Видеорешение
8. Кипяток массой (m=300 г) остыл до температуры 20 градусов. Какое количество теплоты выделилось при этом в окружающую среду ?
Удельная теплоемкость воды (c_в=4200frac{Дж}{кгcdot ^0C})
Ответ дать в килоджоулях
Показать ответ
Показать решение
Видеорешение
9. Кипяток массой (m_в=300 г), находившийся в алюминиевом чайнике массой (m_ч=400 г) остыл до температуры 20 градусов. Какое количество теплоты выделилось при этом в окружающую среду ?
Удельная теплоемкость воды (c_в=4200frac{Дж}{кгcdot ^0C}), Удельная теплоемкость алюминия (c_а=920frac{Дж}{кгcdot ^0C})
Показать ответ
Показать решение
Видеорешение
10. Какое количество теплоты (Q) потребуется для нагревания воды, массой (m_в=50 г) на (20: ^0C) ?
Удельная теплоемкость воды (c_в=4200frac{Дж}{кгcdot ^0C})
Показать ответ
Показать решение
Видеорешение
11. Какое количество теплоты (Q) потребуется для нагревания медной детали, массой (m_д=1300 г) на (200: ^0C)
Удельная теплоемкость меди (c_м=400frac{Дж}{кгcdot ^0C})
Ответ дать в килоджоулях
Показать ответ
Показать решение
Видеорешение
12. Вычислить количество теплоты, необходимое для того, чтобы повысить температуру стального бруса массой 7 тонн на 140 (^0C) .
Удельная теплоемкость стали (c=500frac{Дж}{кгcdot ^0C})
Ответ дать в мегаджоулях.
Показать ответ
Показать решение
Видеорешение
13. Жидкости, массой (m=2кг) , передали количество теплоты (Q=252 кДж) и ее температура повысилась с (t_1= 15: ^0C) до температуры (t_2= 45: ^0C). Найти удельную теплоемкость этой жидкости.
Показать ответ
Показать решение
Видеорешение
14. Вода получила от нагревателя количество теплоты (Q=84 кДж), ее температура возрасла от (t_1=0 : ^0C) до температуры кипения (t_2=100 : ^0C) . Найти массу этой воды.
Удельная теплоемкость воды (c=4200dfrac{Дж}{кгcdot ^0C})
Показать ответ
Показать решение
Видеорешение
15. Воде массой (m=2кг) , передали количество теплоты (Q=252 кДж). На сколько градусов возросла температура воды? Удельная теплоемкость воды (c=4200frac{Дж}{кгcdot ^0C})
Показать ответ
Показать решение
Видеорешение
16. До какой температуры нагреется вода, массой (m = 300 г) , взятая при температуре (t_1=2 : ^0C), если ей сообщить количество теплоты (Q=119,7 кДж),
Удельная теплоемкость воды (c=4200frac{Дж}{кгcdot ^0C})
Показать ответ
Показать решение
Видеорешение
17. Найти удельную теплоемкость меди, если для нагревания медной детали массой (m_д=650 г) на (400: ^0C) потребовалось количество теплоты (Q=104 кДж)
Показать ответ
Показать решение
Видеорешение
22. Каким должен быть минимальный объем надувной лодки массой 50 кг, чтобы взять на борт груз массой 500 кг?
Плотность воды (rho_в=1000frac{кг}{м^3}). Удастся ли птичке поплавать на нем?
Показать ответ
Показать решение
Видеорешение