Задачи на комбинаторику с решением 11 класс егэ

Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий

Без метода (8 шт.)

Категория:
Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Элементы
комбинаторики

Комбинаторика – это
раздел элементарной математики, связанный с изучением количества комбинаций,
подчинённых тем или иным условиям, которые можно составить из заданного
конечного множества элементов (безразлично, какой природы; это могут быть
буквы, цифры, какие-либо предметы и т.п.).

1. Непосредственные подсчеты

Для решения комбинаторных задач существуют различные
способы грамотного подсчета, исключающие возможность потери какой-либо
комбинации элементов.

Логический перебор: При
логическом переборе выписывают все комбинации элементов, придерживаясь
некоторого правила.

Пример 1. В случайном
эксперименте симметричную монету бросают: а) дважды; б) трижды. Определите все
возможные комбинации выпадения орла и решки.

Решение. Выпадение
орла обозначим буквой О, решки – буквой Р.

а)
Записываем на первом месте букву О: ОО, ОР. Теперь на первом месте записываем
букву Р: РО, РР. В итоге получаем 4 комбинации  выпадения орла и решки: ОО, ОР,
РО, РР.

б)
В каждой комбинации, полученной в предыдущей задаче, добавляем слева букву О: ООО,
ООР, ОРО, ОРР. Аналогично слева приписываем букву Р: РОО, РОР, РРО, РРР.
В итоге получаем 8 комбинаций.

Ответ:
8.

Пример 2. Сколько четных
двузначных чисел можно составить из цифр 0, 1, 2, 5, 8, 9?

Решение. Составим
таблицу: слева от первого столбца таблицы поместим цифры десятков двузначных
чисел, выше первой строки – цифры единиц.

	0	2	8
2	20	22	28
5	50	52	58
8	80	82	88
9	90	92	98

Искомых чисел будет столько же, сколько клеток в таблице,
то есть 5·3=15.

Ответ:15.

Иногда подсчет вариантов облегчают графы. Так
называют геометрические фигуры, состоящие из точек (их называют вершинами)
и соединяющих их отрезков (называемых ребрами графа). Для удобства
иллюстрации условия задачи с помощью графа его вершины-точки могут быть
заменены кругами или прямоугольниками, а ребра-отрезки – любыми линиями.

Полный граф: При
решении задач с помощью полного графа проводят все возможные ребра.

Пример 3. Андрей, Борис,
Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько
партий было сыграно?

Решение.
Рассмотрим полный граф с четырьмя вершинами, обозначенными по первым буквам
имен каждого из 4 мальчиков. Отрезки-ребра обозначают шахматные партии,
сыгранные каждой парой мальчиков. Из рисунка видно, что граф имеет 6 ребер,
следовательно, и партий было сыграно 6.

Ответ:
6.

Граф-дерево

При
решении некоторых задач удобно использовать граф, называемый деревом (за внешнее
сходство с деревом).

Пример 4. Антон, Борис и Василий
купили 3 билета на футбольный матч на 1, 2 и 3-е места первого ряда. Сколькими способами
они могут занять имеющиеся три места?

Решение. Изобразим
перебор способов с помощью графа-дерева, помещая в вершины графа первые буквы
имен друзей А, Б и В.

В
итоге получаем 6 способов.

Ответ: 6.

2. Правило умножения

Перебрать и подсчитать всевозможные комбинации из
данных элементов, используя наглядные средства, несложно, когда их количество
невелико. Однако при большом количестве элементов этот перебор затруднителен, и
тогда используют правила комбинаторики. Правило умножения (правило «и») — одно
из основных правил комбинаторики.

Согласно
ему, если элемент множества А может быть выбран m способами,
а элемент множества B — n способами,
то упорядоченная пара (A, B) может
быть составлена m•n способами. Правило
обобщается на произвольную длину последовательности.

Пример 5. Сколько
трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если:

а)
числа не повторяются;

б)
числа могут повторяться.

Решение.

а)
Первую цифру выбираем 5 способами, вторую цифру – 4 способами, третью – 3
способами. Всего 5•4•3 =60 трехзначных
чисел.

б)
Всего 5•5•5 =125
трехзначных чисел.

Ответ: а) 60;
б) 125.

3. Правило сложения

Правило
сложения (правило «или») – одно из основных правил комбинаторики, утверждающее,
что, если элемент множества A можно выбрать m способами,
элемент множества B можно выбрать n способами,
и множества A
и
B
не
имеют общих элементов, то выбор одного из элементов множеств A или B осуществляется
m+n способами.

Пример 6. На блюдце лежит 8
яблок и 6 груш. Сколькими способами можно

взять
плод с блюдца?

Решение. Всего
способов 6 +8 =14 .

Ответ: 14.

4. Перестановки

Перестановками называют
комбинации, состоящие из одних и тех же n различных
элементов
и отличающиеся только порядком их расположения. Число всех возможных
перестановок из n различных элементов P_n= n!, где n!=1•2 •3•…• (n —1) • n ; 1!11; 0!=0.

Например,
из трех элементов a, b и c можно
образовать 3!=1•2•3 = 6
перестановок: abc, acb, bac, bca, cab, cba.

Пример 7. Сколькими
способами можно обозначить вершины куба буквами A, B, C, D, E, F, G, K?

Решение. Число
способов обозначить восемь вершин куба данными различными буквами (которых
также восемь) равно P₈ = 8!= 40320

Ответ:
40320.

5. Размещения

Размещениями называют
комбинации, составленные из n различных элементов по
m
элементов,
которые отличаются либо составом элементов, либо их порядком. Число всех
возможных размещений

В
частности, при m = n получаем = n!=P_n .

Например,
из четырех элементов a, b, c и d можно образовать

размещений по два элемента: ab, ba,
ac, ca, ad, da, bc, cb, bd, db,
cd, dc.

Пример 8. Сколько можно
составить сигналов из 6 флажков различного цвета,

взятых
по 2?

Решение.

Ответ:
30.

1.6. Сочетания

Сочетаниями называют
комбинации, составленные из n различных элементов по
m
элементов,
которые отличаются только составом элементов. Число всех возможных сочетаний

Например,
из пяти элементов a, b, c, d и e можно
образовать

сочетаний
по три элемента: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

Числа
размещений, перестановок и сочетаний связаны равенством

Пример 9. Сколькими способами
читатель может выбрать две книжки из пяти

имеющихся?

Решение.

Ответ:
10.

5 ноября 2020

В закладки

Обсудить

Жалоба

Задачи по комбинаторике

Подборка задач по комбинаторике с краткими пояснениями и ответами.

Комбинаторика — это наука, с который каждый встречается в повседневной жизни: сколько способов выбрать трёх дежурных для уборки класса или сколько способов составить слово из данных букв. В целом, комбинаторика позволяет вычислить, сколько различных комбинаций, согласно некоторым условиям, можно составить из заданных объектов (одинаковых или разных).

В ЕГЭ по математике базового уровня — задача №10.

komb.docx
komb.pdf

Задача 1: Сколькими способами можно составить список из 5 учеников?

Задача 2: В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?

Задача 3: Расписание на день содержит 5 уроков. Определить количество возможных расписаний при выборе из 14 предметов, при условии, что ни один предмет не стоит дважды.

Задача 4: Сколько различных трехцветных флагов можно сделать, комбинируя синий, красный и белый цвета?

Задача 5: В классе 24 ученика. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

Задача 6: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Задача 7: Сколькими различными способами можно избрать из 15 человек делегацию в составе 3 человек?

Задача 8: В магазине продаются блокноты 7 разных видов и ручки 4 разных видов. Сколькими способами можно выбрать покупку из двух разных блокнотов и одной ручки?

Задача 9: Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Задача 10: Сколькими способами можно разместить 6 пассажиров в четырехместной каюте?

Задача 11: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

Задача 12: Бригадир должен отправить на работу бригаду из 4 человек. Сколько бригад по 4 человека в каждой можно составить из 13 человек?

Задача 13: При встрече 16 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Задача 14: Группа учащихся в 30 человек пожелала обменяться своими фотокарточками. Сколько всего фотокарточек потребовалось для этого?

Задача 15: Сколько различных плоскостей можно провести через 10 точек, если никакие три из них не лежат на одной прямой и никакие четыре точки не лежат в одной плоскости?

Задача 16: Сколько существует различных семизначных телефонных номеров?

Задача 17: Сколько существует различных семизначных телефонных номеров, если в каждом номере нет повторяющихся цифр?

Задача 18: Сколько существует таких перестановок 7 учеников, при которых 3 определенных ученика находятся рядом друг с другом?

Задача 19: На книжной полке стоит собрание сочинений в 30 томах. Сколькими различными способами их можно переставить, чтобы: а) тома 1 и 2 стояли рядом; б) тома 3 и 4 рядом не стояли?

Задача 20: Сколько существует трёхзначных чисел, все цифры которых нечётные и различные?

Задача 21: У одного мальчика имеется 10 марок для обмена, а у другого – 8. Сколькими способами они могут обменять 2 марки одного на 2 марки другого?

Решение заданий ЕГЭ
Элементы комбинаторики,
статистики и теории
вероятностей

Айшаев Мухадин Муратович

Айшаев Мухадин Муратович
учитель математики
МКОУ «Средняя общеобразовательная школа с.п.Кара-Суу» и преподаватель «Лицея для одаренных детей» г.Нальчик Айшаев Кязим Мухадинович
«Решение заданий ЕГЭ по теме «Элементы комбинаторики,
статистики и теории
вероятностей»

Введение

• Задания открытого банка заданий ЕГЭ. В презентацию включен необходимый теоретический материал и образцы решений заданий (практика), а также задачи для самостоятельного решения (домашнее задание) и ответы к ним. Может быть полезна учащимся для самостоятельной подготовки к ЕГЭ.

Для успешного решения задач этого типа необходимо:

• Уметь строить и исследовать простейшие математические модели
• Моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры
• Моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин
• Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения

Повторить материал по темам:

• Элементы комбинаторики
• Поочередный и одновременный выбор
• Формулы числа сочетаний и перестановок. Бином Ньютона
• Элементы статистики
• Табличное и графическое представление данных
• Числовые характеристики рядов данных
• Элементы теории вероятностей
• Вероятности событий
• Примеры использования вероятностей и статистики при решении прикладных задач

Классическое определение вероятности

• Вероятностью Р наступления случайного события А называется отношение m к n, где n – это число всех возможных исходов эксперимента, а m – это число всех благоприятных исходов.

• Формула представляет собой так называемое классическое определение вероятности по Лапласу, пришедшее из области азартных игр, где теория вероятностей применялась для определения перспективы выигрыша.

Формула классической теории вероятностей

Число благоприятных исходов

Число всех равновозможных исходов

Вероятность события =

Вероятность события — это десятичная дробь, а не целое число!

Перестановки

• Перестановкой множества из n  элементов называется расположение элементов в определенном порядке.

Число перестановок можно вычислить по формуле Pn=n!

Размещения

• Размещениями множества из n различных элементов по m (m≤n) элементов называются комбинации, которые составлены из данных n элементов по m элементов и отличаются либо самими элементами, либо порядком элементов.

Сочетания

• Сочетаниями из n различных элементов по k элементов называются комбинации, которые составлены из данных n элементов по k элементов и отличаются хотя бы одним элементом (иначе говоря, k -элементные подмножества данного множества из n элементов).

Задача 1:В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

• Решение: Всего возможных комбинаций при вбрасывании двух кубиков: 6 * 6 = 36.
  Из них благоприятные исходы можно перечислить: 2+6;6+2; 3+5;5+3; 4+4.
• Таким образом, всего благоприятных исходов 5. Вероятность найдем, как отношение числа 5 благоприятных исходов к числу всех возможных комбинаций 36.
  = 0,13888… Округлим до сотых. Ответ: 0, 14.

•  

Задача 2: В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.

• Задача 2: В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
• Решение: Условие можно толковать так: какова вероятность, что все 4 раза выпадет решка. Вероятность того, что решка выпадет
• 1 раз равна ,
• 2 раза равна =(Теорема об умножении вероятностей),
• 3 раза равна =,
• а 4 раза равна ()4==0,0625.
• Ответ: 0,0625

•  

Задача 3: Игральный кубик подбрасывают дважды. Определите вероятность того, что при двух бросках выпадет разное количество очков. Результат округлите до сотых.

• Решение: Всего возможных комбинаций: 6 * 6 = 36.
  Из них благоприятные исходы можно перечислить:
  1-й кубик 2-й кубик
  1 очко 2, 3, 4, 5 или 6 очков. Благоприятных исходов 5.
  2 очка 1, 3, 4, 5 или 6 очков. Благоприятных исходов 5.
  3 очка 1, 2, 4, 5 или 6 очков. Благоприятных исходов 5.
  4 очка 1, 2, 3, 5 или 6 очков. Благоприятных исходов 5.
  5 очков 1, 2, 3, 4 или 6 очков. Благоприятных исходов 5.
  6 очков 1, 2, 3, 4 или 5 очков. Благоприятных исходов 5.
  Хотя проще было бы посчитать число неблагоприятных для нас исходов. Когда выпадет одинаковое число очков 1 и 1, 2 и 2, 3 и 3, 4 и 4, 5 и 5, 6 и 6. Таких исходов 6. Всего исходов 36. Тогда благоприятных исходов 36 – 6 = 30. Итак, всего благоприятных исходов 30. Найдем отношение 30/36 = 0,83333…
• Ответ. 0,83

Для самостоятельного
решения

• В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.(ответ: 0,11)
• В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.(ответ: 0,14)
• В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.(ответ: 0,17)
• В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых. (ответ: 0,01)
• В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых. (ответ: 0,07)

Задача 4: Вова точно помнит, что в формуле азотной кислоты подряд идут буквы H, N, O и что есть один нижний индекс – то ли двойка, то ли тройка. Сколько имеется вариантов, в которых индекс стоит не на втором месте?

• Решение: По условию индекс может стоять либо на первом, либо на втором месте:
• H2NO HNO2
• H3NO HNO3
• 2 + 2 = 4
• Ответ: 4

Задача 5: Сколько разных типов гамет может дать гибрид, гетерозиготный по 3 независимым признакам?

• а, в, с – признаки
• 1 случай – гамета не обладает ни одним из этих признаков – только 1тип
• 2 случай – одним из этих признаков: а; в; с – 3 типа
• 3 случай — двумя из трех признаков: ав, ас, вс – 3 типа
• 4 случай – всеми тремя признаками: авс – 1 тип
• 1+3+3+1=8 типов гамет
• Ответ: 8

Задача 6: Перечислить все трехзначные числа, в записи которых встречаются только цифры 1 и 2.

• 111 сотни десятки единицы
• 112 а в с
• 121 1 1 1
• 122 8 2 2 2
• 211 222=8
• 212
• 221
• 222

•  

Задача 7:Три друга – Антон (А), Борис (Б) и Виктор (В) – приобрели два билета на футбольный матч. Сколько различных вариантов посещения футбольного матча для троих друзей?

• А Б В
• (АБ)
• (АВ) 3 варианта посещения
• (БВ)
• Сочетание из 3 по 2
• С3= =3
• Ответ: 3

•  

2

Задача 8: Из группы теннисистов, в которую входят четыре человека – Антонов (А), Григорьев (Г), Сергеев (С) и Федоров (Ф), тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?

• А Г С Ф – число сочетаний из 4 по 2
• АГ
• АС
• АФ С4==6
• ГС
• ГФ
• СФ
• Ответ: 6

•  

2

Задача 9: Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из 5 языков: русского, английского, французского, немецкого, итальянского, на любой другой из этих 5 языков?
Число размещений: А5= =20
Ответ: 20

•  

2

Задача 10: Три друга – Антон, Борис и Виктор – приобрели два билета на футбольный матч на 1-е и 2-е места первого ряда стадиона. Сколько у друзей есть вариантов занять эти два места на стадионе?

• А Б В
• Число сочетаний из 3 по 2: 3 способа
• Количество перестановок: Р2=2!=2
• СР=3
• или А-размещения
• А3==6

•  

2

Задача 11: Сколько двузначных чисел можно составить, используя цифры 1, 2, 3, при условии, что цифра в числе не может повторяться?

• 12 21 23 32 13 31
• А3=
• Ответ: 6

•  

2

Задача 12: В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.

• Задача 12: В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
• Решение: Всего участвует 20 спортсменок, из них из Китая 20-(8+7)=5 спортсменок.
• Вероятность того, что спортсменка, выступающая первой, окажется из Китая будет
• Р =
• Ответ: 0,25

•  

Задача 13: В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.

• n=25
• m=23 билета без вопроса о грибах
• P(A)===0,92
• Ответ: 0,92

•  

Для самостоятельного
решения
1. В соревнованиях по толканию ядра участвуют 9 спортсменов из Дании, 3 спортсмена из Швеции, 8 спортсменов из Норвегии и 5 — из Финляндии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Финляндии. (0,2)
2. В соревнованиях по толканию ядра участвуют 4 спортсмена из Македонии, 9 спортсменов из Сербии, 7 спортсменов из Хорватии и 5 — из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Македонии.(0,16)
3. В чемпионате по гимнастике участвуют 50 спортсменок: 22 из Великобритании, 19 из Франции, остальные — из Германии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Германии.(0,18)
4. В чемпионате по гимнастике участвуют 40 спортсменок: 12 из Аргентины, 9 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Парагвая.(0,475)
5. В чемпионате по гимнастике участвуют 64 спортсменки: 20 из Японии, 28 из Китая, остальные — из Кореи. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Кореи. (0,25).
Задача 14: В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

• Задача 14: В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
• А = {Насос не подтекает}
• n=1000
• m=1000-5=995насосов не подтекают
• P(A)===0,995
• Ответ: 0,995

•  

Задача 15: Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

• Задача 15: Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
• А={Сумка качественная}
• n=100
• m=100-8 без скрытых дефектов
• P(A)===0,92
• Ответ: 0,92

•  

Задача 16: В среднем из 50 аккумуляторов, поступивших в продажу 7 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.

• Решение: 50-7=43 – исправных аккумуляторов
• Вероятность – покупка исправного аккумулятора

43 — Число благоприятных исходов
50 — Число всех равновозможных исходов
Р =
Ответ: 0,86

•  

Для самостоятельного решения

• Фабрика выпускает сумки. В среднем на 180 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. (Ответ:0,96 )
• Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. (Ответ: 0,96)
• В среднем из 1400 садовых насосов, поступивших в продажу, 7 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. (0,995)
• В среднем из 500 садовых насосов, поступивших в продажу, 4 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.(0,992)
• Люба включает телевизор. Телевизор включается на случайном канале. В это время по шести каналам из сорока восьми показывают документальные фильмы. Найдите вероятность того, что Люба попадет на канал, где документальные фильмы не идут. (0,875)
• В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. (0,4)

Произведение вероятностей

• Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно.
• Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:

Сложение вероятностей

• Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
• Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

Список использованной литературы

• А.Л. Семенов, И.В. Ященко «Самое полное издание типовых вариантов заданий ЕГЭ 2015. Математика»;
• http://mathege.ru/ — открытый банк заданий по математике.

Подготовка к ЕГЭ по математике (В4) Решение комбинаторных задач

Зарьянцева В.П.

Комбинаторика

Правило

Формулы

суммы

произведения

Перестановки

Размещения

Сочетания

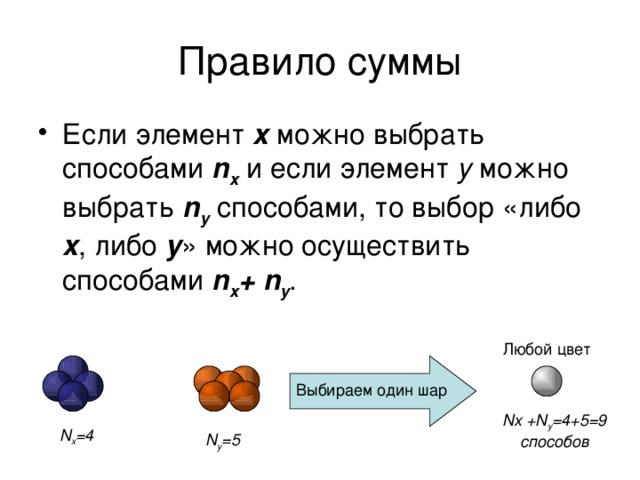
Правило суммы

• Если элемент x можно выбрать способами n x и если элемент y можно выбрать n y способами, то выбор «либо x , либо y » можно осуществить способами n x + n y .

Любой цвет

Выбираем один шар

Nx +N y =4+5=9 способов

N x =4

N y =5

Пример 1

• В коробке 10 тетрадей в клетку и 5 тетрадей в линию. Сколькими способами можно выбрать одну тетрадь?
• Решение: или – логическая сумма
• 10+5=15 (выбор неважен)

• Пример1. Сколько существует способов выбрать кратное двум или трем число из множества чисел : 2,3,4,15,16,20,21, 75,28 ?

• Решение:
• к1=5 –кратное 2 (2,4,16,20,28),

к2=4 – кратное 3 (3,15,21,75)

• к1+к2 = 5+4 = 9

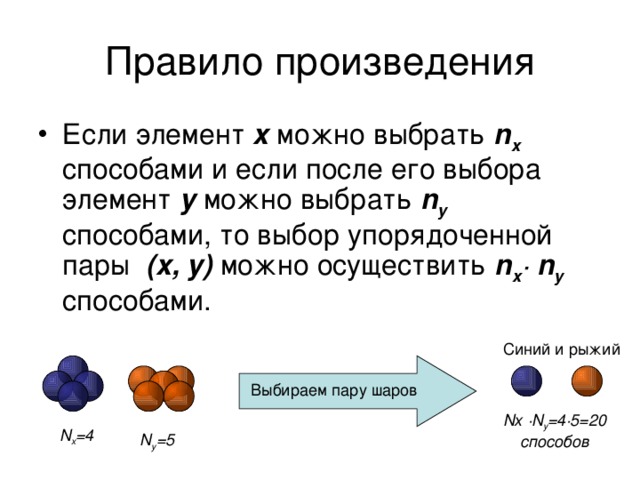
Правило произведения

• Если элемент x можно выбрать n x способами и если после его выбора элемент y можно выбрать n y способами, то выбор упорядоченной пары (x, y) можно осуществить n x ∙ n y способами.

Синий и рыжий

Выбираем пару шаров

Nx ∙N y =4∙5=20 способов

N x =4

N y =5

Пример 2

• В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?

• 5*3=15

Пример 2. а) Сколько различных двузначных чисел можно составить из цифр 1,3,5,7,9?

Решение: N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то выборка с повторениями)

б) Сколько среди них чисел, кратных 5?

Решение: Число кратно 5, если оканчивается цифрой 5 или 0. В нашем случае – 5.

На первой позиции фиксируем одну из пяти цифр, на второй – 5.

N= 5 х1 =5

• Пример5 . Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех горизонтальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг.

• а ) Сколько всего стран могут использовать такую символику?

• Решение : Цвет верхней полосы можно выбрать одним из 4 способов, второй полосы – одним из трех оставшихся, цвет 3 полосы – одним из 2 оставшихся, а 4 – одним способом. По правилу произведения N= 4х3х2х1=24

• б ) Сколько стран могут использовать такую символику с синей и красной полосами, расположенными рядом?

• Решение : Две полосы, всегда расположенные рядом, можно рассматривать как одну полосу, тогда полос останется 3, из них можно составить 3х2х1=6 разных флагов. Но две полосы (синюю и красную) можно «склеить» по-разному: синяя, а под ней красная, или красная, а под ней синяя. Поэтому общее количество вариантов по правилу суммы равно 6+6=12

• Пример7 . Сколькими способами можно посадить шестерых школьников на скамейку так, чтобы Коля и Оля оказались рядом?

• Решение : Будем считать, что на скамейке 6 пустых мест. Посадить Колю можно шестью способами, после чего Олю посадить рядом с ним одним или двумя способами. Это зависит от того, куда мы посадили Колю – на крайнее место или нет.

• Пусть Коля сидит на краю. Место на краю можно выбрать 2 способами, после чего Олю можно посадить одним способом, после чего оставшиеся 4 места можно занять 4х3х2х1 способами, значит, всего 2х1х4х3х2х2=48 способов

Коля сидит где-то в середине. Место для Коли можно выбрать 4 способами, Олю можно посадить 2 способами, значит, всего

4х2х4х3х2х1=192 способами.

• По правилу сложения 48+192= 240 способов

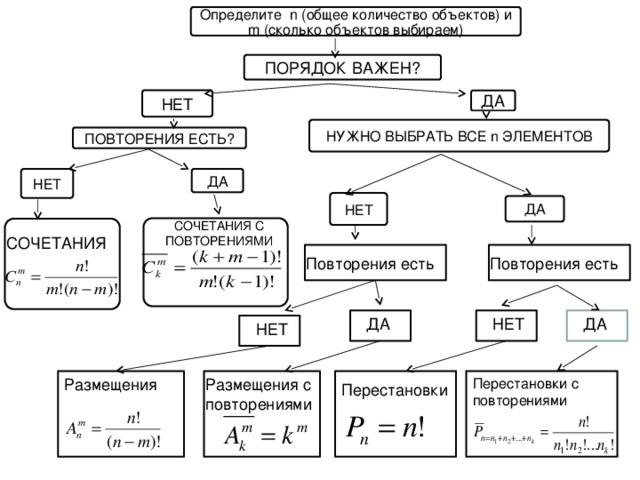
Определите n (общее количество объектов) и m (сколько объектов выбираем)

ПОРЯДОК ВАЖЕН?

НЕТ

ДА

НУЖНО ВЫБРАТЬ ВСЕ n ЭЛЕМЕНТОВ

ПОВТОРЕНИЯ ЕСТЬ?

НЕТ

ДА

НЕТ

ДА

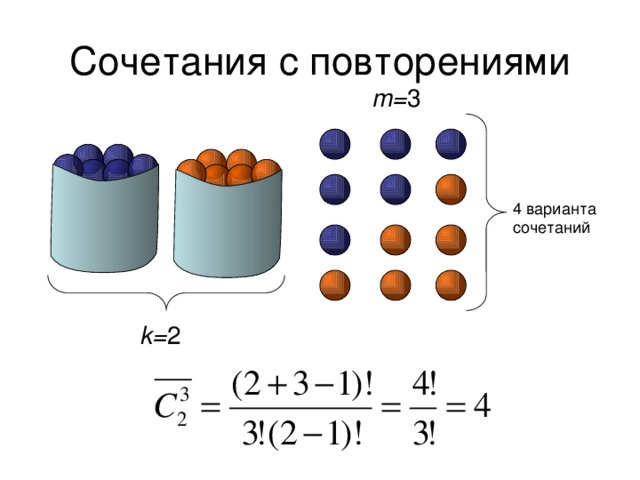
СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ

СОЧЕТАНИЯ

Повторения есть

Повторения есть

ДА

ДА

НЕТ

НЕТ

Перестановки с повторениями

Размещения с повторениями

Размещения

Перестановки

13

Перестановки

Перестановки без повторений

• Перестановками без повторений из n различных элементов называются все возможные последовательности этих n элементов. Число перестановок без повторений из n элементов равняется

по определению

Перестановки без повторений

6 различных перестановок

Сколькими способами 4 человека могут разместиться в четырехместном купе?

Задача 19 . Даны цифр: 1,2,3,4,5,6,7. Сколько различных чисел можно составить из этих цифр? Каждое число является перестановкой из 7 элементов.

Примеры: 1234567, 2354167, 7546321 .

Перестановка-упорядоченное множество.

Число перестановок из n элементов вычисляют по формуле P n =n! .

По условию n=7

Так из 7 цифр можно 7!=1*2*3*4*5*6*7=5040 различных чисел.

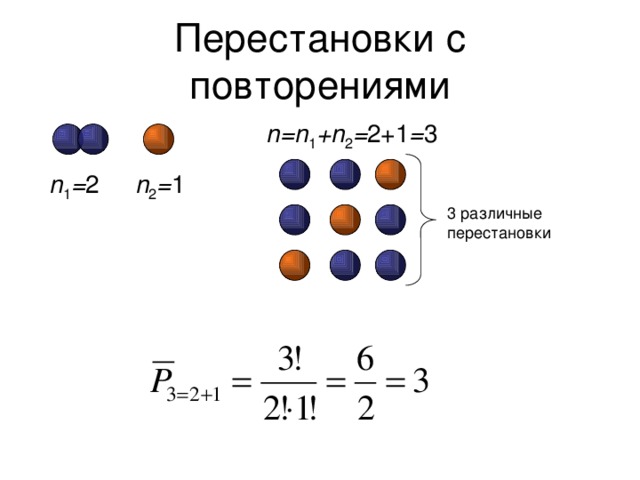
Перестановки с повторениями

• Перестановки с повторением из n элементов k типов
• число элементов 1-го типа n 1 ; число элементов 2-го типа n 2 ; …; число элементов k -го типа n k ,
• все возможные последовательности исходных n элементов. Число перестановок с повторениями обозначают
• подсчитывают так:

Перестановки с повторениями

n=n 1 +n 2 = 2+1 = 3

n 2 = 1

n 1 = 2

3 различные перестановки

Пример 4

• Дворовая футбольная команда выбирает капитана и его заместителя. Сколькими способами это можно сделать, если в команде 11 человек?

Пример 5

• Сколько различных гирлянд можно сделать, если у нас 5 красных, 7 синих и 4 желтых светодиода?

Пример Даны цифр: 1,2,2,3,3,3,4,. Сколько различных чисел можно составить из этих цифр? Каждое число является перестановкой из 7 элементов.

Примеры: 1223334, 4232331,2233314.

Некоторые числа при перестановке одинаковых цифр не меняются.

По условию n = 7, n1=2 , n2 =3

• Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?

• Сколько различных гирлянд получится, если замкнуть гирлянду из предыдущей задачи в кольцо?

Размещения

(выборки)

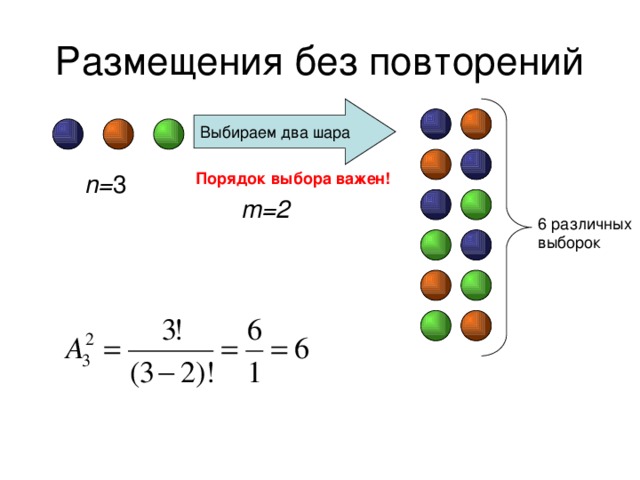
Размещения без повторений

• Размещениями без повторений из n различных элементов по m элементов называются все такие последовательности m различных элементов, выбранных из исходных n , которые отличаются друг от друга или порядком следования элементов, или составом элементов.
• Число размещений без повторений из n элементов по m обозначается символом

Размещения без повторений

Выбираем два шара

n= 3

Порядок выбора важен!

m=2

6 различных выборок

Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин .

Пример

• Из группы в 15 человек выбирается 4 участника эстафеты 800+400+200+100. Сколькими способами можно расставить спортсменов по этапам эстафеты?

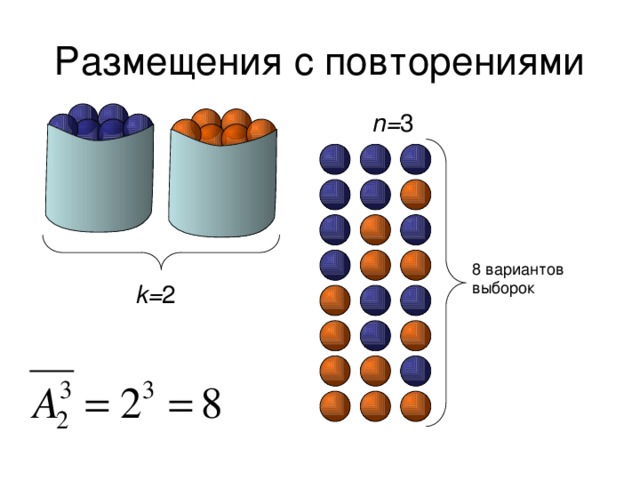
Размещения с повторениями

• Размещения с повторениями из элементов k типов по m элементов ( k и m могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличаются друг от друга или порядком следования элементов, или составом элементов.

Размещения с повторениями

n= 3

8 вариантов выборок

k= 2

Пример 8

• Назовем натуральное число «симпатичным», если в его записи встречаются только нечетные цифры. Сколько существует четырехзначных «симпатичных» чисел?
• k=5 порядок важен

Шифр сейфа состоит из 6 цифр, которые должны набираться последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра?

Сочетания

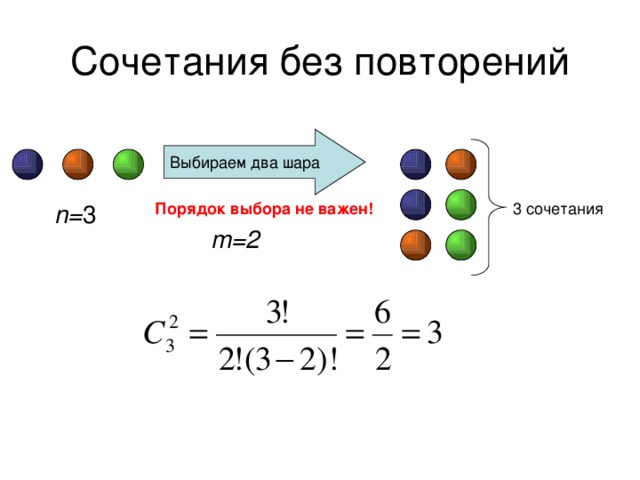
Сочетания без повторений

• Сочетаниями без повторений из n различных элементов по m элементов называются все такие последовательности m различных элементов, выбранных из исходных n , которые отличаются друг от друга составом элементов.

Сочетания без повторений

Выбираем два шара

Порядок выбора не важен!

n= 3

3 сочетания

m=2

Пример 9

• Сколькими способами можно выбрать трех дежурных из группы в 20 человек?

Сколькими способами можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков.

Сочетания с повторениями

• Сочетаниями с повторениями из элементов k типов по m элементов ( m и k могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличают друг от друга составом элементов.

Сочетания с повторениями

m= 3

4 варианта сочетаний

k= 2

Пример 10

В вазе стоят 10 красных и 4 розовых гвоздики. Все цветы на внешний вид одинаковы. Сколькими способами можно выбрать 3 цветка из вазы?

Решение Так как по условию задачи все цветы на внешний вид одинаковы, то мы получаем формулу без повторений. Вы выбираем цветы в букет, порядок выбора не важен, следовательно, мы получаем формулу сочетаний без повторений: два типа цветов, выбираем три цветка.

В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить 12 открыток для поздравлений?

• Один выбор (анализ) элементов или несколько? Если один, то см. п.3
• Каким союзом варианты выбора (анализа) соединяются? «И» – правило произведения, «или» – правило суммы.

Для каждого выбора задаются следующие вопросы:

• Все элементы используются? Если «да», то это перестановки. Переходим к п. 5.
• Порядок выбора элементов важен? Если «да», то это размещения, «нет» – сочетания.
• Есть ли одинаковые элементы? Если «да» – то формула с повторениями, «нет» – без повторений.

Сколько различных гирлянд можно сделать из 10 светодиодов разного цвета?

При замыкании линии в кольцо перестановки, являющиеся циклическими сдвигами относительно друг друга, становятся одинаковыми. Возьмем, например, следующую перестановку и посмотрим, сколько других перестановок явлюяются ее циклическим сдвигом: 1. ккккксссссссжжжж 2. кккксссссссжжжжк 3. ккксссссссжжжжкк … 15. жжккккксссссссжж 16. жккккксссссссжжж Следовательно, все перестановки разбиваются на группы по 16 цепочек в группе. Итак, число кольцевых гирлянд будет

13

Пример 11

• Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?

• У людоеда в подвале томятся 25 пленников.
• а) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин?
• б) А сколько есть способов выбрать троих, чтобы отпустить на свободу?

Решение 25*24*23 = 13800 способов. 

Заметим, что в предыдущем пункте каждую тройку пленников мы посчитали  3·2·1 = 6 раз. Поскольку теперь их порядок нам неважен, то ответом будет число  13800 : 6 = 2300.

Волонтеры разделились на две равные группы для розыска заблудившегося ребенка. Среди них только 4 знакомы с местностью. Каким числом способов они могут разделиться так, чтобы в каждую группу вошло 2 человека, знающих местность, если всего их 16 человек?

Решение Мы делим всех волонтеров на две равные группы, то есть выбираем участников первой группы, а все остальные переходят в другую группу. Один выбор. Теперь рассмотрим этот выбор первой группы. Выбор состоит из выбора волонтеров, знающих местность, и выбора волонтеров, незнающих местность. Следовательно, будем соединять эти два числа правилом произведения . Найдем число выборов волонтеров, знающих местность. Всего таких волонтеров 4 человека. Нам нужно 2. Порядок выбора не важен. Сочетания без повторений.

Найдем число выборов волонтеров, незнающих местность. Всего их 16-4=12 , выбираем шесть человек (ровно половину). Общее число выборов:

• Сколько существует натуральных чисел, меньших 256 10 , таких, что в записи каждого числа в двоичной системе счисления будет равное количество единиц и значащих нулей. В ответе укажите целое число.

Решение Переведем данное число из десятичной системы счисления в двоичную. 256 10 =100000000 2 Следовательно, числа меньше данного состоят из восьми, семи, шести, пяти, четырех, трех, двух и одного разряда.

1) Рассмотрим восьмиразрядные числа. 1ХХХХХХХ. Так как мы точно знаем сколько нулей и единиц, то мы используем формулу перестановки с повторениями.

2) Рассмотрим семиразрядные числа. Очевидно, что такие числа не удовлетворяют условию задачи, так как не могут состоять из одинакового числа единиц и нулей. Аналогичный вывод можно сделать о пятиразрядных, трехразрядных и одноразрядных числах.

3) Рассмотрим шестиразрядные числа. Рассуждая аналогично п.1 получаем:

4) Четырехразрядные числа.

5) Двухразрядное число только одно 10 2

Итак, у нас может быть или восьмиразрядное число, или шестиразрядное число, или четырехразрядное число, или двухразрядное число. Правило суммы.

Пример 15

• В коробке находятся 16 шариков – 4 красных, 4 синих и 8 черных. Из коробки наугад вынули два шарика. Какое из перечисленных сообщений несет в себе наибольший объем информации?
• Один из вынутых шариков – красного цвета, а другой – синего;
• Один из вынутых шариков – синего цвета, а другой – черного;
• Оба вынутых шарика красного цвета;
• Оба вынутых шарика черного цвета;
• Цвета вынутых шариков отличаются друг от друга;
• Вынуты шарики одного и того же цвета.

Сколькими способами можно расставить белые фигуры (короля, ферзя, 2 ладьи, 2 слонов и 2 коней) на первой линии шахматной доски?

Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа, не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно.

Решение

В этой задаче нам обязательно нужно использовать цифры 2, 4 и 5. Но они могут стоять на разных местах и в разном порядке. У нас три «важные» и две «неважные» цифры в числе — два типа цифр. Это перестановки с повторениями.

Теперь посчитаем сколько различных перестановок «важных» цифр между собой. Это перестановки без повторений

Итак у нас 60 различных перестановок. Теперь посчитаем, сколько различных «неважных» цифр может быть в каждой из этих перестановок. Мы выбираем две «неважные» цифры из шести. Порядок выбора важен . Это размещения без повторений .

В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?

• Решение:
• Каждая авиалиния соединяет два города. В качестве первого города можно взять любой из 20 городов (город А), а в качестве второго – любой из 19 оставшихся (город В). Перемножив эти числа, получаем 20 • 19 = 380.
• Однако при этом подсчете каждая авиалиния учтена дважды (первый раз, когда в качестве первого города был выбран город А, а второго – город В, а второй раз – наоборот). Таким образом, число авиалиний равно 380:2 = 190.

Сборник задач по теории вероятностей

(с решениями)

Разработка предназначена для   учащихся  9–11  классов для подготовки к ОГЭ и ЕГЭ по математике.

УМК любой

Цель: показать решение типовых задач по данной теме, закрепить умение учащихся решать данные задачи, подготовить учеников к сдаче ОГЭ и ЕГЭ

Методические рекомендации по использованию ресурса:                    Работу можно применить:

• при проведении урока по систематизации и закреплении знаний учащихся
• при проведении консультаций.

Источники информации:                                                       Открытый банк ЕГЭ ФИПИ  http://fipi.ru/                                                       

Теория вероятностей

Классическое определение вероятности
Вероятностью события A называется отношение числа благоприятных для A исходов к числу всех равновозможных исходов: Р (А) =  
где n — общее число равновозможных исходов, m — число исходов, благоприятствующих событию A.
Противоположные события
Событие, противоположное событию A, обозначают Ā. При проведении испытания всегда происходит ровно одно из двух противоположных событий и  
   Объединение несовместных событий
Два события A и B называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию A, так и событию B.
Если события A и B несовместны, то вероятность их объединения равна сумме вероятностей событий  A и B:               P(A U B) =P(A) + P(B)                          

Пересечение независимых событий
Два события A и B называют независимыми, если вероятность каждого из них не зависит от появления или непоявления другого события.
Событие C называют пересечением событий A и B                     (пишут C = A∩B), если событие C означает, что произошли оба события A и B.
Если события A и B независимы, то вероятность их пересечения равна произведению вероятностей  событий A и B:
 P(A∩B) = P(A) • P(B)

Формула сложения вероятностей совместных событий:

                           P(A U B) =P(A) + P(B)  – P(A∩B)

1. Из 1000 собранных на заводе телевизоров 5 штук бракованных. Эксперт проверяет один наугад выбранный телевизор из этой 1000. Найдите вероятность того, что проверяемый телевизор окажется бракованным.
 Решение.  При выборе телевизора наугад возможны 1000 исходов, событию A «выбранный телевизор — бракованный» благоприятны 5 исходов. По определению вероятности                       P(A) = 5÷1000 = 0,005. Ответ: 0,005.

2. В урне 9 красных, 6 жёлтых и 5 зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?                                                                       Решение. Общее число исходов равно числу шаров: 9 + 6 + 5 = 20. Число исходов, благоприятствующих данному событию, равно 6. Искомая вероятность равна 6÷20 = 0,3.  Ответ: 0,3.

 3. Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.

Решение. Вероятность события равна отношению количества благоприятных случаев к количеству всех случаев. Благоприятными случаями являются 3 случая, когда игру начинает Петя, Игорь или Антон, а количество всех случаев 6. Поэтому искомое отношение равно 3:6=0,5. Ответ: 0,5.

4. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

Решение: Обозначим через А событие «команда России во второй группе». Тогда количество благоприятных событий m  = 4 (четыре карточки с номером 2), а общее число равновозможных событий n = 16 (16 карточек) по определению вероятности         Р= 4: 16 = 0,25. Ответ:0,25

5.  В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.

Решение. Всего спортсменов 11 + 6 + 3 = 20 человек. Поэтому вероятность того, что первым будет стартовать спортсмен не из России равна 9:20 = 0,45. Ответ: 0,45.

 6. На каждые 1000 электрических лампочек приходится 5 бракованных. Какова вероятность купить исправную лампочку? 

Решение. На каждые 1000 лампочек приходится 5 бракованных, всего их 1005. Вероятность купить исправную лампочку будет равна доле исправных лампочек на каждые 1005 лампочек, то есть  1000:1005=0,995.Ответ: 0,995.

7. В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт  в магазин? 6 : 8=0,75.

8. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?

Решение. Каждая команда попадет в группу с вероятностью 0,25. Таким образом, вероятность того, что команда не   попадает в группу равна 1-0,25=0,75. Ответ:0,75

9. На турнир по шахматам прибыло 26 участников в том числе Коля и Толя. Для проведения жеребьевки первого тура участников случайным образом разбили на две группы по 13 человек. Найти вероятность того, что Коля и Толя попадут в разные группы.                                                                                               Решение. Всего 26 мест. Пусть Коля займет случайное место в любой группе. Останется 25 мест, из них в другой группе 13. Исходом считаем выбор места для Толи. Благоприятных исходов 13. Р=13/25 = 0,52. Ответ:0,52                                                                     

10. В классе 16 учащихся, среди них два друга —Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе.                                                                    Решение. Если Сергею первому досталось некоторое место, то Олегу остаётся 15 мест. Из них 3 — в той же группе, где Сергей. Искомая вероятность равна 3/15. Ответ:0,2                                                                                                     

11. В классе 21 учащийся, среди них два друга — Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.                                                                                                        Решение. Пусть один из друзей  находится в некоторой группе. Вместе с ним в группе окажутся 6 человек из 20 оставшихся учащихся. Вероятность того, что друг  окажется среди этих 6 человек, равна 6 : 20 = 0,3.          Ответ: 0,3

12. Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 спортсменов, среди которых 7 участников из России, в том числе Платон Карпов. Найдите вероятность того, что в первом туре Платон Карпов будет играть с каким-либо спортсменом из России? 6:15=0,4. Ответ:0,4.                                                                       

13. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 участника из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России?   2: 25=0,08. Ответ: 0,08.

14. В классе 26 учащихся, среди них два друга —   Сергей и Андрей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Сергей и Андрей окажутся в одной группе. Ответ  12 : 25 = 0,48.

15. В классе 21 ученик, среди них 2 друга – Тоша и Гоша. На уроке физкультуры класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Тоша и Гоша попали в одну группу. Ответ 6 : 20 = 0,3.

16. В классе 21 учащийся, среди них две подруги — Аня и Нина. Класс случайным образом делят на семь групп, по 3 человека в каждой. Найдите вероятность того, что Аня и Нина окажутся в одной группе.             Ответ: 2: 20 = 0,1.                                                     

17. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.                                                      Ответ. 6 : 12= 0,5 ( 6 делений между 12 и 7, всего 12 делений)

18. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 6, но не дойдя до отметки 9 часов. 3:12 = 0,25

 При решении задач с монетами число всех возможных исходов можно посчитать по формуле  п=2ª, где α –количество бросков

19.   В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орел выпадет ровно 1 раз.

Решение. Всего возможны четыре исхода: решка-решка, решка-орёл, орёл-решка, орёл-орёл. Орёл выпадает ровно один раз в двух случаях, поэтому вероятность того, что орёл выпадет ровно один раз равна  2:4=0,5.  Ответ: 0,5.

20. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу. Ответ: 1:4=0,25

21. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл не выпадет ни разу.  Решение. 1:8=0,125  Ответ. 0,125                                                                                    

22. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно 2 раза.                                                                           Решение. Составим список возможных вариантов. Бросают 2 раза может выпасть О — Орел, Р — Решка:
ОО, ОР, РО, РР. Всего 4 исхода из них только один случай удовлетворяет условию.   Вероятность (P) = 1 / 4 = 0.25.   Ответ: 0.25

23. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что решка не выпадет ни разу.                                                                            Решение. Всего исходов   = 16, благоприятных  1 ( ОООО).  1:16 = 0,0625. Ответ: 0,0625                                                                                     

При решении задач с кубиками число всех возможных исходов можно посчитать по формуле  п=6ª, где α –количество бросков 

24. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.                                                                                                          Решение. При бросании кубика равновозможных  шесть различных исходов. Событию «выпадет нечётное число очков» удовлетворяют три случая: когда на кубике выпадает 1, 3 или 5 очков. Поэтому вероятность того, что на кубике выпадет нечётное число очков равна 3:6=0,5. Ответ: 0,5.

25.  Определите вероятность того, что при бросании кубика выпало число очков, не большее 3.

Решение. При бросании кубика равновозможны шесть различных исходов. Событию «выпадет не больше трёх очков» удовлетворяют три случая: когда на кубике выпадает 1, 2, или 3 очка. Поэтому вероятность того, что на кубике выпадет не больше трёх очков равна  3:6=0,5 Ответ: 0,5.                                                                  

26. Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.

Решение. При бросании кубика 6²= 36 различных исходов. Событию «выпадет больше трёх очков» удовлетворяют три случая: когда на кубике выпадает 4, 5, или 6 очков , благоприятных исходов 9 (4,4; 4,5; 4,6; 5,4; 5,5; 5,6;  6,4; 6,5; 6,6.)                       Ответ: 9: 36 = 0,25.

27. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.                                      Решение. При бросании кубика 6³= 216  различных исходов, благоприятных  14.  14 : 216 = 0,07.  Ответ: 0,07.     

28.   Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.

Решение. Всего трехзначных чисел 900. На пять делится каждое пятое их них, то есть таких чисел 900:5=180. Вероятность того, что Коля выбрал трехзначное число, делящееся на 5, определяется отношением количества трехзначных чисел, делящихся на 5, ко всему количеству трехзначных чисел: 180:900=0,2.  Ответ: 0,2.

29.Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?

Решение. Всего было подготовлено 50 билетов. Среди них 9 были однозначными. Таким образом, вероятность того, что наугад взятый учеником билет имеет однозначный номер равна 9:50=0,18. Ответ: 0,18.

30. В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?

Решение. Всего в мешке жетонов — 50. Среди них 45 имеют двузначный номер. Таким образом, вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число равна  45 : 50 = 0,9.  Ответ: 0.9. 

31. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на 3?                                           3 : 10 = 0,3.  Ответ: 0,3.

Противоположные события.

32.  Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Решение. Вероятность того, что ручка пишет хорошо, равна 1 − 0,19 = 0,81.  Ответ: 0,81.

  33. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8°C     равна 0,87. Найдите вероятность того, что в случайный момент времени у здорового человека температура тела окажется 36,8°C или выше.  Ответ. 1-0,87=0,13                                    

34. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.

Решение. По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035. Ответ: 0,035.

Несовместные и независимые события.                                                 35. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.                                          Решение. Суммарная вероятность несовместных событий равна сумме вероятностей этих событий: P=0,6+ 0,1 = 0,7.  Ответ: 0,7.

36. Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.

Решение. Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:  P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07. Ответ: 0,07.

                                                                                                                       37. Вероятность того, что на тесте по химии учащийся П. верно решит больше 8 задач, равна 0,48. Вероятность того, что П. верно решит больше 7 задач, равна 0,54. Найдите вероятность того, что П. верно решит ровно 8 задач. Решение. Вероятность решить несколько задач складывается из суммы вероятностей решить каждую из этих задач. Больше 8:  решить 9-ю, 10-ю … Больше 7:  решить 8-ю, 9-ю, 10-ю …Вероятность решить 8-ю = 0,54-0,48=0,06.  Ответ:0.06

38. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет меньше 4?    Ответ: 4 : 10 = 0,4.

 39. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Решение. Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна 0,8•0,8•0,8•0,2•0,2=0,02048.  Ответ:0.02048.

40. Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение. Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09. Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91.   Ответ: 0,91.

41. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

Решение. Вероятность того, что батарейка исправна, равна 0,94. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,94·0,94 = 0,8836.   Ответ: 0,8836.

42.   Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Решение. Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156.   Ответ: 0,156.

43.   В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).

Решение. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что все три продавца заняты равна                       (0,3)³ = 0,027.    Ответ: 0,027.

   44. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.

Решение. Рассмотрим события A = «в автобусе меньше 15 пассажиров» и  В = «в автобусе от 15 до 19 пассажиров». Их сумма — событие A + B = «в автобусе меньше 20 пассажиров». События A и  В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B).

 Тогда, используя данные задачи, получаем: 0,94 = 0,56 + P(В), откуда P(В) = 0,94 − 0,56 = 0,38.Ответ: 0,38.

45. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.

Ответ: 0,35.

 46.Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение. Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года». События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:  P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B)

 откуда, используя данные из условия, получаем     0,97 = P(A) + 0,89.Тем самым, для искомой вероятности имеем: P(A) = 0,97 − 0,89 = 0,08.   Ответ: 0,08.

 

 47. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.

Решение. Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды: P(XXO) = 0,8·0,8·0,2 = 0,128; P(XOO) = 0,8·0,2·0,8 = 0,128; P(OXO) = 0,2·0,2·0,2 = 0,008;  P(OOO) = 0,2·0,8·0,8 = 0,128.Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:

 P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.   Ответ: 0,392.

48. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. 

Решение. Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025. Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975. Ответ: 0,9975.

 49. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение. Рассмотрим событиеА = кофе закончится в первом автомате, В = кофе закончится во втором автомате.

Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. Поскольку P(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятность х = 0,52. Ответ: 0,9975.

50. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение. Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135. Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055.  Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055 = 0,019.                       Ответ: 0,019.

51. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Решение. Джон попадает в муху, если схватит пристрелянный револьвер и попадет из него, или если схватит непристрелянный револьвер и попадает из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·0,9 = 0,36 и 0,6·0,2 = 0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,36 + 0,12 = 0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Его вероятность равна 1 − 0,48 = 0,52. Ответ. 0,52

 

 52. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.

Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.

Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Решение. В силу независимости событий, вероятность успешно сдать экзамены на лингвистику: 0,6·0,8·0,7 = 0,336, вероятность успешно сдать экзамены на коммерцию: 0,6·0,8·0,5 = 0,24, вероятность успешно сдать экзамены и на «Лингвистику», и на «Коммерцию»: 0,6·0,8·0,7·0,5 = 0,168. Успешная сдача экзаменов на «Лингвистику» и на «Коммерцию» — события совместные, поэтому вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Тем самым, поступить на одну из этих специальностей абитуриент может с вероятностью 0,336 + 0,24 − 0,168 = 0,408.  Ответ: 0,408.

53. По отзывам покупателей Иван Иванович оценил надёжность двух интернет- магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.                                                                                          Решение. Вероятность того, что первый магазин не доставит товар равна 1 − 0,9 = 0,1. Вероятность того, что второй магазин не доставит товар равна 1 − 0,8 = 0,2. Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар) равна произведению вероятностей этих событий: 0,1 · 0,2 = 0,02.  Ответ: 0,02.

54.Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры. Решение. Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5·0,5·0,5 = 0,125.   Ответ: 0,125.

  

55. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

Решение.  Анализ пациента может быть положительным по двум причинам: А) пациент болеет гепатитом, его анализ верен; B) пациент не болеет гепатитом, его анализ ложен. Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем: Р(А)=0,9•0.05=0,045;                                         Р(В)= 0,01•0,95=0,0095  ,Р(А+В)=Р(А)(В)=0,045+0,0095=0,0545.

 Ответ:0,0545.

  56. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.

Решение. Ситуация, при которой батарейка будет забракована, может сложиться в результате событий: A = батарейка действительно неисправна и забракована справедливо или В = батарейка исправна, но по ошибке забракована. Это несовместные события, вероятность их суммы равна сумме вероятностей эти событий. Имеем: Р(А+В)=Р(А)+Р(В)=0,02•0,99+0,98•0,01=0,0198+0,0098=0,0296 Ответ: 0,0296.

 57. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).

Решение. Пусть A — событие, состоящее в том, что мишень поражена стрелком с первого выстрела, B — событие, состоящее в том, что мишень поражена со второго выстрела. Вероятность события A равна P(A) = 0,7. Событие B наступает, если, стреляя первый раз, стрелок промахнулся, а, стреляя второй раз, попал. Это независимые события, их вероятность равна произведению вероятностей этих событий: P(B) = 0,3·0,7 = 0,21. События A и B несовместные, вероятность их суммы равна сумме вероятностей этих событий:  P (A + B) = P(A) + P(B) = 0,7 + 0,21 = 0,91.   Ответ: 0,91.

58.Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча — с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А.

Решение. Рассмотрим все возможные исходы жеребьёвки.

 · КомандаА в матче в обоих матчах первой владеет мячом.

 · КомандаА в матче в обоих матчах не владеет мячом первой.

 · КомандаА в матче с командой В владеет мячом первой, а в матче с командой С — второй.

 · КомандаА в матче с командой С владеет мячом первой, а в матче с командой В — второй.

Из четырех исходов один является благоприятным, вероятность его наступления равна 1:4=0,25. Ответ: 0,25.

59. Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.

Решение. Вероятность промаха равна 1 − 0,5 = 0,5. Вероятность того, что стрелок первые три раза попал в мишени равна 0,53 = 0,125. Откуда, вероятность события, при котором стрелок сначала три раза попадает в мишени, а четвёртый раз промахивается равна 0,125 · 0,5 = 0,0625.     Ответ: 0,0625.

60. Перед началом матча по футболу судья бросает монету, чтобы определить, какая из команд будет первой владеть мячом. Команда «Байкал» играет по очереди с командами

«Амур», «Енисей», «Иртыш». Найти вероятность того, что команда «Байкал» будет первой  владеть мячом только в игре с «Амуром».

Решение. Монету бросают 3 раза.

Для команды «Байкал» возможные исходы в трех бросках {О О О},{Р О О}, {О Р О}, {О О Р},                  {Р Р О},{Р О Р}, {О Р Р},{Р Р Р}. Всего исходов 8, благоприятныx1(выпадение орла в первой игре)  {О Р Р, 1:8=0,125.Ответ 0,125.

61.У Пети в кармане лежат  шесть монет: четыре монеты по рублю и две монеты по два рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность  того, что теперь две двухрублевые монеты лежат в одном кармане.

 Решение. Пронумеруем монеты: рублевые – 1, 2, 3, 4;  двухрублевые – 5, 6. {123} {124} {125} {126} {134} {135} {136} {145} {146} {156} {234} {235} {236} {245} {246} {256} {345} {346} {356} {456} 

 n = 20     – число всех исходов .Взять три монеты можно так: (числа в порядке возрастания,чтобы не пропустить комбинацию)  m = 8  – число благоприятных  исходов

(комбинации, в которых монеты 5 и 6 (двухрублевые) не взяты или взяты обе. 8:20=0,4